Abstract
Magnetic nanofibers belong to the geometries which are intensively investigated in simulations and experiments due to their unique magnetic properties, varying in their lengths, cross-sections, and bending radii. Besides basic research of different magnetization reversal processes and magnetization dynamics in bent nanofibers, these structures are of potential interest for data storage applications, data transport, or other tasks in spintronics devices. While previous simulations concentrated on the domain wall transport through coupled bent nanofibers, creating networks with many in- and outputs to establish nanofiber-based domain wall logics, here we show the influence of the constricted area, in which a rotating magnetic field is applied in the middle of bent or straight magnetic nanofibers, on the magnetization dynamics. Our micromagnetic simulations, performed by Magpar, reveal a strong impact not only of this area, but also of the curvature of the nanofiber as well as of an additional Dzyaloshinskii–Moriya interaction (DMI).
1. Introduction
Nanofibers with magnetic properties, due to their specific spatial symmetry, can be the source of exotic states of magnetization, states that do not exist in larger-scale magnetic objects [1,2,3]. These unusual effects are, on the one hand, due to the shape of the fiber itself, i.e., its geometry and curvature, but on the other hand, they may also have their origin in atomistic interactions [4,5].
Typical energies taken into account in simulations based on micromagnetic methods are the magnetocrystalline energy, the exchange energy, and the demagnetization field (“shape anisotropy”) as well as the magnetoelastic energy [6,7,8]. Several of these micromagnetic simulators have been developed during recent years and have been used to simulate magnetic nanofibers or nanowires, such as the object-oriented micromagnetic framework (OOMMF) [9], the LLG Micromagnetic Simulator [10], MicroMagus [11], or Mumax3 [12]. Such micromagnetic simulators usually average over atomic-based effects, while they are more related to fast prototyping and/or practical, technology-related tasks.
On the other hand, the Dzyaloshinskii–Moriya interaction (DMI), an antisymmetric exchange with atomic origin, is known to influence domain wall dynamics and to enable the formation of skyrmions [13,14,15]. In recent years, several research groups thus investigated the implementation of the DMI in micromagnetic simulation programs, such as OOMMF, MuMax3, Fidimag, or others [16,17,18].
Besides the special magnetic properties of magnetic nanofibers which resulted in large interest regarding basic research of these structures, the potential applications in spintronics are another reason to examine magnetic nanofibers. Here, the racetrack memory should especially be mentioned, being one potential form of future memory storage device [19,20,21]. Diverse other groups have suggested fiber-based solutions for data storage and transport and investigated the impact of fiber geometries, potential connections between multiple fibers, etc. [22,23,24].
In previous studies, we investigated single and coupled magnetic nanofibers bent in the form of a semi-circle, with one or more “input” positions in which a rotating magnetic field was applied, detecting domain wall motion along the “output” positions at the open ends of these semi-circles, to establish domain wall logics and show truth tables with different operators, depending on the rotational direction of the external magnetic fields [25,26,27]. Here, we concentrate on a single magnetic semi-circle, simulated with and without DMI, and vary the area of the applied external magnetic field to serve as a base for potential data storage and transport spintronics devices.
It should be mentioned that such dynamic simulations can not only be useful for the aforementioned spintronics applications, such as the racetrack memory, but also for neuro-inspired devices in the research area of neuromorphic computing [28,29,30]. In ferromagnetic wires, data in the form of domain walls can be inserted and propagate through magnetic wires. The magnetic properties given in this paper are graphically and numerically represented by magnetization vectors; the vectors change their orientation in time and space, representing transported data.
From the methodological point of view, the issue considered here is a classic example of the problem of information obtained in an experiment conducted on a different scale, while phenomena occurring at the quantum level are responsible for the obtained results. Quantum phenomena existing at an atomic scale are associated with the existence of electron spin and spin–orbit interaction, and manifest as the specific crystallographic symmetries, sensed at the nanoscale, thus one order of magnitude larger, covering a countable set of atoms. In turn, going even further, the microscopic approach used here is basically a classical one, described by deterministic equations of the space–time evolution of the magnetization vector. As we know, a classical physical measurement contains averaged information about a large number of phenomena taking place on the atomic scale. However, there is something additional in the current research with magnetic structures, namely, the effects observed with micromagnetic simulations can be actively modified by changing the shape (symmetry) of the tested sample. This is due to the existence of uncompensated demagnetization fields on the surface of the material. Therefore, a sample in the form of a straight fiber with a length of 1570 nm and a semi-circular sample of the same length were tested in this work.
Hence, at the very beginning, the question arises how the specific crystallographic symmetries and the related interaction discovered by Dzyaloshinskii (1957) and Moriya (1960) will translate into the results of micromagnetic simulations, treated as a testing tool on a classical scale. Historically, for the first time, the study of this interesting interaction involved a hematite (α-Fe2O3) crystal. This material exhibited ferromagnetism, resulting from the existence of four sublattices—each with its own arrangement of spins/magnetic moments—in which the spin moments were reoriented with respect to the rhombohedral direction [111]. Going beyond such a local view, the bulk phase of the α-Fe2O3 crystal, indispensable for the occurrence of the DMI, belongs to the trigonal system—the system separated from the hexagonal one—and possesses the R3c space group. This means that the essential feature of the trigonal system is that three of the four crystallographic axes of the system lie in one plane and have the same length. The fourth axis has a different unit length, is a threefold-symmetry axis, and, importantly, is oriented perpendicular to the plane.
For the vast majority of spintronic nanodevices, the magnetic structures are made in the form of very thin layers; they are flat structures. Therefore, the appearance of the DMI in a ferromagnetic material should significantly disturb the dynamics of a typical two-dimensional system, which results from the essence of the symmetry of the R3 c space group symmetry. In other words, it is possible to efficiently control the in-plane dynamics via the introduction of strong enough perpendicular effects.
2. Materials and Methods
The micromagnetic simulations reported in this paper were performed by the Parallel Finite Element Micromagnetics Package (Magpar), based on dynamic solution of the Landau–Lifshitz–Gilbert equation of motion [31]. The DMI plug-in, here taking into account a DMI constant of 6 × 10−3 J/m2, as well as the possibilities to apply external magnetic fields with freely definable time-dependence at defined positions and collect data from specific volumes were implemented in our previous studies [25,26,27].
The simulated geometries are depicted in Figure 1. The field rotates clockwise at a frequency of 0.5 GHz; the magnetic induction amplitude equals 1T, resulting in regularly changed magnetization orientation in the area P0 (red and blue) and thus in the nucleation of domain walls. The lengths of both wires are 1570 nm, their cross-section is 10 nm × 60 nm.
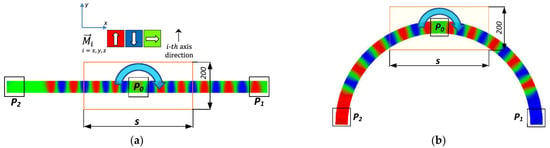
Figure 1.
The external rotating field was applied in rectangular regions of width 200 nm, height 10 nm, and adjustable lengths s of 1 nm, 5 nm, 10 nm, 20 nm, 30 nm, 40 nm, 50 nm, 60 nm, 100 nm, 200 nm, and 500 nm. At the square locations P0, P1, and P2 with lateral dimensions 60 nm × 60 nm, the magnetization was detected. P0 senses the external field directly. (a) Straight nanofiber; (b) bent nanofiber.
The simulation parameters were chosen as follows, in accordance with typical literature values and identical to our previous simulations [25,26,27]: saturation magnetization JS = 1.005 T, exchange constant A = 1.3·10−11 J/T, anisotropy constant zero as usual for permalloy (Py), and damping constant α = 0.02. The magnetoelastic anisotropy was neglected.
3. Results
The micromagnetic simulations, combined with the DMI, superpose energy at the mesoscopic level and its micromagnetic representation, i.e., the exchange energy between electrons’ magnetic moments as a result of spin–orbit coupling given by the Hamiltonian
with the exchange constant J and the magnetic moments pi and pj, and the Dzyaloshinskii–Moriya interaction energy as a result of broken inversion in crystallographic symmetry
with the DMI constant D, where
while senses the direction parallel to . However, due to
the term is related to a direction perpendicular to .
The results of these simulations are given below and in the Supplementary Materials for different lengths s of the applied magnetic field, depicting the magnetization dynamics during 40 ns after switching on the rotating magnetic field in the areas P0, P1, and P2, as defined in Figure 1. It should be mentioned that simulations of domain walls inserted in magnetic nanowires usually apply defined areas of specific shapes, typically much broader or thicker than the nanowire itself, to insert the domain walls [4,32,33,34]. Here, the nucleation of domain walls is oppositely performed directly inside the nanowire, which can be assumed to be less reliable than the aforementioned common method.
Firstly, Figure 2 shows that directly inside the input area, none of the signals is symmetric. This is based on the length of the detection area P0 of 80 nm, as opposed to the much shorter length of the input area of 1 nm. On the other hand, time-asymmetries are visible in the simulations taking into account the DMI as an antisymmetric exchange.
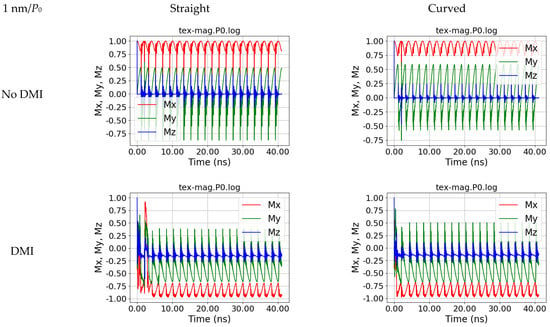
Figure 2.
Magnetization dynamics in position P0, i.e., at the position of the applied external magnetic field, for a straight and a curved nanofiber, simulated without and with DMI, for s = 1 nm.
Neither output P1 nor P2 shows significant oscillations due to the small input area of the applied rotating magnetic field, as depicted in Figure 3 and Figure 4.
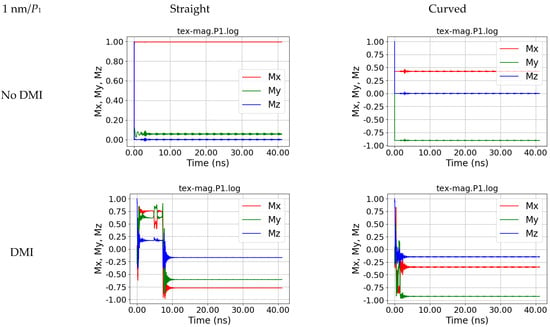
Figure 3.
Magnetization dynamics in position P1, i.e., at the right end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 1 nm.
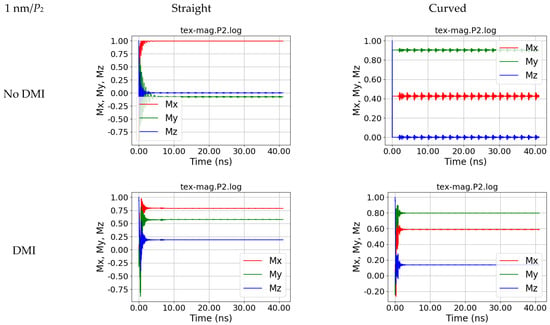
Figure 4.
Magnetization dynamics in position P2, i.e., at the left end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 1 nm.
This situation can be examined by investigating the spatially resolved magnetization components, as visible with time-resolution in the form of movies in the Supplementary Materials and as an exemplary image series of My in Figure 5. Here, it is visible that the rotating magnetic field with a length s = 1 nm can change the magnetization in the middle of the straight nanofiber, as visible by the large oscillations in Figure 2 (no DMI, straight fiber); however, the induced domains are not stable, but lose their magnetic orientation during propagation to the ends of the fiber. In this way, no stable domain walls are introduced into the system.
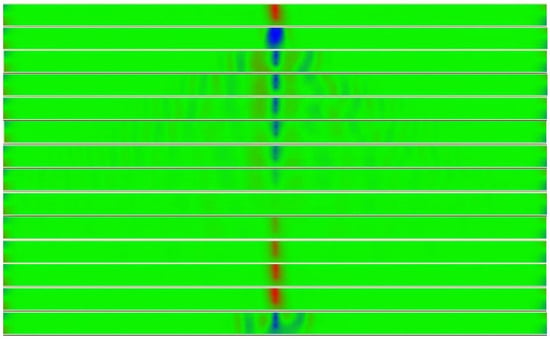
Figure 5.
Magnetization dynamics of a straight nanofiber, simulated without DMI, for s = 1 nm. The figure shows the evolution in time of the magnetization component My (from top to bottom).
Interestingly, a length of the input area of 5 nm, i.e., still much smaller than the detection area, is already sufficient to show nearly fully symmetrical oscillations in P0, as depicted in Figure 6. For the curved nanofiber, simulated without DMI, now oscillations become visible, starting around 17 ns after the introduction of the external magnetic field in P1 (Figure 7) and after around 11 ns in P2 (Figure 8).
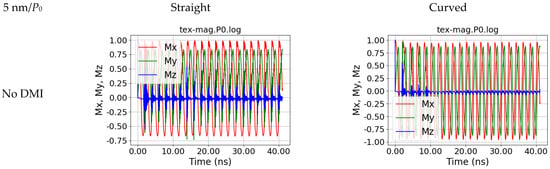
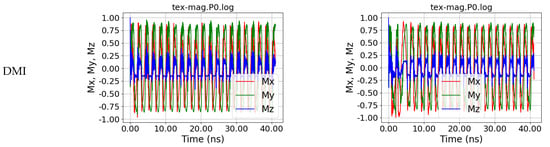
Figure 6.
Magnetization dynamics in position P0, i.e., at the position of the applied external magnetic field, for a straight and a curved nanofiber, simulated without and with DMI, for s = 5 nm.
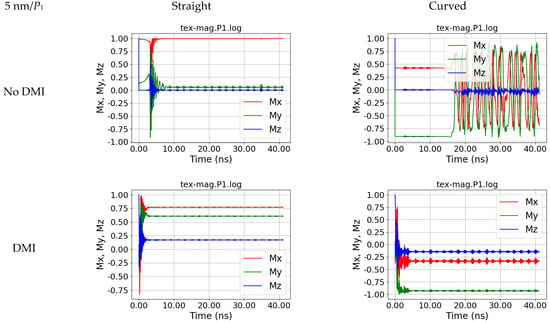
Figure 7.
Magnetization dynamics in position P1, i.e., at the right end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 5 nm.
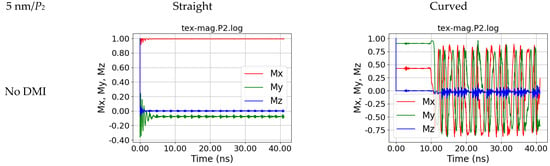
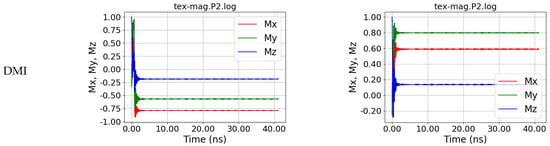
Figure 8.
Magnetization dynamics in position P2, i.e., at the left end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 5 nm.
As an example of such stable oscillations which reach at least one of the fiber ends, Figure 9 depicts snapshots of the magnetization dynamics of My in the curved sample without DMI for the case s = 5 nm. As visible here, domain walls propagate to both ends, P1 and P2, of the curved nanowire, while reaching the left end P2 earlier than the right end P1, as also visible in the comparison of Figure 7 and Figure 8.
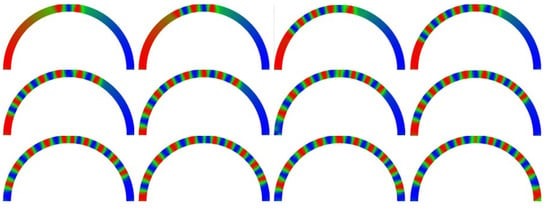
Figure 9.
Magnetization dynamics of a curved nanofiber, simulated without DMI, for s = 5 nm. The figure shows the evolution in time of the magnetization component My (from left to right and top to bottom).
Increasing the length of the input area to 20 nm leads to oscillations also being visible in the straight fiber, simulated without DMI (Figure 10). Neither here nor for input area lengths up to 200 nm are oscillations visible in the nanofibers simulated including DMI (Supplementary Materials, Figures S5–S23).
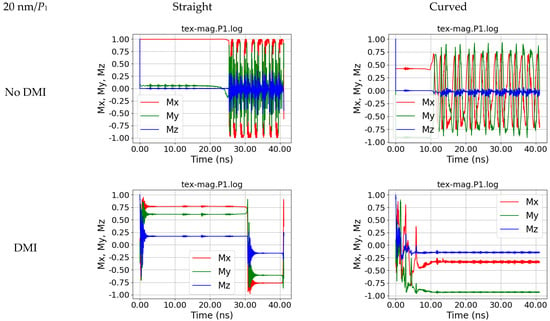
Figure 10.
Magnetization dynamics in position P1, i.e., at the right end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 20 nm.
For larger lengths of the magnetic field area, several simulations without DMI showed oscillations during the first 40 nm, as also visible for the case of a 50 nm length in Figure 11 and Figure 12, while others showed no oscillations for the straight or the curved samples (cf. Supplementary Materials). Generally, no large oscillations are visible for the simulations including the DMI. The small amplitude fluctuations visible, e.g., in Figure 12 for the samples with DMI, are residues of regular domain wall annihilations.
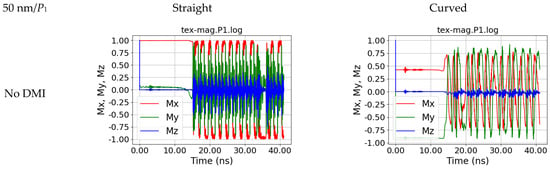
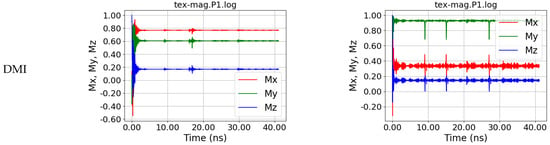
Figure 11.
Magnetization dynamics in position P1, i.e., at the right end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 50 nm.
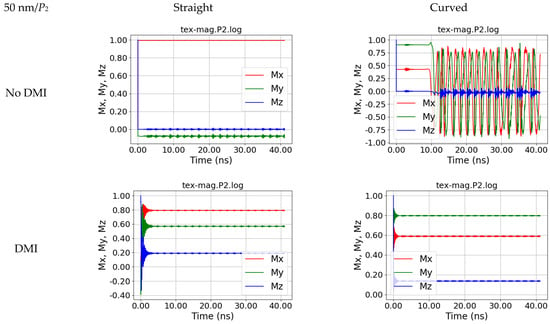
Figure 12.
Magnetization dynamics in position P2, i.e., at the left end of the fiber, for a straight and a curved nanofiber, simulated without and with DMI, for s = 50 nm.
While these simulations are not fully deterministic, i.e., repetitions with different start scenarios may lead to different durations until oscillations become visible at the defined output areas, it is obvious that no simulations with DMI, neither of the straight nor of the curved fiber, show oscillations. Our simulations thus reveal that the DMI can be used to suppress domain wall propagation through nanofibers.
Another point which should be mentioned is that for external magnetic field widths longer than 50 nm, the z-component of the magnetization in P0 is equal to zero after an initial peak in the case of simulations without DMI, while all simulations with DMI show a small z-oscillation in position P0 which can also be attributed to “echoes” of domain wall annihilations near this point. For a better visualization of these effects, movies of the magnetization dynamics of all four cases (with and without DMI, straight and curved samples) for s = 10 nm, 60 nm, and 500 nm are presented in the Supplementary Materials.
Additionally, Figure 13 shows the time evolution of a curved nanofiber with DMI, simulated for s = 500 nm, in which small-amplitude fluctuations near the left end (P2) as well as nucleation, propagation, and annihilation along the right part of the fiber, i.e., between P0 and P1, are visible. Generally, in the systems with DMI, domains can be formed, but do not propagate stably to either end of the nanofiber, but are partly annihilated after the formation of a few domains.

Figure 13.
Magnetization dynamics of a curved nanofiber, simulated with DMI, for s = 500 nm. The figure shows the evolution in time of the magnetization component My (from left to right and top to bottom).
4. Conclusions and Outlook
Micromagnetic simulations by Magpar, supplemented by plug-ins allowing adding the DMI as well as external magnetic fields with definable time-dependence at defined positions and collecting data from specific volumes, were used to investigate the impact of the area, in which a rotating external magnetic field is applied, on the magnetization dynamics in nanofibers. Our simulations showed that starting from a width of the area of the magnetic field of 5 nm, areas with alternating magnetization are produced by the rotating magnetic field, separated by domain walls. However, propagation of these domain walls is, independent from the fiber curvature, only possible in fibers without DMI, showing that the Dzyaloshinskii–Moriya interaction can suppress domain wall motion in magnetic nanofibers.
Future simulations will also investigate the time-dependent wavelengths of the spin-waves, i.e., the propagation of the exchange-coupled spins, by detecting the time-dependence of the exchange energy.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym15010234/s1, Figures S1–S24, showing all other magnetization dynamics graphs simulated within this study; videos of the magnetization dynamics of s = 10 nm, 60 nm, and 500 nm, depicting the y-component of the magnetization (cf. Figure 1 for the color code).
Author Contributions
Conceptualization, T.B. and A.E.; methodology, T.B. and P.S.; software, P.S.; validation, T.B. and A.E.; formal analysis, T.B.; investigation, T.B.; writing—original draft preparation, T.B. and A.E.; writing—review and editing, all authors; visualization, T.B. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—490988677—and Bielefeld University of Applied Sciences.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ryu, K.-S.; Thomas, L.; Yang, S.-H.; Parkin, S.S.P. Current induced tilting of domain walls in high velocity motion along perpendicularly magnetized micron-sized Co/Ni/Co racetracks. Appl. Phys. Express 2012, 5, 093006. [Google Scholar] [CrossRef]
- Yang, S.-H.; Ryu, K.-S.; Parkin, S.S.P. Domain-wall velocities of up to 750 m s−1 driven by exchange-coupling torque in synthetic antiferromagnets. Nat. Nanotechnol. 2015, 10, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Alejos, O.; Raposo, V.; Sanchez-Tejerina, L.; Martinez, E. Efficient and controlled domain wall nucleation for magnetic shift registers. Sci. Rep. 2017, 7, 11909. [Google Scholar] [CrossRef]
- Garg, C.; Yang, S.-H.; Phung, T.; Pushp, A.; Parkin, S.S.P. Dramatic influence of curvature of nanowire on chiral domain wall velocity. Sci. Adv. 2017, 3, e1602804. [Google Scholar] [CrossRef] [PubMed]
- Blachowicz, T.; Ehrmann, A. Magnetization reversal in bent nanofibers of different cross sections. J. Appl. Phys. 2018, 124, 152112. [Google Scholar] [CrossRef]
- Fidler, J.; Schrefl, T. Micromagnetic modelling—The current state of the art. J. Phys. D Appl. Phys. 2000, 33, R135–R156. [Google Scholar] [CrossRef]
- Zhu, B.; Lo, C.C.H.; Lee, S.J. Micromagnetic modeling of the effects of stress on magnetic properties. J. Appl. Phys. 2001, 89, 7009. [Google Scholar] [CrossRef]
- Hertel, R. Micromagnetic simulations of magnetostatically coupled Nickel nanowires. J. Appl. Phys. 2001, 90, 5752. [Google Scholar] [CrossRef]
- Han, M.G. Terahertz permeability of hard ferromagnetic L10-FePt alloy nanowire. Nanotechnology 2022, 34, 105703. [Google Scholar] [CrossRef]
- Dong, X.W.; Wang, R.F. Chirality-selection of magnetic domain walls in the Y-shaped nanostrips under small magnetic fields. J. Magn. Magn. Mater. 2019, 473, 26–31. [Google Scholar] [CrossRef]
- Berkov, D.V.; Boone, C.T.; Krivorotov, I.N. Micromagnetic simulations of magnetization dynamics in a nanowire induced by a spin-polarized current injected via a point contact. Phys. Rev. B 2011, 83, 054420. [Google Scholar] [CrossRef]
- Bran, C.; Fernandez-Roldan, J.A.; del Real, R.P.; Asenjo, A.; Chen, Y.-S.; Zhang, J.L.; Zhang, X.S.; Rodríguez, A.F.; Foerster, M.; Aballe, L.; et al. Unveiling the Origin of Multidomain Structures in Compositionally Modulated Cylindrical Magnetic Nanowires. ACS Nano 2020, 14, 12819–12827. [Google Scholar] [CrossRef] [PubMed]
- Han, D.-S.; Kim, N.-H.; Kim, J.-S.; Yin, Y.X.; Koo, J.-W.; Cho, J.H.; Lee, S.M.; Kläui, M.; Swagten, H.J.M.; Koopmans, B.; et al. Asymmetric Hysteresis for Probing Dzyaloshinskii–Moriya Interaction. Nano Lett. 2016, 16, 4438–4446. [Google Scholar] [CrossRef] [PubMed]
- Koyama, T.; Nakatani, Y.; Ieda, J.I.; Chiba, D. Electric field control of magnetic domain wall motion via modulation of the Dzyaloshinskii-Moriya interaction. Sci. Adv. 2018, 4, eaav0265. [Google Scholar] [CrossRef] [PubMed]
- Staggers, T.L.; Jacob, L.Y.; Pollard, S.D. Domain wall velocity asymmetries driven by saturation magnetization gradients without a Dzyaloshinskii-Moriya interaction. J. Magn. Magn. Mater. 2022, 558, 169500. [Google Scholar] [CrossRef]
- Cortés-Ortuno, D.; Beg, M.; Nehruji, V.; Breth, L.; Pepper, R.; Kluyver, T.; Downing, G.; Hesjedal, T.; Hatton, P.; Lancester, T. Proposal for a micromagnetic standard problem for materials with Dzyaloshinskii–Moriya interaction. New J. Phys. 2018, 20, 113015. [Google Scholar] [CrossRef]
- Puliafito, V.; Khymyn, R.; Carpentieri, M.; Azzerboni, B.; Tiberkevich, V.; Slavin, A.; Finocchio, G. Micromagnetic modeling of terahertz oscillations in an antiferromagnetic material driven by the spin Hall effect. Phys. Rev. B 2019, 99, 024405. [Google Scholar] [CrossRef]
- Silvani, R.; Kuepferling, M.; Tacchi, S.; Carlotti, G. Impact of the interfacial Dzyaloshinskii-Moriya interaction on the band structure of one-dimensional artificial magnonic crystals: A micromagnetic study. J. Magn. Magn. Mater. 2021, 539, 168342. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Rial, J.; Proenca, M.P. A Novel Design of a 3D Racetrack Memory Based on Functional Segments in Cylindrical Nanowire Arrays. Nanomaterials 2020, 10, 2403. [Google Scholar] [CrossRef]
- Khan, A.A.; Ollivier, S.; Longofono, S.; Hempel, G.; Castrillon, J.; Jones, A.K. Brain-inspired Cognition in Next-generation Racetrack Memories. ACM Trans. Embed. Comput. Syst. 2022, 21, 79. [Google Scholar] [CrossRef]
- Gaididei, Y.; Goussev, A.; Kravchuk, V.P.; Pylypovskyi, O.V.; Robbins, J.M.; Sheka, D.D.; Slastikov, V.; Vasylkevych, S. Magnetization in narrow ribbons: Curvature effects. J. Phys. A Math. Theor. 2017, 50, 385401. [Google Scholar] [CrossRef]
- Heinz, B.; Brächer, T.; Schneider, M.; Wang, Q.; Lägel, B.; Friedel, A.M.; Breitbach, D.; Steinert, S.; Meyer, T.; Kewenig, M.; et al. Propagation of Spin-Wave Packets in Individual Nanosized Yttrium Iron Garnet Magnonic Conduits. Nano Lett. 2020, 20, 4220–4227. [Google Scholar] [CrossRef] [PubMed]
- Mamun, A.; Klöcker, M.; Blachowicz, T.; Sabantina, L. Investigation of the Morphological Structure of Needle-Free Electrospun Magnetic Nanofiber Mats. Magnetochemistry 2022, 8, 25. [Google Scholar] [CrossRef]
- Blachowicz, T.; Steblinski, P.; Grzybowski, J.; Ehrmann, A. Magnetization Dynamics in Nanofiber Networks. In Proceedings of the 2021 IEEE 11th International Conference on “Nanomaterials: Applications & Properties” (NAP-2021), Odessa, Ukraine, 5–11 September 2021; pp. 1–4. [Google Scholar]
- Blachowicz, T.; Grzybowski, J.; Steblinski, P.; Ehrmann, A. Neuro-inspired signal processing in ferromagnetic nanofibers. Biomimetics 2021, 6, 32. [Google Scholar] [CrossRef]
- Blachowicz, T.; Steblinski, P.; Grzybowski, J.; Ehrmann, A. Domain wall nucleation, propagation and annihilation in coupled bent ferromagnetic nanofibers with rotating local input fields. J. Magn. Magn. Mater. 2022, 546, 168925. [Google Scholar] [CrossRef]
- Blachowicz, T.; Ehrmann, A. Magnetic elements for neuromorphic computing. Molecules 2020, 25, 2550. [Google Scholar] [CrossRef]
- Kuncic, Z.; Nakayama, T. Neuromorphic nanowire networks: Principles, progress and future prospects for neuro-inspired information processing. Adv. Phys. X 2021, 6, 1894234. [Google Scholar] [CrossRef]
- Sbiaa, R. Multistate Magnetic Domain Wall Devices for Neuromorphic Computing. Phys. Stat. Sol. Rap. Res. Lett. 2021, 15, 2100125. [Google Scholar] [CrossRef]
- Scholz, W.; Fidler, J.; Schrefl, T.; Suess, D.; Dittrich, R.; Forster, H.; Tsiantos, V. Scalable parallel micromagnetic solvers for magnetic nanostructures. Comput. Mater. Sci. 2003, 28, 366–383. [Google Scholar] [CrossRef]
- Nasirpouri, F.; Peighambari-Sattari, S.-M.; Bran, C.; Palmero, E.M.; Eguiarte, E.B.; Vazquez, M.; Patsopoulos, A.; Kechrakos, D. Geometrically designed domain wall trap in tri-segmented nickel magnetic nanowires for spintronics devices. Sci. Rep. 2019, 9, 9010. [Google Scholar] [CrossRef] [PubMed]
- Al Bahri, M.; Borie, B.; Jin, T.L.; Sbiaa, R.; Kläui, M.; Piramanayagam, S.N. Staggered Magnetic Nanowire Devices for Effective Domain-Wall Pinning in Racetrack Memory. Phys. Rev. Appl. 2019, 11, 024023. [Google Scholar] [CrossRef]
- Masciocchi, G.; Fattouhi, M.; Kehlberger, A.; Lopez-Diaz, L.; Syskaki, M.-A.; Kläui, M. Strain-controlled domain wall injection into nanowires for sensor applications. J. Appl. Phys. 2021, 130, 183903. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).