Abstract
The chirality of the interaction between the local magnetic moments in small transition-metal alloy clusters is investigated in the framework of density-functional theory. The Dzyaloshinskii–Moriya (DM) coupling vectors between the Fe atoms in Fe2X and Fe3X with X = Cu, Pd, Pt, and Ir are derived from independent ground-state energy calculations for different noncollinear orientations of the local magnetic moments. The local-environment dependence of and the resulting relative stability of different chiral magnetic orders are analyzed by contrasting the results for different adatoms X and by systematically varying the distance between the adatom X and the Fe clusters. One observes that the adatoms trigger most significant DM couplings in Fe2X, often in the range of 10–30 meV. Thus, the consequences of breaking the inversion symmetry of the Fe dimer are quantified. Comparison between the symmetric and antisymmetric Fe-Fe couplings shows that the DM couplings are about two orders of magnitude weaker than the isotropic Heisenberg interactions. However, they are in general stronger than the anisotropy of the symmetric couplings. In Fe3X, alloying induces interesting changes in both the direction and strength of the DM couplings, which are the consequence of breaking the reflection symmetry of the Fe trimer and which depend significantly on the adatom-trimer distance. A local analysis of the chirality of the electronic energy shows that the DM interactions are dominated by the spin-orbit coupling at the adatoms and that the contribution of the Fe atoms is small but not negligible.
1. Introduction
Systematic investigations of the magnetism of small clusters and low-dimensional systems over past decades have unfolded a wealth of remarkable possibilities of tuning and optimizing the magnetic characteristics of materials for specific technological and scientific purposes. Besides the most basic average magnetization and magnetic order, a major focus of attention has been dedicated to understanding the magneto-anisotropic effects, which originate in subtle relativistic contributions to the electronic structure such as spin-orbit coupling (SOC) [1]. A central property in this context is the magnetic anisotropy energy (MAE) which measures the spin-orientation dependence of the total electronic energy, which determines the low-temperature direction of the magnetic monodomains with respect to the lattice structure as well as its stability in the face of finite-temperature fluctuations and external fields [2,3,4,5,6,7,8]. Furthermore, recent studies have highlighted the importance of relativistic corrections on the magnetic interactions among the local atomic magnetic moments. Indeed, the spin-orbit-driven anisotropy of the magnetic interactions is known to condition the shape and stability of both ground-state and metastable magnetic configurations. Particularly interesting are competing interactions and antisymmetric Dzyaloshinskii–Moriya (DM) couplings that favor the development of noncollinear magnetic orders, such as extended spin-density waves and localized chiral magnetic textures [9,10,11,12,13]. Consequently, understanding the microscopic origin of the anisotropy and chirality of the interactions between local magnetic moments represents one of the major challenges in this field.
Symmetry and the absence thereof are obviously indissociable from magnetic anisotropy. Manipulating the composition, structure, and interfaces of magnetic systems has always been a major route in the development of artificially made magnetic materials [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Most previous theoretical studies of the electronic origin of chiral magnetism have been focused on extended low-dimensional systems (e.g., wires, stripes, thin films, and multilayers) [10,11,12,13,29,30,31,32,33,34,35,36,37,38]. Yang et al. analyzed the DM interaction between nearest neighbors in Co/Pt bilayers using first principles calculations [12]. The DM interaction was found to be the largest at the interfacial Co layer, where the effects of the spin-orbit energy associated with the adjacent Pt atoms are strongest. The authors concluded that the DM interaction is an indirect 3-site coupling in agreement with [9,39]. Within this interpretation, the mechanism behind the DM coupling can be regarded as analogous to the indirect Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction [40,41,42]. However, the role of the 5d substrates in the chiral properties of the 3d coatings is still not quite clear [43]. For instance, Kashid et al. have performed a theoretical analysis of the chiral magnetic order in free-standing planar 3d–5d biatomic metallic chains using a tight-binding model and ab initio calculations [11]. In the case of FePt and CoPt chains, they found that the DM interaction can compete with the symmetric Heisenberg exchange interaction and with the local magnetocrystalline anisotropy. They also confirmed that the strength of the DM interaction is proportional to the strength of the SOC at the 5d atoms, which confirms the dominant role of the latter. Recently, Meyer et al. have successfully mapped the quantum electronic calculations onto an effective atomistic spin model appropriate for ultrathin Co and Mn films [35,44,45,46,47]. Thus, by combining electronic structure theory and real space modeling, the stability of magnetic skyrmions in the absence of external magnetic fields could be theoretically predicted and subsequently experimentally confirmed [35].
Studies of the magnetic anisotropy of finite clusters have been mostly focused on the dependence of the total energy on the orientation of the magnetization of monodomains [1,2,15,22,23,24,25,48]. These investigations have revealed a complicated, non-perturbative behavior of the magnetic anisotropy energy (MAE) as a function of cluster size, structure, bond length, and d-band filling. In particular, a considerable size-dependent enhancement of the cluster MAE with respect to the corresponding crystals and thin films has been observed, together with remarkable multiaxial energy landscapes. As in the case of extended nanostructures, alloying has been a most valuable means of optimizing the MAE of finite clusters. For instance, alloying magnetic 3d transition metals (TMs) with the highly polarizable and heavier 4d and 5d elements has allowed one to optimize the MAE of nanoalloys as a function of size and composition [14,15,16,21,22,23,24,25]. However, very little quantitative information is currently available on the degree of anisotropy of the magnetic interactions, particularly concerning the chiral DM couplings. It is the purpose of the present paper to address this problem by calculating the DM interactions in small Fe clusters. There is a particular emphasis on assessing how the DM interactions can be triggered by breaking the point group symmetry of the clusters and quantifying the actual changes in these chiral coupling as a function of the cluster structure.
The reminder of the paper is organized as follows. In the following Section 2, the bilinear expansion of the electronic energy as a function of the orientations of the local magnetic moments at the different cluster atoms i is presented, from which the DM pseudovectors characterizing the anisotropic antisymmetric couplings between the moments and at nearest neighbor (NN) atoms are derived. In Section 3, the method used for obtaining is outlined, including the main technical details on the underlying density-functional calculations for different noncollinear orientations of and . Our results for the DM couplings in Fe2X and Fe3X clusters with X = Cu, Pd, Pt, and Ir are presented and discussed in Section 4. The importance of the dimer-adatom hybridizations to the chiral interactions between the Fe atoms is quantified by varying the dimer-adatom distance systematically. The results for are correlated to the various local contributions to the spin-orbit (SO) energy. In addition, the DM interactions are contrasted with the corresponding isotropic Heisenberg couplings, as well as with the anisotropy of the symmetric couplings. Finally, Section 5 summarizes our conclusions.
2. Classical Spin Model: Symmetric and Antisymmetric Couplings
In order to derive the effective pairwise interaction between the local magnetic moments at the Fe atoms, we expand the total electronic energy of the clusters to second order in the orientations of the local magnetic moments . The most general quadratic approximation of the interaction energy adopts the form of the classical spin Hamiltonian
where are the interaction matrices and are the orientations of the local magnetic moments [49]. Notice that Equation (1) takes into account not only all possible pair interactions between local magnetic moments and but also the local contribution to the electronic energy for , which is often referred to as a local contribution to the magnetocrystalline anisotropy energy. Although fully unrestricted at the quadratic (i.e., pairwise interaction) level, the model can in principle be extended in order to incorporate three-spin interactions and beyond [50,51,52].
Without a loss of generality, H can be expressed in terms of irreducible contributions as the sum
where the rotational invariant Heisenberg term is given by
with , the anisotropic symmetric term is given by
with and the anisotropic antisymmetric term is given by
with . The focus of this work is on the antisymmetric contribution known as the Dzyaloshinskii–Moriya (DM) interaction [53,54,55,56]. This term can be written in a geometrically more transparent form as
where is a pseudovector known as the DM vector. The magnitude of depends on the details of the electronic structure and on the strength of the SOC of the compounds [12], whereas the orientation of is to a large extent conditioned by the point-group symmetry of the nanostructure around the bond connecting i and j [54]. The orientation of (direction and sense) defines both the favored rotation sense as well as the optimal rotation plane of the local magnetic moments. According to Equation (6) a positive (negative) value of means that the sense of rotation of the local magnetic moments from toward is an unfavorable (favorable) configuration. For example, if is pointing along the positive z axis, then a counterclockwise [clockwise ] sense of rotation from toward within the plane yields the highest [lowest] pair-interaction energy.
The relation between the point-group symmetry of the lattice and the possible orientation of the DM vector has been discussed by Moriya who established a number of useful symmetry rules [54]. Three of them are particularly relevant for the following discussion. Consider two local magnetic moments and located at and , with being the vector connecting them and C denoting the point bisecting the segment . Moriya has shown that the DM interaction satisfies the following symmetry constraints [54]:
- (i)
- If the structure has an inversion symmetry with respect to C then .
- (ii)
- If the structure has a mirror symmetry plane perpendicular to passing through C then is perpendicular to .
- (iii)
- is perpendicular to any mirror symmetry plane of the structure that includes the bond connecting and .
In order to verify the validity of these rules, it suffices to recall that the local magnetic moments, having spin and angular momentum origin, are pseudovectors while the DM energy is of course a scalar. Let us finally underscore that the antisymmetric nature of the DM coupling favors noncollinear magnetic order with a precise local chirality, thus providing the driving force that stabilizes spiral magnetic orders and vortex magnetic patterns.
3. Electronic Calculations
In order to determine the local-environment dependence of the DM interaction in small Fe clusters with non-magnetic adatoms, we perform independent density-functional theory (DFT) calculations for different noncollinear magnetic configurations that are imposed by constraining the directions of the local magnetic moments at each Fe atom. The DM pseudovectors between the Fe atoms are then obtained as a function of the geometry of the cluster by building appropriate total energy differences between equivalent configurations with opposite chiralities. As an example, Figure 1a,b show two representative magnetic configurations of Fe2X, one exhibiting counterclockwise and the other clockwise chiralities, from which the z component of the DM vector is obtained. The contribution of scalar and symmetric magnetic interactions and cancel out in this energy difference, since they are independent of the chirality of otherwise identical magnetic configurations [see Section 2]. In the case of Fe3X the interactions between all the pairs of Fe atoms have to be taken into account. One possibility to determine is then to consider the magnetic configurations displayed in Figure 1c,d, from which follows. The remaining components and are determined in an analogous way by considering further magnetic configurations in which the local magnetic moments point out of the Fe2X or Fe3 plane. The symmetric couplings , the isotropic part , and the anisotropies are obtained by performing independent selfconsistent calculations for parallel and antiparallel orientations of the local Fe moments along the x, y and z axes. Thus, the antisymmetric DM contributions to the total energy vanish and the symmetric couplings can be derived by building the energy differences between the corresponding antiparallel and parallel alignments.
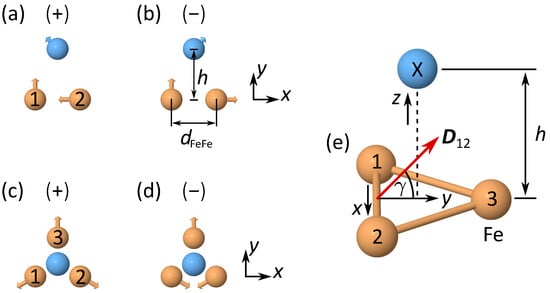
Figure 1.
Illustration of representative magnetic configurations in Fe2X and Fe3X clusters having opposite chiralities indicated by and . The orange spheres indicate the Fe atoms and the blue spheres the adatom X. The arrows show the directions of the local magnetic moments . In (a,b), corresponding to Fe2X, the magnetic moments at the Fe atoms turn in counterclockwise or clockwise sense as we move from Fe(1) to Fe(2). Similarly, in (c,d), top views of Fe3X are shown, where the turn counterclockwise and clockwise , respectively, as we move from Fe(1) to Fe(2). In (e) the Fe3X cluster is illustrated including the DM-interaction vector and the angle that it forms with the y axis.
The spin polarization at the adatoms, as well as the modulus of the local magnetic moments at the Fe atoms, remain unconstrained in all the calculations. In this way, these electronic degrees of freedom are optimized for each orientation of the Fe magnetic moments and the most stable solution of the Kohn–Sham equations is obtained [57,58]. In practice, in the case of Fe, the sizes of local magnetic moments are largely independent of their orientation, since changing the intra-atomic spin-density redistribution involves relatively large energies. Indeed, the intra-atomic exchange energy is of the order of 1 eV, which is significantly larger than the exchange coupling constants controlling the orientations of [59,60,61,62,63,64]. This also justifies our analysis in terms of the classical spin model introduced in Section 2.
No constraints are imposed on the magnetic moments of the adatoms X, since our focus lies on the Fe atoms, their magnetic configurations, and their effective interactions. Furthermore, we do not intend to determine the magnetic couplings involving the adatoms, whose magnetic moments are small and strongly dependent on the cluster geometry. This by no means implies that the adatom contribution to the magnetic coupling is unimportant. In fact, significant local magnetic moments are induced at the adatoms X as a result of the proximity with the Fe atoms, which tend to increase as the adatom-cluster distance decreases. Although the orientations of are in general noncollinear, the tendency thereby is to align parallel to . Consequently, the adatom contribution to the changes in the total energy as a function of the orientation of the Fe moments is central to our study. Moreover, as already discussed, the adatoms break the inversion symmetry of the Fe dimer, thus triggering the appearance of DM interaction between Fe atoms [54]. In the case of Fe3, the adatom-induced symmetry breaking unfolds new components of . Furthermore, heavy open d-shell adatoms such as Pd, Pt, and Ir exhibit a particularly large SOC, which enhances all magneto-anisotropic phenomena and, in particular, the DM couplings [9,12,54].
The first-principles calculations have been performed in the framework of Hohenberg–Kohn–Sham’s density functional theory [65,66] as implemented in the Vienna ab initio simulation package (VASP) [67,68]. The spin-polarized Kohn–Sham equations are solved using an augmented plane-wave basis set, taking into account the interaction between the valence electrons and ionic cores through the projector-augmented wave (PAW) method [69]. The exchange and correlation energy-functional is described by the Perdew–Burke–Ernzerhof (PBE) parameterization of the generalized-gradient approximation (GGA) [70]. In order to gain insight into the role of electron correlations on the DM interactions, we have also performed the calculations by using the local-density approximation (LDA) [71,72,73] and the GGA proposed by Perdew and Wang (PW) [74,75,76,77].
From a technical perspective, the numerical convergence and stability of the calculations is significantly improved by considering the fractional occupations of Kohn–Sham orbitals with a Gaussian smearing. The width of the Gaussian is subsequently decreased stepwise in the range until the entropy contribution to the free energy is less than 10−3 eV/atom. Concerning the expansion of the Kohn–Sham orbitals, a cut-off energy eV has been used for the plane-wave basis set. The self-consistent relaxation of the electronic degrees of freedom is pursued until the total electronic-energy change between subsequent optimization steps is smaller than 10−6 eV. This is sufficient for our purposes, as we are interested in determining the energy differences of the order of 10−4–10−3 eV. The dimensions of the supercell are chosen to be large enough (at least 12 Å) so that any spurious interactions between the cluster images are negligible. As in any finite-cluster calculation, the wave vector is set to , since no integration in the Brillouin zone is necessary.
In order to constrain the orientation of the local magnetic moments at each Fe atom i along specific directions (), the penalty function
is added to the usual Hohenberg–Kohn energy functional, where specifies the weight of the penalty term in the Hamiltonian [78,79]. The local magnetic moments entering Equation (7) are obtained by integrating the magnetization density within the corresponding Wigner–Seitz sphere , i.e.,
Once self-consistency is reached, the spin-orbit interactions are introduced by using the method implemented in Ref. [80].
The equilibrium geometry of the clusters are determined by performing unconstrained relaxations of all atomic positions until the forces are smaller than 0.01 eV/Å. The resulting equilibrium distances are listed in Table 1. In the case of Fe3X, the Fe atoms actually form an isosceles triangle whose shape changes somewhat as the height h between the Fe3 plane and the adatom X is varied. For simplicity, we ignore in the following these minor distortions and consider equilateral Fe3 with the adatom X located above its center. The effects of symmetry breaking and adatom-cluster hybridizations on the DM interaction are then investigated as a function of the height between X and the Fe3 plane.

Table 1.
Equilibrium configurations of Fe2X and Fe3X clusters with X = Cu, Pd, Pt, and Ir. The equilibrium distances and , as well as the height between the adatom X and the center of the Fe2 dimer or the centre of the Fe3 triangle, are given in Å. In the case of Fe3X, average values are shown ignoring minor distortions of the Fe trimer.
4. Results
This section presents and discusses our results on Fe2X and Fe3X clusters for X = Cu, Pd, Pt, and Ir. In Section 4.1, the effects of the different adatoms as the triggering source of the DM coupling in Fe2X are quantified by systematically varying the adatom-dimer distance. The trends for different adatoms are contrasted. The microscopic origin of the DM interaction is analyzed from a local perspective in Section 4.2 by computing the adatom-resolved contributions of the SOC to the chirality energy . In Section 4.3 the symmetric isotropic and anisotropy interactions in Fe2X are quantified and the results are compared to the corresponding antisymmetric DM couplings. Finally, in Section 4.4, the changes in the modulus and orientation of the DM vector between two Fe atoms, which are induced by the adatom in Fe3X are quantified as a function of the distance between the adatom and the Fe3 plane. The trends for different X are identified and compared with the behavior found in Fe2X.
4.1. DM Interaction in Fe2X Clusters
The presence of the adatom breaks the inversion symmetry of the pure dimer and unlocks the DM interaction between the Fe atoms. In accordance with Moriya’s symmetry considerations (see Section 2 and [54]) we obtain that is perpendicular to the plane defined by the Fe2X triangle (i.e., ). The calculated z component for X = Cu, Pd, Pt, and Ir are shown in Figure 2 as a function of the distance h between X and the center of the Fe2 dimer bond. A rich variety of behaviors is found for the considered adatoms, which have different chemical properties, d-band fillings, and the SOC strengths.
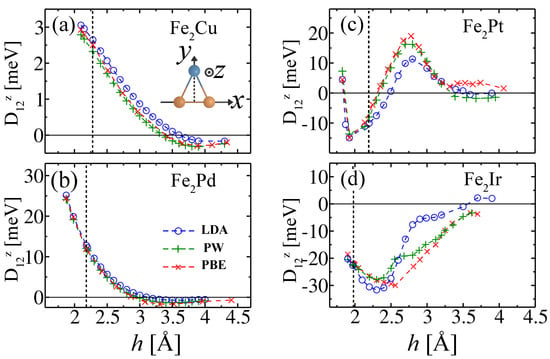
Figure 2.
Dzyaloshinskii–Moriya vector component between the Fe atoms in Fe2X clusters with X = Cu, Pd, Pt, and Ir as a function of the distance h between X and the center of the Fe2 dimer [see inset of (a)]. The vertical dashed lines indicate the equilibrium height . The symbols correspond to independent ab initio calculations, using different approximations to the exchange and correlation energy functional as indicated in the inset of (b).
Probably the simplest or softest way of breaking the symmetry of the Fe dimer and thereby trigger a possible DM coupling is by adding a non-magnetic light atom with a closed d shell similar to Cu. Figure 2a shows that the effects are, already in this case, quite remarkable. The induced DM coupling between the Fe atoms is significant, reaching values of about 2 meV at the equilibrium distance. Stronger effects are expected by considering heavier 4d atoms, particularly if the d-band is no longer completely filled. This is indeed the case when a Pd atom is added. Figure 2b shows an enhancement by about a factor 10 of the strength of the induced DM coupling between the Fe atoms, as compared to Fe2Cu. It is, however, remarkable that the dependence of on the adatom-dimer distance is qualitatively similar in these two cases. In Fe2Cu, the z component is positive and largest around the equilibrium configuration (Å). This means that an in-plane clockwise rotation of the local magnetic moments at the Fe atoms is favored with respect to a counterclockwise rotation [see also Figure 1a,b]. In contrast, at large distances, where the adatom-dimer interaction is weak, –3.5 Å) changes sign and goes over a minimum before vanishing in the limit of , where the consequences of breaking the inversion symmetry become negligible. In the case of Fe2Pd a qualitatively similar trend is observed. However, the strength of the DM coupling is significantly larger, particularly at short distances, where the adatom-dimer hybridization is strong. This can be qualitatively understood by recalling that, in Pd, the 4d shell is open and the nuclear charge is larger, which both results in a much stronger and more effective SOC.
The trend to stronger DM couplings is confirmed when the even heavier Pt and Ir adatoms are considered. In these cases, reaches values of up to 20–30 meV. Furthermore, the dependence on h and on the adatom-dimer hybridization is far richer. Indeed, in Fe2Pt and Fe2Ir, oscillates as a function of h, which demonstrates interesting possibilities of manipulating the chiral magnetic coupling through alloying. For example, in Fe2Pt, the favored chirality changes twice as h increases: First, at a short height Å, from a clockwise rotation of , which corresponds to , to a counterclockwise rotation , which corresponds to . Second, at larger h, the favored sense of rotation changes again from counterclockwise to clockwise at –2.5 Å. Notice that the oscillations of are quite important in Fe2Pt, their values range from meV to 10–20 meV in the counterclockwise, respectively, and clockwise sense of rotation.
The importance of d-band fillings becomes clear by comparing the results for Pt and Ir, which have similar atomic numbers and thus comparably strong SOCs. In the case of Fe2Ir, starting from a large negative value meV at the smallest considered height Å, becomes even stronger at larger distances reaching its maximum absolute value meV at a height –2.6 Å, which is larger than the equilibrium height Å (see Table 1). Around , depends linearly on h, with an important derivative , which indicates the possibility of interesting couplings between magnetic chirality and stress or lattice vibrations. For heights beyond the largest , increases monotonically () approaching zero in the limit of large h. In this context, it is interesting to note that a similar oscillation of the orientation of the DM vector and an exponential decrease in the DM-interaction strength as a function of interatomic distance have been derived from low-temperature inelastic scanning tunneling spectroscopy on a pair of Fe atoms deposited on Pt(111) [32].
Three different local and gradient-corrected approximations to the exchange and correlation (XC) functional have been considered in order to assess the role of correlations on the SO energies and DM interactions. The results shown in Figure 2 show that they all yield similar trends as a function of the distance between the nonmagnetic adatom and the Fe dimer. The quantitative differences between the functionals are in almost all cases clearly smaller than the changes in as a function of h or composition. This is quite remarkable since the behaviors found for the various considered adatoms differ widely (see Figure 2). Notice, however, that in the case of Fe2Pt and Fe2Ir, where the absolute values of are particularly large, the quantitative differences between the results for different functionals can be significant (up to 15 meV), which demonstrates that electron correlations can have a significant impact on the DM couplings.
4.2. Microscopic Origin of the Dzyaloshinskii–Moriya Interactions in Fe2X Clusters
Besides quantifying the strength and orientation of the DM interactions, understanding their microscopic origin is also of considerable interest. Indeed, a more detailed insight on this subtle relativistic effect from a theoretical point of view should be helpful to the experimental search for new materials relevant for technological applications. In this context, it has been proposed [9] that the DM coupling can be regarded as an indirect interaction between two magnetic atoms with local magnetic moments and (for example Fe or Co atoms) mediated by a third often non-magnetic atom exhibiting strong SOC (for example Pt). According to this picture, different relative cantings of the local magnetic moments and result in changes of the SOC energy, which occur for the most part at the heavy non-magnetic atoms. This dominant dependence of the contribution of the nonmagnetic, though strongly spin-polarizable atoms, to the SO energy is regarded as the driving force behind the DM interaction [12]. A further interesting alternative perspective has been proposed in [13]. In this case, the DM interaction is regarded as the result of spin-flip hoppings of electrons between the magnetic moments and , whereby the spin flips are triggered by spin-orbit scattering at the non-magnetic nearby atoms [13]. Moreover, previous theoretical studies on 3d TM chains, monolayers and multilayers deposited on 5d substrates have shown that the chiral coupling between 3d TM atoms are often associated with changes in the SOC energy originating mainly at the adjacent 5d atoms of the support, rather than at the actual magnetic materials [9,11,13,43]. It is therefore very interesting to investigate if a similar situation applies to the chiral properties triggered on Fe dimers by adatoms.
In order to clarify the origin of the DM interaction in the Fe2X clusters, we have analyzed our ab initio calculations from a local perspective. In Figure 3, the results are given for the changes in the SO energy upon changing the chirality of the magnetic configuration in Fe2X from clockwise [, Figure 1b] to counterclockwise [, Figure 1a]. First of all, one observes that, in the case of Cu and Pd, the chirality of the spin-orbit energy accurately accounts for the corresponding chirality of the total electronic energy . Some deviations are found in the case of the Pt adatom while, in the case of Ir, the quantitative discrepancies between and are significant. This demonstrates that the changes in the kinetic and Coulomb energies of the electrons as a function of chirality, possibly related to redistributions of the spin- and orbital-polarized density, cannot be neglected when heavy TM atoms are involved. Particularly, in the case of Fe2Ir at a relatively large Ir-dimer distance ( Å), the actual DM couplings derived from are orders of magnitude larger than those derived from the spin-orbit contributions alone. Nevertheless, it also true that, except in Fe2Ir, is in general able to account for both the sign and approximate strength of , including the non-monotonic behavior as a function of h found in Fe2Pt. Concerning the atom specific contributions to , one observes that the adatoms dominate the chirality of the spin-orbit energy, not only for 4d and 5d TMs but also in the case of Cu. Notice, moreover, that the contribution of the Fe atoms is sometimes significant. In particular, in the case of Cu, the chirality of the SO energy at the Fe atoms is responsible for the change of sign of for Å.
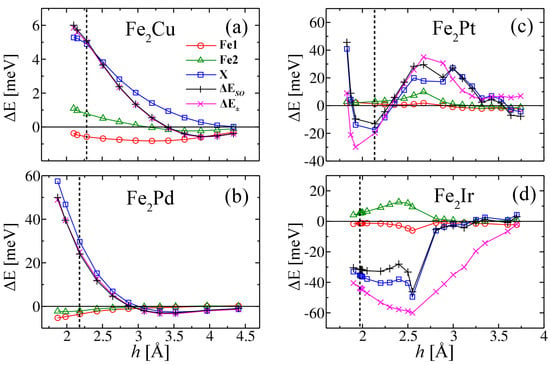
Figure 3.
Local contributions to the chirality of the spin-orbit (SO) energy at the different atoms i in Fe2X as a function of the adatom-dimer distance h. Results are given for the Fe(1) atom (red circles), the Fe(2) atom (green triangles), and the adatom X (blue squares). The plus signs and crosses show, respectively, the chirality of the SO energy and of the total electronic energy . Notice the dominant role played by the changes in the local SOC energy at the adatoms.
The results shown in Figure 3 also provide a useful insight on the role of the d-band filling of the adatoms X regarding the total energy asymmetry . One observes that Fe2Cu, the lightest adatom with a closed 3d shell, exhibits the smallest meV among the considered clusters. Pd and Pt, which have a similar d-band filling, yield comparable largest values of –35 meV, despite Pt being much heavier than Pd. In contrast, Ir, which has one more d hole than Pt, shows a greatly increased maximum meV. This is consistent with the conclusions drawn by Belabbes et al., in whose work the DM interactions are regarded as the result of spin-flip hoppings between magnetic compounds triggered by spin-orbit scattering at often heavy non-magnetic elements [13]. As these authors point out, active d-band states at both the magnetic and intermediate nonmagnetic alloy components are necessary for the spin-flip processes to occur. Therefore, a lower d-band filling at the adatoms facilitates the indirect spin-flip hoppings between the Fe atoms, thus resulting in a larger DM coupling.
4.3. Symmetric Magnetic Interactions in Fe2X Clusters
The stability of noncollinear magnetic configurations and the morphology of spin textures such as domain walls, spin-density waves, and skyrmions are conditioned by the importance of the antisymmetric DM couplings , which favor noncollinear spin arrangements [see Equation (6)], relative to the symmetric isotropic couplings , which, in the absence of frustrations, favor collinear alignments of the local moments [see Equation (3)]. Furthermore, the anisotropies of the symmetric couplings including the local anisotropies define, together with , the shape and orientation of the magnetic configurations in both collinear and noncollinear situations [see Equation (4)]. It is therefore very interesting to analyze the dependence of and on the local environment of the magnetic moments in Fe2X and to compare them with the corresponding DM couplings.
In Figure 4, the symmetric Heisenberg interactions in Fe2X are shown as a function of the distance h between Fe2 and the adatom X = Cu, Pd, Pt, and Ir for the different orientations and z of the Fe moments . These couplings are given by the difference between the electronic energies obtained in independent calculations for parallel and antiparallel alignments of the local magnetic moments along [see Equation (4)]. The corresponding isotropic couplings are shown as well. In Fe2Cu and Fe2Pd, the dependencies of on h are qualitatively similar. In contrast to the results for shown in Figure 2a,b, decreases with decreasing dimer-adatom distance. In other words, decreases as the hybridization between the Fe d-orbitals and the adatom increases. This trend to decouple the Fe local magnetic moments by the adatom contrasts strongly with the behavior found for the DM interaction, where the adatom plays the role of a mediator, enhancing as it approaches the dimer. In the case of Fe2Pt and Fe2Ir, the symmetric couplings are further reduced in comparison with Fe2Cu and Fe2Pd. Moreover, one observes that oscillates strongly as a function of h deviating by about 10% from its large-h value. Similar strong oscillations have been observed in of Fe2Pt and Fe2Ir [Figure 2c,d], which reflects a much stronger modification of the electronic properties due to the presence of these adatoms. However, note that the presence of the adatom does not result in a clear enhancement of the symmetric Heisenberg coupling , as it is the case for . In fact, the symmetric couplings are not triggered, despite being certainly affected by the symmetry breaking adatoms. They are already present in the isolated Fe clusters [2,81,82].
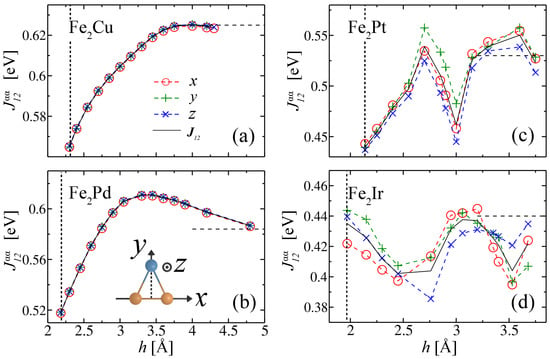
Figure 4.
Symmetric anisotropic Heisenberg coupling constants between Fe magnetic moments pointing along the direction y and z in Fe2X clusters. Results are given for X = Cu, Pd, Pt, and Ir as a function of the distance h between the adatom X and the center of the Fe2 dimer. See Equations (1)–(5) and the inset of (b). The black full curves show the corresponding isotropic couplings . The dashed horizontal lines for large h indicate the calculated for the isolated dimer at the corresponding equilibrium distances given in Table 1. The vertical dashed lines indicate the equilibrium height .
For large h, in the limit of isolated Fe2, one observes that is finite and positive, which corresponds to the known ferromagnetic alignment of the Fe moments in the dimer ground state [81,82,83]. Notice that the large-h value of decreases as we move from X = Cu to X = Ir. This is a consequence of the fact that the considered Fe-Fe distance, assumed for simplicity to be independent of h, is larger for the heavier adatoms (see Table 1). The quantitative values of are in the range of 0.4–0.6 eV. They are larger than typical Fe-bulk values, which is in agreement with the temperature dependence of the average magnetic moment of Fe2 obtained in functional-integral d-band-model calculations [82]. The comparison with the DM couplings reported in Figure 2, which are of the order of 1–30 meV, shows that a misalignment of Fe moments by an angle of only 1/100–1/10 radians yields exchange energies comparable to the DM energy. Previous theoretical studies have shown that the ratio between the DM and exchange couplings depends strongly on the considered magnetic material and its interfaces. The values of of the order of 1/100, as in this work, are not uncommon [44,84,85,86]. However, the situations have been also found in which is of the order of 1 or even larger [32,87,88].
The anisotropy of the symmetric couplings , shown in Figure 5 reveals the SOC effects the exchange couplings. One observes that is quantitatively comparable, though it is in general weaker than for the corresponding adatom. Although both symmetric and antisymmetric anisotropic interactions are a consequence of SOC, the effect of the adatoms is clearly stronger on the DM couplings than on the anisotropy of the Heisenberg couplings, particularly in the case of the heavier adatoms having strong SOC (e.g., Pt and Ir). In the case of Cu and Pd, the anisotropies are very small, of the order of 0.2–0.6 meV, with an even weaker dependence on h. In fact, they are very similar to the anisotropies in the isolated dimer: meV and meV. In contrast, becomes orders of magnitude stronger when the heavier Pt and Ir atoms are added (see Figure 5). Accordingly, the distance dependence of is also much stronger baring no relation to the values in the isolated dimer even at a relatively large adatom-dimer distance.
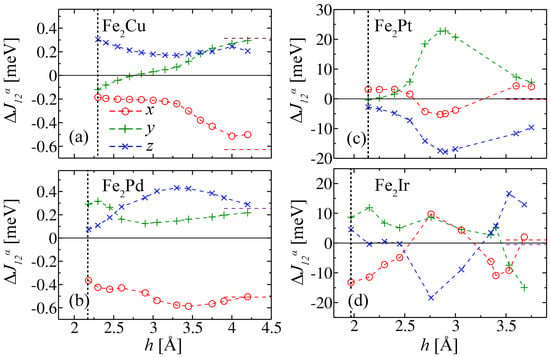
Figure 5.
Anisotropy of the symmetric Heisenberg coupling constants between Fe magnetic moments pointing along the direction y and z in Fe2X clusters. See Equations (1)–(5) and the inset of Figure 4b. Results are given for X = Cu, Pd, Pt, and Ir as a function of the distance h between the adatom X and the center of the Fe2 dimer. The dashed horizontal lines for large h correspond to (red) and (purple) for the isolated dimer at the corresponding equilibrium distances given in Table 1. The vertical dashed lines indicate the equilibrium height .
4.4. DM Interaction in Fe3X Clusters
The Fe3X clusters with an equilateral basis exhibit mirror symmetry planes perpendicular to the bonds connecting the Fe atoms and passing through the middle of the vectors connecting them [see Figure 1]. In accordance with Moriya’s symmetry considerations (see Section 2 and [54]), we obtain that is perpendicular to (i.e., ). In contrast to Fe2X, the adatom affects not only the absolute value of the but also its orientation. In Figure 6, the absolute value and the angle between and the positive y axis are shown as a function of the distance h between X and the center of the Fe3 triangle. As shown in Figure 1e, the positive y axis is the direction perpendicular to the bond between Fe(1) and Fe(2) pointing toward Fe(3) within the Fe-trimer plane.
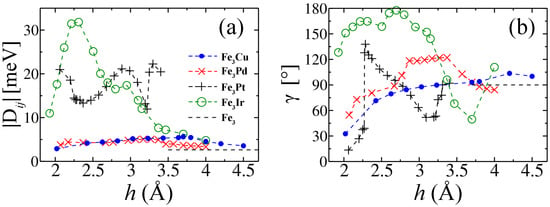
Figure 6.
(a) Absolute value of the Dzyaloshinskii–Moriya vector between a pair of Fe atoms in Fe3X clusters with X = Cu, Pd, Pt, and Ir and the Fe3 triangle as a function of the distance h between the adatom X and the center of the Fe3 triangle. (b) Angle between and the positive y axis as a function of h [see Figure 1c–e]. For symmetry reasons . The symbols are the result of independent DFT calculations, whereas the lines connecting them are a guide to the eye.
In Fe3Cu and Fe3Pd, the absolute value of the DM vector depends weakly on h remaining in the range = 3–6 meV. Notice that in Fe3X does not vanish for large h, as in Fe2X, since the inversion symmetry with respect to the center of the bond between Fe(1) and Fe(2) is already broken by the presence of Fe(3). In fact, calculations for Fe3 yield meV in good agreement with the results for Fe3X at large h. The DM coupling strengths in Fe3Cu and Fe3Pd are very similar, although the spin-orbit coupling in Pd is much larger than in Cu. This behavior is completely different from what is observed in Fe2Cu and Fe2Pd, where is much stronger in the case of Pd [see Figure 2a,b]. One concludes that the hybridization with the additional Fe atom in Fe3X critically modifies the DM interaction between the other two Fe atoms. Therefore, besides the properties of the adatoms, the DM interaction is strongly affected by the local environment of the atoms, as given by the geometry of the nanoclusters and the resulting hybridizations.
Concerning the orientation of , the differences between Fe3Cu and Fe3Pd become more significant quantitatively, although some common qualitative trends are shared. At short distances, is tilted pointing toward the adatom and forming an angle ° with the y axis for Cu and ° for Pd [see Figure 6b as well as Figure 1e]. As the distance h increases, move rapidly toward the normal to the Fe3 plane in the direction of the adatom, showing some oscillations and, in particular, a maximum ° for Fe3Pd at Å. Finally, ° is reached at large adatom-cluster distances, which corresponds to the result obtained for in the case of pure Fe3. The geometry of the clusters qualitatively conditions the orientation of , whereas the Cu or Pd adatoms are important in order to define the precise direction of the DM vector with respect to the cluster structure. It is important to note that the orientation of (direction and sense) defines both the favored rotation sense as well as the optimal rotation plane of the local magnetic moments of the interacting atoms. For example, if is pointing along the z axis, a clockwise [counterclockwise ] rotation direction within the plane is the most [least] favorable.
The significantly heavier Pt and Ir adatoms yield distinctive strong distance dependencies of . In the case of Fe3Pt, the absolute value exhibits oscillations between the maxima –22 meV at Å, 2.9 Å and 3.3 Å and the minima –14 meV at Å and 3.2 Å. In the case of Fe3Ir, increases for small h from meV at Å to meV at Å. As in the case of Fe2X, Ir yields the strongest DM couplings among the considered Fe3X. For large distances, rapidly decreases to meV at Å with an intermediate local maximum meV at Å. Notice that the influence of the Pt and Ir adatoms is still significant, even at the largest considered h. The fact that Pt and Ir show such different behaviors, although the atomic numbers are similar, emphasizes the role of the d-band filling on the DM coupling, in agreement with the conclusion drawn for Fe2X clusters.
The Pt and Ir adatoms also have a major influence on the orientation of . In the case of Fe3Pt and at short distances Å, is close to the positive y axis with °. As the distance h is increased, rapidly rotates to ° at Å, with its component now being negative. For even larger h, rotates back, first in the direction of the normal to the Fe3 plane and then further toward the positive y axis, with almost linearly decreasing until ° is reached at Å. Finally, this is followed by an increase toward ° at Å. In the case of Fe3Ir, the orientation dependence is far smoother. Starting from ° at Å, gradually rotates toward the negative y axis reaching ° at Å, i.e., almost parallel to the negative y axis. Subsequently, reorients itself toward the z axis and beyond it, until ° is reached at Å. At even larger h, rotates again approaching the normal to the Fe3 plane with ° at Å. In summary, both the absolute value as well as the orientation of exhibit non-monotonous behaviors as a function of h. Therefore, they open the most interesting possibilities of manipulating the chirality in a magnetic nanostructure.
5. Conclusions
The chirality of the magnetic interactions between Fe atoms in Fe2X and Fe3X clusters with X = Cu, Pd, Pt, and Ir has been investigated in the framework of density-functional theory. In Fe2X clusters, the adatoms trigger the DM interaction by breaking the inversion symmetry of the dimer, thereby unraveling a rich variety of chiral magnetic behaviors that strongly depend on the nature of the adatom as well as on their distance to the Fe atoms. Three different local and gradient-corrected approximations to the exchange and correlation functional have been considered, which yield qualitatively very similar trends, as well some significant quantitative differences. The microscopic origin of the adatom-induced DM coupling has been investigated by computing the contributions of the different atoms to the chirality of the spin-orbit energy in Fe2X. The results show that the DM couplings originate primarily on the spin-orbit energy of the adatoms, even in the case of a light atom such as Cu, which has a complete d shell. These trends are consistent with previous interpretations of the DM couplings as the result of indirect interactions with heavy open-d-shell atoms [9].
Adatoms showing stronger spin-orbit coupling generally result in stronger and more interesting DM couplings. Furthermore, the d-band filling of the adatom has also been found to be a most relevant parameter for controlling the chiral magnetic properties of the clusters. In fact, the strength of spin-orbit coupling alone is not enough in order to define the significance of the symmetry breaking effect. In particular, we have found that increasing the number of d holes upon changing Pt by Ir results in stronger and more complex DM interactions. Comparison between the symmetric and antisymmetric Fe-Fe couplings in Fe2X shows that the DM couplings are about two orders of magnitude weaker than the isotropic Heisenberg interactions. However, they are in general stronger and more sensitive to dimer-adatom hybridizations than the anisotropy of the symmetric couplings.
The results reported in this work motivate further investigations on larger clusters and nanoalloys in order to understand the size and environment dependence of the DM interaction. The role of cluster symmetry and the possibilities of tuning it by means of alloying should be particularly emphasized. Furthermore, in order to stress the role of the d-band filling, it is interesting to expand the investigation to other magnetic transition metals, for example, Ni, Co, Mn, and Cr. In particular, Mn and Cr, with a nearly half-filled d-band, are promising candidates for an exceptionally strong DM coupling [13]. Finally, a more thorough analysis of the anisotropy of the magnetic interactions in small clusters requires the examination of all contributions to the interaction energy, including the symmetric and thus nonchiral interactions and for different adatoms. Using these ab initio-derived interactions in the framework of phenomenological spin models, it would be possible to investigate the magnetic energy landscapes of the clusters, including metastable magnetic configurations as well as the relevant transition states connecting them. In this way, a quantitative material specific study of dynamical processes such as magnetic relaxation and magnetization reversals would be possible.
Author Contributions
B.J., S.R. and G.M.P. have contributed equally to all parts of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Computer resources provided by the IT Service Center of the University of Kassel and by the Center for Scientific Computing of the University of Frankfurt are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bansmann, J.; Baker, S.H.; Binns, C.; Blackman, J.A.; Bucher, J.P.; Dorantes-Dávila, J.; Dupuis, V.; Favre, L.; Kechrakos, D.; Kleibert, A.; et al. Magnetic and Structural Properties of Isolated and Assembled Clusters. Surf. Sci. Rep. 2005, 56, 189–275. [Google Scholar] [CrossRef]
- Pastor, G.M.; Dorantes-Dávila, J.; Pick, S.; Dreyssé, H. Magnetic Anisotropy of 3d Transition-Metal Clusters. Phys. Rev. Lett. 1995, 75, 326–329. [Google Scholar] [CrossRef]
- Dorantes-Dávila, J.; Pastor, G.M. Magnetic Anisotropy of One-Dimensional Nanostructures of Transition Metals. Phys. Rev. Lett. 1998, 81, 208–211. [Google Scholar] [CrossRef]
- Lau, J.T.; Föhlisch, A.; Nietubyc, R.; Reif, M.; Wurth, W. Size-Dependent Magnetism of Deposited Small Iron Clusters Studied by X-Ray Magnetic Circular Dichroism. Phys. Rev. Lett. 2002, 89, 057201. [Google Scholar] [CrossRef]
- Gambardella, P.; Dallmeyer, A.; Maiti, K.; Malagoli, M.C.; Eberhardt, W.; Kern, K.; Carbone, C. Ferromagnetism in One-Dimensional Monatomic Metal Chains. Nature 2002, 416, 301–304. [Google Scholar] [CrossRef]
- Gambardella, P.; Rusponi, S.; Veronese, M.; Dhesi, S.S.; Grazioli, C.; Dallmeyer, A.; Cabria, I.; Zeller, R.; Dederichs, P.H.; Kern, K.; et al. Giant Magnetic Anisotropy of Single Cobalt Atoms and Nanoparticles. Science 2003, 300, 1130–1133. [Google Scholar] [CrossRef]
- Dorantes-Dávila, J. Magnetic Reorientation Transitions along the Crossover from One-Dimensional to Two-Dimensional Transition-Metal Nanostructures. Phys. Rev. B 2005, 72, 085427. [Google Scholar] [CrossRef]
- Berger, L.; Labaye, Y.; Tamine, M.; Coey, J.M.D. Ferromagnetic Nanoparticles with Strong Surface Anisotropy: Spin Structures and Magnetization Processes. Phys. Rev. B 2008, 77, 104431. [Google Scholar] [CrossRef]
- Fert, A.; Levy, P.M. Role of Anisotropic Exchange Interactions in Determining the Properties of Spin-Glasses. Phys. Rev. Lett. 1980, 44, 1538–1541. [Google Scholar] [CrossRef]
- Bode, M.; Heide, M.; von Bergmann, K.; Ferriani, P.; Heinze, S.; Bihlmayer, G.; Kubetzka, A.; Pietzsch, O.; Blügel, S.; Wiesendanger, R. Chiral Magnetic Order at Surfaces Driven by Inversion Asymmetry. Nature 2007, 447, 190–193. [Google Scholar] [CrossRef]
- Kashid, V.; Schena, T.; Zimmermann, B.; Mokrousov, Y.; Blügel, S.; Shah, V.; Salunke, H.G. Dzyaloshinskii-Moriya Interaction and Chiral Magnetism in 3d–5d Zigzag Chains: Tight-binding Model and ab initio Calculations. Phys. Rev. B 2014, 90, 054412. [Google Scholar] [CrossRef]
- Yang, H.; Thiaville, A.; Rohart, S.; Fert, A.; Chshiev, M. Anatomy of Dzyaloshinskii-Moriya Interaction at Co/Pt Interfaces. Phys. Rev. Lett. 2015, 115, 267210. [Google Scholar] [CrossRef]
- Belabbes, A.; Bihlmayer, G.; Bechstedt, F.; Blügel, S.; Manchon, A. Hund’s Rule-Driven Dzyaloshinskii-Moriya Interaction at 3d-5d Interfaces. Phys. Rev. Lett. 2016, 117, 247202. [Google Scholar] [CrossRef]
- Zitoun, D.; Respaud, M.; Fromen, M.C.; Casanove, M.J.; Lecante, P.; Amiens, C.; Chaudret, B. Magnetic Enhancement in Nanoscale CoRh Particles. Phys. Rev. Lett. 2002, 89, 037203. [Google Scholar] [CrossRef]
- Antoniak, C.; Lindner, J.; Spasova, M.; Sudfeld, D.; Acet, M.; Farle, M.; Fauth, K.; Wiedwald, U.; Boyen, H.G.; Ziemann, P.; et al. Enhanced Orbital Magnetism in Fe50Pt50 Nanoparticles. Phys. Rev. Lett. 2006, 97, 117201. [Google Scholar] [CrossRef]
- Fromen, M.C.; Morillo, J.; Casanove, M.J.; Lecante, P. Structure and Chemical Order in Co–Rh Nanoparticles. EPL 2006, 73, 885. [Google Scholar] [CrossRef]
- Yin, S.; Moro, R.; Xu, X.; de Heer, W.A. Magnetic Enhancement in Cobalt-Manganese Alloy Clusters. Phys. Rev. Lett. 2007, 98, 113401. [Google Scholar] [CrossRef]
- Tournus, F.; Tamion, A.; Blanc, N.; Hannour, A.; Bardotti, L.; Prével, B.; Ohresser, P.; Bonet, E.; Epicier, T.; Dupuis, V. Evidence of L10 Chemical Order in CoPt Nanoclusters: Direct Observation and Magnetic Signature. Phys. Rev. B 2008, 77, 144411. [Google Scholar] [CrossRef]
- Wang, R.M.; Dmitrieva, O.; Farle, M.; Dumpich, G.; Ye, H.Q.; Poppa, H.; Kilaas, R.; Kisielowski, C. Layer Resolved Structural Relaxation at the Surface of Magnetic FePt Icosahedral Nanoparticles. Phys. Rev. Lett. 2008, 100, 017205. [Google Scholar] [CrossRef]
- Gruner, M.E.; Rollmann, G.; Entel, P.; Farle, M. Multiply Twinned Morphologies of FePt and CoPt Nanoparticles. Phys. Rev. Lett. 2008, 100, 087203. [Google Scholar] [CrossRef]
- Muñoz-Navia, M.; Dorantes-Dávila, J.; Zitoun, D.; Amiens, C.; Chaudret, B.; Casanove, M.J.; Lecante, P.; Jaouen, N.; Rogalev, A.; Respaud, M.; et al. Magnetic Properties of CoNRhM Nanoparticles: Experiment and Theory. Faraday Discuss. 2008, 138, 181–192. [Google Scholar] [CrossRef]
- Muñoz-Navia, M.; Dorantes-Dávila, J.; Zitoun, D.; Amiens, C.; Jaouen, N.; Rogalev, A.; Respaud, M.; Pastor, G.M. Tailoring the Magnetic Anisotropy in CoRh Nanoalloys. Appl. Phys. Lett. 2009, 95, 233107. [Google Scholar] [CrossRef]
- Muñoz-Navia, M.; Dorantes-Dávila, J.; Respaud, M.; Pastor, G.M. Theoretical Study of the Magnetic Moments and Anisotropy Energy of CoRh Nanoparticles. Eur. Phys. J. D 2009, 52, 171–174. [Google Scholar] [CrossRef]
- Entel, P.; Gruner, M.E. Large-Scale ab initio simulations of Binary Transition Metal Clusters for Storage Media Materials. J. Phys. Condens. Matter 2009, 21, 064228. [Google Scholar] [CrossRef]
- Tournus, F.; Blanc, N.; Tamion, A.; Hillenkamp, M.; Dupuis, V. Dispersion of Magnetic Anisotropy in Size-Selected CoPt Clusters. Phys. Rev. B 2010, 81, 220405. [Google Scholar] [CrossRef]
- Mokkath, J.H.; Pastor, G.M. First-Principles Study of Structural, Magnetic, and Electronic Properties of Small Fe-Rh Alloy Clusters. Phys. Rev. B 2012, 85, 054407. [Google Scholar] [CrossRef]
- Mokkath, J.H.; Pastor, G.M. Interplay between Chemical and Magnetic Order in FeRh Clusters. J. Phys. Chem. C 2012, 116, 17228–17238. [Google Scholar] [CrossRef]
- Negulyaev, N.N.; Dorantes-Dávila, J.; Niebergall, L.; Juárez-Reyes, L.; Pastor, G.M.; Stepanyuk, V.S. Alloying Route to Tailor Giant Magnetic Anisotropy in Transition-Metal Nanowires. Phys. Rev. B 2013, 87, 054425. [Google Scholar] [CrossRef]
- Ferriani, P.; von Bergmann, K.; Vedmedenko, E.Y.; Heinze, S.; Bode, M.; Heide, M.; Bihlmayer, G.; Blügel, S.; Wiesendanger, R. Atomic-Scale Spin Spiral with a Unique Rotational Sense: Mn Monolayer on W(001). Phys. Rev. Lett. 2008, 101, 027201. [Google Scholar] [CrossRef]
- Menzel, M.; Mokrousov, Y.; Wieser, R.; Bickel, J.E.; Vedmedenko, E.; Blügel, S.; Heinze, S.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Information Transfer by Vector Spin Chirality in Finite Magnetic Chains. Phys. Rev. Lett. 2012, 108, 197204. [Google Scholar] [CrossRef]
- Polesya, S.; Mankovsky, S.; Bornemann, S.; Ködderitzsch, D.; Minár, J.; Ebert, H. Skyrmion Magnetic Structure of an Ordered FePt Monolayer Deposited on Pt(111). Phys. Rev. B 2014, 89, 184414. [Google Scholar] [CrossRef]
- Khajetoorians, A.A.; Steinbrecher, M.; Ternes, M.; Bouhassoune, M.; dos Santos Dias, M.; Lounis, S.; Wiebe, J.; Wiesendanger, R. Tailoring the Chiral Magnetic Interaction between Two Individual Atoms. Nat. Commun. 2016, 7, 10620. [Google Scholar] [CrossRef]
- Nandy, A.K.; Kiselev, N.S.; Blügel, S. Interlayer Exchange Coupling: A General Scheme Turning Chiral Magnets into Magnetic Multilayers Carrying Atomic-Scale Skyrmions. Phys. Rev. Lett. 2016, 116, 177202. [Google Scholar] [CrossRef]
- Zimmermann, B.; Legrand, W.; Maccariello, D.; Reyren, N.; Cros, V.; Blügel, S.; Fert, A. Dzyaloshinskii-Moriya Interaction at Disordered Interfaces from ab initio Theory: Robustness against Intermixing and Tunability through Dusting. Appl. Phys. Lett. 2018, 113, 232403. [Google Scholar] [CrossRef]
- Meyer, S.; Perini, M.; von Malottki, S.; Kubetzka, A.; Wiesendanger, R.; von Bergmann, K.; Heinze, S. Isolated Zero Field Sub-10 nm Skyrmions in Ultrathin Co Films. Nat. Commun. 2019, 10, 3823. [Google Scholar] [CrossRef]
- Lászlóffy, A.; Rózsa, L.; Palotás, K.; Udvardi, L.; Szunyogh, L. Magnetic Structure of Monatomic Fe Chains on Re(0001): Emergence of Chiral Multispin Interactions. Phys. Rev. B 2019, 99, 184430. [Google Scholar] [CrossRef]
- Jadaun, P.; Register, L.F.; Banerjee, S.K. The Microscopic Origin of DMI in Magnetic Bilayers and Prediction of Giant DMI in New Bilayers. NPJ Comput. Mater. 2020, 6, 1–6. [Google Scholar] [CrossRef]
- Mahfouzi, F.; Kioussis, N. First-Principles Calculation of the Dzyaloshinskii-Moriya Interaction: A Green’s Function Approach. Phys. Rev. B 2021, 103, 094410. [Google Scholar] [CrossRef]
- Smith, D.A. New mechanisms for magnetic anisotropy in localised S-state moment materials. J. Magn. Magn. Mater. 1976, 1, 214–225. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Zimmermann, B.; Heide, M.; Bihlmayer, G.; Blügel, S. First-Principles Analysis of a Homochiral Cycloidal Magnetic Structure in a Monolayer Cr on W(110). Phys. Rev. B 2014, 90, 115427. [Google Scholar] [CrossRef]
- Perini, M.; Meyer, S.; Dupé, B.; von Malottki, S.; Kubetzka, A.; von Bergmann, K.; Wiesendanger, R.; Heinze, S. Domain Walls and Dzyaloshinskii-Moriya Interaction in Epitaxial Co/Ir(111) and Pt/Co/Ir(111). Phys. Rev. B 2018, 97, 184425. [Google Scholar] [CrossRef]
- Perini, M.; Meyer, S.; Kubetzka, A.; Wiesendanger, R.; Heinze, S.; von Bergmann, K. Electrical Detection of Domain Walls and Skyrmions in Co Films Using Noncollinear Magnetoresistance. Phys. Rev. Lett. 2019, 123, 237205. [Google Scholar] [CrossRef]
- Meyer, S.; Schmitt, M.; Vogt, M.; Bode, M.; Heinze, S. Dead Magnetic Layers at the Interface: Moment Quenching through Hybridization and Frustration. Phys. Rev. Res. 2020, 2, 012075. [Google Scholar] [CrossRef]
- Spethmann, J.; Meyer, S.; von Bergmann, K.; Wiesendanger, R.; Heinze, S.; Kubetzka, A. Discovery of Magnetic Single- and Triple-q States in Mn/Re(0001). Phys. Rev. Lett. 2020, 124, 227203. [Google Scholar] [CrossRef] [PubMed]
- Yanes, R.; Chubykalo-Fesenko, O.; Kachkachi, H.; Garanin, D.A.; Evans, R.; Chantrell, R.W. Effective Anisotropies and Energy Barriers of Magnetic Nanoparticles with Néel Surface Anisotropy. Phys. Rev. B 2007, 76, 064416. [Google Scholar] [CrossRef]
- Udvardi, L.; Szunyogh, L.; Palotás, K.; Weinberger, P. First-Principles Relativistic Study of Spin Waves in Thin Magnetic Films. Phys. Rev. B 2003, 68, 104436. [Google Scholar] [CrossRef]
- Michaud, F.; Mila, F. Phase Diagram of the Spin-1 Heisenberg Model with Three-Site Interactions on the Square Lattice. Phys. Rev. B 2013, 88, 094435. [Google Scholar] [CrossRef]
- Krönlein, A.; Schmitt, M.; Hoffmann, M.; Kemmer, J.; Seubert, N.; Vogt, M.; Küspert, J.; Böhme, M.; Alonazi, B.; Kügel, J.; et al. Magnetic Ground State Stabilized by Three-Site Interactions: Fe/Rh(111). Phys. Rev. Lett. 2018, 120, 207202. [Google Scholar] [CrossRef] [PubMed]
- Harada, K.; Kawashima, N. Quadrupolar Order in Isotropic Heisenberg Models with Biquadratic Interaction. Phys. Rev. B 2002, 65, 052403. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A Thermodynamic Theory of “Weak” Ferromagnetism of Antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Keffer, F. Moriya Interaction and the Problem of the Spin Arrangements in βMnS. Phys. Rev. 1962, 126, 896–900. [Google Scholar] [CrossRef]
- Moriya, T. New Mechanism of Anisotropic Superexchange Interaction. Phys. Rev. Lett. 1960, 4, 228–230. [Google Scholar] [CrossRef]
- Gyorffy, B.L.; Pindor, A.J.; Staunton, J.; Stocks, G.M.; Winter, H. A First-Principles Theory of Ferromagnetic Phase Transitions in Metals. J. Phys. F Met. Phys. 1985, 15, 1337. [Google Scholar] [CrossRef]
- Thomas, L.; Parkin, S. Current Induced Domain-Wall Motion in Magnetic Nanowires in Handbook of Magnetism and Advanced Magnetic Materials, Vol. 2: Micromagnetism; Kronmüller, H., Parkin, S., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2007; pp. 942–982. [Google Scholar]
- Garibay-Alonso, R.; Dorantes-Dávila, J.; Pastor, G.M. Temperature-Dependent Magnetic Properties of Ultrathin Fe Films: Interplay between Local Environment and Itinerant Ferromagnetism. Phys. Rev. B 2006, 73, 224429. [Google Scholar] [CrossRef]
- Töws, W.; Pastor, G.M. Theoretical Study of the Temperature Dependence of the Magnon Dispersion Relation in Transition-Metal Wires and Monolayers. Phys. Rev. B 2012, 86, 054443. [Google Scholar] [CrossRef]
- Garibay-Alonso, R. Finite-Temperature Magnetism of Ni Monolayers: Interplay between Flips and Amplitude Fluctuations of the Local Moments. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Garibay-Alonso, R.; Dorantes-Dávila, J.; Pastor, G.M. Noncollinear Spin-Fluctuation Theory of Transition-Metal Magnetism: Role of Transverse Spin Fluctuations in Fe. Phys. Rev. B 2015, 91, 184408. [Google Scholar] [CrossRef]
- Riemer, S.; Dorantes-Dávila, J.; Pastor, G.M. Finite Temperature Magnetic Properties of Small Fe Chains and Clusters on Pt(111). Phys. Rev. B 2016, 93, 134414. [Google Scholar] [CrossRef]
- Tanveer, M.; Ruiz-Díaz, P.; Pastor, G.M. Electronic and Magnetic Properties of Spiral Spin-Density-Wave States in Transition-Metal Chains. Phys. Rev. B 2016, 94, 094403. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for ab initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1930; Volume 26, pp. 376–385. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Wang, Y.; Perdew, J.P. Correlation Hole of the Spin-Polarized Electron Gas, with Exact Small-Wave-Vector and High-Density Scaling. Phys. Rev. B 1991, 44, 13298–13307. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Hobbs, D.; Kresse, G.; Hafner, J. Fully Unconstrained Noncollinear Magnetism within the Projector Augmented-Wave Method. Phys. Rev. B 2000, 62, 11556–11570. [Google Scholar] [CrossRef]
- Haynes, P.D.; Payne, M.C. Corrected Penalty-Functional Method for Linear-Scaling Calculations within Density-Functional Theory. Phys. Rev. B 1999, 59, 12173–12176. [Google Scholar] [CrossRef]
- Steiner, S.; Khmelevskyi, S.; Marsmann, M.; Kresse, G. Calculation of the Magnetic Anisotropy with Projected-Augmented-Wave Methodology and the Case Study of Disordered Fe1−xCox Alloys. Phys. Rev. B 2016, 93, 224425. [Google Scholar] [CrossRef]
- Pastor, G.M.; Dorantes-Dávila, J.; Bennemann, K.H. Spin-fluctuation energies in transition-metal clusters. Phys. Rev. B 2004, 70, 064420. [Google Scholar] [CrossRef]
- Garibay-Alonso, R.; Dorantes-Dávila, J.; Pastor, G.M. Electronic spin-fluctuation theory of finite-temperature cluster magnetism: Size and environment dependence in FeN. Phys. Rev. B 2009, 79, 134401. [Google Scholar] [CrossRef]
- Pastor, G.M.; Dorantes-Dávila, J.; Bennemann, K.H. Size and structural dependence of the magnetic properties of small 3d-transition-metal clusters. Phys. Rev. B 1989, 40, 7642–7654. [Google Scholar] [CrossRef] [PubMed]
- Meyer, S. Complex Spin Structures in Frustrated Ultrathin Films. Ph.D. Thesis, Institut für Theoretische Physik und Astrophysik, Mathematisch-Naturwissenschaftliche Fakultät, Christian-Albrechts-Universität zu Kiel, Kiel, Germany, 2020. Available online: https://macau.uni-kiel.de/receive/macau_mods_00000764 (accessed on 8 December 2022).
- Riemer, S. Electronic Theory of the Magnetic Order, Anisotropy and Reversal Processes in Rolled-Up Stripes and Thin Films. Ph.D. Thesis, Institut für Physik, Fachbereich Mathematik und Naturwissenschaften, Universität Kassel, Kassel, Germany, 2022. [Google Scholar]
- Meyer, S.; Xu, B.; Verstraete, M.; Bellaiche, L.; Dupé, B. Spin-Current Driven Dzyaloshinskii-Moriya Interaction in the Multiferroic BiFeO3 from First-Principles. arXiv 2022, arXiv:2210.15591. [Google Scholar]
- Nembach, H.T.; Shaw, J.M.; Weiler, M.; Jué, E.; Silva, T.J. Linear Relation between Heisenberg Exchange and Interfacial Dzyaloshinskii–Moriya Interaction in Metal Films. Nat. Phys. 2015, 11, 825–829. [Google Scholar] [CrossRef]
- Meyer, S.; Dupé, B.; Ferriani, P.; Heinze, S. Dzyaloshinskii-Moriya Interaction at an Antiferromagnetic Interface: First-principles Study of Fe/Ir Bilayers on Rh(001). Phys. Rev. B 2017, 96, 094408. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).