Abstract
The cross fusion of quantum mechanics and information science forms quantum information science. Quantum logic gates and quantum entanglement are very important building blocks in quantum information processing. In this paper, we propose one-step schemes for realizing quantum swap gates and generating two-mode entangled coherent states via circuit QED. In our scheme, due to the adiabatic elimination of the excited state of the qutrit under the condition of large detuning, the decoherence of the spontaneous emission of the qutrit can be ignored. The fidelity of the quantum swap gate remains at a very high level. In addition, we also explore the nonclassical properties of two-mode entangled coherent states prepared in our scheme by addressing the second-order correlation function and intermodal squeezing. In particular, two classes of entangled coherent states demonstrate distinct entanglement and nonclassical behavior.
1. Introduction
Quantum information processing has been one of the most exciting disciplines in recent years, with astonishing achievements in the independent manipulation of individual atoms, photons, ions, and magnons [1,2,3,4,5,6,7,8,9]. Quantum information processing has greatly changed the concept of information processing and attracted the enthusiasm of many researchers [10,11,12,13,14,15,16,17,18]. Various different physical systems have been proposed as suitable candidates for implementing quantum information processing in recent years, such as cavity quantum electrodynamics (CQED) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] and circuit quantum electrodynamics (QED) [19,20,21,22,23,24,25]. Circuit QED, such as superconducting devices, can be easily fabricated to implement large-scale quantum computing and have been demonstrated to have a relatively long decoherence time; the solid-state qubits play an important role in building quantum computers and entanglement. Strikingly, circuit QED exhibits an unprecedented level of flexibility, scalability, and tunability, specifically concerning its improvements in coherence time [19,20,21,22,23,24,25]. As a result, we also focus on circuit QED systems to implement quantum information processing tasks.
Circuit QED mainly studies the interaction of artificial atoms with microwave photons stored in resonators, and is an analog of cavity QED [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. In the context of circuit QED, artificial atoms usually refer to superconducting or other solid quantum qubits; the microwave resonators, which are comprised of superconducting quantum circuits and can provide a simple and reliable way for the manipulation and measurement of superconducting qubits, have been considered good memory elements in quantum information processing. The simplest circuit QED system consists of a single superconducting qubit coupled to a microwave resonator. This system is a specially suited platform to achieve quantum computation and quantum information processing and has allowed the realization of strong, ultrastrong, and beyond ultrastrong coupling between a superconducting qubit and a microwave resonator [26,27,28,29,30,31,32,33,34,35,36,37,38]. Circuit QED has the following advantages over cavity QED: (i) The dipole moment of a superconducting qubit is four orders of magnitude larger than that of an atom. Moreover, the size of the superconducting resonator is small and can have the strength of a large vacuum field. Therefore, the circuit QED can easily achieve strong coupling experimentally. (ii) Circuit QED has excellent integration and scalability. This is because it uses photolithographic microfabrication, which allows multiple superconducting qubits to be pinned into a single superconducting resonator. (iii) The circuit QED can significantly improve the coherence time of the qubits. This is because the superconducting resonator can effectively suppress the influence of the electromagnetic noise caused by the environment on the superconducting qubits in the resonator [26,27,28,29,30,31,32,33,34,35,36,37,38].
It has two important basic elements, such as entangled states and quantum logic gates, among more sophisticated quantum circuits and communication protocols. Here, we proposed an alternative scheme to realize a quantum swap gate and generate entangled coherent states using a qutrit to induce the effective interaction of two resonators. The operations of our model only involve the two lower states of the circuit QED system. Therefore, the operations are not affected by decoherence due to spontaneous emission of the upper state [26,27,28,29,30,31,32,33,34,35,36,37,38]. The quantum swap gate can be directly realized using a single step, which can reduce the number of unitary operations required to save quantum resources in actual quantum information processing. The fidelity of the quantum swap gate is very high in the existence of cavity dissipation. In addition, our model can be extended to prepare two-mode entangled coherent states in circuit QED, and we analyze the entangled and nonclassical properties of entangled coherent states. Furthermore, one of the favorable features of our scheme is that the structure is very simple and is feasible with the current experimental condition [26,27,28,29,30,31,32,33,34,35,36,37,38].
2. Swap Gate for Photonic Qubits
The concrete qutrit level structure and corresponding transitions are shown in Figure 1. Consider a system consisting of two superconducting circuit (SC) coplanar waveguide resonators connected by a -type SC flux qutrit (coupler) (Figure 1b). The resonators (Figure 1a) are dispersively coupled to the transitions and , with the coupling strengths being and and the detunings being and The classical fields (relevant frequencies are and ) drive, off-resonantly, the energy transitions and with Rabi frequencies and The Hamiltonian of the whole system, assuming , is written as
where is the free part, describes the resonator interacting with the qutrit, and is the Hamiltonian between the qutrit and classical fields. Here, and are the annihilation operators associated with the two resonators, respectively. In the following, we assume that and are real numbers for simplicity. Then, the Hamiltonian of the qutrit interacting with the resonators and the classical field in the interaction picture is [39,40,41,42,43]
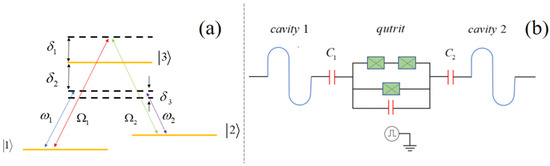
Figure 1.
(a) The concrete qutrit level structure and corresponding transitions.; (b) SC coplanar waveguide resonators connected by a -type SC flux qutrit (coupler).
Under the large detuning conditions that and the excited level can be adiabatically eliminated and can be replaced by the following Hamiltonian
where and The first two terms describe the photon-number-dependent Stark shifts, while the latter terms describe the Raman coupling. The parameters were appropriately adjusted so that Then, Introducing the new dressed state basis and projection operators and [44], and then performing a unitary transformation on i.e., we can obtain an effective Hamiltonian
Under the condition we can neglect the fast oscillating terms. Then, is reduced to
Performing the further unitary transformation on this Hamiltonian, it can be further simplified to
with The parameter must be chosen appropriately, so that Then, we have [40]
Assume that the qutrit is initially in the state which is the eigenstate of the qutrit operator with the eigenvalue 1. Then, the qutrit state remains unchanged, and the resonator field state is decoupled with the qutrit part. In this case, the effective Hamiltonian describes the evolution of the resonator field as
Using such a Hamiltonian, we can realize swap gate operation very conveniently. For this purpose, we take our initial field of the bimodal resonator to be in Fock states, i.e., , and the time evolution of the whole system can easily be expressed as where we have defined The operator directly acts on the two-mode Fock state of the resonators. This will lead to
Supposing that or initially, after the interaction time , we can realize the swap gate for a photonic qubit using the operator of as follows
It is worth noting that the non-standardized phase factors can be eliminated by appropriately setting the phases of subsequent logic operations. In the above analysis, we did not take into account the influence of decoherence on the scheme. The main decoherence channels in circuit QED commonly arise from upper state spontaneous emission and resonator decay. In our scheme, the excited level does not participate in the qutrit–resonator interaction due to the large detuning. Therefore, the adverse effect of the spontaneous emission from the upper state can be ignored. However, in order to realize the swap gate, the two coherent states in two modes must exchange their information; thus, the resonator decay may be the important noise source in the gate operation [40,41,42]. When considering the decay of the resonator, the master equation of the system is described by In order to check the validity of the scheme, we provide the evolution of the system and calculate the fidelity of the gate operation by using a numerical calculation. The fidelity is given by:
where is the actual output state under dissipation according to the master equation, and is the output state of an ideal system without decay. For the initial state of the system , we plot the fidelity of the photonic qutrit phase gate vs , as shown in Figure 2. From that, it can be seen that the gate fidelity monotonically drops when grows during the gate implementation. However, the fidelity exceeds 99.8% when is smaller than 0.1.
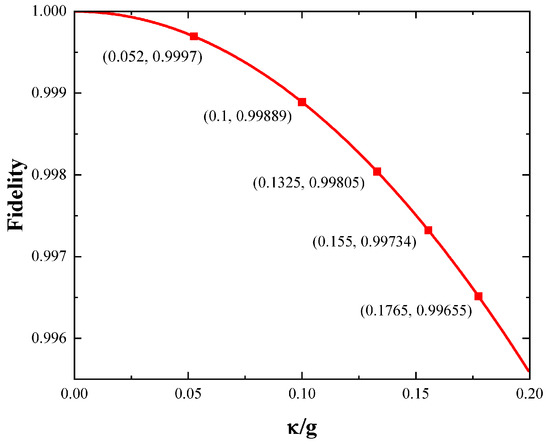
Figure 2.
Fidelity of swap gate vs where .
3. Preparation of Entangled Coherent State
Quantum superposition represents the state obtained by numerous possible linear combinations of several quantum states of a quantum system and involves the uncertainty of a particle (or multiple particles) being in multiple states at the same time. A quantum entanglement state originating from quantum superposition is a special kind of quantum state that describes, by definition, a composite system (with two or more member systems), and this quantum state cannot be decomposed into the direct product of the respective quantum states of the member systems. There is no way to write the entangled state as a direct product of each individual state. Therefore, entangled states composited by different particles are not independent of each other. For example, in an entangled state, particle A cannot be described independently of particle B, due to the fact that A and B are strongly correlated with each other. The essence of quantum entanglement is the interference superposition of quantum fluctuations. From the viewpoint of a wave, the quantum system in entanglement is a quantum superposition state. In the view of particle property, the entangled system shows that the members correlate with each other and are nonseparable. In this sense, quantum entanglement is a kind of quantum superposition state, which cannot be written as a direct product of partial particle states. However, the converse is not true. After all, there are several quantum superposition states that can be written as the direct product of member systems; they are the separable quantum state. The entangled coherent states, which are continuous variable entangled states, play an important role in quantum information. They are not only helpful for quantum mechanics to prevail over the local hidden theory, but are also valuable in quantum information processes (quantum teleportation, [6] quantum dense coding, and quantum cryptography).
In this section, we consider using the above Hamiltonian to prepare a two-mode entangled coherent state. When resonator a is initially prepared in the normalized symmetric or antisymmetric superposition state of two coherent states (the normalization factors are ), the other resonator is in a vacuum state . Thus, the initial state of the system can be expressed as After an interaction time t, the state evolves into
Using the concept of concurrence for bipartite entangled nonorthogonal states, the concurrence of the final state can be calculated as [31,45,46,47]
In order to observe how the system parameters affect concurrence, we performed numerical simulations for the influence of the initial state parameter and effective coupling strength . In Figure 3, we have plotted the concurrence with respect to dimensionless time , which indicates the concurrence of the antisymmetric superposition state of two coherent states can reach a maximum value of 1 with a different . From Figure 3, we can see that concurrence of the symmetric superposition state of two coherent states is very small, with while the maximum value of concurrence will heighten with increasing values of , even nearing 1 when The relation between the concurrence of a symmetric or antisymmetric superposition state and dimensionless time , with different values, can be shown in Figure 4. We find that different coupling constants will affect the period of concurrence; the larger the coupling constant, the shorter the period for a fixed The concurrence of the antisymmetric superposition state of two coherent states is usually bigger than the symmetric case. In fact, after a straightforward calculation, we found that when the evolution time (where ) and the reach the unit, the maximally entangled antisymmetric superposition state of two coherent states can be obtained with a random [31]. Nevertheless, for the symmetric superposition state of two coherent states, the rises with the increase in [31]. As is known to all, for a realistic quantum system, system decay plays an important role. In this sense, we make a direct numerical calculation when taking into account the decay of the cavity modes. From Figure 5, it can be observed that concurrence decreases fast while increases; the larger the decay coefficient, the smaller the concurrence; and the symmetric and antisymmetric superposition states of two coherent states show no significant difference. Obviously, after considering the decay, the concurrences of both the symmetric and antisymmetric superposition states cannot reach 1. The maximum value of the antisymmetric superposition state is only 0.8, indicating that the decay has a very large impact on the degree of entanglement.
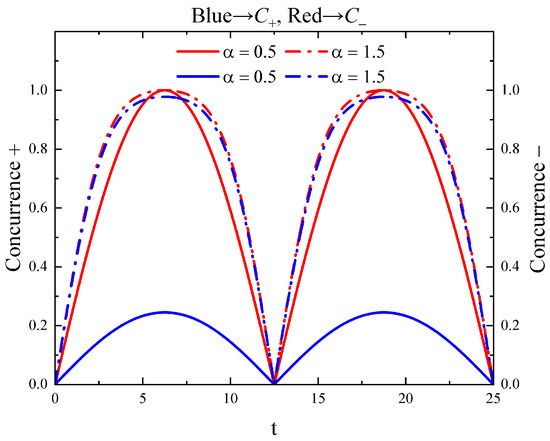
Figure 3.
Concurrence versus dimensionless time t for .
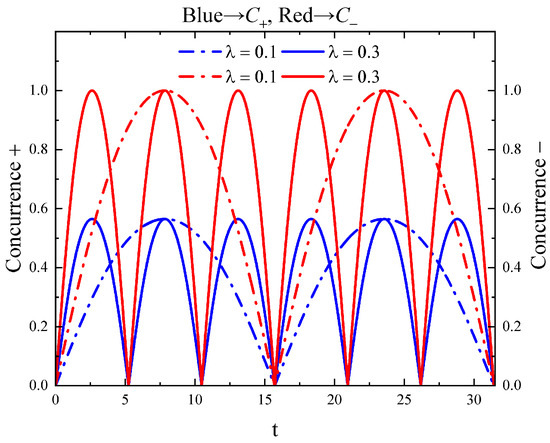
Figure 4.
Concurrence versus dimensionless time t for .
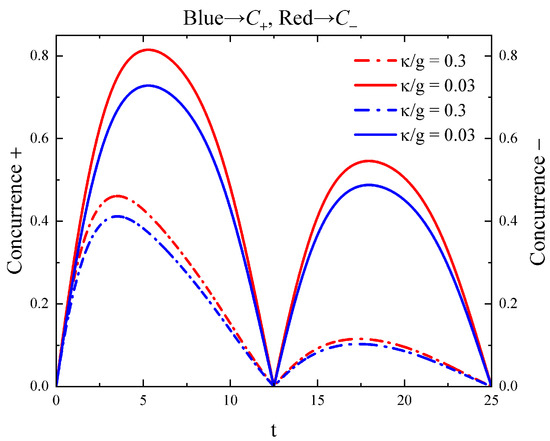
Figure 5.
Concurrence versus dimensionless time t for .
4. Criteria of Nonclassicality
The nonclassicality of optical fields has been a hot topic in the development of quantum optics and quantum information processing [37,38]. Usually, the nonclassicality manifests itself in specific properties of quantum statistics, such as antibunching, sub-Poissonian photon statistics, squeezing in one of the quadratures, etc. In recent years, people extensively know that it is the principle of superposition in quantum mechanics that produces various kinds of non-classical effects of quantum states. From the perspective of quantum optics, there are different witnesses of the nonclassicality of the radiation field. For example, single and multimode squeezing conditions reveal the nonclassical character of a state due to field fluctuation [48,49,50,51,52,53,54,55,56,57,58,59].
4.1. Antibunching
The antibunching effect is a remarkable manifestation of nonclassicality. With the second-order correlation function, one can distinguish between the possibly different statistical regimes. In particular, < 0 means photons do not like to be together and tend to separate or emerge in different places. > 0 means photons are inclined to come in flocks, and tend to stay in the same place, = 0 implies photons are randomly distributed. We cannot seek out the orientation of a single photon. In other words, can reflect repulsive properties or attractive features of two photons. The second-order correlation function is defined as [60]
In order to clearly see the influence of system decay on the second-order correlation function, from Figure 6, Figure 7, Figure 8 and Figure 9, we have plotted the second-order correlation function with respect to dimensionless time for different decay coefficients, respectively. We can clearly see the bunching phenomena in Figure 6, and the antibunching effect in Figure 8. For the symmetric superposition state of two coherent states (Figure 6 and Figure 7), both the long time limit and short time limit, the photon bunching effect is mainly shown. When the decays are not too large, the red line displays an antibunching effect, although the probability is very small. The quantum statistical properties of the second-order correlation function become more complicated as shown below for the symmetric case. It is worth noting that may have an inflection, and the photon statistics may change slightly in the red line. This leads to an interesting phenomenon that can slightly trigger the photon statistics transition from the classical bunching to the antibunching effect. Not surprisingly, the antibunching effect of the two-mode field will decrease while the dissipation increases. Moreover, numerical calculations show that the antisymmetric superposition state of two coherent states only exhibits an antibunching effect, and of both cases will trend to close to 0 under long-term conditions with decay.
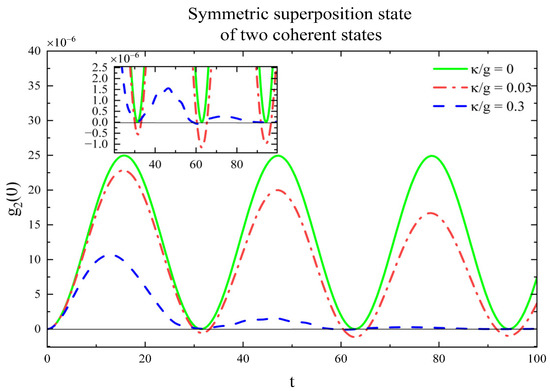
Figure 6.
Under short-term condition with respect to the parameter .
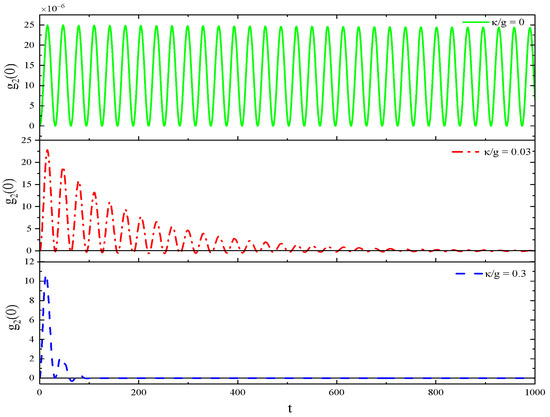
Figure 7.
Under long-term condition with respect to the parameter .
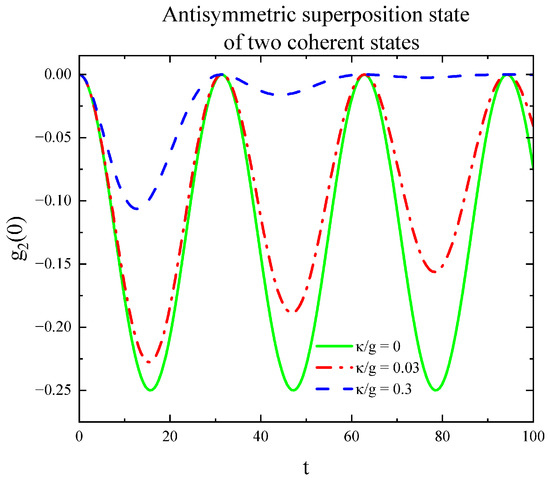
Figure 8.
Under short-term condition antibunching effect vs .
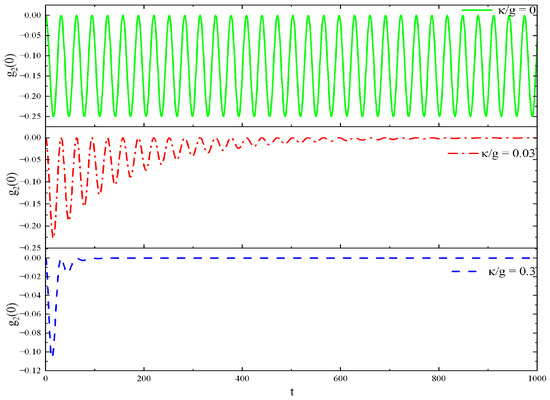
Figure 9.
Under long-term condition antibunching effect vs .
4.2. Squeezing
Squeezing is the key ingredient in measuring nonclassical light. In quantum theory, the squeezed effect is another non-classical phenomenon peculiar to the quantum light field [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. We know that the coherent state is the state where the amplitude fluctuation of the light field has the minimum uncertainty value, and its two orthogonal components both take the minimum uncertainty value of 1/4, which is usually called the vacuum fluctuation of the light field. The squeezed state reflects the non-classical characteristics of the light field by means of a noise level even lower than that of the coherent state light field (laser field). That is, the noise fluctuation of an orthogonal phase component in the squeezed light is lower than that of the corresponding orthogonal phase component in the laser field. Therefore, in practical applications, if this component is used to transmit information, the signal-to-noise ratio can be higher than that of the coherent state light field, which has broad application prospects in optical communication, weak signal detection, and quantum non-destructive measurement.
In order to attain the squeezing effect, which delineates the nonclassicality of a field in the context of the fluctuations in the quadratures and of the field, we have the intermodal quadrature operators, defined as [61]
The criteria for the nonclassical signature in the field are given in terms of the variances in the quadratures as follows:
We investigated the presence of intermodal squeezing using the criterion given in Equations (14) and (15). The outcome of the investigation is plotted in Figure 10 and Figure 11, which clearly show the existence of intermodal squeezing for the symmetric superposition state of two coherent states. From Figure 11, it is evident that squeezing is absent in the antisymmetric superposition state case. In other words, the antisymmetric superposition state of two coherent states does not exhibit two-mode quadrature squeezing, which is ascribed to variances in the quadratures where both X and Y are greater than 0.25. It is worth mentioning here that this is the exact opposite of a second-order correlation function, which exhibits a nonclassical property in the antisymmetric superposition state of two coherent states. On the other hand, the squeezing effect of the nonclassical property only appears when it is in the symmetric superposition state. From Figure 10, it is easy to observe that when will be bigger than 0.25, and vice versa. When taking into account the decay of the resonators, we find that the squeezing effect will decrease. However, variances in the quadratures of the antisymmetric superposition state of two coherent states will trend to approach 0.25 when .
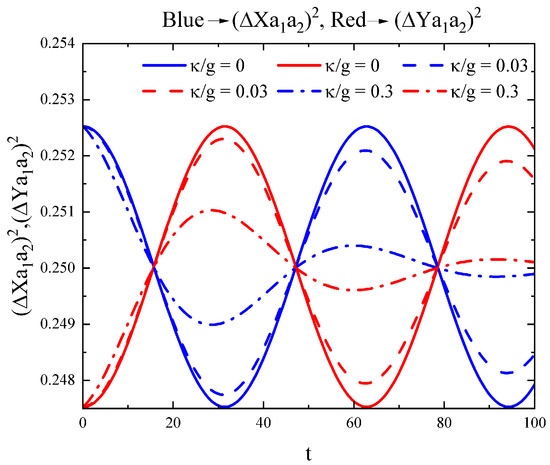
Figure 10.
Intermodal squeezing of the symmetric superposition state of two coherent states with respect to the dimensionless parameter .
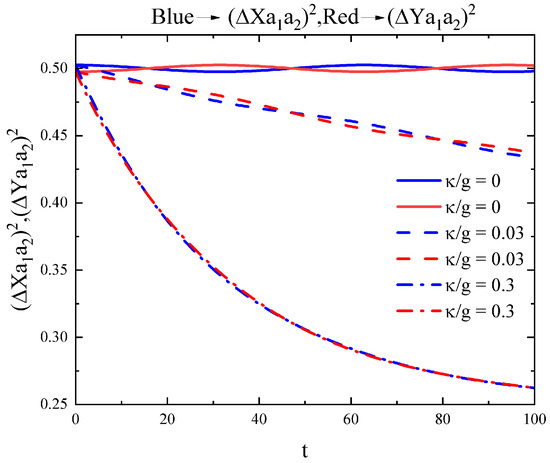
Figure 11.
Intermodal squeezing of the antisymmetric superposition state of two coherent states with respect to the dimensionless parameter .
5. Conclusions
In conclusion, we have studied the beam-splitter-type coupling interaction between two resonators via circuit QED. It has been shown that circuit QED can realize a quantum swap gate and prepare two-mode entangled coherent states using a single step. The numerical results show that the fidelity of the quantum swap gate is very high, even when dissipation is bigger than 0.2. More interestingly, it has been found that two-mode entangled coherent states prepared from our model, i.e., the symmetric and antisymmetric superposition states of two coherent states, demonstrate different entanglement behavior. The antisymmetric state can reach the unit under less severe conditions with the random . That is to say, it is easier to reach maximum entanglement with the antisymmetric case. Furthermore, we have discussed the nonclassical nature of two-mode entangled coherent states prepared from our model, i.e., the symmetric and antisymmetric superposition states of two coherent states, using antibunching and squeezing criteria, found that they have exhibited different quantum statistical properties when taking into account symmetric and antisymmetric cases. The symmetric superposition state clearly shows the existence of intermodal squeezing, but cannot exhibit an antibunching effect. Nevertheless, the antisymmetric case can reveal antibunching phenomena, while the squeezing effect disappears.
Author Contributions
Conceptualization, S.T. and Z.Z.; methodology, S.T.; software, Z.Z.; validation, Z.Z., X.J. and S.T.; formal analysis, S.T.; investigation, S.T.; resources, S.T.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, S.T.; visualization, Z.Z.; supervision, S.T.; project administration, S.T.; funding acquisition, S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Hunan Provincial Natural Science Foundation of China under Grant Nos. 2020JJ4146 and 2020JJ4002, the Open Fund project of the Key Laboratory of Optoelectronic Control and Detection Technology of University of Hunan Province under Grant No. PC20K02, the open fund project of the Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education under Grant No. QSQC1907, and the Science and Technology Plan Project of Hunan Province under Grant No. 2016TP1020.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict.
References
- Su, S.L.; Shen, H.Z.; Liang, E.; Zhang, S. One-step construction of the multiple-qubit Rydberg controlled-phase gate. Phys. Rev. A 2018, 98, 032306. [Google Scholar] [CrossRef]
- Su, S.L.; Gao, Y.; Liang, E.; Zhang, S. Fast Rydberg antiblockade regime and its applications in quantum logic gates. Phys. Rev. A 2017, 95, 022319. [Google Scholar] [CrossRef]
- Kang, Y.H.; Shi, Z.-C.; Song, J.; Xia, Y. Heralded atomic nonadiabatic holonomic quantum computation with Rydberg blockade. Phys. Rev. A 2020, 102, 022617. [Google Scholar] [CrossRef]
- Kang, Y.H.; Shi, Z.-C.; Huang, B.H.; Song, J.; Xia, Y. Flexible scheme for the implementation of nonadiabatic geometric quantum computation. Phys. Rev. A 2020, 101, 032322. [Google Scholar] [CrossRef]
- Su, S.L.; Guo, F.Q.; Tian, L.; Zhu, X.Y.; Yan, L.L.; Liang, E.J.; Feng, M. Nondestructive Rydberg parity meter and its applications. Phys. Rev. A 2020, 101, 012347. [Google Scholar] [CrossRef]
- Zheng, R.H.; Kang, Y.H.; Su, S.L.; Song, J.; Xia, Y. Robust and high-fidelity nondestructive Rydberg parity meter. Phys. Rev. A 2020, 102, 012609. [Google Scholar] [CrossRef]
- Zheng, R.H.; Xiao, Y.; Su, S.L.; Chen, Y.H.; Shi, Z.-C.; Song, J.; Xia, Y.; Zheng, S.B. Fast and dephasing-tolerant preparation of steady Knill-Laflamme-Milburn states via dissipative Rydberg pumping. Phys. Rev. A 2021, 103, 052402. [Google Scholar] [CrossRef]
- Zou, X.B.; Pahlke, K.; Mathis, W. Generation of two-mode nonclassical states and a quantum-phase-gate operation in trapped-ion cavity QED. Phys. Rev. A 2002, 65, 064303. [Google Scholar] [CrossRef]
- Xiong, W.; Tian, M.; Zhang, G.Q. Strong long-range spin-spin coupling via a Kerr magnon interface. Phys. Rev. B 2022, 105, 245310. [Google Scholar] [CrossRef]
- Shao, X.Q.; Zhu, A.D.; Zhang, S.; Chung, J.S.; Yeon, K.H. Efficient scheme for implementing an N-qubit Toffoli gate by a single resonant interaction with cavity quantum electrodynamics. Phys. Rev. A 2007, 75, 034307. [Google Scholar] [CrossRef]
- Su, S.L.; Liang, E.; Zhang, S.; Wen, J.J.; Sun, L.L.; Jin, Z.; Zhu, A.D. One-step implementation of the Rydberg-Rydberg-interaction gate. Phys. Rev. A 2016, 93, 012306. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q. Directional quantum state transfer in a dissipative Rydberg-atom-cavity system. Phys. Rev. A 2019, 99, 032348. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q.; Wu, J.H.; Yi, X.X. Dissipation-induced W state in a Rydberg-atom-cavity system. Opt. Lett. 2018, 43, 1639–1642. [Google Scholar] [CrossRef] [PubMed]
- Li, D.X.; Shao, X.Q.; Wu, J.H.; Yi, X.X. Engineering steady-state entanglement via dissipation and quantum Zeno dynamics in an optical cavity. Opt. Lett. 2017, 42, 3904–3907. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.H.; Shi, Z.-C.; Song, J.; Xia, Y. Effective discrimination of chiral molecules in optical cavity. Opt. Lett. 2020, 45, 4952–4955. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Shu, C.C.; Dong, D.; Nori, F. Vanishing and Revival of Resonance Raman Scattering. Phys. Rev. Lett. 2019, 123, 223202. [Google Scholar] [CrossRef]
- Guo, Y.; Luo, X.; Ma, S.; Shu, C.C. All-optical generation of quantum entangled states with strictly constrained ultrafast laser pulses. Phys. Rev. A 2019, 100, 023409. [Google Scholar] [CrossRef]
- Ma, S.; Xue, S.B.; Guo, Y.; Shu, C.C. Numerical detection of Gaussian entanglement and its application to the identification of bound entangled Gaussian states. Quantum Inf. Process. 2020, 19, 225. [Google Scholar] [CrossRef]
- Liu, T.; Guo, B.Q.; Yu, C.S. One-step implementation of a hybrid Fredkin gate with quantum memories and single superconducting qubit in circuit QED and its applications. Opt. Express 2018, 26, 4498–4511. [Google Scholar] [CrossRef]
- Liu, T.; Su, Q.P.; Xiong, S.J. Generation of a macroscopic entangled coherent state using quantum memories in circuit QED. Sci. Rep. 2016, 6, 1–15. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Y.; Guo, B.Q. Circuit QED: Cross-Kerr effect induced by a superconducting qutrit without classical pulses. Quantum Inf. Process. 2017, 16, 1–16. [Google Scholar] [CrossRef]
- Liu, T.; Xiong, S.J.; Cao, X.Z. Efficient transfer of an arbitrary qutrit state in circuit quantum electrodynamics. Optics. Lett. 2015, 40, 5602–5605. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Su, Q.P.; Yang, J.H. Transferring arbitrary d-dimensional quantum states of a superconducting transmon qudit in circuit QED. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.Q.; Huang, J.F.; Liu, Y.X.; Kuang, L.M.; Sun, C.P. Quantum switch for single-photon transport in a coupled superconducting transmission-line-resonator array. Phys. Rev. A 2009, 80, 014301. [Google Scholar] [CrossRef]
- Zhou, L.; Gao, Y.B.; Song, Z.; Sun, C.P. Coherent output of photons from coupled superconducting transmission line resonators controlled by charge qubits. Phys. Rev. A 2008, 77, 013831. [Google Scholar] [CrossRef]
- Xiong, W.; Jin, D.Y.; Jing, J.; Lam, C.H.; You, J.Q. Controllable coupling between a nanomechanical resonator and a coplanar-waveguide resonator via a superconducting flux qubit. Phys. Rev. A 2015, 92, 032318. [Google Scholar] [CrossRef]
- Xiong, W.; Chen, J.J.; Fang, B.L.; Wang, M.F.; Ye, L.; You, J.Q. Strong tunable spin-spin interaction in a weakly coupled nitrogen vacancy spin-cavity electromechanical system. Phys. Rev. B 2021, 103, 174106. [Google Scholar] [CrossRef]
- Xiong, W.; Qiu, Y.Y.; Wu, L.A.; You, J.Q. Amplification of the coupling strength in a hybrid quantum system. New, J. Phys. 2018, 20, 043037. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Yang, C.P. Generation of generalized hybrid entanglement in cavity electro–optic systems. Quantum. Sci. Technol. 2021, 6, 025003. [Google Scholar]
- Zhang, F.Y.; Wu, Q.C.; Yang, C.P. Non-Hermitian shortcut to adiabaticity in Floquet cavity electromagnonics. Phys. Rev. A 2022, 106, 012609. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, Z.; Li, C. Controllable preparation of entangled coherent states with superconducting system. Phys. Lett. A 2012, 376, 2418–2421. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, B.; Chen, Z. Controllable quantum information network with a superconducting system. Ann. Phys. 2014, 346, 103–112. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Chen, X.Y.; Li, C. Long-distance quantum information transfer with strong coupling hybrid solid system. Sci. Rep. 2015, 5, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Yang, X.C.; Mei, F. Controllable high-fidelity quantum state transfer and entanglement generation in circuit QED. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Zhao, P.; Zhong, W. Violation of Bell’s inequalities by continuous probing of a two-qubit system. Quantum Inf. Processing 2021, 20, 1–14. [Google Scholar] [CrossRef]
- Xu, P.; Zhao, S.M. Fast population transfer and entanglement preparation among four superconducting flux qubits. Laser Phys. Lett. 2020, 17, 105203. [Google Scholar] [CrossRef]
- Ji, Y.H.; Liu, Y.M. Controllable preparation of two-mode entangled coherent states in circuit QED. Chin. Phys. B 2014, 23, 110303. [Google Scholar] [CrossRef]
- Ji, Y.H.; Liu, Y.M. Preparation and non-classical characteristics of two-mode entangled coherent state. Optik 2016, 127, 3211–3217. [Google Scholar] [CrossRef]
- Zhou, L.; Xiong, H. A macroscopical entangled coherent state generator in a V configuration atom system. J. Phys. B-AT. Mol. Opt. 2008, 41, 025501. [Google Scholar] [CrossRef]
- Zheng, S.B. Efficient scheme for realizing beam-splitter-type coupling for two cavity modes. Opt. Commun 2007, 277, 349–352. [Google Scholar] [CrossRef]
- Villas-Boas, C.J.; de Almeida, N.G.; Serra, R.M. Squeezing arbitrary cavity-field states through their interaction with a single driven atom. Phys. Rev. A 2003, 68, 061801. [Google Scholar] [CrossRef]
- Serra, R.M.; Villas-Boas, C.J.; de Almeida, N.G. Frequency up-and down-conversions in two-mode cavity quantum electrodynamics. Phys. Rev. A 2005, 71, 045802. [Google Scholar] [CrossRef]
- Zou, X.; Dong, Y.; Guo, G. Schemes for realizing frequency up-and down-conversions in two-mode cavity QED. Phys. Rev. A 2006, 73, 025802. [Google Scholar] [CrossRef]
- Solano, E.; Agarwal, G.S.; Walther, H. Strong-driving-assisted multipartite entanglement in cavity QED. Phys. Rev. Lett. 2003, 90, 027903. [Google Scholar] [CrossRef]
- Wang, X.G.; Sanders, B.C. Multipartite entangled coherent states. Phys. Rev. A 2001, 65, 012303. [Google Scholar] [CrossRef]
- Mu, Q.X.; Ma, Y.H. Generation of two-mode entangled coherent states via a cavity QED system. J. Phys. A-Math. Theor. 2009, 42, 225304. [Google Scholar] [CrossRef]
- Mu, Q.X.; Ma, Y.H.; Zhou, L. Generating an entangled coherent state of two cavity modes in a three-level Λ-type atomic system. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 3241. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’Ko, V.I.; Nikonov, D.E. Even and odd coherent states for multimode parametric systems. Phys. Rev. A 1995, 51, 3328. [Google Scholar] [CrossRef]
- Ansari, N.A.; Man’ko, V.I. Photon statistics of multimode even and odd coherent light. Phys. Rev. A 1994, 50, 1942. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Man’ko, M.A.; Man’ko, V.I. Differential parametric formalism for the evolution of Gaussian states: Nonunitary evolution and invariant states. Entropy 2020, 22, 586. [Google Scholar] [CrossRef]
- Buzek, V.; Vidiella-Barranco, A.; Knight, P.L. Superpositios of coherent states: Squeezing and dissipation. Phys. Rev. A 1992, 45, 6570–6585. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Guo, G. Nonclassical properties of even and odd coherent states. Phys. Lett. A 1989, 136, 281–283. [Google Scholar] [CrossRef]
- Hillery, M. Amplitude-squared squeezing of the electromagnetic field. Phys. Rev. A 1987, 36, 3796. [Google Scholar] [CrossRef] [PubMed]
- Gerry, C.C. Proposal for generating even and odd coherent states. Opt. Commun. 1992, 91, 247–251. [Google Scholar] [CrossRef]
- Walls, D.F. Squeezed states of light. Nature 1983, 306, 141–146. [Google Scholar] [CrossRef]
- Schleich, W.; Wheeler, J.A. Oscillations in photon distribution of squeezed states. JOSA B 1987, 4, 1715–1722. [Google Scholar] [CrossRef]
- Schrade, G.; Akulin, V.M.; Man’ko, V.I. Photon statistics of a two-mode squeezed vacuum. Phys. Rev. A 1993, 48, 2398. [Google Scholar] [CrossRef]
- Lynch, R. Phase fluctuations in a squeezed state using measured phase operators. JOSA B 1987, 4, 1723–1726. [Google Scholar] [CrossRef]
- Grønbech-Jensen, N.; Christiansen, P.L.; Ramanujam, P.S. Phase properties of squeezed states. JOSA B 1989, 6, 2423–2429. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer Press: Berlin, Germany, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).