Review of the Applications of Kalman Filtering in Quantum Systems
Abstract
1. Introduction
2. Realization of Kalman Filtering in Quantum Systems
3. Applications of Kalman Filtering in Quantum Systems
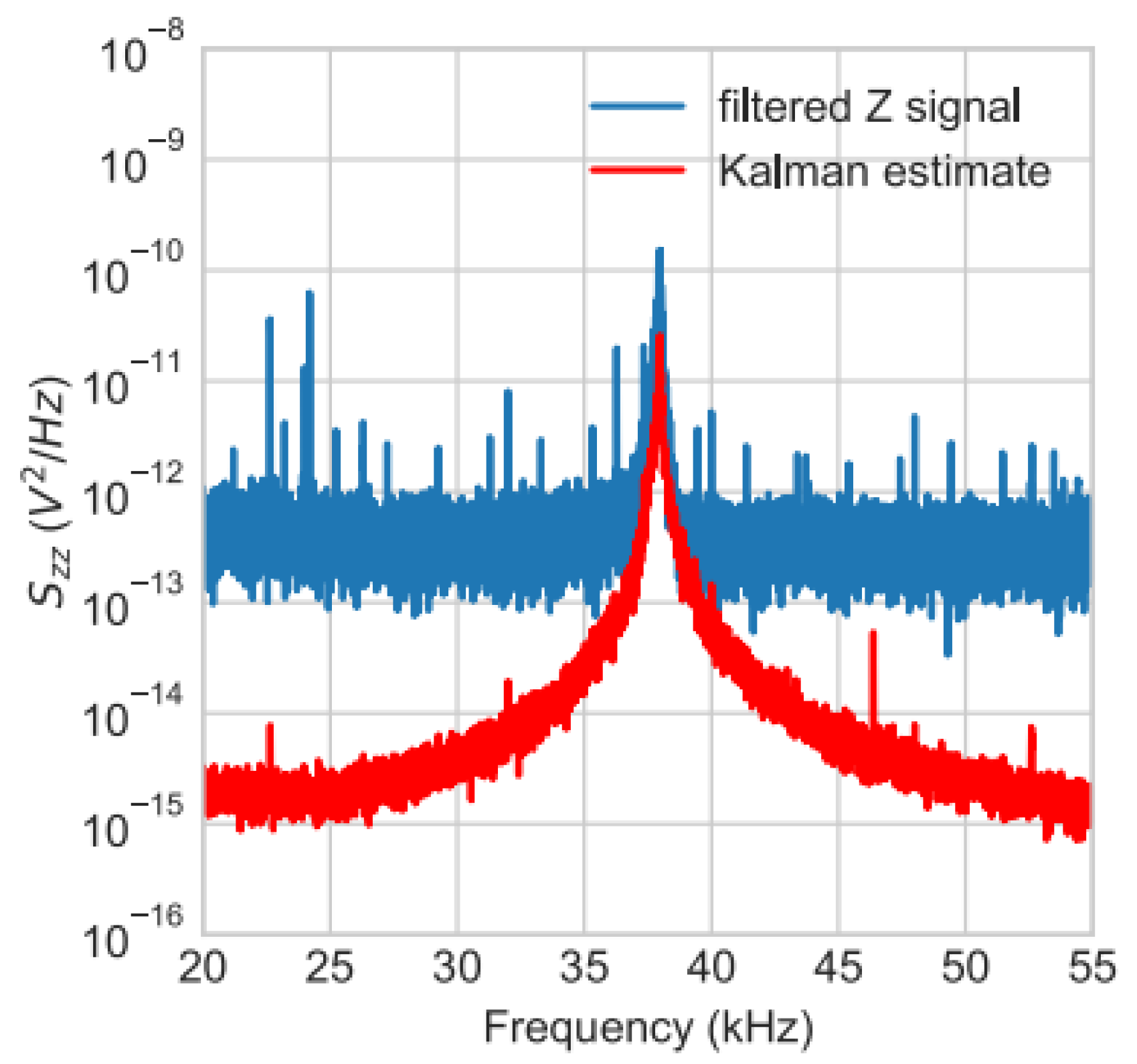
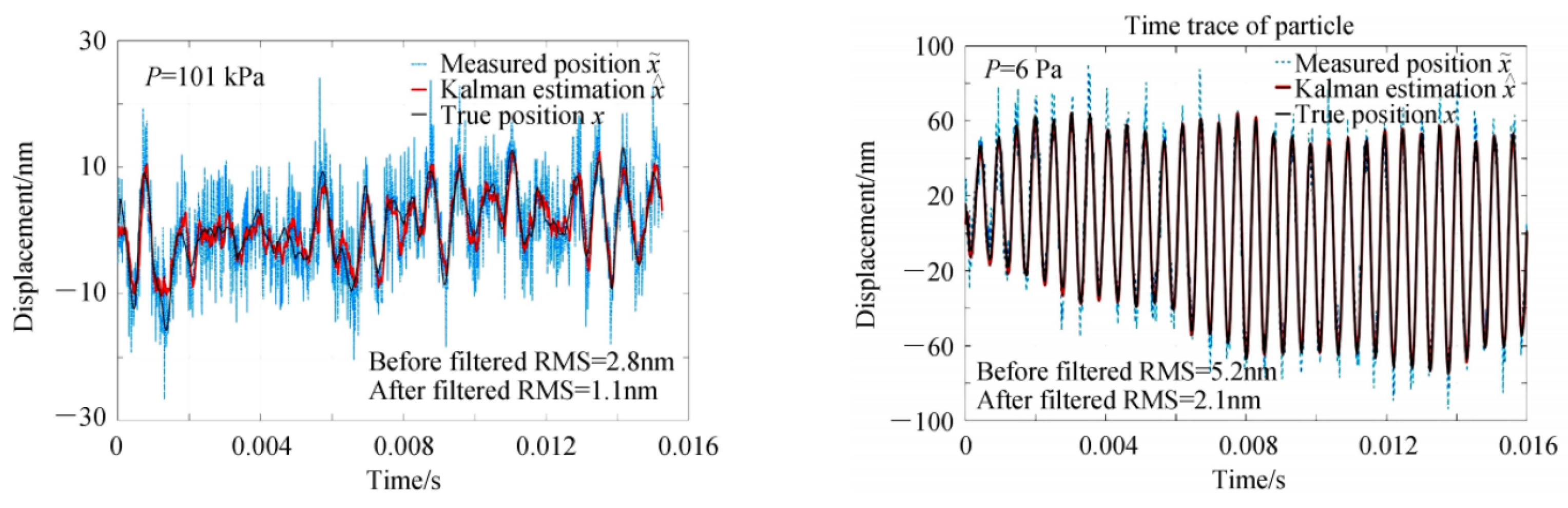
3.1. Position Estimation and Feedback Control
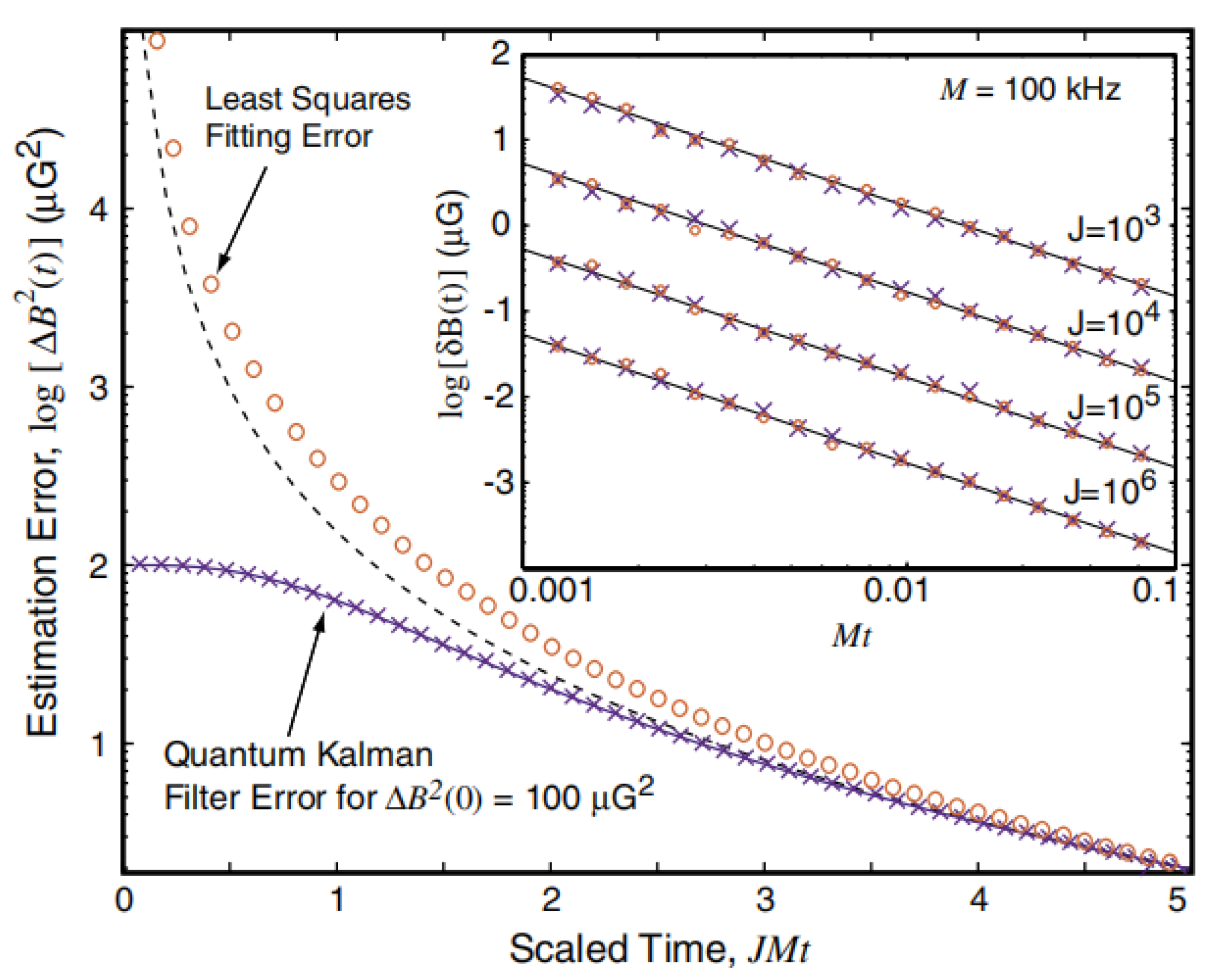
3.2. Magnetic Field Estimation
3.3. Waveform Estimation and Tracking of Optical Pump
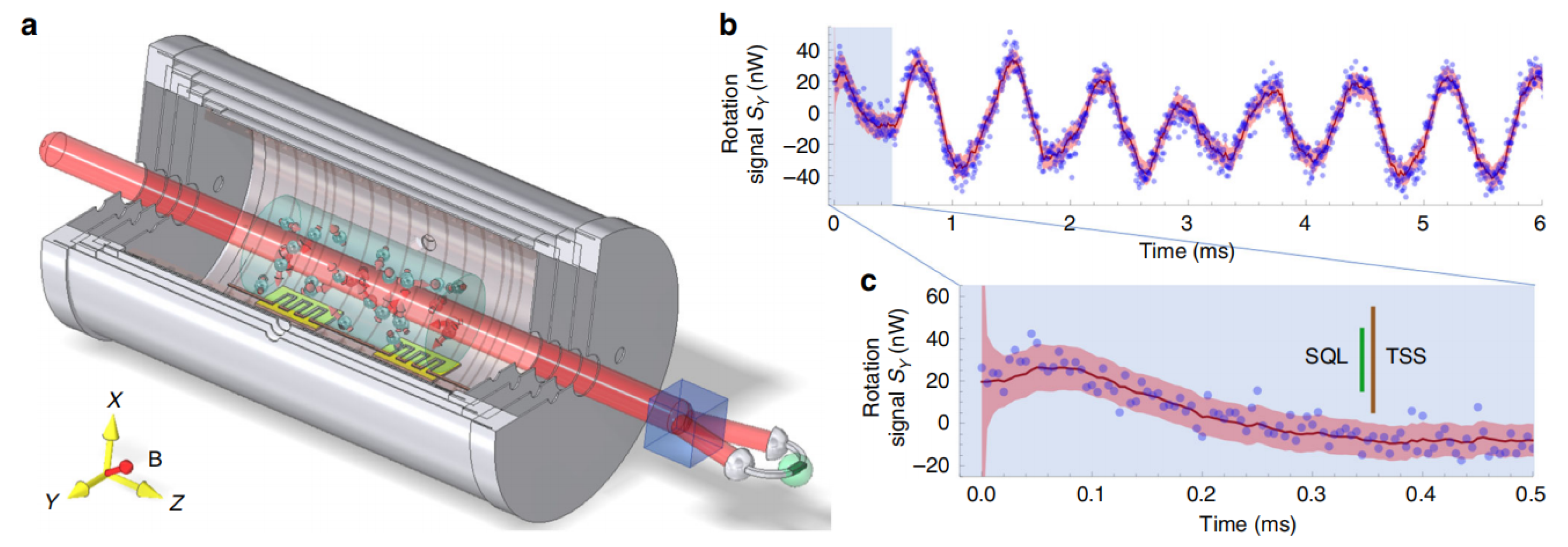
3.4. Estimation of Spin Components and Noise Squeezing
3.5. Density Matrix Estimation in Quantum Tomography
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yonezawa, H.; Nakane, D.; Wheatley, T.A.; Iwasawa, K.; Takeda, S.; Arao, H.; Ohki, K.; Tsumura, K.; Berry, D.W.; Ralph, T.C.; et al. Quantum-Enhanced Optical-Phase Tracking. Science 2012, 337, 1514–1517. [Google Scholar] [CrossRef] [PubMed]
- Korayem, A.H.; Khajepour, A.; Fidan, B. A Review on Vehicle-Trailer State and Parameter Estimation. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5993–6010. [Google Scholar] [CrossRef]
- Kitching, J.; Knappe, S.; Donley, E.A. Atomic Sensors—A Review. IEEE Sens. J. 2011, 11, 1749–1758. [Google Scholar] [CrossRef]
- Wieczorek, W.; Hofer, S.G.; Hoelscher-Obermaier, J.; Riedinger, R.; Hammerer, K.; Aspelmeyer, M. Optimal State Estimation for Cavity Optomechanical Systems. Phys. Rev. Lett. 2015, 114, 223601. [Google Scholar] [CrossRef]
- Rossi, M.; Mason, D.; Chen, J.; Tsaturyan, Y.; Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 2018, 563, 53–58. [Google Scholar] [CrossRef]
- Geremia, J.M.; Stockton, J.K.; Mabuchi, H. Real-Time Quantum Feedback Control of Atomic Spin-Squeezing. Science 2004, 304, 270–273. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Tsang, M.; Wiseman, H.M.; Caves, C.M. Fundamental Quantum Limit to Waveform Estimation. Phys. Rev. Lett. 2011, 106, 090401. [Google Scholar] [CrossRef]
- Tsang, M. Optimal waveform estimation for classical and quantum systems via time-symmetric smoothing. Phys. Rev. A 2009, 80, 033840. [Google Scholar] [CrossRef]
- Iwasawa, K.; Makino, K.; Yonezawa, H.; Tsang, M.; Davidovic, A.; Huntington, E.; Furusawa, A. Quantum-Limited Mirror-Motion Estimation. Phys. Rev. Lett. 2013, 111, 163602. [Google Scholar] [CrossRef] [PubMed]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Jacobs, K. Quantum Measurement Theory and Its Applications; Cambridge University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Kalman, R. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82D, 35–45. [Google Scholar] [CrossRef]
- Kalman, R.; Bucy, R. New Results in Linear Filtering and Prediction Theory. ASME J. Basic Eng. Ser. D 1973, 83, 95–108. [Google Scholar] [CrossRef]
- Jacobs, K. Stochastic Processes for Physicists Understanding Noisy Systems; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Costa, P.J. Adaptive model architecture and extended Kalman-Bucy filters. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 525–533. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Cooper, S.; Durrant-Whyte, H. A Kalman filter model for GPS navigation of land vehicles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994; Volume 1, pp. 157–163. [Google Scholar] [CrossRef]
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial Applications of the Kalman Filter: A Review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef]
- Carron, A.; Todescato, M.; Carli, R.; Schenato, L.; Pillonetto, G. Machine learning meets Kalman Filtering. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 4594–4599. [Google Scholar] [CrossRef]
- Doherty, A.C.; Jacobs, K. Feedback control of quantum systems using continuous state estimation. Phys. Rev. A 1999, 60, 2700–2711. [Google Scholar] [CrossRef]
- Brettorst, G.L. Bayesian Spectrum Analysis and Parameter Estimation; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- van Trees, H.L.; Bell, K.L.; Tian, Z. Detection, Estimation, and Modulation Theory. Part I: Detection, Estimation and Filtering Theory; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Bain, A.; Crisan, D. Fundamentals of Stochastic Filtering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Caves, C.M.; Milburn, G.J. Quantum-mechanical model for continuous position measurements. Phys. Rev. A 1987, 36, 5543–5555. [Google Scholar] [CrossRef] [PubMed]
- Czerwinski, A. Dynamics of Open Quantum Systems—Markovian Semigroups and Beyond. Symmetry 2022, 14, 1752. [Google Scholar] [CrossRef]
- Czerwinski, A. Entanglement Dynamics Governed by Time-Dependent Quantum Generators. Axioms 2022, 11, 589. [Google Scholar] [CrossRef]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series: With Engineering Applications; The MIT Press: Cambridge, MA, USA, 1949. [Google Scholar]
- Jacobs, K.; Steck, D.A. A straightforward introduction to continuous quantum measurement. Contemp. Phys. 2006, 47, 279–303. [Google Scholar] [CrossRef]
- Verstraete, F.; Doherty, A.C.; Mabuchi, H. Sensitivity optimization in quantum parameter estimation. Phys. Rev. A 2001, 64, 032111. [Google Scholar] [CrossRef]
- Doherty, A.C.; Tan, S.M.; Parkins, A.S.; Walls, D.F. State determination in continuous measurement. Phys. Rev. A 1999, 60, 2380–2392. [Google Scholar] [CrossRef]
- Geremia, J.M.; Stockton, J.K.; Doherty, A.C.; Mabuchi, H. Quantum Kalman Filtering and the Heisenberg Limit in Atomic Magnetometry. Phys. Rev. Lett. 2003, 91, 250801. [Google Scholar] [CrossRef] [PubMed]
- Kong, J.; Jiménez-Martínez, R.; Troullinou, C.; Lucivero, V.G.; Tóth, G.; Mitchell, M.W. Measurement-induced, spatially-extended entanglement in a hot, strongly-interacting atomic system. Nat. Commun. 2020, 11, 2415. [Google Scholar] [CrossRef]
- Jiménez-Martínez, R.; Kołodyński, J.; Troullinou, C.; Lucivero, V.G.; Kong, J.; Mitchell, M.W. Signal Tracking Beyond the Time Resolution of an Atomic Sensor by Kalman Filtering. Phys. Rev. Lett. 2018, 120, 040503. [Google Scholar] [CrossRef] [PubMed]
- Audenaert, K.M.R.; Scheel, S. Quantum tomographic reconstruction with error bars: A Kalman filter approach. New J. Phys. 2009, 11, 023028. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Hornberger, K.; Gerlich, S.; Haslinger, P.; Nimmrichter, S.; Arndt, M. Colloquium: Quantum interference of clusters and molecules. Rev. Mod. Phys. 2012, 84, 157–173. [Google Scholar] [CrossRef]
- Bera, S.; Motwani, B.; Singh, T.P.; Ulbricht, H. A proposal for the experimental detection of CSL induced random walk. Sci. Rep. 2015, 5, 7664. [Google Scholar] [CrossRef]
- Jain, V.; Gieseler, J.; Moritz, C.; Dellago, C.; Quidant, R.; Novotny, L. Direct Measurement of Photon Recoil from a Levitated Nanoparticle. Phys. Rev. Lett. 2016, 116, 243601. [Google Scholar] [CrossRef]
- Setter, A.; Toroš, M.; Ralph, J.F.; Ulbricht, H. Real-time Kalman filter: Cooling of an optically levitated nanoparticle. Phys. Rev. A 2018, 97, 033822. [Google Scholar] [CrossRef]
- Monmasson, E.; Cirstea, M.N. FPGA Design Methodology for Industrial Control Systems—A Review. IEEE Trans. Ind. Electron. 2007, 54, 1824–1842. [Google Scholar] [CrossRef]
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G.; Hong, S.; Kiesel, N.; Kugi, A.; Aspelmeyer, M. Real-time optimal quantum control of mechanical motion at room temperature. Nature 2021, 595, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Hu, H.; Li, N.; Chen, X.; Shu, X.; Liu, C.; Fu, Z.; Gao, X. Displacement of Optically Trapped Microsphere in Vacuum Based on Kalman Filter. Acta Photonica Sin. 2020, 49, 0512004. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Wang, S.; Zeng, G. Polarization-state tracking based on Kalman filter in continuous-variable quantum key distribution. Opt. Express 2019, 27, 26689–26700. [Google Scholar] [CrossRef]
- Ruppert, M.G.; Karvinen, K.S.; Wiggins, S.L.; Moheimani, S.O.R. A Kalman Filter for Amplitude Estimation in High-Speed Dynamic Mode Atomic Force Microscopy. IEEE Trans. Control Syst. Technol. 2016, 24, 276–284. [Google Scholar] [CrossRef]
- Cheiney, P.; Fouché, L.; Templier, S.; Napolitano, F.; Battelier, B.; Bouyer, P.; Barrett, B. Navigation-Compatible Hybrid Quantum Accelerometer Using a Kalman Filter. Phys. Rev. Appl. 2018, 10, 034030. [Google Scholar] [CrossRef]
- Budker, D.; Romalis, M. Optical magnetometry. Nat. Phys. 2007, 3, 227–234. [Google Scholar] [CrossRef]
- Colangelo, G.; Ciurana, F.M.; Bianchet, L.C.; Sewell, R.J.; Mitchell, M.W. Simultaneous tracking of spin angle and amplitude beyond classical limits. Nature 2017, 543, 525–528. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
- Tralshawala, N.; Claycomb, J.R.; Miller, J.H. Practical SQUID instrument for non-destructive testing. Appl. Phys. Lett 1997, 71, 1573. [Google Scholar] [CrossRef]
- Xia, H.; Baranga, A.B.; Hoffman, D.; Romalis, M.V. Magnetoencephalography with an atomic magnetometer. Appl. Phys. Lett. 2006, 89, 211104. [Google Scholar] [CrossRef]
- Xu, S.; Crawford, C.W.; Rochester, S.; Yashchuk, V.; Budker, D.; Pines, A. Submillimeter-resolution magnetic resonance imaging at the Earth’s magnetic field with an atomic magnetometer. Phys. Rev. A 2008, 78, 013404. [Google Scholar] [CrossRef]
- Alexandrov, E.B. Recent Progress in Optically Pumped Magnetometers. Phys. Scr. 2003, 2003, 27. [Google Scholar] [CrossRef]
- Sutton, G.J.; Bitmead, R.R. Experiences with model predictive control applied to a nonlinear constrained submarine. In Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No.98CH36171), Tampa, FL, USA, 18 December 1998; Volume 2, pp. 1370–1375. [Google Scholar] [CrossRef]
- Miller, J.B. Chapter 7—Nuclear Quadrupole Resonance Detection of Explosives. In Counterterrorist Detection Techniques of Explosives; Yinon, J., Ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; pp. 157–198. [Google Scholar]
- Bison, G.; Wynands, R.; Weis, A. A laser-pumped magnetometer for the mapping of human cardiomagnetic fields. Appl. Phys. B 2003, 76, 325–328. [Google Scholar] [CrossRef]
- Auzinsh, M.; Budker, D.; Kimball, D.F.; Rochester, S.M.; Stalnaker, J.E.; Sushkov, A.O.; Yashchuk, V.V. Can a Quantum Nondemolition Measurement Improve the Sensitivity of an Atomic Magnetometer? Phys. Rev. Lett. 2004, 93, 173002. [Google Scholar] [CrossRef]
- Novikova, I.; Mikhailov, E.E.; Xiao, Y. Excess optical quantum noise in atomic sensors. Phys. Rev. A 2015, 91, 051804. [Google Scholar] [CrossRef]
- Troullinou, C.; Jiménez-Martínez, R.; Kong, J.; Lucivero, V.G.; Mitchell, M.W. Squeezed-Light Enhancement and Backaction Evasion in a High Sensitivity Optically Pumped Magnetometer. Phys. Rev. Lett. 2021, 127, 193601. [Google Scholar] [CrossRef]
- Wolfgramm, F.; Cerè, A.; Beduini, F.A.; Predojević, A.; Koschorreck, M.; Mitchell, M.W. Squeezed-Light Optical Magnetometry. Phys. Rev. Lett. 2010, 105, 053601. [Google Scholar] [CrossRef]
- Horrom, T.; Singh, R.; Dowling, J.P.; Mikhailov, E.E. Quantum-enhanced magnetometer with low-frequency squeezing. Phys. Rev. A 2012, 86, 023803. [Google Scholar] [CrossRef]
- Otterstrom, N.; Pooser, R.C.; Lawrie, B.J. Nonlinear optical magnetometry with accessible in situ optical squeezing. Opt. Lett. 2014, 39, 6533–6536. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Mølmer, K. Estimating a fluctuating magnetic field with a continuously monitored atomic ensemble. Phys. Rev. A 2020, 102, 063716. [Google Scholar] [CrossRef]
- Bao, H.; Duan, J.; Jin, S.; Lu, X.; Li, P.; Qu, W.; Wang, M.; Novikova, I.; Mikhailov, E.E.; Zhao, K.F.; et al. Spin squeezing of 1011 atoms by prediction and retrodiction measurements. Nature 2020, 581, 159–163. [Google Scholar] [CrossRef] [PubMed]
- Shah, V.; Vasilakis, G.; Romalis, M.V. High Bandwidth Atomic Magnetometery with Continuous Quantum Nondemolition Measurements. Phys. Rev. Lett. 2010, 104, 013601. [Google Scholar] [CrossRef]
- Behbood, N.; Martin Ciurana, F.; Colangelo, G.; Napolitano, M.; Tóth, G.; Sewell, R.J.; Mitchell, M.W. Generation of Macroscopic Singlet States in a Cold Atomic Ensemble. Phys. Rev. Lett. 2014, 113, 093601. [Google Scholar] [CrossRef]
- Isayama, T.; Takahashi, Y.; Tanaka, N.; Toyoda, K.; Ishikawa, K.; Yabuzaki, T. Observation of Larmor spin precession of laser-cooled Rb atoms via paramagnetic Faraday rotation. Phys. Rev. A 1999, 59, 4836–4839. [Google Scholar] [CrossRef]
- Stockton, J.K.; Geremia, J.M.; Doherty, A.C.; Mabuchi, H. Robust quantum parameter estimation: Coherent magnetometry with feedback. Phys. Rev. A 2004, 69, 032109. [Google Scholar] [CrossRef]
- Amorós-Binefa, J.; Kołodyński, J. Noisy atomic magnetometry in real time. New J. Phys. 2021, 23, 123030. [Google Scholar] [CrossRef]
- Kuzmich, A.; Mandel, L.; Bigelow, N.P. Generation of Spin Squeezing via Continuous Quantum Nondemolition Measurement. Phys. Rev. Lett. 2000, 85, 1594–1597. [Google Scholar] [CrossRef]
- Mølmer, K.; Madsen, L.B. Estimation of a classical parameter with Gaussian probes: Magnetometry with collective atomic spins. Phys. Rev. A 2004, 70, 052102. [Google Scholar] [CrossRef]
- Petersen, V.; Mølmer, K. Estimation of fluctuating magnetic fields by an atomic magnetometer. Phys. Rev. A 2006, 74, 043802. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Budker, D.; Gawlik, W.; Kimball, D.F.; Rochester, S.M.; Yashchuk, V.V.; Weis, A. Resonant nonlinear magneto-optical effects in atoms. Rev. Mod. Phys. 2002, 74, 1153–1201. [Google Scholar] [CrossRef]
- Albarelli, F.; Rossi, M.A.C.; Paris, M.G.A.; Genoni, M.G. Ultimate limits for quantum magnetometry via time-continuous measurements. New J. Phys. 2017, 19, 123011. [Google Scholar] [CrossRef]
- Dang, H.B.; Maloof, A.C. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Grangier, P.; Levenson, J.A.; Poizat, J.P. Quantum non-demolition measurements in optics. Nature 1998, 396, 537–542. [Google Scholar] [CrossRef]
- Vitagliano, G.; Hyllus, P.; Egusquiza, I.L.; Tóth, G. Spin Squeezing Inequalities for Arbitrary Spin. Phys. Rev. Lett. 2011, 107, 240502. [Google Scholar] [CrossRef]
- Mooney, C.Z. Monte Carlo Simulation; Sage Publications, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Tóth, G.; Mitchell, M.W. Generation of macroscopic singlet states in atomic ensembles. New J. Phys. 2010, 12, 053007. [Google Scholar] [CrossRef]
- Warszawski, P.; Wiseman, H.M.; Doherty, A.C. Solving quantum trajectories for systems with linear Heisenberg-picture dynamics and Gaussian measurement noise. Phys. Rev. A 2020, 102, 042210. [Google Scholar] [CrossRef]
- Czerwinski, A.; Szlachetka, J. Efficiency of photonic state tomography affected by fiber attenuation. Phys. Rev. A 2022, 105, 062437. [Google Scholar] [CrossRef]
- Czerwinski, A.; Czerwinski, K. Statistical Analysis of the Photon Loss in Fiber-Optic Communication. Photonics 2022, 9, 568. [Google Scholar] [CrossRef]
- Horn, R.T.; Kolenderski, P.; Kang, D.; Abolghasem, P.; Scarcella, C.; Frera, A.D.; Tosi, A.; Helt, L.G.; Zhukovsky, S.V.; Sipe, J.E.; et al. Inherent polarization entanglement generated from a monolithic semiconductor chip. Sci. Rep. 2013, 3, 2314. [Google Scholar] [CrossRef] [PubMed]
- Czerwinski, A. Selected Concepts of Quantum State Tomography. Optics 2022, 3, 268–286. [Google Scholar] [CrossRef]
- Czerwinski, A. Entanglement quantification enhanced by dark count correction. Int. J. Quantum Inf. 2022, 20, 2250021. [Google Scholar] [CrossRef]
- Man’Ko, V.; Markovich, L. Optimal Nonlinear Filtering of Quantum State. IEEE Trans. Inf. Theory 2017, 64, 4784–4791. [Google Scholar] [CrossRef]
- Aguirre, C.; Mendes, R.V. Signal recognition and adapted filtering by non-commutative tomography. IET Signal Process. 2014, 8, 67–75. [Google Scholar] [CrossRef]
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, K.; Kong, J.; Wang, Y.; Lu, X.-M. Review of the Applications of Kalman Filtering in Quantum Systems. Symmetry 2022, 14, 2478. https://doi.org/10.3390/sym14122478
Ma K, Kong J, Wang Y, Lu X-M. Review of the Applications of Kalman Filtering in Quantum Systems. Symmetry. 2022; 14(12):2478. https://doi.org/10.3390/sym14122478
Chicago/Turabian StyleMa, Kezhao, Jia Kong, Yihan Wang, and Xiao-Ming Lu. 2022. "Review of the Applications of Kalman Filtering in Quantum Systems" Symmetry 14, no. 12: 2478. https://doi.org/10.3390/sym14122478
APA StyleMa, K., Kong, J., Wang, Y., & Lu, X.-M. (2022). Review of the Applications of Kalman Filtering in Quantum Systems. Symmetry, 14(12), 2478. https://doi.org/10.3390/sym14122478




