Symmetry Reductions, Cte Method and Interaction Solutions for Sharma-Tasso-Olver-Burgers Equation
Abstract
:1. Introduction
2. Preliminaries of Lie Point Symmetry and CTE Method
2.1. Method of Lie Point Symmetry
2.2. Method of CTE Method
3. Lie Point Symmetry and Similarity Reductions of STOB Equation
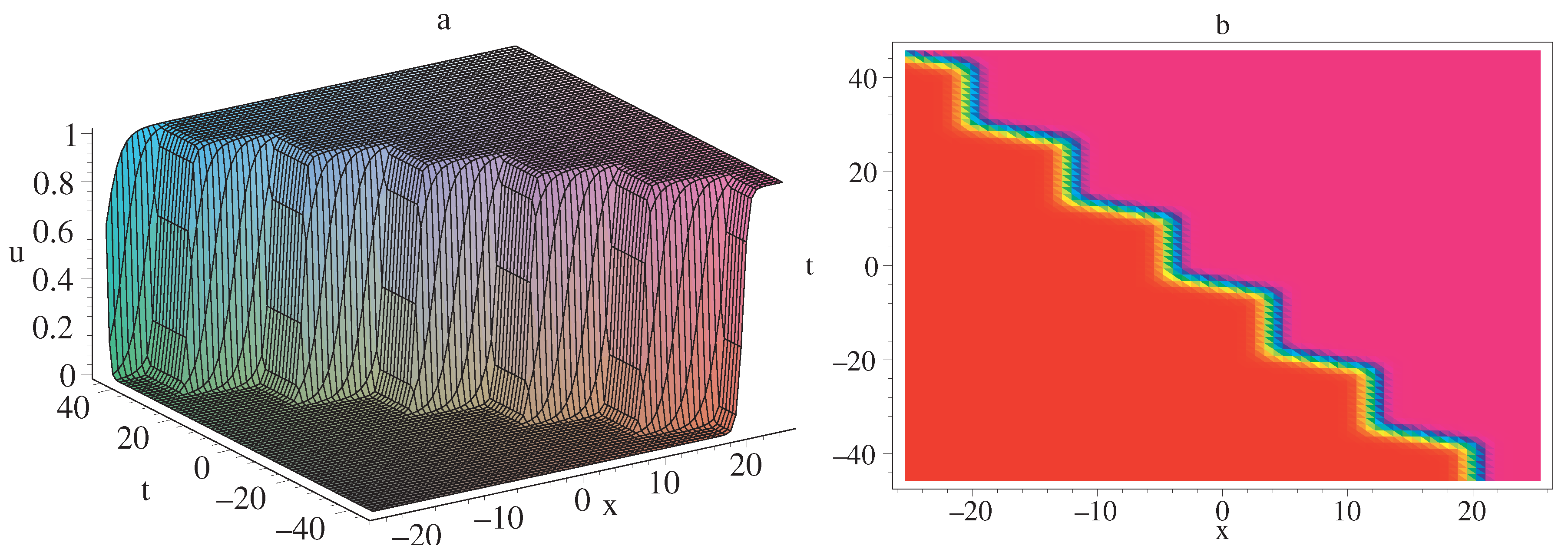
4. CTE Solvability and Interaction Solutions of STOB Equation
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property for partial differential equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin, Germany, 1991. [Google Scholar]
- Rogers, C.; Schief, W.K. Bäcklund and Darboux transformations geometry and modern applications in soliton theory. In Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Tang, X.Y.; Lou, S.Y.; Zhang, Y. Localized excitations in (2+1)-dimensional systems. Phys. Rev. E 2002, 66, 046601. [Google Scholar] [CrossRef]
- Jin, X.W.; Shen, S.J.; Yang, Z.Y.; Lin, J. Magnetic lump motion in saturated ferromagnetic films. Phys. Rev. E 2022, 105, 014205. [Google Scholar] [CrossRef]
- Dai, C.Q.; Chen, R.P.; Wang, Y.Y.; Fan, Y. Dynamics of light bullets in inhomogeneous cubic-quintic-septimal nonlinear media with PT-symmetric potentials. Nonlinear Dyn. 2017, 87, 1675–1683. [Google Scholar] [CrossRef]
- Fang, Y.; Wu, G.Z.; Wang, Y.Y.; Dai, C.Q. Data-driven femtosecond optical soliton excitations and parameters discovery of the high-order NLSE using the PINN. Nonlinear Dyn. 2021, 105, 603–616. [Google Scholar] [CrossRef]
- Dai, C.Q.; Zhang, J.F. Controlling effect of vector and scalar crossed double-Ma breathers in a partially nonlocal nonlinear medium with a linear potential. Nonlinear Dyn. 2020, 100, 1621–1628. [Google Scholar] [CrossRef]
- Dai, C.Q.; Wang, Y.Y.; Fan, Y.; Zhang, J.F. Interactions between exotic multi-valued solitons of the (2+1)-dimensional Korteweg-de Vries equation describing shallow water wave. Appl. Math. Model. 2020, 80, 506–515. [Google Scholar] [CrossRef]
- Dai, C.Q.; Fan, Y.; Wang, Y.Y. Three-dimensional optical solitons formed by the balance between different-order nonlinearities and high-order dispersion/diffraction in parity-time symmetric potentials. Nonlinear Dyn. 2019, 98, 489–499. [Google Scholar] [CrossRef]
- Olver, P.J. Application of Lie Group to Differential Equation; Springer: Berlin, Germany, 1986. [Google Scholar]
- Bluman, G.W.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Springer: New York, NY, USA, 2002. [Google Scholar]
- Jiang, H.J.; Xiang, J.J.; Dai, C.Q.; Wang, Y.Y. Nonautonomous bright soliton solutions on continuous wave and cnoidal wave backgrounds in blood vessels. Nonlinear Dyn. 2014, 75, 201–207. [Google Scholar] [CrossRef]
- Shin, H.J. Multisoliton complexes moving on a cnoidal wave background. Phys. Rev. E 2005, 71, 036628. [Google Scholar] [CrossRef]
- Gao, X.N.; Lou, S.Y.; Tang, X.Y. Bosonization, singularity analysis, nonlocal symmetry reductions and exact solutions of supersymmetric KdV equation. J. High Energy Phys. 2013, 2013, 29. [Google Scholar] [CrossRef]
- Cheng, X.P.; Lou, S.Y.; Chen, C.L.; Tang, X.Y. Interactions between solitons and other nonlinear Schrödinger waves. Phys. Rev. E 2014, 89, 043202. [Google Scholar] [CrossRef] [PubMed]
- Ren, B. Interaction solutions for mKP equation with nonlocal symmetry reductions and CTE method. Phys. Scr. 2015, 90, 065206. [Google Scholar] [CrossRef]
- Ren, B.; Cheng, X.P.; Lin, J. The (2+1)-dimensional Konopelchenko-Dubrovsky equation: Nonlocal symmetries and interaction solutions. Nonlinear Dyn. 2016, 86, 1855. [Google Scholar] [CrossRef]
- Ren, B. Painlevé analysis, nonlocal symmetry and explicit interaction solutions for supersymmetric mKdVB equation. AIP Adv. 2016, 6, 085205. [Google Scholar] [CrossRef]
- Ren, B.; Lou, Z.M.; Liang, Z.F.; Tang, X.Y. Nonlocal symmetry and explicit solutions for Drinfel’d-Sokolov-Wilson system. Eur. Phys. J. Plus 2016, 131, 441. [Google Scholar] [CrossRef]
- Ren, B. Symmetry reduction related with nonlocal symmetry for Gardner equation. Commun. Nonlinear Sci. Numer. Simulat. 2017, 42, 456–463. [Google Scholar] [CrossRef]
- Ren, B. Painlevé analysis and exact solutions of bosonized N = 1 supersymmetric Burgers equation. Open Phys. 2015, 13, 205–209. [Google Scholar] [CrossRef]
- Ren, B.; Gao, X.N.; Yu, J.; Liu, P. Exact solutions of supersymmetric Burgers equation with bosonization procedure. Open Math. 2015, 13, 502–509. [Google Scholar] [CrossRef]
- Lian, Z.J.; Lou, S.Y. Symmetries and exact solutions of the Sharma-Tass-Olver equation. Nonlinear Anal. 2005, 63, e1167–e1177. [Google Scholar] [CrossRef]
- Hu, H.C.; Li, Y.Y.; Zhu, H.D. Residual symmetry, interaction solutions and consistent tanh expansion solvability for the third-order Burgers equation. Chaos Soliton Fractals 2018, 108, 77–81. [Google Scholar] [CrossRef]
- Pu, H.; Jia, M. CTE Solvability, Exact Solutions and nonlocal Symmetries of the Sharma-Tasso-Olver equation. Commun. Theor. Phys. 2015, 64, 623–629. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Akinyemi, L.; Rezazadeh, H.; Inc, M. Non-topological, topological and rogue wave Soliton solutions for Sharma Tasso Olver equation. J. Ocean. Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Miao, Z.W.; Hu, X.R.; Chen, Y. Interaction phenomenon to (1+1)-dimensional Sharma-Tasso-Olver-Burgers equation. Appl. Math. Lett. 2021, 112, 106722. [Google Scholar] [CrossRef]
- Yan, Z.W.; Lou, S.Y. Soliton molecules in Sharma-Tasso-Olver-Burgers equation. Appl. Math. Lett. 2020, 104, 106271. [Google Scholar] [CrossRef]
- Hosseini, K.; Akbulut, A.; Baleanu, D.; Salahshour, S. The Sharma-Tasso-Olver-Burgers equation: Its conservation laws and kink solitons. Commun. Theor. Phys. 2022, 74, 025001. [Google Scholar] [CrossRef]
- Wang, G.W.; Kara, A.H. Nonlocal symmetry analysis, explicit solutions and conservation laws for the fourth-order Burgers’ equation. Chaos Soliton Fractals 2015, 81, 290–298. [Google Scholar] [CrossRef]
- Jin, X.W.; Lin, J. Rogue wave, interaction solutions to the KMM system. J. Magn. Magn. Mater. 2020, 502, 166590. [Google Scholar] [CrossRef]
- Cheng, W.; Li, B. CRE solvability, exact soliton-cnoidal wave interaction solutions, and nonlocal symmetry for the modified Boussinesq equation. Adv. Math. Phys. 2016, 2016, 4874392. [Google Scholar] [CrossRef]
- Wang, S.; Tang, X.Y.; Lou, S.Y. Soliton fission and fusion: Burgers equation and Sharma-Tasso-Olver equation. Chaos Soliton Fractals 2004, 21, 231–239. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Ren, B.; Wang, W.-L. Symmetry Reductions, Cte Method and Interaction Solutions for Sharma-Tasso-Olver-Burgers Equation. Symmetry 2022, 14, 1690. https://doi.org/10.3390/sym14081690
Yu J, Ren B, Wang W-L. Symmetry Reductions, Cte Method and Interaction Solutions for Sharma-Tasso-Olver-Burgers Equation. Symmetry. 2022; 14(8):1690. https://doi.org/10.3390/sym14081690
Chicago/Turabian StyleYu, Jun, Bo Ren, and Wan-Li Wang. 2022. "Symmetry Reductions, Cte Method and Interaction Solutions for Sharma-Tasso-Olver-Burgers Equation" Symmetry 14, no. 8: 1690. https://doi.org/10.3390/sym14081690
APA StyleYu, J., Ren, B., & Wang, W.-L. (2022). Symmetry Reductions, Cte Method and Interaction Solutions for Sharma-Tasso-Olver-Burgers Equation. Symmetry, 14(8), 1690. https://doi.org/10.3390/sym14081690







