Abstract
The flow of a viscous incompressible fluid outflowing from a uniformly moving point source is considered. An exact solution to the problem is found in the way that the velocity decreases inversely with the radial coordinate. It is shown that a spherical volume of fluid is carried away by the source, the radius of which is inversely proportional with respect to the velocity of motion. In this case, a cylindrical discontinuity arises in the region of forming a wake behind the body, the dimensions of which are determined by the magnitude of the external pressure and do not depend on the velocity of the source. The obtained solutions are governed by hydrodynamical fields of flows which can be recognized as special invariants at symmetry reduction.
1. Introduction
The problem for the motion of bodies in a viscous fluid has numerous applications and has been studied in sufficient detail [1,2,3,4,5,6,7,8]. The greatest attention is traditionally paid to the description of the fluid flow near a moving body, where the velocity field depends significantly on the shape and size of the object under study [1,2,3,4,5,6,7,8]. At the same time, at sufficiently large distances, there must obviously be a universal solution, which will depend on a certain set of parameters characterizing the properties of the fluid and the specific mode of motion of the body. Moreover, taking into account the asymptotic nature of the description of the flow, the real body can be replaced by a source of momentum of zero size. In this paper, we consider a point source moving at a constant velocity in a viscous incompressible fluid. The main and only assumption is the hypothesis of a hyperbolic decrease in velocity with distance from the source, which is a direct consequence of the momentum flux conservation.
2. Problem Statement
We consider a point source moving uniformly in a viscous incompressible fluid that fills the surrounding space. It is required to determine the parameters of the flow that decays (to be uniform or at rest) with sufficient distance from the source. To solve the problem, let us go to the spherical coordinate system associated with the source. The coordinate system is non-inertial, and its origin moves together with the source. In this case, the stationary distribution of pressure and velocity is described by the Navier–Stokes equation and the continuity equation:
Equation (1) is written in an invariant form. Here, is the fluid flow velocity, is the pressure, is the constant density of the fluid, is the coefficient of kinematic viscosity, is the Hamilton operator, square brackets denote the vector product of vectors, and the dot denotes the scalar product.
As for boundary conditions to the system of Equation (1), we accept the conditions of pressure constancy and velocity uniformity at infinity:
is the external pressure, is the velocity of the body, which is assumed to be constant and being directed in the opposite direction with respect to the polar axis, so that at , the fluid flows onto the body under study. We assume that the velocity and pressure are periodic functions with respect to the variables , , and do not tend to infinity anywhere, except for the origin and the line , which corresponds to the trace area. The introduced assumption means that the speed and pressure can be infinite at every point on the line . We assume that the velocity at infinity is equal to , where is not equal to zero (), since the description of the motion is asymptotic. Thus, we are not considering a physical infinity, but a mathematical one. It is assumed that the region is finite, but at the first stage of the study of fluid motion, we formally assume that it is infinite. It is obvious that the exact solution, which will be announced below, will be valid for .
4. Investigation of Hydrodynamic Fields
Analysis of these equations shows that they are solvable only in the class of potential flows. Note that the requirement of belonging to the class of potential flows is a direct consequence of the assumption of a hyperbolic decrease of velocity field with distance from the source. Thus, the system of Equation (1) is reduced to the Bernoulli equation and to the condition that the rotor of velocity should be equal to zero, which altogether, after a simple integration, leads to the following equations:
is an arbitrary constant having the dimension of viscosity .
Taking into account that, in accordance with the boundary conditions, the components of the potentials and are periodic, as well as that the features of the velocity and pressure are admissible only in the wake region, we write the general solution of Equation (5) in the form of a Fourier series [9,10]:
where , , are the eigenfunctions of the Laplace operator, , , , are arbitrary constants.
To analyze the results to be obtained, we restrict ourselves to the case of an axisymmetric flow (when the azimuthal component of the potential is equal to zero) and, according to (6), of the assumption of only the first term to be present in the poloidal component ( and ).
We substitute the obtained expressions into (4) and then afterwards introduce the current function, and we obtain:
Expression (7) determines the dependence of the velocity on the coordinates , and at the same time, they are equations for the stream function . After solving these equations and substituting Formula (7) into the Bernoulli Equation (5), we will determine the pressure and the stream function, which, for convenience, can be represented as:
where . In the case of a source as the origin of the flow field, the parameter is positive, and in the case of a sink, in Formula (8) it is necessary to change the sign in the terms containing the first powers of . Then we should obtain expressions for the hydrodynamic fields.
Analysis of Formula (8) shows that a spherical volume of radius of fluid is carried away by the moving source, inside which the velocity component along the axis of motion of the body is positive, while the velocity of the external flow is negative (Figure 1, Figure 2 and Figure 3). Moreover, the fluid flows out of the trace area, which has zero thickness, and the parameter determines the amount of fluid flowing out of a segment of unit length per unit time.
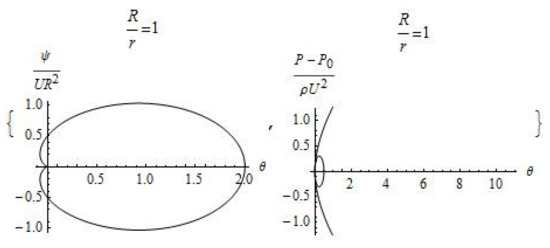
Figure 1.
Plot of the dimensionless stream functions and pressure ( and ).
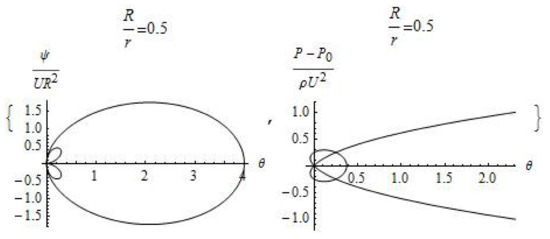
Figure 2.
Plot of the dimensionless stream functions and pressure ( and ).

Figure 3.
Plot of the dimensionless stream functions and pressure ( and ).
The velocity of motion is equal to zero at the point of intersection of the lines on which the stream function is equal to zero. The pressure, in accordance with the Bernoulli Equation (5), at a given point takes on a maximum value equal to the sum of the external pressure and the kinetic energy of the external flow. The area of reduced pressure is separated from the external flow by a paraboloid of revolution, the center of which is located at distance in front of the body. The zone of zero pressure covers all surface of the moving body and turns to be a cylindrical surface at a distance of sufficiently large meanings of , the radius of which does not depend on the velocity of motion and is determined by the pressure at infinity and by the density of the fluid:
In the case of a moving sink or drain as a origin of flow (), the fluid flows into the wake’s area and, as in case of the aforementioned source motion, a cylindrical space area of discontinuity of radius is to be formed behind the body.
We note that the obtained solution corresponds to the problem of flow around a half-of-infinite thread, on which sources or sinks of fluid are located, and is the power per unit length of the thread.
We note that Formulas (8) and (9) actually describe the formation of a cavitation cushion (cylindrical wake) (Figure 4, Figure 5 and Figure 6). Fluid flows into this trace, which can be used to create new pneumatic and hydrotransport devices. For example, this exact solution of simplified Navier–Stokes equations can help to transport goods over long distances. A similar experimental approach is presented in article [11], and this article provides a theoretical justification for a new method of momentum transfer in liquids.
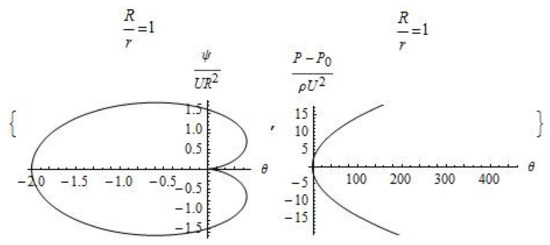
Figure 4.
Plot of the dimensionless stream functions and pressure ( and ).
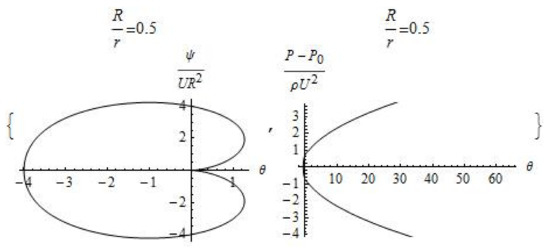
Figure 5.
Plot of the dimensionless stream functions and pressure ( and ).
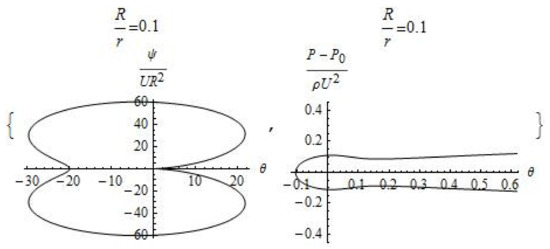
Figure 6.
Plot of the dimensionless stream functions and pressure ( and ).
An additional important remark should be mentioned regarding the physical essence of the suggested class of solutions as follows: as for the negative value of pressure P, we know physically reasonable cases of flows when pressure is transformed to be negative (according to the results of profound work by the academician L.I. Sedov regarding the conditions for boiling in the fluid flows: in the vicinity of or inside the bubbles during the boiling in the fluid flows, pressure appears to be negative, but these are very special conditions for the flow of fluids). Namely, such fluids are incapable of taking tensile loads (at negative pressure), whereas the abovementioned physical mechanism may be treated as a phenomenon of boiling a liquid as soon as its pressure is lowered below zero locally [11,12,13].
5. Conclusions
In this article, a new exact solution of simplified Navier–Stokes equations is obtained. It describes the flow of a fluid generated by a point source. This exact solution of simplified Navier–Stokes equations is similar in its form to the potential flow for an ideal fluid. It is shown that there are two flow regimes. The assumed size of space of a cylindrical discontinuity in a fluid is determined. The trace length does not depend on the velocity of the moving source in the fluid. The obtained new exact solution of simplified Navier–Stokes equations can become a fundamental basis for the development of new engineering approaches for the design of pneumatic and hydraulic transport.
The obtained solutions are governed by hydrodynamical fields of flows which can be recognized as special invariants at symmetry reduction. The final state of such maximal symmetry reduction can be presented as Hopf bifurcation of zeroth order which can be considered to be a prototype for the study of a dynamical chaos for the trajectories of non-stationary solutions [14,15,16,17].
Author Contributions
Conceptualization, E.Y.P. and S.V.E.; methodology, E.Y.P.; software, E.Y.P.; validation, E.Y.P., S.V.E. and D.D.L.; formal analysis, E.Y.P.; investigation, E.Y.P.; resources (are not available); data curation, E.Y.P.; writing—original draft preparation, E.Y.P.; writing—review and editing, E.Y.P.; visualization, E.Y.P.; supervision, S.V.E.; project administration, D.D.L.; funding acquisition is not applicable. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stokes, G.G. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1880; Volume 1. [Google Scholar]
- Moiseyev, N.N.; Rumyantsev, V.V. Dynamic Stability of Bodies Containing Fluid; Springer: New York, NY, USA, 1968. [Google Scholar]
- Ratner, B.D.; Hoffman, A.S.; Schoen, F.J.; Lemons, J.E. (Eds.) Nanomedicine, Biomaterials Science: An Introduction to Materials in Medicine; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Humphrey, J.D.; Delange, S.L. An Introduction to Biomechanics: Solids and Fluids, Analysis and Design; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Planas, G.; Sueur, F. On the “viscous incompressible fluid + rigid body” system with Navier conditions. Ann. Inst. H. Poincaré Anal. Non Linéaire 2014, 31, 55–80. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Prosviryakov, E.Y.; Burmasheva, N.V.; Christianto, V. Towards understanding the algorithms for solving the Navier-Stokes equations. Fluid Dyn. Res. 2021, 53, 044501. [Google Scholar] [CrossRef]
- Aristov, S.N.; Knyazev, D.V.; Polyanin, A.D. Exact solutions of the Navier–Stokes equations with the linear dependence of velocity components on two space variables. Theor. Found. Chem. Eng. 2009, 43, 642–662. [Google Scholar] [CrossRef]
- Drazin, P.G.; Riley, N. The Navier–Stokes Equations: A Classification of Flows and Exact Solutions; Cambridge University Press: Cambridge, UK, 2006; 196p. [Google Scholar]
- Aristov, S.N. An Exact Solution to the Point Source Problem. Dokl. Phys. 1995, 40, 346–348. [Google Scholar]
- Aristov, S.N. Stationary Cylindrical Vortex in a Viscous Fluid. Dokl. Phys. 2001, 46, 251–253. [Google Scholar] [CrossRef]
- Leporini, M.; Terenzi, A.; Marchetti, B.; Giacchetta, G.; Corvaro, F. Experiences in numerical simulation of wax deposition in oil and multiphase pipelines: Theory versus reality. J. Pet. Sci. Eng. 2019, 174, 997–1008. [Google Scholar] [CrossRef]
- Sedov, L.I. Mechanics of Continuous Media; World Scientific: Singapore, 1997; Volume 1. [Google Scholar]
- Liu, Y.; Peng, Y. Study on the Collapse Process of Cavitation Bubbles Including Heat Transfer by Lattice Boltzmann Method. J. Mar. Sci. Eng. 2021, 9, 219. [Google Scholar] [CrossRef]
- Ershkov, S.V. Non-stationary helical flows for incompressible 3D Navier–Stokes equations. Appl. Math. Comput. 2016, 274, 611–614. [Google Scholar] [CrossRef]
- Ershkov, S.V. About existence of stationary points for the Arnold-Beltrami-Childress (ABC) flow. Appl. Math. Comput. 2016, 276, 379–383. [Google Scholar] [CrossRef][Green Version]
- Ershkov, S.V.; Shamin, R.V. A Riccati-type solution of 3D Euler equations for incompressible flow. J. King Saud Univ. - Sci. 2020, 32, 125–130. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Rachinskaya, A.; Prosviryakov, E.Y.; Shamin, R.V. On the semi-analytical solutions in hydrodynamics of ideal fluid flows governed by large-scale coherent structures of spiral-type. Symmetry 2021, 13, 2307. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).