Intuitionistic Fuzzy Topology Based on Intuitionistic Fuzzy Logic

Abstract

There are many symmetries in intuitionistic fuzzifying topology. In the present paper, the notion of intuitionistic fuzzifying topology as an extension of fuzzifying topology and a preliminary of the research on bi-intuitionistic fuzzy topology is introduced. A theory of intuitionistic fuzzy topology with the semantic method of intuitionistic fuzzy logic is established.

1. Introduction

Symmetry takes place not only in geometry but also in other branches of mathematics. In particular, there are many symmetries in groups, rings, fields, lattices, fuzzy logic, topology, and fuzzy topology. In fuzzy topology, the intuitionistic fuzzifying topology is one of the most basic notions. Intuitionism is a very important mathematical property, and it exists in many research areas, such as vector space, metric space, and partially ordered sets. By abstracting the common properties of intuitionistic fuzzy sets, the intuitionistic fuzzy structures were proposed. We already see that serious research on this topic is absolutely necessary, even in hindsight.

Fuzzy sets were introduced by L. A. Zadeh [1] in 1965. In 1983, Atanassov proposed the concept of intuitionistic fuzzy set [2]. Some basic results on intuitionistic fuzzy sets were published in [3,4], and the book [5] offers a comprehensive study and applications of intuitionistic fuzzy sets. In fact, intuitionistic fuzzy sets are a topic of research by many scholars [6,7]. In particular, elements of intuitionistic fuzzy logic and, in the area of applications, were studied by Atanassov and co-workers (see [5,8,9]). According to Ref. [10], the kind of topologies defined by Chang [11] and Goguen [12] is called the topologies of fuzzy subset, and is called L-topological spaces if a lattice L of membership values has been chosen. From another side, Höhle in [13] proposed the term L-fuzzy topology to be a map from $\mathcal{P}\left(\mathcal{X}\right)$ to $\mathcal{X}$. The authors in [14,15] defined an L-fuzzy topology to be a map from $L^{\mathcal{X}}$ of $\mathcal{X}$. Çoker [16,17] established the intuitionistic fuzzy topological space. The intuitionistic fuzzy topology is a family $\tau$ of intuitionistic fuzzy subsets of a non-empty set $\mathcal{X}$, and $\tau$ satisfies the basic conditions of classical topologies [18]. Ying, in 1991–1993 [19,20,21], used a semantical method of multi-valued logic to develop methodically fuzzifying topology. Now, we suggest the following problems: What are the details of the many-valued theories beyond the level of intuitionistic predicates calculus? To provide a partial answer to this issue in topology, we use a semantical method of intuitionistic fuzzy logic to develop methodically intuitionistic fuzzifying topology. Intuitionistic fuzzifying topology is an extension of fuzzifying topology and introductory research on bi-intuitionistic fuzzy topology. The rest of this paper is organized as follows. The next section contains necessary concepts and properties. Section 3 is exclusively devoted to intuitionistic fuzzy logics. In Section 4, the concept of bi-intuitionistic fuzzy topological spaces is defined and some examples are introduced. In Section 5, in the intuitionistic fuzzifying topology, we discuss the neighborhood system of a point. In Section 6, we introduce the concepts of intuitionistic fuzzifying closure, intuitionistic fuzzifying boundary, intuitionistic fuzzifying derived set, and intuitionistic fuzzifying interior. The goal of the last section is to conclude this paper with a succinct but precise recapitulation of our main findings, and to give some lines for future research.

2. Preliminaries

First, we recall some necessary notations that will be used throughout the whole paper.

Definition 1

([2]). Let $\mathcal{X}$ be a non-empty set. An intuitionistic fuzzy set ($\mathcal{IF}$ set for short) $\widehat{\mathcal{A}}$, is an object having the form $(m\widehat{\mathcal{A}},n\widehat{\mathcal{A}})$, where the functions $m\widehat{\mathcal{A}}:\mathcal{X}\to [0,1]$ and $n\widehat{\mathcal{A}}:\mathcal{X}\to [0,1]$ denote the degree of membership (namely $m\widehat{\mathcal{A}}\left(x\right)$) and the degree of non-membership (namely $n\widehat{\mathcal{A}}\left(x\right)$) of each element $x\in \mathcal{X}$ to the set $\widehat{\mathcal{A}}$, respectively, and $0\le m\widehat{\mathcal{A}}\left(x\right)+n\widehat{\mathcal{A}}\left(x\right)\le 1$ for each $x\in \mathcal{X}$. The set of all intuitionistic fuzzy set of $\mathcal{X}$ is denoted by $\mathcal{IF}\left(\mathcal{X}\right)$. Note that an intuitionistic fuzzy set becomes a fuzzy set when we dispense with non-membership.

The next definitions present some basic set-theoretic operations for intuitionistic fuzzy sets.

Definition 2

([4]). Let $\mathcal{X}$ be a non-empty set, and $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right)$. Then

(a) $\widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}$ if and only if $m\widehat{\mathcal{A}}\left(x\right)\le m\widehat{\mathcal{B}}\left(x\right)$ and $n\widehat{\mathcal{A}}\left(x\right)\ge n\widehat{\mathcal{B}}\left(x\right)$ for all $x\in \mathcal{X}$;

(b) $\widehat{\mathcal{A}}=\widehat{\mathcal{B}}$ if and only if $\widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}$ and $\widehat{\mathcal{B}}\subseteq \widehat{\mathcal{A}}$;

(c) $\neg \widehat{\mathcal{A}}=(n\widehat{\mathcal{A}},m\widehat{\mathcal{A}})$;

(d) $\widehat{\mathcal{A}}\cap \widehat{\mathcal{B}}=(m\widehat{\mathcal{A}}\wedge m\widehat{\mathcal{B}},n\widehat{\mathcal{A}}\vee n\widehat{\mathcal{B}}))$;

(e) $\widehat{\mathcal{A}}\cup \widehat{\mathcal{B}}=(m\widehat{\mathcal{A}}\vee m\widehat{\mathcal{B}},n\widehat{\mathcal{A}}\wedge n\widehat{\mathcal{B}})$.

Definition 3

([16]). Let $\left\{{\widehat{\mathcal{A}}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\}\subseteq \mathcal{IF}\left(\mathcal{X}\right)$. Then

(a) ${\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }=\left({\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }}m{\widehat{\mathcal{A}}}_{\lambda }\left(x\right),{\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigvee }}n{\widehat{\mathcal{A}}}_{\lambda }\left(x\right)\right)$;

(b) ${\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }=\left({\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigvee }}m{\widehat{\mathcal{A}}}_{\lambda }\left(x\right),{\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }}n{\widehat{\mathcal{A}}}_{\lambda }\left(x\right)\right)$;

(c) $\widehat{1}=(1,0)$ and $\widehat{0}=(0,1)$.

Remark 1.

(1) If $\mathcal{A}\in \mathcal{P}\left(\mathcal{X}\right)$, then $\mathcal{A}$ is identified with an $\mathcal{IF}$ set $\widehat{\mathcal{A}}$ of $\mathcal{X}$ such that $m\widehat{\mathcal{A}}=\mathcal{A}$ and $n\widehat{\mathcal{A}}=\mathcal{X}-\mathcal{A}$;

(2) If $\tilde{\mathcal{A}}\in \Im \left(\mathcal{X}\right)$ ($\Im \left(\mathcal{X}\right)$ is the set of all fuzzy subsets of $\mathcal{X}$), then $\tilde{\mathcal{A}}$ is identified with an $\mathcal{IF}$ set $\widehat{\mathcal{A}}$ of $\mathcal{X}$ such that $m\widehat{\mathcal{A}}=\tilde{\mathcal{A}}$ and $n\widehat{\mathcal{A}}=1-n\tilde{\mathcal{A}}$ [2];

(3) $\widehat{\mathcal{A}}\in \mathcal{IF}\left(\mathcal{X}\right)$ is called normal if and only if there exists $x\in \mathcal{X}$ such that $\widehat{\mathcal{A}}\left(x\right)=(1,0)$. The set of all normal $\mathcal{IF}$ sets of $\mathcal{X}$ will be denoted by ${\mathcal{IF}}^{\mathcal{N}}\left(\mathcal{X}\right)$;

(4) The dual complement of $\widehat{\mathcal{A}}$, denoted by $\neg \widehat{\mathcal{A}}$, is defined as follows:

$$\neg \widehat{\mathcal{A}}\left(x\right)=\neg \left(\widehat{\mathcal{A}}\left(x\right)\right)=(n\widehat{\mathcal{A}}\left(x\right),m\widehat{\mathcal{A}}\left(x\right)).$$

3. Intuitionistic Fuzzy Logic

Now, we give the intuitionistic fuzzy logical and corresponding intuitionistic fuzzy set-theoretical notions. Let

$$\mathcal{Z}=\left\{(\alpha ,\beta )\left|(\alpha ,\beta )\in [0,1]\times [0,1],\alpha +\beta \le 1\right\}\right..$$

By an intuitionistic fuzzy well formed formula $\phi$ we mean any proposition with respect to which we assign an element $(a,b)\in \mathcal{Z}$. We say that $a=m\left(\phi \right)$ and $b=n\left(\phi \right)$ and called them the truth degree and the falsity degree of $\phi$, respectively. Let $\mathcal{M}$ denote the set of all intuitionistic fuzzy well formed formula and consider the function $\mathcal{V}:\mathcal{M}⟶\mathcal{Z}$. If $\phi \in \mathcal{M}$ and $\mathcal{V}\left(\phi \right)=(a,b)$ we write $\left[\phi \right]=(a,b)$. We say that $\phi$ is valid (or a tautology) and we type $\vDash \phi$ if $\left[\phi \right]=(1,0)$.

Definition 4.

(1) The binary relation “=”, “<”, “≤”, “∧” and “∨” and the unary operation “¬” on $\mathcal{Z}$ are defined as:

(a) $(\alpha ,\beta )=(\gamma ,\delta )$ if and only if $\alpha =\gamma$ and $\beta =\delta$;

(b) $(\alpha ,\beta )\le (\gamma ,\delta )$ if and only if $\alpha \le \gamma$ and $\beta \ge \delta$;

(c) $(\alpha ,\beta )<(\gamma ,\delta )$ if and only if $\alpha <\gamma$ and $\beta >\delta$;

(d) $[(\alpha ,\beta )\wedge (\gamma ,\delta )]:=(min\left\{\alpha ,\gamma \right\},max\left\{\beta ,\delta \right\})$;

(e) $[(\alpha ,\beta )\vee (\gamma ,\delta )]:=(max\left\{\alpha ,\gamma \right\},min\left\{\beta ,\delta \right\})$;

(f) $[\neg (\alpha ,\beta \left)\right]:=(\beta ,\alpha )$.

(2) (a) The intuitionistic fuzzy implications $“\to ,\dot{\to }”\in {\mathcal{Z}}^{\mathcal{Z}\times \mathcal{Z}}$ are defined as follows:

$$[(\alpha ,\beta )\to (\gamma ,\delta )]=\left(min(1,1-\alpha +\gamma ,1-\delta +\beta ),max(0,\alpha -\gamma ,\delta -\beta )\right),$$

$$\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]=\left(min(1,\beta +\gamma ),max(0,\alpha +\delta -1)\right);$$

(b) For each $\alpha \in {\mathcal{Z}}^{\mathcal{X}}$ (i.e., $\alpha :\mathcal{X}\to \mathcal{Z}$), we have

$$[\forall x\alpha \left(x\right)]:=\underset{x\in \mathcal{X}}{\bigwedge }\alpha \left(x\right):=\left(\underset{x\in \mathcal{X}}{\bigwedge }m\alpha \left(x\right),\underset{x\in \mathcal{X}}{\bigvee }n\alpha \left(x\right)\right).$$

For example, if $\alpha :\mathcal{X}\to \mathcal{Z}$ and $\mathcal{X}=\{a,b,c\}$, where $\alpha \left(a\right)=(0.3,0.6)$, $\alpha \left(b\right)=(0.4,0.3)$ and $\alpha \left(c\right)=(0.5,0.1)$, then $[\forall x\alpha (x\left)\right]=(0.3,0.6)$.

(3) (a)

$$\left[\right(\alpha ,\beta )⋏(\gamma ,\delta \left)\right]:=[\neg ((\alpha ,\beta )\to \neg (\gamma ,\delta )\left)\right],$$

$$[(\alpha ,\beta )⊼(\gamma ,\delta )]:=[\neg ((\alpha ,\beta )\dot{\to }\neg (\gamma ,\delta ))];$$

(b)

$$\left[\right(\alpha ,\beta )⋎(\gamma ,\delta \left)\right]:=[\neg (\alpha ,\beta )\to (\gamma ,\delta \left)\right],$$

$$[(\alpha ,\beta )⊻(\gamma ,\delta )]:=[\neg (\alpha ,\beta )\dot{\to }(\gamma ,\delta )];$$

(4) (a)

$$\left[\right(\alpha ,\beta )⟷(\gamma ,\delta \left)\right]:=\left[\right((\alpha ,\beta )\to (\gamma ,\delta ))\wedge ((\gamma ,\delta )\to (\alpha ,\beta )\left)\right],$$

$$\left[(\alpha ,\beta )\dot{⟷}(\gamma ,\delta )\right]:=[\left((\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right)\wedge \left((\gamma ,\delta )\dot{\to }(\alpha ,\beta )\right)].$$

For example, if $(\alpha ,\beta )=(0.6,0.3)$ and $(\gamma ,\delta )=(0.5,0.4)$, then

$\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]=(0.9,0.1)$ and $\left[\right(\gamma ,\delta )\to (\alpha ,\beta \left)\right]=(1,0)$.

Therefore $\left[\right(\alpha ,\beta )⟷(\gamma ,\delta \left)\right]=(0.9,0.1)\wedge (1,0)=(0.9,0.1)$.

Similarly, $\left[(\alpha ,\beta )\dot{⟷}(\gamma ,\delta )\right]=(0.9,0)$.

(b) $[\exists x\alpha (x\left)\right]:=[\neg (\forall x\neg \left(\alpha \right(x\left)\right)\left)\right]$;

(5) Let $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right)$,

(a) $[x\in \widehat{\mathcal{A}}]:=\left[\widehat{\mathcal{A}}\left(x\right)\right]$;

The intuitionistic fuzzy inclusions “⊆ and ⋐”, and the intuitionistic fuzzy equalities “$\equiv ,\approx ,\dot{\equiv }$ and $\dot{\approx }$” between two intuitionistic fuzzy sets are defined as follows:

(b) $[\widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}]:=[\forall x(x\in \widehat{\mathcal{A}}\to x\in \widehat{\mathcal{B}})]$;

(c) $[\widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}]:=[(\widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}})\wedge (\widehat{\mathcal{B}}\subseteq \widehat{\mathcal{A}})]$;

(d) $[\widehat{\mathcal{A}}\approx \widehat{\mathcal{B}}]:=[(\widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}})⋏(\widehat{\mathcal{B}}\subseteq \widehat{\mathcal{A}})]$;

(e) $[\widehat{\mathcal{A}}⋐\widehat{\mathcal{B}}]:=[\forall x(x\in \widehat{\mathcal{A}}\dot{\to }x\in \widehat{\mathcal{B}})]$;

(f) $\left[\widehat{\mathcal{A}}\dot{\equiv }\widehat{\mathcal{B}}\right]:=[(\widehat{\mathcal{A}}⋐\widehat{\mathcal{B}})\wedge (\widehat{\mathcal{B}}⋐\widehat{\mathcal{A}})]$;

(g) $\left[\widehat{\mathcal{A}}\dot{\approx }\widehat{\mathcal{B}}\right]:=[(\widehat{\mathcal{A}}⋐\widehat{\mathcal{B}})⊼(\widehat{\mathcal{B}}⋐\widehat{\mathcal{A}})]$.

(6) Let $f:\mathcal{X}\to \mathcal{Y}$ be a function, $\widehat{\mathcal{A}}\in \mathcal{IF}\left(\mathcal{X}\right)$ and $\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{Y}\right)$.

The image $f\left(\widehat{\mathcal{A}}\right)$ of $\widehat{\mathcal{A}}$ under f is an intuitionistic fuzzy set in $\mathcal{Y}$ defined by:

$f\left(\widehat{\mathcal{A}}\right)\left(y\right)=(f\left(m\widehat{\mathcal{A}}\right)\left(y\right),1-f(1-n\widehat{\mathcal{A}})\left(y\right))\forall y\in \mathcal{Y}$.

The inverse image $f^{-1}\left(\widehat{\mathcal{B}}\right)$ of $\widehat{\mathcal{B}}$ under f is an intuitionistic fuzzy set in $\mathcal{X}$ defined by:

$f^{-1}\left(\widehat{\mathcal{B}}\right)=(f^{-1}\left(m\widehat{\mathcal{B}}\right)\left(x\right),f^{-1}\left(n\widehat{\mathcal{B}}\right)\left(x\right))\forall x\in \mathcal{X}$.

Theorem 1.

$(\mathcal{Z},\le ,\wedge ,\vee ,\neg )$ is a complete completely distributive lattice with least element $(0,1)$ and greatest element $(1,0)$, this is equipped with an order reversing involution $“\neg ”$.

Remark 2.

(1) The completely distributive law in $\mathcal{Z}$ is of the form:

$$\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\underset{(\alpha ,\beta )\in {\wp }_{\lambda }}{\bigvee }(\alpha ,\beta )=\underset{f\in \underset{\lambda \in \mathsf{\Lambda }}{\pi }{\wp }_{\lambda }}{\bigvee }\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }f\left(\lambda \right),$$

where ${\wp }_{\lambda }\subseteq \mathcal{Z}$ for all $\lambda \in \mathsf{\Lambda }$.

(2) It is clear that $(\mathcal{Z},\le )$ is not totally ordered set (Indeed, $(\frac{1}{4},\frac{1}{3}),(\frac{1}{2},\frac{1}{2})\in \mathcal{Z}$, but $(\frac{1}{4},\frac{1}{3})$ is not comparable with $(\frac{1}{2},\frac{1}{2})$ by the relation $“\le ”$.

Theorem 2.

Let $(\alpha ,\beta ),(\gamma ,\delta )\in \mathcal{Z}$. Then

(1) $[\neg (\alpha ,\beta )]=\left[(\alpha ,\beta )\dot{\to }(0,1)\right]$;

(2) $[(\alpha ,\beta )⋏(\gamma ,\delta )]=\left(max(0,\alpha -\delta ,\gamma -\beta ),min(1,1-\alpha +\delta ,1-\gamma +\beta )\right)$

(3) $[(\alpha ,\beta )⋎(\gamma ,\delta )]=\left(min(1,1-\beta +\gamma ,1-\delta +\alpha ),max(0,\beta -\gamma ,\delta -\alpha )\right)$

(4) $\left[\right(\alpha ,\beta )⊼(\gamma ,\delta \left)\right]=(max(0,\alpha +\gamma -1),min(1,\beta +\delta \left)\right)$;

(5) $\left[\right(\alpha ,\beta )⊻(\gamma ,\delta \left)\right]=(min(1,\alpha +\gamma ),max(0,\beta +\delta -1\left)\right)$;

(6) $\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]=[\neg (\alpha ,\beta )⋎(\gamma ,\delta \left)\right]$;

(7) $\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]=[\neg (\alpha ,\beta )⊻(\gamma ,\delta )]$;

(8) $[\neg \left((\alpha ,\beta )\wedge (\gamma ,\delta )\right)]=[\neg (\alpha ,\beta )\vee \neg (\gamma ,\delta )]$;

(9) $[\neg \left((\alpha ,\beta )\vee (\gamma ,\delta )\right)]=[\neg (\alpha ,\beta )\wedge \neg (\gamma ,\delta )]$;

(10) $\left[\right(\alpha ,\beta )⋎(\gamma ,\delta \left)\right]=[\neg (\neg (\alpha ,\beta )⋏\neg (\gamma ,\delta )\left)\right]$;

(11) $\left[\right(\alpha ,\beta )⊻(\gamma ,\delta \left)\right]=[\neg (\neg (\alpha ,\beta )⊼\neg (\gamma ,\delta )\left)\right]$.

Proof. 

(1) $\left[(\alpha ,\beta )\dot{⟶}(0,1)\right]=(min(1,\beta +0),max(0,\alpha +1-1))=(\beta ,\alpha )=[\neg (\alpha ,\beta )]$;

(2) $\left[\right(\alpha ,\beta )⋏(\gamma ,\delta \left)\right]=[\neg ((\alpha ,\beta )⟶\neg (\gamma ,\delta )\left)\right]=[\neg ((\alpha ,\beta )⟶(\delta ,\gamma )\left)\right]$

$=\neg (min(1,1-\alpha +\delta ,1-\gamma +\beta ),max(0,\alpha -\delta ,\gamma -\beta \left)\right)$

$=(max(0,\alpha -\delta ,\gamma -\beta ),min(1,1-\alpha +\delta ,1-\gamma +\beta \left)\right)$;

(3) $\left[\right(\alpha ,\beta )⋎(\gamma ,\delta \left)\right]=[\neg (\neg (\alpha ,\beta )⋏\neg (\gamma ,\delta )\left)\right]=[\neg ((\beta ,\alpha )⋏(\delta ,\gamma )\left)\right]$

$=[\neg (\neg \left(\right(\beta ,\alpha )⟶\neg (\delta ,\gamma \left)\right)\left)\right]=\left[\right(\beta ,\alpha )⟶(\gamma ,\delta \left)\right]$

$=(min(1,1-\beta +\gamma ,1-\delta +\alpha ),max(0,\beta -\gamma ,\delta -\alpha \left)\right)$;

(4) $[(\alpha ,\beta )⊼(\gamma ,\delta )]=[\neg ((\alpha ,\beta )\dot{⟶}\neg (\gamma ,\delta ))]=[\neg \left((\alpha ,\beta )\dot{⟶}(\delta ,\gamma )\right)]$

$=\neg (min(1,\beta +\delta ),max(0,\alpha +\gamma -1\left)\right)=(max(0,\alpha +\gamma -1),min(1,\beta +\delta \left)\right)$;

(5) $[(\alpha ,\beta )⊻(\gamma ,\delta )]=[\neg (\alpha ,\beta )\dot{⟶}(\gamma ,\delta )]=\left[(\beta ,\alpha )\dot{⟶}(\gamma ,\delta )\right]=(min(1,\alpha +\gamma ),max(0,\beta +\delta -1))$;

(6) $[\neg (\alpha ,\beta )⋎(\gamma ,\delta \left)\right]=[\neg (\neg (\alpha ,\beta ))⟶(\gamma ,\delta \left)\right]=\left[\right(\alpha ,\beta )⟶(\gamma ,\delta \left)\right]$;

(7) $[\neg (\alpha ,\beta )⊻(\gamma ,\delta )]=[\neg (\neg (\alpha ,\beta ))\dot{⟶}(\gamma ,\delta )]=\left[(\alpha ,\beta )\dot{⟶}(\gamma ,\delta )\right]$;

(8) $[\neg ((\alpha ,\beta )\wedge (\gamma ,\delta )\left)\right]=\neg (min(\alpha ,\gamma ),max(\beta ,\delta \left)\right)=(max(\beta ,\delta ),min(\alpha ,\gamma \left)\right)=\left[\right(\beta ,\alpha )\vee (\delta ,\gamma \left)\right]=[\neg (\alpha ,\beta )\vee \neg (\gamma ,\delta \left)\right]$;

(9) The proof is similar to that of (8);

(10) $[\neg (\neg (\alpha ,\beta )⋏\neg (\gamma ,\delta )\left)\right]=[\neg ((\beta ,\alpha )⋏(\delta ,\gamma )\left)\right]=\neg (max(0,\beta -\gamma ,\delta -\alpha ),min(1,1-\beta +\gamma ,1-\delta +\alpha \left)\right)=(min(1,1-\beta +\gamma ,1-\delta +\alpha ),max(0,\beta -\gamma ,\delta -\alpha \left)\right)=\left[\right(\alpha ,\beta )⋎(\gamma ,\delta \left)\right]$;

(11) $[\neg (\neg (\alpha ,\beta )⊼\neg (\gamma ,\delta )\left)\right]=[\neg ((\beta ,\alpha )⊼(\delta ,\gamma )\left)\right]=\neg (max(0,\beta +\delta -1),min(1,\alpha +\gamma \left)\right)=(min(1,\alpha +\gamma ),max(0,\beta +\delta -1\left)\right)=\left[\right(\alpha ,\beta )⊻(\gamma ,\delta \left)\right]$. □

Theorem 3.

(1) ⊼ and ⋏ are isotone functions;

(2) $(\mathcal{Z},⊼,(1,0\left)\right)$ is a commutative monoid;

(3) $(\mathcal{Z},⋏)$ is a commutative semi-group such that $\left[\right(\alpha ,\beta )⋏(1,0\left)\right]=\left[\right(1,0)⋏(\alpha ,\beta \left)\right]=(1-\beta ,\beta )$;

(4) ⊼ is distributive over arbitrary joins, i.e.,

$$(\alpha ,\beta )⊼\underset{j\in \mathsf{\Lambda }}{\bigvee }\left({\gamma }_j,{\delta }_j\right)=\underset{j\in \mathsf{\Lambda }}{\bigvee }\left((\alpha ,\beta )⊼({\gamma }_j,{\delta }_j)\right),$$

for every $(\alpha ,\beta )\in \mathcal{Z},\{({\gamma }_j,{\delta }_j):j\in \mathsf{\Lambda }\}\subseteq \mathcal{Z}$.

Proof. 

(1) To prove that ⊼ is isotone function, suppose that $(\alpha ,\beta )\le ({\alpha }_1,{\beta }_1)$ and $(\gamma ,\delta )\le ({\gamma }_1,{\delta }_1)$. Then $\alpha \le {\alpha }_1$, $\beta \ge {\beta }_1$, $\gamma \le {\gamma }_1$ and $\delta \ge {\delta }_1$. Hence, $\alpha +\gamma -1\le {\alpha }_1+{\gamma }_1-1$ and $\beta +\delta \ge {\beta }_1+{\delta }_1$. Therefore,

$\left[\right(\alpha ,\beta )⊼(\gamma ,\delta \left)\right]=(max(0,\alpha +\gamma -1),min(1,\beta +\delta \left)\right)$

$\le (max(0,{\alpha }_1+{\gamma }_1-1),min(1,{\beta }_1+{\delta }_1))=[({\alpha }_1,{\beta }_1)⊼({\gamma }_1,{\delta }_1)]$.

Similarly, from Theorem 2 (2) ⋏ is isotone function.

(2) To prove the commutative law, suppose that $(\alpha ,\beta ),(\gamma ,\delta )\in \mathcal{Z}$.

$\left[\right(\alpha ,\beta )⊼(\gamma ,\delta \left)\right]=(max(0,\alpha +\gamma -1),min(1,\beta +\delta \left)\right)$

$=(max(0,\gamma +\alpha -1),min(1,\delta +\beta \left)\right)=\left[\right(\gamma ,\delta )⊼(\alpha ,\beta \left)\right]$.

Now, we want to prove ⊼ is associative. Therefore, we prove that $\left[\right((\alpha ,\beta )⊼(\gamma ,\delta ))⊼(\lambda ,\xi \left)\right]=\left[\right(\alpha ,\beta )⊼((\gamma ,\delta )⊼(\lambda ,\xi )\left)\right]$ i.e.,

$(max(0,max(0,\alpha +\gamma -1)+\lambda -1),min(1,min(1,\beta +\delta )+\xi \left)\right)=(max(0,\alpha +max(0,\gamma$

$+\lambda -1)-1),min(1,\beta +min(1,\delta +\xi \left)\right))$. To prove that,

$L.H.S=max(0,max(0,\alpha +\gamma -1)+\lambda -1)=max(0,\alpha +max(0,\gamma +\lambda -1)-1)=R.H.S$.

First, we prove that $L.H.S\ge R.H.S$. If $R.H.S=0$, then the result holds.

If $max(0,\gamma +\lambda -1)=0$, then $L.H.S\ge max(0,\alpha -1)=R.H.S$. If $max(0,\gamma +\lambda -1)=\gamma +\lambda -1$, then $R.H.S=\alpha +\gamma +\lambda -2$. Now, If $\alpha +\gamma \ge 1$, then $L.H.S=max(0,\alpha +\gamma +\lambda -2)\ge R.H.S$. If $\alpha +\gamma \le 1$, then $L.H.S=0=R.H.S$. Thus $L.H.S\ge R.H.S$.

Second, we prove that $L.H.S\le R.H.S$. If $\gamma +\lambda -1\ge 0$ and $\alpha +\gamma -1\ge 0$, then $R.H.S=max(0,\alpha +\gamma +\lambda -2)\ge \alpha +\gamma +\lambda -2=L.H.S$. If $\gamma +\lambda -1<0$ and $\alpha +\gamma -1\ge 0$, then $R.H.S=0=max(0,\gamma +\lambda -1+\alpha -1)=L.H.S$. If $\gamma +\lambda -1<0$ and $\alpha +\gamma -1<0$, then $R.H.S=0=L.H.S$. Hence $L.H.S\le R.H.S$. Therefore, $L.H.S=R.H.S$.

Similarly, $min(1,min(1,\beta +\delta )+\xi )=min(1,\beta +min(1,\delta +\xi \left)\right)$. Therefore, the associative law holds.

Now, $\left[\right(\alpha ,\beta )⊼(1,0\left)\right]=(max(0,\alpha +1-1),min(1,\beta +0\left)\right)=(\alpha ,\beta )=\left[\right(1,0)⊼(\alpha ,\beta \left)\right]$. Hence $(\mathcal{Z},⊼,(1,0\left)\right)$ is a commutative moniod.

(3) The proof is similar to the proof of (2);

(4) $[(\alpha ,\beta )⊼{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\gamma }_j,{\delta }_j)]=[(\alpha ,\beta )⊼({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j)]$

$=(max(0,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j+\alpha -1),min(1,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j+\beta ))$

$=({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}max(0,{\gamma }_j+\alpha -1),{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}min(1,{\delta }_j+\beta ))$

$={\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}(max(0,{\gamma }_j+\alpha -1),min(1,{\delta }_j+\beta ))$

$=\left[{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}((\alpha ,\beta )⊼({\gamma }_j,{\delta }_j))\right]$. □

Theorem 4.

(1) If $(\alpha ,\beta )\le ({\alpha }_1,{\beta }_1)$, then $[({\alpha }_1,{\beta }_1)\to (\gamma ,\delta )]\le [(\alpha ,\beta )\to (\gamma ,\delta )]$, and $[({\alpha }_1,{\beta }_1)\dot{\to }$

$(\gamma ,\delta )]\le \left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]$.

(2) If $(\gamma ,\delta )\le ({\gamma }_1,{\delta }_1)$, then $[(\alpha ,\beta )\to (\gamma ,\delta )]\le [(\alpha ,\beta )\to ({\gamma }_1,{\delta }_1)]$, and $\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]\le \left[(\alpha ,\beta )\dot{\to }({\gamma }_1,{\delta }_1)\right]$;

(3) (a) $\left[\right(0,1)\to (\gamma ,\delta \left)\right]=(1,0)$, $\left[(0,1)\dot{\to }(\gamma ,\delta )\right]=(1,0)$, $\left[\right(1,0)\to (\gamma ,\delta \left)\right]=(\gamma ,1-\gamma )$, and $\left[(1,0)\dot{\to }(\gamma ,\delta )\right]=(\gamma ,\delta )$.

(b) $\left[\right(\alpha ,\beta )\to (1,0\left)\right]=(1,0)$, $\left[(\alpha ,\beta )\dot{\to }(1,0)\right]=(1,0)$, $\left[\right(\alpha ,\beta )\to (0,1\left)\right]=(\beta ,1-\beta )$, and $\left[(\alpha ,\beta )\dot{\to }(0,1)\right]=\neg (\alpha ,\beta )$.

(c) $\left[\right(\alpha ,\beta )⊼(1,0\left)\right]=(\alpha ,\beta )$, and $\left[\right(\alpha ,\beta )⊼(0,1\left)\right]=(0,1)$;

(4) (a) $(\alpha ,\beta )\le (\gamma ,\delta )$ if and only if $\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]=(1,0)$

(b) $\beta +\gamma \ge 1$ if and only if $\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]=(1,0)$;

(5) (a) $\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]=[\neg (\gamma ,\delta )\to \neg (\alpha ,\beta \left)\right]$;

(b) $\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]=[\neg (\gamma ,\delta )\dot{\to }\neg (\alpha ,\beta )]$;

(6) $(\lambda ,\xi )\le \left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]$ if and only if $\left[\right(\lambda ,\xi )⊼(\alpha ,\beta \left)\right]\le (\gamma ,\delta )$;

(7)

$$\left[\right(\gamma ,\delta )\to (\lambda ,\xi \left)\right]\le \left[\right((\alpha ,\beta )⋏(\gamma ,\delta ))\to ((\alpha ,\beta )⋏(\lambda ,\xi )\left)\right];$$

(8)

$$\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]\le \left[\right((\lambda ,\xi )\to (\alpha ,\beta ))\to ((\lambda ,\xi )\to (\gamma ,\delta )\left)\right];$$

$$\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]\le \left[\left((\lambda ,\xi )\dot{\to }(\alpha ,\beta )\right)\dot{\to }\left((\lambda ,\xi )\dot{\to }(\gamma ,\delta )\right)\right];$$

(9)

$$\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]\le \left[\right((\gamma ,\delta )\to (\lambda ,\xi ))\to ((\alpha ,\beta )\to (\lambda ,\xi )\left)\right];$$

(10)

$$[(\alpha ,\beta )⊼(\gamma ,\delta )\dot{\to }(\lambda ,\xi )]=\left[(\alpha ,\beta )\dot{\to }\left((\gamma ,\delta )\dot{\to }(\lambda ,\xi )\right)\right];$$

(11) $(\gamma ,\delta )\le \left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right];$

(12)

$$\underset{j\in \mathsf{\Lambda }}{\bigwedge }[({\alpha }_j,{\beta }_j)\to ({\gamma }_j,{\delta }_j)]\le [\underset{j\in \mathsf{\Lambda }}{\bigvee }({\alpha }_j,{\beta }_j)\to \underset{j\in \mathsf{\Lambda }}{\bigvee }({\gamma }_j,{\delta }_j)];$$

$$\underset{j\in \mathsf{\Lambda }}{\bigwedge }\left[({\alpha }_j,{\beta }_j)\dot{\to }({\gamma }_j,{\delta }_j)\right]\le \left[\underset{j\in \mathsf{\Lambda }}{\bigvee }({\alpha }_j,{\beta }_j)\dot{\to }\underset{j\in \mathsf{\Lambda }}{\bigvee }({\gamma }_j,{\delta }_j)\right];$$

$$\underset{j\in \mathsf{\Lambda }}{\bigwedge }[({\alpha }_j,{\beta }_j)\to ({\gamma }_j,{\delta }_j)]\le [\underset{j\in \mathsf{\Lambda }}{\bigwedge }({\alpha }_j,{\beta }_j)\to \underset{j\in \mathsf{\Lambda }}{\bigwedge }({\gamma }_j,{\delta }_j)];$$

$$\underset{j\in \mathsf{\Lambda }}{\bigwedge }\left[({\alpha }_j,{\beta }_j)\dot{\to }({\gamma }_j,{\delta }_j)\right]\le \left[\underset{j\in \mathsf{\Lambda }}{\bigwedge }({\alpha }_j,{\beta }_j)\dot{\to }\underset{j\in \mathsf{\Lambda }}{\bigwedge }({\gamma }_j,{\delta }_j)\right];$$

(13)

$$\left[\right(\alpha ,\beta )\to ((\gamma ,\delta )\wedge (\lambda ,\xi )\left)\right]=\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]\wedge \left[\right(\alpha ,\beta )\to (\lambda ,\xi \left)\right];$$

$$\left[(\alpha ,\beta )\dot{\to }((\gamma ,\delta )\wedge (\lambda ,\xi ))\right]=\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]\wedge \left[(\alpha ,\beta )\dot{\to }(\lambda ,\xi )\right];$$

(14)

$$\vDash (\alpha ,\beta )⊼(\gamma ,\delta )\to (\alpha ,\beta )\wedge (\gamma ,\delta );$$

$$\vDash \left((\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right)\to ((\alpha ,\beta )\to (\gamma ,\delta )).$$

Proof. 

(1) $[({\alpha }_1,{\beta }_1)⟶(\gamma ,\delta )]=(min(1,1-{\alpha }_1+\gamma ,1-\delta +{\beta }_1),max(0,{\alpha }_1-\gamma ,\delta -{\beta }_1))$.

Since $(\alpha ,\beta )\le ({\alpha }_1,{\beta }_1)$, then $\alpha \le {\alpha }_1$ and ${\beta }_1\le \beta$. Therefore,

$min(1,1-{\alpha }_1+\gamma ,1-\delta +{\beta }_1)\le min(1,1-\alpha +\gamma ,1-\delta +\beta )$ and $max(0,\alpha -\gamma ,\delta -\beta )\le max(0,{\alpha }_1-\gamma ,\delta -{\beta }_1)$. Hence

$[({\alpha }_1,{\beta }_1)⟶(\gamma ,\delta )]\le (min(1,1-\alpha +\gamma ,1-\delta +\beta ),max(0,\alpha -\gamma ,\delta -\beta ))=[(\alpha ,\beta )⟶(\gamma ,\delta )]$.

Similarly, $\left[({\alpha }_1,{\beta }_1)\dot{⟶}(\gamma ,\delta )\right]\le \left[(\alpha ,\beta )\dot{⟶}(\gamma ,\delta )\right]$.

(2) The proof is similar to that of (1).

(3) Since $\alpha +\beta \le 1$ and $\gamma +\delta \le 1$, the result holds.

(4) (a) Since $(\alpha ,\beta )\le (\gamma ,\delta )$, then $\alpha \le \gamma$ and $\delta \le \beta$. Hence

$\left[\right(\alpha ,\beta )⟶(\gamma ,\delta \left)\right]=(min(1,1-\alpha +\gamma ,1-\delta +\beta ),max(0,\alpha -\gamma ,\delta -\beta \left)\right)=(1,0)$.

Conversely, if $\left[\right(\alpha ,\beta )⟶(\gamma ,\delta \left)\right]=(1,0)$, then $min(1,1-\alpha +\gamma ,1-\delta +\beta )=1$ or $1-\alpha +\gamma \ge 1$ and $1-\delta +\beta \ge 1$. Therefore, $\alpha \le \gamma$ and $\delta \le \beta$. Hence $(\alpha ,\beta )\le (\gamma ,\delta )$. Additionally, the result holds if we choose $max(0,\alpha -\gamma ,\delta -\beta )=0$.

(b) Since $\beta +\gamma \ge 1$, $\alpha +\beta \le 1$ and $\gamma +\delta \le 1$, then $\alpha +\delta \le 1$. Therefore, the result holds.

(5) Follows from Definition 4 (2).

(6) $(\lambda ,\xi )\le \left[(\alpha ,\beta )\dot{⟶}(\gamma ,\delta )\right]$

⇔

$(\lambda ,\xi )\le (min(1,\beta +\gamma ),max(0,\alpha +\delta -1\left)\right)$

⇔

$\lambda \le min(1,\beta +\gamma )$ and $\xi \ge max(0,\alpha +\delta -1)$

⇔

$\lambda \le \beta +\gamma$ and $\xi \ge \alpha +\delta -1$

• $\stackrel{\alpha +\beta \le 1}{\iff }\lambda +\alpha -1\le \gamma$ and $\xi +\beta \ge \delta$

⇔

$max(0,\lambda +\alpha -1)\le \gamma$ and $min(1,\xi +\beta )\ge \delta$

⇔

$(max(0,\lambda +\alpha -1),min(1,\xi +\beta \left)\right)\le (\gamma ,\delta )$

⇔

$\left[\right(\lambda ,\xi )⊼(\alpha ,\beta \left)\right]\le (\gamma ,\delta )$.

(7) $R.H.S=\left[\right((\alpha ,\beta )⋏(\gamma ,\delta ))\to ((\alpha ,\beta )⋏(\lambda ,\xi )\left)\right]$

$=\left[\right(max(0,\alpha -\delta ,\gamma -\beta ),min(1,1-\alpha +\delta ,1-\gamma +\beta ))\to (max(0,\alpha -\xi ,\lambda -\beta ),min(1,1$

$-\alpha +\xi ,1-\lambda +\beta \left)\right)]$

$=(min(1,1-max(0,\alpha -\delta ,\gamma -\beta )+max(0,\alpha -\xi ,\lambda -\beta ),1-min(1,1-\alpha +\xi ,1-\lambda +\beta )+min(1,1-\alpha +\delta ,1-\gamma +\beta )),max(0,max(0,\alpha -\delta ,\gamma -\beta )-max(0,\alpha -\xi ,\lambda -\beta ),min(1,1-\alpha +\xi ,1-\lambda +\beta )-min(1,1-\alpha +\delta ,1-\gamma +\beta )\left)\right)$

$=(min(1,min(1,1-\alpha +\delta ,1-\gamma +\beta )+max(0,\alpha -\xi ,\lambda -\beta )),max(0,max(0,\alpha -\delta ,\gamma -\beta )-max(0,\alpha -\xi ,\lambda -\beta )\left)\right)$

$\ge (min(1,min(1,1-\xi +\delta ,1-\gamma +\lambda )),max(0,max(0,\gamma -\lambda ,\xi -\delta )\left)\right)$

$=(min(1,1-\gamma +\lambda ,1-\xi +\delta ),max(0,\gamma -\lambda ,\xi -\delta \left)\right)=\left[\right(\gamma ,\delta )⋏(\lambda ,\xi \left)\right]=L.H.S.$

(8) $\left[\right((\lambda ,\xi )\to (\alpha ,\beta ))\to ((\lambda ,\xi )\to (\gamma ,\delta )\left)\right]$

$=\left[\right(min(1,1-\lambda +\alpha ,1-\beta +\xi ),max(0,\lambda -\alpha ,\beta -\xi ))\to (min(1,1-\lambda +\gamma ,1-\delta +\xi ),max(0,\lambda -\gamma ,\delta -\xi )\left)\right]$

$=(min(1,1-min(1,1-\lambda +\alpha ,1-\beta +\xi )+min(1,1-\lambda +\gamma ,1-\delta +\xi ),1-max(0,\lambda -\gamma ,\delta -\xi )+max(0,\lambda -\alpha ,\beta -\xi )),max(0,min(1,1-\lambda +\alpha ,1-\beta +\xi )-min(1,1-\lambda +\gamma ,1-\delta +\xi ),max(0,\lambda -\gamma ,\delta -\xi )-max(0,\lambda -\alpha ,\beta -\xi )\left)\right)$

$=(min(1,1-min(1,1+\alpha -\lambda ,1-\beta +\xi )+min(1,1-\lambda +\gamma ,1-\delta +\xi )),max(0,max(0,$

$\lambda -\gamma ,\delta -\xi )-max(0,\lambda -\alpha ,\beta -\xi \left)\right))$

$\ge (min(1,1-\alpha +\gamma ,1-\delta +\beta ),max(0,\alpha -\gamma ,\delta -\beta \left)\right)=\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]$.

Similarly, $\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]\le \left[\left((\lambda ,\xi )\dot{\to }(\alpha ,\beta )\right)\dot{\to }\left((\lambda ,\xi )\dot{\to }(\gamma ,\delta )\right)\right].$

(9) The proof is similar to that of (8).

(10) $[(\alpha ,\beta )⊼(\gamma ,\delta )\dot{\to }(\lambda ,\xi )]=(max(0,\alpha +\gamma -1),min(1,\beta +\delta ))\dot{\to }(\lambda ,\xi )$

$=(min(1,min(1,\beta +\delta )+\lambda ),max(0,max(0,\alpha +\gamma -1)+\xi -1\left)\right)$

$=(min(1,\beta +min(1,\delta +\lambda )),max(0,\alpha +max(0,\gamma +\xi -1)-1\left)\right)$

$=\left[(\alpha ,\beta )\dot{\to }(min(1,\delta +\lambda ),max(0,\gamma +\xi -1))\right]$

$=\left[(\alpha ,\beta )\dot{\to }\left((\gamma ,\delta )\dot{\to }(\lambda ,\xi )\right)\right]$.

(11) Obvious.

(12) ${\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}[({\alpha }_j,{\beta }_j)\to ({\gamma }_j,{\delta }_j)]$

$={\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}(min(1,1-{\alpha }_j+{\gamma }_j,1-{\delta }_j+{\beta }_j),max(0,{\alpha }_j-{\gamma }_j,{\delta }_j-{\beta }_j))$

$=({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}min(1,1-{\alpha }_j+{\gamma }_j,1-{\delta }_j+{\beta }_j),{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}max(0,{\alpha }_j-{\gamma }_j,{\delta }_j-{\beta }_j))$

$=(min(1,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}(1-{\alpha }_j+{\gamma }_j),{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}(1-{\delta }_j+{\beta }_j)),max(0,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\alpha }_j-{\gamma }_j),{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\delta }_j-{\beta }_j)))$

$\le (min(1,1-{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\alpha }_j+{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j,1-{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j+{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\beta }_j),max(0,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\alpha }_j-{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j-{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\beta }_j))$

$=[({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\alpha }_j,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\beta }_j)⟶({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j)]=[{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\alpha }_j,{\beta }_j)⟶{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\gamma }_j,{\delta }_j)]$.

Also,

${\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}\left[({\alpha }_j,{\beta }_j)\dot{⟶}({\gamma }_j,{\delta }_j)\right]={\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}(min(1,{\beta }_j+{\gamma }_j),max(0,{\alpha }_j+{\delta }_j-1))$

$=({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}min(1,{\beta }_j+{\gamma }_j),{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}max(0,{\alpha }_j+{\delta }_j-1))$

$\le (min(1,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\beta }_j+{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j),max(0,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\alpha }_j+{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j-1))$

$=\left[({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\alpha }_j,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\beta }_j)\dot{⟶}({\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}{\gamma }_j,{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigwedge }}{\delta }_j)\right]=\left[{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\alpha }_j,{\beta }_j)\dot{⟶}{\displaystyle \underset{j\in \mathsf{\Lambda }}{\bigvee }}({\gamma }_j,{\beta }_j)\right]$.

The proofs of the other statements are similar.

(13) $\left[\right(\alpha ,\beta )\to ((\gamma ,\delta )\wedge (\lambda ,\xi )\left)\right]=\left[\right(\alpha ,\beta )⟶(\gamma \wedge \lambda ,\delta \vee \xi \left)\right]$

$=(min(1,1-\alpha +\gamma \wedge \lambda ,1-\delta \vee \xi +\beta ),max(0,\alpha -\gamma \wedge \lambda ,\delta \vee \xi -\beta \left)\right)$

$=(min(1,(1-\alpha +\gamma )\wedge (1-\alpha +\lambda ),(1-\delta +\beta )\wedge (1-\xi +\beta )),max(0,(\alpha -\gamma )\vee (\alpha -\lambda ),(\delta -\beta )\vee (\xi -\beta )\left)\right)$

$=(min(1,1-\alpha +\gamma ,1-\alpha +\lambda ,1-\delta +\beta ,1-\xi +\beta ),max(0,\alpha -\gamma ,\alpha -\lambda ,\delta -\beta ,\xi -\beta \left)\right)$

$=\left(min(1,1-\alpha +\gamma ,1-\delta +\beta ),max(0,\alpha -\gamma ,\delta -\beta )\right)\wedge$

$\left(min(1,1-\alpha -\lambda ,1-\xi +\beta ),max(0,\alpha -\lambda ,\xi -\beta )\right)$

$=\left[\right(\alpha ,\beta )\to (\gamma ,\delta \left)\right]\wedge \left[\right(\alpha ,\beta )\to (\lambda ,\xi \left)\right]$.

Similarly, we can prove that

$\left[(\alpha ,\beta )\dot{\to }((\gamma ,\delta )\wedge (\lambda ,\xi ))\right]=\left[(\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right]\wedge \left[(\alpha ,\beta )\dot{\to }(\lambda ,\xi )\right].$

(14) $\left[\right(\alpha ,\beta )⊼(\gamma ,\delta )\to (\alpha ,\beta )\wedge (\gamma ,\delta \left)\right]$

$=\left[\right(max(0,\alpha +\gamma -1),min(1,\beta +\delta ))\to (min(\alpha ,\gamma ),max(\beta ,\delta )\left)\right]$

$=(min(1,1-max(0,\alpha +\gamma -1)+min(\alpha ,\gamma ),1-max(\beta ,\delta )+min(1,\beta +\delta )),max(0,$

$max(0,\alpha +\gamma -1)-min(\alpha ,\gamma ),max(\beta ,\delta )-min(1,\beta +\delta )\left)\right)=(1,0)$.

Similarly, $[\left((\alpha ,\beta )\dot{\to }(\gamma ,\delta )\right)\to ((\alpha ,\beta )\to (\gamma ,\delta ))]=(1,0)$. □

Lemma 1.

Let $\widehat{\mathcal{A}},\widehat{\mathcal{B}},\widehat{\mathcal{C}}\in \mathcal{IF}\left(\mathcal{X}\right).$ Then

(1) $\vDash \widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}\to (\widehat{\mathcal{B}}\subseteq \widehat{\mathcal{C}}\to \widehat{\mathcal{A}}\subseteq \widehat{\mathcal{C}})$;

(2) $\vDash \widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}\to (\widehat{\mathcal{B}}\equiv \widehat{\mathcal{C}}\to \widehat{\mathcal{A}}\equiv \widehat{\mathcal{C}})$;

(3) $\vDash \widehat{\mathcal{A}}\approx \widehat{\mathcal{B}}\to (\widehat{\mathcal{B}}\approx \widehat{\mathcal{C}}\to \widehat{\mathcal{A}}\approx \widehat{\mathcal{C}})$;

(4) $\vDash \widehat{\mathcal{B}}\subseteq \widehat{\mathcal{C}}\to (\widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\subseteq \widehat{\mathcal{C}})$;

(5) $\vDash \widehat{\mathcal{B}}\equiv \widehat{\mathcal{C}}\to (\widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\equiv \widehat{\mathcal{C}})$;

(6) $\vDash \widehat{\mathcal{B}}\approx \widehat{\mathcal{C}}\to (\widehat{\mathcal{A}}\approx \widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\approx \widehat{\mathcal{C}})$;

(7) $\vDash \widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}\to \neg \left(\widehat{\mathcal{B}}\right)\subseteq \neg \left(\widehat{\mathcal{A}}\right)$;

(8) $\vDash \widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}\to \neg \left(\widehat{\mathcal{B}}\right)\equiv \neg \left(\widehat{\mathcal{A}}\right)$;

(9) $\vDash \widehat{\mathcal{A}}\approx \widehat{\mathcal{B}}\to \neg \left(\widehat{\mathcal{B}}\right)\approx \neg \left(\widehat{\mathcal{A}}\right)$.

Lemma 2.

Let $\left\{{\widehat{\mathcal{A}}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\},\left\{{\widehat{\mathcal{B}}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\}\subseteq \mathcal{IF}\left(\mathcal{X}\right).$

(1) $\vDash \forall (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\subseteq {\widehat{\mathcal{B}}}_{\lambda })\to {\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }\subseteq {\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{B}}}_{\lambda }$;

(2) $\vDash \forall (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\equiv {\widehat{\mathcal{B}}}_{\lambda })\to {\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }\equiv {\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{B}}}_{\lambda }$;

(3) $\vDash \forall (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\approx {\widehat{\mathcal{B}}}_{\lambda })\to {\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }\approx {\displaystyle \bigcap _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{B}}}_{\lambda }$;

(4) $\vDash \forall (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\subseteq {\widehat{\mathcal{B}}}_{\lambda })\to {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }\subseteq {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{B}}}_{\lambda }$;

(5) $\vDash \forall (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\equiv {\widehat{\mathcal{B}}}_{\lambda })\to {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }\equiv {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{B}}}_{\lambda }$;

(6) $\vDash \forall (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\approx {\widehat{\mathcal{B}}}_{\lambda })\to {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{A}}}_{\lambda }\approx {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\widehat{\mathcal{B}}}_{\lambda }$.

Lemma 3.

Let $f:\mathcal{X}\to \mathcal{Y}$ be a function, $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right)$ and $\widehat{\mathcal{C}},\widehat{\mathcal{D}}\in \mathcal{IF}\left(\mathcal{Y}\right)$. Then

(1) $\vDash \widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}\to f\left(\widehat{\mathcal{A}}\right)\subseteq f\left(\widehat{\mathcal{B}}\right)$;

(2) $\vDash \widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}\to f\left(\widehat{\mathcal{A}}\right)\equiv f\left(\widehat{\mathcal{B}}\right)$;

(3) $\vDash \widehat{\mathcal{A}}\approx \widehat{\mathcal{B}}\to f\left(\widehat{\mathcal{A}}\right)\approx f\left(\widehat{\mathcal{B}}\right)$;

(4) $\vDash \widehat{\mathcal{C}}\subseteq \widehat{\mathcal{D}}\to f^{-1}\left(\widehat{\mathcal{C}}\right)\subseteq f^{-1}\left(\widehat{\mathcal{D}}\right)$;

(5) $\vDash \widehat{\mathcal{C}}\equiv \widehat{\mathcal{D}}\to f^{-1}\left(\widehat{\mathcal{C}}\right)\equiv f^{-1}\left(\widehat{\mathcal{D}}\right)$;

(6) $\vDash \widehat{\mathcal{C}}\approx \widehat{\mathcal{D}}\to f^{-1}\left(\widehat{\mathcal{C}}\right)\approx f^{-1}\left(\widehat{\mathcal{D}}\right)$.

Remark 3.

Lemmas 1–3 are true when we replace “$\subseteq ,\to ,\equiv$ and ≈” by “$⋐,\dot{\to },\dot{\equiv }$ and $\dot{\approx }$”, respectively.

Lemma 4.

Let $\widehat{\mathcal{A}},\widehat{\mathcal{B}},\widehat{\mathcal{C}}\in \mathcal{IF}\left(\mathcal{X}\right).$ Then

(1) $\vDash \widehat{\mathcal{A}}⋐\widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\subseteq \widehat{\mathcal{B}}$;

(2) $\vDash \widehat{\mathcal{A}}\dot{\approx }\widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\dot{\equiv }\widehat{\mathcal{B}}$;

(3) $\vDash \widehat{\mathcal{A}}\dot{\equiv }\widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}$;

(4) $\vDash \widehat{\mathcal{A}}\dot{\approx }\widehat{\mathcal{B}}\to \widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}$;

(5) $\vDash \widehat{\mathcal{A}}⋐\widehat{\mathcal{B}}⊼\widehat{\mathcal{B}}⋐\widehat{\mathcal{C}}\to \widehat{\mathcal{A}}⋐\widehat{\mathcal{C}}$;

(6) $\vDash \widehat{\mathcal{A}}\dot{\equiv }\widehat{\mathcal{B}}⊼\widehat{\mathcal{B}}\dot{\equiv }\widehat{\mathcal{C}}\to \widehat{\mathcal{A}}\dot{\equiv }\widehat{\mathcal{C}}$.

Lemma 5.

Let $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right).$ Then the following are equivalent:

(1) $\widehat{\mathcal{A}}\left(x\right)=\widehat{\mathcal{B}}\left(x\right)$;

(2) $\vDash \widehat{\mathcal{A}}\equiv \widehat{\mathcal{B}}$;

(3) $\vDash \widehat{\mathcal{A}}\dot{\equiv }\widehat{\mathcal{B}}$;

(4) $\vDash \widehat{\mathcal{A}}\approx \widehat{\mathcal{B}}$;

(5) $\vDash \widehat{\mathcal{A}}\dot{\approx }\widehat{\mathcal{B}}$.

4. Bi-Intuitionistic Fuzzy Topological Space

Now, we introduce the definition of the bi-intuitionistic fuzzy topology and other related topologies. Additionally, we give some examples.

Definition 5.

Let $\mathcal{X}$ be a universe of discourse, $\tau \in \mathcal{IF}\left(\mathcal{IF}\right(\mathcal{X}\left)\right)(\tau :\mathcal{IF}(\mathcal{X})\to \mathcal{Z})$, satisfy the following axioms:

(1) $\vDash \widehat{1}\in \tau ,\vDash \widehat{0}\in \tau$;

(2) For any $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right)$, $\vDash \widehat{\mathcal{A}}\in \tau \wedge \widehat{\mathcal{B}}\in \tau \to \widehat{\mathcal{A}}\cap \widehat{\mathcal{B}}\in \tau$;

(3) ⊧ For any $\left\{{\widehat{\mathcal{A}}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\}\subseteq \mathcal{IF}\left(\mathcal{X}\right)$,

$$\vDash \forall \lambda (\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\in \tau )\to \bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\in \tau .$$

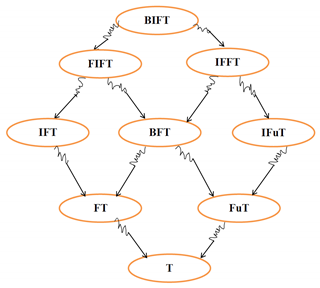
Then, τ is called a bi-intuitionistic fuzzy topology (BIFT for short) and $(X,\tau )$ is a bi-intuitionistic fuzzy topological space. Specially, if $\tau \in \mathcal{P}\left(\mathcal{IF}\right(\mathcal{X}\left)\right)(\tau :\mathcal{IF}(\mathcal{X})\to \{0,1\left\}\right)$, then τ is an intuitionistic fuzzy topology (IFT for short), if $\tau \in \mathcal{IF}\left(\mathcal{P}\right(\mathcal{X}\left)\right)(\tau :\mathcal{P}(\mathcal{X})\to \mathcal{Z})$, then τ is called an intuitionistic fuzzifying topology (IFuT for short), if $\tau \in IF\left(\mathcal{F}\right(\mathcal{X}\left)\right)(\tau :\mathcal{F}(\mathcal{X})\to \mathcal{Z})$, then τ is called an intuitionistic-fuzzy fuzzy topology (IFFT for short), if $\tau \in \mathcal{F}\left(\mathcal{IF}\right(\mathcal{X}\left)\right)(\tau :\mathcal{IF}(\mathcal{X})\to [0,1\left]\right)$, then τ is a fuzzy intuitionistic fuzzy topology (FIFT for short), if $\tau \in \mathcal{F}\left(\mathcal{F}\right(\mathcal{X}\left)\right)(\tau :\mathcal{F}(\mathcal{X})\to [0,1\left]\right)$, then τ is a bifuzzy topology (BFT for short), if $\tau \in \mathcal{F}\left(\mathcal{P}\right(\mathcal{X}\left)\right)(\tau :\mathcal{P}(\mathcal{X})\to [0,1\left]\right)$, then τ is a fuzzifying topology (FuT for short), if $\tau \in \mathcal{P}\left(\mathcal{F}\right(\mathcal{X}\left)\right)(\tau :\mathcal{F}(\mathcal{X})\to \{0,1\left\}\right)$, then τ is a fuzzy topology (FT for short), and if $\tau \in \mathcal{P}\left(\mathcal{P}\right(\mathcal{X}\left)\right)(\tau :\mathcal{P}(\mathcal{X})\to \{0,1\left\}\right)$, then τ is a classical topology (T for short). For any $\widehat{\mathcal{A}}\in \mathcal{IF}\left(\mathcal{X}\right)$, we always suppose that $\tau \left(\widehat{\mathcal{A}}\right)=(m\tau \left(\widehat{\mathcal{A}}\right),n\tau \left(\widehat{\mathcal{A}}\right))$; the number $m\tau \left(\widehat{\mathcal{A}}\right)$ is the openness degree of $\widehat{\mathcal{A}}$, while the number $n\tau \left(\widehat{\mathcal{A}}\right)$ is the non-openness degree of $\widehat{\mathcal{A}}$.

Remark 4.

The conditions in Definition 4 may be rewritten respectively as follows:

(1)${}^{{}^{\prime }}$$\tau \left(\widehat{1}\right)=(1,0)=\tau \left(\widehat{0}\right)$;

(2)${}^{{}^{\prime }}$ For any $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right)$,

$$m\tau \left(\widehat{\mathcal{A}}\right)\wedge m\tau \left(\widehat{\mathcal{B}}\right)\le m\tau (\widehat{\mathcal{A}}\cap \widehat{\mathcal{B}})\mathrm{and}n\tau (\widehat{\mathcal{A}}\cap \widehat{\mathcal{B}})\le n\tau \left(\widehat{\mathcal{A}}\right)\vee n\tau \left(\widehat{\mathcal{B}}\right);$$

(3)${}^{{}^{\prime }}$ For any $\left\{{\widehat{\mathcal{A}}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\}\subseteq \mathcal{IF}\left(\mathcal{X}\right)$,

$$\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }m\tau \left({\widehat{\mathcal{A}}}_{\lambda }\right)\le m\tau \left(\bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\right)\mathrm{and}n\tau \left(\bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\right)\le \underset{\lambda \in \mathsf{\Lambda }}{\bigvee }n\tau \left({\widehat{\mathcal{A}}}_{\lambda }\right).$$

Remark 5.

In the above diagram, and in the sequel, the symbol $\mathcal{H}⇝\mathcal{K}$ means that the concept $\mathcal{K}$ is a special case of the concept $\mathcal{H}$:

Theorem 5.

Let $\mathcal{X}$ be a non-empty set.

(1) If τ is a BIFT, then $\tau \left|{}_{\mathcal{F}\left(\mathcal{X}\right)}\right.$ is a IFFT;

(2) If τ is a BIFT, then $\tau \left|{}_{\mathcal{P}\left(\mathcal{X}\right)}\right.$ is a IFuT;

(3) If τ is a FIFT, then $\tau \left|{}_{\mathcal{F}\left(\mathcal{X}\right)}\right.$ is a BFT;

(4) If τ is a FIFT, then $\tau \left|{}_{\mathcal{P}\left(\mathcal{X}\right)}\right.$ is a FuT;

(5) If τ is a IFFT, then $\tau \left|{}_{\mathcal{P}\left(\mathcal{X}\right)}\right.$ is a IFuT;

(6) If τ is a BFT, then $\tau \left|{}_{\mathcal{P}\left(\mathcal{X}\right)}\right.$ is a FuT;

(7) If τ is a IFT, then $\tau \left|{}_{\mathcal{F}\left(\mathcal{X}\right)}\right.$ is a FT;

(8) If τ is a IFT, then $\tau \left|{}_{\mathcal{P}\left(\mathcal{X}\right)}\right.$ is a T;

(9) If τ is a FT, then $\tau \left|{}_{\mathcal{P}\left(\mathcal{X}\right)}\right.$ is a T.

Theorem 6.

(1) τ is a IFuT if and only if for any $(\alpha ,\beta )\in \mathcal{Z}$, ${\tau }_{(\alpha ,\beta )}$ is a classical topology, where

${\tau }_{(\alpha ,\beta )}=\left\{\mathcal{A}:\tau \left(\mathcal{A}\right)\ge (\alpha ,\beta )\right\}=\left\{\mathcal{A}:m\tau \left(\mathcal{A}\right)\ge \alpha ,n\tau \left(\mathcal{A}\right)\le \beta \right\}$ is the $(\alpha ,\beta )$-level set of τ.

(2) τ is BIFT if and only if for any $(\alpha ,\beta )\in \mathcal{Z}$, ${\tau }_{(\alpha ,\beta )}$ is a IFT.

Proof. 

We only prove (1) as (2) is similar.

($⟹:$) Suppose $(\alpha ,\beta )\in \mathcal{Z}$. We prove that ${\tau }_{(\alpha ,\beta )}$ is an ordinary topology.

(1) Since $\tau \left(\mathcal{X}\right)=\tau \left(\varphi \right)=(1,0)\ge (\alpha ,\beta )$, then $\mathcal{X},\varphi \in {\tau }_{(\alpha ,\beta )}$.

(2) Suppose $\mathcal{A},\mathcal{B}\in {\tau }_{(\alpha ,\beta )}$. Then $\tau \left(\mathcal{A}\right)\ge (\alpha ,\beta )$ and $\tau \left(\mathcal{B}\right)\ge (\alpha ,\beta )$. So, $\tau (\mathcal{A}\cap \mathcal{B})\ge \tau \left(\mathcal{A}\right)\wedge \tau \left(\mathcal{B}\right)\ge (\alpha ,\beta )$. Therefore $\mathcal{A}\cap \mathcal{B}\in {\tau }_{(\alpha ,\beta )}$.

(3) Suppose $\left\{{\mathcal{A}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\}\subseteq {\tau }_{(\alpha ,\beta )}$. Then for each $\lambda \in \mathsf{\Lambda }$, we have $\tau \left({\mathcal{A}}_{\lambda }\right)\ge (\alpha ,\beta )$. So, ${\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }}\tau \left({\mathcal{A}}_{\lambda }\right)\ge (\alpha ,\beta )$. Hence $\tau \left({\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\right)\ge {\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }}\tau \left({\mathcal{A}}_{\lambda }\right)\ge (\alpha ,\beta )$. Therefore ${\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\in {\tau }_{(\alpha ,\beta )}$.

$(:⟸)$ We prove that $\tau$ is an intuitionistic fuzzifying topology.

(1) For any $(\alpha ,\beta )\in \mathcal{Z}$, $\mathcal{X}\in {\tau }_{(\alpha ,\beta )}$. Then, for any $(\alpha ,\beta )\in \mathcal{Z}$, $\tau \left(\mathcal{X}\right)\ge (\alpha ,\beta )$. Therefore, $\tau \left(\mathcal{X}\right)\ge {\displaystyle \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigvee }}(\alpha ,\beta )=(1,0)$. Hence $\vDash \mathcal{X}\in \tau$. Similar $\vDash \varphi \in \tau$.

(2) Suppose $\mathcal{A},\mathcal{B}\subseteq \mathcal{X}$ such that $\tau \left(\mathcal{A}\right)\wedge \tau \left(\mathcal{B}\right)\ge (\alpha ,\beta )$. Then $\tau \left(\mathcal{A}\right)\ge (\alpha ,\beta )$ and $\tau \left(\mathcal{B}\right)\ge (\alpha ,\beta )$. Hence $\mathcal{A},\mathcal{B}\in {\tau }_{(\alpha ,\beta )}$. Thus, $\mathcal{A}\cap \mathcal{B}\in {\tau }_{(\alpha ,\beta )}$, i.e., $\tau (\mathcal{A}\cap \mathcal{B})\ge (\alpha ,\beta )$. Therefore, $\tau (\mathcal{A}\cap \mathcal{B})\ge \tau \left(\mathcal{A}\right)\wedge \tau \left(\mathcal{B}\right)$.

(3) Suppose $\left\{{\mathcal{A}}_{\lambda }\left|\lambda \in \mathsf{\Lambda }\right\}\right.\subseteq \mathcal{P}\left(\mathcal{X}\right)$ such that ${\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }}\tau \left({\mathcal{A}}_{\lambda }\right)\ge (\alpha ,\beta )$. Then $\left\{{\mathcal{A}}_{\lambda }\left|\lambda \in \mathsf{\Lambda }\right\}\right.\subseteq {\tau }_{(\alpha ,\beta )}$ and so ${\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\in {\tau }_{(\alpha ,\beta )}$. Hence $\tau \left({\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\right)\ge (\alpha ,\beta )$. Therefore $\tau \left({\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\right)\ge {\displaystyle \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }}\tau \left({\mathcal{A}}_{\lambda }\right)$. □

Example 1.

(1) If τ is a IFuT and $\tau \left(\mathcal{P}\left(\mathcal{X}\right)\right)\subseteq \left\{(0,1),(1,0)\right\}$, then τ is an ordinary topology.

(2) If τ is a FIFT and for each $\tilde{\mathcal{A}}\in \Im \left(\mathcal{X}\right)$, $m\tau \left(\tilde{\mathcal{A}}\right)+n\tau \left(\tilde{\mathcal{A}}\right)=1$, then τ is a fuzzifying topology.

Example 2.

Suppose that τ is an intuitionistic fuzzifying topology and $\check{\tau }\in \mathcal{IF}\left(\mathcal{IF}\left(\mathcal{X}\right)\right)$ is defined as $\widehat{\mathcal{A}}\in \check{\tau }:=\exists \mathcal{A}((\mathcal{A}\in \tau )\wedge \mathcal{A}\equiv \widehat{\mathcal{A}})$. Then $\check{\tau }$ is a bi-intuitionistic fuzzy topology such that $\check{\tau }{|}_{\mathcal{P}\left(\mathcal{X}\right)}=\tau$. In fact, it suffices to check the three conditions in Definition 5.

(1) $\check{\tau }\left(\tilde{1}\right)=\check{\tau }\left(\tilde{0}\right)=(1,0)$.

(2)

$$\begin{array}{ccc}\hfill \check{\tau }(\widehat{\mathcal{A}}\cap \widehat{\mathcal{B}})& =& \underset{\mathcal{C}\in \mathcal{P}\left(\mathcal{X}\right)}{\bigvee }\left(\tau \left(\mathcal{C}\right)\wedge [\mathcal{C}\equiv \widehat{\mathcal{A}}\cap \widehat{\mathcal{B}}]\right)\hfill \\ & =& \underset{\mathcal{A},\mathcal{B}\subseteq \mathcal{X}}{\bigvee }\left(\tau (\mathcal{A}\cap \mathcal{B})\wedge [\mathcal{A}\cap \mathcal{B}\equiv \widehat{\mathcal{A}}\cap \widehat{\mathcal{B}}]\right)\hfill \\ & \ge & \underset{\mathcal{A},\mathcal{B}\subseteq \mathcal{X}}{\bigvee }\left(\tau \left(\mathcal{A}\right)\wedge \tau \left(\mathcal{B}\right)\wedge [\mathcal{A}\equiv \widehat{\mathcal{A}}]\wedge [\mathcal{B}\equiv \widehat{\mathcal{B}}]\right)\hfill \\ & =& \underset{\mathcal{A},\mathcal{B}\subseteq \mathcal{X}}{\bigvee }\left(\tau \left(\mathcal{A}\right)\wedge [\mathcal{A}\equiv \widehat{\mathcal{A}}]\right)\wedge \underset{\mathcal{A},\mathcal{B}\subseteq \mathcal{X}}{\bigvee }\left(\tau \left(\mathcal{B}\right)\wedge [\mathcal{B}\equiv \widehat{\mathcal{B}}]\right)\hfill \\ & =& \check{\tau }\left(\widehat{\mathcal{A}}\right)\wedge \check{\tau }\left(\widehat{\mathcal{B}}\right).\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \left[\bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\in \check{\tau }\right]& =& \underset{\mathcal{C}\subseteq \mathcal{X}}{\bigvee }\left(\tau \left(\mathcal{C}\right)\wedge \left[\mathcal{C}\equiv \bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\right]\right)\hfill \\ & =& \underset{{\mathcal{A}}_{\lambda }\subseteq \mathcal{X}}{\bigvee }\left(\tau \left(\bigcup _{\lambda \in \mathsf{\Lambda }}{\mathcal{A}}_{\lambda }\right)\wedge \left[\bigcup _{\lambda \in \mathsf{\Lambda }}{\mathcal{A}}_{\lambda }\equiv \bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\right]\right)\hfill \\ & \ge & \underset{{\mathcal{A}}_{\lambda }\subseteq \mathcal{X}}{\bigvee }\left(\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\tau \left({\mathcal{A}}_{\lambda }\right)\wedge \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }[{\mathcal{A}}_{\lambda }\equiv {\widehat{\mathcal{A}}}_{\lambda }]\right)\hfill \\ & =& \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\underset{{\mathcal{A}}_{\lambda }\subseteq \mathcal{X}}{\bigvee }\left(\tau \left({\mathcal{A}}_{\lambda }\right)\wedge [{\mathcal{A}}_{\lambda }\equiv {\widehat{\mathcal{A}}}_{\lambda }]\right)\hfill \\ & =& \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\check{\tau }\left({\widehat{\mathcal{A}}}_{\lambda }\right).\hfill \end{array}$$

Example 3.

Suppose that τ is an inituitionistic fuzzifying topology and $\breve{\tau }\in \mathcal{IF}\left(\mathcal{IF}\left(\mathcal{X}\right)\right)$ is defined as

$$\widehat{\mathcal{A}}\in \breve{\tau }:=\forall (\alpha ,\beta )\left({\widehat{\mathcal{A}}}_{\left[\right(\alpha ,\beta \left)\right]}\in \tau \right),$$

where ${\tau }_{\left[\right(\alpha ,\beta \left)\right]}=\left\{\widehat{\mathcal{A}}:\tau \left(\widehat{\mathcal{A}}\right)>(\alpha ,\beta )\right\}$=$\left\{\widehat{\mathcal{A}}:m\tau \left(\widehat{\mathcal{A}}\right)>\alpha ,n\tau \left(\widehat{\mathcal{A}}\right)<\beta \right\}$ is the strong $\left[\right(\alpha ,\beta \left)\right]$-level set of τ. Then $\breve{\tau }$ is a bi-intuitionistic fuzzy topology such that $\breve{\tau }\left|{}_{\mathcal{P}\left(\mathcal{X}\right)}=\tau \right.$. To show this, it suffices to check all conditions in Definition 5.

(1) Since $\widehat{1}\left(x\right)=(1,0)$ and $(\alpha ,\beta )\le (1,0)$, then ${\widehat{1}}_{\left[\right(\alpha ,\beta \left)\right]}=\mathcal{X}$ and $\tau \left(\widehat{1}\right)=(1,0)$. Hence $[\widehat{1}\in \breve{\tau }]=\breve{\tau }\left(\widehat{1}\right)={\displaystyle \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }}(1,0)=(1,0)$. Similarly, $[\widehat{0}\in \breve{\tau }]=(1,0)$.

(2)

$$\begin{array}{ccc}\hfill \breve{\tau }(\widehat{\mathcal{A}}\cap \widehat{\mathcal{B}})& =& \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\tau \left({(\widehat{\mathcal{A}}\cap \widehat{\mathcal{B}})}_{\left[\right(\alpha ,\beta \left)\right]}\right)\hfill \\ & =& \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\tau \left({\widehat{\mathcal{A}}}_{\left[\right(\alpha ,\beta \left)\right]}\cap {\widehat{\mathcal{B}}}_{\left[\right(\alpha ,\beta \left)\right]}\right)\hfill \\ & \ge & \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\left(\tau \left({\widehat{\mathcal{A}}}_{\left[\right(\alpha ,\beta \left)\right]}\right)\wedge \tau \left({\widehat{\mathcal{B}}}_{\left[\right(\alpha ,\beta \left)\right]}\right)\right)\hfill \\ & =& \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\tau \left({\widehat{\mathcal{A}}}_{\left[\right(\alpha ,\beta \left)\right]}\right)\wedge \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\tau \left({\widehat{\mathcal{B}}}_{\left[\right(\alpha ,\beta \left)\right]}\right)\hfill \\ & =& \breve{\tau }\left(\widehat{\mathcal{A}}\right)\wedge \breve{\tau }\left(\widehat{\mathcal{B}}\right).\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \breve{\tau }\left(\bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\right)& =& \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\tau \left(\bigcup _{\lambda \in \mathsf{\Lambda }}{\left({\widehat{\mathcal{A}}}_{\lambda }\right)}_{\left[\right(\alpha ,\beta \left)\right]}\right)\hfill \\ & \ge & \underset{(\alpha ,\beta )\in \mathcal{Z}}{\bigwedge }\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\tau \left({\left({\widehat{\mathcal{A}}}_{\lambda }\right)}_{\left[\right(\alpha ,\beta \left)\right]}\right)=\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\breve{\tau }\left({\widehat{\mathcal{A}}}_{\lambda }\right).\hfill \end{array}$$

Definition 6.

The family of bi-intuitionistic fuzzy closed sets, denoted by $\mathcal{F}\in \mathcal{IF}\left(\mathcal{IF}\right(\mathcal{X}\left)\right)$, is defined as $\widehat{\mathcal{A}}\in \mathcal{F}:=\neg \left(\widehat{\mathcal{A}}\right)\in \tau$, i.e., $\mathcal{F}\left(\widehat{\mathcal{A}}\right)=\tau (\neg \left(\widehat{\mathcal{A}}\right))$, or equivalently $m\mathcal{F}\left(\widehat{\mathcal{A}}\right)=m\tau (\neg \left(\widehat{\mathcal{A}}\right))$ and $n\mathcal{F}\left(\widehat{\mathcal{A}}\right)=n\tau (\neg \left(\widehat{\mathcal{A}}\right))$.

Theorem 7.

(1) $\mathcal{F}\left(\widehat{1}\right)=\mathcal{F}\left(\widehat{0}\right)=(1,0)$;

(2) for any $\widehat{\mathcal{A}},\widehat{\mathcal{B}}\in \mathcal{IF}\left(\mathcal{X}\right)$, $\vDash \widehat{\mathcal{A}}\in \mathcal{F}\wedge \widehat{\mathcal{B}}\in \mathcal{F}\to \widehat{\mathcal{A}}\cup \widehat{\mathcal{B}}\in \mathcal{F}$;

(3) for any $\left\{{\widehat{\mathcal{A}}}_{\lambda }:\lambda \in \mathsf{\Lambda }\right\}\subseteq \mathcal{IF}\left(\mathcal{X}\right)$,

$$\vDash \forall \lambda \left(\lambda \in \mathsf{\Lambda }\dot{\to }{\widehat{\mathcal{A}}}_{\lambda }\in \mathcal{F}\right)\to \bigcup _{\lambda \in \mathsf{\Lambda }}{\widehat{\mathcal{A}}}_{\lambda }\in \mathcal{F}.$$

In the sequel, we discuss only intuitionistic fuzzifying topological spaces as a preliminary of the research on bi-intuitionistic fuzzy topology.

5. Intuitionistic Fuzzifying Neighborhood Structure of a Point

In this section, we introduce the definition of the intuitionistic fuzzifying neighborhood structure of a point and study its properties.

Definition 7.

Let $x\in \mathcal{X}$. The intuitionistic fuzzifying neighborhood system of x, denoted by ${\widehat{\mathcal{N}}}_x\in \mathcal{IF}\left(\mathcal{P}\left(\mathcal{X}\right)\right)$, is defined as follows:

$$\mathcal{A}\in {\widehat{\mathcal{N}}}_x:=\exists \mathcal{B}\left(\mathcal{B}\in \tau \wedge \mathcal{B}\in \mathcal{M}(x,\mathcal{A})\right),$$

where $\mathcal{M}(x,\mathcal{A})=\left\{\mathcal{B}:\mathcal{B}\subseteq \mathcal{X},x\in \mathcal{B}\subseteq \mathcal{A}\right\}$.

Lemma 6.

${\displaystyle \underset{x\in \mathcal{A}}{\bigwedge }}{\displaystyle \underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }}\tau \left(\mathcal{B}\right)=\tau \left(\mathcal{A}\right)$.

Proof. 

First, for each $x\in \mathcal{A}$, we have ${\displaystyle \underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }}\tau \left(\mathcal{B}\right)\ge \tau \left(\mathcal{A}\right)$. So,

$$\underset{x\in \mathcal{A}}{\bigwedge }\underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{B}\right)\ge \tau \left(\mathcal{A}\right).$$

Second, for any $f\in {\displaystyle \prod _{x\in \mathcal{A}}}\mathcal{M}(x,\mathcal{A})$ we have ${\displaystyle \bigcup _{x\in \mathcal{A}}}f\left(x\right)=\mathcal{A}$. Therefore

$$\tau \left(\mathcal{A}\right)=\tau \left(\bigcup _{x\in \mathcal{A}}f\left(x\right)\right)\ge \underset{x\in \mathcal{A}}{\bigwedge }\tau \left(f\left(x\right)\right).$$

So,

$$\tau \left(\mathcal{A}\right)\ge \underset{f\in \prod _{x\in \mathcal{A}}\mathcal{M}(x,\mathcal{A})}{\bigvee }\underset{x\in \mathcal{A}}{\bigwedge }\tau \left(f\left(x\right)\right)=\underset{x\in \mathcal{A}}{\bigwedge }\underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{B}\right).$$

□

Corollary 1.

$\tau \left(\mathcal{A}\right)={\displaystyle \underset{x\in \mathcal{A}}{\bigwedge }}{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)$.

Theorem 8.

For any $x\in \mathcal{X}$ and $\mathcal{A}\in \mathcal{P}\left(\mathcal{X}\right)$,

$$\vDash \mathcal{A}\in \tau ⟷\forall x\left(x\in \mathcal{A}\dot{\to }\exists \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\wedge \mathcal{B}\subseteq \mathcal{A}\right)\right).$$

Proof. 

$$\begin{array}{ccc}\hfill \left[\forall x\left(x\in \mathcal{A}\dot{\to }\exists \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\wedge \mathcal{B}\subseteq \mathcal{A}\right)\right)\right]& =& \underset{x\in \mathcal{A}}{\bigwedge }\underset{\mathcal{B}\subseteq \mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\hfill \\ & =& \underset{x\in \mathcal{A}}{\bigwedge }\underset{\mathcal{B}\subseteq \mathcal{A}}{\bigvee }\underset{\mathcal{C}\in \mathcal{M}(x,\mathcal{B})}{\bigvee }\tau \left(\mathcal{C}\right)\hfill \\ & =& \underset{x\in \mathcal{A}}{\bigwedge }\underset{\mathcal{C}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{C}\right)\hfill \\ & =& \underset{x\in \mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=\tau \left(\mathcal{A}\right).\hfill \end{array}$$

□

Theorem 9.

The mapping $\widehat{\mathcal{N}}:\mathcal{X}\to {\mathcal{IF}}^{\mathcal{N}}\left(\mathcal{X}\right)$, $x\mapsto {\widehat{\mathcal{N}}}_x$, has the following properties:

(1) For any $x\in \mathcal{A}$, $\vDash \mathcal{A}\in {\widehat{\mathcal{N}}}_x\to x\in \mathcal{A}$;

(2) For any $x\in \mathcal{A},\mathcal{B}$, $\vDash \mathcal{A}\in {\widehat{\mathcal{N}}}_x\wedge \mathcal{B}\in {\widehat{\mathcal{N}}}_x\to \mathcal{A}\cap \mathcal{B}\in {\widehat{\mathcal{N}}}_x$;

(3) For any $x\in \mathcal{A},\mathcal{B}$, $\vDash \mathcal{A}\subseteq \mathcal{B}\dot{\to }\left(\mathcal{A}\in {\widehat{\mathcal{N}}}_x\to \mathcal{B}\in {\widehat{\mathcal{N}}}_x\right)$;

(4) For any $x,\mathcal{A}$, $\vDash \mathcal{A}\in {\widehat{\mathcal{N}}}_x\to \exists \mathcal{C}\left((\mathcal{C}\in {\widehat{\mathcal{N}}}_x)\wedge (\mathcal{C}\subseteq \mathcal{A})\wedge \forall (y\in \mathcal{C}\dot{\to }\mathcal{C}\in {\widehat{\mathcal{N}}}_y)\right)$.

Conversely, if a mapping $\widehat{\mathcal{N}}$ satisfies (2) and (3), then τ is an intuitionistic fuzzifying topology which is defined $\mathcal{A}\in \tau :=\forall x\left(x\in \mathcal{A}\dot{\to }\mathcal{A}\in {\widehat{\mathcal{N}}}_x\right)$.

Specially, if it satisfies (1) and (4) also, then for any $x\in \mathcal{X},{\widehat{\mathcal{N}}}_x$ is the neighborhood system of x with respect to τ.

Proof. 

(A) Since ${\widehat{\mathcal{N}}}_x\left(\mathcal{X}\right)={\displaystyle \underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{X})}{\bigvee }}\tau \left(\mathcal{B}\right)\ge \tau \left(\mathcal{X}\right)=(1,0)$, then ${\widehat{\mathcal{N}}}_x$ is normal.

(1) If $\mathcal{A}\left(x\right)=(1,0)$, then $\mathcal{A}\left(x\right)\ge {\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)$. Now, suppose $\mathcal{A}\left(x\right)=(0,1)$. We need to prove that ${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=(0,1)$. Indeed,

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)& =& \underset{\mathcal{B}\in \mathcal{P}\left(\mathcal{X}\right)}{\bigvee }\left(\tau \left(\mathcal{B}\right)\wedge x\in \mathcal{B}\wedge \mathcal{B}\subseteq \mathcal{A}\right)\hfill \\ & =& \underset{x\in \mathcal{B}}{\bigvee }\left(\tau \left(\mathcal{B}\right)\wedge \mathcal{B}\subseteq \mathcal{A}\right)=\underset{x\in \mathcal{B}}{\bigvee }\left(\tau \left(\mathcal{B}\right)\wedge (0,1)\right)\hfill \\ & =& \underset{x\in \mathcal{B}}{\bigvee }\left(m\tau \left(\mathcal{B}\right)\wedge 0,n\tau \left(\mathcal{B}\right)\vee 1\right)\hfill \\ & =& \underset{x\in \mathcal{B}}{\bigvee }(0,1)=(0,1).\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{N}}}_x(\mathcal{A}\cap \mathcal{B})& =& \underset{x\in \mathcal{C}\subseteq \mathcal{A}\cap \mathcal{B}}{\bigvee }\tau \left(\mathcal{C}\right)\hfill \\ & =& \underset{x\in {\mathcal{C}}_1\subseteq \mathcal{A},x\in {\mathcal{C}}_2\subseteq \mathcal{B}}{\bigvee }\tau ({\mathcal{C}}_1\cap {\mathcal{C}}_2)\hfill \\ & \ge & \underset{x\in {\mathcal{C}}_1\subseteq \mathcal{A},x\in {\mathcal{C}}_2\subseteq \mathcal{B}}{\bigvee }\left(\tau \left({\mathcal{C}}_1\right)\wedge \tau \left({\mathcal{C}}_2\right)\right)\hfill \\ & =& \underset{x\in {\mathcal{C}}_1\subseteq \mathcal{A}}{\bigvee }\tau \left({\mathcal{C}}_1\right)\wedge \underset{x\in {\mathcal{C}}_2\subseteq \mathcal{B}}{\bigvee }\tau \left({\mathcal{C}}_2\right)\hfill \\ & =& \underset{{\mathcal{C}}_1\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left({\mathcal{C}}_1\right)\wedge \underset{{\mathcal{C}}_2\in \mathcal{M}(x,\mathcal{B})}{\bigvee }\tau \left({\mathcal{C}}_2\right)={\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\wedge {\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right).\hfill \end{array}$$

(3) If $[\mathcal{A}\subseteq \mathcal{B}]=(0,1)$, then the result holds. Suppose $[\mathcal{A}\subseteq \mathcal{B}]=(1,0)$ and so to complete the proof we need to prove that ${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\le {\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)$. Now, $\mathcal{M}(x,\mathcal{A})\subseteq \mathcal{M}(x,\mathcal{B})$.

Then

$${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=\underset{\mathcal{C}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{C}\right)\le \underset{\mathcal{C}\in \mathcal{M}(x,\mathcal{B})}{\bigvee }\tau \left(\mathcal{C}\right)={\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right).$$

Thus $[\mathcal{A}\in {\widehat{\mathcal{N}}}_x\dot{\to }\mathcal{B}\in {\widehat{\mathcal{N}}}_x]=(1,0)$.

(4)

$$\begin{array}{c}\hfill \left[\exists \mathcal{C}\left((\mathcal{C}\in {\widehat{\mathcal{N}}}_x)\wedge (\mathcal{C}\subseteq \mathcal{A})\wedge \forall (y\in \mathcal{C}\dot{\to }\mathcal{C}\in {\widehat{\mathcal{N}}}_y)\right)\right]\\ & =& \underset{\mathcal{C}\subseteq \mathcal{A}}{\bigvee }\left({\widehat{\mathcal{N}}}_x\left(\mathcal{C}\right)\wedge \underset{y\in \mathcal{C}}{\bigwedge }{\widehat{\mathcal{N}}}_y\left(\mathcal{C}\right)\right)\hfill \\ & =& \underset{\mathcal{C}\subseteq \mathcal{A}}{\bigvee }\left({\widehat{\mathcal{N}}}_x\left(\mathcal{C}\right)\wedge \tau \left(\mathcal{C}\right)\right)\hfill \\ & =& \underset{\mathcal{C}\subseteq \mathcal{A}}{\bigvee }\tau \left(\mathcal{C}\right)\ge \underset{x\in \mathcal{C}\subseteq \mathcal{A}}{\bigvee }\tau \left(\mathcal{C}\right)\hfill \\ & =& \underset{\mathcal{C}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{C}\right)={\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right).\hfill \end{array}$$

(B) Conversely, we prove that $\tau \left(\mathcal{A}\right)={\displaystyle \underset{x\in \mathcal{A}}{\bigwedge }}{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)$ is an intuitionistic fuzzifying topology.

(1) (a) $\tau \left(\varphi \right)={\displaystyle \underset{x\in \varphi }{\bigwedge }}{\widehat{\mathcal{N}}}_x\left(\varphi \right)=(1,0)$.

(b) For any $x\in \mathcal{X}$ and since ${\mathcal{N}}_x$ is normal, then there exists $\mathcal{A}\in \mathcal{P}\left(\mathcal{X}\right)$ such that ${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=(1,0)$. Thus, from Condition (3) we have ${\widehat{\mathcal{N}}}_x\left(\mathcal{X}\right)\ge {\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=(1,0)$. Therefore, $\tau \left(\mathcal{X}\right)={\displaystyle \underset{x\in \mathcal{X}}{\bigwedge }}{\widehat{\mathcal{N}}}_x\left(\mathcal{X}\right)=(1,0)$.

(2) Applying Condition (2) we have

$$\begin{array}{ccc}\hfill \tau (\mathcal{A}\cap \mathcal{B})& =& \underset{x\in \mathcal{A}\cap \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{A}\cap \mathcal{B})\hfill \\ & \ge & \underset{x\in \mathcal{A}\cap \mathcal{B}}{\bigwedge }\left({\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\wedge {\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\hfill \\ & =& \underset{x\in \mathcal{A}\cap \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\wedge \underset{x\in \mathcal{A}\cap \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\hfill \\ & \ge & \underset{x\in \mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\wedge \underset{x\in \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)=\tau \left(\mathcal{A}\right)\wedge \tau \left(\mathcal{B}\right).\hfill \end{array}$$

(3) Applying Condition (3) we have

$$\begin{array}{ccc}\hfill \tau \left(\bigcup _{\lambda \in \mathsf{\Lambda }}{\mathcal{A}}_{\lambda }\right)& =& \underset{x\in {\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }}{\bigwedge }{\widehat{\mathcal{N}}}_x\left({\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\right)\hfill \\ & =& \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\underset{x\in {\mathcal{A}}_{\lambda }}{\bigwedge }{\widehat{\mathcal{N}}}_x\left({\displaystyle \bigcup _{\lambda \in \mathsf{\Lambda }}}{\mathcal{A}}_{\lambda }\right)\hfill \\ & \ge & \underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\underset{x\in {\mathcal{A}}_{\lambda }}{\bigwedge }{\widehat{\mathcal{N}}}_x\left({\mathcal{A}}_{\lambda }\right)=\underset{\lambda \in \mathsf{\Lambda }}{\bigwedge }\tau \left({\mathcal{A}}_{\lambda }\right).\hfill \end{array}$$

(4) From Condition (4), ${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\le {\displaystyle \underset{\mathcal{B}\subseteq \mathcal{A}}{\bigvee }}\left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\wedge {\displaystyle \underset{y\in \mathcal{B}}{\bigwedge }}{\widehat{\mathcal{N}}}_y\left(\mathcal{B}\right)\right)$ and from Condition (1), if $[x\in \mathcal{B}]=(0,1)$, then ${\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)=(0,1)$. So,

$${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\le \underset{x\in \mathcal{B}\subseteq \mathcal{A}}{\bigvee }\left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\wedge \underset{y\in \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_y\left(\mathcal{B}\right)\right)=\underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\underset{y\in \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_y\left(\mathcal{B}\right)=\underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{B}\right).$$

On the other hand, for each $\mathcal{B}\in \mathcal{M}(x,\mathcal{A})$, from Condition (3) we obtain ${\displaystyle \underset{y\in \mathcal{B}}{\bigwedge }}{\widehat{\mathcal{N}}}_y\left(\mathcal{B}\right)\le {\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\le {\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)$. Therefore,

$${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\ge \underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\underset{y\in \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_y\left(\mathcal{B}\right)=\underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }\tau \left(\mathcal{B}\right).$$

Therefore, we obtain ${\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)={\displaystyle \underset{\mathcal{B}\in \mathcal{M}(x,\mathcal{A})}{\bigvee }}\tau \left(\mathcal{B}\right).$ □

6. Intuitionistic Fuzzifying Fundamental Concepts

In this section, the concepts of intuitionistic fuzzifying closure, intuitionistic fuzzifying boundary, intuitionistic fuzzifying derived set, and intuitionistic fuzzifying interior are investigated. Additionally, the relations among these concepts are derived.

Definition 8.

The intuitionistic fuzzifying derived (resp. closure, interior, boundary) operation will be denoted by $\widehat{\mathcal{D}}$ (resp. $\widehat{Cl}$, $\widehat{Int}$, $\widehat{b}$) $\in {\left(\mathcal{IF}\left(\mathcal{X}\right)\right)}^{\mathcal{P}\left(\mathcal{X}\right)}$ and defined as follows:

$x\in \widehat{\mathcal{D}}\left(\mathcal{A}\right):=\forall \mathcal{B}(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }\mathcal{B}\cap (\mathcal{A}-\left\{x\right\})\ne \varphi )$;

$x\in \widehat{Cl}\left(\mathcal{A}\right):=\forall \mathcal{B}((\mathcal{B}\supseteq \mathcal{A})\wedge \mathcal{B}\in \mathcal{F}\dot{\to }x\in \mathcal{B})$;

$x\in \widehat{Int}\left(\mathcal{A}\right):=\mathcal{A}\in {\widehat{\mathcal{N}}}_x$;

$x\in \widehat{b}\left(\mathcal{A}\right):=x\in \widehat{Cl}\left(\mathcal{A}\right)\wedge \widehat{Cl}(\mathcal{X}-\mathcal{A})$.

Theorem 10.

For any $x,\mathcal{A}$ (1) $\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)=\neg ({\widehat{\mathcal{N}}}_x((\mathcal{X}-\mathcal{A})\cup \left\{x\right\})$;

(2) $\vDash \mathcal{A}\in \mathcal{F}⟷\widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}$.

Proof. 

(1)

$$\begin{array}{ccc}\hfill \widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)& =& \underset{\mathcal{B}\cap (\mathcal{A}-\{x\left\}\right)=\varphi }{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left(\underset{\mathcal{B}\subseteq (\mathcal{X}-\mathcal{A})\cup \left\{x\right\}}{\bigvee }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left({\widehat{\mathcal{N}}}_x((\mathcal{X}-\mathcal{A})\cup \left\{x\right\})\right).\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill [\widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}]& =& \left[\forall x\left(x\in \widehat{\mathcal{D}}\left(\mathcal{A}\right)\dot{\to }x\in \mathcal{A}\right)\right]\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{A}}{\bigwedge }\neg \left(\widehat{\mathcal{D}}\left(\mathcal{A}\right)\right)\left(x\right)\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x((\mathcal{X}-\mathcal{A})\cup \left\{x\right\})\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})=\tau (\mathcal{X}-\mathcal{A})=\mathcal{F}\left(\mathcal{A}\right).\hfill \end{array}$$

□

Lemma 7.

$\vDash \widehat{Cl}\left(\mathcal{A}\right)\equiv \neg ((\mathcal{X}-\mathcal{A})\in {\widehat{\mathcal{N}}}_x)$.

Proof. 

$$\begin{array}{ccc}\hfill \widehat{Cl}\left(\mathcal{A}\right)\left(x\right)& =& \underset{x\in \mathcal{X}-\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigwedge }\neg \left(\mathcal{F}\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left(\underset{x\in \mathcal{X}-\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }\mathcal{F}\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left(\underset{x\in \mathcal{X}-\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }\tau (\mathcal{X}-\mathcal{B})\right)\hfill \\ & =& \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right).\hfill \end{array}$$

□

Corollary 2.

(1) $\vDash \widehat{Cl}\left(\mathcal{A}\right)\dot{\equiv }\neg ((\mathcal{X}-\mathcal{A})\in {\widehat{\mathcal{N}}}_x)$;

(2) $\vDash \widehat{Cl}\left(\mathcal{A}\right)\dot{\approx }\neg ((\mathcal{X}-\mathcal{A})\in {\widehat{\mathcal{N}}}_x)$

Theorem 11.

(1) $\widehat{Cl}\left(\varphi \right)=\varphi$;

(2) For any $\mathcal{A},\vDash \mathcal{A}⋐\widehat{Cl}\left(\mathcal{A}\right)$;

(3) For any $\mathcal{A},\mathcal{B}$, if $[\mathcal{A}\subseteq \mathcal{B}]=(1,0)$, then $\vDash \widehat{Cl}\left(\mathcal{A}\right)\subseteq \widehat{Cl}\left(\mathcal{B}\right)$;

(4) For any, $\vDash \widehat{Cl}(\mathcal{A}\cup \mathcal{B})\equiv \widehat{Cl}\left(\mathcal{A}\right)\cup \widehat{Cl}\left(\mathcal{B}\right)$.

Proof. 

(1) $\widehat{Cl}\left(\varphi \right)\left(x\right)=\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{X}\right)\right)=\neg (1,0)=(0,1)=\varphi \left(x\right)$.

(2)

$$\begin{array}{ccc}\hfill [\mathcal{A}⋐\widehat{Cl}\left(\mathcal{A}\right)]& =& \left[\forall x\left(x\in \mathcal{A}\dot{\to }x\in \widehat{Cl}\left(\mathcal{A}\right)\right)\right]\hfill \\ & =& \underset{x\in \mathcal{A}}{\bigwedge }\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)=\underset{x\in \mathcal{A}}{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\hfill \\ & =& \neg \left(\underset{x\in \mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)=\neg (0,1)=(1,0).\hfill \end{array}$$

(3) Suppose that $[\mathcal{A}\subseteq \mathcal{B}]=(1,0)$. Then, from Theorem 9 (3), we have ${\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{B})\le {\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})$. Hence $\neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\le \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{B})\right)$. Therefore, $\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)\le \widehat{Cl}\left(\mathcal{B}\right)\left(x\right)$. Therefore $\vDash \widehat{Cl}\left(\mathcal{A}\right)\subseteq \widehat{Cl}\left(\mathcal{B}\right)$.

(4) Applying (3) above, we obtain $\vDash \widehat{Cl}\left(\mathcal{A}\right)\cup \widehat{Cl}\left(\mathcal{B}\right)\subseteq \widehat{Cl}(\mathcal{A}\cup \mathcal{B})$. Now, we need to prove that $\vDash \widehat{Cl}(\mathcal{A}\cup \mathcal{B})\subseteq \widehat{Cl}\left(\mathcal{A}\right)\cup \widehat{Cl}\left(\mathcal{B}\right)$. For any $x\in \mathcal{X}$,

$$\begin{array}{ccc}\hfill \widehat{Cl}(\mathcal{A}\cup \mathcal{B})\left(x\right)& =& \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-(\mathcal{A}\cup \mathcal{B}))\right)\hfill \\ & =& \neg \left({\widehat{\mathcal{N}}}_x\left((\mathcal{X}-\mathcal{A})\cap (\mathcal{X}-\mathcal{B})\right)\right)\hfill \\ & \le & \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\wedge {\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{B})\right)\hfill \\ & =& \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\vee \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{B})\right)\hfill \\ & =& \widehat{Cl}\left(\mathcal{A}\right)\left(x\right)\vee \widehat{Cl}\left(\mathcal{B}\right)\left(x\right).\hfill \end{array}$$

□

Theorem 12.

For any $x,\mathcal{A}$,

(1) $\vDash \widehat{Cl}\left(\mathcal{A}\right)\dot{\approx }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)$, $\vDash \widehat{Cl}\left(\mathcal{A}\right)\dot{\equiv }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)$ and $\vDash \widehat{Cl}\left(\mathcal{A}\right)\equiv \mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)$;

(2) $\vDash x\in \widehat{Cl}\left(\mathcal{A}\right)⟷\forall \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }\mathcal{A}\cap \mathcal{B}\ne \varphi \right)$;

(3) $\vDash \mathcal{A}\in \mathcal{F}\to \widehat{Cl}\left(\mathcal{A}\right)\dot{\equiv }\mathcal{A}$;

(4) $\vDash \mathcal{A}\in \mathcal{F}\to \widehat{Cl}\left(\mathcal{A}\right)\equiv \mathcal{A}$.

Proof. 

(1) If $\mathcal{A}\left(x\right)=(1,0)$, then $\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)=\neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)=\neg (0,1)=(1,0)$, and so $\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)=\mathcal{A}\left(x\right)=\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)$. If $\mathcal{A}\left(x\right)=(0,1)$, then $\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)=\neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)=\neg \left({\widehat{\mathcal{N}}}_x((\mathcal{X}-\mathcal{A})\cup \left\{x\right\})\right)=\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)=(\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right))\left(x\right)$. Therefore, by Lemma 5, the results hold.

(2)

$$\begin{array}{ccc}\hfill \left[\forall \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }\mathcal{A}\cap \mathcal{B}\ne \varphi \right)\right]& =& \underset{\mathcal{A}\cap \mathcal{B}=\varphi }{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left(\underset{\mathcal{A}\cap \mathcal{B}=\varphi }{\bigvee }\left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\right)\hfill \\ & =& \neg \left(\underset{\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }\left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\right)\hfill \\ & =& \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)=\widehat{Cl}\left(\mathcal{A}\right)\left(x\right).\hfill \end{array}$$

(3)

$$\begin{array}{c}\hfill \mathcal{F}\left(\mathcal{A}\right)=[\widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}]=[\widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}]\wedge [\mathcal{A}⋐\mathcal{A}]\le [\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}]\\ & =& [\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}]\wedge [\mathcal{A}⋐\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)]\le [\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\dot{\equiv }\mathcal{A}]\hfill \\ & =& \left[\widehat{Cl}\left(\mathcal{A}\right)\dot{\equiv }\mathcal{A}\right].\hfill \end{array}$$

(4) $\vDash \mathcal{A}\in \mathcal{F}\to \widehat{Cl}\left(\mathcal{A}\right)\dot{\equiv }\mathcal{A}\to \widehat{Cl}\left(\mathcal{A}\right)\equiv \mathcal{A}$. □

Theorem 13.

For any $\mathcal{A},\mathcal{B},$$\vDash \mathcal{B}\dot{\approx }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\to \mathcal{B}\in \mathcal{F}$.

Proof. 

If $[\mathcal{A}\subseteq \mathcal{B}]=(0,1)$, then $[\mathcal{B}\dot{\approx }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)]=(0,1)$. Suppose $[\mathcal{A}\subseteq \mathcal{B}]=(1,0)$. Then

$$\begin{array}{ccc}\hfill [\mathcal{B}⋐\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)]& =& \left[\forall x\left(x\in \mathcal{B}\dot{\to }x\in \mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\right)\right]\hfill \\ & =& \underset{x\in \mathcal{B}}{\bigwedge }[x\in \mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)]\hfill \\ & =& \underset{x\in \mathcal{B}}{\bigwedge }\left(m\mathcal{A}\left(x\right)\vee m\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right),n\mathcal{A}\left(x\right)\wedge n\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)\right)\hfill \\ & =& \underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }(m\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right),n\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right))=\underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)\hfill \\ & =& \underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x((\mathcal{X}-\mathcal{A})\cup \left\{x\right\})\right)\hfill \\ & =& \underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\hfill \\ & =& \neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right).\hfill \end{array}$$

$$\begin{array}{ccc}\hfill [\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{B}]& =& \left[\forall x\left(x\in \mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\dot{\to }x\in \mathcal{B}\right)\right]\hfill \\ & =& \left[\forall x\left(x\notin \mathcal{B}\dot{\to }\neg \left(x\in \mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\right)\right)\right]\hfill \\ & =& \underset{x\notin \mathcal{B}}{\bigwedge }\neg \left(x\in \mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\right)\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }\neg \left(m\mathcal{A}\left(x\right)\vee m\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right),n\mathcal{A}\left(x\right)\wedge n\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)\right)\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }\neg \left(m\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right),n\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)\right)\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }\neg \left(\widehat{\mathcal{D}}\left(\mathcal{A}\right)\left(x\right)\right)\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A}).\hfill \end{array}$$

Suppose $\mathcal{B}\dot{\approx }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)>(t,t_o).$ Then

$$(max\left(0,m\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)+m\underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})-1\right),$$

$$min\left(1,n\left(\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\right)+n\underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right))>(t,t_o).$$

First,

$$m\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)+m\underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})-1>t.$$

Hence

$$m\underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})>1-m\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)+t.$$

For any $x\in \mathcal{X}-\mathcal{B}$,

$$m{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})>1-m\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)+t,$$

then

$$m\left(\underset{x\in \mathcal{C}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }\tau \left(\mathcal{C}\right)\right)>1-m\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)+t,$$

i.e., there exists ${\mathcal{C}}_x$ such that $x\in {\mathcal{C}}_x\subseteq \mathcal{X}-\mathcal{A}$ and

$$m\tau \left({\mathcal{C}}_x\right)>1-m\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)+t>t.$$

Therefore,

$$m\mathcal{F}\left(\mathcal{B}\right)=m\tau (\mathcal{X}-\mathcal{B})=m\underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{B})\ge m\left(\underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }\tau \left({\mathcal{C}}_x\right)\right)>t.$$

Second, $n\left(\neg \left({\displaystyle \underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }}{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\right)+n{\displaystyle \underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }}{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})<t_o$. Hence,

$$n\underset{x\in \mathcal{B}-\mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})<t_o-n\left(\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\right).$$

There exists $x^{\prime }\in \mathcal{X}-\mathcal{B}$ such that

$$n\left({\widehat{\mathcal{N}}}_{x^{\prime }}(\mathcal{X}-\mathcal{A})\right)<t_o-n\left(\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\right).$$

Thus

$$n\left(\underset{x^{\prime }\in \mathcal{C}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }\tau \left(\mathcal{C}\right)\right)<t_o-n\left(\neg \left(\underset{x\in \mathcal{B}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\right).$$

So, $n\left(\tau \left(\mathcal{C}\right)\right)<t_o$. Therefore,

$$\begin{array}{ccc}\hfill n\mathcal{F}\left(\mathcal{B}\right)& =& n\tau (\mathcal{X}-\mathcal{B})\hfill \\ & =& n\left(\underset{x\in \mathcal{X}-\mathcal{B}}{\bigwedge }{\mathcal{N}}_x(\mathcal{X}-\mathcal{B})\right)\le n\left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{B})\right)\hfill \\ & \le & n\left(\underset{x\in \mathcal{C}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }\tau \left(\mathcal{C}\right)\right)\le n\tau \left(\mathcal{C}\right)<t_o.\hfill \end{array}$$

Hence $\mathcal{F}\left(\mathcal{B}\right)=\left(m\mathcal{F}\left(\mathcal{B}\right),n\mathcal{F}\left(\mathcal{B}\right)\right)>(t,t_o)$. Therefore, $\mathcal{F}\left(\mathcal{B}\right)\ge [\mathcal{B}\dot{\approx }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)]$. We obtain $\vDash \mathcal{B}\dot{\approx }\mathcal{A}\cup \widehat{\mathcal{D}}\left(\mathcal{A}\right)\to \mathcal{B}\in \mathcal{F}$. □

Theorem 14.

For any $x,\mathcal{A},\mathcal{B}$,

(1) $\vDash (\mathcal{B}\in \tau )\wedge (\mathcal{B}\subseteq \mathcal{A})\to \mathcal{B}⋐\widehat{Int}\left(\mathcal{A}\right)$;

(2) $\vDash \mathcal{A}\dot{\equiv }\widehat{Int}\left(\mathcal{A}\right)⟷\mathcal{A}\in \tau$, and the statement is true when we replace “$\dot{\equiv }$” by “$\dot{\approx }$”;

(3) $\vDash x\in \widehat{Int}\left(\mathcal{A}\right)⟷(x\in \mathcal{A})\wedge (x\in \neg \left(\widehat{\mathcal{D}}(\mathcal{X}-\mathcal{A})\right))$, and the statement is true when we replace “∧” by “⊼”;

(4) $\vDash \widehat{Int}\left(\mathcal{A}\right)\equiv \neg \left(\widehat{Cl}(\mathcal{X}-\mathcal{A})\right)$, and the statement is true when we replace “≡” by “$\dot{\equiv }$” or by “$\dot{\approx }$”;

(5) $\vDash \mathcal{B}\dot{\equiv }\widehat{Int}\left(\mathcal{A}\right)\to \mathcal{B}\in \tau$, and the statement is true when we replace “$\dot{\equiv }$” by “$\dot{\approx }$”.

Proof. 

(1) If $[\mathcal{B}\subseteq \mathcal{A}]=(0,1)$, then

$$\left[\right(\mathcal{B}\in \tau )\wedge (\mathcal{B}\subseteq \mathcal{A}\left)\right]=\tau \left(\mathcal{B}\right)\wedge (0,1)=(0,1).$$

If $[\mathcal{B}\subseteq \mathcal{A}]=(1,0)$, then

$$\begin{array}{ccc}\hfill [\mathcal{B}⋐\widehat{Int}\left(\mathcal{A}\right)]& =& \left[\forall x\left(x\in \mathcal{B}\dot{\to }x\in \widehat{Int}\left(\mathcal{A}\right)\right)\right]\hfill \\ & \le & \underset{x\in \mathcal{B}}{\bigwedge }\left[(1,0)\dot{\to }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right]\hfill \\ & =& \underset{x\in \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\ge \underset{x\in \mathcal{B}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\hfill \\ & =& \tau \left(\mathcal{B}\right)=[\mathcal{B}\in \tau ]=\left[\right(\mathcal{B}\in \tau )\wedge (1,0\left)\right]\hfill \\ & =& \left[\right(\mathcal{B}\in \tau )\wedge (\mathcal{B}\subseteq \mathcal{A}\left)\right].\hfill \end{array}$$

(2) $\left[\mathcal{A}\dot{\equiv }\widehat{Int}\left(\mathcal{A}\right)\right]=[\mathcal{A}⋐\widehat{Int}\left(\mathcal{A}\right)]\wedge [\widehat{Int}\left(\mathcal{A}\right)⋐\mathcal{A}].$ First,

$$\begin{array}{ccc}\hfill [\widehat{Int}\left(\mathcal{A}\right)⋐\mathcal{A}]& =& \left[\forall x\left(x\in \widehat{Int}\left(\mathcal{A}\right)\dot{\to }x\in \mathcal{A}\right)\right]\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{A}}{\bigwedge }\left[(1,0)\dot{\to }\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right)\right]\hfill \\ & =& \underset{x\in \mathcal{X}-\mathcal{A}}{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right)\hfill \\ & =& \neg \left(\underset{x\in \mathcal{X}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right)=\neg (0,1)=(1,0).\hfill \end{array}$$

Second,

$$\begin{array}{ccc}\hfill [\mathcal{A}⋐\widehat{Int}\left(\mathcal{A}\right)]& =& \left[\forall x\left(x\in \mathcal{A}\dot{\to }x\in \widehat{Int}\left(\mathcal{A}\right)\right)\right]\hfill \\ & =& \underset{x\in \mathcal{A}}{\bigwedge }\left[(1,0)\dot{\to }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right]=\underset{x\in \mathcal{A}}{\bigwedge }{\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=\tau \left(\mathcal{A}\right)=[\mathcal{A}\in \tau ].\hfill \end{array}$$

(3) If $\mathcal{A}\left(x\right)=(0,1)$, then $\widehat{Int}\left(\mathcal{A}\right)\left(x\right)=(0,1)$ and the result holds. If $\mathcal{A}\left(x\right)=(1,0)$, then

$$[x\in \widehat{\mathcal{D}}(\mathcal{X}-\mathcal{A})]=\widehat{\mathcal{D}}(\mathcal{X}-\mathcal{A})\left(x\right)=\neg \left({\widehat{\mathcal{N}}}_x(\mathcal{A}\cup \left\{x\right\})\right)=\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right).$$

Hence

$$[x\in \neg \left(\widehat{\mathcal{D}}(\mathcal{X}-\mathcal{A})\right)]=\neg \left(\widehat{\mathcal{D}}(\mathcal{X}-\mathcal{A})\right)\left(x\right)={\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)=[x\in \widehat{Int}\left(\mathcal{A}\right)].$$

Therefore,

$$[(x\in \mathcal{A})\wedge x\in \neg \left(\widehat{\mathcal{D}}(\mathcal{X}-\mathcal{A})\right)]=[x\in \widehat{Int}\left(\mathcal{A}\right)].$$

(4) Follows from Lemma 7.

(5) From (4) above, Theorems 12 and 13 (1) we have

$$\left[\mathcal{B}\dot{\equiv }\widehat{Int}\left(\mathcal{A}\right)\right]\equiv [\neg \left(\mathcal{B}\right)\dot{\equiv }\neg \left(\widehat{Int}\left(\mathcal{A}\right)\right)]\equiv [\mathcal{X}-\mathcal{B}\dot{\equiv }\widehat{Cl}(\mathcal{X}-\mathcal{A})]\le [\mathcal{X}-\mathcal{B}\in \mathcal{F}]=[\mathcal{B}\in \tau ].$$

□

Lemma 8.

$$\vDash x\in \widehat{b}\left(\mathcal{A}\right)⟷\forall \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }\left((\mathcal{B}\cap \mathcal{A}\ne \varphi )\wedge (\mathcal{B}\cap (\mathcal{X}-\mathcal{A})\ne \varphi )\right)\right).$$

Proof. 

$$\begin{array}{c}\hfill \left[\forall \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }\left((\mathcal{B}\cap \mathcal{A}\ne \varphi )\wedge (\mathcal{B}\cap (\mathcal{X}-\mathcal{A})\ne \varphi )\right)\right)\right]\\ & =& \left[\forall \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }(\mathcal{B}\cap \mathcal{A}\ne \varphi )\right)\right]\wedge \left[\forall \mathcal{B}\left(\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }(\mathcal{B}\cap (\mathcal{X}-\mathcal{A})\ne \varphi )\right)\right]\hfill \\ & =& \underset{\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigwedge }\left[\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }(0,1)\right]\wedge \underset{\mathcal{B}\subseteq \mathcal{A}}{\bigwedge }\left[\mathcal{B}\in {\widehat{\mathcal{N}}}_x\dot{\to }(0,1)\right]\hfill \\ & =& \underset{\mathcal{B}\subseteq \mathcal{A}}{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\wedge \underset{\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigwedge }\neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left(\underset{\mathcal{B}\subseteq \mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\wedge \neg \left(\underset{\mathcal{B}\subseteq \mathcal{X}-\mathcal{A}}{\bigvee }{\widehat{\mathcal{N}}}_x\left(\mathcal{B}\right)\right)\hfill \\ & =& \neg \left({\widehat{\mathcal{N}}}_x\left(\mathcal{A}\right)\right)\wedge \neg \left({\widehat{\mathcal{N}}}_x(\mathcal{X}-\mathcal{A})\right)\hfill \\ & =& \neg \left(\widehat{Int}\left(\mathcal{A}\right)\left(x\right)\right)\wedge \neg \left(\widehat{Int}(\mathcal{X}-\mathcal{A})\left(x\right)\right)\hfill \\ & =& \widehat{Cl}(\mathcal{X}-\mathcal{A})\left(x\right)\wedge \widehat{Cl}\left(\mathcal{A}\right)\left(x\right)\hfill \\ & =& \widehat{b}\left(\mathcal{A}\right)\left(x\right).\hfill \end{array}$$

□

Theorem 15.

For any $\mathcal{A}$,

(1) $\vDash \widehat{b}\left(\mathcal{A}\right)\equiv \widehat{b}(\mathcal{X}-\mathcal{A})$;

(2) $\neg \left(\widehat{b}\left(\mathcal{A}\right)\right)\equiv \widehat{Int}\left(\mathcal{A}\right)\cup \widehat{Int}(\mathcal{X}-\mathcal{A})$;

(3) $\vDash \widehat{Cl}\left(\mathcal{A}\right)\equiv \mathcal{A}\cup \widehat{b}\left(\mathcal{A}\right)$, and so $\vDash \widehat{b}\left(\mathcal{A}\right)⋐\mathcal{A}⟷\mathcal{A}\in \mathcal{F}$.

(4) $\vDash \widehat{Int}\left(\mathcal{A}\right)\equiv \mathcal{A}\cap \neg \left(\widehat{b}\left(\mathcal{A}\right)\right)$, and so $\vDash (\widehat{b}\left(\mathcal{A}\right)\cap \mathcal{A}\dot{\equiv }\widehat{0})⟷\mathcal{A}\in \tau$.

Proof. 

(1) obvious.

(2) From Theorem 14 (4), we obtain

$$\widehat{Int}\left(\mathcal{A}\right)\left(x\right)\vee \widehat{Int}(\mathcal{X}-\mathcal{A})\left(x\right)=\neg \left(\widehat{Cl}(\mathcal{X}-\mathcal{A})\left(x\right)\right)\vee \neg \left(\widehat{Int}\left(\mathcal{A}\right)\left(x\right)\right)=\neg \left(\widehat{b}\left(\mathcal{A}\right)\left(x\right)\right).$$

(3) If $\mathcal{A}\left(x\right)=(1,0)$, then $\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)=(\mathcal{A}\cup \widehat{b}\left(\mathcal{A}\right))\left(x\right)=(1,0)$. If $\mathcal{A}\left(x\right)=(0,1)$, then $(\mathcal{A}\cup \widehat{b}\left(\mathcal{A}\right))\left(x\right)=\widehat{b}\left(\mathcal{A}\right)\left(x\right)=\neg \left(\widehat{Int}\left(\mathcal{A}\right)\left(x\right)\right)\wedge \neg \left(\widehat{Int}(\mathcal{X}-\mathcal{A})\left(x\right)\right)=(1,0)\wedge \neg (\widehat{Int}(\mathcal{X}-\mathcal{A})$

$\left(x\right))=\neg \left(\widehat{Int}(\mathcal{X}-\mathcal{A})\left(x\right)\right)=\widehat{Cl}\left(\mathcal{A}\right)\left(x\right)$. From Theorem 10 (2), we have $\vDash \mathcal{A}\in \mathcal{F}⟷\widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A}⟷(\widehat{\mathcal{D}}\left(\mathcal{A}\right)⋐\mathcal{A})\wedge (\mathcal{A}⋐\mathcal{A})⟷(\widehat{\mathcal{D}}\left(\mathcal{A}\right)\cup \mathcal{A}⋐\mathcal{A})⟷\widehat{Cl}\left(\mathcal{A}\right)⋐\mathcal{A}⟷\mathcal{A}\cup \widehat{b}\left(\mathcal{A}\right)⋐\mathcal{A}⟷(\mathcal{A}⋐\mathcal{A})\wedge (\widehat{b}\left(\mathcal{A}\right)⋐\mathcal{A})⟷(1,0)\wedge (\widehat{b}\left(\mathcal{A}\right)⋐\mathcal{A})⟷\widehat{b}\left(\mathcal{A}\right)⋐\mathcal{A}$.

(4) $\widehat{Int}\left(\mathcal{A}\right)\left(\mathcal{A}\right)\equiv \neg \left(\widehat{Cl}(\mathcal{X}-\mathcal{A})\right)\equiv \neg ((\mathcal{X}-\mathcal{A})\cup \widehat{b}(\mathcal{X}-\mathcal{A}))\equiv \mathcal{A}\cap \neg \left(\widehat{b}(\mathcal{X}-\mathcal{A})\right)=\mathcal{A}\cap \neg \left(\widehat{b}\left(\mathcal{A}\right)\right)$. From Theorem 14 (2), we obtain $\vDash \widehat{b}\left(\mathcal{A}\right)\cap \mathcal{A}\dot{\equiv }\widehat{0}⟷\neg \left(\widehat{b}\left(\mathcal{A}\right)\right)\cup (\mathcal{X}-\mathcal{A})\dot{\equiv }\widehat{1}$

$⟷\mathcal{A}⋐\neg \left(\widehat{b}\left(\mathcal{A}\right)\right)⟷\mathcal{A}\cap \neg \left(\widehat{b}\left(\mathcal{A}\right)\right)\dot{\equiv }\mathcal{A}⟷\widehat{Int}\left(\mathcal{A}\right)\dot{\equiv }\mathcal{A}⟷\mathcal{A}\in \tau$. □

Remark 6.

All statements in Theorem 15 are true when we replace “≡” by “$\dot{\equiv }$” or by “$\dot{\approx }$”.

7. Conclusions

As an extension of fuzzifying topology, we discussed intuitionistic fuzzifying neighborhood system of a point. Additionally, we introduced the concepts of intuitionistic fuzzifying closure, intuitionistic fuzzifying boundary, intuitionistic fuzzifying derived set and intuitionistic fuzzifying interior. These concepts provide a theoretical basis for the further study of intuitionistic fuzzifying topology. In this regard, it is interesting to develop a mathematical framework that contains continuity, speration axioms, compactness, and vector spaces. Additionally, we believe that it would be interesting to apply the intuitionistic fuzzy logic to other structures such as proximity, uniformity, topogenous, syntopogenous, homotopy, etc. We intend to investigate some of these issues in future research works. We believe that it is very important to apply both fuzzy logic and intuitionistic fuzzy logic to convex spaces.