Intuitionistic Fuzzy Rough Aczel-Alsina Average Aggregation Operators and Their Applications in Medical Diagnoses

Abstract

Managing ambiguous and asymmetric types of information is a very challenging task under the consideration of classical data. Furthermore, Aczel-Alsina aggregation operators are the new developments in fuzzy sets theory. However, when decision-makers need to use these structures in fuzzy rough structures, these operators fail to deal with such types of values, as fuzzy rough structures use lower and upper approximation spaces. Thus, an encasement of an intuitionistic fuzzy set has a chance of data loss, whereas an intuitionistic fuzzy rough set can resolve the problem of data loss. Motivated by the notion of intuitionistic fuzzy rough sets and new aggregation operators i.e., intuitionistic fuzzy Aczel-Alsina operators, this paper firstly initiates some basic Aczel-Alsina operational rules for intuitionistic fuzzy rough numbers. Secondly, based on these newly defined operational rules, we have developed some new aggregation operators, such as intuitionistic fuzzy rough Aczel-Alsina weighted average (IFRAAWA), intuitionistic fuzzy rough Aczel-Alsina ordered weighted average (IFRAAOWA), and intuitionistic fuzzy rough Aczel-Alsina hybrid average (IFRAAHA) aggregation operators. Moreover, the properties of these aggregation operators have been initiated. These operators can help in evaluating awkward and asymmetric information in real-life problems. The use of aggregation operators in medical diagnosis and MADM is an efficient method that can help in healthcare and decision-making applications. To present an effective use of these developed operators in medical diagnosis and the selection of the best next-generation firewall, we have established an algorithm along with a numerical example to provide authenticity and clarity to the established work. Furthermore, a comparative analysis of the introduced work shows the superiority of the introduced approach.

1. Introduction

1.1. Evolution of Medical Diagnosis

Accurately locating a patient’s disease is the most important and challenging task in medicine. Patient history and health assessment procedures are symptomatic approaches. Diagnosis is the first element in the health field, which depends on patient history to start the treatment. In the 19th century, auxiliary procedures were added to the field of medical microbiology and biochemistry. In the late 19th and 20th century, some further advancements were made, such as electron microscopy, biophysics, immunology, and physiology. These findings have altered the consequences of the diagnosis techniques used in the confirmation of patient ailment. In recent days, due to the large volume of data used by experts working in the medical field, a single practitioner can never hope to cover such uncertain data in an inaccurate way. In other words, we can say that modern medicine has the potential to organize and accomplish a large amount of data. In recent times, a modern computer can be more helpful for assisting doctors, and it can help them to solve these problems. One of the first attempts in this regard was made by Ledley and Lusted in 1959 [1]. Additionally, some problems in the medical field can be resolved by using the method provided in [2].

1.2. Fuzzy Set Theory in Medical Fields

Zadeh [3] opened the path for researchers by introducing the concept of a fuzzy set (FS), which generalizes the classical set theory. Researchers working in the medical field emphasize developing new methods that can code and process medical data in effective ways. Dealing with such an issue, Smets has made some effective efforts in showing the use of fuzzy set theory (FST) in medical diagnosis as shown in [4]. To prepare the medical relationship and fuzzy logic to design the diagnostic process, FST might be the acceptable groundwork for forming a computerized diagnostic structure as given in [5]. In his research, Steimann [6] explored how FS formulizes gradation, a natural characteristic of medicine that is incompatible with the discrete nature of classical approaches. Phuong and Kreinovich [7] proposed that FST and fuzzy logics are highly appropriate and valid foundations for evolving knowledge-based structures in medicine. Phuong et al. [8] established a case-based reasoning for medical diagnoses under the environment of FST. Moreover, Samuel and Balamurugan [9] used fuzzy max-min techniques in medical diagnosis applications. Kuncheva and Steimann [10] determined that diagnostic accuracy can be obtained using a FS, thus establishing fuzzy diagnosis. Mahmood [11] proposed Dombi aggregation operators (AO) based on bipolar complex fuzzy information and provided its applications to MADM problems.

Although an FS has a large number of applications in medical diagnosis, we cannot restrict it to this notion because it is a limited notion. A FS uses $“ȹ\left(\mathrm{a}\right)”$ as a membership grade (MG) belonging to [0 1]. However, researchers noticed that FSs only use one aspect such as MG, which can be used for a limited number of decision-making problems. There are some situations in which we must discuss MG and non-membership grades (NMG) in one structure. To manage this situation, Atanassov [12] introduced the notion of the intuitionistic fuzzy set (IFS), which uses the conditions $sum\left(\mathsf{ȹ}\left(\mathrm{a}\right), \mathsf{\theta }\left(\mathrm{a}\right)\right)\in \left[0 1\right]$, where $\mathsf{ȹ}\left(\mathrm{a}\right) \mathrm{and} \mathsf{\theta }\left(\mathrm{a}\right)$ are MG and NMG, respectively. IFS is a more generalized structure, and it has a large range of applications in medical diagnosis. De et al. [13] used Sanchez’s method for medical diagnosis and extended this idea with the concept of IFS theory. Many new methodologies are being used for the analysis of diagnosing a patient, and valuable results can be obtained. Luo and Zhao [14] introduced IF distance measures and applied these structures to medical diagnosis. Furthermore, Das et al. [15] established a medical diagnosis method using the concept of fuzzy logic and IF logic. Mahanta and Panda [16] proposed the application of an IFS for medical diagnosis and pattern recognition. Dhivya and Sridevi [17] used novel similarity measure and found their applications in pattern recognition and medical diagnosis. Some new developments in AOs based on t-norms and t-conorm have been made by Senapati et al. [18], and they have established Aczel-Alsina (AA) average AOs. In [19], Xu initiated IF-weighted average AOs. Moreover, based on AA t-norms and t-conorms, many developments have been made, and some interval-valued AA average aggregation operators have been provided in [20]; some AA geometric aggregation operators are given in [21]. Furthermore, Xu and Yager [22] established some geometric AOs based on the IFS. Moreover, Seikh and Mandal [23] introduced IF Dombi AOs and provided their applications. Huang [24] explored the notion of IF Hamacher AOs and provided its application in MADM problems. Ali et al. [25] explored a graphical method for ranking IFSs using uncertainty and entropy. Kahn et al. [26] introduced IF divergences and provided critical investigation and uses in figure skating.

The rough set (RS) theory presented by Pawlak [27] is the new mathematical apparatus for discussing more imprecise and uncertain data. Using the idea of upper and lower approximation in RS theory, hidden information can be expressed in the form of a decision rule. Roughness in semigroups and ordered ternary semigroups can be observed in [28,29]. To assess sustainable mining’s contribution to sustainable development goals, Deveci et al. [30] proposed an RS-based ordinal priority approach. The hybrid notion of FSs and RSs plays a role as a bridge between these notions. Dubois and Prade [31] originated the concept of the fuzzy rough set (FRS). Moreover, Ayub et al. [32] initiated the structure of a linear Diophantine fuzzy rough set. Furthermore, the idea of the IF rough set (IFRS) has been provided by Cornelis et al. [33] as a new development in RS theory. Based on this advanced structure of IFRSs, some new developments have been made, such as Chinram et al. [34] proposing EDAS methods for MCGDMs based on IFRSs. Furthermore, Akram et al. [35] anticipated the definition of an intuitionistic fuzzy N-soft rough set.

1.3. Motivation for Introduced Work

We can see from references [20,21] that the theories developed for AA aggregation operators are based on IFNs. Note that the IFS lacks the property to consider the upper and upper approximation operators. So, when decision-makers come up with $\left\{\left(0.5, 0.1\right), \left(0.3, 0.4\right)\right\}$ for IFRN, then the notions developed in references [20,21] cannot tackle these kinds of data. Thus, there is a need to develop notions based on AA operational laws to overcome these issues.

The theory addressed in this research is significant and more appropriate for assessing the above dilemmas as it can handle complicated, risk-illustrating, and asymmetric information. The AA t-norm and t-conorm principles were developed to handle ambiguity and inconsistent behavior in real-world scenarios. Due to the parameter p, where $0<p<+\infty$, these norms have undergone significant modification and are different from the current standards. The main contribution of the analysis is to discuss AA norms under the notions of IFRS. AA developed the core theory of the AA t-norm and t-conorm based on classical information, which is a very important and useful concept utilized for assessing uncomfortable and inaccurate information in real-world applications. The fundamental idea behind the AA t-norm and t-conorm is that they are significantly changed in comparison to the current t-norms (Hamacher). The theory of symmetry and the mathematical analysis of diagnosed information and related operators are closely related.

Given the analysis above, we can conclude that general decision-making problems are becoming increasingly complex. The ability to select the best option(s) for the MADM problems and communicate the dubious information in a demonstrably more valuable way is a significant challenge. Additionally, it is crucial to control how to take input disputes into account. Below is an illustration of this analysis’s main contribution:

• To examine the addition, multiplication, scoring value, and accuracy value of the AA operational laws in the IFR circumstances.
• To cover the issues faced by intuitionistic fuzzy AA aggregation operators, the theme is to establish the notions for IFRAAWA, IFRAAOWA, and IFRAAHA aggregation operators.
• To examine the superiority and practicality of the generated works, a MADM technique was investigated.
• To graphically illustrate the sensitivity analysis with the aid of various examples, where the primary theme of this study is also shown in the form of Figure 1.

The rest of the article is given as follows: In Section 2, we have overviewed the basic notions for FS, IFS, RS, IFRS, and some basic operational laws. In Section 3, we have introduced new Aczel-Alsina operational laws based on IFRSs. In Section 4, we have developed some new aggregation operators based on Aczel-Alsina operative rules such as IFR Aczel-Alsina Average (weighted, ordered weighted, hybrid) aggregation operators. Section 5 deals with an algorithm for the introduced work and numerical examples to show the effective use of the proposed work. Section 6 discusses the comparative assessment of the initiated work. Section 7 deals with the concluding remarks.

2. Preliminaries

Medical diagnosis is the procedure for deciding which disease or state explains a person’s syndrome. The theory of a fuzzy set in the medical field starts from [4], and all generalized structures can work in this field. Many new developments have been initiated and used for the assessment of medical diagnoses. The intuitionistic fuzzy rough set is more robust structure introduced by Cornelis et al. [33]. It can deal with more imprecise data and provide more space for decision-makers. We will use this structure for later discussion.

In the followings, we will review some basic definitions of FS, IFS, RS, IFRS, Aczel-Alsina t-norm and t-conorm, and some basic Aczel-Alsina operational laws.

2.1. Basics of Aczel-Alsina t-norm and t-conorm

Here in this subsection, we discuss and overview the notions of the AA t-norm and t-conorm, intuitionistic fuzzy AA operational laws, and their aggregation operators that have been proposed in the literature.

Definition 1

[18]. Let $‘\mathfrak{T}’$ and $‘\mathcal{S}’$ denote the t-norm and t-conorm of the Aczel-Alsinsa product and sum, respectively. Then, for two IFSs $ℳ$ and $\mathcal{N},$ the generalized intersection and union turn into AA product and AA sum, as given below

$$ℳ\mathsf{\otimes }\mathcal{N}=\left\{\left(\mathrm{a}, \mathfrak{T}\left\{{\mathsf{ȹ}}_{ℳ}\left(\mathrm{a}\right), {\mathsf{ȹ}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}, \mathcal{S}\left\{{\mathsf{\theta }}_{ℳ}\left(\mathrm{a}\right),{ \mathsf{\theta }}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}\right)|\mathrm{a}\in \mathsf{Ƿ}\right\}$$

$$ℳ\mathsf{\oplus }\mathcal{N}=\left\{\left(\mathrm{a}, \mathcal{S}\left\{{\mathsf{ȹ}}_{ℳ}\left(\mathrm{a}\right), {\mathsf{ȹ}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}, \mathfrak{T}\left\{{\mathsf{\theta }}_{ℳ}\left(\mathrm{a}\right),{ \mathsf{\theta }}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}\right)|\mathrm{a}\in \mathsf{Ƿ}\right\}.$$

Definition 2

[12]. An intuitionistic fuzzy set (IFS) is of the shape$\mathsf{Ǧ}=\left\{\left(\mathrm{a}, \mathsf{ȹ}\left(\mathrm{a}\right), \mathsf{\theta }\left(\mathrm{a}\right)\right)|\mathrm{a}\in \mathsf{Ƿ}\right\}$, where $0\le \mathsf{ȹ}\left(\mathrm{a}\right)+\mathsf{\theta }\left(\mathrm{a}\right)\le 1$ and $\mathsf{ȹ}\left(\mathrm{a}\right), \mathsf{\theta }\left(\mathrm{a}\right)$ MG and non-membership grade (NMG), respectively.

Definition 3

[18]. Let $\mathsf{Ǧ}=\left\{\left({\mathsf{ȹ}}_{\mathsf{Ǧ}},{ \mathsf{\theta }}_{\mathsf{Ǧ}}\right)\right\}, {\mathsf{Ǧ}}_1=\left\{\left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_1},{ \mathsf{\theta }}_{{\mathsf{Ǧ}}_1}\right)\right\}$ and ${\mathsf{Ǧ}}_2=\left\{\left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_2},{ \mathsf{\theta }}_{{\mathsf{Ǧ}}_2}\right)\right\}$ be three IFNs and $\mathcal{Q}\ge 1$ and $\mathsf{\tau }>0$, then AA t-norm and t-conorm operations for IFNs can be defined as

• ${\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2=\left\{\left(\left(1-{\mathrm{e}}^{-{\left({\left(-\log \left(1-{\mathsf{ȹ}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\mathsf{ȹ}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left({\mathrm{e}}^{-{\left({\left(-\log \left({\mathsf{\theta }}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\mathsf{\theta }}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\right\},$
• ${\mathsf{Ǧ}}_1\mathsf{\otimes }{\mathsf{Ǧ}}_2=\left\{\left({\mathrm{e}}^{-{\left({\left(-\log \left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(\left(1-{\mathrm{e}}^{-{\left({\left(-\log \left(1-{\mathsf{\theta }}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\mathsf{\theta }}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\right\},$
• $\mathsf{\tau }\mathsf{Ǧ}=\left\{\left(\left(1-{\mathrm{e}}^{-{\left(\mathsf{\tau }{\left(-\log \left(1-{\mathsf{ȹ}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left({\mathrm{e}}^{-{\left(\mathsf{\tau }{\left(-\log \left({\mathsf{\theta }}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\right\},$
• ${\mathsf{Ǧ}}^{\mathsf{\tau }}=\left\{\left(\left({\mathrm{e}}^{-{\left(\mathsf{\tau }{\left(-\log \left({\mathsf{ȹ}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(1-{\mathrm{e}}^{-{\left(\mathsf{\tau }{\left(-\log \left(1-{\mathsf{\theta }}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\right\}.$

Now using the above operational laws, some intuitionistic fuzzy AA weighted average aggregation operators are defined in literature as

Definition 4

[18]. Let ${\mathsf{Ǧ}}_{\mathrm{i}}=\left\{\left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_{\mathrm{i}}},{ \mathsf{\theta }}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right)\right\} \left(\mathrm{i}=1, 2, \dots , \mathrm{n}\right)$ be the collection for IFNs, then IFAAWA operators are defined as

${\mathrm{IFAAWA}}_{\mathsf{\varpi }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_{\mathrm{n}}\right)={\oplus }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathsf{\varpi }}_{\mathrm{i}}{\mathsf{Ǧ}}_{\mathrm{i}}\right)$

$=\left\{\begin{array}{c}\left(\left(1-{\mathrm{e}}^{-{\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}\left({\left(-\log \left(1-{\mathsf{ȹ}}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left({\mathrm{e}}^{-{\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}\left({\left(-\log \left({\mathsf{\theta }}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

Definition 5

[18]. Let ${\mathsf{Ǧ}}_{\mathrm{i}}=\left\{\left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_{\mathrm{i}}},{ \mathsf{\theta }}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right)\right\} \left(\mathrm{i}=1, 2, \dots , \mathrm{n}\right)$ be the collection for IFNs, then IF AA ordered weighted average (IFAAOWA) operators are defined by mapping

${\mathrm{IFAAOWA}}_{{\mathsf{\varpi }}^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_{\mathrm{n}}\right)={\oplus }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathsf{\varpi }}_{\mathrm{i}}^{\star }{\mathsf{Ǧ}}_{\mathfrak{O}\left(\mathrm{i}\right)}\right)$$=\left\{\begin{array}{c}\left(\left(1-{\mathrm{e}}^{-{\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}^{\star }\left({\left(-\log \left(1-{\mathsf{ȹ}}_{{\mathsf{ȹ}}_{\mathfrak{O}\left(\mathrm{i}\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \right),\\ \left(\left({\mathrm{e}}^{-{\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}^{\star }\left({\left(-\log \left({\mathsf{\theta }}_{{\mathsf{ȹ}}_{\mathfrak{O}\left(\mathrm{i}\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$ where ${\mathsf{\varpi }}^{\star }=\left({\mathsf{\varpi }}_1^{\star }, {\mathsf{\varpi }}_2^{\star }, \dots , {\mathsf{\varpi }}_{\mathrm{n}}^{\star }\right)$ be the WVs for IFNs ${\mathsf{Ǧ}}_{\mathrm{i}} \left(\mathrm{i}=1, 2, \dots , \mathrm{n}\right)$ with the condition that ${\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}^{\star }=1$ and $\left(\mathfrak{O}\left(1\right), \mathfrak{O}\left(2\right), \dots , \mathfrak{O}\left(\mathrm{n}\right)\right)$ are the permutation of $\left(\mathrm{i}=1, 2,3, \dots , \mathrm{n}\right)$, including ${\mathsf{Ǧ}}_{\mathfrak{O}\left(\mathrm{n}-1\right)}\ge {\mathsf{Ǧ}}_{\mathfrak{O}\left(\mathrm{n}\right)}.$

Definition 6

[18]. Let ${\mathsf{Ǧ}}_{\mathrm{i}}=\left\{\left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_{\mathrm{i}}},{ \mathsf{\theta }}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right)\right\} \left(\mathrm{i}=1, 2, \dots , \mathrm{n}\right)$ be the family for IFNs, then IFAAHA operators are defined by

${\mathrm{IFAAHA}}_{\mathsf{\varpi }, {\mathsf{\varpi }}^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_{\mathrm{n}}\right)={\oplus }_{\mathrm{i}=1}^{\mathrm{n}}\left({\mathsf{\varpi }}_{\mathrm{i}}^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(\mathrm{i}\right)}\right)$

$=\left\{\begin{array}{c}\left(\left(1-{\mathrm{e}}^{-{\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}^{\star }\left({\left(-\log \left(1-{\mathsf{ȹ}}^{\therefore }{}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(\mathrm{i}\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \right),\\ \left(\left({\mathrm{e}}^{-{\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\varpi }}_{\mathrm{i}}^{\star }\left({\left(-\log \left({\mathsf{\theta }}^{\therefore }{}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(\mathrm{i}\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

Now we can see that all the above theories that exist in the literature contain MG and NMG in the form of IFNs, but if the decision-makers come up with intuitionistic fuzzy rough data such as ${\mathsf{Ǧ}}_{\mathrm{i}}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{\mathrm{i}}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{\mathrm{i}}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{\mathrm{i}}}\right)\right\}$, then all the above theories fail to handle such a situation. So, there is a need to develop notions that can handle these issues freely. The main focus of the study is to introduce some intuitionistic fuzzy rough Aczel-Alsina aggregation operators so that more complex information can be handled.

2.2. Some Elementary Notions

In this subsection, we must discuss the core notions of FS, RS, and IFRS and their score function and accuracy function.

Definition 7

[3]. A fuzzy set is of the shape $\mathsf{Ǧ}=\left\{\left(\mathrm{a}, \mathsf{ȹ}\left(\mathrm{a}\right)\right)|\mathrm{a}\in \mathsf{Ƿ}\right\}$, where $\mathsf{ȹ}\left(\mathrm{a}\right)\in \left[0, 1\right]$ and represents membership grade (MG).

Definition 8

[27]. Let $\mathsf{Ƿ}$ denote a general set and $\mathsf{Ɣ}\subseteq \mathsf{Ƿ}\times \mathsf{Ƿ}$ be a random crisp relation on $\mathsf{Ƿ}.$ Let ${\mathsf{Ɣ}}^{*}$ is a set-valued map (SVMP)${\mathsf{Ɣ}}^{*}: \mathsf{Ƿ}\to P\left(\mathsf{Ƿ}\right)$ described as ${\mathsf{Ɣ}}^{*}\left(\mathrm{a}\right)=\left\{\mathfrak{b}\in \mathsf{Ƿ}:\left(\mathrm{a}, \mathfrak{b}\right)\in \mathsf{Ɣ} and \mathrm{a}\in \mathsf{Ƿ}\right\},$then $\left(\mathsf{Ƿ}, \mathsf{Ɣ}\right)$ is an approximation space. Now, let$\mathscr{H}\subseteq \mathsf{Ƿ}$, then the lower approximation (LRA) and upper approximations (URA) of $\mathscr{H}$ w.r.t $\left(\mathsf{Ƿ}, \mathsf{Ɣ}\right)$ are described by

$$\underbrace{\mathsf{Ɣ}}(\mathscr{H})=\left\{\langle \left(\mathrm{a}\in \mathsf{Ƿ}: {\mathsf{Ɣ}}^{*}\left(\mathrm{a}\right)\subseteq \mathscr{H}\right)\rangle \right\}$$

$$\overbrace{\mathsf{Ɣ}}(\mathscr{H})=\left\{\langle \left(\mathrm{a}\in \mathsf{Ƿ}: {\mathsf{Ɣ}}^{*}\left(\mathrm{a}\right)\mathsf{⨅}\mathscr{H}\ne \varnothing \right)\rangle \right\}$$

The pair $\left(\underbrace{\mathsf{Ɣ}}(\mathscr{H}), \overbrace{\mathsf{Ɣ}}(\mathscr{H})\right)$ is called a rough set (RS), where $\underbrace{\mathsf{Ɣ}}(\mathscr{H})\ne \overbrace{\mathsf{Ɣ}}(\mathscr{H})$. Furthermore, $\underbrace{\mathsf{Ɣ}}(\mathscr{H}), \overbrace{\mathsf{Ɣ}}(\mathscr{H}):P\left(\mathsf{Ƿ}\right)\to P\left(\mathsf{Ƿ}\right)$ are called crisp LR and UR approximation operators, according to $\left(\mathsf{Ƿ}, \mathsf{Ɣ}\right).$

Definition 9

[33]. Let $\mathsf{Ƿ}$ denote the universal set and $\mathsf{Ɣ}\in IFS\left(\mathsf{Ƿ}\times \mathsf{Ƿ}\right)$ be the intuitionistic fuzzy relation. Then, pair $\left(\mathsf{Ɣ}, \mathsf{Ƿ}\right)$ is called the IF approximation space.

Now, for any$\mathscr{H}\subseteq \mathsf{Ƿ}$, the LRA and URA of $\mathscr{H}$ w.r.t $\left(\mathsf{Ƿ}, \mathsf{Ɣ}\right)$ are given by

$$\underbrace{\mathsf{Ɣ}}(\mathscr{H})=\left\{\langle \left(\mathrm{a}: {\underbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right), {\underbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\right)|\mathrm{a}\in \mathsf{Ƿ}\rangle \right\}$$

$$\overbrace{\mathsf{Ɣ}}(\mathscr{H})=\{\langle (\mathrm{a}: {\overbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right), {\overbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right))|\mathrm{a}\in \mathsf{Ƿ}\rangle \}$$

where ${\underbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)={\mathsf{\bigwedge }}_{d\in \mathsf{Ƿ}}\left[{\mathsf{ȹ}}_{\mathsf{Ɣ}}\left(\mathrm{a}, d\right)\mathsf{\bigwedge }{\mathsf{ȹ}}_{\mathscr{H}}\left(d\right)\right],{\underbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)={\mathsf{\bigvee }}_{d\in \mathsf{Ƿ}}\left[{\mathsf{\theta }}_{\mathsf{Ɣ}}\left(\mathrm{a}, d\right)\mathsf{\bigvee }{\mathsf{\theta }}_{\mathscr{H}}\left(d\right)\right]$ and ${\overbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)={\mathsf{\bigvee }}_{d\in \mathsf{Ƿ}}\left[{\mathsf{ȹ}}_{\mathsf{Ɣ}}\left(\mathrm{a}, d\right)\mathsf{\bigvee }{\mathsf{ȹ}}_{\mathscr{H}}\left(d\right)\right],{\overbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)={\mathsf{\bigwedge }}_{d\in \mathsf{Ƿ}}\left[{\mathsf{\theta }}_{\mathsf{Ɣ}}\left(\mathrm{a}, d\right)\mathsf{\bigwedge }{\mathsf{\theta }}_{\mathscr{H}}\left(d\right)\right]$ with $0\le {\overbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)+{\overbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\le 1, 0\le {\underbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)+{\underbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\le 1.$ As $\underbrace{\mathsf{Ɣ}}(\mathscr{H}) and \overbrace{\mathsf{Ɣ}}(\mathscr{H})$ are IFSs, so $\underbrace{\mathsf{Ɣ}}(\mathscr{H}), \overbrace{\mathsf{Ɣ}}(\mathscr{H}):IFS\left(\mathsf{Ƿ}\right)\to IFS\left(\mathsf{Ƿ}\right)$ are LR and UR approximation operators. Then, pair $\mathsf{Ɣ}(\mathscr{H})=\left(\underbrace{\mathsf{Ɣ}}(\mathscr{H}), \overbrace{\mathsf{Ɣ}}(\mathscr{H})\right)=\left\{\mathrm{a}:\left( {\underbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right), {\underbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\right), \left({\overbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right), {\overbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\right)|\mathrm{a}\in \mathsf{Ƿ}\right\}$ is called the IFRS. For simplicity, $\mathsf{ȹ}(\mathscr{H})=\left(\underbrace{\mathsf{Ɣ}}(\mathscr{H}), \overbrace{\mathsf{Ɣ}}(\mathscr{H})\right)=\left\{\mathrm{a}:\left( {\underbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right), {\underbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\right), \left({\overbrace{{\mathsf{ȹ}}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right), {\overbrace{{\mathsf{\theta }}_{\mathsf{Ɣ}}}}_{\mathscr{H}}\left(\mathrm{a}\right)\right)|\mathrm{a}\in \mathsf{Ƿ}\right\}$ can be represented as $\mathsf{Ɣ}(\mathscr{H})=\left\{\left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right), \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right\}$, known as intuitionistic fuzzy rough numbers (IFRNs).

Definition 10

[34]. To compare two IFRNs, we need to define the score function and accuracy function for IFRNs $\mathsf{Ǧ}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right), \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right\}$, as follows

$Sc\left(\mathsf{Ǧ}\right)=\frac{1}{4}\left(2+{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}+{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}-{\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}-{\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right), Sc\left(\mathsf{Ǧ}\right)\in \left[0, 1\right]$ and

$Ac\left(\mathsf{Ǧ}\right)=\frac{1}{4}\left(2+{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}+{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}+{\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}+{\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right), Ac\left(\mathsf{Ǧ}\right)\in \left[0, 1\right].$

Definition 11

[34]. If ${\mathsf{Ǧ}}_1=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right\}$ and ${\mathsf{Ǧ}}_2=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right\}$ are two IFRNs, then

• If $Sc\left({\mathsf{Ǧ}}_1\right)>Sc\left({\mathsf{Ǧ}}_2\right)$ then ${\mathsf{Ǧ}}_1>{\mathsf{Ǧ}}_2,$
• If$Sc\left({\mathsf{Ǧ}}_1\right)<Sc\left({\mathsf{Ǧ}}_2\right)$then ${\mathsf{Ǧ}}_1<{\mathsf{Ǧ}}_2,$
• If $Sc\left({\mathsf{Ǧ}}_1\right)=Sc\left({\mathsf{Ǧ}}_2\right)$ then

  (1)

  If $Ac\left({\mathsf{Ǧ}}_1\right)>Ac\left({\mathsf{Ǧ}}_2\right)$ then ${\mathsf{Ǧ}}_1>{\mathsf{Ǧ}}_2,$

  (2)

  If $Ac\left({\mathsf{Ǧ}}_1\right)<Ac\left({\mathsf{Ǧ}}_2\right)$ then ${\mathsf{Ǧ}}_1<{\mathsf{Ǧ}}_2,$

  (3)

  If $Ac\left({\mathsf{Ǧ}}_1\right)=Ac\left({\mathsf{Ǧ}}_2\right)$ then ${\mathsf{Ǧ}}_1={\mathsf{Ǧ}}_2.$

3. Aczel-Alsina Intuitionistic Fuzzy Rough Operational Laws

In this part, we will establish Aczel-Alsina operational rules for intuitionistic fuzzy rough sets with examples and examine some fundamental characteristics of these introduced operational laws.

Definition 12.

Let $‘\mathfrak{T}’$ and $‘\mathcal{S}’$ denote the t-norm and t-conorm of the Aczel-Alsinsa product and sum, respectively. Then, for two IFRSs $ℳ$ and $\mathcal{N},$ the generalized intersection and union turn into AA product and AA sum as given below

$ℳ\mathsf{\otimes }\mathcal{N}=\left\{\begin{array}{c}\left(\mathrm{a}, \mathfrak{T}\left\{{\underbrace{\mathsf{ȹ}}}_{ℳ}\left(\mathrm{a}\right), {\underbrace{\mathsf{ȹ}}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}, \mathcal{S}\left\{{\underbrace{\mathsf{\theta }}}_{ℳ}\left(\mathrm{a}\right), {\underbrace{\mathsf{\theta }}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}\right),\\ \left(\mathrm{a}, \mathfrak{T}\left\{{\overbrace{\mathsf{ȹ}}}_{ℳ}\left(\mathrm{a}\right), {\overbrace{\mathsf{ȹ}}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}, \mathcal{S}\left\{{\overbrace{\mathsf{\theta }}}_{ℳ}\left(\mathrm{a}\right), {\overbrace{\mathsf{\theta }}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}\right)|\mathrm{a}\in \mathsf{Ƿ}\end{array}\right\}$$ℳ\mathsf{\oplus }\mathcal{N}=\left\{\begin{array}{c}\left(\mathrm{a}, \mathcal{S}\left\{{\underbrace{\mathsf{ȹ}}}_{ℳ}\left(\mathrm{a}\right), {\underbrace{\mathsf{ȹ}}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}, \mathfrak{T}\left\{{\underbrace{\mathsf{\theta }}}_{ℳ}\left(\mathrm{a}\right), {\underbrace{\mathsf{\theta }}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}\right),\\ \left(\mathrm{a}, \mathcal{S}\left\{{\mathsf{ȹ}}_{ℳ}\left(\mathrm{a}\right), {\overbrace{\mathsf{ȹ}}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}, \mathfrak{T}\left\{{\overbrace{\mathsf{\theta }}}_{ℳ}\left(\mathrm{a}\right), {\overbrace{\mathsf{\theta }}}_{\mathcal{N}}\left(\mathrm{a}\right)\right\}\right)|\mathrm{a}\in \mathsf{Ƿ}\end{array}\right\}.$

Definition 13.

Let $\mathsf{Ǧ}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right), \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right\}, {\mathsf{Ǧ}}_1=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right\}$ and ${\mathsf{Ǧ}}_2=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right\}$ be three IFRSs and $\mathcal{Q}\ge 1$ and$\tau >0$, then AA t-norm and t-conorm operations for IFRSs can be defined as

• ${\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2=\left\{\begin{array}{c}\left(\right(1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}), \left(e^{-{\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)),\\ \left(\right(1-e^{-{\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}), \left(e^{-{\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right))\end{array}\right\},$
• ${\mathsf{Ǧ}}_1\mathsf{\otimes }{\mathsf{Ǧ}}_2=\left\{\begin{array}{c}\left(e^{-{\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(\left(1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(e^{-{\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(\left(1-e^{-{\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\},$
• $\tau \mathsf{Ǧ}=\left\{\begin{array}{c}\left(\left(1-e^{-{\left(\tau {\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left(\tau {\left(-\log \left({\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left(\tau {\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left(\tau {\left(-\log \left({\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\},$
• ${\mathsf{Ǧ}}^{\tau }=\left\{\begin{array}{c}\left(\left(e^{-{\left(\tau {\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(1-e^{-{\left(\tau {\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(e^{-{\left(\tau {\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(1-e^{-{\left(\tau {\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}.$

Example 1.

Let $\mathsf{Ǧ}=\left\{\left(0.5, 0.2\right), \left(0.3, 0.5\right)\right\}, {\mathsf{Ǧ}}_1=\left\{\left(0.4, 0.3\right), \left(0.6, 0.1\right)\right\}$ and ${\mathsf{Ǧ}}_2=\left\{\left(0.2, 0.7\right), \left(0.3, 0.5\right)\right\}$ be three IFRSs and $\mathcal{Q}=3$and$\tau =2,$ then we obtain

• ${\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\left(-\log \left(1-0.4\right)\right)}^3+{\left(-\log \left(1-0.2\right)\right)}^3\right)}^{\frac{1}{3}}}\right), \left(e^{-{\left({\left(-\log \left(0.3\right)\right)}^3+{\left(-\log \left(0.7\right)\right)}^3\right)}^{\frac{1}{3}}}\right)\right),\\ \left(\left(1-e^{-{\left({\left(-\log \left(1-0.6\right)\right)}^3+{\left(-\log \left(1-0.3\right)\right)}^3\right)}^{\frac{1}{3}}}\right), \left(e^{-{\left({\left(-\log \left(0.1\right)\right)}^3+{\left(-\log \left(0.5\right)\right)}^3\right)}^{\frac{1}{3}}}\right)\right)\end{array}\right\},$
  $=\left\{\left(0.2037, 0.5901\right), \left(0.3334, 0.3645\right)\right\},$
• ${\mathsf{Ǧ}}_1\mathsf{\otimes }{\mathsf{Ǧ}}_2=\left\{\begin{array}{c}\left(e^{-{\left({\left(-\log \left(0.4\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(0.2\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(\left(1-e^{-{\left({\left(-\log \left(1-0.3\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-0.7\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(e^{-{\left({\left(-\log \left(0.6\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(0.3\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(\left(1-e^{-{\left({\left(-\log \left(1-0.1\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-0.5\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\},$
  $=\left\{\left(0.4773, 0.4098\right), \left(0.5851, 0.2602\right)\right\},$
• $2\mathsf{Ǧ}=\left\{\begin{array}{c}\left(\left(1-e^{-{\left(2{\left(-\log \left(1-0.5\right)\right)}^3\right)}^{\frac{1}{3}}}\right), \left(e^{-{\left(2{\left(-\log \left(0.2\right)\right)}^3\right)}^{\frac{1}{3}}}\right)\right),\\ \left(\left(1-e^{-{\left(2{\left(-\log \left(1-0.3\right)\right)}^3\right)}^{\frac{1}{3}}}\right), \left(e^{-{\left(2{\left(-\log \left(0.5\right)\right)}^3\right)}^{\frac{1}{3}}}\right)\right)\end{array}\right\},$
  $=\left\{\left(0.3156, 0.4145\right), \left(0.1773, 0.6843\right)\right\},$
• ${\mathsf{Ǧ}}^2=\left\{\begin{array}{c}\left(\left(e^{-{\left(2{\left(-\log \left(0.5\right)\right)}^3\right)}^{\frac{1}{3}}}\right), \left(1-e^{-{\left(2{\left(-\log \left(1-0.2\right)\right)}^3\right)}^{\frac{1}{3}}}\right)\right),\\ \left(\left(e^{-{\left(2{\left(-\log \left(0.3\right)\right)}^3\right)}^{\frac{1}{3}}}\right), \left(1-e^{-{\left(2{\left(-\log \left(1-0.5\right)\right)}^3\right)}^{\frac{1}{3}}}\right)\right)\end{array}\right\},$
  $=\left\{\left(0.6843, 0.1149\right), \left(0.5174, 0.3156\right)\right\}.$

Theorem 1.

Suppose$\mathsf{Ǧ}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\underbrace{\theta }}_{\mathsf{Ǧ}}\right), \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\overbrace{\theta }}_{\mathsf{Ǧ}}\right)\right\}, {\mathsf{Ǧ}}_1=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_1}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_1}\right)\right\}$and${\mathsf{Ǧ}}_2=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_2}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_2}\right)\right\}$be three IFRNs, then

(1)

${\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2={\mathsf{Ǧ}}_2\mathsf{\oplus }{\mathsf{Ǧ}}_1$

(2)

${\mathsf{Ǧ}}_1\mathsf{\otimes }{\mathsf{Ǧ}}_2={\mathsf{Ǧ}}_2\mathsf{\otimes }{\mathsf{Ǧ}}_1$

(3)

$\tau \left({\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2\right)=\tau {\mathsf{Ǧ}}_1\mathsf{\oplus }\tau {\mathsf{Ǧ}}_2, \tau >0$

(4)

$\left({\tau }_1+{\tau }_2\right)\mathsf{Ǧ}={\tau }_1\mathsf{Ǧ}+{\tau }_2\mathsf{Ǧ}, {\tau }_1, {\tau }_2>0$

(5)

${\left({\mathsf{Ǧ}}_1\mathsf{\otimes }{\mathsf{Ǧ}}_2\right)}^{\tau }={\mathsf{Ǧ}}_1{}^{\tau }\mathsf{\otimes }{\mathsf{Ǧ}}_2{}^{\tau }, \tau >0$

(6)

${\mathsf{Ǧ}}^{{\tau }_1}\mathsf{\otimes }{\mathsf{Ǧ}}^{{\tau }_2}={\mathsf{ȹ}}^{\left({\tau }_1+{\tau }_2\right)}.$

Proof of Theorem 1.

For three IFRNs $\mathsf{Ǧ}, {\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_3$ and $\tau , {\tau }_1, {\tau }_2>0,$ we can get

(1)

$$\begin{gathered} {\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \\ \left(e^{-{\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)& \right),\\ \left(\left(1-e^{-{\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \\ \left(e^{-{\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)& \right)\end{array}\right\} \\ =\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{\theta }}}_1\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\} \end{gathered}$$

$={\mathsf{Ǧ}}_2\mathsf{\oplus }{\mathsf{Ǧ}}_1.$

(2)

Straightforward

(3)

Let $\xi =1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}$

Then $\log \left(1-\xi \right)=e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}.}$ Using this, we can get

$\tau ({\mathsf{Ǧ}}_2\mathsf{\oplus }{\mathsf{Ǧ}}_1) =\tau \left(\right\{\begin{array}{c}\left(\left(1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{{\mathsf{Ǧ}}_2}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{\theta }}}_1\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\left\}\right),$

$$\begin{gathered} =\left(\right\{\begin{array}{c}\left(\left(1-e^{-{\left({\tau \left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \\ \left(e^{-{\left({\tau \left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)& \right),\\ \left( \left(1-e^{-{\left({\tau \left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \\ \left(e^{-{\left({\tau \left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)& \right)\end{array}\left\}\right), \end{gathered}$$

$=\left(\left\{\begin{array}{c}\left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{\ae }}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(e^{-\left(\tau {\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right),\\ \left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(e^{-\left(\tau {\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}\right)$

$\mathsf{\oplus }\left(\left\{\begin{array}{c}\left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(e^{-\left(\tau {\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right),\\ \left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(e^{-\left(\tau {\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}\right)$

$=\tau {\mathsf{Ǧ}}_1\mathsf{\oplus }\tau {\mathsf{Ǧ}}_2.$

(4)

${\tau }_1\mathsf{Ǧ}+{\tau }_2\mathsf{Ǧ}=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\tau }_1{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\tau }_1{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\tau }_1{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\tau }_1{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$\mathsf{\oplus }\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\tau }_2{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\tau }_2{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\tau }_2{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\tau }_2{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left(\left({\tau }_1+{\tau }_2\right){\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left(\left({\tau }_1+{\tau }_2\right){\left(-\log \left({\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left(\left({\tau }_1+{\tau }_2\right){\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left(\left({\tau }_1+{\tau }_2\right){\left(-\log \left({\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$=\left({\tau }_1+{\tau }_2\right)\mathsf{Ǧ}.$

(5)

${({\mathsf{Ǧ}}_1\mathsf{\oplus }{\mathsf{Ǧ}}_2)}^{\tau } ={\left\{\begin{array}{c}\left(e^{-{\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), (\left(1-e^{-{\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)),\\ \left(e^{-{\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), (\left(1-e^{-{\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right))\end{array}\right\}}^{\tau }$

$=\{\begin{array}{c}\left(e^{-{\left({\tau (\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left({\mathsf{ȹ}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}})}), (\left({1-e}^{-{\left({\tau (\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}})}\right)\right),\\ (e^{-{\left({\tau \left(\right(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right))}^{\mathcal{Q}}+{\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}})}), (\left(1-e^{-{\left({\tau (\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}})}\right))\end{array})$

$=\left\{\begin{array}{c}\left(e^{-\left(\tau {\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-(\tau {\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)),\\ \left(e^{-(\tau {\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}})}\right), \left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}$

$\mathsf{\otimes }\left\{\begin{array}{c}\left(e^{-\left(\tau {\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right),\\ \left(e^{-\left(\tau {\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left(\tau {\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}$

$={\mathsf{Ǧ}}_1{}^{\tau }\mathsf{\otimes }{\mathsf{Ǧ}}_2{}^{\tau }.$

(6)

${\mathsf{Ǧ}}_1{}^{{\tau }_1}\mathsf{\otimes }{\mathsf{Ǧ}}_2{}^{{\tau }_2}=\left\{\begin{array}{c}\left(e^{-\left({\tau }_1{\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left({\tau }_1{\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right),\\ \left(e^{-\left({\tau }_1{\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left({\tau }_1{\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}$

$\mathsf{\otimes }\left\{\begin{array}{c}\left(e^{-\left({\tau }_2{\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left({\tau }_2{\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right),\\ \left(e^{-\left({\tau }_2{\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left({\tau }_2{\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}$

$=\left\{\begin{array}{c}\left(e^{-\left(\left({\tau }_1+{\tau }_2\right){\left({\left(-\log \left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left(\left({\tau }_1+{\tau }_2\right){\left({\left(-\log \left(1-{\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right),\\ \left(e^{-\left(\left({\tau }_1+{\tau }_2\right){\left({\left(-\log \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right), \left(\left(1-e^{-\left(\left({\tau }_1+{\tau }_2\right){\left({\left(-\log \left(1-{\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}\right)}\right)\right)\end{array}\right\}$

$={\mathsf{Ǧ}}^{\left({\tau }_1+{\tau }_2\right)}$ □

4. Aczel-Alsina Intuitionistic Fuzzy Rough Average Aggregation Operators

In this part, we aim to initiate the notion of the IFRAA weighted average, IFRAA ordered weighted average, and IFRAA hybrid AOs.

Definition 14.

Let ${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\} \left(i=1, 2, \dots , n\right)$ be the family for IFRNs and$\varpi =\left({\varpi }_1, {\varpi }_2, \dots , {\varpi }_n\right)$ be the weight vectors (WVs) for IFRNs ${\mathsf{Ǧ}}_i \left(i=1, 2, \dots , n\right)$ with the condition that ${\displaystyle \sum }_{i=1}^n{\varpi }_i=1.$ Then, the IFRAAWA aggregation operators are the mappings $IFRAAWA:{\left({\Xi }^{\wr }\right)}^n\to {\Xi }^{\wr }$ given by

$$IFRAAWA\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }_i{\mathsf{Ǧ}}_i\right)={\varpi }_1{\mathsf{Ǧ}}_1+{\varpi }_2{\mathsf{Ǧ}}_2+\dots +{\varpi }_n{\mathsf{Ǧ}}_n$$

Now we prove that the results obtain from IFRAAWA operators are again IFRNs.

Theorem 2.

Let ${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\} \left(i=1, 2, \dots , n\right)$be the collection for IFRNs, then the aggregated values obtain by using IFRAAWA operators are again an IFRNs, and$IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }_i{\mathsf{Ǧ}}_i\right)$

$$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$$

(1)

where$\varpi =\left({\varpi }_1, {\varpi }_2, \dots , {\varpi }_n\right)$be the WVs for IFRNs${\mathsf{Ǧ}}_i \left(i=1, 2, \dots , n\right)$with condition that${\displaystyle \sum }_{i=1}^n{\varpi }_i=1.$

Proof of Theorem 2.

We use the method of mathematical induction to prove this result.

Step 1.

For $n=1$, by using intuitionistic fuzzy rough Aczel-Aslina operation, we get ${\varpi }_1{\mathsf{Ǧ}}_1=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\mathsf{\varpi }}_1{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_1{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\},$

${\varpi }_2{\mathsf{Ǧ}}_2=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\varpi }_2{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\mathsf{\varpi }}_2{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\varpi }_2{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_2{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}.$□

By using definition (10), we get

$IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2\right)={\oplus }_{i=1}^2\left({\varpi }_i{\mathsf{Ǧ}}_i\right)={\varpi }_1{\mathsf{Ǧ}}_1\oplus {\varpi }_2{\mathsf{Ǧ}}_2$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_1{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_1{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$\oplus \left\{\begin{array}{c}\left(\left(1-e^{-{\left({\varpi }_2{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_1{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_1{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$$\begin{gathered} =\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{{\varpi }_2\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \\ (e^{-{\left({\varpi }_1{\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{{\varpi }_2\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}})}& \right),\\ \left(\left(1-e^{-{\left({\varpi }_1{\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{{\varpi }_2\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right), \\ \left(e^{-{\left({\varpi }_1{\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_1}\right)\right)}^{\mathcal{Q}}+{{\varpi }_2\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_2}\right)\right)}^{\mathcal{Q}}\right)}^{\frac{1}{\mathcal{Q}}}}\right)& \right)\end{array}\right\} \end{gathered}$$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^2{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^2{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^2{\mathsf{\varpi }}_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^2{\varpi }_i\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

Hence Equation (1) is true for $n=2.$

Now suppose that Equation (1) is true for $n={\mathsf{{\rm K}}}^{\divideontimes },$ i.e.,

$IFRAAW{A}_{\mathsf{\varpi }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}\left({\varpi }_i{\mathsf{Ǧ}}_i\right)$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

Now for $n={\mathsf{{\rm K}}}^{\divideontimes }+1,$ we get

$IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_{{\mathsf{{\rm K}}}^{\divideontimes }}, {\mathsf{Ǧ}}_{{\mathsf{{\rm K}}}^{\divideontimes }+1}\right)={\oplus }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}\left({\varpi }_i{\mathsf{Ǧ}}_i\right)\oplus \left({\varpi }_{{\mathsf{{\rm K}}}^{\divideontimes }+1}{\mathsf{Ǧ}}_{{\mathsf{{\rm K}}}^{\divideontimes }+1}\right)$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }}{\varpi }_i\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$\oplus \left\{\begin{array}{c}\left(\left(1-e^{-{\left({\varpi }_{{\mathsf{{\rm K}}}^{\divideontimes }+1}\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\varpi }_{{\mathsf{{\rm K}}}^{\divideontimes }+1}\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\varpi }_{{\mathsf{{\rm K}}}^{\divideontimes }+1}\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\varpi }_{{\mathsf{{\rm K}}}^{\divideontimes }+1}\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }+1}{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }+1}{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }+1}{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^{{\mathsf{{\rm K}}}^{\divideontimes }+1}{\varpi }_i\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

Hence, the result is true for $n={\mathsf{{\rm K}}}^{\divideontimes }+1$, and hence it is true for any $n.$

Next, we present some fundamental properties of the IFRAAWA aggregation operators.

Property 1 (Idempotency).

If all${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\}$are equal i.e.,${\mathsf{Ǧ}}_i=\mathsf{Ǧ}$for all$i$, then

$$IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)=\mathsf{Ǧ}.$$

Proof of Property 1.

As ${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\}=\mathsf{Ǧ} \left(i=1, 2, 3, \dots , n\right),$ then by using Equation (1), we get

$IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }_i{\mathsf{Ǧ}}_i\right)$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left(\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left(\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left(\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left(\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}$

$=\left\{\begin{array}{c}\left(\left(1-e^{\log \left(1-{\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)}\right), \left(e^{\log \left({\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)}\right)\right),\\ \left(\left(1-e^{\log \left(1-{\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}\right)}\right),\left(e^{\log \left({\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)}\right)\right)\end{array}\right\}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\underbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right), \left({\overbrace{\mathsf{ȹ}}}_{\mathsf{Ǧ}}, {\overbrace{\mathsf{\theta }}}_{\mathsf{Ǧ}}\right)\right\}=\mathsf{Ǧ}.$□

Property 2 (Boundedness).

Suppose${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\}$is the family of IFRNs. Let${\mathsf{Ǧ}}^{-}=\min \left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)$and${\mathsf{Ǧ}}^{+}=\max \left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right),$then

$${\mathsf{Ǧ}}^{-}\le IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)\le {\mathsf{Ǧ}}^{+}.$$

Proof of Property 2. 

Let ${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\}$ be the family of IFRNs and suppose ${\mathsf{Ǧ}}^{-}=\min \left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)=\left\{\left({\underbrace{{\mathsf{ȹ}}^{-}}}_{\mathsf{Ǧ}}, {\underbrace{{\mathsf{\theta }}^{-}}}_{\mathsf{Ǧ}}\right), \left({\overbrace{{\mathsf{ȹ}}^{-}}}_{\mathsf{Ǧ}}, {\overbrace{{\mathsf{\theta }}^{-}}}_{\mathsf{Ǧ}}\right)\right\}$ and ${\mathsf{Ǧ}}^{+}=\max \left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)=\left\{\left({\underbrace{{\mathsf{ȹ}}^{+}}}_{\mathsf{Ǧ}}, {\underbrace{{\mathsf{\theta }}^{+}}}_{\mathsf{Ǧ}}\right), \left({\overbrace{{\mathsf{ȹ}}^{+}}}_{\mathsf{Ǧ}}, {\overbrace{{\mathsf{\theta }}^{+}}}_{\mathsf{Ǧ}}\right)\right\}.$ Now we have ${\underbrace{{\mathsf{ȹ}}^{-}}}_{\mathsf{Ǧ}}=\underset{i}{\min } \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right), {\underbrace{{\mathsf{\theta }}^{-}}}_{\mathsf{Ǧ}}=\underset{i}{\max } \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), {\underbrace{{\mathsf{ȹ}}^{+}}}_{\mathsf{Ǧ}}=\underset{i}{\max } \left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right), {\underbrace{{\mathsf{\theta }}^{+}}}_{\mathsf{Ǧ}}=\underset{i}{\min } \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)$ and ${\overbrace{{\mathsf{ȹ}}^{-}}}_{\mathsf{Ǧ}}=\underset{i}{\min } \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right), {\overbrace{{\mathsf{\theta }}^{-}}}_{\mathsf{Ǧ}}=\underset{i}{\max } \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), {\overbrace{{\mathsf{ȹ}}^{+}}}_{\mathsf{Ǧ}}=\underset{i}{\max } \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right), {\overbrace{{\mathsf{\theta }}^{+}}}_{\mathsf{Ǧ}}=\underset{i}{\min } \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right).$ Hence, we get

$1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\underbrace{{\mathsf{ȹ}}^{-}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le 1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le 1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\underbrace{{\mathsf{ȹ}}^{+}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}$

and $1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\overbrace{{\mathsf{ȹ}}^{-}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le 1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le 1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\overbrace{{\mathsf{ȹ}}^{+}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}},$

$e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{{\mathsf{\theta }}^{+}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{{\mathsf{\theta }}^{-}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}$

and $e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\overbrace{{\mathsf{\theta }}^{+}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\le e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\overbrace{{\mathsf{\theta }}^{-}}}_{\mathsf{Ǧ}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}.$

therefore ${\mathsf{Ǧ}}^{-}\le IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)\le {\mathsf{Ǧ}}^{+}.$ □

Property 3 (Monotonicity).

Let${\mathsf{Ǧ}}_i and {\mathsf{Ǧ}}^{\prime }{}_i\left(i=1, 2, 3, \dots , n\right)$be the two collections of IFRNs, then if${\mathsf{Ǧ}}_i \le {\mathsf{Ǧ}}^{\prime }{}_i$for all$i$, then

$$IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)\le IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}^{\prime }{}_1, {\mathsf{Ǧ}}_2^{\prime }, \dots , {\mathsf{Ǧ}}^{\prime }{}_n\right).$$

Proof of property 3.

Straightforward

Now, we introduce the IFRAA-ordered weighted average AOs. □

Definition 15.

Let ${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\} \left(i=1, 2, \dots , n\right)$ be the family for IFRNs and ${\varpi }^{\star }=\left({\varpi }^{\star }{}_1, {\varpi }^{\star }{}_2, \dots , {\varpi }^{\star }{}_n\right)$ be the WVs for IFRNs ${\mathsf{Ǧ}}_i \left(i=1, 2, \dots , n\right)$ with the condition that ${\displaystyle \sum }_{i=1}^n{\varpi }^{\star }{}_i=1.$ Then, the IFRAAOWA aggregation operators are the mappings$IFRAAOWA:{\left({\Xi }^{\wr }\right)}^n\to {\Xi }^{\wr }$_, given by

$$IFRAAOWA\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }^{\star }{}_i{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}\right)={\varpi }^{\star }{}_1{\mathsf{Ǧ}}_{\mathfrak{O}\left(1\right)}+{\varpi }^{\star }{}_2{\mathsf{Ǧ}}_{\mathfrak{O}\left(2\right)}+\dots +{\varpi }^{\star }{}_n{\mathsf{Ǧ}}_{\mathfrak{O}\left(n\right)}.$$

where $\left(\mathfrak{O}\left(1\right), \mathfrak{O}\left(2\right), \dots , \mathfrak{O}\left(n\right)\right)$ are the permutation of $\left(i=1, 2,3, \dots , n\right)$ including ${\mathsf{ȹ}}_{\mathfrak{O}\left(n-1\right)}\ge {\mathsf{ȹ}}_{\mathfrak{O}\left(n\right)}.$

Theorem 3.

Let${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\} \left(i=1, 2, \dots , n\right)$be the collection for IFRNs, then IFRAAOWA operators are defined by mapping

$$\begin{gathered} IFRAAOW{A}_{{\varpi }^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }_i^{\star }{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}\right) \\ =\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left({\underbrace{\theta }}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left({\overbrace{\theta }}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\} \end{gathered}$$

(2)

where${\varpi }^{\star }=\left({\varpi }_1^{\star }, {\varpi }_2^{\star }, \dots , {\varpi }_n^{\star }\right)$are the WVs for IFRNs${\mathsf{Ǧ}}_i \left(i=1, 2, \dots , n\right)$with the condition that${\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }=1$and$\left(\mathfrak{O}\left(1\right), \mathfrak{O}\left(2\right), \dots , \mathfrak{O}\left(n\right)\right)$are the permutation of$\left(i=1, 2,3, \dots , n\right)$including${\mathsf{Ǧ}}_{\mathfrak{O}\left(n-1\right)}\ge {\mathsf{Ǧ}}_{\mathfrak{O}\left(n\right)}.$

IFRAAOWA aggregation operators also satisfy some basic properties, given as

Property 1 (Idempotency).

If all${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\}$are equal i.e.,${\mathsf{Ǧ}}_i=\mathsf{Ǧ}$for all$i$then

$$IFRAAOW{A}_{{\mathsf{\varpi }}_i^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)=\mathsf{Ǧ}.$$

Property 2 (Boundedness).

Suppose${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\}$is the family of IFRNs. Let${\mathsf{Ǧ}}^{-}=\min \left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)$and${\mathsf{Ǧ}}^{+}=\max \left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right),$then

$${\mathsf{Ǧ}}^{-}\le IFRAAOW{A}_{{\varpi }_i^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)\le {\mathsf{Ǧ}}^{+}.$$

Property 3 (Monotonicity).

Let${\mathsf{Ǧ}}_i \mathrm{a}nd {\mathsf{Ǧ}}^{\prime }{}_i\left(i=1, 2, 3, \dots , n\right)$be the two collections of IFRNs, then if${\mathsf{Ǧ}}_i \le {\mathsf{Ǧ}}^{\prime }{}_i$for all$i$, then

$$IFRAAOW{A}_{{\varpi }_i^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)\le IFRAAOW{A}_{{\varpi }_i^{\star }}\left({\mathsf{Ǧ}}^{\prime }{}_1, {\mathsf{Ǧ}}_2^{\prime }, \dots , {\mathsf{Ǧ}}^{\prime }{}_n\right).$$

It is clear by Definition (14) that IFRAAWA operators can only weight IFRNs, and by Definition (15), it is clear that IFRAAOWA operators can only weight the ordered position of IFRNs. As a result, weights represent different aspects of both IFRAAWA and IFRAAOWA operators. To cover this drawback, we will introduce an IFR Aczel-Alsina hybrid average (IFRAAHA) aggregation operator that can weigh IFRNs as well as their ordered position.

Definition 16.

Let ${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\} \left(i=1, 2, \dots , n\right)$ be the collection for IFRNs. Then, IFRAAHA aggregation operators are the mappings$IFRAAHA:{\left({\Xi }^{\wr }\right)}^n\to {\Xi }^{\wr }$ given by

$$IFRAAH{A}_{\varpi , {\varpi }^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }_i^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(i\right)}\right)={\varpi }^{\star }{}_1{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(1\right)}+{\varpi }^{\star }{}_2{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(2\right)}+\dots +{\varpi }^{\star }{}_n{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n\right)}$$

where ${\varpi }^{\star }=\left\{{\varpi }_1^{\star }, {\varpi }_2^{\star }, {\varpi }_3^{\star }, \dots , {\varpi }_n^{\star }\right\}$ are the WVs associated with IFRAAHA operators with the condition that ${\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }; {\mathsf{Ǧ}}^{\therefore }{}_i=n{\varpi }_i{\mathsf{Ǧ}}_i \left(i=1, 2, 3, \dots , n\right), \left({\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(1\right)}, {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(2\right)}, {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(3\right)}, \dots , {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n\right)}\right)$ is the permutation of the family of weighted IFRNs $\left({\mathsf{Ǧ}}^{\therefore }{}_1, {\mathsf{Ǧ}}^{\therefore }{}_2, {\mathsf{Ǧ}}^{\therefore }{}_3, \dots , {\mathsf{Ǧ}}^{\therefore }{}_n\right)$, such that ${\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n-1\right)}\ge {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n\right)},$ $\varpi =\left\{{\varpi }_1, {\varpi }_2, {\varpi }_3, \dots , {\varpi }_n\right\}$ are the WVs of ${\mathsf{Ǧ}}_i \left(i=1, 2, 3, \dots , n\right)$ with the condition ${\displaystyle \sum }_{i=1}^n{\varpi }_i$ and $n$ is the balancing coefficient.

Theorem 4.

Let${\mathsf{Ǧ}}_i=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\theta }}_{{\mathsf{Ǧ}}_i}\right)\right\} \left(i=1, 2, \dots , n\right)$be the collection for IFRNs, then the aggregated result contained by IFRAAHA operators are again IFRNs given by

$$\begin{gathered} IFRAAH{A}_{\varpi , {\varpi }^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)={\oplus }_{i=1}^n\left({\varpi }_i^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(i\right)}\right) \\ =\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left(1-{\underbrace{{\mathsf{ȹ}}^{\therefore }}}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left({\underbrace{{\theta }^{\therefore }}}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left(1-{\overbrace{{\mathsf{ȹ}}^{\therefore }}}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i^{\star }\left({\left(-\log \left({\overbrace{{\theta }^{\therefore }}}_{{\mathsf{Ǧ}}_{\mathfrak{O}\left(i\right)}}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\} \end{gathered}$$

(3)

Proof of Theorem 4.

Similar to the proof of Theorem 1, we can prove this result. □

Theorem 5.

The IFRAAWA and IFRAAOWA operator are special cases of the IFRAAHA operators.

Proof of Theorem 5.

• Let ${\varpi }^{\star }={\left(\frac{1}{n}, \frac{1}{n}, \frac{1}{n}, \dots , \frac{1}{n}\right)}^{\mathbb{T}}.$ Then

$IFRAAH{A}_{\varpi , {\varpi }^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)=\left({\varpi }_1^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(1\right)}\right)\oplus \left({\varpi }_2^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(2\right)}\right)\oplus \left({\varpi }_3^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(3\right)}\right)\oplus \dots \oplus \left({\varpi }_n^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n\right)}\right)$

$=\frac{1}{n}\left({\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(1\right)}\oplus {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(2\right)}\oplus {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(3\right)}\oplus \dots \oplus {\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n\right)}\right)$

$=\left({\varpi }_1{\mathsf{Ǧ}}_1\oplus {\varpi }_2{\mathsf{Ǧ}}_2\oplus {\varpi }_3{\mathsf{Ǧ}}_3\oplus \dots \oplus {\varpi }_n{\mathsf{Ǧ}}_n\right)$

$=IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right).$

2.

Let $\varpi ={\left(\frac{1}{n}, \frac{1}{n}, \frac{1}{n}, \dots , \frac{1}{n}\right)}^{\mathbb{T}}.$ Then

$IFRAAH{A}_{\varpi , {\varpi }^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right)=\left({\varpi }_1^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(1\right)}\right)\oplus \left({\varpi }_2^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(2\right)}\right)\oplus \left({\varpi }_3^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(3\right)}\right)\oplus \dots \oplus \left({\varpi }_n^{\star }{\mathsf{Ǧ}}^{\therefore }{}_{\mathfrak{O}\left(n\right)}\right)$$=\left({\varpi }_1^{\star }{\mathsf{Ǧ}}_{\mathfrak{O}\left(1\right)}\right)\oplus \left({\varpi }_2^{\star }{\mathsf{Ǧ}}_{\mathfrak{O}\left(2\right)}\right)\oplus \left({\varpi }_3^{\star }{\mathsf{Ǧ}}_{\mathfrak{O}\left(3\right)}\right)\oplus \dots \oplus \left({\varpi }_n^{\star }{\mathsf{Ǧ}}_{\mathfrak{O}\left(n\right)}\right)$

$=IFRAAOW{A}_{{\varpi }^{\star }}\left({\mathsf{Ǧ}}_1, {\mathsf{Ǧ}}_2, \dots , {\mathsf{Ǧ}}_n\right).$ □

5. Multi-Attribute Decision Making (MADM Technique Based on Intuitionistic Fuzzy Rough Aczel-Alsina Weighted Average Aggregation Operators

In this part of the article, to show the effective use of the proposed approach, we introduce the MADM approach to show the reliability of our work. Let ${\mathcal{J}}^{\divideontimes }=\left\{{\mathcal{J}}_1^{\divideontimes }, {\mathcal{J}}_2^{\divideontimes }, {\mathcal{J}}_3^{\divideontimes }, \dots , {\mathcal{J}}_m^{\divideontimes }\right\}$ be the family of different alternatives and $Y=\left\{Y_1, Y_2, Y_3, \dots , Y_n\right\}$ be a family of attributes. Furthermore, suppose that $\varpi ={\left({\varpi }_1, {\varpi }_2, {\varpi }_3, \dots , {\varpi }_n\right)}^{\mathbb{T}}$ are the WVs of attributes $Y \left(i=1, 2, 3, \dots , n\right)$ with the condition that ${\displaystyle \sum }_{i=1}^n{\varpi }_i=1.$ Suppose the decision analyst provide their assessment of each alternative corresponding to their attributes in the shape of IFRNs ${\mathsf{Ǧ}}_{\mathsf{\upsilon }i}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\},$ then the decision matrix can be expressed as

$\mathfrak{K}={\left({\mathsf{Ǧ}}_{\mathsf{\upsilon }i}\right)}_{m\times n}=\left[\begin{array}{cccc}\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{11}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{11}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{11}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{11}}\right)\right\}& \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{12}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{12}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{12}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{12}}\right)\right\}& \cdots & \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{1n}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{1n}}\right), \left({\stackrel{\mathsf{⏞}}{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{1n}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{1n}}\right)\right\}\\ \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{21}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{21}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{21}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{21}}\right)\right\}& \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{22}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{22}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{22}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{22}}\right)\right\}& \cdots & \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{2n}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{2n}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{2n}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{2n}}\right)\right\}\\ ⋮& ⋮& \ddots & \ddots \\ \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{m1}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{m1}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{m1}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{m1}}\right)\right\}& \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{m2}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{m2}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{m2}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{m2}}\right)\right\}& \cdots & \left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{mn}}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{mn}}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_{mn}}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_{mn}}\right)\right\}\end{array}\right].$

Step 1.

Standardize the above-given matrix by using the formula given below

$${\mathfrak{K}}^{\colon\colon }=\{\begin{array}{c}{\left({\mathsf{Ǧ}}_{\mathsf{\upsilon }i}\right)}^c;for cost type parameters\\ {\mathsf{Ǧ}}_{\mathsf{\upsilon }i};for benefit type parameters\end{array}$$

where ${\left({\mathsf{Ǧ}}_{\mathsf{\upsilon }i}\right)}^c=\left\{\left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right\}$ is the complement of ${\mathsf{Ǧ}}_{\mathsf{\upsilon }i}=\left\{\left({\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right), \left({\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}, {\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right\}.$

Step 2.

Aggregate IFRNs ${\mathsf{Ǧ}}_{\mathsf{\upsilon }i} \left(i=1, 2, 3, \dots , n\right) and \left(\mathsf{\upsilon }=1, 2, 3, \dots , m\right)$ for each alternative ${\mathcal{J}}_{\mathsf{\upsilon }}^{\divideontimes } \left(\mathsf{\upsilon }=1, 2, 3, \dots , m\right)$ by using IFRAAWA aggregation operators ${\mathsf{Ǧ}}_{\mathsf{\upsilon }}=IFRAAW{A}_{\varpi }\left({\mathsf{Ǧ}}_{\mathsf{\upsilon }1}, {\mathsf{Ǧ}}_{\mathsf{\upsilon }2}, \dots , {\mathsf{Ǧ}}_{\mathsf{\upsilon }n}\right)={\oplus }_{i=1}^n\left({\varpi }_i{\mathsf{Ǧ}}_{\mathsf{\upsilon }i}\right)$

$=\left\{\begin{array}{c}\left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\underbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right), \left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\underbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right),\\ \left(\left(1-e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left(1-{\overbrace{\mathsf{ȹ}}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right),\left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\varpi }_i\left({\left(-\log \left({\overbrace{\mathsf{\theta }}}_{{\mathsf{Ǧ}}_i}\right)\right)}^{\mathcal{Q}}\right)\right)}^{\frac{1}{\mathcal{Q}}}}\right)\right)\end{array}\right\}.$

Step 3.

Calculate the score values for each alternative by using the formula given in Definition (10).

Step 4.

Rank the results obtain from Step 3 and then choose the best alternative.

5.1. Applications

In this subsection, we will discuss possible applications of introduced aggregation operators in medical diagnosis and MADM problems.

5.1.1. Medical Diagnosis

Medical diagnosis is the activity of describing which disease or state presents a person’s syndrome. To reach an accurate decision, experts try to diagnose the disease according to the patient’s symptoms. Medical diagnosis is a method in which a physician chooses one disease over another based on a person’s symptoms. FST helps health experts who are dealing with linguistic ideas and removes the loss of accuracy. FSs have been successfully used in medical diagnoses that can be seen in [4]. In the following, we will use IFRNs for medical diagnosis. A graphical presentation of medical diagnosis is given in Figure 2.

Example 2.

Let ${\mathcal{J}}^{\divideontimes }=\left\{{\mathcal{J}}_1^{\divideontimes }=Coronavirus, {\mathcal{J}}_2^{\divideontimes }=Asthma, {\mathcal{J}}_3^{\divideontimes }=Tuberculosis, {\mathcal{J}}_4^{\divideontimes }=Pneumonia, {\mathcal{J}}_5^{\divideontimes }=Mesothelioma\right\}$ be the set of five diseases as alternatives and $Y=\left\{Y_1=Chest pain, Y_2=Fever, Y_3=Fatigue, Y_4=Cough, Y_5=Body aches\right\}$ is the set of attributes. Suppose decision analyst supply their data in the shape of IFRNs given in 

Table 1. Intuitionistic fuzzy rough data.

	${\mathit{Y}}_1$$=\mathit{C}\mathit{h}\mathit{e}\mathit{s}\mathit{t} \mathit{p}\mathit{a}\mathit{i}\mathit{n}$	${\mathit{Y}}_2$$=\mathit{F}\mathit{e}\mathit{v}\mathit{e}\mathit{r}$	${\mathit{Y}}_3$$=\mathit{F}\mathit{a}\mathit{t}\mathit{i}\mathit{g}\mathit{u}\mathit{e}$	${\mathit{Y}}_4$$=\mathit{C}\mathit{o}\mathit{u}\mathit{g}\mathit{h}$	${\mathit{Y}}_5$$=\mathit{B}\mathit{o}\mathit{d}\mathit{y} \mathit{a}\mathit{c}\mathit{h}\mathit{e}\mathit{s}$
${\mathcal{J}}_1^{\divideontimes }$=$Coron\mathrm{a}virus$	$\left\{\begin{array}{c}\left(0.21, 0.32\right),\\ \left(0.41, 0.17\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.29, 0.30\right),\\ \left(0.14, 0.12\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.22, 0.23\right),\\ \left(0.19, 0.17\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.21, 0.22\right),\\ \left(0.29, 0.27\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.12, 0.13\right),\\ \left(0.15, 0.16\right)\end{array}\right\}$
${\mathcal{J}}_2^{\divideontimes }$=$Asthm\mathrm{a}$	$\left\{\begin{array}{c}\left(0.21, 0.32\right),\\ \left(0.14, 0.15\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.26, 0.35\right),\\ \left(0.44, 0.13\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.21, 0.37\right),\\ \left(0.54, 0.16\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.22, 0.27\right),\\ \left(0.24, 0.36\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.60, 0.17\right),\\ \left(0.61, 0.21\right)\end{array}\right\}$
${\mathcal{J}}_3^{\divideontimes }$=$Tuberculosis$	$\left\{\begin{array}{c}\left(0.32, 0.33\right),\\ \left(0.44, 0.41\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.52, 0.16\right),\\ \left(0.47, 0.18\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.62, 0.11\right),\\ \left(0.54, 0.13\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.42, 0.13\right),\\ \left(0.54, 0.16\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.52, 0.41\right),\\ \left(0.40, 0.43\right)\end{array}\right\}$
${\mathcal{J}}_4^{\divideontimes }=Pneumoni\mathrm{a}$	$\left\{\begin{array}{c}\left(0.12, 0.23\right),\\ \left(0.34, 0.41\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.51, 0.30\right),\\ \left(0.47, 0.19\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.11, 0.23\right),\\ \left(0.37, 0.14\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.51, 0.33\right),\\ \left(0.32, 0.19\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.41, 0.42\right),\\ \left(0.27, 0.16\right)\end{array}\right\}$
${\mathcal{J}}_5^{\divideontimes }$=$Mesotheliom\mathrm{a}$	$\left\{\begin{array}{c}\left(0.25, 0.36\right),\\ \left(0.47, 0.18\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.12, 0.38\right),\\ \left(0.14, 0.21\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.19, 0.20\right),\\ \left(0.21, 0.21\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.17, 0.10\right),\\ \left(0.16, 0.29\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.21, 0.27\right),\\ \left(0.26, 0.62\right)\end{array}\right\}$

 and$\varpi ={\left(0.22, 0.19, 0.11, 0.27, 0.21\right)}^{\mathbb{T}}$ are the WVs of attributes $Y\left(i=1, 2, 3, \dots , n\right)$ with condition that ${\displaystyle \sum }_{i=1}^n{\varpi }_i=1.$ We want to diagnose which disease Mr.$X$is suffering from. Now, we use a step-wise algorithm to elaborate on this disease.

Step 1.

There is no need to normalize the matrix given in Table 1 because all attributes are of the same type.

Step 2.

Suppose that $\mathcal{Q}=1.$ We use the IFRAAWA AOs to compute general alternative values ${\mathsf{Ǧ}}_{\mathsf{\upsilon }}$ of five alternatives ${\mathcal{J}}_{\mathsf{\upsilon }}^{\divideontimes }\left(\mathsf{\upsilon }=1, 2, 3, 4, 5\right).$ Then

${\mathsf{Ǧ}}_1=\left\{\left(0.0966, 0.5937\right), \left(0.1789, 0.5329\right)\right\},{\mathsf{Ǧ}}_2=\left\{\left(0.1713, 0.5953\right), \left(0.1653, 0.4538\right)\right\},$

${\mathsf{Ǧ}}_3=\left\{\left(0.1140, 0.5213\right), \left(0.1890, 0.4739\right)\right\}$

${\mathsf{Ǧ}}_4=\left\{\left(0.1560, 0.5014\right), \left(0.1423, 0.5460\right)\right\}, {\mathsf{ȹ}}_5=\left\{\left(0.1863, 0.5461\right), \left(0.1663, 0.5473\right)\right\}$

Step 3.

We calculate the score values for each evaluated alternative.

$Sc\left({\mathsf{Ǧ}}_1\right)=0.2872, Sc\left({\mathsf{Ǧ}}_2\right)=0.3218, Sc\left({\mathsf{Ǧ}}_3\right)=0.3269,$

$Sc\left({\mathsf{Ǧ}}_4\right)=0.3127, Sc\left({\mathsf{Ǧ}}_5\right)=0.3148$

Step 4.

Rank the evaluated values and we can observe that ranking results are as follows

${\mathcal{J}}_3^{\divideontimes }\ge {\mathcal{J}}_2^{\divideontimes }\ge {\mathcal{J}}_5^{\divideontimes }\ge {\mathcal{J}}_4^{\divideontimes }\ge {\mathcal{J}}_1^{\divideontimes }.$

Because the score value for alternative ${\mathcal{J}}_1^{\divideontimes }=Coronavirus$ is the highest, so it means that Mr. $X$ is suffering from coronavirus disease.

5.1.2. Selection of Next-Generation Firewall (NGFW)

Firewalls are the typical security tools for most companies, but in recent scenarios, NGFW is the only type of firewall that can supply genuine security. NGFWs are the more leading version of security tools. They provide stable and active filtering and VPN support to guarantee that all associations between the network, internet, and firewall are sound and secure. In the next example, we will establish the selection of the best firewall. The graphical expression of NGFW is given in Figure 3.

Example 3.

Suppose a multi-national company $“X”$ wants to strengthen the security of its wireless network, and suppose that this company wants to buy the best next-generation firewall for its company. The company hires an expert who can give his suggestion in the selection of the best next ‘NGFW’ based on his experience and knowledge. Suppose ${\mathcal{J}}^{\divideontimes }=\left\{{\mathcal{J}}_1^{\divideontimes }, {\mathcal{J}}_2^{\divideontimes }, {\mathcal{J}}_3^{\divideontimes }, {\mathcal{J}}_4^{\divideontimes }, {\mathcal{J}}_5^{\divideontimes }\right\}$ denote the set of different alternatives and $Y=\left\{Y_1=application and user control, Y_2=Integrated intrusion prevention, Y_3=advance malware detection, Y_4=leverages threat intelligence feeds, Y_5=decrypt outboud SSL\right\}$ denote the set of different attributes. Let $\varpi ={\left(0.20, 0.16, 0.24, 0.21, 0.19\right)}^{\mathbb{T}}$ be the WVs of attributes. Suppose an expert supplies his assessment of each alternative corresponding to the respective attribute in the form of IFRNs as given in

Table 2. Intuitionistic fuzzy rough data.

	${\mathit{Y}}_1$	${\mathit{Y}}_2$	${\mathit{Y}}_3$	${\mathit{Y}}_4$	${\mathit{Y}}_5$
${\mathcal{J}}_1^{\divideontimes }$	$\left\{\begin{array}{c}\left(0.22, 0.13\right),\\ \left(0.11, 0.27\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.51, 0.19\right),\\ \left(0.15, 0.16\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.19, 0.18\right),\\ \left(0.13, 0.15\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.29, 0.59\right),\\ \left(0.39, 0.27\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.13, 0.23\right),\\ \left(0.14, 0.26\right)\end{array}\right\}$
${\mathcal{J}}_2^{\divideontimes }$	$\left\{\begin{array}{c}\left(0.51, 0.35\right),\\ \left(0.24, 0.25\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.17, 0.18\right),\\ \left(0.19, 0.20\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.51, 0.24\right),\\ \left(0.24, 0.19\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.26, 0.37\right),\\ \left(0.34, 0.37\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.15, 0.27\right),\\ \left(0.16, 0.28\right)\end{array}\right\}$
${\mathcal{J}}_3^{\divideontimes }$	$\left\{\begin{array}{c}\left(0.32, 0.13\right),\\ \left(0.10, 0.11\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.21, 0.22\right),\\ \left(0.23, 0.34\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.61, 0.20\right),\\ \left(0.57, 0.27\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.47, 0.17\right),\\ \left(0.14, 0.36\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.19, 0.29\right),\\ \left(0.20, 0.30\right)\end{array}\right\}$
${\mathcal{J}}_4^{\divideontimes }$	$\left\{\begin{array}{c}\left(0.12, 0.13\right),\\ \left(0.14, 0.15\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.52, 0.25\right),\\ \left(0.34, 0.43\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.11, 0.23\right),\\ \left(0.37, 0.14\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.21, 0.43\right),\\ \left(0.52, 0.21\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.21, 0.31\right),\\ \left(0.22, 0.32\right)\end{array}\right\}$
${\mathcal{J}}_5^{\divideontimes }$	$\left\{\begin{array}{c}\left(0.25, 0.36\right),\\ \left(0.47, 0.18\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.12, 0.38\right),\\ \left(0.14, 0.21\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.19, 0.20\right),\\ \left(0.21, 0.21\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.19, 0.15\right),\\ \left(0.23, 0.27\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.23, 0.33\right),\\ \left(0.24, 0.34\right)\end{array}\right\}$

. Now for our convenience, we will apply IFRAAWA aggregation operators to select the best alternative.

Step 1.

There is no need to normalize the matrix given in Table 1 because all attributes are of the same type.

Step 2.

Suppose that $\mathcal{Q}=1.$ We use the IFRAAWA AOs to compute general alternative values ${\mathsf{Ǧ}}_{\mathsf{\upsilon }}$ of five alternatives ${\mathcal{J}}_{\mathsf{\upsilon }}^{\divideontimes }\left(\mathsf{\upsilon }=1, 2, 3, 4, 5\right).$ Then

${\mathsf{Ǧ}}_1=\left\{\left(0.1397, 0.4908\right), \left(0.1046, 0.4805\right)\right\},{\mathsf{Ǧ}}_2=\left\{\left(0.1667, 0.5302\right), \left(0.1016, 0.5369\right)\right\},$

${\mathsf{Ǧ}}_3=\left\{\left(0.1633, 0.5081\right), \left(0.1507, 0.4766\right)\right\}$

${\mathsf{Ǧ}}_4=\left\{\left(0.1334, 0.6040\right), \left(0.1725, 0.5792\right)\right\}, {\mathsf{Ǧ}}_5=\left\{\left(0.0839, 0.5788\right), \left(0.0888, 0.5918\right)\right\}$

Step 3.

We calculate the score values for each evaluated alternative.

$Sc\left({\mathsf{Ǧ}}_1\right)=0.3182, Sc\left({\mathsf{Ǧ}}_2\right)=0.3003, Sc\left({\mathsf{Ǧ}}_3\right)=0.3323,$

$Sc\left({\mathsf{Ǧ}}_4\right)=0.2806, Sc\left({\mathsf{Ǧ}}_5\right)=0.2505$

Step 4.

Rank the evaluated values and we can observe that ranking results are as follows

${\mathcal{J}}_3^{\divideontimes }\ge {\mathcal{J}}_1^{\divideontimes }\ge {\mathcal{J}}_2^{\divideontimes }\ge {\mathcal{J}}_4^{\divideontimes }\ge {\mathcal{J}}_5^{\divideontimes }.$ From the above analysis, we can observe that ${\mathcal{J}}_3^{\divideontimes }$ is the best NGFW.

6. Comparative Analysis

In this part, we must introduce a comparative analysis of the introduced work with some existing notions to show that our work is more reliable and effective. We will compare our work with the IFWA [19], IFWG [22], IFDWA [23], IFWDG [23], IFHWA [24], IFAAWA [18], IFAAOWA [18], IFAAHA [18] and IFRWA [34] methods.

We use the data given in

Table 3. Intuitionistic fuzzy rough data.

	${\mathcal{J}}_1^{\divideontimes }$	${\mathcal{J}}_2^{\divideontimes }$	${\mathcal{J}}_3^{\divideontimes }$	${\mathcal{J}}_4^{\divideontimes }$	${\mathcal{J}}_5^{\divideontimes }$
$Y_1$	$\left\{\begin{array}{c}\left(0.12, 0.31\right),\\ \left(0.42, 0.15\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.62, 0.18\right),\\ \left(0.41, 0.21\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.42, 0.32\right),\\ \left(0.13, 0.18\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.51, 0.29\right),\\ \left(0.59, 0.17\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.42, 0.29\right),\\ \left(0.19, 0.14\right)\end{array}\right\}$
$Y_2$	$\left\{\begin{array}{c}\left(0.29, 0.33\right),\\ \left(0.18, 0.16\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.19, 0.53\right),\\ \left(0.27, 0.31\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.10, 0.13\right),\\ \left(0.14, 0.56\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.12, 0.32\right),\\ \left(0.54, 0.23\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.13, 0.12\right),\\ \left(0.15, 0.16\right)\end{array}\right\}$
$Y_3$	$\left\{\begin{array}{c}\left(0.23, 0.35\right),\\ \left(0.49, 0.14\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.25, 0.61\right),\\ \left(0.74, 0.10\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.12, 0.61\right),\\ \left(0.31, 0.23\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.22, 0.37\right),\\ \left(0.14, 0.15\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.29, 0.28\right),\\ \left(0.27, 0.26\right)\end{array}\right\}$
$Y_4$	$\left\{\begin{array}{c}\left(0.21, 0.32\right),\\ \left(0.43, 0.14\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.15, 0.59\right),\\ \left(0.71, 0.14\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.41, 0.33\right),\\ \left(0.39, 0.10\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.61, 0.18\right),\\ \left(0.17, 0.15\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.25, 0.14\right),\\ \left(0.29, 0.20\right)\end{array}\right\}$
$Y_5$	$\left\{\begin{array}{c}\left(0.52, 0.26\right),\\ \left(0.74, 0.12\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.11, 0.80\right),\\ \left(0.17, 0.12\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.15, 0.15\right),\\ \left(0.11, 0.41\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.18, 0.41\right),\\ \left(0.26, 0.11\right)\end{array}\right\}$	$\left\{\begin{array}{c}\left(0.30, 0.41\right),\\ \left(0.13, 0.15\right)\end{array}\right\}$

and all other data in Example 1 to evaluate the overall results. The evaluated results are given in

Table 4. Comparative evaluations.

Methods	Score Values	Ranking Results
IFWA [19]	No result	$\times$
IFWG [22]	No result	$\times$
IFDWA [23]	No result	$\times$
IFDWG [23]	No result	$\times$
IFHWA [24]	No result	$\times$
IFAAWA [18]	No result	$\times$
IFAAOWA [18]	No result	$\times$
IFAAHA [18]	No result	$\times$
IFRWA [34]	$Sc\left({\mathsf{ȹ}}_1\right)=0.3389,$ $Sc\left({\mathsf{ȹ}}_2\right)=0.3050,$ $Sc\left({\mathsf{ȹ}}_3\right)=0.2905,$ $Sc\left({\mathsf{ȹ}}_4\right)=0.3315,$ $Sc\left({\mathsf{ȹ}}_5\right)=0.3133$	${\mathcal{J}}_1^{\divideontimes }\ge {\mathcal{J}}_4^{\divideontimes }\ge {\mathcal{J}}_5^{\divideontimes }\ge {\mathcal{J}}_2^{\divideontimes }\ge {\mathcal{J}}_3^{\divideontimes }$
IVIFAAWA [20]	No result	$\times$
IVIFAAG [21]	No result	$\times$
IFRAAWA (proposed)	$Sc\left({\mathsf{ȹ}}_1\right)=0.34016,$ $Sc\left({\mathsf{ȹ}}_2\right)=0.3050,$ $Sc\left({\mathsf{ȹ}}_3\right)=0.29015,$ $Sc\left({\mathsf{ȹ}}_4\right)=0.3385,$ $Sc\left({\mathsf{ȹ}}_5\right)=0.3133,$	${\mathcal{J}}_1^{\divideontimes }\ge {\mathcal{J}}_4^{\divideontimes }\ge {\mathcal{J}}_5^{\divideontimes }\ge {\mathcal{J}}_2^{\divideontimes }\ge {\mathcal{J}}_3^{\divideontimes }.$
IFRAAOWA (proposed)	$Sc\left({\mathsf{ȹ}}_1\right)=0.34073,$ $Sc\left({\mathsf{ȹ}}_2\right)=0.2996,$ $Sc\left({\mathsf{ȹ}}_3\right)=0.2788,$ $Sc\left({\mathsf{ȹ}}_4\right)=0.3280,$ $Sc\left({\mathsf{ȹ}}_5\right)=0.3215$	${\mathcal{J}}_1^{\divideontimes }\ge {\mathcal{J}}_4^{\divideontimes }\ge {\mathcal{J}}_5^{\divideontimes }\ge {\mathcal{J}}_2^{\divideontimes }\ge {\mathcal{J}}_3^{\divideontimes }$
IFRAAHA (proposed)	$Sc\left({\mathsf{ȹ}}_1\right)=0.1826,$ $Sc\left({\mathsf{ȹ}}_2\right)=0.1529,$ $Sc\left({\mathsf{ȹ}}_3\right)=0.1472,$ $Sc\left({\mathsf{ȹ}}_4\right)=0.1726,$ $Sc\left({\mathsf{ȹ}}_5\right)=0.1585$	${\mathcal{J}}_1^{\divideontimes }\ge {\mathcal{J}}_4^{\divideontimes }\ge {\mathcal{J}}_5^{\divideontimes }\ge {\mathcal{J}}_2^{\divideontimes }\ge {\mathcal{J}}_3^{\divideontimes }$

.

• From the inspection of the above table, we can see that all existing notions are inaccessible for handling the IFR data, whereas the proposed technique can do so. So, our work is more general.
• Furthermore, note that all results are the same in all IFRAAWA operators, IFRAAOWA operators, and IFRAAHA operators, which show the authenticity and reliability of the introduced work.
• Moreover, we can see that IFWA [19], IFWG [22], IFDWA [23], IFWDG [23], and IFHA [24] operators can handle intuitionistic fuzzy data effectively. However, there are many decision-making situations where we need intuitionistic fuzzy rough data. Our work provides more space for decision-makers to use IFR data according to their situation. Hence, in comparison to all aspects, we can see that established operators are more reliable, and effective, providing assistance to decision-makers.
• Note that IFRSs use a lower and upper approximation in their structure, so there is no chance of data loss, whereas IFS lacks this property. So, IFAAWA [18], IFAAOWA [18], and IFAAHA [18] fail to deal with all information given in Table 3, whereas the proposed aggregation operators can handle this situation. So, the introduced work is more advanced.
• We can see from Table 4 that the idea given by Senapati et al. [20,21] can only deal with interval-valued IFS that use the MG and NMG in the form of intervals that are the subset of [0, 1]. However, the data given in Table 3 consist of IFRNs. So, there is a need to develop such kind of notions that can handle IFR data. So, the proposed operators can handle more complex data and are superior to existing notions.
• From Table 4, we can observe that IFRAAWA operators are more advanced operators than that IFRWA operator established on [34]. This means that when we replace the parameter term $\mathcal{Q}=1$ in the developed operator, then IFRAAWA operators reduce to IFRWA. Consequently, as compared with the Chinram et al. [34] method, our methods are more general.
• The computational complexity of our techniques is less complex than those of the IFRWA [32] operator, IFROWA [32], and IFRHA [32] operator. The suggested solutions then include a parameter that can alter the aggregate value by the actual decision needs and capture numerous already-existing IF aggregation operations. Accordingly, the benefit is that the suggested operators come with a better level of consensus and adaptability.
• The primary advantage of our recommended method over Chinram’s IFRHA operator [34] is that the IFRAAWA operator has the appealing property of monotonically growing for the parameter, allowing decision-makers to select the optimal value on their risk preferences.

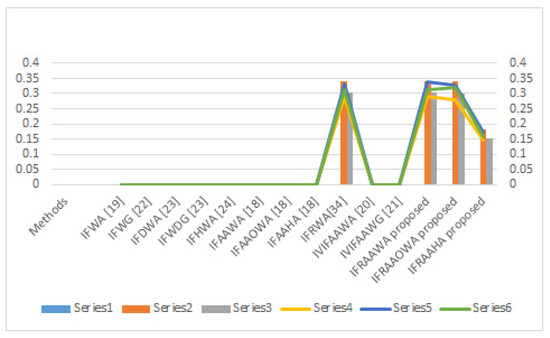
Figure 4 shows the graphical presentation of the comparative analysis given in Table 4.

Note that IFRSs use a lower and upper approximation in their structure so there is no chance of data loss, whereas IFS lacks this property. So, IFAAWA [18], IFAAOWA [18], and IFAAHA [18] fail to deal with all information given in Table 3, while proposed aggregation operators can handle this situation. So, the introduced work is more advanced.

7. Conclusions

Due to advancements in FS structures, researchers have attempted to find out valuable and helpful results from new theories. As the IFRS is more advanced than the intuitionistic fuzzy set, IFRS provides more space for decision-makers. So, based on IFRSs and intuitionistic fuzzy Aczel-Alsina operational laws, here in this paper we have established some fundamental Aczel-Alsina operational laws for IFRNs. Moreover, we have proved the basic properties, as AOs are fruitful tools to convert overall data into a single value. Impressed by this quality of aggregation operators, we have initiated the notions of IFRAA weighted average, IFRAA ordered weighted average, and IFRAA hybrid average aggregation operators. Furthermore, the properties of these AOs have been elaborated. We have initiated an algorithm for introduced work along with a numerical example to show the effective use of these operators in decision-making problems. Furthermore, a comparative analysis of established work shows the authenticity and superiority of the introduced work.

This work is also limited, and it has some gaps; when decision-makers come up with information such as $\left\{\left(0.5, 0.6\right), \left(0.3, 0.8\right)\right\}$, then the basic condition for intuitionistic fuzzy rough set fails to handle this type of data. Here, there is a need for a stronger structure such as a Pythagorean fuzzy rough set to tackle that kind of information. Moreover, if the decision-maker considers the picture fuzzy data that include the abstinence grade, then these introduced notions fail to handle that type of information.

In the future, we can extend these notions to Pythagorean fuzzy soft rough sets, as given in [36,37]. Moreover, this work can be precisely generalized to a stronger structure, as given in [38]. Additionally, we can establish a fuzzy 2D algorithm for the developed approach, as given in [39].