Motion along a Space Curve with a Quasi-Frame in Euclidean 3-Space: Acceleration and Jerk

Abstract

The resolution of the acceleration and jerk vectors of a particle moving on a space curve in the Euclidean 3-space is considered. By applying this resolution and Siacci’s theorem, alternative resolutions of acceleration and jerk vectors are derived based on the quasi-frame. In the osculating plane, the acceleration vector is resolved as the sum of its tangential and radial components. In addition, in the osculating and rectifying planes, the jerk vector is resolved along the tangential direction and two special radial directions. The maximum permissible speed on a space curve at all trajectory points is established via the jerk vector formula. Finally, some examples are presented to illustrate how the results work.

1. Introduction

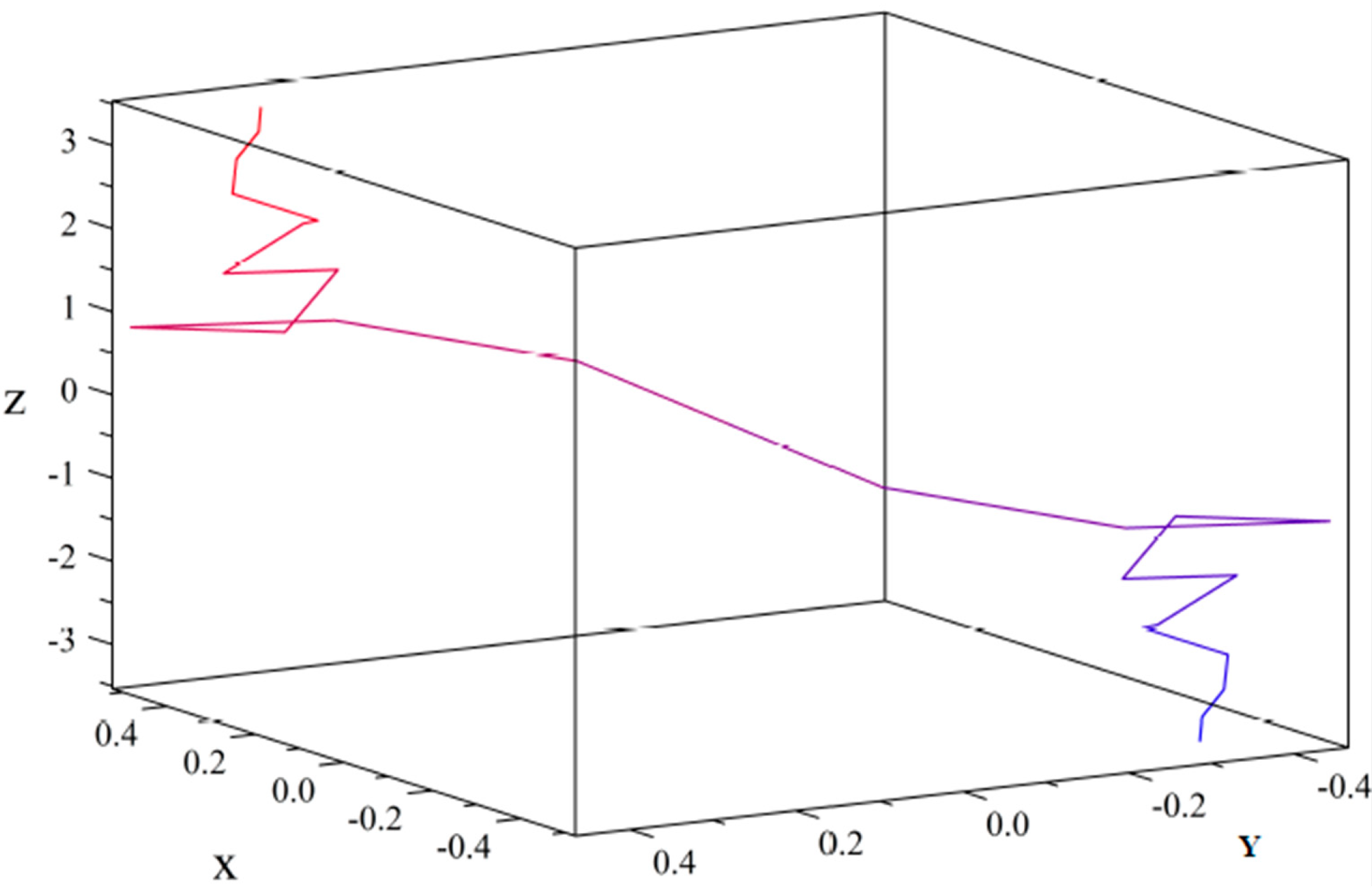
The geometry of motion in a 3-dimensional space has constantly been crucial in terms of understanding physical phenomena. Specifically, the mathematical description of a particle’s motion as a consequence of geometrical analysis is a subject that is required in a wide variety of applications, such as water wave theory, relativity, non-linear optics, sigma models, fluid dynamics, and so on. In Newtonian physics, the force acting on a particle, as defined by the equation $F=m\mathbb{A}$, is proportional to its acceleration $\mathbb{A}$. In certain cases, it is simpler to deal with the acceleration vector when decomposing it into normal and tangential components. However, it is more practical to represent the acceleration vector as the sum of its tangential and radial components when the angular momentum of the particle is constant.

In 1879, for the osculating plane to the curve, Siacci [1] described the acceleration vector as the sum of two particular oblique components. Subsequently in 1944, Whittaker [2] dealt with Siacci’s theorem for the plane and gave a geometrical proof of it. Although Siacci’s formulas are very remarkable, his formulation of the theorem is inaccurate and his proof is burdensome. Therefore, in 2011, Casey [3] used the Serret–Frenet frame to prove Siacci’s theorem in space. Subsequently, in the Finsler manifold ${\mathbf{F}}^3$, in 2012, Küçükarslan et al. [4] investigated Siacci’s theorem for curves. In 2017, Özen et al. [5] investigated Siacci’s theorem for the curves on regular surfaces in $E^3$ according to the Darboux frame. Recently, in 2020, Özen et al. [6] studied Siacci’s theorem for the curves in $E^3$ according to the modified orthogonal frame. In the same year, Özen [7] studied Siacci’s theorem for the curves in Minkowski 3-space by using the Serret–Frenet frame.

In contrast, the jerk vector $\mathbb{J}$ is the time derivative of the acceleration vector. Thus, for a particle with a constant mass, the equality $\mathbb{J}=\left(1/m\right)\left(\mathrm{d}F/\mathrm{d}t\right)$ is satisfied. In the literature, there has been considerable interest in the resolution of the jerk vector for the curves in $E^3$, and several methods and frames for studying the resolution of the jerk vector have been proposed, for example, the Serret–Frenet frame [8,9], the modified orthogonal frame [6], and the Bishop frame [10]. Acceleration varies abruptly when a machinist operates a high-speed train, a stock-car racer races on a track, or a gymnast does gymnastic exercises. Estimating the lower threshold of merely an observable shock and the highest values of the jerk that humans can tolerate without undue discomfort is critical in these situations (see [11]). In addition, in 2017, Tsirlin [12], using the jerk vector formula, gave the maximum permissible speed on a space curve at all trajectory points.

The Serret–Frenet frame is inadequate for studying the space curves in which the curvatures have discrete zero points as, in this case, the principal normal and binormal vectors are discontinuous at points of inflections or along the straight sections of the curve. Therefore, to solve this problem, Dede et al. [13] introduced a new adapted frame along a space curve as an alternative frame to the Serret–Frenet frame and denoted this as the quasi-frame. Numerous studies on the quasi-frame have been discussed; see for example, optical Hasimoto map [14], Berry phase of the linearly polarized light wave along an optical fiber and its electromagnetic curves [15], magnetic flux flows with Heisenberg ferromagnetic spin [16], and evolution of the ruled surfaces [17].

Motivated by these papers, we consider a particle moving on a space curve according to a quasi-frame in the Euclidean 3-space under the influence of arbitrary forces.

The paper is organized as follows: In Section 2, we present some basic definitions concerning the Serret–Frenet frame and quasi-frame in the Euclidean 3-spac $E^3$ and the relation between them. In Section 3, we resolve the acceleration vector $\mathbb{A}$ and the jerk vector $\mathbb{J}$ of a particle moving on a space curve according to the quasi basis. Moreover, we give alternative resolutions of acceleration and jerk vectors. In Section 4, we provide informative examples to demonstrate how our results work.

2. Preliminaries

We give some preliminaries in this part that will be used in our later discussion.

The Euclidean space $E^3=\left({\mathbb{R}}^3,⟨·,·⟩\right)$ is a metric space with the standard inner product $⟨·,·⟩$, which given by

$$⟨G,H⟩=g_1{h}_1+g_2{h}_2+g_3{h}_3,$$

for any two vectors $G=\left(g_1,g_2,g_3\right)$ and $H=\left(h_1,h_2,h_3\right)$ in $E^3$. Based on this metric, the norm of a vector $G\in E^3$ is given by $∥G∥=\sqrt{⟨G,G⟩}$. A curve $\zeta =\zeta \left(\ell \right):I\subseteq \mathbb{R}\to E^3$ is a unit speed curve if $∥{\zeta }^{\prime }\left(\ell \right)∥=1$ for all $\ell \in I$. In this case, ℓ is called arc-length parameter of the curve $\zeta \left(\ell \right)$.

Let $\zeta \left(\ell \right)$ be a space curve in $E^3$, parameterized by arc-length ℓ. Denote by $\top \left(\ell \right),\aleph \left(\ell \right)$, $\mathfrak{B}\left(\ell \right)$ the moving Serret–Frenet frame along the unit speed curve $\zeta \left(\ell \right)$, where $\top \left(\ell \right)$, $\aleph \left(\ell \right)$, and $\mathfrak{B}\left(\ell \right)$ are the unit tangent, principal normal, and binormal vectors defined as

$$\top \left(\ell \right)={\zeta }^{\prime }\left(\ell \right),\aleph \left(\ell \right)=\frac{{\zeta }^{\prime \prime }\left(\ell \right)}{∥{\zeta }^{″}\left(\ell \right)∥},\mathfrak{B}\left(\ell \right)=\top \left(\ell \right)\times \aleph \left(\ell \right),$$

(1)

respectively. In contrast, the Serret–Frenet formulas are defined by

$$\left[\begin{array}{c}{\top }^{\prime }\left(\ell \right)\\ {\aleph }^{\prime }\left(\ell \right)\\ {\mathfrak{B}}^{\prime }\left(\ell \right)\end{array}\right]=\left[\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right]\left[\begin{array}{c}\top \left(\ell \right)\\ \aleph \left(\ell \right)\\ \mathfrak{B}\left(\ell \right)\end{array}\right],$$

(2)

where $\kappa (\ell )$ is the curvature function and $\tau \left(\ell \right)$ is the torsion function defined as follows: $\kappa =\kappa (\ell )=∥{\top }^{\prime }\left(\ell \right)∥$, $\tau =\tau \left(\ell \right)=-⟨{\mathfrak{B}}^{\prime }\left(\ell \right),\aleph \left(\ell \right)⟩$, Ref. [18].

Now, as an alternative to the Serret–Frenet frame, which is donated by { $\top \left(\ell \right)$, ${\aleph }_q\left(\ell \right)$, ${\mathfrak{B}}_q\left(\ell \right)$, $\varrho$}, the quasi-frame (or simply q -frame) along a space curve $\zeta \left(\ell \right)$, where $\top \left(\ell \right)$, ${\aleph }_q\left(\ell \right)$, ${\mathfrak{B}}_q\left(\ell \right)$, and $\varrho$ are the unit tangent, quasi-normal, quasi-binormal, and projection vectors, respectively, and they are defined as follows:

$$\top \left(\ell \right)={\zeta }^{\prime }\left(\ell \right),{\aleph }_q\left(\ell \right)=\frac{\top \times \varrho }{∥\top \times \varrho ∥},{\mathfrak{B}}_q\left(\ell \right)=\top \times {\aleph }_q,$$

(3)

where $\varrho$ is the projection vector and can be chosen as $\varrho =\left(1,0,0\right)$ or $\varrho =\left(0,1,0\right)$ or $\varrho =\left(0,0,1\right)$. For simplicity, we choose the projection vector $\varrho =\left(1,0,0\right)$ in this paper. However, the q-frame is singular in all cases where ⊤ and $\varrho$ are parallel. Thus, in those cases where ⊤ and $\varrho$ are parallel, the projection vector $\varrho$ can be chosen as $\varrho =\left(0,1,0\right)$ or $\varrho =\left(0,0,1\right)$. We can define the Euclidean angle $\theta$ between the principal normal ℵ and quasi-normal ${\aleph }_q$ vectors. Then, the relation between the q-frame and the classical Serret–Frenet frame is given as follows:

$$\left[\begin{array}{c}\top \left(\ell \right)\\ {\aleph }_q\left(\ell \right)\\ {\mathfrak{B}}_q\left(\ell \right)\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & sin\theta \\ 0& -sin\theta & cos\theta \end{array}\right]\left[\begin{array}{c}\top \left(\ell \right)\\ \aleph \left(\ell \right)\\ \mathfrak{B}\left(\ell \right)\end{array}\right].$$

(4)

Thus, we have

$$\left[\begin{array}{c}\top \left(\ell \right)\\ \aleph \left(\ell \right)\\ \mathfrak{B}\left(\ell \right)\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{array}\right]\left[\begin{array}{c}\top \left(\ell \right)\\ {\aleph }_q\left(\ell \right)\\ {\mathfrak{B}}_q\left(\ell \right)\end{array}\right].$$

(5)

By taking the derivative of (4) with respect to ℓ, then substituting (2) and (5) into the results, we obtain the variation equations of the q-frame in the following form:

$$\left[\begin{array}{c}{\top }^{\prime }\left(\ell \right)\\ {\aleph }_q^{\prime }\left(\ell \right)\\ {\mathfrak{B}}_q^{\prime }\left(\ell \right)\end{array}\right]=\left[\begin{array}{ccc}0& {\kappa }_1& {\kappa }_2\\ -{\kappa }_1& 0& {\kappa }_3\\ -{\kappa }_2& -{\kappa }_3& 0\end{array}\right]\left[\begin{array}{c}\top \left(\ell \right)\\ {\aleph }_q\left(\ell \right)\\ {\mathfrak{B}}_q\left(\ell \right)\end{array}\right],$$

(6)

where

$$\begin{array}{ccc}\hfill {\kappa }_1\left(\ell \right)& =& \kappa \left(\ell \right)cos\theta ,{\kappa }^2\left(\ell \right)={\kappa }_1^2\left(\ell \right)+{\kappa }_2^2\left(\ell \right),\hfill \\ \hfill {\kappa }_2\left(\ell \right)& =& -\kappa \left(\ell \right)sin\theta ,\theta =-arctan\left(\frac{{\kappa }_2}{{\kappa }_1}\right),\hfill \\ \hfill {\kappa }_3\left(\ell \right)& =& {\theta }^{\prime }\left(\ell \right)+\tau \left(\ell \right),\hfill \end{array}$$

(7)

The triple $\left({\kappa }_1,{\kappa }_2,{\kappa }_3\right)$ is called the quasi-curvature functions of $\zeta \left(\ell \right)$, Ref. [13].

Example 1.

Assume that a particle $\mathbb{P}$ moves along a helical curve over a clothoid (Cornu spiral or Euler spiral) [19] in $E^3$, and the position vector of $\mathbb{P}$ in Cartesian coordinates is expressed as

$$\mathcal{X}=\left(\frac{1}{\sqrt{2}}{\int }_0^{t}cos\left(\frac{\pi u^2}{2}\right)\mathrm{d}u,\frac{1}{\sqrt{2}}{\int }_0^{t}sin\left(\frac{\pi u^2}{2}\right)\mathrm{d}u,\frac{t}{\sqrt{2}}\right),$$

(8)

where ${\int }_0^{t}cos\left(\frac{\pi u^2}{2}\right)\mathrm{d}u$ and ${\int }_0^{t}sin\left(\frac{\pi u^2}{2}\right)\mathrm{d}u$ are called Fresnel integrals. Recently, this curve has had many applications in real life, for example, the highway, railway route design, or roller coasters, etc. Thus, we can determine the velocity, acceleration, and jerk vectors as

$$\begin{array}{c}\hfill \mathbb{V}=\left(\frac{1}{\sqrt{2}}cos\left(\frac{\pi t^2}{2}\right),\frac{1}{\sqrt{2}}sin\left(\frac{\pi t^2}{2}\right),\frac{1}{\sqrt{2}}\right),\\ \hfill a=\left(\frac{-\pi t}{\sqrt{2}}sin\left(\frac{\pi t^2}{2}\right),\frac{\pi t}{\sqrt{2}}cos\left(\frac{\pi t^2}{2}\right),0\right),\\ \hfill \mathbb{J}=\left(\frac{-{\pi }^2{t}^2}{\sqrt{2}}cos\left(\frac{\pi t^2}{2}\right)-\frac{\pi }{\sqrt{2}}sin\left(\frac{\pi t^2}{2}\right),\frac{-{\pi }^2{t}^2}{\sqrt{2}}sin\left(\frac{\pi t^2}{2}\right)+\frac{\pi }{\sqrt{2}}cos\left(\frac{\pi t^2}{2}\right),0\right).\end{array}$$

(9)

From (9), we can write the following equalities:

$$\mathrm{d}x=\frac{1}{\sqrt{2}}cos\left(\frac{\pi t^2}{2}\right)\mathrm{d}t,\mathrm{d}y=\frac{1}{\sqrt{2}}sin\left(\frac{\pi t^2}{2}\right)\mathrm{d}t,\mathrm{d}z=\frac{1}{\sqrt{2}}\mathrm{d}t.$$

Using ${\left(\mathrm{d}\ell \right)}^2={\left(\mathrm{d}x\right)}^2+{\left(\mathrm{d}y\right)}^2+{\left(\mathrm{d}z\right)}^2$, we obtain

$$\frac{\mathrm{d}\ell }{\mathrm{d}t}=1,\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}=0,\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}=0.$$

Therefore, the arc-length $\ell =\ell \left(t\right)=t$ can be used to parameterize the oriented curve traced out by the particle $\mathbb{P}$ as

$$\delta \left(\ell \right)=\left(\frac{1}{\sqrt{2}}{\int }_0^{\ell }cos\left(\frac{\pi u^2}{2}\right)\mathrm{d}u,\frac{1}{\sqrt{2}}{\int }_0^{\ell }sin\left(\frac{\pi u^2}{2}\right)\mathrm{d}u,\frac{\ell }{\sqrt{2}}\right).$$

(10)

Then, from (1) we can obtain the Serret–Frenet frame as:

$$\top =\left(\frac{1}{\sqrt{2}}cos\left(\frac{\pi {\ell }^2}{2}\right),\frac{1}{\sqrt{2}}sin\left(\frac{\pi {\ell }^2}{2}\right),\frac{1}{\sqrt{2}}\right),$$

$$\aleph =\left(\frac{-\ell }{\left|\ell \right|}sin\left(\frac{\pi {\ell }^2}{2}\right),\frac{\ell }{\left|\ell \right|}cos\left(\frac{\pi {\ell }^2}{2}\right),0\right),$$

and

$$\mathfrak{B}=\left(\frac{-\ell }{\sqrt{2}\left|\ell \right|}cos\left(\frac{\pi {\ell }^2}{2}\right),\frac{-\ell }{\sqrt{2}\left|\ell \right|}sin\left(\frac{\pi {\ell }^2}{2}\right),\frac{\ell }{\sqrt{2}\left|\ell \right|}\right)$$

and the curvature and the torsion as $\kappa =\pi \left|\ell \right|/\sqrt{2}$. Thus, we note that the Serret–Frenet frame is inadequate for studying the space curves whose curvatures have discrete zero points because, as we have shown, the principal normal and binormal vectors are discontinuous at $\ell =0$, and the curvature is not differentiable as well. Furthermore, the curve forms a symmetrical double spiral.

Therefore, to solve this problem and prevent the occurrence of two reverse oriented principal normal and binormal vectors, we use the q-frame as an alternative frame to the Serret–Frenet frame (Figure 1). If we consider (3) and choose the projection vector $\varrho =\left(0,0,1\right)$, we get the following q-frame:

$$\top =\left(\frac{1}{\sqrt{2}}cos\left(\frac{\pi {\ell }^2}{2}\right),\frac{1}{\sqrt{2}}sin\left(\frac{\pi {\ell }^2}{2}\right),\frac{1}{\sqrt{2}}\right),$$

$${\aleph }_q=\left(\frac{1}{\sqrt{2}}sin\left(\frac{\pi {\ell }^2}{2}\right),\frac{-1}{\sqrt{2}}cos\left(\frac{\pi {\ell }^2}{2}\right),0\right),$$

$${\mathfrak{B}}_q=\left(\frac{1}{2}cos\left(\frac{\pi {\ell }^2}{2}\right),\frac{1}{2}sin\left(\frac{\pi {\ell }^2}{2}\right),\frac{-1}{2}\right).$$

Figure 1. Helical curve over clothoid.

3. Main Results

In this section, we obtain a new resolution of the acceleration and jerk vectors for a particle via the q-frame. Thereafter, in the osculating plane, we give alternative resolutions of the acceleration vector along the radial direction and tangential direction. In addition, in the osculating and rectifying planes, the jerk vector is resolved along the tangential direction and two special radial directions.

Theorem 1.

Assume that the particle $\mathbb{P}$ with mass m moves along an analytic space curve $\zeta =\zeta \left(\ell \right)$ with the q-frame. Then the acceleration vector $\mathbb{A}$ and the jerk $\mathbb{J}$ vector of $\mathbb{P}$ at time t with a q-frame can be expressed as

$$\mathbb{A}=\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\top +\sqrt{{\kappa }_1^2\left(\ell \right)+{\kappa }_2^2\left(\ell \right)}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^{2}cos\theta {\aleph }_q-\sqrt{{\kappa }_1^2\left(\ell \right)+{\kappa }_2^2\left(\ell \right)}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^{2}sin\theta {\mathfrak{B}}_q,$$

(11)

and

$$\mathbb{J}=\frac{\mathrm{d}\mathbb{A}}{\mathrm{d}t}=C_{\top }\top +C_{{\aleph }_q}{\aleph }_q+C_{{\mathfrak{B}}_q}{\mathfrak{B}}_q,$$

(12)

where

$$C_{\top }=\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}-\left({\kappa }_1^2+{\kappa }_2^2\right){\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3,$$

$$\begin{array}{ccc}\hfill C_{{\aleph }_q}& =& cos\theta \left[3\sqrt{{\kappa }_1^2+{\kappa }_2^2}\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right)+{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]\hfill \\ & & +sin\theta \left[\left({\kappa }_3-{\theta }^{\prime }\right)\sqrt{{\kappa }_1^2+{\kappa }_2^2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\right],\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill C_{{\mathfrak{B}}_q}& =& -sin\theta \left[3\sqrt{{\kappa }_1^2+{\kappa }_2^2}\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right)+{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]\hfill \\ & & +cos\theta \left[\left({\kappa }_3-{\theta }^{\prime }\right)\sqrt{{\kappa }_1^2+{\kappa }_2^2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\right].\hfill \end{array}$$

Proof. 

According to a q-frame, let a particle $\mathbb{P}$ with mass $m>0$ move on a space curve in Euclidean space $E^3$ under the effect of arbitrary forces. Let $\mathcal{X}$ be the position vector of $\mathbb{P}$ at time t with an arbitrary fixed origin O in the space $E^3$. Let $\zeta$ parametrized by the arc-length ℓ described at time t be the oriented curve traced out by $\mathbb{P}$. Therefore, the unit tangent vector for the curve $\zeta$ is given as

$$\top =\frac{\mathrm{d}\mathcal{X}}{\mathrm{d}\ell }.$$

(13)

Then, from (6), (7), and (13), we deduce the velocity $\mathbb{V}$, the acceleration vector $\mathbb{A}$, and the jerk $\mathbb{J}$ vector of $\mathbb{P}$ at time t with q-frame as

$$\begin{array}{c}\hfill \mathbb{V}=\frac{\mathrm{d}\mathcal{X}}{\mathrm{d}t}=\frac{\mathrm{d}\ell }{\mathrm{d}t}\top ,\\ \hfill \mathbb{A}=\frac{\mathrm{d}\mathbb{V}}{\mathrm{d}t}=\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\top +{\kappa }_1{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^2{\aleph }_q+{\kappa }_2{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^2{\mathfrak{B}}_q,\end{array}$$

(14)

or

$$\mathbb{A}=\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\top +\sqrt{{\kappa }_1^2\left(\ell \right)+{\kappa }_2^2\left(\ell \right)}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^{2}cos\theta {\aleph }_q-\sqrt{{\kappa }_1^2\left(\ell \right)+{\kappa }_2^2\left(\ell \right)}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^{2}sin\theta {\mathfrak{B}}_q,$$

and

$$\mathbb{J}=\frac{\mathrm{d}\mathbb{A}}{\mathrm{d}t},$$

which implies that (11) and (12) hold. The proof is complete. □

Theorem 2.

(Siacci’s Theorem according to Quasi-Frame). Assume that the particle $\mathbb{P}$ with mass m moves along an analytic space curve $\zeta =\zeta \left(\ell \right)$ with the q-frame. Suppose that the component of its angular momentum, which is along the vector $\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right)$, never vanishes. Then, the acceleration vector $\mathbb{A}$ of $\mathbb{P}$ can be expressed as

$$\begin{array}{ccc}\hfill \mathbb{A}& =& \left(\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}+\frac{{\lambda }_1\sqrt{{\kappa }_1^2+{\kappa }_2^2}}{{\lambda }_2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^2\right)\top +\left(\frac{-n\sqrt{{\kappa }_1^2+{\kappa }_2^2}}{{\lambda }_2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^2\right){\mathbf{e}}_{\mathbf{n}}\hfill \\ & =& A_t\top +A_n{\mathbf{e}}_{\mathbf{n}},\hfill \end{array}$$

(15)

where $A_t$ lies along the tangent line of ζ, whereas $A_n$ is directed from the particle $\mathbb{P}$ to the foot of the perpendicular, that is, from the origin to osculating plane to ζ at $\mathbb{P}$.

Proof. 

The acceleration and jerk vectors in (11) and (12) can be expressed as follows:

$$\mathbb{A}=\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\top +\sqrt{{\kappa }_1^2+{\kappa }_2^2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^2\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right),$$

(16)

and

$$\begin{array}{ccc}& & \mathbb{J}=\left[\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}-\left({\kappa }_1^2+{\kappa }_2^2\right){\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\right]\top \hfill \\ & & +\left[3\sqrt{{\kappa }_1^2+{\kappa }_2^2}\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right)+{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)\hfill \\ & & +\left[\left({\kappa }_3-{\theta }^{\prime }\right)\sqrt{{\kappa }_1^2+{\kappa }_2^2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\right]\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right).\hfill \end{array}$$

(17)

We can observe that, because $\left\{\top ,{\aleph }_q,{\mathfrak{B}}_q\right\}$ is a right-handed orthonormal basis, the vectors $\left\{\top ,\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right),\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right)\right\}$ form a right-handed orthonormal system. Let a particle $\mathbb{P}$ move on a space curve $\zeta =\zeta \left(\ell \right)$. As a result, according to the q-frame, $\mathbb{P}$ has a position vector. Assume that the position vector of $\mathbb{P}$ be resolved as follows:

$$\mathcal{X}={\lambda }_1\top -{\lambda }_2\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)+{\lambda }_3\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right),$$

(18)

where

$${\lambda }_1=⟨\mathcal{X},\top ⟩,-{\lambda }_2=⟨\mathcal{X},\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)⟩,{\lambda }_3=⟨\mathcal{X},\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right)⟩.$$

(19)

Denote by $\mathbf{n}$ and ${\mathbf{n}}^{*}$ the vectors

$$\mathbf{n}={\lambda }_1\top -{\lambda }_2\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right),{\mathbf{n}}^{*}={\lambda }_1\top +{\lambda }_3\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right),$$

(20)

which lie in the osculating plane and rectifying plane to $\mathcal{C}$ at $\mathbb{P}$, respectively. Then, we have

$$n^2=⟨\mathbf{n},\mathbf{n}⟩={\lambda }_1^2+{\lambda }_2^2,{\left(n^{*}\right)}^2=⟨{\mathbf{n}}^{*},{\mathbf{n}}^{*}⟩={\lambda }_1^2+{\lambda }_3^2,$$

(21)

where n and $n^{*}$ are the lengths of the vectors $\mathbf{n}$ and ${\mathbf{n}}^{*}$, respectively. It is well known that the angular momentum vector ${\mathbf{L}}^O$ of $\mathbb{P}$ about O is given by

$${\mathbf{L}}^O=\mathcal{X}\times m\mathbb{V}.$$

Thus, from (14) and (18), we have

$${\mathbf{L}}^O=m{\lambda }_3\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)+m{\lambda }_2\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right).$$

(22)

Now we aim to resolve the acceleration vector $\mathbb{A}$ in (11) along the radial direction and tangential direction in the osculating plane, as well as the jerk vector $\mathbb{J}$ in (12) along the tangential direction, radial direction in the osculating plane, and radial direction in the rectifying plane. Let us begin by expressing the vector $\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)$ in terms of $\mathbf{n}$ and ⊤. Considering (20), we can deduce that this is possible if and only if ${\lambda }_2\ne 0$. We can assure that ${\lambda }_2$ is nonzero by assuming the physical condition that the angular momentum component along the vector $\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right)$ never vanishes. Second, let us represent the vector $\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right)$ in terms of ${\mathbf{n}}^{*}$ and ⊤. Considering (20), this is possible if and only if ${\lambda }_3\ne 0$. We can assure that ${\lambda }_3$ is nonzero by assuming the second physical condition that the angular momentum component along the vector $\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)$ never vanishes. Thus, we obtain the following equations:

$$cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q=\frac{1}{{\lambda }_2}\left(-\mathbf{n}+{\lambda }_1\top \right),sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q=\frac{1}{{\lambda }_3}\left({\mathbf{n}}^{*}-{\lambda }_1\top \right).$$

(23)

Hence, in view of (21), $n\ne 0$ and $n^{*}\ne 0$. Therefore, we can define the unit vectors ${\mathbf{e}}_{\mathbf{n}}$ and ${\mathbf{e}}_{{\mathbf{n}}^{*}}$ as:

$${\mathbf{e}}_{\mathbf{n}}=\frac{1}{n}\mathbf{n},{\mathbf{e}}_{{\mathbf{n}}^{*}}=\frac{1}{n^{*}}{\mathbf{n}}^{*}.$$

(24)

From (23) and (24), we get

$$cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q=\frac{1}{{\lambda }_2}\left(-n{\mathbf{e}}_{\mathbf{n}}+{\lambda }_1\top \right),sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q=\frac{1}{{\lambda }_3}\left(n^{*}{\mathbf{e}}_{{\mathbf{n}}^{*}}-{\lambda }_1\top \right).$$

(25)

Substituting (25) into (16) and (17), we can obtain the acceleration vector $\mathbb{A}$ as in (15). The proof is complete. □

With the help of Theorem 2 and substituting (25) into (17), we can state the following theorem.

Theorem 3.

Assume that the particle $\mathbb{P}$ with mass m moves along an analytic space curve $\zeta =\zeta \left(\ell \right)$ with the q-frame. Suppose that the component of its angular momentum never vanishes. Then, the jerk $\mathbb{J}$ of $\mathbb{P}$ can be expressed as

$$\begin{array}{ccc}\hfill \mathbb{J}& =& \left[\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}-\left({\kappa }_1^2+{\kappa }_2^2\right){\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3+3\sqrt{{\kappa }_1^2+{\kappa }_2^2}\frac{{\lambda }_1}{{\lambda }_2}\frac{\mathrm{d}\ell }{\mathrm{d}t}\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right.\hfill \\ & & \left.+\frac{{\lambda }_1}{{\lambda }_2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)-\frac{{\lambda }_1\left({\kappa }_3-{\theta }^{\prime }\right)}{{\lambda }_3}\sqrt{{\kappa }_1^2+{\kappa }_2^2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\right]\top \hfill \\ & & +\left[-\frac{3n}{{\lambda }_2}\sqrt{{\kappa }_1^2+{\kappa }_2^2}\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right)-\frac{n}{{\lambda }_2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]{\mathbf{e}}_{\mathbf{n}}\hfill \\ & & +\left[\frac{n^{*}\left({\kappa }_3-{\theta }^{\prime }\right)}{{\lambda }_3}\sqrt{{\kappa }_1^2+{\kappa }_2^2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\right]{\mathbf{e}}_{{\mathbf{n}}^{*}}.\hfill \\ & =& J_t\top +J_n{\mathbf{e}}_{\mathbf{n}}+J_{n^{*}}{\mathbf{e}}_{{\mathbf{n}}^{*}},\hfill \end{array}$$

(26)

where $J_t$ is the component that lies on the tangent line of ζ, whereas $J_n$ is the component that lies on the line passing through the particle $\mathbb{P}$ towards the foot of the perpendicular, that is, from the origin to osculating plane to ζ at $\mathbb{P}$, and $J_{n^{*}}$ is the component that lies on the line passing through the particle $\mathbb{P}$ towards the foot of the perpendicular, that is, from the origin to rectifying plane to ζ at $\mathbb{P}$.

Remark 1.

We note that if ${\kappa }_3=0$, then the q-frame $\left\{\top \left(\ell \right),{\aleph }_q\left(\ell \right),{\mathfrak{B}}_q\left(\ell \right)\right\}$ becomes the Bishop frame. In this case, Theorem 3 reduces to Theorem 1 in [10].

Corollary 1.

Assume that the particle $\mathbb{P}$ moves along an analytic space curve with the q-frame and lies in the osculating plane, which does not contain the origin of space, in Euclidean 3-space. Suppose that the component of its angular momentum never vanishes along the normal vector of this plane. Then, the jerk vector becomes

$$\begin{array}{ccc}\hfill \mathbb{J}& =& \left[\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}-\left({\kappa }_1^2+{\kappa }_2^2\right){\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3+3\sqrt{{\kappa }_1^2+{\kappa }_2^2}\frac{{\lambda }_1}{{\lambda }_2}\frac{\mathrm{d}\ell }{\mathrm{d}t}\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right.\hfill \\ & & \left.+\frac{{\lambda }_1}{{\lambda }_2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]\top \hfill \\ & & +\left[-\frac{3n}{{\lambda }_2}\sqrt{{\kappa }_1^2+{\kappa }_2^2}\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)\left(\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}\right)-\frac{n}{{\lambda }_2}{\left(\frac{\mathrm{d}\ell }{\mathrm{d}t}\right)}^3\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]{\mathbf{e}}_{\mathbf{n}}.\hfill \end{array}$$

Proof. 

Consider ${\kappa }_3-{\theta }^{\prime }=\tau$ in Theorem 3, and set $\tau =0$ for the planar case to complete the proof directly. □

Corollary 2.

Assume that the particle $\mathbb{P}$ moves with a uniform motion with a speed ≫ along an analytic space curve with the q-frame in Euclidean 3-space such that the jerk satisfies the condition $∥\mathbb{J}∥\le j_{max}$. Then the maximum speed admissible on the curve at all trajectory points must satisfy

$$\gg \le \frac{\sqrt[3]{j_{max}}}{\sqrt[6]{max\Phi \left(\ell \right)}},$$

where

$$\Phi \left(\ell \right)={\Phi }_1^2+{\Phi }_2^2+{\Phi }_3^2+\frac{2{\lambda }_1}{n}{\Phi }_1{\Phi }_2+\frac{2{\lambda }_1}{n^{*}}{\Phi }_1{\Phi }_3+\frac{2{\lambda }_1^2}{n{n}^{*}}{\Phi }_2{\Phi }_3,$$

and

$${\Phi }_1\left(\ell \right)=\left[\frac{{\lambda }_1}{{\lambda }_2}\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)-\left({\kappa }_1^2+{\kappa }_2^2\right)-\frac{{\lambda }_1\left({\kappa }_3-{\theta }^{\prime }\right)}{{\lambda }_3}\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right],$$

$${\Phi }_2\left(\ell \right)=-\frac{n}{{\lambda }_2}\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right),$$

$${\Phi }_3\left(\ell \right)=\frac{n^{*}\left({\kappa }_3-{\theta }^{\prime }\right)}{{\lambda }_3}\sqrt{{\kappa }_1^2+{\kappa }_2^2}.$$

Proof. 

In the case of uniform motion, let the particle $\mathbb{P}$ move along a curve with a uniform motion with $\mathrm{d}\ell /\mathrm{d}t=\gg$, ${\mathrm{d}}^2\ell /\mathrm{d}{t}^2=0$, and ${\mathrm{d}}^3\ell /\mathrm{d}{t}^3=0$. Thus, from Theorem 3, we get

$$\begin{array}{ccc}\hfill J_t& =& \left[\frac{{\lambda }_1}{{\lambda }_2}\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)-\left({\kappa }_1^2+{\kappa }_2^2\right)-\frac{{\lambda }_1\left({\kappa }_3-{\theta }^{\prime }\right)}{{\lambda }_3}\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right]{\gg }^3\hfill \\ & =& {\Phi }_1\left(\ell \right){\gg }^3,\hfill \end{array}$$

$$J_n=-\left[\frac{n}{{\lambda }_2}\frac{\mathrm{d}}{\mathrm{d}\ell }\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)\right]{\gg }^3={\Phi }_2\left(\ell \right){\gg }^3,$$

and

$$J_{n^{*}}=\left[\frac{n^{*}\left({\kappa }_3-{\theta }^{\prime }\right)}{{\lambda }_3}\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right]{\gg }^3={\Phi }_3\left(\ell \right){\gg }^3.$$

Then

$$\begin{array}{ccc}\hfill ∥\mathbb{J}∥& =& {\gg }^3\sqrt{{\Phi }_1^2+{\Phi }_2^2+{\Phi }_3^2+\frac{2{\lambda }_1}{n}{\Phi }_1{\Phi }_2+\frac{2{\lambda }_1}{n^{*}}{\Phi }_1{\Phi }_3+\frac{2{\lambda }_1^2}{n{n}^{*}}{\Phi }_2{\Phi }_3}\hfill \\ & =& {\gg }^3\sqrt{\Phi },\hfill \end{array}$$

which implies that

$$\gg \le \frac{\sqrt[3]{j_{max}}}{\sqrt[6]{max\Phi \left(\ell \right)}}.$$

The proof is complete. □

4. Applications

In this section, we present applications of the results derived to calculate the components of acceleration and jerk vectors with respect to a q-frame by applying Theorems 1–3 and Corollaries 1 and 2.

Example 2.

Consider a particle $\mathbb{P}$ moves along a right-handed circular helix lying on a clylinder, which has a radius a, and the angular frequency Ω of $\mathbb{P}$ is not time dependent. Then, the position vector of $\mathbb{P}$ in Cartesian coordinates is given by

$$\mathcal{X}=\left(acos\left(\Omega t\right),asin\left(\Omega t\right),bt\right),$$

(27)

where t is the time and a, b are positive constants. Let the helix axis be the z-axis, and φ be the helix angle satisfying $tan\phi =\frac{a\Omega }{b}$. The velocity, acceleration, and jerk vectors can be obtained as

$$\mathbb{V}=\left(-a\Omega sin\left(\Omega t\right),a\Omega cos\left(\Omega t\right),b\right),$$

$$\mathbb{A}=\left(-a{\Omega }^{2}cos\left(\Omega t\right),-a{\Omega }^{2}sin\left(\Omega t\right),0\right),$$

and

$$\mathbb{J}=\left(a{\Omega }^{3}sin\left(\Omega t\right),-a{\Omega }^{3}cos\left(\Omega t\right),0\right).$$

From (27), we have

$$\mathrm{d}x=-a\Omega sin\left(\Omega t\right)\mathrm{d}t,\mathrm{d}y=a\Omega cos\left(\Omega t\right)\mathrm{d}t,\mathrm{d}z=b\mathrm{d}t.$$

Using ${\left(\mathrm{d}\ell \right)}^2={\left(\mathrm{d}x\right)}^2+{\left(\mathrm{d}y\right)}^2+{\left(\mathrm{d}z\right)}^2$, the speed ≫ of the particle $\mathbb{P}$, and its first and second derivatives can be given by

$$\gg =\frac{\mathrm{d}\ell }{\mathrm{d}t}=\sqrt{a^2{\Omega }^2+b^2},\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}=0,\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}=0.$$

We see that the arc-length $\ell =\ell \left(t\right)=\gg t$ can be used to parameterize the oriented curve traced out by the particle $\mathbb{P}$ as

$$\zeta \left(\ell \right)=\left(acos\left(\frac{\Omega \ell }{\gg }\right),asin\left(\frac{\Omega \ell }{\gg }\right),\frac{b\ell }{\gg }\right).$$

(28)

Then, from (1) and (28), we can obtain the Serret–Frenet frame as follows:

$$\top =\left(-sin\phi sin\left(\frac{\Omega \ell }{\gg }\right),sin\phi cos\left(\frac{\Omega \ell }{\gg }\right),cos\phi \right),$$

$$\aleph =\left(-cos\left(\frac{\Omega \ell }{\gg }\right),-sin\left(\frac{\Omega \ell }{\gg }\right),0\right),$$

and

$$\mathfrak{B}=\left(cos\phi sin\left(\frac{\Omega \ell }{\gg }\right),-cos\phi cos\left(\frac{\Omega \ell }{\gg }\right),sin\phi \right).$$

In addition, we can get the curvature and the torsion as

$$\kappa =\frac{a{\Omega }^2}{{\gg }^2},\tau =\frac{b\Omega }{{\gg }^2}.$$

From (7), we obtain

$${\kappa }_1=\frac{a{\Omega }^2}{{\gg }^2}cos\theta ,{\kappa }_2=-\frac{a{\Omega }^2}{{\gg }^2}sin\theta ,$$

and

$${\kappa }_3={\theta }^{\prime }\left(\ell \right)+\frac{b\Omega }{{\gg }^2},\theta =-arctan\left(\frac{{\kappa }_2}{{\kappa }_1}\right).$$

Considering (4), we get the following q-frame:

$$\top =\left(-sin\phi sin\left(\frac{\Omega \ell }{\gg }\right),sin\phi cos\left(\frac{\Omega \ell }{\gg }\right),cos\phi \right),$$

$$\begin{array}{ccc}\hfill {\aleph }_q& =& \left(-cos\theta cos\left(\frac{\Omega \ell }{\gg }\right)+sin\theta cos\phi sin\left(\frac{\Omega \ell }{\gg }\right),\right.\hfill \\ & & -cos\theta sin\left(\frac{\Omega \ell }{\gg }\right)-sin\theta cos\phi cos\left(\frac{\Omega \ell }{\gg }\right),\hfill \\ \hfill & & \left.sin\theta sin\phi \right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\mathfrak{B}}_q& =& \left(sin\theta cos\left(\frac{\Omega \ell }{\gg }\right)+cos\theta cos\phi sin\left(\frac{\Omega \ell }{\gg }\right),\right.\hfill \\ & & sin\theta sin\left(\frac{\Omega \ell }{\gg }\right)-cos\theta cos\phi cos\left(\frac{\Omega \ell }{\gg }\right),\hfill \\ & & \left.cos\theta sin\phi \right).\hfill \end{array}$$

Therefore, by applying Theorem 1, we get the acceleration and jerk vectors with the q-frame as follows:

$$\mathbb{A}=a{\Omega }^2\left(cos\theta {\aleph }_q-sin\theta \right){\mathfrak{B}}_q,$$

and

$$\mathbb{J}=\frac{\mathrm{d}\mathbb{A}}{\mathrm{d}t}=-\left(\frac{a^2{\Omega }^4}{\gg }\right)\top +\left(\frac{ab{\Omega }^3}{\gg }\right)sin\theta {\aleph }_q+\left(\frac{ab{\Omega }^3}{\gg }\right)cos\theta {\mathfrak{B}}_q.$$

By considering (19) and (28), we have

$${\lambda }_1=\frac{b\ell }{\gg }cos\phi ,{\lambda }_2=a,{\lambda }_3=\frac{b\ell }{\gg }sin\phi .$$

(29)

In addition, from (18) and (28), we have

$$\begin{array}{ccc}\hfill \zeta \left(\ell \right)& =& \left(\frac{b\ell }{\gg }cos\phi \right)\top -a\left(cos\theta {\aleph }_q-sin\theta {\mathfrak{B}}_q\right)+\left(\frac{b\ell }{\gg }sin\phi \right)\left(sin\theta {\aleph }_q+cos\theta {\mathfrak{B}}_q\right)\hfill \\ & =& \left(\frac{b\ell }{\gg }cos\phi \right)\top -\left(acos\theta -\frac{b\ell }{\gg }sin\phi sin\theta \right){\aleph }_q+\left(asin\theta +\frac{b\ell }{\gg }sin\phi cos\theta \right){\mathfrak{B}}_q.\hfill \end{array}$$

From (21) and (29), we obtain

$$n=\sqrt{{\left(\frac{b\ell }{\gg }\right)}^2{cos}^2\phi +a^2},n^{*}=\frac{b\ell }{\gg }.$$

Therefore, by applying Theorems 1, 2, and 3, we get an alternative resolution of the components of the acceleration and jerk vectors as follows:

$$A_t=\frac{{\Omega }^2{b}^2\ell }{a^2{\Omega }^2+b^2},A_n=-{\Omega }^2\sqrt{\frac{b^4{\ell }^2}{{\left(a^2{\Omega }^2+b^2\right)}^2}+a^2},$$

and

$$J_t=-{\Omega }^2\sqrt{a^2{\Omega }^2+b^2},J_n=0,J_{n^{*}}=b{\Omega }^2.$$

Furthermore, by applying Corollary 2, if the jerk satisfies the condition $∥\mathbb{J}∥\le j_{max}$, we can calculate the maximum permissible speed on a circular helix at all trajectory points as follows:

$${\Phi }_1\left(\ell \right)=\frac{-{\Omega }^2}{a^2{\Omega }^2+b^2},{\Phi }_2\left(\ell \right)=0,{\Phi }_3\left(\ell \right)=\frac{b{\Omega }^2}{{\left(a^2{\Omega }^2+b^2\right)}^{3/2}}.$$

Then

$$\Phi \left(\ell \right)=\frac{a^2{\Omega }^6}{{\left(a^2{\Omega }^2+b^2\right)}^3},$$

which implies that

$$∥\mathbb{J}∥=a{\Omega }^3,$$

and

$$\gg \le \frac{\sqrt[3]{j_{max}}}{\sqrt[6]{max\Phi \left(\ell \right)}}.$$

Then

$${\gg }_{max}=\sqrt{a^2{\Omega }^2+b^2}.$$

Example 3.

Let a particle $\mathbb{P}$ move along the logarithmic spiral curve. Then, the position vector of $\mathbb{P}$ in Cartesian coordinates can be expressed as

$$\mathcal{X}=\left(e^{\Omega t}cos\left(\Omega t\right),0,e^{\Omega t}sin\left(\Omega t\right)\right),$$

(30)

where t is the time and Ω the angular frequency. The velocity, acceleration, and jerk vectors can be obtained as

$$\mathbb{V}=\Omega e^{\Omega t}\left(cos\left(\Omega t\right)-sin\left(\Omega t\right),0,sin\left(\Omega t\right)+cos\left(\Omega t\right)\right),$$

$$\mathbb{A}=2{\Omega }^2{e}^{\Omega t}\left(-sin\left(\Omega t\right),0,cos\left(\Omega t\right)\right),$$

and

$$\mathbb{J}=2{\Omega }^3{e}^{\Omega t}\left(-sin\left(\Omega t\right)-cos\left(\Omega t\right),0,cos\left(\Omega t\right)-sin\left(\Omega t\right)\right).$$

From (30), we have

$$\mathrm{d}x=\Omega e^{\Omega t}\left(cos\left(\Omega t\right)-sin\left(\Omega t\right)\right)\mathrm{d}t,\mathrm{d}y=0\mathrm{d}t,\mathrm{d}z=\Omega e^{\Omega t}\left(sin\left(\Omega t\right)+cos\left(\Omega t\right)\right)\mathrm{d}t.$$

Using ${\left(\mathrm{d}\ell \right)}^2={\left(\mathrm{d}x\right)}^2+{\left(\mathrm{d}y\right)}^2+{\left(\mathrm{d}z\right)}^2$, we obtain

$$\frac{\mathrm{d}\ell }{\mathrm{d}t}=\sqrt{2}\Omega e^{\Omega t},\frac{{\mathrm{d}}^2\ell }{\mathrm{d}{t}^2}=\sqrt{2}{\Omega }^2{e}^{\Omega t},\frac{{\mathrm{d}}^3\ell }{\mathrm{d}{t}^3}=\sqrt{2}{\Omega }^3{e}^{\Omega t}.$$

Therefore, the arc-length $\ell =\ell \left(t\right)=\sqrt{2}\left(e^{\Omega t}-1\right)$ can be used to parameterize the oriented curve traced out by the particle $\mathbb{P}$ as

$${\zeta }^{*}\left(\ell \right)=\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right),0,\frac{\ell +\sqrt{2}}{\sqrt{2}}sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right).$$

(31)

Then, from (1) and (31), we can obtain the Serret–Frenet frame as follows:

$$\top =\frac{1}{\sqrt{2}}\left(cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right),0,cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)+sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right),$$

$$\aleph =\frac{1}{\sqrt{2}}\left(-cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right),0,cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right),$$

and

$$\mathfrak{B}=\left(0,-1,0\right).$$

Moreover, we can get the curvature and the torsion as

$$\kappa =\frac{1}{\ell +\sqrt{2}},\tau =0.$$

From (7), we obtain

$${\kappa }_1=\frac{1}{\ell +\sqrt{2}}cos\theta ,{\kappa }_2=-\frac{1}{\ell +\sqrt{2}}sin\theta ,$$

and

$${\kappa }_3={\theta }^{\prime }\left(\ell \right),\theta =-arctan\left(\frac{{\kappa }_2}{{\kappa }_1}\right).$$

Considering (4), we get the following q-frame:

$$\top =\frac{1}{\sqrt{2}}\left(cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right),0,cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)+sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right),$$

$$\begin{array}{ccc}\hfill {\aleph }_q& =& \left(\frac{1}{\sqrt{2}}cos\theta \left(-cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right),-sin\theta ,\right.\hfill \\ & & \left.\frac{1}{\sqrt{2}}cos\theta \left(cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right)\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\mathfrak{B}}_q& =& \left(\frac{-1}{\sqrt{2}}sin\theta \left(-cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right),-cos\theta ,\right.\hfill \\ & & \left.\frac{-1}{\sqrt{2}}sin\theta \left(cosln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)-sinln\left(\frac{\ell +\sqrt{2}}{\sqrt{2}}\right)\right)\right).\hfill \end{array}$$

Therefore, by applying Theorem 1, we get the acceleration and jerk vectors with the q-frame as follows:

$$\mathbb{A}=\sqrt{2}{\Omega }^2{e}^{\Omega t}\top +\frac{2{\Omega }^2{e}^{2\Omega t}}{\ell +\sqrt{2}}cos\theta {\aleph }_q-\frac{2{\Omega }^2{e}^{2\Omega t}}{\ell +\sqrt{2}}sin\theta {\mathfrak{B}}_q,$$

and

$$\mathbb{J}=\frac{\mathrm{d}\mathbb{A}}{\mathrm{d}t}=C_{\top }\top +C_{{\aleph }_q}{\aleph }_q+C_{{\mathfrak{B}}_q}{\mathfrak{B}}_q,$$

where

$$C_{\top }=\sqrt{2}{\Omega }^3{e}^{\Omega t}-\frac{2\sqrt{2}{\Omega }^3{e}^{3\Omega t}}{{\left(\ell +\sqrt{2}\right)}^2},$$

$$C_{{\aleph }_q}=cos\theta \left[\frac{6{\Omega }^3{e}^{2\Omega t}}{\ell +\sqrt{2}}-\frac{2\sqrt{2}{\Omega }^3{e}^{3\Omega t}}{{\left(\ell +\sqrt{2}\right)}^2}\right],$$

and

$$C_{{\mathfrak{B}}_q}=-sin\theta \left[\frac{6{\Omega }^3{e}^{2\Omega t}}{\ell +\sqrt{2}}-\frac{2\sqrt{2}{\Omega }^3{e}^{3\Omega t}}{{\left(\ell +\sqrt{2}\right)}^2}\right].$$

By considering (19) and (31), we get

$${\lambda }_1=\frac{\ell +\sqrt{2}}{2},{\lambda }_2=\frac{\ell +\sqrt{2}}{2},{\lambda }_3=0.$$

(32)

In addition, from (18) and (31), we have

$${\zeta }^{*}\left(\ell \right)=\left(\frac{\ell +\sqrt{2}}{2}\right)\top -\left(\frac{\ell +\sqrt{2}}{2}\right)cos\theta {\aleph }_q+\left(\frac{\ell +\sqrt{2}}{2}\right)sin\theta {\mathfrak{B}}_q.$$

From (21) and (32), we obtain

$$n=\frac{\ell +\sqrt{2}}{\sqrt{2}}=e^{\Omega t},n^{*}=\frac{\ell +\sqrt{2}}{2}=\frac{1}{\sqrt{2}}{e}^{\Omega t}.$$

Therefore, by applying Theorem 2 and Corollary 1, we get the components of the acceleration and jerk vectors as follows:

$$A_t=2\sqrt{2}{\Omega }^2{e}^{\Omega t},A_n=-2{\Omega }^2{e}^{\Omega t},$$

and

$$J_t=2\sqrt{2}{\Omega }^3{e}^{\Omega t},J_n=-4{\Omega }^3{e}^{\Omega t},J_{n^{*}}=0.$$

5. Conclusions

In terms of the Serret–Frenet frame, various resolutions of acceleration and jerk vectors have been derived in $E^3$. However, the Serret–Frenet frame is inadequate for studying space curves whose curvatures have discrete zero points. As a result, at the aforementioned points, the theories presented in these works are ineffective. However, the q-frame is well defined for all the curves. Therefore, in the present study, we establish the acceleration and jerk vectors in terms of this frame. Our resolutions for the acceleration and jerk vectors are a new contribution to the field. It may be beneficial in the future for some specific applications in various fields of science. As an application, using the jerk vector formula, we established the maximum permissible speed on a space curve at all trajectory points.