Fractional View Analysis of Kuramoto–Sivashinsky Equations with Non-Singular Kernel Operators
Abstract
:1. Introduction
2. Basic Preliminaries
3. General Procedure
3.1. Case I
3.2. Case II
4. Applications
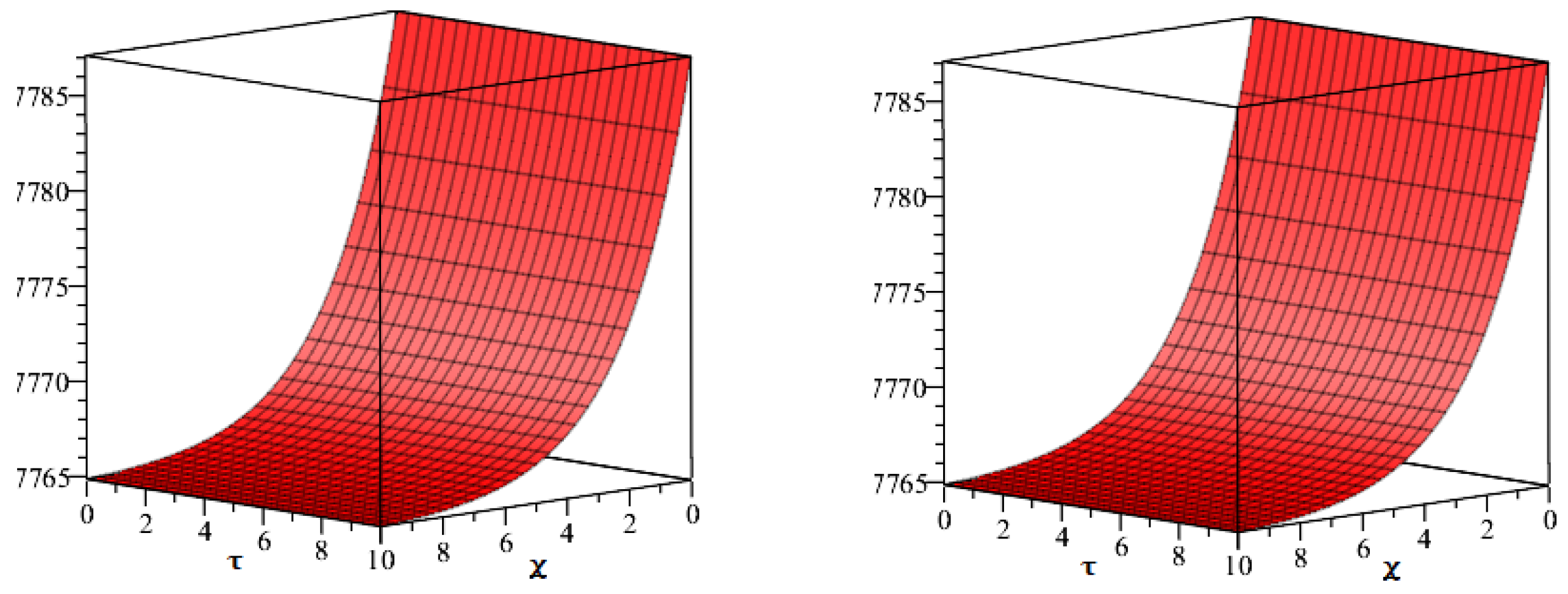
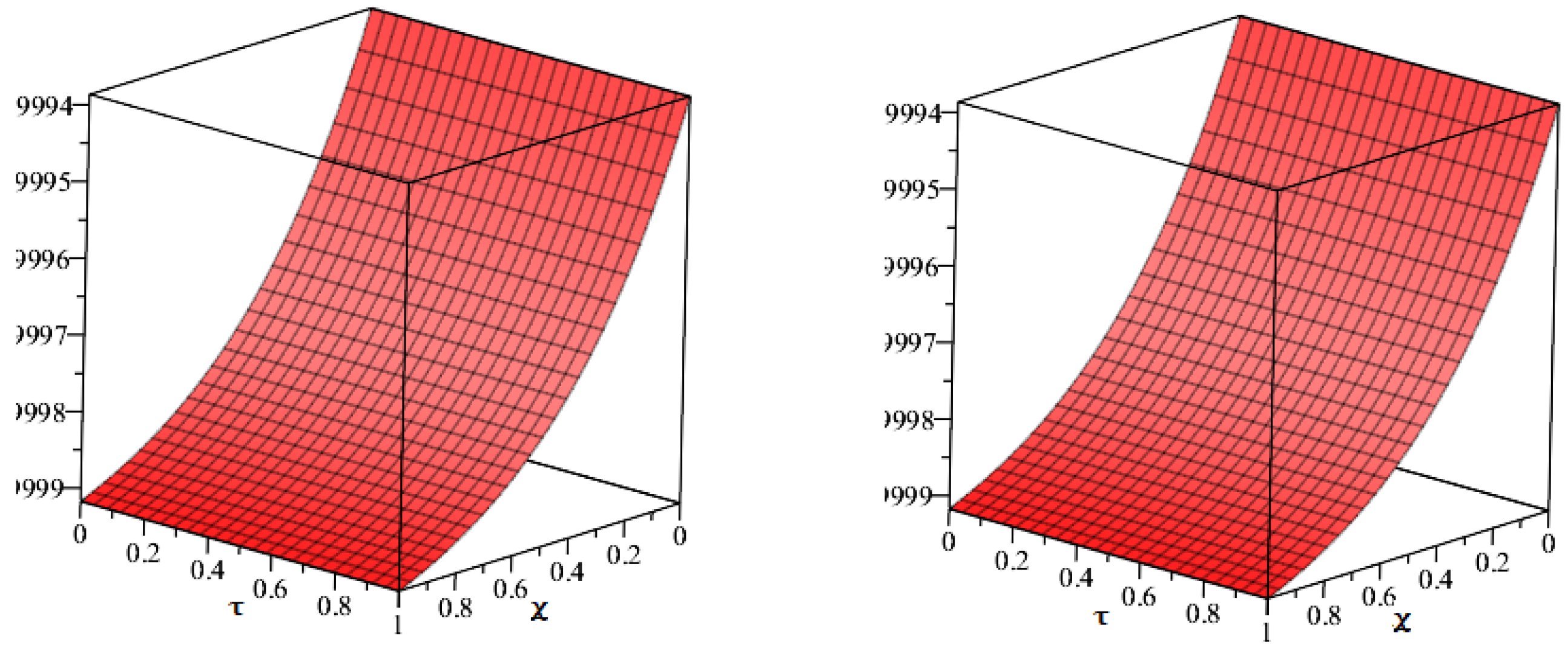
Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Momani, S.; Shawagfeh, N.T. Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 2006, 182, 1083–1092. [Google Scholar] [CrossRef]
- Kiryakova, S.V. Multiple (multiindex) Mittag-Leffler functions and relations to generalized fractional calculus. J. Comput. Appl. Math. 2000, 118, 441–452. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Seifi, S. Homotopy Analysis Method for solving linear and nonlinear fractional diffusion-wave equation. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2006–2012. [Google Scholar] [CrossRef]
- Jafari, H.; Seifi, S. Solving a system of nonlinear fractional partial differential equations using homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1962–1969. [Google Scholar] [CrossRef]
- Millerand, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equation. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Trujillo, J.J. Differential equations of fractional order: Methods, results problems. Appl. Anal. 2001, 78, 153–192. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M. An analytical technique to solve the system of nonlinear fractional partial differential equations. Mathematics 2019, 7, 505. [Google Scholar] [CrossRef] [Green Version]
- Cruz-Duarte, J.M.; Rosales-Garcia, J.; Correa-Cely, C.R.; Garcia-Perez, A.; Avina-Cervantes, J.G. A closed form expression for the Gaussian-based Caputo-Fabrizio fractional derivative for signal processing applications. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 138–148. [Google Scholar] [CrossRef]
- Mukhtar, S.; Noor, S. The Numerical Investigation of a Fractional-Order Multi-Dimensional Model of Navier-Stokes Equation via Novel Techniques. Symmetry 2022, 14, 1102. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Chung, J.D. Analytical Investigation of Fractional-Order Korteweg-De-Vries-Type Equations under Atangana-Baleanu-Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.C.; Zeng, S.D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Singh, B.K. A novel approach for numeric study of 2D biological population model. Cogent Math. 2016, 3, 1261527. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A 2000, 284, 376–384. [Google Scholar] [CrossRef] [Green Version]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgul, A.; De la Sen, M. A Novel Homotopy Perturbation Method with Applications to Nonlinear Fractional Order KdV and Burger Equation with Exponential-Decay Kernel. J. Funct. Spaces 2021, 2021, 8770488. [Google Scholar] [CrossRef]
- Basto, M.; Semiao, V.; Calheiros, F.L. Numerical study of modified Adomian’s method applied to Burgers equation. J. Comput. Appl. Math. 2007, 206, 927–949. [Google Scholar] [CrossRef] [Green Version]
- Adomian, G. Solutions of Nonlinear PDE. Appl. Math. Lett. 1998, 11, 121–123. [Google Scholar] [CrossRef] [Green Version]
- Yee, E. Application of the Decomposition Method to the Solution of the Reaction-Convection-Diffusion Equation. Appl. Math. Comput. 1993, 56, 1–27. [Google Scholar] [CrossRef]
- Inc, M.; Cherruault, Y. A new approach to solve a diffusion-convection problem. Kybernetes 2002, 31, 536–549. [Google Scholar] [CrossRef]
- Adomian, G. Analytical solution of Navier-Stokes flow of a viscous compressible fluid. Found. Phys. Lett. 1995, 8, 389–400. [Google Scholar] [CrossRef]
- Krasnoschok, M.; Pata, V.; Siryk, S.V.; Vasylyeva, N. A subdiffusive Navier-Stokes-Voigt system. Phys. D Nonlinear Phenom. 2020, 409, 132503. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Z.; Li, C.; Chen, Y.Q. Adomian’s method applied to Navier-Stokes equation with a fractional order. In Proceedings of the ASME 2009 IDETC/CIE, San Diego, CA, USA, 30 August–2 September 2009; pp. 1047–1054. [Google Scholar] [CrossRef]
- Siryk, S.V.; Salnikov, N.N. Numerical solution of Burger’s equation by Petrov-Galerkin method with adaptive weighting functions. J. Autom. Inf. Sci. 2012, 44, 50–67. [Google Scholar] [CrossRef]
- Roos, H.-G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008; 604p. [Google Scholar]
- Nonlaopon, K.; Naeem, M.; Zidan, A.M.; Alsanad, A.; Gumaei, A. Numerical investigation of the time-fractional Whitham–Broer–Kaup equation involving without singular kernel operators. Complexity 2021, 2021, 7979365. [Google Scholar] [CrossRef]
- Siryk, S.V.; Salnikov, N.N. Construction of Weight Functions of the Petrov-Galerkin Method for Convection-Diffusion-Reaction Equations in the Three-Dimensional Case. Cybern. Syst. Anal. 2014, 50, 805–814. [Google Scholar]
- Siryk, S.V. A note on the application of the Guermond-Pasquetti mass lumping correction technique for convection-diffusion problems. J. Comput. Phys. 2019, 376, 1273–1291. [Google Scholar] [CrossRef] [Green Version]
- John, V.; Knobloch, P.; Novo, J. Finite elements for scalar convection-dominated equations and incompressible flow problems: A never ending story? Comput. Vis. Sci. 2018, 19, 47–63. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y. Similarity solution and heat transfer characteristics for a class of nonlinear convection-diffusion equation with initial value conditions. Math. Probl. Eng. 2019, 2019, 3467276. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simulat 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Shah, R.; Nonlaopon, K. The analysis of the fractional-order Navier-Stokes equations by a novel approach. J. Funct. Spaces 2022, 2022, 8979447. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.R.; Ahmad, S.; Younis, M.; Baleanu, D. Lump, lump-one stripe, multiwave and breather solutions for the Hunter-Saxton equation. Open Phys. 2021, 19, 1–10. [Google Scholar] [CrossRef]
- Gonzalez-Gaxiola, O.; Leon-Ramirez, A.; Chacon-Acosta, G. Application of the Kudryashov Method for Finding Exact Solutions of the Schamel-Kawahara Equation. Russ. J. Nonlinear Dyn. 2022, 18, 203–215. [Google Scholar] [CrossRef]
- Akinyemi, L. Two improved techniques for the perturbed nonlinear Biswas-Milovic equation and its optical solitons. Optik 2021, 243, 167477. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Akgul, A.; Mahariq, I.; Kafle, J. A comparative analysis of the fractional-order coupled Korteweg-De Vries equations with the Mittag-Leffler law. J. Math. 2022, 2022, 8876149. [Google Scholar] [CrossRef]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 741–750. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Al-Qurashi, M.; Shah, R.; Baleanu, D. Modified modelling for heat like equations within Caputo operator. Energies 2020, 13, 2002. [Google Scholar] [CrossRef]
- Wu, G.C.; Lee, E.W.M. Fractional variational iteration method and its application. Phys. A Lett. 2010, 374, 2506–2509. [Google Scholar] [CrossRef]
- Rawashdeh, M.S. The fractional natural decomposition method: Theories and applications. Math. Methods Appl. Sci. 2017, 40, 2362–2376. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, R.; Khan, H.; Arif, M. Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions. Math. Methods Appl. Sci. 2020, 43, 199–212. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical Investigation of Noyes-Field Model for Time-Fractional Belousov-Zhabotinsky Reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Taneco-Hernández, M.A.; Morales-Delgado, V.F.; Gómez-Aguilar, J.F. Fractional Kuramoto-Sivashinsky equation with power law and stretched Mittag-Leffler kernel. Phys. Stat. Mech. Its Appl. 2019, 527, 121085. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Tsuzuki, T. Persistent propagation of concentration waves in dissipative media far from thermal equilibrium. Prog. Theor. Phys. 1976, 55, 356–369. [Google Scholar] [CrossRef] [Green Version]
- Sivashinsky, G.L. Instabilities, pattern-formation, and turbulence in flames. Ann. Rev. Fluid Mech. 1983, 15, 179–199. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Shu, C.-W. Local discontinuous Galerkin methods for the Kuramoto-Sivashinsky equations and the Ito-type coupled KdV equations. Comput. Methods Appl. Mech. Eng. 2006, 195, 3430–3447. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup equations within modified analytical approaches. Axioms 2019, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Akrivis, G.D. Finite difference discretization of the Kuramoto-Sivashinsky equation. Numer. Math. 1992, 63, 1–11. [Google Scholar] [CrossRef]
- Khater, A.H.; Temsah, R.S. Numerical solutions of the generalized Kuramoto-Sivashinsky equation by Chebyshev spectral collocation methods. Comput. Math. Appl. 2008, 56, 1465–1472. [Google Scholar] [CrossRef] [Green Version]
- Kurulay, M.; Secer, A.; Akinlar, A. A new approximate analytical solution of Kuramoto-Sivashinsky equation using Homotopy analysis method. Appl. Math. Inf. Sci. 2013, 7, 267–271. [Google Scholar] [CrossRef]
- Porshokouhi, M.G.; Ghanbari, B. Application of He’s variational iteration method for solution of the family of Kuramoto-Sivashinsky equations. J. King Saud Univ. Sci. 2011, 23, 407–411. [Google Scholar] [CrossRef] [Green Version]
- Ye, L.; Yan, G.; Li, T. Numerical method based on the Lattice Boltzmann model for the Kuramoto-Sivashinsky equation. J. Sci. Comput. 2011, 49, 195–210. [Google Scholar] [CrossRef]
- Lakestania, M.; Dehghan, M. Numerical solutions of the generalized Kuramoto-Sivashinsky equation using B-spline functions. Appl. Math. Model. 2012, 36, 605–617. [Google Scholar] [CrossRef]
- Singh, B.K.; Arora, G.; Kumar, P. A note on solving the fourth-order Kuramoto-Sivashinsky equation by the compact finite difference scheme. Ain Shams Eng. J. 2016, 9, 1581–1589. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. New approach to find exact solutions of time-fractional Kuramoto-Sivashinsky equation. Physica A 2015, 434, 240–245. [Google Scholar] [CrossRef]
- Kbiri Alaoui, M.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical investigation of fractional-order cahn-hilliard and gardner equations using two novel techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Zhou, M.X.; Kanth, A.S.V.; Aruna, K.; Raghavendar, K.; Rezazadeh, H.; Inc, M.; Aly, A.A. Numerical Solutions of Time Fractional Zakharov-Kuznetsov Equation via Natural Transform Decomposition Method with Nonsingular Kernel Derivatives. J. Funct. Spaces 2021, 2021, 9884027. [Google Scholar] [CrossRef]




| 0.2 | 3.8763631750 | 2.5603465160 | 1.2452127610 | 5.2357898000 | 5.2357898000 | |
| 0.4 | 3.5383874710 | 2.3370987630 | 1.1366159900 | 5.1930879000 | 5.1930879000 | |
| 0.1 | 0.6 | 3.2298917490 | 2.1333562800 | 1.0375564680 | 4.1981581000 | 4.1981581000 |
| 0.8 | 2.9481307140 | 1.9472375180 | 9.4701581360 | 4.2586011000 | 4.2586011000 | |
| 1 | 2.6909407330 | 1.7773682470 | 8.6440866950 | 3.7555413000 | 3.7555413000 | |
| 0.2 | 3.9051956730 | 2.6213609880 | 1.2791603100 | 2.1671579400 | 2.1671579400 | |
| 0.4 | 3.5647273900 | 2.3928150910 | 1.1676250400 | 1.9986175500 | 1.9986175500 | |
| 0.2 | 0.6 | 3.2539153040 | 2.1841946000 | 1.0658420020 | 1.7896316100 | 1.7896316100 |
| 0.8 | 2.9700833590 | 1.9936660840 | 9.7285869800 | 1.6517202000 | 1.6517202000 | |
| 1 | 2.7109715270 | 1.8197396140 | 8.8799030700 | 1.5011082500 | 1.5011082500 | |
| 0.2 | 3.9074452580 | 2.6557920700 | 1.3018392060 | 4.9107369000 | 4.9107369000 | |
| 0.4 | 3.5667759500 | 2.4242396230 | 1.1883219200 | 4.5079263000 | 4.5079263000 | |
| 0.3 | 0.6 | 3.2557659070 | 2.2128595690 | 1.0847147790 | 4.0994474000 | 4.0994474000 |
| 0.8 | 2.9717650370 | 2.0198233190 | 9.9007783700 | 3.7675803000 | 3.7675803000 | |
| 1 | 2.7125122030 | 1.8436205320 | 9.0371291300 | 3.4266623600 | 3.4266623600 | |
| 0.2 | 3.8968119170 | 2.6758919850 | 1.3174768270 | 8.7943159000 | 8.7943159000 | |
| 0.4 | 3.5570453110 | 2.4425629700 | 1.2025719880 | 8.0772351000 | 8.0772351000 | |
| 0.4 | 0.6 | 3.2469220340 | 2.2296233550 | 1.0977604780 | 7.3192632000 | 7.3192632000 |
| 0.8 | 2.9636656620 | 2.0350980460 | 1.0019587770 | 6.7334404000 | 6.7334404000 | |
| 1 | 2.7051309960 | 1.8575742050 | 9.1456888300 | 6.1222165000 | 6.1222165000 | |
| 0.2 | 3.8780476890 | 2.6863820070 | 1.3278652660 | 1.3857894800 | 1.3857894800 | |
| 0.4 | 3.5399297510 | 2.4521513270 | 1.2120676190 | 1.2686543800 | 1.2686543800 | |
| 0.5 | 0.6 | 3.2312565220 | 2.2383331580 | 1.1063856400 | 1.1569079000 | 1.1569079000 |
| 0.8 | 2.9494198080 | 2.0431014380 | 1.0098849110 | 1.0559300400 | 1.0559300400 | |
| 1 | 2.6920845170 | 1.8648358860 | 9.2176004600 | 9.6577706000 | 9.6577706000 |
| 0.2 | 1.1612667280 | 8.5363755450 | 4.6919140870 | 6.8704703900 | 6.8704703900 | |
| 0.4 | 1.0028798100 | 7.3867676970 | 4.0850054000 | 6.4548098400 | 6.4548098400 | |
| 0.1 | 0.6 | 8.5796886930 | 6.3106175850 | 3.4749449090 | 5.2095715600 | 5.2095715600 |
| 0.8 | 7.3807877630 | 5.4320275680 | 2.9966494870 | 4.5965813960 | 4.5965813960 | |
| 1 | 6.3324213410 | 4.6587557540 | 2.5671651650 | 3.8830543490 | 3.8830543490 | |
| 0.2 | 1.1160913160 | 8.6892447100 | 5.1845663050 | 1.1940940770 | 1.1940940770 | |
| 0.4 | 9.5808260400 | 7.4580679400 | 4.4481235990 | 1.0209619810 | 1.0209619810 | |
| 0.2 | 0.6 | 8.2234346360 | 6.4003333330 | 3.8152844530 | 8.7191431200 | 8.7191431200 |
| 0.8 | 7.0730673850 | 5.5073221600 | 3.2871888450 | 7.5931629400 | 7.5931629400 | |
| 1 | 6.0790881850 | 4.7343696780 | 2.8276390620 | 6.5661087000 | 6.5661087000 | |
| 0.2 | 1.0067944450 | 8.0987732900 | 5.0016428380 | 1.1911411150 | 1.1911411150 | |
| 0.4 | 8.6901621500 | 6.9989668720 | 4.3390394210 | 1.0664429710 | 1.0664429710 | |
| 0.3 | 0.6 | 7.4103967680 | 5.9579371980 | 3.6734954620 | 8.6287146800 | 8.6287146800 |
| 0.8 | 6.3622255760 | 5.1148008530 | 3.1528398080 | 7.3897444000 | 7.3897444000 | |
| 1 | 5.4643673440 | 4.3930339730 | 2.7080310190 | 6.3491630400 | 6.3491630400 | |
| 0.2 | 8.3045099900 | 6.7775158900 | 4.1126291900 | 5.7818811000 | 5.7818811000 | |
| 0.4 | 7.1575681000 | 5.8461304340 | 3.5574295280 | 5.2192393400 | 5.2192393400 | |
| 0.4 | 0.6 | 6.1227594040 | 4.9964493820 | 3.0308304070 | 4.2382858300 | 4.2382858300 |
| 0.8 | 5.2830801080 | 4.3157643950 | 2.6276198470 | 3.8863255800 | 3.8863255800 | |
| 1 | 4.4867499390 | 3.6559842940 | 2.2061448310 | 2.8322174000 | 2.8322174000 | |
| 0.2 | 5.5952845800 | 4.4690695900 | 2.2473572590 | 9.4476480800 | 9.4476480800 | |
| 0.4 | 4.8042354800 | 3.8370013900 | 1.9289146280 | 8.1259504900 | 8.1259504900 | |
| 0.5 | 0.6 | 4.1587226470 | 3.3280270810 | 1.6892932770 | 6.6521422000 | 6.6521422000 |
| 0.8 | 3.5512618890 | 2.8378305440 | 1.4304267840 | 5.9170930300 | 5.9170930300 | |
| 1 | 3.0596603570 | 2.4469397700 | 1.2382106280 | 4.9847282600 | 4.9847282600 |
| 0.2 | 7.60000000 | 7.10000000 | 3.40000000 | 1.10000000 | 1.10000000 | |
| 0.4 | 5.13000000 | 5.10000000 | 6.10000000 | 1.20000000 | 1.20000000 | |
| 0.1 | 0.6 | 3.35000000 | 4.10000000 | 3.00000000 | 0.00000000 | 0.0000000 |
| 0.8 | 2.31000000 | 3.80000000 | 8.20000000 | 1.00000000 | 1.00000000 | |
| 1 | 1.52000000 | 1.80000000 | 1.00000000 | 1.10000000 | 1.10000000 | |
| 0.2 | 5.49000000 | 5.10000000 | 1.00000000 | 1.40000000 | 1.40000000 | |
| 0.4 | 3.63000000 | 2.80000000 | 1.20000000 | 1.30000000 | 1.30000000 | |
| 0.2 | 0.6 | 2.38000000 | 3.60000000 | 4.20000000 | 1.50000000 | 1.50000000 |
| 0.8 | 1.70000000 | 3.10000000 | 7.50000000 | 1.10000000 | 1.10000000 | |
| 1 | 9.80000000 | 1.00000000 | 2.00000000 | 0.00000000 | 0.00000000 | |
| 0.2 | 9.90000000 | 1.10000000 | 9.10000000 | 1.30000000 | 1.30000000 | |
| 0.4 | 7.60000000 | 7.00000000 | 3.40000000 | 0.00000000 | 0.00000000 | |
| 0.3 | 0.6 | 4.60000000 | 9.00000000 | 5.20000000 | 1.30000000 | 1.30000000 |
| 0.8 | 3.60000000 | 1.30000000 | 1.90000000 | 0.00000000 | 0.00000000 | |
| 1 | 1.20000000 | 2.00000000 | 2.00000000 | 1.10000000 | 1.10000000 | |
| 0.2 | 7.06000000 | 1.15000000 | 1.80000000 | 1.20000000 | 1.20000000 | |
| 0.4 | 4.64000000 | 7.30000000 | 1.20000000 | 1.50000000 | 1.50000000 | |
| 0.4 | 0.6 | 3.17000000 | 4.80000000 | 5.00000000 | 1.30000000 | 1.30000000 |
| 0.8 | 2.00000000 | 1.50000000 | 2.60000000 | 0.00000000 | 0.00000000 | |
| 1 | 1.55000000 | 2.70000000 | 1.80000000 | 1.10000000 | 1.10000000 | |
| 0.2 | 2.19300000 | 3.09000000 | 4.70000000 | 1.20000000 | 1.20000000 | |
| 0.4 | 1.45500000 | 2.09000000 | 3.10000000 | 8.10000000 | 8.10000000 | |
| 0.5 | 0.6 | 9.81000000 | 1.36000000 | 1.40000000 | 1.30000000 | 1.30000000 |
| 0.8 | 6.66000000 | 8.40000000 | 2.60000000 | 0.00000000 | 0.00000000 | |
| 1 | 4.53000000 | 6.60000000 | 7.00000000 | 1.40000000 | 1.40000000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saad Alshehry, A.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto–Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. https://doi.org/10.3390/sym14071463
Saad Alshehry A, Imran M, Khan A, Shah R, Weera W. Fractional View Analysis of Kuramoto–Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry. 2022; 14(7):1463. https://doi.org/10.3390/sym14071463
Chicago/Turabian StyleSaad Alshehry, Azzh, Muhammad Imran, Adnan Khan, Rasool Shah, and Wajaree Weera. 2022. "Fractional View Analysis of Kuramoto–Sivashinsky Equations with Non-Singular Kernel Operators" Symmetry 14, no. 7: 1463. https://doi.org/10.3390/sym14071463
APA StyleSaad Alshehry, A., Imran, M., Khan, A., Shah, R., & Weera, W. (2022). Fractional View Analysis of Kuramoto–Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry, 14(7), 1463. https://doi.org/10.3390/sym14071463







