Groups and Structures of Commutative Semigroups in the Context of Cubic Multi-Polar Structures

Abstract

In recent years, the m-polar fuzziness structure and the cubic structure have piqued the interest of researchers and have been commonly implemented in algebraic structures like groupoids, semigroups, groups, rings and lattices. The cubic m-polar (${\mathcal{C}}_m\mathcal{P}$) structure is a generalization of m-polar fuzziness and cubic structures. The intent of this research is to extend the ${\mathcal{C}}_m\mathcal{P}$ structures to the theory of groups and semigroups. In the present research, we preface the concept of the ${\mathcal{C}}_m\mathcal{P}$ groups and probe many of its characteristics. This concept allows the membership grade and non-membership grade sequence to have a set of m-tuple interval-valued real values and a set of m-tuple real values between zero and one. This new notation of group (semigroup) serves as a bridge among ${\mathcal{C}}_m\mathcal{P}$ structure, classical set and group (semigroup) theory and also shows the effect of the ${\mathcal{C}}_m\mathcal{P}$ structure on a group (semigroup) structure. Moreover, we derive some fundamental properties of ${\mathcal{C}}_m\mathcal{P}$ groups and support them by illustrative examples. Lastly, we vividly construct semigroup and groupoid structures by providing binary operations for the ${\mathcal{C}}_m\mathcal{P}$ structure and provide some dominant properties of these structures.

1. Introduction

An algebraic (system) structure is a random set with one or more finitary operations defined in it. Algebraic structures include a wide range of structures such as semigroups, groups, rings, fields, vector spaces, lattices, categories and so on. In mathematics, the theory of groups is one of the most critical aspects of algebra. This theory provides a useful framework for analyzing an element that appears in the symmetric form. Group theory is inextricably linked to symmetry in some areas of science such as geometry and chemistry. In some areas of chemistry, it is an essential tool to classify and study the symmetries of atoms, molecules, crystal structure and regular polyhedral structure (see [1,2]). Semigroup theory, a new algebraic structure, is a thriving branch of modern algebra and it is a generalization of a group because a semigroup is a non-empty set together with an associative binary operation and need not have an element which has an inverse. Algebraic structures have been used in numerous domains; in particular, a semigroup is utilized in the theory of automata, network analogy, formal languages and so on.

There are numerous things inherently ambiguous, uncertain and inaccurate in the real world, and these things cannot be dealt with effectively using mathematical techniques that are traditionally used to deal with vagueness and uncertainties. However, one can use a wider range of pioneering theories, such as the theory of fuzzy structures ($\mathcal{FS}s$) [3], the theory of bipolar fuzzy ($\mathcal{BF}$) structures [4], the theory of interval-valued fuzzy ($\mathcal{IVF}$) structures [5] and the theory of cubic structures ($\mathcal{CS}s$) [6] for dealing with vagueness and uncertainties. Zadeh [3] demonstrated the concept of $\mathcal{FS}s$ in 1965 as an essential mathematical structure to characterize and assemble the objects/elements whose boundary is ambiguous. This concept permits the membership degree ($\mathcal{MD}$) of a crisp object/element over the interval $I=[0,1]$; that is, every crisp object/element assigns a degree of membership. $\mathcal{FS}s$ have grown stupendously over the years, giving rise to the idea of fuzzy groups proposed in [7]. After that, this concept was extended to many hybrid structures such as the $\mathcal{IVF}$ structure which permits the $\mathcal{MD}$ and non-membership degree ($\mathcal{N}-\mathcal{MD}$) of a crisp object/element over the interval $[0,1]$ and $\mathcal{CS}$ combined with $\mathcal{IVF}$ structure and $\mathcal{FS},$ which permits the $\mathcal{MD}$ and $\mathcal{N}-\mathcal{MD}$ of a crisp object/element over the intervals $\left[I\right]=\left[\right[0,1\left]\right]$ and $I=[0,1],$ respectively. As a new hybrid structure of $\mathcal{FS}s,$ the theory of bipolar and intuitionistic fuzzy structures is well known and is propounded by Zhang [4] and Atanassov [8], respectively. In [4], Zhang used a grade of membership which is a positive fuzzy value and a grade of non-membership which is a negative fuzzy value for each ordinary object. In [8], Atanassov used a grade of membership and a grade of non-membership for each ordinary object, where the sum of them is less than or equal to one. After that, these hybrid aspects of $\mathcal{FS}s$ were connected to algebraic structures, especially in group theory (see [9,10,11]). For more information about hybrid fuzziness structures, see [12].

In 2014, Chen and co-workers [13] presented the conceptualization of m-polar fuzzy (${}_m\mathcal{PF}$) structures by using a grade of membership which is an m-tuple fuzzy value for each object. This concept stems from ordinary sets and $\mathcal{FS}s,$ and it is one of the most popular extensions of $\mathcal{BF}$ structures. The notions of $\mathcal{FS}s$ and $\mathcal{BF}$ structures are specific cases of the notion of ${}_m\mathcal{PF}$ structure; thus, an ${}_m\mathcal{PF}$ structure differs from a $\mathcal{FS}$ and a $\mathcal{BF}$ structure in the sense that each object contains m-components. Following the introduction of the ${}_m\mathcal{PF}$ structure by Chen and co-workers [13], a lot of publications on generalizations of ${}_m\mathcal{PF}$ structures were conducted, for instance, polarity of generalized neutrosophic sets [14], polarity of $\mathcal{IVF}$ structures [15] and polarity of intuitionistic (spherical) fuzzy structures [16,17].

Following the generalization of ${}_m\mathcal{PF}$ structures, numerous mathematicians used the concept of generalized ${}_m\mathcal{PF}$ structures in a wide range of scientific and technological fields. In group theory, the ${}_m\mathcal{PF}$ group was first implemented by Farooq and co-workers [18]. They proposed the notion of the ${}_m\mathcal{PF}$ subgroup and described the concepts of the ${}_m\mathcal{PF}$ coset and the ${}_m\mathcal{PF}$ quotient subgroup. In addition, the ${}_m\mathcal{PF}$ structure was studied by Al-Masarwah and Ahmad [19,20] in BCK and BCI algebras, Sarwar and Akram [21] in matroid theory, and Akram and Shahzadi [22] in Hypergraphs. In polarity of hybrid fuzziness structures, Kang et al. [16], Muhiuddin and Al-Kadi [23], Dogra and Pal [24] and Borzooei et al. [14] applied multipolar intuitionistic fuzzy structures, multipolar $\mathcal{IVF}$ structures, picture ${}_m\mathcal{PF}$ structures and multipolar generalized neutrosophic structures, respectively, to BCK and BCI algebras. Uluçay and Ṣahin [25] constructed a bridge among neutrosophic multiset theory, classical set theory and classical group theory. They demonstrated the effect of neutrosophic multisets on a group structure. Basumatary et al. [26] studied and discussed several results in neutrosophic multi-topological group theory. In addition, many researchers studied some real-life applications based on polarity of hybrid fuzziness structures such as Siraj et al. [27], Akram et al. [28,29] and Hashmi et al. [30].

As a combination between $\mathcal{CS}$ and ${}_m\mathcal{PF}$ structure and to solve various complex and uncertain problems, Riaz and Hashmi [31] in 2019 propounded the theory of the ${\mathcal{C}}_m\mathcal{P}$ structure by using a grade of $\mathcal{N}-\mathcal{MD}$ which is a multi-fuzzy value and a grade of $\mathcal{MD}$ which is a multi-fuzzy interval value for each ordinary object. This notion manipulates not only multi-attributed information but also cubic information. After that, Garg et al. [32] presented some new laws and produced some results concerning the ${\mathcal{C}}_m\mathcal{P}$ structure. In real-life issues, they applied the concept of the ${\mathcal{C}}_m\mathcal{P}$ structure in medical diagnosis and pattern recognition. In [33,34], Riaz et al. studied the topological structures and some real-life applications based on the ${\mathcal{C}}_m\mathcal{P}$ structure. In the context of graph theory, Muhiuddin and co-workers [35] initiated and studied the polarity of cubic graphs. Al-Masarwah and Alshehri [36] for the first time applied the theory of the ${\mathcal{C}}_m\mathcal{P}$ structure to algebraic structures, especially $BCK/BCI$ algebras. They originated the concepts of ${\mathcal{C}}_m\mathcal{P}$ subalgebras and ${\mathcal{C}}_m\mathcal{P}$ (closed) ideals and discussed many dominant properties of these concepts. Moreover, they established the ${\mathcal{C}}_m\mathcal{P}$ extension property for a ${\mathcal{C}}_m\mathcal{P}$ ideal. By extending the works of [11,18] and inspired by the above works, the idea of the ${\mathcal{C}}_m\mathcal{P}$ groups is presented by combining the notions of ${}_m\mathcal{PF}$ groups and cubic groups, and characterizations of them according to the properties of ${\mathcal{C}}_m\mathcal{P}$ structures are provided in this present article. 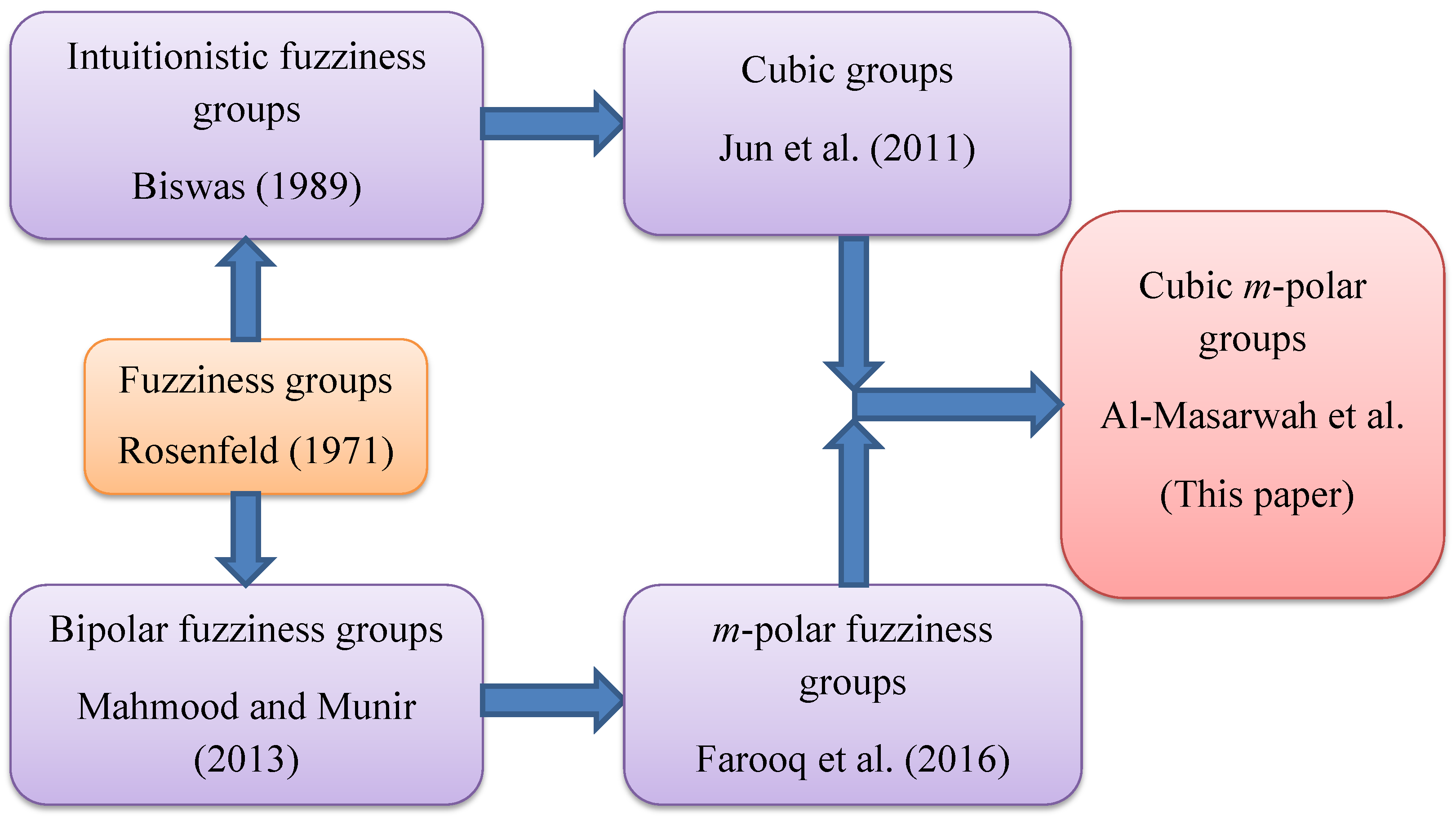Figure 1 depicts a novel hybrid extension of cubic groups and ${}_m\mathcal{PF}$ groups known as ${\mathcal{C}}_m\mathcal{P}$ groups to demonstrate the novelty of this extended algebraic structure.

Figure 1. Contributions toward ${\mathcal{C}}_m\mathcal{P}$ groups. (Biswas [9], Jun [11], Rosenfeld [7], Mahmood and Munir [10], Farooq et al. [18]).

This work is the first attempt to investigate and utilize the ${\mathcal{C}}_m\mathcal{P}$ structures in group theory. The proposed work is arranged as follows. In Section 2, some key principles with respect to groups and ${\mathcal{C}}_m\mathcal{P}$ structures are given to understand the proposed work. In Section 3, we preface the idea of the ${\mathcal{C}}_m\mathcal{P}$ groups and probe many of its characteristics. In this regard, we show the effect of ${\mathcal{C}}_m\mathcal{P}$ structures on a group theory. Then, we derive some fundamental results of ${\mathcal{C}}_m\mathcal{P}$ groups and support them by illustrative examples. In Section 4, we vividly construct semigroup and groupoid structures by providing binary operations for the ${\mathcal{C}}_m\mathcal{P}$ structure and provide some dominant properties of these structures. Finally, the conclusion and some potential future studies of this work are offered in Section 5.

Table 1 contains a list of acronyms used in the study article.

Table 1. List of acronyms.

Acronyms	Representation
$\mathcal{FS}(s)$	Fuzzy structure(s)
$\mathcal{BF}$	Bipolar fuzzy
$\mathcal{IVF}$	Interval-valued fuzzy
$\mathcal{CS}(s)$	Cubic structure(s)
${}_m\mathcal{PF}$	m-polar fuzzy
${\mathcal{C}}_m\mathcal{P}$	Cubic m-polar
$\mathcal{MD}$	Membership degree
$\mathcal{N}-\mathcal{MD}$	Non-membership degree

2. Basic Definitions

In this segment, we review some key notions for each area, i.e., ${}_m\mathcal{PF}$ structure [13], $\mathcal{CS}$ [6], $\mathcal{IVF}$ structure [5] and ${\mathcal{C}}_m\mathcal{P}$ structure [31]. In what follows, let I be the interval $[0,1].$

A groupoid consists of a non-empty set equipped with a binary operation. A semigroup is an associative groupoid $\mathbb{A},$ i.e., $(yr)s=y(rs)$ for all $y,r,s\in \mathbb{A}.$ A monoid is a semigroup $\mathbb{B}$ with a neutral element $e\in \mathbb{B}$ that has the property $ey=ye=y$ for all $y\in \mathbb{B}.$ A group is a monoid $\mathbb{G}$ such that for all $y\in \mathbb{G}$ there exists an inverse $y^{-1}$ such that $y^{-1}y=y{y}^{-1}=e.$

An interval number $\tilde{o}$ is defined as $[o^{-},o^{+}],$ where $0\le o^{-}\le o^{+}\le 1.$ The set of all intervals is symbolized by $\left[I\right].$ The interval $[o,o]$ is indicated by the number $o\in I$ in what follows. For the interval numbers $\widetilde{o_l}=[o_l^{-},o_l^{+}],\widetilde{{\epsilon }_l}=[{\epsilon }_l^{-},{\epsilon }_l^{+}]\in \left[I\right],$ where $l\in \Delta .$ We describe

• $\widetilde{o_l}\overline{\wedge }\widetilde{{\epsilon }_l}=[o_l^{-}\wedge {\epsilon }_l^{-},o_l^{+}\wedge {\epsilon }_l^{+}],$
• $\widetilde{o_l}\overline{\vee }\widetilde{{\epsilon }_l}=[o_l^{-}\vee {\epsilon }_l^{-},o_l^{+}\vee {\epsilon }_l^{+}],$
• $\widetilde{o_1}⪯\widetilde{o_2}\iff o_1^{-}\le o_2^{-}$ and $o_1^{+}\le o_2^{+},$
• $\widetilde{o_1}=\widetilde{o_2}\iff o_1^{-}=o_2^{-}$ and $o_1^{+}=o_2^{+}.$

To say that $\widetilde{o_1}\prec \widetilde{o_2}$ (resp. $\widetilde{o_1}\succ \widetilde{o_2}),$ we mean $\widetilde{o_1}⪯\widetilde{o_2}$ and $\widetilde{o_1}\ne \widetilde{o_2}$ (resp. $\widetilde{o_1}⪰\widetilde{o_2}$ and $\widetilde{o_1}\ne \widetilde{o_2}).$

Definition 1

([5]). An $\mathcal{IVF}$ structure $\tilde{\xi }$ of $\mathbb{G}(\ne \varphi )$ is a mapping

$$\tilde{\xi }:\mathbb{G}\to \left[I\right]$$

defined as

$$\tilde{\xi }=\{⟨y,{\xi }^{+}(y),{\xi }^{-}(y)⟩\mid y\in \mathbb{G}\},$$

where ${\xi }^{+}:\mathbb{G}\to I$ and ${\xi }^{-}:\mathbb{G}\to I$ are $\mathcal{FS}s$ on $\mathbb{G}.$

Definition 2

([6]). A $\mathcal{CS}$ of $\mathbb{G}(\ne \varphi )$ is a mapping

$${\mathcal{C}}_{(\tilde{\xi },\zeta )}:\mathbb{G}\to \left[I\right]\times I$$

defined as

$${\mathcal{C}}_{(\tilde{\xi },\zeta )}=\{⟨y,\tilde{\xi }(y),\zeta (y)⟩\mid y\in \mathbb{G}\},$$

where $\tilde{\xi }:\mathbb{G}\to \left[I\right]$ is an $\mathcal{IVF}$ structure on $\mathbb{G}$ and $\zeta :\mathbb{G}\to I$ is a $\mathcal{FS}$ on $\mathbb{G}.$

Definition 3

([13]). An ${}_m\mathcal{PF}$ structure (or an $I^m$ structure) of $\mathbb{G}(\ne \varphi )$ is a mapping

$${\tilde{\mathcal{C}}}_{{\tilde{\zeta }}_m}:\mathbb{G}\to I^m$$

defined as

$${\tilde{\mathcal{C}}}_{{\tilde{\zeta }}_m}=\left\{⟨y,{\tilde{\zeta }}^{(j)}(y)⟩\mid y\in \mathbb{G}\mathrm{and}j\in \{1,2,\dots ,m\}\right\},$$

where for $j\in \{1,2,\dots ,m\},$ ${\tilde{\zeta }}^{(j)}:\mathbb{G}\to I^m$ is the j-th projection mapping.

As a connection between an ${}_m\mathcal{PF}$ structure and a group theory, the idea of an ${}_m\mathcal{PF}$ group was first implemented by Farooq and co-workers [18] as follows:

Definition 4.

An ${}_m\mathcal{PF}$ structure ${\tilde{\mathcal{C}}}_{{\tilde{\zeta }}_m}$ is called an ${}_m\mathcal{PF}$ group of $\mathbb{G}$ if for all $y,z\in \mathbb{G},$

(1) 

${\tilde{\zeta }}^{(j)}(yz)\ge {\tilde{\zeta }}^{(j)}(y)\wedge {\tilde{\zeta }}^{(j)}(z),$

(2) 

${\tilde{\zeta }}^{(j)}(y^{-1})\ge {\tilde{\zeta }}^{(j)}(y),$

for all $j\in \{1,2,\dots ,m\}.$

As a combination between a $\mathcal{CS}$ and an ${}_m\mathcal{PF}$ structure, Riaz and Hashmi [31] propounded the theory of ${\mathcal{C}}_m\mathcal{P}$ structure as follows:

Definition 5.

A ${\mathcal{C}}_m\mathcal{P}$ structure of $\mathbb{G}(\ne \varphi )$ is a mapping

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}:\mathbb{G}\to {\left[I\right]}^m\times I^m$$

defined as

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}=\left\{⟨y,({\tilde{\tilde{\xi }}}^{(j)}(y),{\tilde{\zeta }}^{(j)}(y))⟩\mid y\in \mathbb{G}andj\in \{1,2,\dots ,m\}\right\},$$

where for $j\in \{1,2,\dots ,m\},$ ${\tilde{\tilde{\xi }}}^{(j)}:\mathbb{G}\to {\left[I\right]}^m$ and ${\tilde{\zeta }}^{(j)}:\mathbb{G}\to I^m$ are the j-th projection mappings.

That is,

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}=\left\{⟨y,([{\tilde{\xi }}^{(-j)}(y),{\tilde{\xi }}^{(+j)}(y)],{\tilde{\zeta }}^{(j)}(y))⟩\mid y\in \mathbb{G}andj\in \{1,2,\dots ,m\}\right\},$$

where ${\tilde{\xi }}^{(-j)},$ ${\tilde{\xi }}^{(+j)}$ and ${\tilde{\zeta }}^{(j)}$ are $\mathcal{FS}s$ of $\mathbb{G}$ with ${\tilde{\xi }}^{(-j)}\le {\tilde{\xi }}^{(+j)}$ for all $j\in \{1,2,\dots ,m\}.$

Definition 6

([31]). Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be two ${\mathcal{C}}_m\mathcal{P}$ structures over $\mathbb{G}.$ Then the equal operation for these structures is defined as follows: ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\iff \tilde{\tilde{\xi }}(y)=\tilde{\tilde{\gamma }}(y)$ and $\tilde{\zeta }(y)=\tilde{\delta }(y)$ for all $y\in \mathbb{G}.$

That is, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\iff {\tilde{\xi }}^{(-j)}(y)={\tilde{\gamma }}^{(-j)}(y),$ ${\tilde{\xi }}^{(+j)}(y)={\tilde{\gamma }}^{(+j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y)={\tilde{\delta }}^{(j)}(y)$ for all $y\in \mathbb{G}$ for all $j\in \{1,2,\dots ,m\}$ and $y\in \mathbb{G}.$

Definition 7

([31]). Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be two ${\mathcal{C}}_m\mathcal{P}$ structures over $\mathbb{G}.$ Then the subset for these structures under P-ordering and R-ordering operations, respectively, is defined as follows:

(1) 

${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}{\tilde{\subseteq }}_P{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\iff \tilde{\tilde{\xi }}(y)⪯\tilde{\tilde{\gamma }}(y)$ and $\tilde{\zeta }(y)\le \tilde{\delta }(y)$ for all $y\in \mathbb{G}.$

That is, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}{\tilde{\subseteq }}_P{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\iff {\tilde{\xi }}^{(-j)}(y)\le {\tilde{\gamma }}^{(-j)}(y),$ ${\tilde{\xi }}^{(+j)}(y)\le {\tilde{\gamma }}^{(+j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y)\le {\tilde{\delta }}^{(j)}(y)$ for all $j\in \{1,2,\dots ,m\}$ and $y\in \mathbb{G}.$

(2) 

${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}{\tilde{\subseteq }}_R{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\iff \tilde{\tilde{\xi }}(y)⪯\tilde{\tilde{\gamma }}(y)$ and $\tilde{\zeta }(y)\ge \tilde{\delta }(y)$ for all $y\in \mathbb{G}.$

That is, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}{\tilde{\subseteq }}_P{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\iff {\tilde{\xi }}^{(-j)}(y)\le {\tilde{\gamma }}^{(-j)}(y),$ ${\tilde{\xi }}^{(+j)}(y)\le {\tilde{\gamma }}^{(+j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y)\ge {\tilde{\delta }}^{(j)}(y)$ for all $j\in \{1,2,\dots ,m\}$ and $y\in \mathbb{G}.$

3. Cubic m-Polar Groups

In this segment, we initiate ${\mathcal{C}}_m\mathcal{P}$ groups and normal ${\mathcal{C}}_m\mathcal{P}$ subgroups, and investigate their fundamental properties. Throughout this article, let $(\mathbb{G},\diamond )$ be a group with the identity element “e” and a binary operation “⋄”. Here, $y^{-1}$ is the inverse of $y\in \mathbb{G},$ and we use $yz$ instead of $y\diamond z$ $\forall y,z\in \mathbb{G}.$

Definition 8.

Let $\mathbb{G}$ be a group and let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ structure. Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ groupoid over $\mathbb{G}$ if for all $y,z\in \mathbb{G},$

(1) 

${\tilde{\tilde{\xi }}}^{(j)}(yz)⪰{\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z),$

(2) 

${\tilde{\zeta }}^{(j)}(yz)\le {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)$

for all $j\in \{1,2,\dots ,m\}.$

A ${\mathcal{C}}_m\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}$ if the ${\mathcal{C}}_m\mathcal{P}$ groupoid satisfies:

(1) 

${\tilde{\tilde{\xi }}}^{(j)}(y^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y),$

(2) 

${\tilde{\zeta }}^{(j)}(y^{-1})\le {\tilde{\zeta }}^{(j)}(y)$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Example 1.

Let $({\mathbb{Z}}_3,{+}_3)$ be a group and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}:{\mathbb{Z}}_3\to {\left[I\right]}^3\times I^3$ be a ${\mathcal{C}}_3\mathcal{P}$ structure over ${\mathbb{Z}}_3$ defined by:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}=\left\{\begin{array}{cc}⟨0,\hfill & ([0.8,0.9],0.2),\left(\right[0.7,0.8],0.3),\hfill \\ & ([0.6,0.7],0.4)⟩,\hfill \\ ⟨1,\hfill & ([0.7,0.9],0.3),([0.6,0.8],0.4),\hfill \\ & ([0.4,0.6],0.5)⟩,\hfill \\ ⟨2,\hfill & ([0.7,0.9],0.3),([0.6,0.8],0.4),\hfill \\ & ([0.4,0.6],0.5)⟩.\hfill \end{array}\right\}$$

It is not difficult to demonstrate that ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ is a ${\mathcal{C}}_3\mathcal{P}$ group over ${\mathbb{Z}}_3.$ However, the ${\mathcal{C}}_3\mathcal{P}$ structure

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}=\left\{\begin{array}{cc}⟨0,\hfill & ([0.6,0.8],0.4),([0.7,0.8],0.3),\hfill \\ & ([0.6,0.7],0.4)⟩,\hfill \\ ⟨1,\hfill & ([0.7,0.9],0.3),([0.6,0.8],0.4),\hfill \\ & ([0.4,0.6],0.5)⟩,\hfill \\ ⟨2,\hfill & ([0.7,0.9],0.3),([0.6,0.8],0.4),\hfill \\ & ([0.4,0.6],0.5)⟩.\hfill \end{array}\right\}$$

is not a ${\mathcal{C}}_3\mathcal{P}$ group of ${\mathbb{Z}}_3,$ since ${\tilde{\tilde{\gamma }}}^{(1)}(0)={\tilde{\tilde{\gamma }}}^{(1)}(1+2)=[0.6,0.8]⪯[0.7,0.9]={\tilde{\tilde{\gamma }}}^{(1)}(1)\overline{\wedge }{\tilde{\tilde{\gamma }}}^{(1)}(2)$ and ${\tilde{\delta }}^{(1)}(0)={\tilde{\delta }}^{(1)}(1+2)=0.4\ge 0.3={\tilde{\delta }}^{(1)}(1)\vee {\tilde{\delta }}^{(1)}(2).$

Definition 8 and Example 1 illustrate that a ${\mathcal{C}}_m\mathcal{P}$ group is an extension case of a cubic group and an ${}_m\mathcal{PF}$ group.

Next, we define the inverse of a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$

Definition 9.

Let $\mathbb{G}$ be a group and let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ structure. Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}^{-1}$ is defined as:

$${\mathsf{\Xi }}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}^{-1}=\left\{⟨y,({\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y),{\tilde{\zeta }}^{{(j)}^{-1}}(y))⟩\mid y\in \mathbb{G}\mathrm{and}j\in \{1,2,\dots ,m\}\right\},$$

where

$${\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y)={\tilde{\tilde{\xi }}}^{(j)}(y^{-1})=[{\tilde{\xi }}^{(-j)}(y^{-1}),{\tilde{\xi }}^{(+j)}(y^{-1})]$$

and

$${\tilde{\zeta }}^{{(j)}^{-1}}(y)={\tilde{\zeta }}^{(j)}(y^{-1})$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Here, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}^{-1}$ is the inverse of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ over $\mathbb{G}.$

The next theorem suggests the necessary and sufficient condition under which the inverse of the ${\mathcal{C}}_m\mathcal{P}$ group will be a ${\mathcal{C}}_m\mathcal{P}$ group.

Theorem 1.

Let $\mathbb{G}$ be a group. A ${\mathcal{C}}_m\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ over $\mathbb{G}$ is a ${\mathcal{C}}_m\mathcal{P}$ group if and only if ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}^{-1}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$

Proof. 

Let $y,z\in \mathbb{G}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$ Then,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(yz)& =& {\tilde{\tilde{\xi }}}^{(j)}({(yz)}^{-1})\hfill \\ & =& {\tilde{\tilde{\xi }}}^{(j)}(z^{-1}{y}^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(z^{-1})\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y^{-1})\hfill \\ & =& {\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(z)\overline{\wedge }{\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{{(j)}^{-1}}(yz)& =& {\tilde{\zeta }}^{(j)}({(yz)}^{-1})\hfill \\ & =& {\tilde{\zeta }}^{(j)}(z^{-1}{y}^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(z^{-1})\vee {\tilde{\zeta }}^{(j)}(y^{-1})\hfill \\ & =& {\tilde{\zeta }}^{{(j)}^{-1}}(z)\vee {\tilde{\zeta }}^{{(j)}^{-1}}(y).\hfill \end{array}$$

Moreover,

$$\begin{array}{c}\hfill {\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y^{-1})={\tilde{\tilde{\xi }}}^{(j)}({(y^{-1})}^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y^{-1})={\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y)\end{array}$$

and

$$\begin{array}{c}\hfill {\tilde{\zeta }}^{{(j)}^{-1}}(y^{-1})={\tilde{\zeta }}^{(j)}({(y^{-1})}^{-1})\le {\tilde{\zeta }}^{(j)}(y^{-1})={\tilde{\zeta }}^{{(j)}^{-1}}(y)\end{array}$$

for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Thus, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}^{-1}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$

Conversely, let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}^{-1}$ be a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$ Then,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(yz)& =& {\tilde{\tilde{\xi }}}^{(j)}({({(yz)}^{-1})}^{-1})\hfill \\ & =& {\tilde{\tilde{\xi }}}^{{(j)}^{-1}}({(yz)}^{-1})\hfill \\ & =& {\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(z^{-1}{y}^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(z^{-1})\overline{\wedge }{\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y^{-1})\hfill \\ & =& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{(j)}(yz)& =& {\tilde{\zeta }}^{(j)}({({(yz)}^{-1})}^{-1})\hfill \\ & =& {\tilde{\zeta }}^{{(j)}^{-1}}({(yz)}^{-1})\hfill \\ & =& {\tilde{\zeta }}^{{(j)}^{-1}}(z^{-1}{y}^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{{(j)}^{-1}}(z^{-1})\vee {\tilde{\zeta }}^{{(j)}^{-1}}(y^{-1})\hfill \\ & =& {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z).\hfill \end{array}$$

Moreover,

$$\begin{array}{c}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y^{-1})={\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y)={\tilde{\tilde{\xi }}}^{{(j)}^{-1}}({(y^{-1})}^{-1})⪰{\tilde{\tilde{\xi }}}^{{(j)}^{-1}}(y^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y)\end{array}$$

and

$$\begin{array}{c}\hfill {\tilde{\zeta }}^{(j)}(y^{-1})={\tilde{\zeta }}^{{(j)}^{-1}}(y)={\tilde{\zeta }}^{{(j)}^{-1}}({(y^{-1})}^{-1})\le {\tilde{\zeta }}^{{(j)}^{-1}}(y^{-1})\le {\tilde{\zeta }}^{(j)}(y)\end{array}$$

for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Hence, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$    □

Theorem 2.

Let $\mathbb{G}$ be a group and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group. Then,

(i) 

${\tilde{\tilde{\xi }}}^{(j)}(e)⪰{\tilde{\tilde{\xi }}}^{(j)}(y)$ and ${\tilde{\zeta }}^{(j)}(e)\le {\tilde{\zeta }}^{(j)}(y)$ $\forall y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

(ii) 

${\tilde{\tilde{\xi }}}^{(j)}(y^{-1})={\tilde{\tilde{\xi }}}^{(j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y^{-1})={\tilde{\zeta }}^{(j)}(y)$ $\forall y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Proof. 

(i) Since ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G},$ then

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(e)& =& {\tilde{\tilde{\xi }}}^{(j)}(y{y}^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y)\hfill \\ & =& {\tilde{\tilde{\xi }}}^{(j)}(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{(j)}(e)& =& {\tilde{\zeta }}^{(j)}(y{y}^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(y^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& {\tilde{\zeta }}^{(j)}(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

(ii) Since ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G},$ therefore ${\tilde{\tilde{\xi }}}^{(j)}(y^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y^{-1})\le {\tilde{\zeta }}^{(j)}(y)$ for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Replacing y by $y^{-1},$ it is obtained that ${\tilde{\tilde{\xi }}}^{(j)}(y)⪰{\tilde{\tilde{\xi }}}^{(j)}(y^{-1})$ and ${\tilde{\zeta }}^{(j)}(y)\le {\tilde{\zeta }}^{(j)}(y^{-1})$ for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Thus, ${\tilde{\tilde{\xi }}}^{(j)}(y^{-1})={\tilde{\tilde{\xi }}}^{(j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y^{-1})\le {\tilde{\zeta }}^{(j)}(y)$ $\forall y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$    □

Theorem 3.

Let $\mathbb{G}$ be a group and let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ structure of $\mathbb{G}.$ If ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group, then ${\tilde{\tilde{\xi }}}^{(j)}(y^n)⪰{\tilde{\tilde{\xi }}}^{(j)}(y)$ and ${\tilde{\zeta }}^{(j)}(y^n)\le {\tilde{\zeta }}^{(j)}(y)$ for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Proof. 

Since ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G},$ then

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y^n)& ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y^{n-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }\dots \overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y)\hfill \\ & =& {\tilde{\tilde{\xi }}}^{(j)}(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{(j)}(y^n)& \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(y^{n-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(y)\vee \dots \vee {\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& {\tilde{\zeta }}^{(j)}(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$    □

The next Theorem suggests the necessary and sufficient condition under which a ${\mathcal{C}}_m\mathcal{P}$ structure will be a ${\mathcal{C}}_m\mathcal{P}$ group.

Theorem 4.

Let $\mathbb{G}$ be a group and let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ structure of $\mathbb{G}.$ Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group if and only if ${\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)$ and ${\tilde{\zeta }}^{(j)}(y{z}^{-1})\le {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(y)$ for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Proof. 

Since ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G},$ therefore

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})& ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{(j)}(y{z}^{-1})& \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Conversely, assume the given conditions are satisfied. Then,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y^{-1})& =& {\tilde{\tilde{\xi }}}^{(j)}(e{y}^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(e)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(y)\hfill \\ & =& {\tilde{\tilde{\xi }}}^{(j)}(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{(j)}(y^{-1})& =& {\tilde{\zeta }}^{(j)}(e{y}^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(e)\vee {\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& {\tilde{\zeta }}^{(j)}(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Moreover,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(yz)& =& {\tilde{\tilde{\xi }}}^{(j)}(y{(z^{-1})}^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z^{-1})\hfill \\ & ⪰& {\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tilde{\zeta }}^{(j)}(yz)& =& {\tilde{\zeta }}^{(j)}(y{(z^{-1})}^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z^{-1})\hfill \\ & \le & {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)\hfill \end{array}$$

for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Hence, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group of $\mathbb{G}.$    □

Theorem 5.

Let $\mathbb{G}$ be a group and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group. Then, the following are equivalent for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\},$

(i) 

${\tilde{\tilde{\xi }}}^{(j)}(yz)={\tilde{\tilde{\xi }}}^{(j)}(zy)$ and ${\tilde{\zeta }}^{(j)}(yz)={\tilde{\zeta }}^{(j)}(zy).$

(ii) 

${\tilde{\tilde{\xi }}}^{(j)}(yz{y}^{-1})={\tilde{\tilde{\xi }}}^{(j)}(z)$ and ${\tilde{\zeta }}^{(j)}(yz{y}^{-1})={\tilde{\zeta }}^{(j)}(z).$

(iii) 

${\tilde{\tilde{\xi }}}^{(j)}(yz{y}^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(z)$ and ${\tilde{\zeta }}^{(j)}(yz{y}^{-1})\le {\tilde{\zeta }}^{(j)}(z).$

(iv) 

${\tilde{\tilde{\xi }}}^{(j)}(yz{y}^{-1})⪯{\tilde{\tilde{\xi }}}^{(j)}(z)$ and ${\tilde{\zeta }}^{(j)}(yz{y}^{-1})\ge {\tilde{\zeta }}^{(j)}(z).$

Proof. 

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group and $y,z\in \mathbb{G}.$ Then, for all $j\in \{1,2,\dots ,m\},$ we have

• $(i)\Rightarrow (ii):$

  $${\tilde{\tilde{\xi }}}^{(j)}(yz{y}^{-1})={\tilde{\tilde{\xi }}}^{(j)}(y^{-1}yz)={\tilde{\tilde{\xi }}}^{(j)}(z)\mathrm{and}{\tilde{\zeta }}^{(j)}(yz{y}^{-1})={\tilde{\zeta }}^{(j)}(y^{-1}yz)={\tilde{\zeta }}^{(j)}(z).$$
  Thus, condition $(ii)$ holds.
• $(ii)\Rightarrow (iii):$ Immediate.
• $(iii)\Rightarrow (iv):$

  $${\tilde{\tilde{\xi }}}^{(j)}(yz{y}^{-1})⪯{\tilde{\tilde{\xi }}}^{(j)}(y^{-1}yz{(y^{-1})}^{-1})={\tilde{\tilde{\xi }}}^{(j)}(z)\mathrm{and}{\tilde{\zeta }}^{(j)}(yz{y}^{-1})\ge {\tilde{\zeta }}^{(j)}(y^{-1}yz{(y^{-1})}^{-1})={\tilde{\zeta }}^{(j)}(z).$$
  Therefore, condition $(iii)$ holds.
• $(iv)\Rightarrow (i):$

  $${\tilde{\tilde{\xi }}}^{(j)}(yz)={\tilde{\tilde{\xi }}}^{(j)}(yzy{y}^{-1})⪯{\tilde{\tilde{\xi }}}^{(j)}(zy)\mathrm{and}{\tilde{\zeta }}^{(j)}(yz)\ge {\tilde{\zeta }}^{(j)}(yzy{y}^{-1})={\tilde{\zeta }}^{(j)}(zy).$$
  Hence, condition $(i)$ holds.

    □

Definition 10.

Let $\mathbb{H}$ be a subgroup of a group $\mathbb{G}.$ Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be two ${\mathcal{C}}_m\mathcal{P}$ structures of $\mathbb{G}$ and $\mathbb{H},$ respectively, such that ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ ${\tilde{\subseteq }}_P$ (resp., ${\tilde{\subseteq }}_R$) ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$ If ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ is itself a ${\mathcal{C}}_m\mathcal{P}$ group of $\mathbb{H},$ then ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ subgroup of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ over $\mathbb{G}$ and denoted by ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\precsim {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$

Example 2.

Let us assume the group $({\mathbb{Z}}_3,{+}_3)$ and a ${\mathcal{C}}_3\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ given in Example 1. Define a ${\mathcal{C}}_3\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ over $({\mathbb{Z}}_3,{+}_3)$ by:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}=\left\{\begin{array}{cc}⟨0,\hfill & ([0.6,0.7],0.1),([0.5,0.6],0.2),\hfill \\ & ([0.4,0.5],0.3)⟩,\hfill \\ ⟨1,\hfill & ([0.5,0.7],0.2),([0.4,0.6],0.3),\hfill \\ & ([0.2,0.4],0.4)⟩,\hfill \\ ⟨2,\hfill & ([0.5,0.7],0.2),([0.4,0.6],0.3),\hfill \\ & ([0.2,0.4],0.4)⟩.\hfill \end{array}\right\}$$

It is clear that ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ ${\tilde{\subseteq }}_P$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ itself is a ${\mathcal{C}}_3\mathcal{P}$ group over ${\mathbb{Z}}_3.$ Thus, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ is a ${\mathcal{C}}_3\mathcal{P}$ subgroup of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ over ${\mathbb{Z}}_3,$ and denoted by ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}\precsim {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}.$

From Definition 10 and Example 2, it is clear that a ${\mathcal{C}}_m\mathcal{P}$ subgroup is itself a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}.$

Definition 11.

Let $\mathbb{G}$ be a group, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ subgroup of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ over $\mathbb{G}.$ Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ is called a normal ${\mathcal{C}}_m\mathcal{P}$ subgroup of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m},$ denoted by ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\widetilde{⊳}{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ if

$${\tilde{\tilde{\gamma }}}^{(j)}(yz)={\tilde{\tilde{\gamma }}}^{(j)}(zy)and{\tilde{\delta }}^{(j)}(yz)={\tilde{\delta }}^{(j)}(zy)$$

(1)

for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Example 3.

Let $(S_3,\circ )$ be a symmetric group, where $S_3=\{e,(12),(13),(23),(123),(132)\}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}:S_3\to {\left[I\right]}^3\times I^3$ be a ${\mathcal{C}}_3\mathcal{P}$ structure over $S_3$ defined by:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}(y)=\left\{\begin{array}{cc}⟨([0.7,0.9],0.2),([0.5,0.7],0.2),([0.6,0.8],0.2)⟩,\hfill & y\in A_1,\hfill \\ ⟨([0.4,0.6],0.6),([0.3,0.5],0.6),([0.4,0.6],0.6)⟩,\hfill & y\in A_2,\hfill \\ ⟨([0.6,0.8],0.3),([0.5,0.7],0.3),([0.6,0.8],0.3)⟩,\hfill & y\in A_3,\hfill \end{array}\right\}$$

where $A_1=\left\{e\right\},A_2=\{(12),(13),(23)\}$ and $A_3=\{(123),(132)\}.$ Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ is a ${\mathcal{C}}_3\mathcal{P}$ group of $S_3.$ Since ${\tilde{\tilde{\gamma }}}^{(j)}(yz)={\tilde{\tilde{\gamma }}}^{(j)}(zy)$ and ${\tilde{\delta }}^{(j)}(yz)={\tilde{\delta }}^{(j)}(zy)$ for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\},$ then ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ is a ${\mathcal{C}}_3\mathcal{P}$ normal subgroup over $S_3.$

Remark 1.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group over $\mathbb{G}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ subgroup of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ over $\mathbb{G}.$ If $\mathbb{G}$ is abelian group, then ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ is a normal ${\mathcal{C}}_m\mathcal{P}$ subgroup of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ over $\mathbb{G}.$

Example 4.

Let us consider the ${\mathcal{C}}_3\mathcal{P}$ group ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ over ${\mathbb{Z}}_3$ in Example 1. Since ${\mathbb{Z}}_3$ is an abelian group, then ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ is a normal ${\mathcal{C}}_3\mathcal{P}$ subgroup over ${\mathbb{Z}}_3.$

Theorem 6.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be a normal ${\mathcal{C}}_m\mathcal{P}$ subgroup of $\mathbb{G}.$ Then, the conditions (1) and $(H)$ are equivalent, where

$$\begin{array}{c}(H) \left\{{\tilde{\tilde{\gamma }}}^{(j)}(yz{y}^{-1})={\tilde{\tilde{\gamma }}}^{(j)}(z)and{\tilde{\delta }}^{(j)}(yz{y}^{-1})={\tilde{\delta }}^{(j)}(z)\right\}\hfill \end{array}$$

for all $y.z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Proof. 

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be a normal ${\mathcal{C}}_m\mathcal{P}$ subgroup of $\mathbb{G}.$ Taking $z{y}^{-1}$ instead of z in (1) and by Theorem 5 (ii), we have

$${\tilde{\tilde{\gamma }}}^{(j)}(yz{y}^{-1})={\tilde{\tilde{\gamma }}}^{(j)}(z)\mathrm{and}{\tilde{\delta }}^{(j)}(yz{y}^{-1})={\tilde{\delta }}^{(j)}(z)$$

for all $y,z\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Conversely, assume that condition $(H)$ holds. Taking $zy$ instead of z in (H), then condition (1) is shown easily.    □

Definition 12.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be any ${\mathcal{C}}_m\mathcal{P}$ structure over $\mathbb{G},$ $\widetilde{[\rho ,\tau ]}\in {\left[I\right]}^m$ and $\tilde{\sigma }\in I^m.$ Define the $\widetilde{[\rho ,\tau ]}$-level and $\tilde{\sigma }$-level of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ as follows:

$${\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}=\left\{y\in \mathbb{G}\mid \tilde{\tilde{\xi }}(y)⪰\widetilde{[\rho ,\tau ]}\right\}and{\tilde{\zeta }}_{\tilde{\sigma }}=\left\{y\in \mathbb{G}\mid \tilde{\zeta }(y)\le \tilde{\sigma }\right\}.$$

That is,

$${\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}=\left\{y\in \mathbb{G}\mid {\tilde{\tilde{\xi }}}^{(j)}(y)⪰[{\rho }_j,{\tau }_j]\right\}and{\tilde{\zeta }}_{\tilde{\sigma }}=\left\{y\in \mathbb{G}\mid {\tilde{\zeta }}^{(j)}(y)\le {\sigma }_j\right\},$$

where $[{\rho }_j,{\tau }_j]\in \left[I\right]$ and ${\sigma }_j\in I$ for each $j\in \{1,2,\dots ,m\}.$

The following theorem reflects on $\widetilde{[\rho ,\tau ]}$-level and $\tilde{\sigma }$-level of a ${\mathcal{C}}_m\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$ It actually tells about the condition imposed on $\widetilde{[\rho ,\tau ]}$-level and $\tilde{\sigma }$-level of a ${\mathcal{C}}_m\mathcal{P}$ structure under which a ${\mathcal{C}}_m\mathcal{P}$ structure will be a ${\mathcal{C}}_m\mathcal{P}$ group.

Theorem 7.

Let $\mathbb{G}$ be a group and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ structure over $\mathbb{G}.$ Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group if $\widetilde{[\rho ,\tau ]}$-level, ${\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}$ and $\tilde{\sigma }$-level, ${\tilde{\zeta }}_{\tilde{\sigma }}$ are crisp subgroups of $\mathbb{G}.$

Proof. 

Let $y,z\in \mathbb{G},$ with $[{\rho }_j,{\tau }_j]={\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)$ and ${\sigma }_j={\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)$ for all $j\in \{1,2,\dots ,m\}.$ Then, $[{\rho }_j,{\tau }_j]\in \left[I\right]$ and ${\sigma }_j\in I.$ It is observed that

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y)& ⪰& [{\rho }_j,{\tau }_j]={\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)\hfill \\ \hfill {\tilde{\zeta }}^{(j)}(y)& \le & {\sigma }_j={\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)\hfill \end{array}$$

for all $j\in \{1,2,\dots ,m\}.$ Moreover,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(z)& ⪰& [{\rho }_j,{\tau }_j]={\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)\hfill \\ \hfill {\tilde{\zeta }}^{(j)}(z)& \le & {\sigma }_j={\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)\hfill \end{array}$$

for all $j\in \{1,2,\dots ,m\}.$ Thus,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y)& ⪰& [{\rho }_j,{\tau }_j],\hfill \\ \hfill {\tilde{\zeta }}^{(j)}(y)& \le & {\sigma }_j,\hfill \\ \hfill {\tilde{\tilde{\xi }}}^{(j)}(z)& ⪰& [{\rho }_j,{\tau }_j],\hfill \\ \hfill {\tilde{\zeta }}^{(j)}(z)& \le & {\sigma }_j.\hfill \end{array}$$

It follows that $y,z\in {\tilde{\tilde{\xi }}}_{\widetilde{[\rho ,\tau ]}}$ and $y,z\in {\tilde{\zeta }}_{\tilde{\sigma }}.$ Since ${\tilde{\tilde{\xi }}}_{\widetilde{[\rho ,\tau ]}}$ and ${\tilde{\zeta }}_{\tilde{\sigma }}$ are crisp subgroups of $\mathbb{G},$ then $y{z}^{-1}\in {\tilde{\tilde{\xi }}}_{\widetilde{[\rho ,\tau ]}}$ and $y{z}^{-1}\in {\tilde{\zeta }}_{\tilde{\sigma }}.$ Therefore,

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})& ⪰& [{\rho }_j,{\tau }_j]={\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)\hfill \\ \hfill {\tilde{\zeta }}^{(j)}(y{z}^{-1})& \le & {\sigma }_j={\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)\hfill \end{array}$$

for all $j\in \{1,2,\dots ,m\}.$ Since $y,z$ are arbitrary elements of $\mathbb{G},$ then ${\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)$ and ${\tilde{\zeta }}^{(j)}(y{z}^{-1})\le {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z).$ Thus, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ is a ${\mathcal{C}}_m\mathcal{P}$ group of $\mathbb{G}.$    □

Theorem 8.

Let $\mathbb{G}$ be a group and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group of $\mathbb{G}.$ Then, the nonempty set

$$\mathsf{\Omega }=\{y\in G\mid {\tilde{\tilde{\xi }}}^{(j)}(y)={\tilde{\tilde{\xi }}}^{(j)}(e),{\tilde{\zeta }}^{(j)}(y)={\tilde{\zeta }}^{(j)}(e)\forall j\in \{1,2,\dots ,m\}\}$$

forms a crisp subgroup of $\mathbb{G}.$

Proof. 

Let $y,z\in \mathsf{\Omega }.$ Then, ${\tilde{\tilde{\xi }}}^{(j)}(y)={\tilde{\tilde{\xi }}}^{(j)}(e),$ ${\tilde{\tilde{\xi }}}^{(j)}(z)={\tilde{\tilde{\xi }}}^{(j)}(e),$ ${\tilde{\zeta }}^{(j)}(y)={\tilde{\zeta }}^{(j)}(e)$ and ${\tilde{\zeta }}^{(j)}(z)={\tilde{\zeta }}^{(j)}(e)$ for all $j\in \{1,2,\dots ,m\}.$ It follows that

$${\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z^{-1})={\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)={\tilde{\tilde{\xi }}}^{(j)}(e)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(e)={\tilde{\tilde{\xi }}}^{(j)}(e)$$

and

$${\tilde{\zeta }}^{(j)}(y{z}^{-1})\le {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z^{-1})={\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)={\tilde{\zeta }}^{(j)}(e)\vee {\tilde{\zeta }}^{(j)}(e)={\tilde{\zeta }}^{(j)}(e)$$

for all $j\in \{1,2,\dots ,m\}.$ Since ${\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})⪯{\tilde{\tilde{\xi }}}^{(j)}(e)$ and ${\tilde{\zeta }}^{(j)}(y{z}^{-1})\ge {\tilde{\zeta }}^{(j)}(e)$ for all $j\in \{1,2,\dots ,m\},$ then ${\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})={\tilde{\tilde{\xi }}}^{(j)}(e)$ and ${\tilde{\zeta }}^{(j)}(y{z}^{-1})={\tilde{\zeta }}^{(j)}(e),$ implying that $y{z}^{-1}\in \mathsf{\Omega }$ and $\mathsf{\Omega }$ is a crisp subgroup of $\mathbb{G}.$    □

The following Theorem reflects on $\widetilde{[\rho ,\tau ]}$-level and $\tilde{\sigma }$-level of a ${\mathcal{C}}_m\mathcal{P}$ group ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$ From Definition 12, we notice that $\widetilde{[\rho ,\tau ]}$-level and $\tilde{\sigma }$-level are crisp sets. From the next theorem, we will know that $\widetilde{[\rho ,\tau ]}$-level and $\tilde{\sigma }$-level are crisp subgroups of $\mathbb{G}.$

Theorem 9.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ group over a group $\mathbb{G}.$ Then, for all $\widetilde{[\rho ,\tau ]}\in {\left[I\right]}^m$ and $\tilde{\sigma }\in I^m,$ $\widetilde{[\rho ,\tau ]}$-level, ${\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}\ne \varnothing$ and $\tilde{\sigma }$-level, ${\tilde{\zeta }}_{\tilde{\sigma }}\ne \varnothing$ of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ are crisp subgroups of $\mathbb{G}.$

Proof. 

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ be a ${\mathcal{C}}_m\mathcal{P}$ subgroup of a group $\mathbb{G},$ $\widetilde{[\rho ,\tau ]}\in {\left[I\right]}^m$ and $\tilde{\sigma }\in I^m.$ Let $y,z\in {\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}.$ By assumption,

$${\tilde{\tilde{\xi }}}^{(j)}(y{z}^{-1})⪰{\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z^{-1})={\tilde{\tilde{\xi }}}^{(j)}(y)\overline{\wedge }{\tilde{\tilde{\xi }}}^{(j)}(z)⪰[{\rho }_j,{\tau }_j]$$

for all $j\in \{1,2,\dots ,m\}.$ Hence, $y{z}^{-1}\in {\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}.$ Similarly, let $y,z\in {\tilde{\zeta }}_{\tilde{\sigma }}.$ Then,

$${\tilde{\zeta }}^{(j)}(y{z}^{-1})\le {\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z^{-1})={\tilde{\zeta }}^{(j)}(y)\vee {\tilde{\zeta }}^{(j)}(z)\le {\sigma }_j$$

for all $j\in \{1,2,\dots ,m\}.$ Hence, $y{z}^{-1}\in {\tilde{\zeta }}_{\tilde{\sigma }}.$ Therefore, ${\tilde{\tilde{\xi }}}_{(\widetilde{[\rho ,\tau ]}}$ and ${\tilde{\zeta }}_{\tilde{\sigma }}$ are crisp subgroups of $\mathbb{G}.$    □

4. Commutative Semigroup Structures of Cubic m-Polar Structures

In this section, we construct a commutative semigroup structure and a commutative groupoid structure by providing binary operations for the ${\mathcal{C}}_m\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$. In the current section,

• We use the group $\mathbb{G}$ as the universe set (domain of discourse).
• ${\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}}$ denotes the collection of all ${\mathcal{C}}_m\mathcal{P}$ structures over $\mathbb{G}.$

Definition 13.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be two ${\mathcal{C}}_m\mathcal{P}$ structures on a set $\mathbb{G}.$ Then, the symmetric difference of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\psi }},\tilde{\mu })}_m},$ denoted by ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m},$ is defined as ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }},\tilde{\zeta }\boxminus \tilde{\delta })}_m}$ in which

$$\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }}:\mathbb{G}\to {\left[I\right]}^{m}and\tilde{\zeta }\boxminus \tilde{\delta }:\mathbb{G}\to I^m,$$

where

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }})(y)& =& \left[{(\tilde{\xi }\boxminus \tilde{\gamma })}^{-(j)}(y),{(\tilde{\xi }\boxminus \tilde{\gamma })}^{+(j)}(y)\right]\hfill \\ & =& \left[|{\tilde{\xi }}^{-(j)}(y)-{\tilde{\gamma }}^{-(j)}(y)|,|{\tilde{\xi }}^{+(j)}(y)-{\tilde{\gamma }}^{+(j)}(y)|\right]\hfill \end{array}$$

and

$$(\tilde{\zeta }\boxminus \tilde{\delta })(y)=|{\tilde{\zeta }}^{(j)}(y)-{\tilde{\delta }}^{(j)}(y)|$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Example 5.

Consider the set $\mathbb{G}=\{1,\alpha ,{\alpha }^2\}$ under the ordinary multiplication “.”, where ${\alpha }^3=1.$ Then, it is clear that $(\mathbb{G},.)$ is a group. Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}:\mathbb{G}\to {\left[I\right]}^4\times I^4$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}:\mathbb{G}\to {\left[I\right]}^4\times I^4$ be two ${\mathcal{C}}_4\mathcal{P}$ structures on a set $\mathbb{G}$ defined by:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.4,0.8],0.3),([0.3,0.7],0.4),\hfill \\ & ([0.3,0.8],0.4),([0.2,0.3],0.1)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.3,0.8],0.3),([0.1,0.4],0.4),\hfill \\ & ([0.3,0.5],0.4),([0.1,0.2],0.2)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.3,0.8],0.2),([0.3,0.8],0.3),\hfill \\ & ([0.1,0.8],0.4),([0.3,0.8],0.2)⟩.\hfill \end{array}\right\}$$

and

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.2,0.5],0.4),([0.3,0.6],0.2),\hfill \\ & ([0.3,0.4],0.4),([0.3,0.4],0.3)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.3,0.4],0.4),([0.1,0.2],0.3),\hfill \\ & ([0.7,0.9],0.6),([0.1,0.3],0.4)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.3,0.5],0.4),([0.3,0.4],0.3),\hfill \\ & ([0.0,0.4],0.5),([0.3,0.4],0.4)⟩.\hfill \end{array}\right\}$$

Then, the symmetric difference ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}$ of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}$ is given as follows:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }},\tilde{\zeta }\boxminus \tilde{\delta })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.2,0.3],0.1),([0.0,0.1],0.2),\hfill \\ & ([0.0,0.4],0.0),([0.1,0.1],0.2)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.0,0.4],0.1),([0.0,0.2],0.1),\hfill \\ & ([0.4,0.4],0.2),([0.0,0.1],0.2)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.0,0.3],0.2),([0.0,0.4],0.0),\hfill \\ & ([0.1,0.4],0.1),([0.0,0.4],0.2)⟩.\hfill \end{array}\right\}$$

Theorem 10.

$({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus )$ is a commutative groupoid with identity element ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}.$

Proof. 

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m},$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}}.$ Then,

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }})(y)& =& \left[{(\tilde{\xi }\boxminus \tilde{\gamma })}^{-(j)}(y),{(\tilde{\xi }\boxminus \tilde{\gamma })}^{+(j)}(y)\right]\hfill \\ & =& \left[|{\tilde{\xi }}^{-(j)}(y)-{\tilde{\gamma }}^{-(j)}(y)|,|{\tilde{\xi }}^{+(j)}(y)-{\tilde{\gamma }}^{+(j)}(y)|\right]\hfill \\ & =& \left[|{\tilde{\gamma }}^{-(j)}(y)-{\tilde{\xi }}^{-(j)}(y)|,|{\tilde{\gamma }}^{+(j)}(y)-{\tilde{\xi }}^{+(j)}(y)|\right]\hfill \\ & =& \left[{(\tilde{\gamma }\boxminus \tilde{\xi })}^{-(j)}(y),{(\tilde{\gamma }\boxminus \tilde{\xi })}^{+(j)}(y)\right]\hfill \\ & =& (\tilde{\tilde{\gamma }}\boxminus \tilde{\tilde{\xi }})(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (\tilde{\zeta }\boxminus \tilde{\delta })(y)& =& |{\tilde{\zeta }}^{(j)}(y)-{\tilde{\delta }}^{(j)}(y)|\hfill \\ & =& |{\tilde{\delta }}^{(j)}(y)-{\tilde{\zeta }}^{(j)}(y)|\hfill \\ & =& (\tilde{\delta }\boxminus \tilde{\zeta })(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Thus, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}=$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$ Moreover, for all ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m},$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},$ we have ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}=$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }},\tilde{\zeta }\boxminus \tilde{\delta })}_m}\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}}.$ Finally, for any ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},$ we have

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{0}})(y)& =& \left[{(\tilde{\xi }\boxminus \tilde{0})}^{-(j)}(y),{(\tilde{\xi }\boxminus \tilde{0})}^{+(j)}(y)\right]\hfill \\ & =& \left[|{\tilde{\xi }}^{-(j)}(y)-{\tilde{0}}^{-(j)}(y)|,|{\tilde{\xi }}^{+(j)}(y)-{\tilde{0}}^{+(j)}(y)|\right]\hfill \\ & =& \left[{\tilde{\xi }}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)\right]\hfill \\ & =& \tilde{\tilde{\xi }}(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (\tilde{\zeta }⊞\tilde{0})(y)& =& |{\tilde{\zeta }}^{(j)}(y)-{\tilde{0}}^{(j)}(y)|\hfill \\ & =& {\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& \tilde{\zeta }(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Similarly, for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\},$ we obtain, $(\tilde{\tilde{0}}\boxminus \tilde{\tilde{\xi }})(y)=\left[{\tilde{\xi }}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)\right]=\tilde{\tilde{\xi }}(y)$ and $(\tilde{0}⊞\tilde{\zeta })(y)={\tilde{\zeta }}^{(j)}(y)=\tilde{\zeta }(y).$ Therefore,

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$$

Hence, $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus )$ is a commutative groupoid with identity element ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}.$    □

The following example shows that a binary operation ⊟ is not associative in $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus ),$ where $m=4.$ Hence, ⊟ is not associative in $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus ),$ so $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus )$ is not a semigroup.

Example 6.

Let us assume the group $\mathbb{G},$ a ${\mathcal{C}}_4\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}$ and a ${\mathcal{C}}_4\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}$ in Example 5. Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4}:\mathbb{G}\to {\left[I\right]}^4\times I^4$ be another ${\mathcal{C}}_4\mathcal{P}$ structure on a set $\mathbb{G}$ defined by:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.4,0.8],0.6),\left(\right[0.2,0.4],0.3),\hfill \\ & ([0.1,0.6],0.5),\left(\right[0.2,0.3],0.6)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.1,0.6],0.4),\left(\right[0.1,0.3],0.4),\hfill \\ & ([0.4,0.6],0.7),([0.1,0.6],0.5)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.0,0.9],0.5),([0.1,0.6],0.3),\hfill \\ & ([0.3,0.7],0.5),([0.1,0.6],0.3)⟩.\hfill \end{array}\right\}$$

Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}$ is given as in Example 5 and $({\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4})\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4}$ is given as:

$${\tilde{\mathsf{\Xi }}}_{{((\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\gamma }})\boxminus \tilde{\tilde{\chi }},(\tilde{\zeta }\boxminus \tilde{\delta })\boxminus \tilde{\omega })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.2,0.5],0.5),([0.2,0.3],0.1),\hfill \\ & ([0.1,0.2],0.5),([0.1,0.2],0.4)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.1,0.2],0.3),([0.1,0.1],0.3),\hfill \\ & ([0.0,0.2],0.5),([0.1,0.5],0.3)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.0,0.6],0.3),([0.1,0.2],0.3),\hfill \\ & ([0.2,0.3],0.4),([0.1,0.2],0.1)⟩.\hfill \end{array}\right\}$$

Moreover, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4}$ is given as:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }}\boxminus \tilde{\tilde{\chi }},\tilde{\delta }\boxminus \tilde{\omega })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & \left(\right[0.2,0.3],0.2),\left(\right[0.1,0.2],0.1),\hfill \\ & ([0.2,0.2],0.1),([0.1,0.1],0.3)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.2,0.2],0.0),([0.0,0.1],0.1),\hfill \\ & ([0.3,0.3],0.1),([0.0,0.3],0.1)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.3,0.4],0.1),([0.2,0.2],0.0),\hfill \\ & ([0.3,0.3],0.0),([0.2,0.2],0.1)⟩\hfill \end{array}\right\}$$

and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus ({\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4})$ is given as:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}\boxminus (\tilde{\tilde{\gamma }}\boxminus \tilde{\tilde{\chi }}),\tilde{\zeta }\boxminus (\tilde{\delta }\boxminus \tilde{\omega }))}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.2,0.5],0.1),([0.2,0.5],0.3),\hfill \\ & ([0.1,0.6],0.3),([0.1,0.2],0.2)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.1,0.6],0.3),([0.1,0.3],0.3),\hfill \\ & ([0.0,0.2],0.3),([0.1,0.1],0.1)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.0,0.4],0.1),([0.1,0.6],0.3),\hfill \\ & ([0.2,0.5],0.4),([0.1,0.6],0.1)⟩.\hfill \end{array}\right\}$$

Hence, $({\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4})\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4}\ne {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus ({\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_4}).$ Therefore, a binary operation ⊟ is not an associative in $({\mathcal{L}}_{{\mathcal{C}}_4\mathcal{P}},\boxminus ).$

Remark 2.

$({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus )$ is non-idempotent.

The following example shows that $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},\boxminus )$ is non-idempotent, where $m=4.$

Example 7.

Let us assume the group $\mathbb{G}$ and a ${\mathcal{C}}_4\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}$ in Example 5. Then, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\boxminus {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}\boxminus \tilde{\tilde{\xi }},\tilde{\zeta }\boxminus \tilde{\zeta })}_4}(y)=(\widetilde{[0.0,0.0]},\widetilde{0.0})\ne {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}(y)$ for all $y\in \mathbb{G}.$ Hence, $({\mathcal{L}}_{{\mathcal{C}}_4\mathcal{P}},\boxminus )$ is non-idempotent.

Definition 14.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be two ${\mathcal{C}}_m\mathcal{P}$ structures on a set $\mathbb{G}.$ Then, the sum of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m},$ denoted by ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m},$ is defined as a ${\mathcal{C}}_m\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}⊞\tilde{\tilde{\gamma }},\tilde{\zeta }⊞\tilde{\delta })}_m}$ in which

$$\tilde{\tilde{\xi }}⊞\tilde{\tilde{\gamma }}:\mathbb{G}\to {\left[I\right]}^{m}and\tilde{\zeta }⊞\tilde{\delta }:\mathbb{G}\to I^m,$$

where

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}⊞\tilde{\tilde{\gamma }})(y)& =& \left[{(\tilde{\xi }⊞\tilde{\gamma })}^{-(j)}(y),{(\tilde{\xi }⊞\tilde{\gamma })}^{+(j)}(y)\right]\hfill \\ & =& [{\tilde{\xi }}^{-(j)}(y)+{\tilde{\gamma }}^{-(j)}(y)-{\tilde{\xi }}^{-(j)}(y).{\tilde{\gamma }}^{-(j)}(y),\hfill \\ & & {\tilde{\xi }}^{+(j)}(y)+{\tilde{\gamma }}^{+(j)}(y)-{\tilde{\xi }}^{+(j)}(y)·{\tilde{\gamma }}^{+(j)}(y)]\hfill \end{array}$$

and

$$(\tilde{\zeta }⊞\tilde{\delta })(y)={\tilde{\zeta }}^{(j)}(y)+{\tilde{\delta }}^{(j)}(y)-{\tilde{\zeta }}^{(j)}(y)·{\tilde{\delta }}^{(j)}(y)$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Example 8.

Let us assume the group $\mathbb{G}$ in Example 5. Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}:\mathbb{G}\to {\left[I\right]}^3\times I^3$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}:\mathbb{G}\to {\left[I\right]}^3\times I^3$ be two ${\mathcal{C}}_3\mathcal{P}$ structures on a set $\mathbb{G}$ defined by:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.0,0.0],0.3),([0.09,0.1],0.4),\hfill \\ & ([0.18,0.20],0.4)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.27,0.30],0.3),([0.36,0.4],0.4),\hfill \\ & ([0.45,0.5],0.4)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.54,0.6],0.2),([0.63,0.7],0.3),\hfill \\ & ([0.72,0.8],0.4)⟩.\hfill \end{array}\right\}$$

and

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.0,0.0],0.4),([0.01,0.01],0.2),\hfill \\ & ([0.02,0.04],0.4)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.04,0.09],0.4),([0.08,0.16],0.3),\hfill \\ & ([0.12,0.25],0.6)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.18,0.36],0.4),([0.24,0.49],0.3),\hfill \\ & ([0.32,0.64],0.5)⟩.\hfill \end{array}\right\}$$

Then, the sum ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ is given as follows:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}⊞\tilde{\tilde{\gamma }},\tilde{\zeta }⊞\tilde{\delta })}_3}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.0000,0.0000],0.5800),([0.0991,0.1090],0.5200),\hfill \\ & ([0.1964,0.2320],0.6400)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.2992,0.3630],0.5800),([0.4112,0.4960],0.5800),\hfill \\ & ([0.5160,0.6250],0.7600)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.62228,0.74440],0.52),([0.7188,0.8470],0.5100),\hfill \\ & ([0.8096,0.9280],0.7000)⟩.\hfill \end{array}\right\}$$

Theorem 11.

$({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊞)$ is a commutative semigroup with identity element ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}.$

Proof. 

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m},$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}}.$ Then,

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}⊞\tilde{\tilde{\gamma }})(y)& =& \left[{(\tilde{\xi }⊞\tilde{\gamma })}^{-(j)}(y),{(\tilde{\xi }⊞\tilde{\gamma })}^{+(j)}(y)\right]\hfill \\ & =& [{\tilde{\xi }}^{-(j)}(y)+{\tilde{\gamma }}^{-(j)}(y)-{\tilde{\xi }}^{-(j)}(y).{\tilde{\gamma }}^{-(j)}(y),\hfill \\ & & {\tilde{\xi }}^{+(j)}(y)+{\tilde{\gamma }}^{+(j)}(y)-{\tilde{\xi }}^{+(j)}(y).{\tilde{\gamma }}^{+(j)}(y)]\hfill \\ & =& [{\tilde{\gamma }}^{-(j)}(y)+{\tilde{\xi }}^{-(j)}(y)-{\tilde{\gamma }}^{-(j)}(y).{\tilde{\xi }}^{-(j)}(y),\hfill \\ & & {\tilde{\gamma }}^{+(j)}(y)+{\tilde{\xi }}^{+(j)}(y)-{\tilde{\gamma }}^{+(j)}(y).{\tilde{\xi }}^{+(j)}(y)\hfill \\ & =& \left[{(\tilde{\gamma }⊞\tilde{\xi })}^{-(j)}(y),{(\tilde{\gamma }⊞\tilde{\xi })}^{+(j)}(y)\right]\hfill \\ & =& (\tilde{\tilde{\gamma }}⊞\tilde{\tilde{\xi }})(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (\tilde{\zeta }⊞\tilde{\delta })(y)& =& {\tilde{\zeta }}^{(j)}(y)+{\tilde{\delta }}^{(j)}(y)-{\tilde{\zeta }}^{(j)}(y)·{\tilde{\delta }}^{(j)}(y)\hfill \\ & =& {\tilde{\delta }}^{(j)}(y)+{\tilde{\zeta }}^{(j)}(y)-{\tilde{\delta }}^{(j)}(y)·{\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& (\tilde{\delta }⊞\tilde{\zeta })(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Thus, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}=$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$ Moreover, for any ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},$ we have

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}⊞\tilde{\tilde{0}})(y)& =& \left[{(\tilde{\xi }⊞\tilde{0})}^{-(j)}(y),{(\tilde{\xi }⊞\tilde{0})}^{+(j)}(y)\right]\hfill \\ & =& [{\tilde{\xi }}^{-(j)}(y)+{\tilde{0}}^{-(j)}(y)-{\tilde{\xi }}^{-(j)}(y).{\tilde{0}}^{-(j)}(y),\hfill \\ & & {\tilde{\xi }}^{+(j)}(y)+{\tilde{0}}^{+(j)}(y)-{\tilde{\xi }}^{+(j)}(y).{\tilde{0}}^{+(j)}(y)]\hfill \\ & =& \left[{\tilde{\xi }}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)\right]\hfill \\ & =& \tilde{\tilde{\xi }}(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (\tilde{\zeta }⊞\tilde{0})(y)& =& {\tilde{\zeta }}^{(j)}(y)+{\tilde{0}}^{(j)}(y)-{\tilde{\zeta }}^{(j)}(y)·{\tilde{0}}^{(j)}(y)\hfill \\ & =& {\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& \tilde{\zeta }(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Similarly, for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\},$ we obtain, $(\tilde{\tilde{0}}⊞\tilde{\tilde{\xi }})(y)=\left[{\tilde{\xi }}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)\right]=\tilde{\tilde{\xi }}(y)$ and $(\tilde{0}⊞\tilde{\zeta })(y)={\tilde{\zeta }}^{(j)}(y)=\tilde{\zeta }.$ Thus,

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$$

    □

Hence, $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊞)$ is a commutative semigroup and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{0}},\tilde{0})}_m}$ is the identity element of $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊞).$ Thus, $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊞)$ is a monoid.

Remark 3.

$({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊞)$ is non-idempotent.

The following example shows that $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊞)$ is non-idempotent, where $m=4.$

Example 9.

Let us assume the group $\mathbb{G}$ and a ${\mathcal{C}}_4\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}$ in Example 5. Then,

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.64,0.96],0.51),([0.51,0.91],0.64),\hfill \\ & ([0.51,0.96],0.64),([0.36,0.51],0.19)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.51,0.96],0.51),([0.19,0.64],0.64),\hfill \\ & ([0.51,0.75],0.64),([0.19,0.36],0.36)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.51,0.96],0.36),([0.51,0.96],0.51),\hfill \\ & ([0.19,0.96],0.64),([0.51,0.96],0.36)⟩.\hfill \end{array}\right\}$$

for all $y\in \mathbb{G}.$ Therefore, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\ne {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}.$ Hence, $({\mathcal{L}}_{{\mathcal{C}}_4\mathcal{P}},⊞)$ is non-idempotent.

Definition 15.

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}$ be two ${\mathcal{C}}_m\mathcal{P}$ structures on a set $\mathbb{G}.$ Then, the product of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m},$ denoted by ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m},$ is defined as a ${\mathcal{C}}_m\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}⊠\tilde{\tilde{\gamma }},\tilde{\zeta }⊠\tilde{\delta })}_m}$ in which

$$\tilde{\tilde{\xi }}⊠\tilde{\tilde{\gamma }}:\mathbb{G}\to {\left[I\right]}^{m}and\tilde{\zeta }⊠\tilde{\delta }:\mathbb{G}\to I^m,$$

where

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}⊠\tilde{\tilde{\gamma }})(y)& =& \left[{(\tilde{\xi }⊠\tilde{\gamma })}^{-(j)}(y),{(\tilde{\xi }⊠\tilde{\gamma })}^{+(j)}(y)\right]\hfill \\ & =& \left[{\tilde{\xi }}^{-(j)}(y)·{\tilde{\gamma }}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)·{\tilde{\gamma }}^{+(j)}(y)\right]\hfill \end{array}$$

and

$$(\tilde{\zeta }⊠\tilde{\delta })(y)={\tilde{\zeta }}^{(j)}(y)·{\tilde{\delta }}^{(j)}(y)$$

$y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$

Example 10.

Let us assume the group $\mathbb{G}$ in Example 5, a ${\mathcal{C}}_3\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ and ${\mathcal{C}}_3\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ in Example 8. Then, the product ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ of ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_3}$ and ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_3}$ is given as follows:

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }}⊠\tilde{\tilde{\gamma }},\tilde{\zeta }⊠\tilde{\delta })}_3}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.0,0.0],0.12),([0.0009,0.001],0.08),\hfill \\ & ([0.0036,0.008],0.16)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.0108,0.027],0.12),([0.0288,0.064],0.12),\hfill \\ & ([0.054,0.125],0.24)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.0972,0.216],0.08),([0.1512,0.343],0.09),\hfill \\ & ([0.2304,0.512],0.2)⟩.\hfill \end{array}\right\}$$

Theorem 12.

$({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊠)$ is a commutative semigroup.

Proof. 

Let ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m},$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m},$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_m}$ $\in {\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}}.$ Then,

$$\begin{array}{ccc}\hfill ((\tilde{\tilde{\xi }}⊠\tilde{\tilde{\gamma }})⊠\tilde{\tilde{\chi }})(y)& =& \left[{(\tilde{\xi }⊠\tilde{\gamma })}^{-(j)}(y)·{\tilde{\chi }}^{-(j)}(y),{(\tilde{\xi }⊠\tilde{\gamma })}^{+(j)}(y)·{\tilde{\chi }}^{+(j)}(y)\right]\hfill \\ & =& \left[({\tilde{\xi }}^{-(j)}(y)·{\tilde{\gamma }}^{-(j)}(y))·{\tilde{\chi }}^{-(j)}(y),({\tilde{\xi }}^{+(j)}(y)·{\tilde{\gamma }}^{+(j)}(y))·{\tilde{\chi }}^{+(j)}(y)\right]\hfill \\ & =& \left[{\tilde{\xi }}^{-(j)}(y)·({\tilde{\gamma }}^{-(j)}(y)·{\tilde{\chi }}^{-(j)}(y)),{\tilde{\xi }}^{+(j)}(y)·({\tilde{\gamma }}^{+(j)}(y)·{\tilde{\chi }}^{+(j)}(y))\right]\hfill \\ & =& \left[{\tilde{\xi }}^{-(j)}(y)·{(\tilde{\gamma }⊠\tilde{\chi })}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)·{(\tilde{\gamma }⊠\tilde{\chi })}^{+(j)}(y)\right]\hfill \\ & =& (\tilde{\tilde{\xi }}⊠(\tilde{\tilde{\gamma }}⊠\tilde{\tilde{\chi }}))(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill ((\tilde{\zeta }⊠\tilde{\delta })⊠\tilde{\omega })(y)& =& \left[{(\tilde{\zeta }⊠\tilde{\delta })}^{(j)}(y)·{\tilde{\omega }}^{(j)}(y),{(\tilde{\zeta }⊠\tilde{\delta })}^{(j)}(y)·{\tilde{\omega }}^{(j)}(y)\right]\hfill \\ & =& \left[({\tilde{\zeta }}^{(j)}(y)·{\tilde{\delta }}^{(j)}(y))·{\tilde{\omega }}^{(j)}(y),({\tilde{\zeta }}^{(j)}(y)·{\tilde{\delta }}^{(j)}(y))·{\tilde{\omega }}^{(j)}(y)\right]\hfill \\ & =& \left[{\tilde{\zeta }}^{(j)}(y)·({\tilde{\delta }}^{(j)}(y)·{\tilde{\omega }}^{(j)}(y)),{\tilde{\zeta }}^{(j)}(y)·({\tilde{\delta }}^{(j)}(y)·{\tilde{\omega }}^{(j)}(y))\right]\hfill \\ & =& \left[{\tilde{\zeta }}^{(j)}(y)·{(\tilde{\delta }⊠\tilde{\omega })}^{(j)}(y),{\tilde{\zeta }}^{(j)}(y)·{(\tilde{\delta }⊠\tilde{\omega })}^{(j)}(y)\right]\hfill \\ & =& (\tilde{\zeta }⊠(\tilde{\delta }⊠\tilde{\omega }))(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Thus,

$$({\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m})⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_m}={\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊠({\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\chi }},\tilde{\omega })}_m}).$$

Moreover, we have

$$\begin{array}{ccc}\hfill (\tilde{\tilde{\xi }}⊠\tilde{\tilde{\gamma }})(y)& =& \left[{(\tilde{\xi }⊠\tilde{\gamma })}^{-(j)}(y),{(\tilde{\xi }⊠\tilde{\gamma })}^{+(j)}(y)\right]\hfill \\ & =& \left[{\tilde{\xi }}^{-(j)}(y)·{\tilde{\gamma }}^{-(j)}(y),{\tilde{\xi }}^{+(j)}(y)·{\tilde{\gamma }}^{+(j)}(y)\right]\hfill \\ & =& \left[{\tilde{\gamma }}^{-(j)}(y)·{\tilde{\xi }}^{-(j)}(y),{\tilde{\gamma }}^{+(j)}(y)·{\tilde{\xi }}^{+(j)}(y)\right]\hfill \\ & =& \left[{(\tilde{\gamma }⊠\tilde{\xi })}^{-(j)}(y),{(\tilde{\gamma }⊠\tilde{\xi })}^{+(j)}(y)\right]\hfill \\ & =& (\tilde{\tilde{\gamma }}⊠\tilde{\tilde{\xi }})(y)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (\tilde{\zeta }⊠\tilde{\delta })(y)& =& {\tilde{\zeta }}^{(j)}(y)·{\tilde{\delta }}^{(j)}(y)\hfill \\ & =& {\tilde{\delta }}^{(j)}(y)·{\tilde{\zeta }}^{(j)}(y)\hfill \\ & =& (\tilde{\zeta }⊠\tilde{\delta })(y)\hfill \end{array}$$

for all $y\in \mathbb{G}$ and $j\in \{1,2,\dots ,m\}.$ Thus, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}=$ ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\gamma }},\tilde{\delta })}_m}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_m}.$ Therefore, $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊠)$ is a commutative semigroup.    □

Remark 4.

$({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊠)$ is non-idempotent.

The following example shows that $({\mathcal{L}}_{{\mathcal{C}}_m\mathcal{P}},⊠)$ is non-idempotent, where $m=4.$

Example 11.

Let us assume the group $\mathbb{G}$ and a ${\mathcal{C}}_4\mathcal{P}$ structure ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}$ in Example 5. Then,

$${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}⊞{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}=\left\{\begin{array}{cc}⟨1,\hfill & ([0.16,0.64],0.09),([0.09,0.49],0.16),\hfill \\ & ([0.09,0.64],0.16),([0.04,0.09],0.01)⟩,\hfill \\ ⟨\alpha ,\hfill & ([0.09,0.64],0.09),([0.01,0.16],0.16),\hfill \\ & ([0.09,0.25],0.16),([0.01,0.04],0.04)⟩,\hfill \\ ⟨{\alpha }^2,\hfill & ([0.09,0.64],0.04),([0.09,0.64],0.09),\hfill \\ & ([0.01,0.64],0.16),([0.09,0.64],0.04)⟩.\hfill \end{array}\right\}$$

for all $y\in \mathbb{G}.$ Therefore, ${\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}⊠{\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}\ne {\tilde{\mathsf{\Xi }}}_{{(\tilde{\tilde{\xi }},\tilde{\zeta })}_4}.$ Hence, $({\mathcal{L}}_{{\mathcal{C}}_4\mathcal{P}},⊠)$ is non-idempotent.

5. Conclusions

The conception of a ${\mathcal{C}}_m\mathcal{P}$ structure is a generalization of an ${}_m\mathcal{PF}$ structure which deals with a two-pronged approach of decision analysis and data imprecision by taking into consideration both the polarity of the $\mathcal{IVF}$ structure and the ${}_m\mathcal{PF}$ structure, simultaneously. In this article, we originated the idea of ${\mathcal{C}}_m\mathcal{P}$ groups and probed many of its characteristics. We gave an an essential bridge between ordinary group theory and ${\mathcal{C}}_m\mathcal{P}$ group theory. We investigated the effect of the ${\mathcal{C}}_m\mathcal{P}$ structure on group (semigroup) structures. We derived some basic properties of ${\mathcal{C}}_m\mathcal{P}$ groups and supported them by illustrative examples. Finally, we provided one binary operation to assign a groupoid structure to the set of ${\mathcal{C}}_m\mathcal{P}$ structures and two binary operations to assign a semigroup structure to the set of ${\mathcal{C}}_m\mathcal{P}$ structures. Moreover, we thoroughly investigated some important properties of groupoid and semigroup structures, and gave some illustrative examples to support these properties.

The results of this study can be further extended to normed subrings, hemirings, fields and ordered gamma semigroups (see [37,38,39,40]). Furthermore, the conception of a ${\mathcal{C}}_m\mathcal{P}$ structure used in this manuscript can be studied according to the idea in [41], which will be the way for much future research.