Trajectories Derived from Periodic Orbits around the Lagrangian Point L1 and Lunar Swing-Bys: Application in Transfers to Near-Earth Asteroids
Abstract
1. Introduction
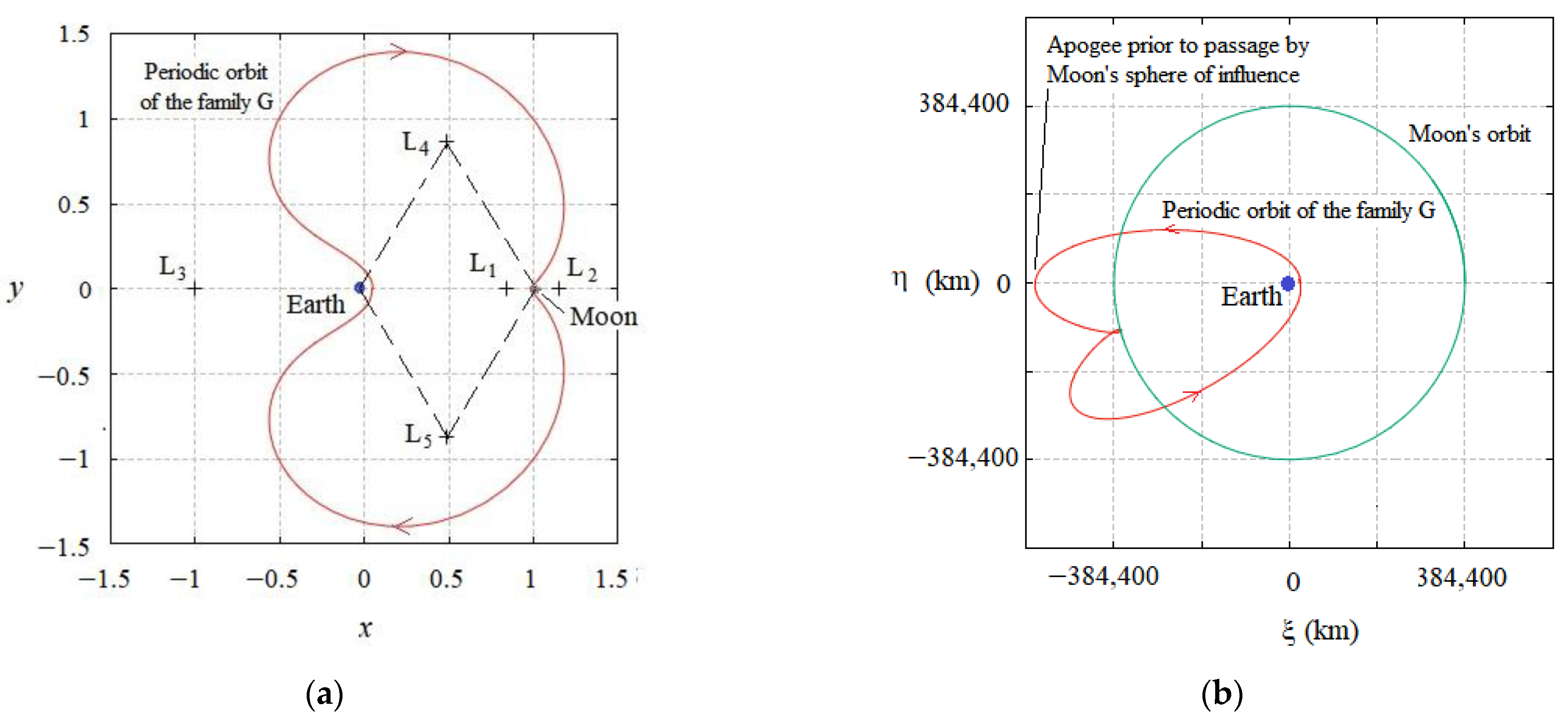
2. Circular Restricted Three-Body Problem (CR3BP) and Family G of the Periodic Orbits around the Lagrangian Point L1
3. Definition of the Trajectories G
3.1. The CR3BP and a First Approach for the TGs
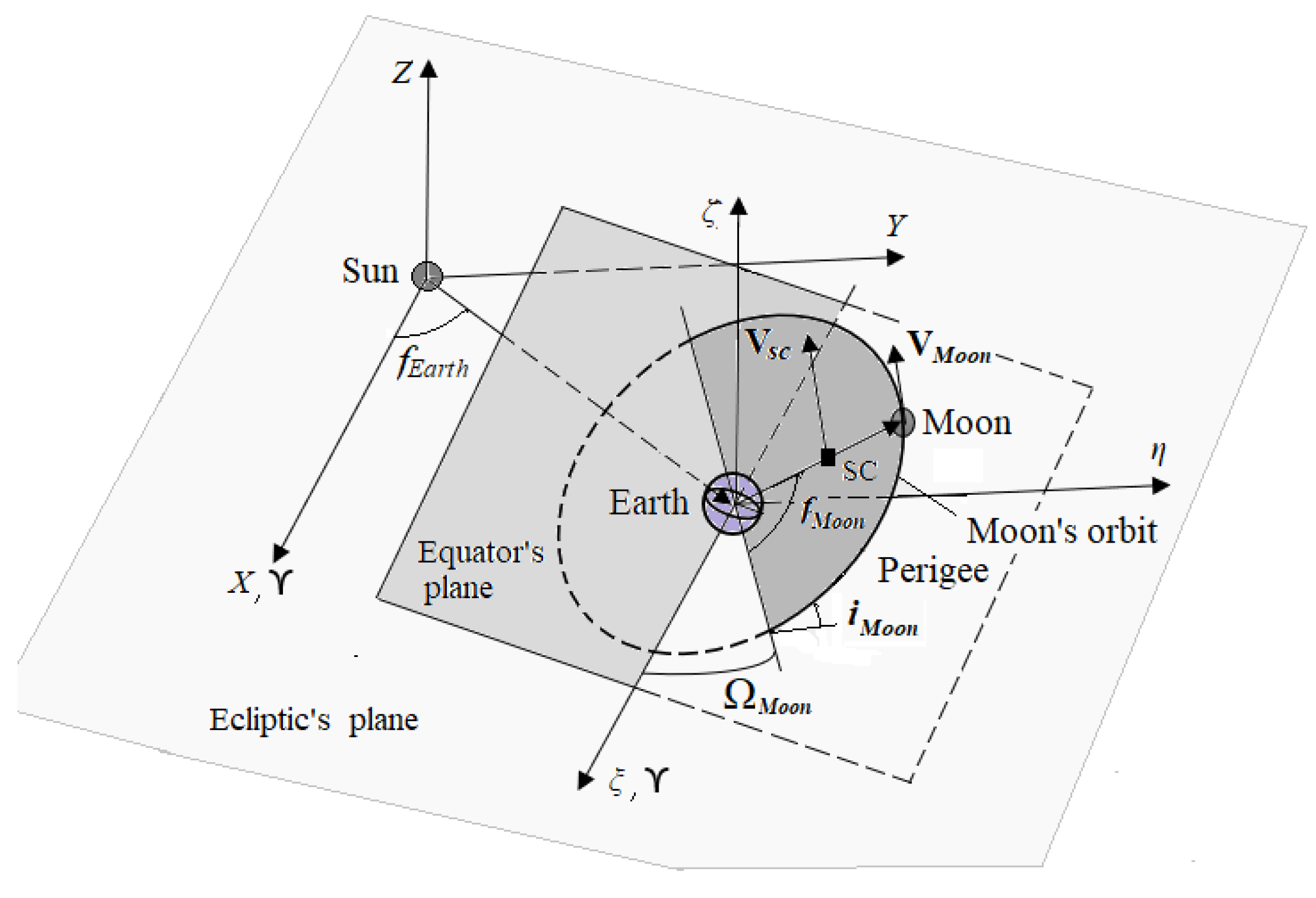
3.2. The Three-Dimensional Restricted Full Four-Body Problem Sun-Earth-Moon-Particle (FR4BP)
3.2.1. The Three-Dimensional Restricted Bicircular Four-body Problem (BCR4BP) and a Second Approach for the TGs
- For , TGs that collide with the Moon are found (they are called “trajectories G of collision”, TGCs).
- For , TGs that have encounters with the Moon, gain energy, and escape from the Earth–Moon system are found (they are called “trajectories G of direct escape”, TGEs).
- For , TGs that approach and have an encounter with the Moon, but do not gain enough energy to escape from the Earth–Moon system, are found (they are called “trajectories G of inversion”, TGIs).
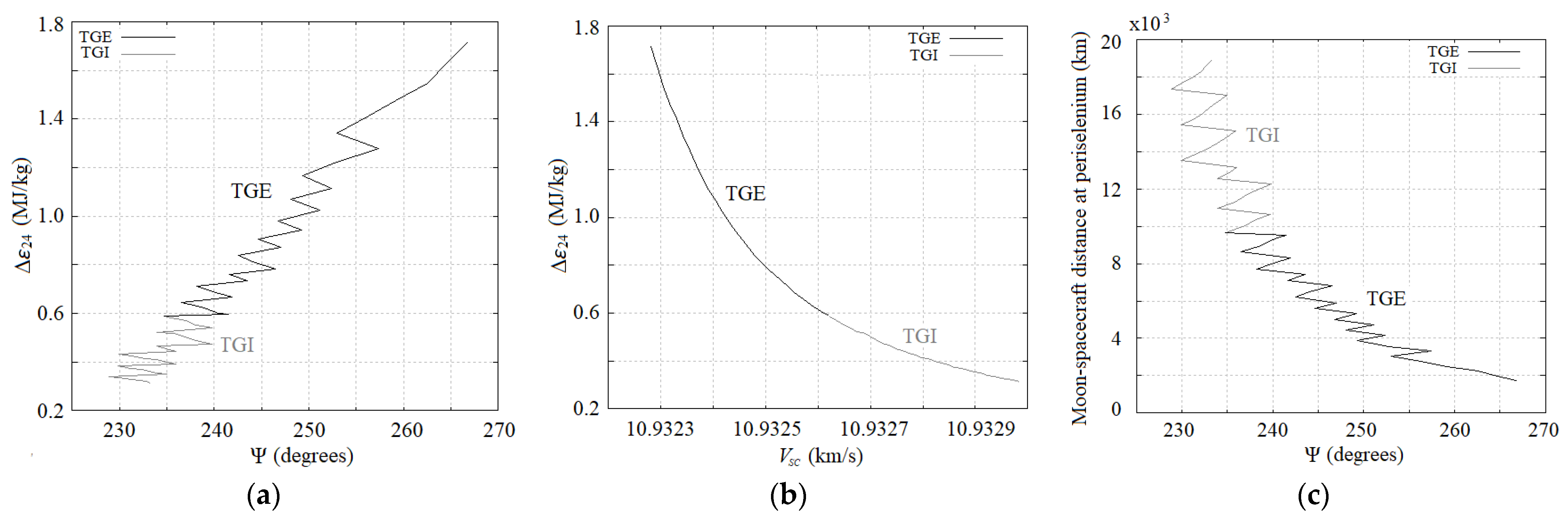
3.2.2. Some Features of the TGs in the BCR4BP
4. Applications
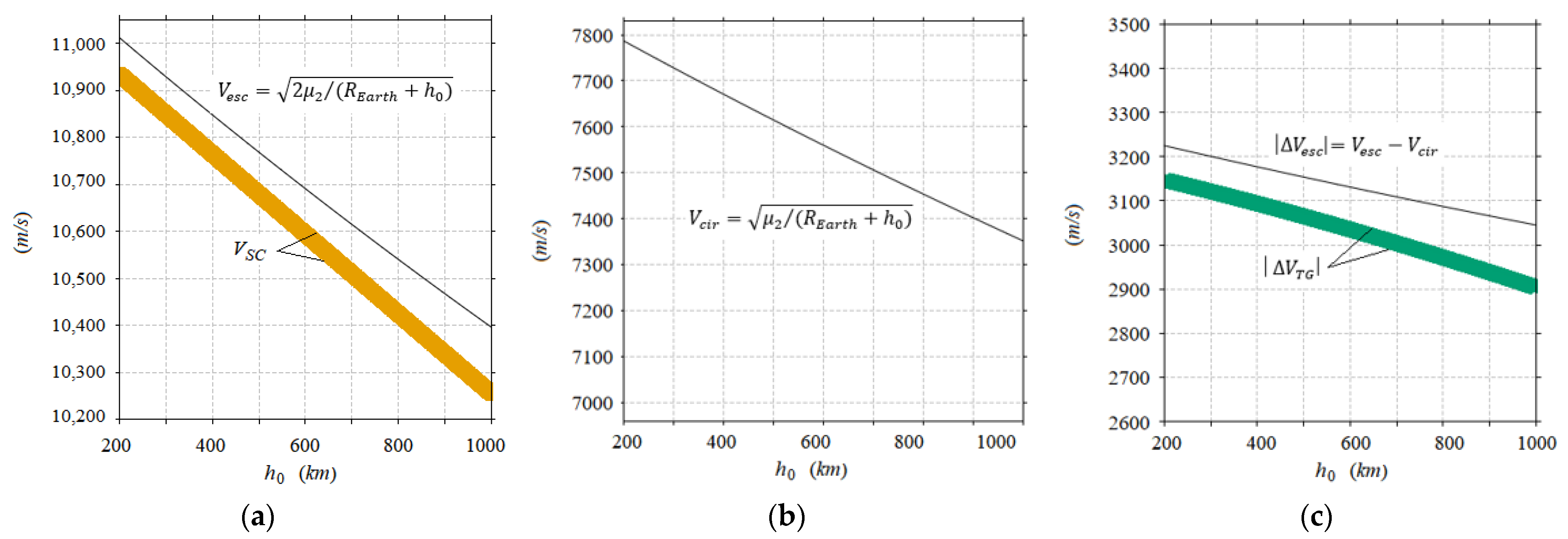
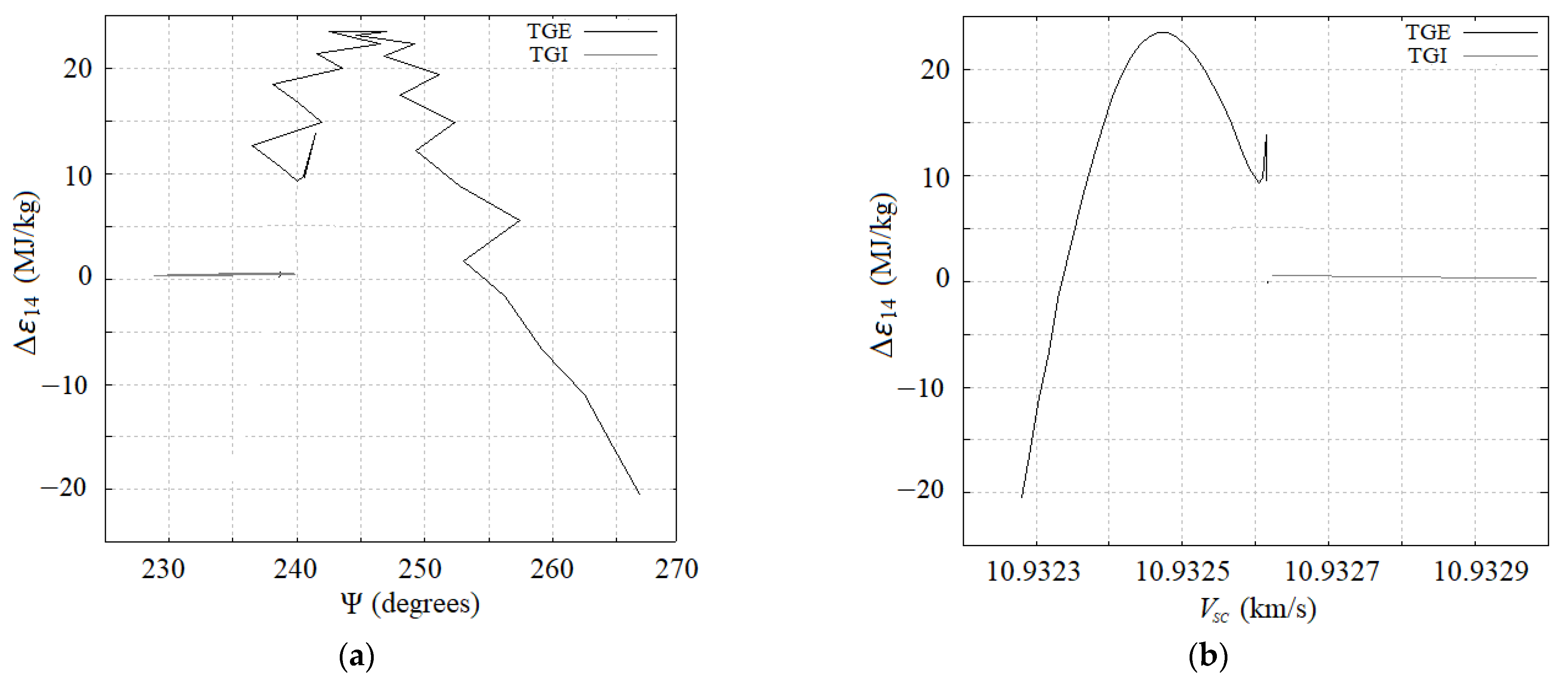
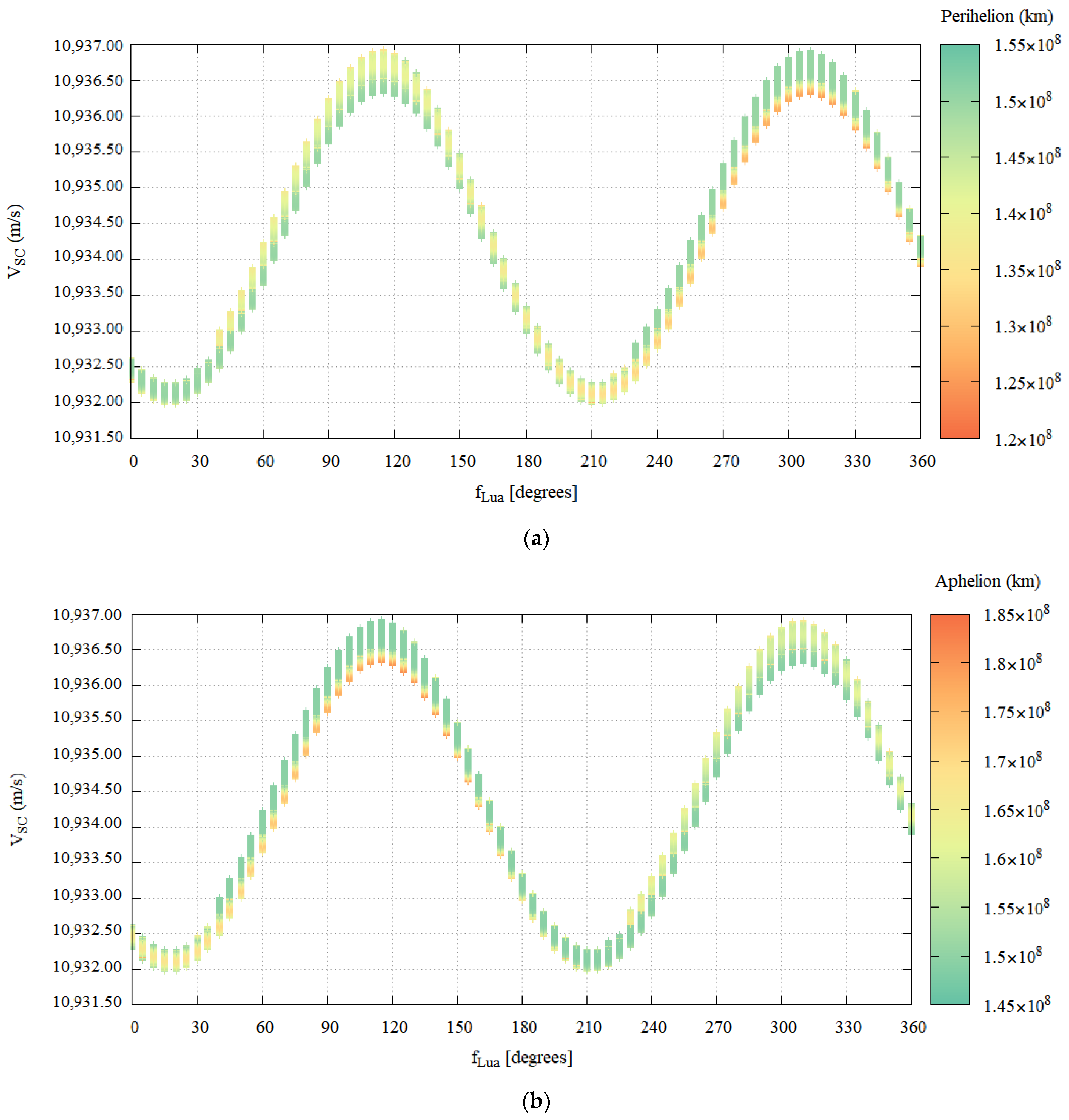
4.1. Limits of the TGs
4.2. Parameters for Planning Transfers to NEAs by TGEs
- Step 1: Choose an NEA and an interval of interest for planning a mission. Once this choice is made, data on the orbits of the NEA, Earth, and Moon (orbital elements or vectors state) must be obtained through an orbit propagator or, for example, from JPL’s Horizons platform for this interval [35].
- Step 2: Considering the data obtained for the NEA’s orbit in step 1, it is necessary to determine if it passes through the primary intercept region, the dates of entry and exit from this region, and the respective position (relative to the Sun), and if its nodes are also in this region. If the nodes are in this region, there is a great probability of finding a TGE able to intercept the chosen NEA. Otherwise, this probability becomes smaller, so even an interception continues to be possible.
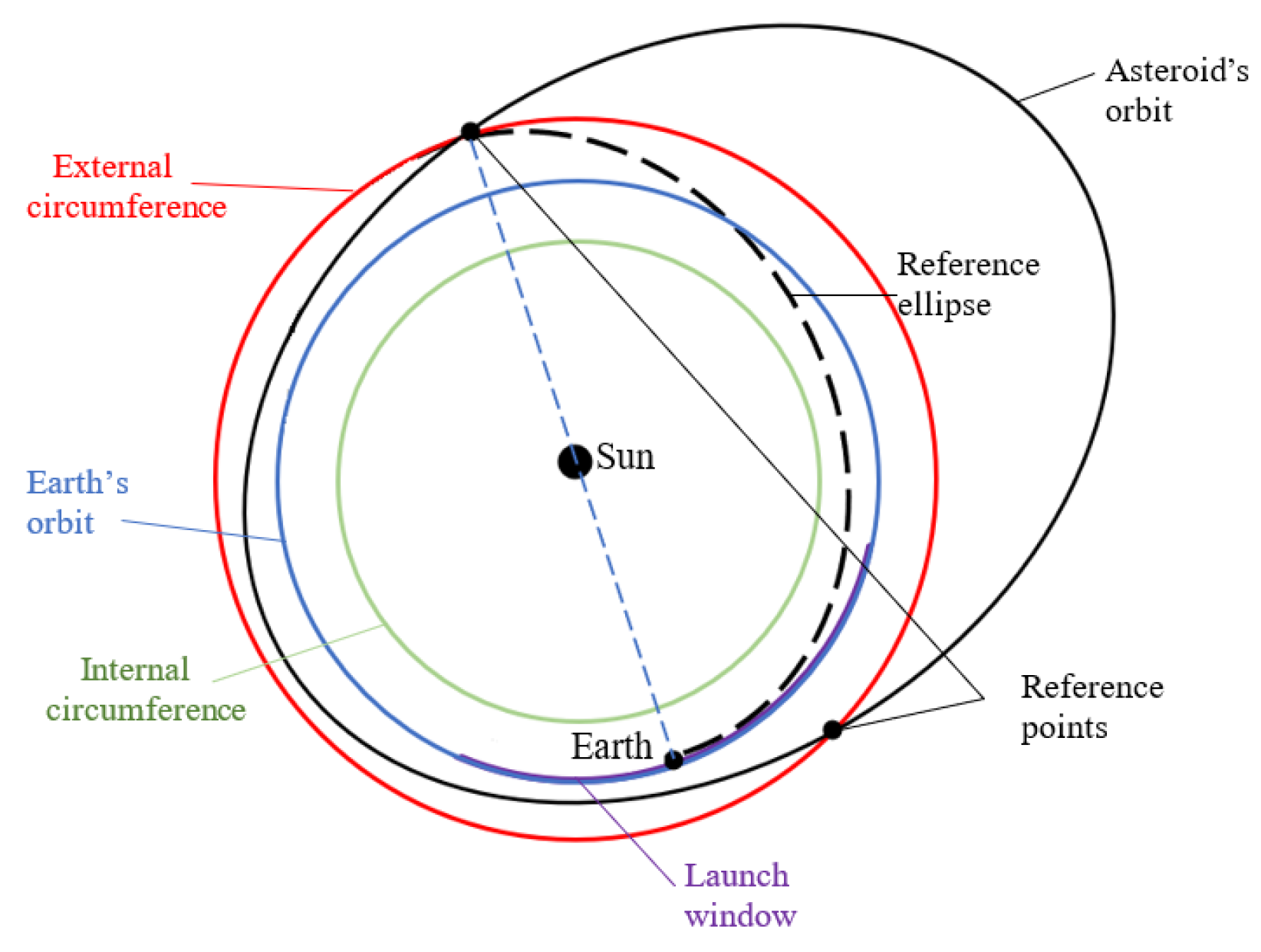
- Step 3. Firstly, considering the case in which the nodes are in the primary intercept region, from the straight lines segments that join these points to the Earth’s orbits through the Sun, it is possible to define the semimajor axes of two references ellipses and their orbital periods. Subtracting half of these orbital periods and adding 20 days (time needed for a TGE to reach the Earth’s sphere of influence) from the dates corresponding to the passages of the NEA through its ascending or descending nodes, two new dates are found, and they will be the starting point for definition (or study) of the launch windows. Figure 10 shows a reference ellipse considering that the points in which the NEA’s orbit entries and exits the intercept region coincide with its nodes. In this example, the semimajor axis is (149,597,870.7 km + 181,272,593.0 km)/2 = 165,435,231.9 km, and half of the orbital period is 212.4 days, plus 20 days, totaling 232.4 days. Then, the date found can be adopted as the beginning of the launch window, since the Earth is within the launch window interval. An interval of three lunar cycles, approximately 82 days, is generally enough to obtain some TGEs able to carry out an Earth–NEA transfer.
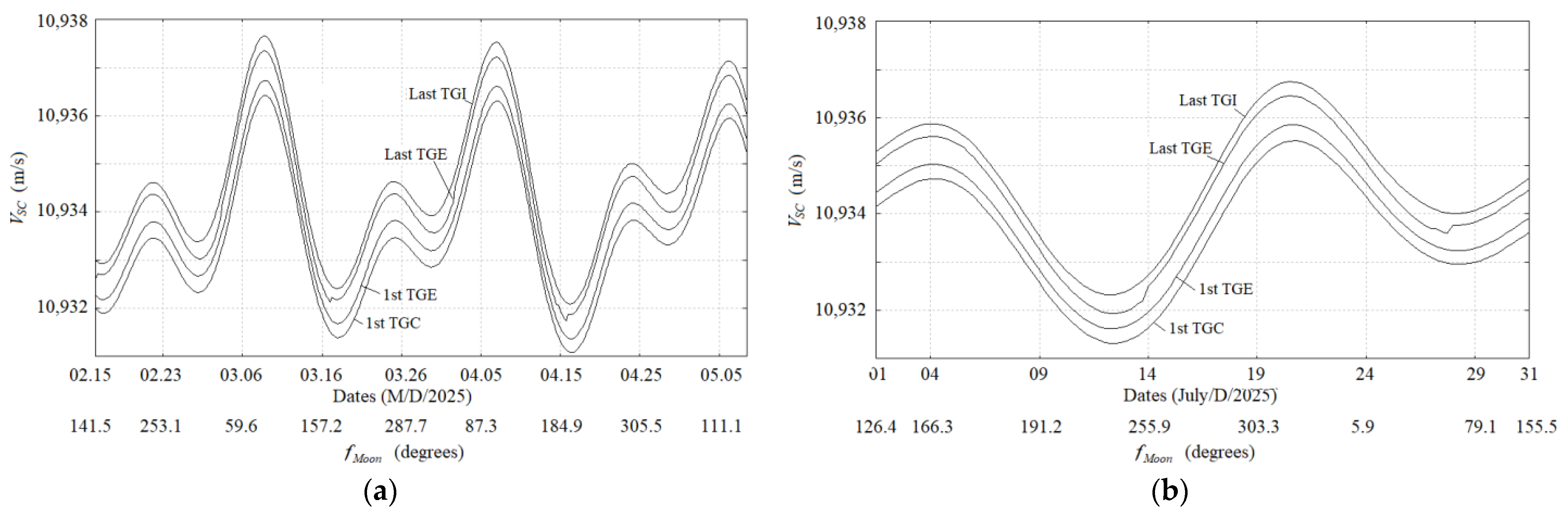
- Step 4. From the new dates found in step 3, intervals containing these dates are defined, and they will be considered the first choice for the launch window. Following this, a set of simulations are conducted to find TGEs able to intercept the NEA chosen. First, the curves VSC × fMoon for these intervals are found; then, from the VSC that defines the TGEs for these intervals, trajectories are propagated to obtain encounters with the NEA.
- Step 5. Analyses of the results.
4.3. Analysis for the Transfers to the 3361 Orpheus (Apollo Class), 99942 Apophis (Aten Class), and 65803 Didymos (Amor Class)
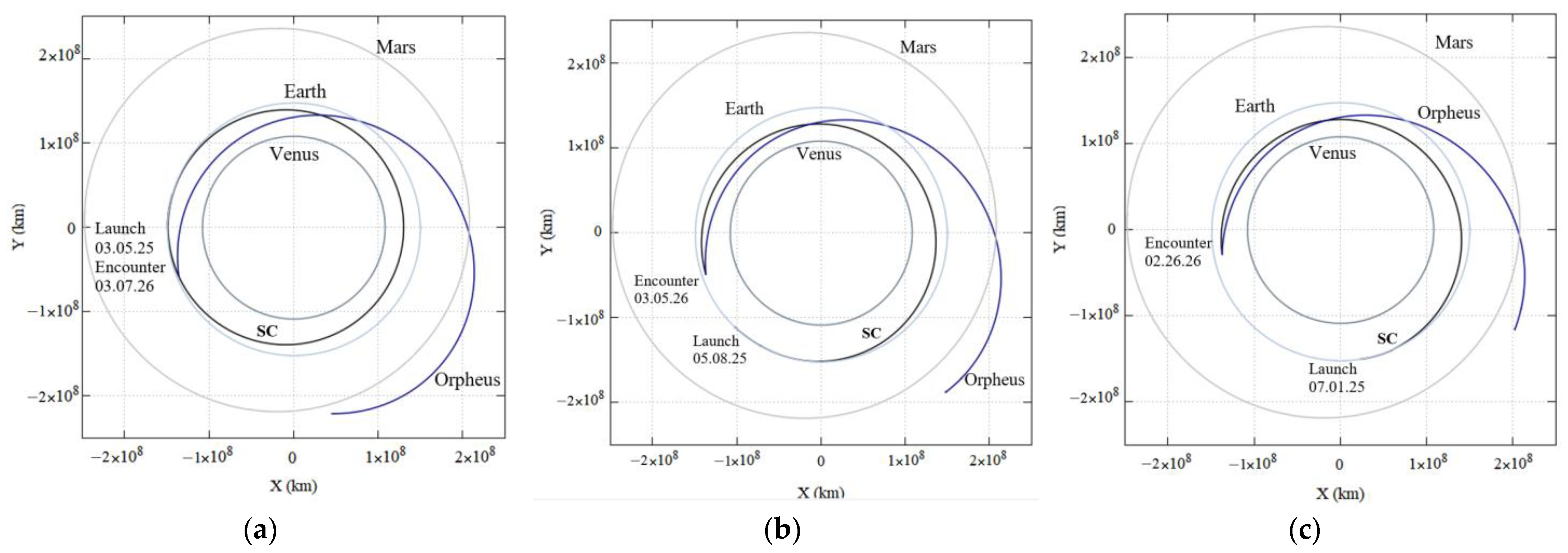
4.3.1. Transfer to the 3361 Orpheus
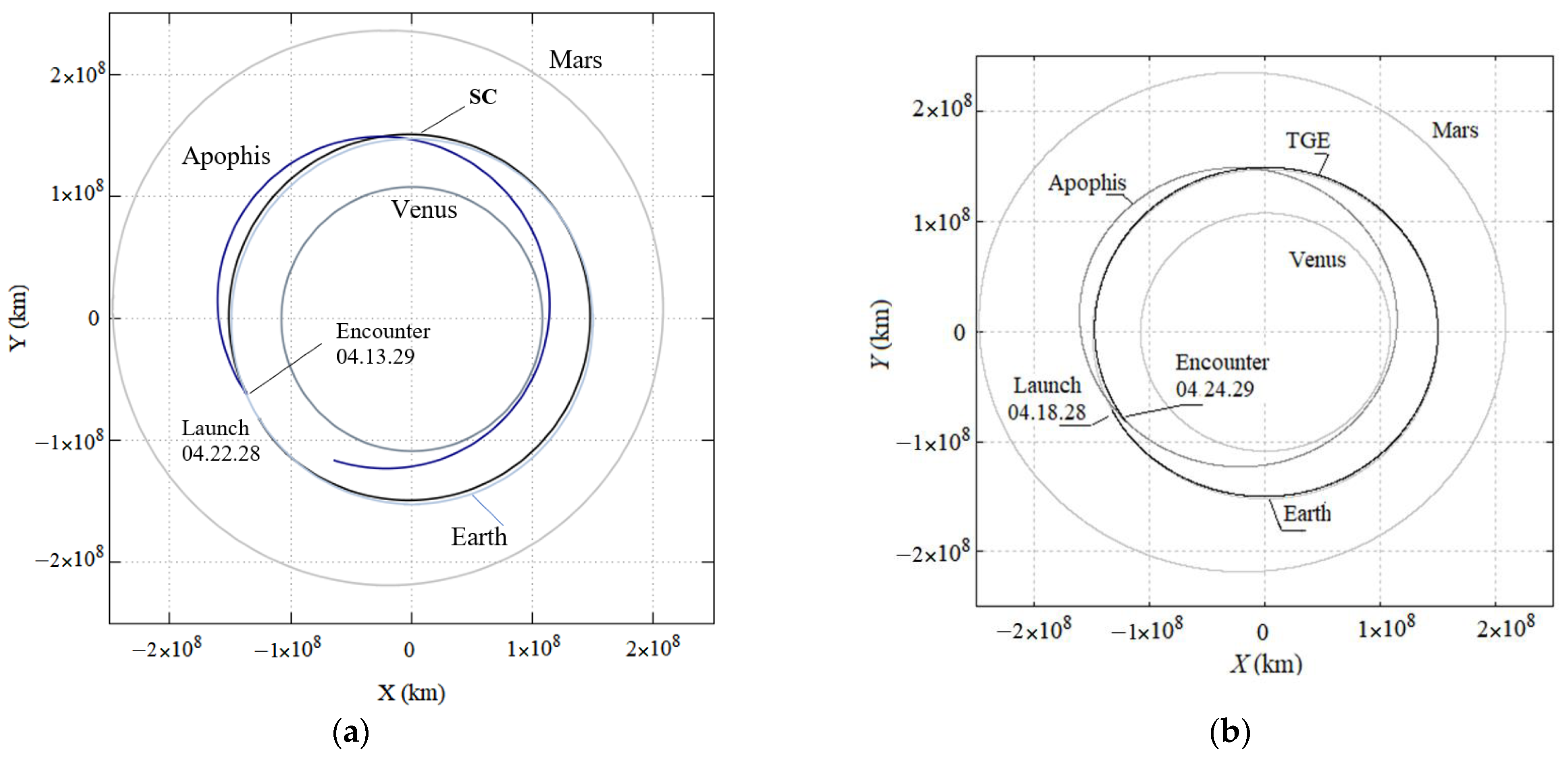
4.3.2. Transfer to the 99942 Apophis
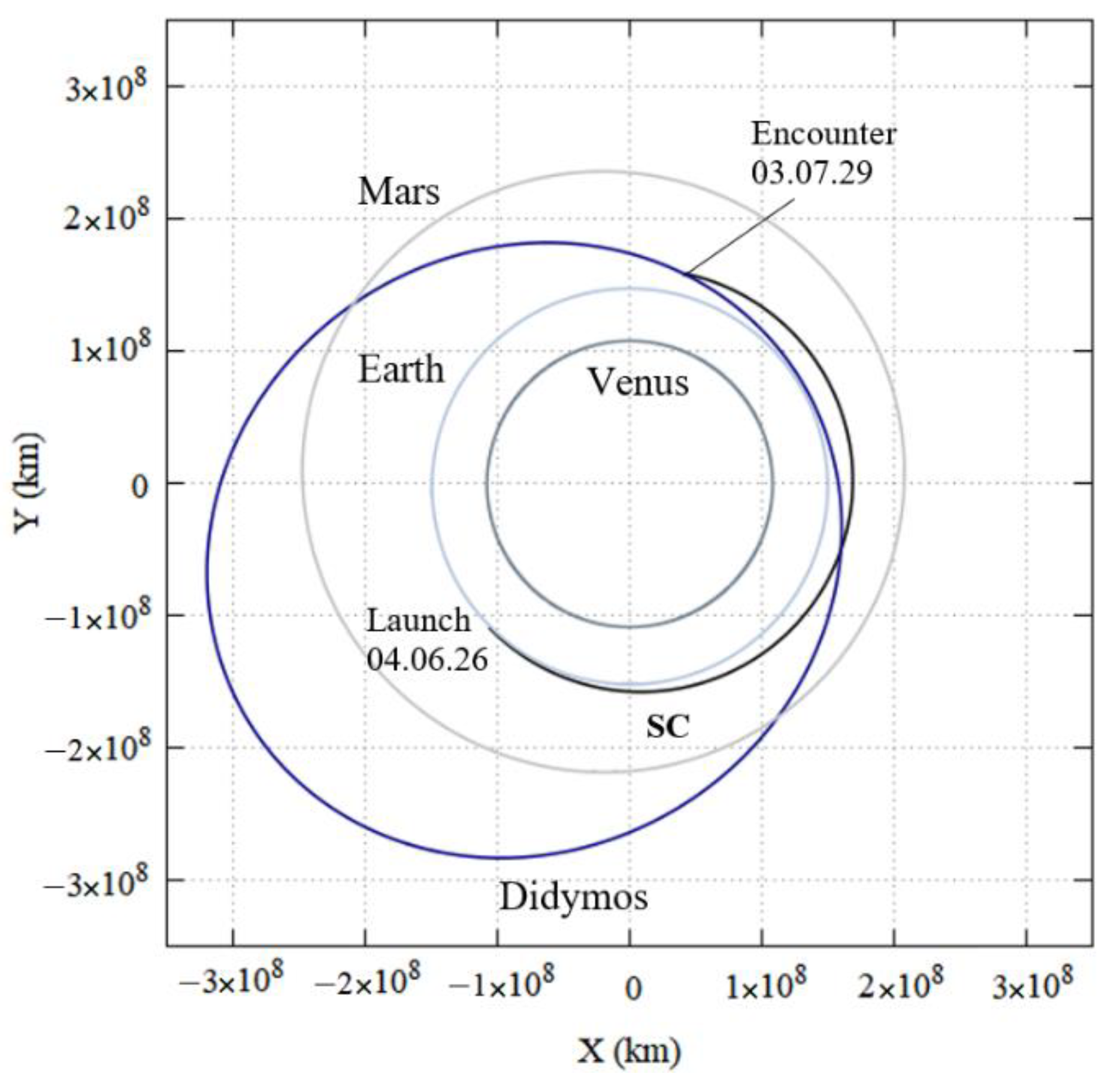
4.3.3. Transfer to the 65803 Didymos
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minor Planet Center. “Latest Published Data,” 2022. Available online: https://www.minorplanetcenter.net/mpc/summary (accessed on 30 March 2022).
- Shoemaker, E.M.; Williams, J.G.; Hellin, E.F.; Wolfe, R.F. Orbital Classes, Collision Rates with Earth, and Origin; Asteroids, T.G., Ed.; University of Arizona Press: Tucson, AZ, USA, 1979; pp. 253–282. [Google Scholar]
- Broucke, R.A. Periodic orbits in the restricted three body problem with earth-moon masses. Tech. Rep. 1968. [Google Scholar]
- de Melo, C.; Macau, E.; Winter, O.; Neto, E.V. Alternative paths for insertion of probes into high inclination lunar orbits. Adv. Space Res. 2007, 40, 58–68. [Google Scholar] [CrossRef]
- de Melo, C.F.; Macau, E.E.N.; Winter, O. Strategies for plane change of Earth orbits using lunar gravity and derived trajectories of family G. Celest. Mech. Dyn. Astron. 2009, 103, 281–299. [Google Scholar] [CrossRef]
- De Melo, C.F.; Macau, E.E.N.; Winter, O.C. Alternative Transfers to the NEOs 99942 Apophis, 1994 WR12, and 2007 UW1 via Derived Trajectories from Periodic Orbits of Family G. Math. Probl. Eng. 2009, 2009, 303604. [Google Scholar] [CrossRef]
- Salazar, F.J.T.; de Melo, C.F.; Macau, E.E.N.; Winter, O. Three-body problem, its Lagrangian points and how to exploit them using an alternative transfer to L4 and L5. Celest. Mech. Dyn. Astron. 2012, 114, 201–213. [Google Scholar] [CrossRef]
- Turco, R.; Toon, O.; Park, C.; Whitten, R.; Pollack, J.; Noerdlinger, P. An analysis of the physical, chemical, optical, and historical impacts of the 1908 Tunguska meteor fall. Icarus 1982, 50, 1–52. [Google Scholar] [CrossRef]
- Shoemaker, E.M. Asteroid and comet bombardment of the Earth. Annu. Rev. Earth Planet. Sci. 1983, 11, 461–494. [Google Scholar] [CrossRef]
- Kerr, R.A. Huge impact tied to mass extinction. Science 1992, 257, 878–880. [Google Scholar] [CrossRef]
- Popova, O.P.; Jenniskens, P.; Emel’yanenko, V.; Kartashova, A.; Biryukov, E.; Khaibrakhmanov, S.; Shuvalov, V.; Rybnov, Y.; Dudorov, A.; Grokhovsky, V.I.; et al. Chelyabinsk airburst, damage assessment, meteorite recovery, and characterization. Science 2013, 342, 1069–1073. [Google Scholar] [CrossRef]
- The Guardian. Scientists Reveal the Full Power of the Chelyabinsk Meteor Explosion. 2013. Available online: https://www.theguardian.com/science/2013/nov/06/chelyabinsk-meteor-russia#:~:text=Travelling%20at%20a%20speed%20of,knock%20people%20off%20their%20feet (accessed on 23 May 2022).
- Chapman, C.R. Space weathering of asteroid surfaces. Annu. Rev. Earth Planet. Sci. 2004, 32, 539–567. [Google Scholar] [CrossRef]
- Prockter, L.; Murchie, S.; Cheng, A.; Krimigis, S.; Farquhar, R.; Santo, A.; Trombka, J. The NEAR shoemaker mission to asteroid 433 eros. Acta Astronaut. 2002, 51, 491–500. [Google Scholar] [CrossRef]
- Kawaguchi, J.; Fujiwara, A.; Uesugi, T. Hayabusa—Its technology and science accomplishment summary and Hayabusa-2. Acta Astronaut. 2008, 62, 639–647. [Google Scholar] [CrossRef]
- Tsuda, Y.; Saiki, T.; Terui, F.; Nakazawa, S.; Yoshikawa, M.; Watanabe, S.-I. Hayabusa2 mission status: Landing, roving and cratering on asteroid Ryugu. Acta Astronaut. 2020, 171, 42–54. [Google Scholar] [CrossRef]
- Lauretta, D.S.; Balram-Knutson, S.S.; Beshore, E.; Boynton, W.V.; D’Aubigny, C.D.; DellaGiustina, D.; Enos, H.L.; Gholish, D.R.; Hergenrother, C.W.; Howell, E.S.; et al. OSIRIS-REx: Sample Return from Asteroid (101955) Bennu. Space Sci. Rev. 2017, 212, 925–984. [Google Scholar] [CrossRef]
- NASA. NASA, SpaceX Launch DART: First Test Mission to Defend Planet Earth. 2021. Available online: https://www.nasa.gov/press-release/nasa-spacex-launch-dart-first-test-mission-to-defend-planet-earth (accessed on 19 April 2022).
- Michel, P.; Cheng, A.; Küppers, M.; Pravec, P.; Blum, J.; Delbo, M.; Green, S.F.; Rosenblatt, P.; Tsiganis, K.; Vincent, J.; et al. Science case for the Asteroid Impact Mission (AIM): A component of the Asteroid Impact & Deflection Assessment (AIDA) mission. Adv. Space Res. 2016, 57, 2529–2547. [Google Scholar]
- Scheirich, P.; Pravec, P.; Thomas, C.A. Observations of Didymos in support of DART and Hera. EPSC-DPS Jt. Meet. 2019, 2019, EPSC-DPS2019. [Google Scholar]
- Lawden, D.F. Perturbation maneuvers. J. Br. Interplanet Soc. 1954, 13, 329–334. [Google Scholar]
- Minovitch, M. A method for determining interplanetary free-fall reconnaissance trajectories. JPL Tec. Memo. 1961, 312, 130. [Google Scholar]
- Broucke, R. The celestial mechanics of gravity assist. Astrodyn. Conf. 1988, 69–78. [Google Scholar]
- Dunham, D.; Davis, S. Optimization of a multiple lunar-swingby trajectory sequence. Astrodyn. Conf. 1985, 1978. [Google Scholar] [CrossRef]
- Prado, F.B.A. Orbital control of a satellite using the gravity of the moon. J. Braz. Soc. Mech. Sci. Eng. 2006, 28, 105–110. [Google Scholar] [CrossRef][Green Version]
- Farquhar, R. Detour to a Comet; Journey of the International Cometary Explorer. Planet. Rep. 1985, 5, 4–6. [Google Scholar]
- NASA Science. ISEE-3/ICE. 24 July 2019. Available online: https://solarsystem.nasa.gov/missions/isee-3-ice/in-depth/ (accessed on 22 September 2021).
- Kawaguchi, J. On the lunar and heliocentric gravity assist experienced in the planet-b (‘nozomi’). Fourth Int. Symp. Space Flight Dyn. Iguassu Falls Braz. 1999, 8–12. [Google Scholar]
- Kawaguchi, J.; Nakatani, I.; Uesugi, T.; Tsuruda, K. Synthesis of an alternative flight trajectory for Mars explorer, Nozomi. Acta Astronaut. 2003, 52, 189–195. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration. “Nozomi,” NASA Space Science Data Coordinated Archive. Available online: https://nssdc.gsfc.nasa.gov/nmc/spacecraft/display.action?id=1998-041A (accessed on 22 September 2021).
- Dunham, D.W.; Guzmán, J.J.; Sharer, P.J. STEREO trajectory and maneuver design. Johns Hopkins APL Tech. Dig. 2009, 28, 104–125. [Google Scholar]
- Ocampo, C. Trajectory analysis for the lunar flyby rescue of AsiaSat-3/HGS-1. Ann. N. Y. Acad Sci. 2005, 1065, 232–253. [Google Scholar] [CrossRef]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Stroemgren, E. Connaissance actuelle des orbites dans le probleme des trois corps. Publ. Og Mindre Meddeler Fra Kbh. Obs. 1933, 100, 1–44. [Google Scholar]
- Jet Propulsion Laboratory (JPL). Horizons System. Available online: https://ssd.jpl.nasa.gov/horizons/ (accessed on 15 May 2022).
- Jet Propulsion Laboratory (JPL). Horizons Web Application. Available online: https://ssd.jpl.nasa.gov/horizons/app.html#/ (accessed on 23 May 2022).




| Property | Orpheus | Apophis | Didymos |
|---|---|---|---|
| Class | Apollo | Aten | Apollo |
| Mass * | 4.66 × 1010 kg | 2.70 × 1010 kg | 5.27 × 1010 kg |
| Dimension | AR = 150 m, L = 300 m | 370 m × 450 m × 170 m | AR = 390 m |
| Absolute Magnitude (H) | 19.03 | 19.70 | 18.07 |
| Semimajor axis | 180,962,886.3 km | 137,994,462.3 km | 246,025,217.4 km |
| Eccentricity | 0.322752 | 0.191195 | 0.383638 |
| Inclination | 2.68° | 3.33° | 3.41° |
| Longitude of ascending node | 189.53° | 204.45° | 73.21° |
| Argument of perihelion | 301.66° | 126.40° | 319.30° |
| Orbital period | 1.33 Years | 0.89 Years | 2.11 Years |
| Property | First Transfer | Second Transfer | Third Transfer |
|---|---|---|---|
| Launch window M/D/Y | 02/15/25–05/08/25 | 02/15/25–05/08/25 | 07/01/25–07/30/25 |
| Launch date M/D/Y | 12 h-03/05/25 | 0 h-05/08/25 | 0 h-07/01/2025 |
| Circular parking LEO altitude (km) | 200 | ||
| VSC (m/s) | 10,935.561 | 10,935.550 | 10,934.480 |
| |ΔVTGE | (m/s) | 3153.635 | 3153.362 | 3152.553 |
| |ΔV| at aphelion (m/s) | 48 | 18 | 12 |
| |ΔVLaunch| (reference) Lambert’s Method * (m/s) | 3330 | ||
| Launch C3 relative to the Earth (106 m2/s2) | −1.530 | −1.531 | −1.55 |
| Impact date, M/D/Y | 03/07/2026 | 03/05/2026 | 02/26/2026 |
| Time of transfer (days) | 367.89 | 301.18 | 230 |
| Distance from Earth at impact (km) | 376,576,144.4 km | 325,347,488.6 km | 89,997,492.0 km |
| Arrival Impact Angles (degrees) | 16.80 | 10.73 | 8.89 |
| Relative velocity at impact (m/s) | 9886.548 | 6383.805 | 6082.983 |
| Property | First Transfer | Second Transfer |
|---|---|---|
| Launch window M/D/Y | 03/03/28 to 06/27/28 | 03/03/28 to 06/27/28 |
| Launch date M/D/Y | 6 h 04/06/28 | 12 h 04/18/28 |
| Circular parking LEO altitude (km) | 200 km | |
| VSC (m/s) | 10,932.494 | 10,935.384 |
| |ΔVTGE | (m/s) | 3150.567 | 3153.458 |
| |ΔV| at aphelion (m/s) | 20 | 18 |
| |ΔVLaunch| (reference) Lambert’s Meth. * (m/s) | 3331 | |
| Launch C3 relative to the Earth (106 m2/s2) | −1.597 | −1.534 |
| Impact date, M/D/Y | 04/13/2029 | 04/24/2029 |
| Time of transfer (days) | 356.69 | 371.39 |
| Distance from Earth at impact (km) | 24,184,985 | 28,267,878 |
| Arrival Impact Angles (degrees) | 22.27 | 7.57 |
| Relative velocity at impact (m/s) | 5220.245 | 4373.068 |
| Launch Window M/D/Y | 03/06/26 to 04/29/26 |
|---|---|
| Launch date M/D/Y | 6 h 04/06/26 |
| Circular parking LEO altitude (km) | 200 |
| VSC (m/s) | 10,932.389 |
| |ΔVTGE | (m/s) | 3144 |
| |ΔV| at perihelion (m/s) | 22 |
| |ΔVLaunch| (reference) Lambert’s Meth. * (m/s) | 3318 |
| Launch C3 relative to the Earth (106 m2/s2) | −1.796 |
| Impact date, M/D/Y | 03/07/2029 |
| Time of transfer (days) | 1086 |
| Distance from Earth at impact (km) | 19,126,666 |
| Arrival Impact Angles (degrees) | 15.04 |
| Relative velocity at impact (m/s) | 9240.300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, R.S.; de Melo, C.F.; Prado, A.F.B.A. Trajectories Derived from Periodic Orbits around the Lagrangian Point L1 and Lunar Swing-Bys: Application in Transfers to Near-Earth Asteroids. Symmetry 2022, 14, 1132. https://doi.org/10.3390/sym14061132
Ribeiro RS, de Melo CF, Prado AFBA. Trajectories Derived from Periodic Orbits around the Lagrangian Point L1 and Lunar Swing-Bys: Application in Transfers to Near-Earth Asteroids. Symmetry. 2022; 14(6):1132. https://doi.org/10.3390/sym14061132
Chicago/Turabian StyleRibeiro, Rebeca S., Cristiano F. de Melo, and Antônio F. B. A. Prado. 2022. "Trajectories Derived from Periodic Orbits around the Lagrangian Point L1 and Lunar Swing-Bys: Application in Transfers to Near-Earth Asteroids" Symmetry 14, no. 6: 1132. https://doi.org/10.3390/sym14061132
APA StyleRibeiro, R. S., de Melo, C. F., & Prado, A. F. B. A. (2022). Trajectories Derived from Periodic Orbits around the Lagrangian Point L1 and Lunar Swing-Bys: Application in Transfers to Near-Earth Asteroids. Symmetry, 14(6), 1132. https://doi.org/10.3390/sym14061132





