Maximal Product and Symmetric Difference of Complex Fuzzy Graph with Application

Abstract

A complex fuzzy set (CFS) is described by a complex-valued truth membership function, which is a combination of a standard true membership function plus a phase term. In this paper, we extend the idea of a fuzzy graph (FG) to a complex fuzzy graph (CFG). The CFS complexity arises from the variety of values that its membership function can attain. In contrast to a standard fuzzy membership function, its range is expanded to the complex plane’s unit circle rather than [0,1]. As a result, the CFS provides a mathematical structure for representing membership in a set in terms of complex numbers. In recent times, a mathematical technique has been a popular way to combine several features. Using the preceding mathematical technique, we introduce strong approaches that are properties of CFG. We define the order and size of CFG. We discuss the degree of vertex and the total degree of vertex of CFG. We describe basic operations, including union, join, and the complement of CFG. We show new maximal product and symmetric difference operations on CFG, along with examples and theorems that go along with them. Lastly, at the base of a complex fuzzy graph, we show the application that would be important for measuring the symmetry or asymmetry of acquaintanceship levels of social disease: COVID-19.

1. Introduction

It is frequently recognized that graphs are basically representations of relations. A graph is a useful means of describing information concerning object relationships. Vertices represent objects, while edges describe relationships.

It can be used to look at combinatorial problems in a lot of different fields, such as algebra, topology, zoology, number theory, geometry, and image capture and clustering.

The graph’s vertices and edges are used to describe objects and the relationships between them, respectively. Vagueness in global issues can emerge in the information that specifies the conditions. FG models are useful mathematical tools for dealing with combinatorial issues in different fields, such as topology, algebra, optimization, computers, and environmental science. Because of the inherent presence of vagueness and ambiguity, FG models are more complex in comparison to simple graphical models. The first time fuzzy set theory was used, it was used to deal with a lot of complicated situations that did not have enough information.

Zadeh [1] proposed the theory of a fuzzy set (FS), which is applicable in several areas, and his FS has a true membership function which is limited to [0,1]. In approximate reasoning, the importance of fuzzy theory is particularly significant in overcoming combinatorial challenges in numerous domains, such as algebra, image segmentation, topology, operational research, medical science, and algebraic structure. Rosenfeld [2] discussed the fuzzy versions of various graph-based theories. Ghorai and Pal [3,4] recently studied the extensions of FG, such as bipolar fuzzy graphs, m-polar fuzzy planner graphs, and m-polar fuzzy graphs. They defined the density of m-polar fuzzy graph techniques as well as a set of operations. Nagoor Gani and Radha [5] discussed a few operations on regular FG. Mathew and Sunitha described some kinds of arcs of FG. Bhattacharya [6] gave some remarks on FG. Atanassov [7] extended the FS to the intuitionistic fuzzy set. Shao et al. [8] developed new notions of the bondage number in intuitionistic fuzzy graphs. Rashmanlou et al. [9,10] discussed briefly a bipolar fuzzy graph with the product of bipolar fuzzy graphs, categorical operations, and related degrees. Rashmanlou et al. [11] were interested in research on interval-valued fuzzy graphs. Zeng et al. [12] invented different properties for single-valued neutrosophic graphs. Shao et al. [13] studied the properties of vague graphs.

Ramot et al. [14] proposed the notion of a “CFS” in 2002. CFSs are an innovative development of Zadeh’s fuzzy sets. Despite all of the benefits of this theory, we still face enormous challenges when attempting to counter various physical conditions using a true membership function. Because of this, it is very important to add a new step to fuzzy set theory that takes into account complex numbers, which are an expansion of real numbers. Complex fuzzy logic is a linear extension of standard fuzzy logic. It lets problems in fuzzy logic that cannot be solved with a simple membership function grow and change in a natural way. This specific set plays a critical role in a variety of executions, particularly intelligent control systems and the prediction of periodic phenomena, where various fuzzy variables are connected in a complicated way that cannot be accurately represented by simple fuzzy operations. Furthermore, these sets are employed to tackle a variety of difficulties, particularly the various periodic aspects and forecasting challenges. One of the far-reaching implications of researching the CFS is that it effectively illustrates data with uncertainty and periodicity. Buckley described fuzzy complex numbers in [15]. Yaqoob et al. [16] studied the complex intuitionistic fuzzy graph and the complex neutrosophic graph. Shoaib et al. [17] proposed the concept of a complex Pythagorean fuzzy graph. Shoaib et al. [18] discussed some properties, symmetric difference and maximal product of picture fuzzy graphs. Gulzar et al. [19,20,21] discussed fuzzy groups.

The CFG is the generalization of the FG. We define the order and size of CFG. Furthermore, we present the degree of vertex and total degree of vertex concepts for CFG. We describe some basic properties, including the join, union, and complement of CFG. We discuss some new operations with maximal product and symmetric difference on CFG with elaboration of examples and related theorems. Lastly, we analyze the application of CFG.

2. Preliminaries

Definition 1

([1]). Fuzzy set is defined as $Q=<p:{\mu }_Q\left(p\right)>,p\in X$, where ${\mu }_Q:A\to [0,1]$ represent the degree of true membership function.

Definition 2

([17]). Let X be a non-empty universal set. A complex fuzzy set Q is defined as $Q=<p:{\mu }_Q\left(p\right)e^{i{\alpha }_Q}>,p\in X$ where ${\mu }_Q:A\to [0,1]$ and ${\alpha }_Q:A\to [0,2\pi ]$.

Definition 3

([22]). FG is a pair $\mathbb{G}=(Q,L)$ with fuzzy set Q on A and a fuzzy relation L on A such that

$$\begin{array}{c}\hfill {\mu }_L\left(pq\right)\le max\{{\mu }_Q\left(p\right),{\mu }_Q\left(q\right)\}\end{array}$$

where ${\mu }_Q$$:A\to [0,1]$ denotes the degree of true membership function and the function ${\mu }_L$: B ⊆ A × A→ [0,1].

3. CFGs

This section presents the idea of complex fuzzy relations and CFG, as well as some of their properties.

Definition 4.

A CFG on a universe Y with underlying set A is an ordered pair $\tau =(Q,L)$; Q is a complex fuzzy set on A and L is a complex fuzzy set on $B\subseteq A\times A$ such that

$$\begin{array}{c}\hfill {\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}\le min\{{\mu }_Q\left(x\right),{\mu }_Q\left(y\right)\}{e}^{imin\{{\alpha }_Q\left(x\right),{\alpha }_Q\left(y\right)\}}\end{array}$$

${\mu }_Q\left(x\right)\in [0,1]$, and ${\alpha }_Q\left(x\right)$∈$[0,2\pi ]$

∀ x, y ∈ A.

Definition 5.

Let $Q=\{x,{\mu }_Q\left(x\right)e^{i{\alpha }_Q\left(x\right)}\}$, $Q_1=\{x,{\mu }_{Q_1}\left(x\right)e^{i{\alpha }_{Q_1}\left(x\right)}\}|x\in Y\}$,

$Q_2=\{x,{\mu }_{Q_2}\left(x\right)e^{i{\alpha }_{Q_2}\left(x\right)}\}|x\in Y\}$, be the three CFSs in Y:

 (i) 

$Q_1\subseteq Q_2$ if and only if ${\mu }_{Q_1}\le {\mu }_{Q_2}$ for amplitude terms and ${\alpha }_{Q_1}\le {\alpha }_{Q_2}$ for phase terms, ∀ x ∈ Y.

 (ii) 

$Q_1=Q_2$ if and only if ${\mu }_{Q_1}={\mu }_{Q_2}$ for amplitude terms and ${\alpha }_{Q_1}={\alpha }_{Q_2}$ for phase terms, ∀ x ∈ Y.

For simplicity, $\mu e^{i\alpha }$ is called the complex fuzzy number where μ ∈ [0,1], and α ∈ $[0,2\pi ]$.

Definition 6.

Let $Q_1=\{x,{\mu }_{Q_1}\left(x\right)e^{i{\alpha }_{Q_1}\left(x\right)}|x\in Y\}$ and $Q_2=\{x,{\mu }_{Q_2}\left(x\right)e^{i{\alpha }_{Q_2}\left(x\right)}|x\in Y\}$ be the two complex picture fuzzy sets in Y, then

 (i) 

$Q_1$∪$Q_2$ =$\{x,max({\mu }_{Q_1}\left(x\right),{\mu }_{Q_2}\left(x\right))e^{imax({\alpha }_{Q_1}\left(x\right),{\alpha }_{Q_2}\left(x\right))}|x\in Y\}$.

 (ii) 

$Q_1$∩$Q_2$ =$\{x,min({\mu }_{Q_1},{\mu }_{Q_2}\left(x\right))e^{imin({\alpha }_{Q_1}\left(x\right),{\alpha }_{Q_2}\left(x\right))}|x\in Y\}$.

Definition 7.

A complex fuzzy set L in Y × Y is called a complex fuzzy relation in Y, characterized by $L=\{xy,{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}|xy\in Y$× Y}, where ${\mu }_L$: Y × Y → [0,1] depicts the membership function of L and ${\alpha }_L\left(xy\right)$∈$2\pi$∀ xy ∈ Y × Y.

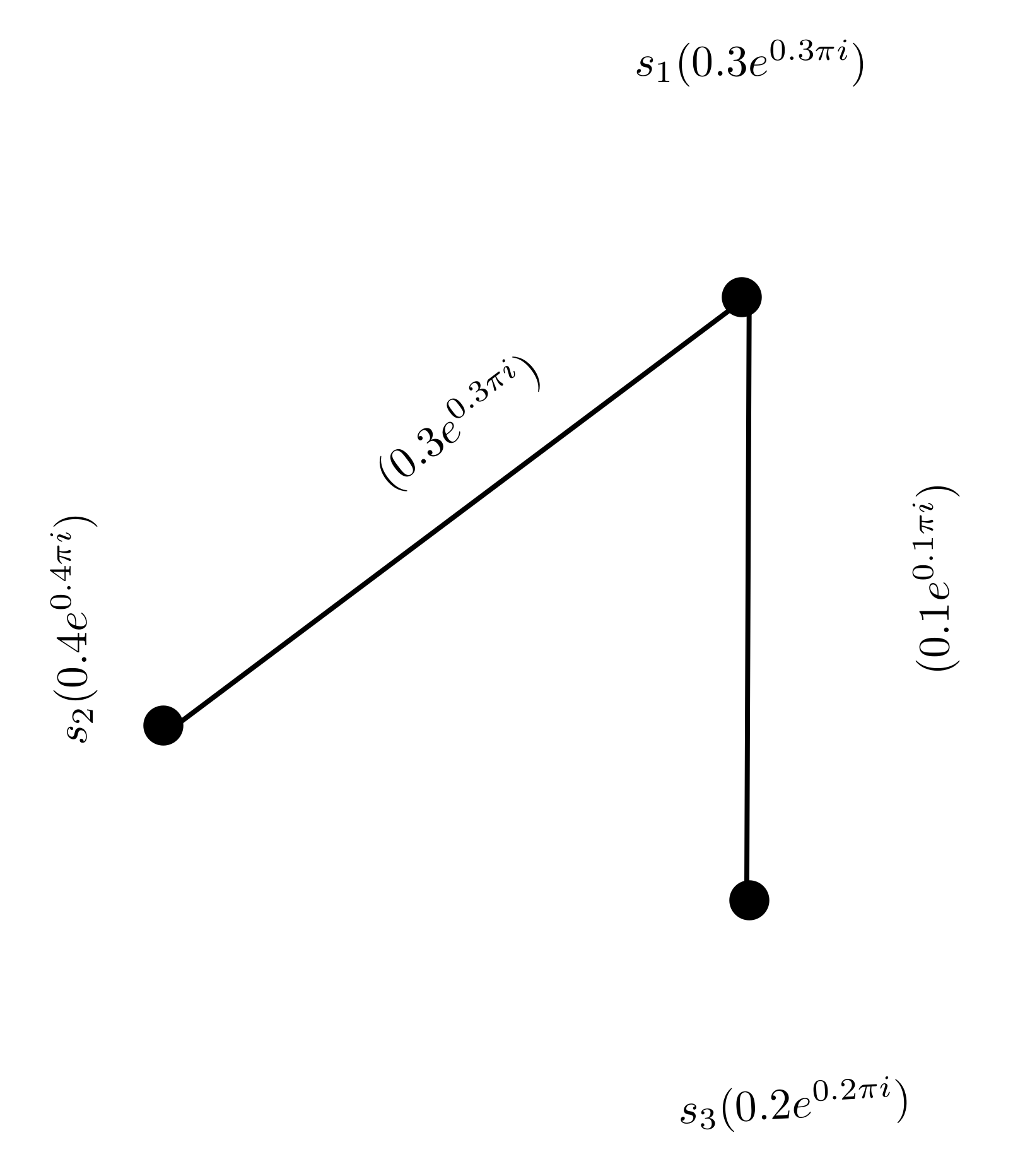
Example 1.

Let G = (A,B) be a graph with $Q=\{s_1,s_3,s_4\}$ as the vertex set and $L=\{s_1{s}_3,s_3{s}_4\}$ as the edge set of G. $\tau =(Q,L)$ is a CFG on A, as given in Figure 1, defined by $Q=$$<(\frac{s_1}{0.3e^{0.2\pi i}},\frac{s_3}{0.3e^{0.3\pi i}},\frac{s_4}{0.3e^{0.3\pi i}})>$ $L=<(\frac{s_1{s}_3}{0.2e^{0.1\pi i}},\frac{s_3{s}_4}{0.2e^{0.2\pi i}})>$.

Definition 8.

Let $Q=\{x,{\mu }_Q\left(x\right)e^{i{\alpha }_Q\left(x\right)}|x\in A\}$ and $L=\{xy,{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}|xy\in B\}$ be the vertex set and edge set of a CFG τ, then the order of a CFG τ is denoted by O(τ) and is defined as O(τ) = ${\displaystyle \sum _{x_i\in A}}{\mu }_Q\left(x_i\right)e^{i{\displaystyle \sum _{x_i\in A}}{\alpha }_Q\left(x_i\right)}$.

The size of a CFG τ is denoted by S(τ ) and is defined as S(τ) = ${\displaystyle \sum _{x_i\in A}}{\mu }_L\left(x_i{y}_j\right)e^{i{\displaystyle \sum _{x_i{y}_j\in A}}{\alpha }_L\left(x_i{y}_j\right)}$.

Example 2.

The order and size of the CFG given in Figure 1 is O(τ) = $0.9e^{0.8\pi i}$ and S(τ) = $0.4e^{0.3\pi i}$, respectively.

Definition 9.

The complement of a CFG τ = (Q,L) on the underlying graph G = (A,B) is a CFG $\overline{\tau }$ = ($\overline{Q}$,$\overline{L}$) defined by

 1. 

$\overline{{\mu }_Q\left(x\right)e^{i{\alpha }_Q\left(x\right)}}$ = ${\mu }_Q\left(x\right)e^{i{\alpha }_Q\left(x\right)}$

 2. 

$$\overline{{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}}=\left\{\begin{array}{cc}min\{{\mu }_Q\left(x\right),{\mu }_Q\left(y\right)\}{e}^{min\{{\alpha }_Q\left(x\right),{\alpha }_Q\left(y\right)\}i}\hfill & if{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}=0,\hfill \\ min\{{\mu }_Q\left(x\right),{\mu }_Q\left(y\right)\}{e}^{min\{{\alpha }_Q\left(x\right),{\alpha }_Q\left(y\right)\}i}-{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}\hfill & if0<{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}\le 1.\hfill \end{array}\right..$$

Example 3.

Consider a CFG τ = (Q,L) on $A=\{s_1,s_2,s_3\}$, which is shown as in Figure 2 where $Q=<(\frac{s_1}{0.3e^{0.3\pi i}},\frac{s_2}{0.4e^{0.4\pi i}},\frac{s_3}{0.2e^{0.2\pi i}})$, $L=<(\frac{s_2{s}_1}{0.3e^{0.3\pi i}},\frac{s_1{s}_3}{0.1e^{0.1\pi i}})$.

Utilizing the Definition 9, the complement of a CFG can be obtained, which is shown as in Figure 3.

Where $\overline{Q}=<(\frac{s_1}{0.3e^{0.3\pi i}},\frac{s_2}{0.4e^{0.4\pi i}},\frac{s_3}{0.2e^{0.2\pi i}})>$ $\overline{L}=<(\frac{s_1{s}_3}{0.1e^{0.1\pi i}},\frac{s_2{s}_3}{0.2e^{0.2\pi i}}))$.

It is easy to see from Figure 3 that $\overline{\tau }$ = $(\overline{Q},\overline{L})$ is a CFG.

Theorem 1.

The complement of a complement of CFG is a CFG itself, that is, $\stackrel{=}{\tau }$ = τ

Proof. 

Suppose that $\tau$ is a CFG. Then, by utilizing Definition 9.

$\stackrel{=}{{\mu }_Q\left(x\right)}\stackrel{=}{e^{i{\alpha }_Q\left(x\right)}}$ = $\overline{{\mu }_Q\left(x\right)}\overline{e^{i{\alpha }_Q\left(x\right)}}$ = ${\mu }_Q\left(x\right)e^{i{\alpha }_Q\left(x\right)}$ for all x ∈ A

if ${\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}=0$ then

$\stackrel{=}{{\mu }_L\left(xy\right)}$$\stackrel{=}{e^{i{\alpha }_L\left(xy\right)}}$ = $min\{\overline{{\mu }_Q\left(x\right)},\overline{{\mu }_Q\left(y\right)}\}$$e^{i min\{\overline{{\alpha }_Q\left(x\right)},\overline{{\alpha }_Q\left(y\right)}\}}$

= $min\{{\mu }_Q\left(x\right),{\mu }_Q\left(y\right)\}$$e^{i min\{{\alpha }_Q\left(x\right),{\alpha }_Q\left(y\right)}\}$$={\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}$

if $0<{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}\le 1$ then

$\stackrel{=}{{\mu }_L\left(xy\right)}$$\stackrel{=}{e^{i{\alpha }_L\left(xy\right)}}$ = $min\{\overline{{\mu }_Q\left(x\right)},\overline{{\mu }_Q\left(y\right)}\}$$e^{i min\{\overline{{\alpha }_Q\left(x\right)},\overline{{\alpha }_Q\left(y\right)}\}}$−$\overline{{\mu }_L\left(xy\right)}$$\overline{e^{i{\alpha }_L\left(xy\right)}}$

$\stackrel{=}{{\mu }_L\left(xy\right)}$$\stackrel{=}{e^{i{\alpha }_L\left(xy\right)}}$ = $min\{\overline{{\mu }_Q\left(x\right)},\overline{{\mu }_Q\left(y\right)}\}$$e^{i min\{\overline{{\alpha }_Q\left(x\right)},\overline{{\alpha }_Q\left(y\right)}\}}$−

$min\{{\mu }_Q\left(x\right),{\mu }_Q\left(y\right)\}{e}^{min\{{\alpha }_Q\left(x\right),{\alpha }_Q\left(y\right)\}i}-{\mu }_L\left(xy\right)e^{i{\alpha }_L\left(xy\right)}$

$\stackrel{=}{{\mu }_L\left(xy\right)}$$\stackrel{=}{e^{i{\alpha }_L\left(xy\right)}}$ = ${\mu }_L\left(xy\right)$$e^{i{\alpha }_L\left(xy\right)}$

for all x, y ∈ A. Hence $\stackrel{=}{\tau }$ = $\tau$. □

Definition 10.

The union τ${}_1$∪τ${}_2$ = $(Q_1\cup Q_2,L_1\cup L_2)$ of two CFGs τ${}_1$ = $(Q_1,L_1)$ and τ${}_2$ = $(Q_2,L_2)$ of the graphs $G_1$ = $(A_1,B_1)$ and $G_2$ = $(A_2,B_2)$, respectively, is defined as follows: $({\mu }_{Q_1}\cup {\mu }_{Q_2})$(x)$e^{i({\alpha }_{Q_1}\cup {\alpha }_{Q_2})}$

$$({\mu }_{Q_1}\cup {\mu }_{Q_2})\left(x\right)e^{i({\alpha }_{Q_1}\cup {\alpha }_{Q_2})\left(x\right)}=\left\{\begin{array}{cc}{\mu }_{Q_1}\left(x\right)e^{i{\alpha }_{Q_1}\left(x\right)}\hfill & ifx\in A_1-A_2,\hfill \\ {\mu }_{Q_2}\left(x\right)e^{i{\alpha }_{Q_2}\left(x\right)}\hfill & ifx\in A_2-A_1,\hfill \\ max\{{\mu }_{Q_1}\left(x\right),{\mu }_{Q_2}\left(x\right)\}{e}^{i max\{{\alpha }_{Q_1}\left(x\right),{\alpha }_{Q_2}\left(x\right)\}}\hfill & ifx\in A_1\cap A_2,\hfill \end{array}\right.$$

$$({\mu }_{L_1}\cup {\mu }_{L_2})\left(xy\right)e^{i({\alpha }_{L_1}\cup {\alpha }_{L_2})\left(xy\right)}=\left\{\begin{array}{cc}{\mu }_{L_1}\left(xy\right)e^{i{\alpha }_{L_1}\left(xy\right)}\hfill & ifxy\in B_1-B_2,\hfill \\ {\mu }_{L_2}\left(xy\right)e^{i{\alpha }_{L_2}\left(xy\right)}\hfill & ifxy\in B_2-B_1,\hfill \\ max\{{\mu }_{L_1}\left(xy\right),{\mu }_{L_2}\left(xy\right)\}{e}^{i max\{{\alpha }_{L_1}\left(xy\right),{\alpha }_{L_2}\left(xy\right)\}}\hfill & ifxy\in B_1\cap B_2,\hfill \end{array}\right.$$

Definition 11.

The ring-sum τ${}_1$⊕τ${}_2$ = $(Q_1\oplus Q_2,L_1\oplus L_2)$ of two CFGs τ${}_1$ = $(Q_1,L_1)$ and τ${}_2$ = $(Q_2,L_2)$ of the graphs $G_1$ and $G_2$, respectively, is defined as follows:

$({\mu }_{Q_1}\oplus {\mu }_{Q_2})\left(x\right)e^{i({\alpha }_{Q_1}\oplus {\alpha }_{Q_2})\left(x\right)}$=(${\mu }_{Q_1}\cup {\mu }_{Q_2})\left(x\right)e^{i({\alpha }_{Q_1}\cup {\alpha }_{Q_2})\left(x\right)}$,

$$({\mu }_{L_1}\otimes {\mu }_{L_2})\left(xy\right)e^{i({\alpha }_{L_1}\cup {\alpha }_{L_2})\left(xy\right)}=\left\{\begin{array}{cc}{\mu }_{L_1}\left(xy\right)e^{i{\alpha }_{L_1}\left(xy\right)}\hfill & ifxy\in B_1-B_2,\hfill \\ {\mu }_{L_2}\left(xy\right)e^{i{\alpha }_{L_2}\left(xy\right)}\hfill & ifxy\in B_2-B_1,\hfill \\ 0\hfill & ifxy\in B_1\cap B_2,\hfill \end{array}\right.$$

Definition 12.

Let τ${}_1$ = $(Q_1,L_1)$ and τ${}_2$ = $(Q_2,L_2)$ be two CFGs of $G_1$ and $G_2$, respectively. The join τ${}_1$$+$τ${}_2$ = $(Q_1+Q_2,L_1+L_2)$ of τ${}_1$ = $(Q_1,L_1)$ and τ${}_2$ = $(Q_2,L_2)$, defined as

 (i) 

$({\mu }_{Q_1}+{\mu }_{Q_2})\left(x\right)e^{i({\alpha }_{Q_1}+{\alpha }_{Q_2})\left(x\right)}$=(${\mu }_{Q_1}\cup {\mu }_{Q_2})\left(x\right)e^{i({\alpha }_{Q_1}\cup {\alpha }_{Q_2})\left(x\right)}$,

 (ii) 

$({\mu }_{L_1}+{\mu }_{L_2})\left(xy\right)e^{i({\alpha }_{L_1}+{\alpha }_{L_2})\left(xy\right)}$=(${\mu }_{L_1}\cup {\mu }_{L_2})\left(xy\right)e^{i({\alpha }_{L_1}\cup {\alpha }_{L_2})\left(xy\right)}$,

 (iii) 

$({\mu }_{L_1}+{\mu }_{L_2})\left(xy\right)e^{i({\alpha }_{L_1}+{\alpha }_{L_2})\left(xy\right)}$ = $min\{{\mu }_{Q_1}\left(x\right),{\mu }_{Q_2}\left(y\right)\}{e}^{i min\{{\alpha }_{Q_1}\left(x\right),{\alpha }_{Q_2}\left(y\right)\}}$ where $B^{\prime }$ is the arcs set joining the nodes of $A_1$ and $A_2$, $A_1\cap A_2=\varnothing$.

Definition 13.

The degree of a vertex x ∈ A in a CFG τ stands for $d_{\tau }\left(x\right)$, and is described as $d_{\tau }\left(x\right)$ = $d_{\mu e^{i\alpha }}\left(x\right)$, where $d_{\mu e^{i\alpha }}\left(x\right)$ = ${\displaystyle \sum _{x,y\ne x\in A}}{\mu }_L\left(xy\right)e^{i{\displaystyle \sum _{x,y\ne x\in A}}{\alpha }_L\left(xy\right)}$

Definition 14.

The total degree of a vertex x ∈ A in a CFG τ stands for $t{d}_{\tau }\left(x\right)$, and is described as $t{d}_{\tau }\left(x\right)$ = $t{d}_{\mu e^{i\alpha }}\left(x\right)$, where $t{d}_{\mu e^{i\alpha }}\left(x\right)$ = ${\displaystyle \sum _{x,y\ne x\in A}}{\mu }_L\left(xy\right)e^{i{\displaystyle \sum _{x,y\ne x\in A}}{\alpha }_L\left(xy\right)}$ + ${\mu }_Q\left(x\right)e^{i{\alpha }_Q\left(x\right)}$

Definition 15.

Let τ${}_1$ and τ${}_2$ be two CFGs. For any vertex x $\in A_1\cup A_2$, there are three cases to consider.

 Case 1: 

Either x $\in A_1-A_2$ or x $\in A_2-A_1$. Then no arc incident at x lies in $B_1\cap B_2$. Thus, for c $\in C_1-C_2$,

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\displaystyle \sum _{xy\in B_1}}$${\mu }_{L_1}\left(xy\right)$$e^{i{\displaystyle \sum _{xy\in B_1}}{\alpha }_{L_1}\left(xy\right)}$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_1}\left(x\right)$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_1}\left(x\right)$. For x $\in A_2-A_1$.

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\displaystyle \sum _{xy\in B_2}}$${\mu }_{L_2}\left(xy\right)$$e^{i{\displaystyle \sum _{xy\in B_2}}{\alpha }_{L_2}\left(xy\right)}$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_2}\left(x\right)$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_2}\left(x\right)$.

 Case 2: 

x $\in A_1\cap A_2$ but no arc incident at x lies in $B_1\cap B_2$. Then any arc incident at x is either $B_1-B_2$ or $B_2-B_1$.

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\displaystyle \sum _{xy\in B_1\cup B_2}}$$({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\cup {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left(xy\right)$

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\displaystyle \sum _{xy\in B_1}}$${\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right)$ + ${\displaystyle \sum _{xy\in B_2}}$${\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)$

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_1}\left(x\right)$ + ${\left(d_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_2}\left(x\right)$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\displaystyle \sum _{xy\in B_1\cup B_2}}$$({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\cup {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left(xy\right)$ + $max\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(x\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(x\right)\}$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\displaystyle \sum _{xy\in B_1}}$${\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right)$ + ${\displaystyle \sum _{xy\in B_2}}$${\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)$ + $max\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(x\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(x\right)\}$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_1}\left(x\right)$ + ${\left(d_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_2}\left(x\right)$ + $max\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(x\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(x\right)\}$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)$ = ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_1}\left(x\right)$ + ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\mathtt{G}}_2}\left(x\right)-min\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(x\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(x\right)\}$

 Case 3: 

$$\begin{array}{cc}\hfill {\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(x\right)& =\sum _{xy\in B_1\cup B_2}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\cup {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left(xy\right)\hfill \\ \hfill & =\sum _{xy\in B_1-B_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right)+\sum _{xy\in B_2-B_1}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)\hfill \\ \hfill & +\sum _{xy\in B_1\cap B_2}max\{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)\}\hfill \\ \hfill & =\sum _{xy\in B_1-B_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right)+\sum _{xy\in B_2-B_1}{\mu }_{L_2}{e}^{i{\alpha }_{L_1}}\left(xy\right)\hfill \\ \hfill & +\sum _{xy\in B_1\cap B_2}max\{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)\}\hfill \\ \hfill & +\sum _{xy\in B_1\cap B_2}min\{{\mu }_{L_1}\left(xy\right),{\mu }_{L_2}\left(xy\right)\}{e}^{imin\{{\alpha }_{L_1}\left(xy\right),{\alpha }_{L_2}\left(xy\right)\}}\hfill \\ \hfill & -\sum _{xy\in B_1\cap B_2}min\{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)\}\hfill \\ \hfill & =\sum _{xy\in B_1}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right)+\sum _{xy\in B_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_1}}\left(xy\right)\hfill \\ \hfill & -\sum _{xy\in B_1\cap B_2}min\{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)\}\hfill \\ \hfill & ={\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(x\right)+{\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(x\right)-\sum _{xy\in B_1\cap B_2}min\{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(xy\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(xy\right)\}\hfill \end{array}$$

In addition,

$$\begin{array}{cc}\hfill \left({\mathrm{td}}_{¯{\mathrm{e}}^{\mathrm{i}\mathrm{ff}}}\right){ø}_1\cup {ø}_2\left(\mathrm{x}\right)& ={\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(x\right)+{\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(x\right)\hfill \\ \hfill & -\sum _{xy\in B_1\cap B_2}min\{{\mu }_{L_1}\left(xy\right),{\mu }_{L_2}\left(xy\right)\}{e}^{i min\{{\alpha }_{L_1}\left(xy\right),{\alpha }_{L_2}\left(xy\right)\}}\hfill \\ \hfill & -min\{{\mu }_{Q_1}\left(x\right),{\mu }_{Q_2}\left(x\right)\}{e}^{i min\{{\alpha }_{Q_1}\left(x\right),{\alpha }_{Q_2}\left(x\right)\}},\hfill \end{array}$$

Example 4.

Suppose that ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs on $A_1=\{s_1,s_2,s_4\}$ and $A_2=\{s_1,s_2,s_3,s_4\}$, respectively, as shown in Figure 4 and Figure 5.

Moreover, ${\tau }_1\cup {\tau }_2$ is shown in Figure 6.

If $s_3$∈$A_2-A_1$, then

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(s_3\right)$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(s_3\right)$ = $0.3e^{0.2\pi i}$

Therefore, $(d_{{\tau }_1\cup {\tau }_2}\left(s_3\right)$ = $d_{{\tau }_2}\left(s_3\right)$ = $0.3e^{0.2\pi i}$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(s_3\right)$ = ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(s_3\right)$ = $0.6e^{0.3\pi i}$

Therefore, $(t{d}_{{\tau }_1\cup {\tau }_2}\left(s_3\right)$ = $t{d}_{{\tau }_2}\left(s_3\right)$ = $0.6e^{0.3\pi i})$

Since $s_4$∈$A_1$∩$A_2$ but there is no edge incident at $s_4$ lies in $B_1\cap B_2$,

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(s_4\right)$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(s_4\right)$ + ${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(s_4\right)$ = $0.4e^{0.5\pi i}$

Therefore, $(d_{{\tau }_1\cup {\tau }_2}\left(s_4\right)$ = $d_{{\tau }_1}\left(s_4\right)$ + $d_{{\tau }_2}\left(s_4\right)$ = ($0.4e^{0.5\pi i}$)

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(s_4\right)$ = ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(s_4\right)$ + ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(s_4\right)$ + $max\{{\mu }_{Q_1}\left(s_4\right),{\mu }_{Q_2}\left(s_4\right)\}{e}^{max\{{\alpha }_{Q_1}\left(s_4\right),{\alpha }_{Q_2}\left(s_4\right)\}i}$

= $0.7e^{0.8\pi i}$

Since $s_2$∈$A_1$∩$A_2$ and $s_1{s}_2$∈$B_1$∩$B_2$,

${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(s_2\right)$ = ${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(s_2\right)$ + ${\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(s_2\right)-min\{{\mu }_{L_1}\left(s_1{s}_2\right),{\mu }_{L_2}\left(s_1{s}_2\right)\}{e}^{min\{{\alpha }_{L_1}\left(s_1{s}_2\right),{\alpha }_{L_2}\left(s_1{s}_2\right)\}i}$ = $0.5e^{0.5\pi i}$

Therefore, $(d_{{\tau }_1\cup {\tau }_2}\left(s_2\right)$ = $0.5e^{0.5\pi i}$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\cup {\tau }_2}\left(s_2\right)$ = ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(s_2\right)$ + ${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(s_2\right)-min\{{\mu }_{L_1}\left(s_1{s}_2\right),{\mu }_{L_2}\left(s_1{s}_2\right)\}{e}^{min\{{\alpha }_{L_1}\left(s_1{s}_2\right),{\alpha }_{L_2}\left(s_1{s}_2\right)\}i}$

+ $max\{{\mu }_{Q_1}\left(s_2\right),{\mu }_{Q_2}\left(s_2\right)\}{e}^{max\{{\alpha }_{Q_1}\left(s_2\right),{\alpha }_{Q_2}\left(s_2\right)\}i}$ = $0.7e^{0.8\pi i}$

Therefore, $(t{d}_{{\tau }_1\cup {\tau }_2}\left(s_2\right)$ = $0.7e^{0.8\pi i}$

Definition 16.

Maximal product ${\tau }_1\ast {\tau }_2=(Q_1\ast Q_2,L_1\ast L_2)$ of two CFGs ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ is defined as

 (i) 

$$\begin{array}{c}\hfill ({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((u_1,u_2)\right)=\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\\ \hfill \forall (u_1,u_2)\in (V_1\times V_2),\end{array}$$

 (ii) 

$$\begin{array}{c}\hfill ({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((m,u_2)(m,w_2)\right)=\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\\ \hfill \forall m\in V_{1}and{u}_2{w}_2\in E_2,\end{array}$$

 (iii) 

$$\begin{array}{c}\hfill ({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((u_1,z)(w_1,z)\right)=\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\\ \hfill \forall z\in V_{2}and{u}_1{w}_1\in E_1.\end{array}$$

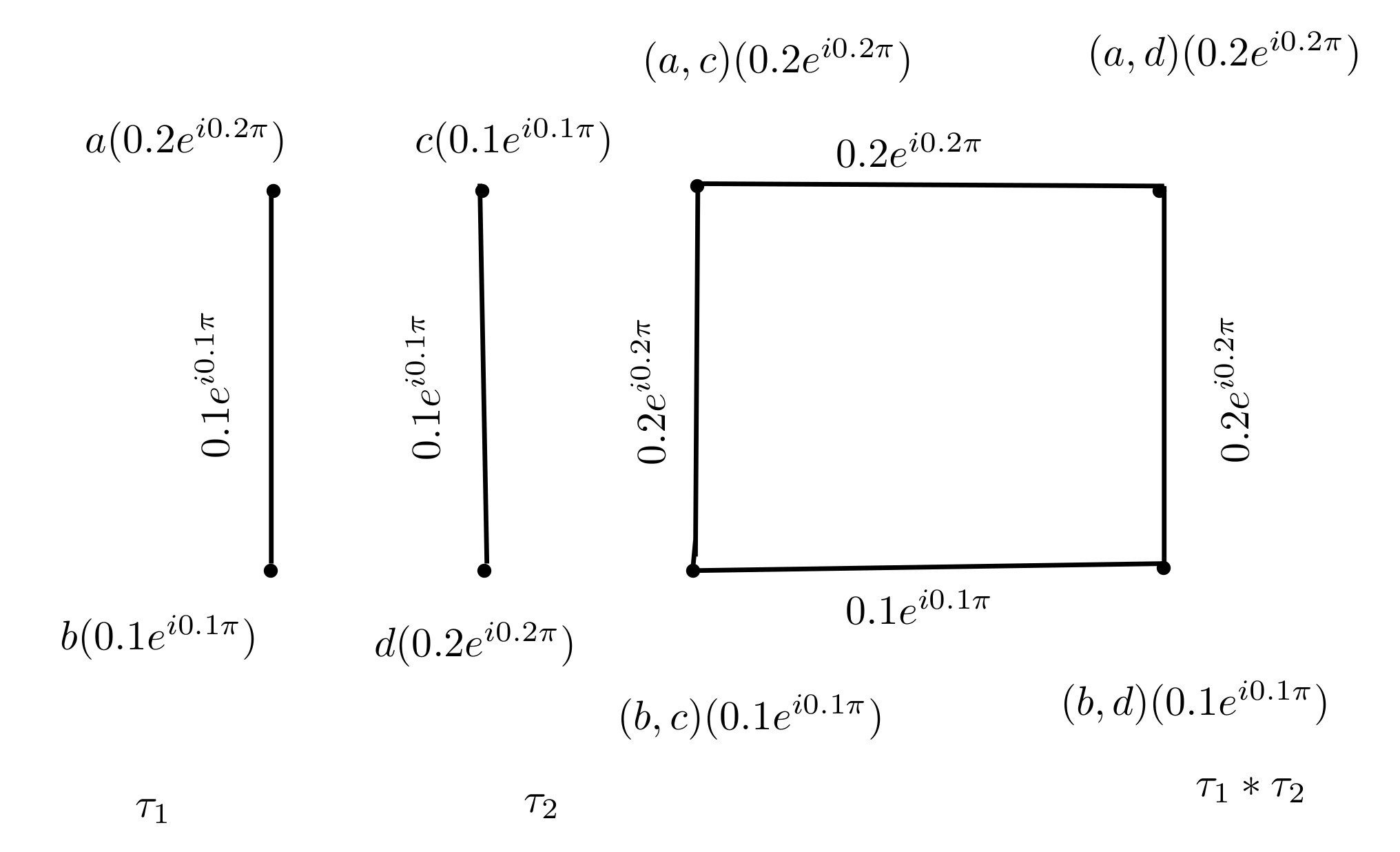
Example 5.

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs, shown in Figure 7 and Figure 8. Their maximal product ${\tau }_1\ast {\tau }_2$ is shown in Figure 9.

For vertex (e,a), we find membership value (Mv) as follows:

$$\begin{array}{cc}\hfill (\mu e_{Q_1}^{i\alpha }\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((e,a)\right)& =\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(e\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(a\right)\}\hfill \\ \hfill & =\vee \{0.1,0.2\}{e}^{i\vee \{0.1,0.2\}}=0.2e^{i0.2\pi },\hfill \end{array}$$

for $e\in V_1$ and $a\in V_2$.

For edge (e,a)(e,b), we find Mv.

$$\begin{array}{cc}\hfill ({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((e,a)(e,b)\right)& =\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(e\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(ab\right)\}\hfill \\ \hfill & =\vee \{0.1,0.1\}{e}^{i\vee \{0.1,0.1\}\pi }=0.1e^{i\vee \{0.1,0.1\}\pi }.\hfill \end{array}$$

for $e\in V_1$ and $ab\in E_2$.

For edge $(e,a)(f,a)$:

$$\begin{array}{cc}\hfill ({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((e,a)(f,a)\right)& =\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(ef\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(a\right)\}\hfill \\ \hfill & =\vee \{0.1,0.2\}{e}^{i\vee \{0.1,0.2\}\pi }=0.2e^{i0.2\pi }.\hfill \end{array}$$

for $a\in V_2$ and $ef\in E_1$. Similarly, Mv for all others nodes and edges can be calculated.

Proposition 1.

Maximal product of two CFGs ${\tau }_1$ and ${\tau }_2$, is a CFG.

Proof. 

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs on crisp graphs

$G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$, respectively and $\left((u_1,u_2)(w_1,w_2)\right)\in E_1\times E_2$.

(i)

if $u_1=w_1=m$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})& \left((m,u_2)(m,w_2)\right)\hfill \\ \hfill & =\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & \le \vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),\wedge \{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\}\hfill \\ \hfill & =\wedge \{\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\},\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(m,u_2),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(m,w_2)\}.\hfill \end{array}$$

(ii)

if $u_2=w_2=z$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})& \left((u_1,z)(w_1,z)\right)\hfill \\ \hfill & =\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \\ \hfill & \le \vee \{\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \\ \hfill & =\wedge \{\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\},\vee \left\{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\right\}\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(u_1,z),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(w_1,z)\}.\hfill \end{array}$$

We conclude that ${\tau }_1\ast {\tau }_2$ is a CFG. □

Theorem 2.

Maximal product of two strong CFGs ${\tau }_1$ and ${\tau }_2$ is a strong CFG.

Proof. 

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two strong CFGs on two crisp graphs and $\left((u_1,u_2)(w_1,w_2)\right)\in E_1\times E_2$.

(i)

if $u_1=w_1=m$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})& \left((m,u_2)(m,w_2)\right)=\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & =\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),\wedge \{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\}\hfill \\ \hfill & =\wedge \{\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\},\vee \left\{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\right\}\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(m,u_2),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(m,w_2)\}.\hfill \end{array}$$

(ii)

if $u_2=w_2=z$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})& \left((u_1,z)(w_1,z)\right)=\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \\ \hfill & =\vee \{\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \\ \hfill & =\wedge \{\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\},\vee \left\{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\right\}\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(u_1,z),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(w_1,z)\}.\hfill \end{array}$$

Hence, ${\tau }_1\ast {\tau }_2$ is a strong CFG. □

Example 6.

Suppose ${\tau }_1$ and ${\tau }_2$ are two strong CFGs as shown in Figure 10.

Hence $G_1\ast G_2$ is also a strong CFG.

Remark 1.

If maximal product of two CFGs ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ is a strong, then ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ not necessary to be strong, in general.

Example 7.

Suppose ${\tau }_1$ and ${\tau }_2$ are two CFGs as in Figure 11 and Figure 12. We can see that the maximal product of two CFGs ${\tau }_1$ and ${\tau }_2$, that is ${\tau }_1\ast {\tau }_2$ in Figure 13.

Then ${\tau }_1$ and ${\tau }_1\ast {\tau }_2$ are strong CFGs, but ${\tau }_2$ is not strong. Since ${\mu }_{L_2}{e}^{i{\alpha }_{L_2}}(u_2,w_2)$ = $0.2e^{i0.2\pi }$, on other hand $\wedge \{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}$ = $\wedge \{0.2e^{i0.2\pi },0.1e^{i0.1\pi }\}$ = $0.1e^{i0.1\pi }$.

Hence ${\mu }_{L_2}{e}^{i{\mu }_{L_2}}(u_2,w_2)\ne \wedge \{{\mu }_{Q_2}{e}^{i{\mu }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\mu }_{Q_2}}\left(w_2\right)\}$.

Remark 2.

The maximal product of two complete CFGs may or may not be a complete CFG because $(u_1,u_2)\in E_1$ and $(w_1,w_2)\in E_2$ do not exist in the definition of the maximal product of two CFGs.

Definition 17.

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs. $\forall (u_1,u_2)\in V_1\times V_2$

$$\begin{array}{cc}\hfill {\left(d_{\mu e^{\alpha }}\right)}_{{\tau }_1\ast {\tau }_2}(u_1,u_2)& =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \end{array}$$

Theorem 3.

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs. If ${\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ge {\mu }_{L_2}{e}^{i{\alpha }_{L_2}}$, and ${\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\ge {\mu }_{L_1}{e}^{i{\alpha }_{L_1}}$. Then for every $\forall (u_1,u_2)\in V_1\times V_2$

$\left(d_{\mu }\right)e_{{\tau }_1\ast {\tau }_2}^{i\alpha }(u_1,u_2)$ =${\left(d\right)}_{G_2}\left(u_2\right){\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right)+{\left(d\right)}_{G_1}\left(u_1\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)$

Proof. 

$$\begin{array}{cc}\hfill {\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1\ast {\tau }_2}(u_1,u_2)& =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i\_\alpha L_1}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & =\sum _{u_2{w}_2\in E_2,u_1=w_1}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)+\sum _{u_1{w}_1\in E_1,u_2=w_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\hfill \\ \hfill & ={\left(d\right)}_{G_2}\left(u_2\right){\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}+{\left(d\right)}_{G_1}\left(u_1\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\hfill \end{array}$$

□

Example 8.

Take the CFGs ${\tau }_1$, ${\tau }_2$, and ${\tau }_1\ast {\tau }_2$ as in Figure 14. Since ${\mu }_{Q_1}\ge {\mu }_{L_2}$, ${\alpha }_{Q_1}\ge {\alpha }_{L_2}$, ${\mu }_{Q_2}\ge {\mu }_{L_1}$, ${\alpha }_{Q_2}\ge {\alpha }_{L_1}$, by Theorem 3.8, we have the following.

$$\begin{array}{ccc}& & {\left(d_{\mu }{e}^{i\alpha }\right)}_{G_1\ast G_2}(a,d)={\left(d\right)}_{G_2}\left(d\right){\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(a\right)\hfill \\ & & +{\left(d\right)}_{G_1}\left(a\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(d\right)=1·\left(0.3e^{i0.3\pi }\right)+1·\left(0.3e^{i0.3\pi }\right)=0.6e^{i0.6\pi },\hfill \end{array}$$

By direct calculations:

$$\begin{array}{ccc}& & \left(d_{\mu }{e}_{G_1\ast G_2}^{i\alpha }(b,d)\right)=0.2e^{i0.2\pi }+0.3e^{i0.3\pi }=0.5e^{i0.5\pi },\hfill \\ & & \left(d_{\mu }{e}_{G_1\ast G_2}^{i\alpha }(a,c)\right)=0.5e^{i0.5\pi },\hfill \\ & & \left(d_{\mu }{e}_{G_1\ast G_2}^{i\alpha }(a,d)\right)=0.6e^{i0.6\pi },\hfill \\ & & \left(d_{\mu }{e}_{G_1\ast G_2}^{i\alpha }(b,c)\right)=0.4e^{i0.4\pi },\hfill \end{array}$$

We conclude from the above calculations that ”the degrees of nodes determined by using the formula of the above theorem and by the directed method are equal”.

Definition 18.

Let ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ be two CFGs. $\forall (u_1,u_2)\in V_1\times V_2$

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\ast {\tau }_2}(u_1,u_2)& =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)+({\alpha }_{Q_1}\ast {\alpha }_{Q_2}(u_1,u_2)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\vee \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & +\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}{e}^{i\vee \{{\alpha }_{Q_1}\left(u_1\right),{\alpha }_{Q_2}\left(u_2\right)\}},\hfill \end{array}$$

Theorem 4.

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs. If ${\mu }_{Q_1}\ge {\mu }_{L_2}$, ${\alpha }_{Q_1}\ge {\alpha }_{L_2}$ and ${\mu }_{Q_2}\ge {\mu }_{L_1}$, ${\alpha }_{Q_2}\ge {\alpha }_{L_1}$. Then for every $\forall (u_1,u_2)\in V_1\times V_2$

${\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\ast {\tau }_2}(u_1,u_2)$ =${\left(d\right)}_{G_2}\left(u_2\right)\mu e_{Q_1}^{i\alpha }\left(u_1\right)+{\left(d\right)}_{G_1}\left(u_1\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)$ + $\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}$

Proof. 

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\ast {\tau }_2}& (u_1,u_2)=\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\ast {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)\hfill \\ \hfill & +({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ast {\mu }_{Q_2}{e}^{i{\alpha }_{Q_1}})(u_1,u_2)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\vee \{{\mu }_{L_1}\left(u_1{w}_1\right),{\mu }_{Q_2}\left(u_2\right)\}{e}^{i\sum _{u_1{w}_1\in E_1,u_2=w_2}\vee \{{\alpha }_{L_1}\left(u_1{w}_1\right),{\alpha }_{Q_2}\left(u_2\right)\}}\hfill \\ \hfill & +\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & =\sum _{u_2{w}_2\in E_2,u_1=w_1}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\hfill \\ \hfill & +max\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & ={\left(d\right)}_{G_2}\left(u_2\right){\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right)+{\left(d\right)}_{G_1}\left(u_1\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)+max\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \end{array}$$

□

Example 9.

Let ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ be two CFGs. If ${\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ge {\mu }_{L_2}{e}^{i{\alpha }_{L_2}}$ and ${\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\ge {\mu }_{L_1}{e}^{i{\alpha }_{L_1}}$.

In Example 9, we calculate total degree of nodes of ${\tau }_1\ast {\tau }_2$ by using Figure 7, Figure 8 and Figure 9. We calculate the total degree of nodes in the maximal product. Choose node (e,a).

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1\ast {\tau }_2}(e,a)& ={\left(d\right)}_{G_2}\left(e\right){\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(a\right)+{\left(d\right)}_{G_1}\left(a\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(e\right)+\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(e\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(a\right)\}\hfill \\ \hfill & =1\left(0.1e^{i0.1\pi }\right)+3\left(0.2e^{i0.2\pi }\right)+\vee (0.2,0.1)e^{i\vee (0.2,0.1)\pi }\hfill \\ \hfill & =(0.1+0.6+0.2)e^{i(0.1+0.6+0.2)\pi }=0.9e^{i0.9\pi }\hfill \end{array}$$

Similarly, we can calculate it for other nodes.

Definition 19.

Symmetric difference ${\tau }_1\oplus {\tau }_2=(Q_1\oplus Q_2,L_1\oplus L_2)$ of two CFGs ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ is defined as

 (i) 

$$\begin{array}{cc}\hfill & ({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})\left((u_1,u_2)\right)=\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \end{array}$$

$$\forall (u_1,u_2)\in (V_1\times V_2)$$

 (ii) 

$$\begin{array}{cc}\hfill & ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((m,u_2)(m,w_2)\right)=\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \end{array}$$

$$\forall m\in V_{1}and{u}_2{w}_2\in E_2$$

 (iii) 

$$\begin{array}{cc}\hfill & ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus {\mu }_{L_2})e^{i{\alpha }_{L_1}}\left((u_1,z)(w_1,z)\right)=\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \end{array}$$

$$\forall z\in V_{2}and{u}_1{w}_1\in E_1$$

(iv)

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)& =\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & forall{u}_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2\hfill \\ \hfill & or\hfill \\ \hfill & =\wedge \{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right),{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\}\hfill \\ \hfill & forall{u}_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2\hfill \end{array}$$

Example 10.

Take ${\tau }_1$ and ${\tau }_2$ as CFGs as shown in Figure 15 and Figure 16. We can see the symmetric difference of two CFGs ${\tau }_1$ and ${\tau }_2$, that is ${\tau }_1\oplus {\tau }_2$ in Figure 17.

For node $(a,f)$, we calculate Mv, IDv and NMv as follows:

$$\begin{array}{ccc}& & ({\mu }_{Q_1}\oplus {\mu }_{Q_2})\left((a,f)\right)e^{i({\alpha }_{Q_1}\oplus {\alpha }_{Q_2})\left((a,f)\right)}=\wedge \{{\mu }_{Q_1}\left(a\right),{\mu }_{Q_2}\left(f\right)\}{e}^{i\wedge \{{\alpha }_{Q_1}\left(a\right),{\alpha }_{Q_2}\left(f\right)\}}\hfill \\ & & =\wedge \{0.2,0.4\}{e}^{i\wedge \{0.2,0.4\}\pi }=0.2e^{i0.2\pi },\hfill \end{array}$$

for $a\in V_1$ and $f\in V_2$.

For arc/edge $(a,d)(a,e)$, we calculate the Mv.

$$\begin{array}{ccc}& & \left({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\right)\oplus \left({\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\right)\left((a,d)(a,e)\right)=\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(a\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(de\right)\}\hfill \\ & & =\wedge \{0.2,0.2\}{e}^{i\wedge \{0.2,0.2\}\pi }=0.2e^{i0.2\pi },\hfill \end{array}$$

for $a\in V_1$ and $de\in E_2$.

Now, for edge $(a,d)(b,d)$ we have

$$\begin{array}{ccc}& & ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((a,d)(b,d)\right)=\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(ab\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(d\right)\}\hfill \\ & & =\wedge \{0.2,0.2\}{e}^{i\wedge \{0.2,0.2\}}=0.2e^{i0.2\pi }.\hfill \end{array}$$

for $ab\in E_1$ and $d\in V_2$.

We can calculate Mv for all other nodes and edges.

Proposition 2.

Symmetric difference of two CFGs ${\tau }_1$ and ${\tau }_2$ is a CFG.

Proof. 

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ are two CFGs on two crisp graphs and $\left((u_1,u_2)(w_1,w_2)\right)\in E_1\times E_2$.

(i)

If $u_1=w_1=m$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})& \left((m,u_2)(m,w_2)\right)=\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & \le \wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),min\{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\}\hfill \\ \hfill & =\wedge \{\wedge \{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\},\wedge \left\{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(m\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\right\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(m,u_2),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(m,w_2)\}.\hfill \end{array}$$

(ii)

If $u_2=w_2=z$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus & {\mu }_{L_2}{e}^{i{\alpha }_{L_2}}ei({\alpha }_{L_1}\oplus {\alpha }_{L_2}))\left((u_1,z)(w_1,z)\right)=\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}ei{\alpha }_{L_1}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \\ \hfill & \le \wedge \{\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\hfill \\ \hfill & =\wedge \{\wedge \{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}{e}^{i{\alpha }_{Q_2}}\left(z\right)\},\wedge \left\{\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}{e}^{i{\alpha }_{Q_2}}\left(z\right)\}\right\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}{e}^{i{\alpha }_{Q_2}})(u_1,z),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}{e}^{i{\alpha }_{Q_2}})(w_1,z)\}.\hfill \end{array}$$

(iii)

If $u_1{w}_1\notin E_1 and u_2{w}_2\in E_2$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}ei{\alpha }_{L_1}\oplus & {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)=\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & \le \wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),min\left\{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right){\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\right\}\}\hfill \\ \hfill & =\wedge \{\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\},\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(u_1,u_2),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2})e^{i{\alpha }_{Q_1}}(w_1,w_2)\}.\hfill \end{array}$$

(iv)

If $u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2$

$$\begin{array}{cc}\hfill ({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\oplus & {\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)=\wedge \{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right),{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\}\hfill \\ \hfill & \le \wedge \{{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right),\wedge \left\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right){\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right)\right\}\}\hfill \\ \hfill & =\wedge \{\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\},\{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\hfill \\ \hfill & =\wedge \{({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(u_1,u_2),({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\oplus {\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(w_1,w_2)\}.\hfill \end{array}$$

Hence, ${\tau }_1⨁{\tau }_2$ is a CFG. □

Definition 20.

Suppose ${\mathit{G}}_1=(Q_1,L_1)$ and ${\mathit{G}}_2=(Q_2,L_2)$ are two CFGs. For any node $(u_1,u_2)\in V_1\times V_2$, we have

$$\begin{array}{cc}\hfill {\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)& =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}⨁{\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}(u_1{w}_1,{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\},\hfill \end{array}$$

Theorem 5.

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,Y_2)$ are two CFGs. If ${\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\ge {\mu }_{L_2}{e}^{i{\alpha }_{L_2}}$ and ${\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\ge {\mu }_{L_1}{e}^{i{\alpha }_{L_1}}$. Then $\forall (u_1,u_2)\in V_1\times V_2$

${\left(d\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)$ = q${\left(d\right)}_{{\tau }_1}\left(u_1\right)+s{\left(d\right)}_{{\tau }_2}\left(u_2\right)$ where s= $\mid V_1\mid -{\left(d\right)}_{G_1}\left(u_1\right)$ and q= $\mid V_2\mid -{\left(d\right)}_{G_2}\left(u_2\right)$.

Proof. 

$$\begin{array}{cc}\hfill {\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)& =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}⨁{\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\hfill \\ \hfill & =\sum _{u_2{w}_2\in E_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)+\sum _{u_1{w}_1\in E_1}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\hfill \\ \hfill & +\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}+\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\hfill \\ \hfill & =q{\left(d_{\mu }\right)}_{{\tau }_1}\left(u_1\right)+s{\left(d_{\mu }\right)}_{{\tau }_2}\left(u_2\right),\hfill \end{array}$$

We conclude that ${\left(d\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)$ = q${\left(d\right)}_{{\tau }_1}\left(u_1\right)+s{\left(d\right)}_{{\tau }_2}\left(u_2\right)$, where s = $\mid V_1\mid -{\left(d\right)}_{G_1}\left(u_1\right)$ and q = $\mid V_2\mid -{\left(d\right)}_{G_2}\left(u_2\right)$. □

Example 11.

In Figure 18, ${\mu }_{Q_1}\ge {\mu }_{L_2}$, ${\psi }_{Q_1}\le {\psi }_{L_2}$, ${\mu }_{Q_2}\ge {\mu }_{L_1}$, and ${\psi }_{Q_2}\le {\psi }_{L_1}$. Then, the total degree of vertex in the symmetric difference is calculated by using the following formula:

$$\begin{array}{ccc}& & {\left(d_{\mu }{e}^{i\alpha }\right)}_{G_1\oplus G_2}(m_1,m_2)=q{\left(d_T\right)}_{G_1}\left(m_1\right)+s{\left(d_T\right)}_{G_2}\left(m_2\right),\hfill \end{array}$$

$$\begin{array}{ccc}& & {\left(d_{\mu e^{i\alpha }}\right)}_{G_1\oplus G_2}(a,c)=1·\left(0.2e^{i0.2\pi }\right)+1·\left(0.2e^{i0.2\pi }\right)=0.4e^{i0.4\pi },\hfill \\ & & {\left(d_{\mu e^{i\alpha }}\right)}_{G_1\oplus G_2}(a,d)=1·\left(0.2e^{i0.2\pi }\right)+1·\left(0.2e^{i0.2\pi }\right)=0.4e^{i0.4\pi },\hfill \end{array}$$

So, ${\left(d\right)}_{G_1\oplus G_2}(a,c)=0.4e^{i0.4\pi }$ and ${\left(d\right)}_{G_1\oplus G_2}(a,d)=0.4e^{i0.4\pi }$. Applying the same technique, we can obtain ${\left(d\right)}_{G_1\oplus G_2}(b,c)={\left(d\right)}_{G_1\oplus G_2}(b,d)=(0.4,0.9,0.9)$. Now by direct calculations we have:

$$\begin{array}{ccc}& & {\left(d_{\mu e^{i\alpha }}\right)}_{G_1\oplus G_2}(a,c)=0.2e^{i0.2\pi }+0.2e^{i0.2\pi }=0.4e^{i0.4\pi },\hfill \\ & & {\left(d_{\mu e^{i\alpha }}\right)}_{G_1\oplus G_2}(a,d)=0.2e^{i0.2\pi }+0.2e^{i0.2\pi }=0.4e^{i0.4\pi },\hfill \\ & & {\left(d_{\mu e^{i\alpha }}\right)}_{G_1\oplus G_2}(b,c)=0.2e^{i0.2\pi }+0.2e^{i0.2\pi }=0.4e^{i0.4\pi },\hfill \\ & & {\left(d_{\mu e^{i\alpha }}\right)}_{G_1\oplus G_2}(b,d)=0.2e^{i0.2\pi }+0.2e^{i0.2\pi }=0.4e^{i0.4\pi }.\hfill \end{array}$$

It is obvious from the above calculations that the degrees of nodes determined by using the formula of the above theorem and by the direct method are equal.

Definition 21.

Let ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,L_2)$ be two CFGs. For any vertex $(u_1,u_2)\in V_1\times V_2$, we have

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)& =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}⨁{\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)\hfill \\ \hfill & +({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}⨁{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}(u_1,u_2)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}(u_1{w}_1,{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\hfill \\ \hfill & +\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\},\hfill \end{array}$$

Theorem 6.

Suppose ${\tau }_1=(Q_1,L_1)$ and ${\tau }_2=(Q_2,Y_2)$ are two CFGs. If

• ${\mu }_{Q_1}\ge {\mu }_{L_2}and{\mu }_{Q_2}\ge {\mu }_{L_1}$ then $\forall (u_1,u_2)\in V_1\times V_2$

  $$\begin{array}{cc}\hfill {\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)& =q{\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(u_1\right)+s{\left(t{d}_{\mu e^{io\alpha }}\right)}_{{\tau }_2}\left(u_2\right)\hfill \\ \hfill & -(q-1){\mu e^{i\alpha }}_{{\tau }_1}\left(u_1\right)-\vee \{{\mu e^{i\alpha }}_{{\tau }_1}\left(u_1\right),{\mu e^{i\alpha }}_{{\tau }_1}\left(u_1\right)\}\hfill \end{array}$$
  $\forall (u_1,u_2)\in V_1\times V_2$, s= $\mid V_1\mid -{\left(d\right)}_{G_1}\left(u_1\right)$ and q= $\mid V_2\mid -{\left(d\right)}_{G_2}\left(u_2\right)$.

Proof. 

$\forall (u_1,u_2)\in V_1\times V_2$

$$\begin{array}{cc}\hfill & {\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1⨁{\tau }_2}(u_1,u_2)\hfill \\ \hfill & =\sum _{(u_1,u_2)(w_1,w_2)\in E_1\times E_2.}({\mu }_{L_1}{e}^{i{\alpha }_{L_1}}⨁{\mu }_{L_2}{e}^{i{\alpha }_{L_2}})\left((u_1,u_2)(w_1,w_2)\right)+({\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}⨁{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}})(u_1,u_2)\hfill \\ \hfill & =\sum _{u_1=w_1,u_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_1,u_2=w_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}\wedge \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(w_1\right),{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}\wedge \{{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(w_2\right)\}\hfill \\ \hfill & +\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & =\sum _{u_2{w}_2\in E_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)+\sum _{u_1{w}_1\in E_1}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\hfill \\ \hfill & +\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}+\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)\hfill \\ \hfill & +\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & =\sum _{u_2{w}_2\in E_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)+\sum _{u_1{w}_1\in E_1}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)+\sum _{u_1{w}_1\notin E_{1}and{u}_2{w}_2\in E_2}{\mu }_{L_2}{e}^{i{\alpha }_{L_2}}\left(u_2{w}_2\right)\}\hfill \\ \hfill & +\sum _{u_1{w}_1\in E_{1}and{u}_2{w}_2\notin E_2}{\mu }_{L_1}{e}^{i{\alpha }_{L_1}}\left(u_1{w}_1\right)+{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right)+{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\hfill \\ \hfill & -\vee \{{\mu }_{Q_1}{e}^{i{\alpha }_{Q_1}}\left(u_1\right),{\mu }_{Q_2}{e}^{i{\alpha }_{Q_2}}\left(u_2\right)\}\hfill \\ \hfill & =q{\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(u_1\right)+s{\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(u_2\right)\hfill \\ \hfill & -(q-1){\mu e^{i\alpha }}_{{\tau }_1}\left(u_1\right)-\vee \{{\mu e^{i\alpha }}_{{\tau }_1}\left(u_1\right),\mu e^{i\alpha }{\tau }_1\left(u_1\right)\}\hfill \end{array}$$

where value of s and q as follows s = $|V_1{|-\left(d\right)}_{G_1}\left(u_1\right)$ and q = $|V_2{|-\left(d\right)}_{G_2}\left(u_2\right)$. □

Example 12.

We find the total degree of nodes by using Example 10.

$$\begin{array}{c}\hfill {\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_1⨁{\tau }_2}(a,e)=q{\left(d_{\mu }\right)}_{{\tau }_1}\left(a\right)+s{\left(d_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(e\right)\end{array}$$

$$\begin{array}{cc}\hfill s& =\mid V_1\mid -{\left(d\right)}_{G_1}\left(a\right)\hfill \\ \hfill & =2-1=1\hfill \end{array}$$

Now,

$$\begin{array}{cc}\hfill q& =\mid V_2\mid -{\left(d\right)}_{G_2}\left(e\right)\hfill \\ \hfill & =4-2=2\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\left({td}_{¯}\right)}_{{ø}_1⨁{ø}_2}(\mathrm{a},\mathrm{e})& =q{\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_1}\left(a\right)+s{\left(t{d}_{\mu e^{i\alpha }}\right)}_{{\tau }_2}\left(e\right)\hfill \\ \hfill & -(s-1){\mu e^{i\alpha }}_{{\tau }_2}\left(e\right)-(q-1){\mu e^{i\alpha }}_{{\tau }_1}\left(a\right)-\vee \{{\mu e^{i\alpha }}_{{\tau }_1}\left(a\right),{\mu e^{i\alpha }}_{{\tau }_2}\left(e\right)\}\hfill \\ \hfill & =2(0.2e^{i0.2\pi }+0.2e^{i0.2\pi })+1(0.3e^{i0.3\pi }+0.3e^{i0.3\pi }+0.2e^{i0.2\pi })\hfill \\ \hfill & -(1-1)\left(0.3e^{i0.3\pi }\right)-(2-1)\left(0.2e^{i0.2\pi }\right)-\vee \{0.2e^{i0.2\pi },0.3e^{i0.3\pi }\}\hfill \\ \hfill & =2(0.4+0.8-0.2-0.3)e^{i0.4+0.8-0.2-0.3\pi }\hfill \\ \hfill & =1.1e^{i1.1\pi }\hfill \end{array}$$

$$\begin{array}{c}\hfill {\left(td\right)}_{{\tau }_1⨁{\tau }_2}(a,e)=1.1e^{i1.1\pi }\end{array}$$

We conclude from the calculations that the total degrees of nodes calculated by the formula of the above theorem and by the direct method are equal.

4. Application of CFG

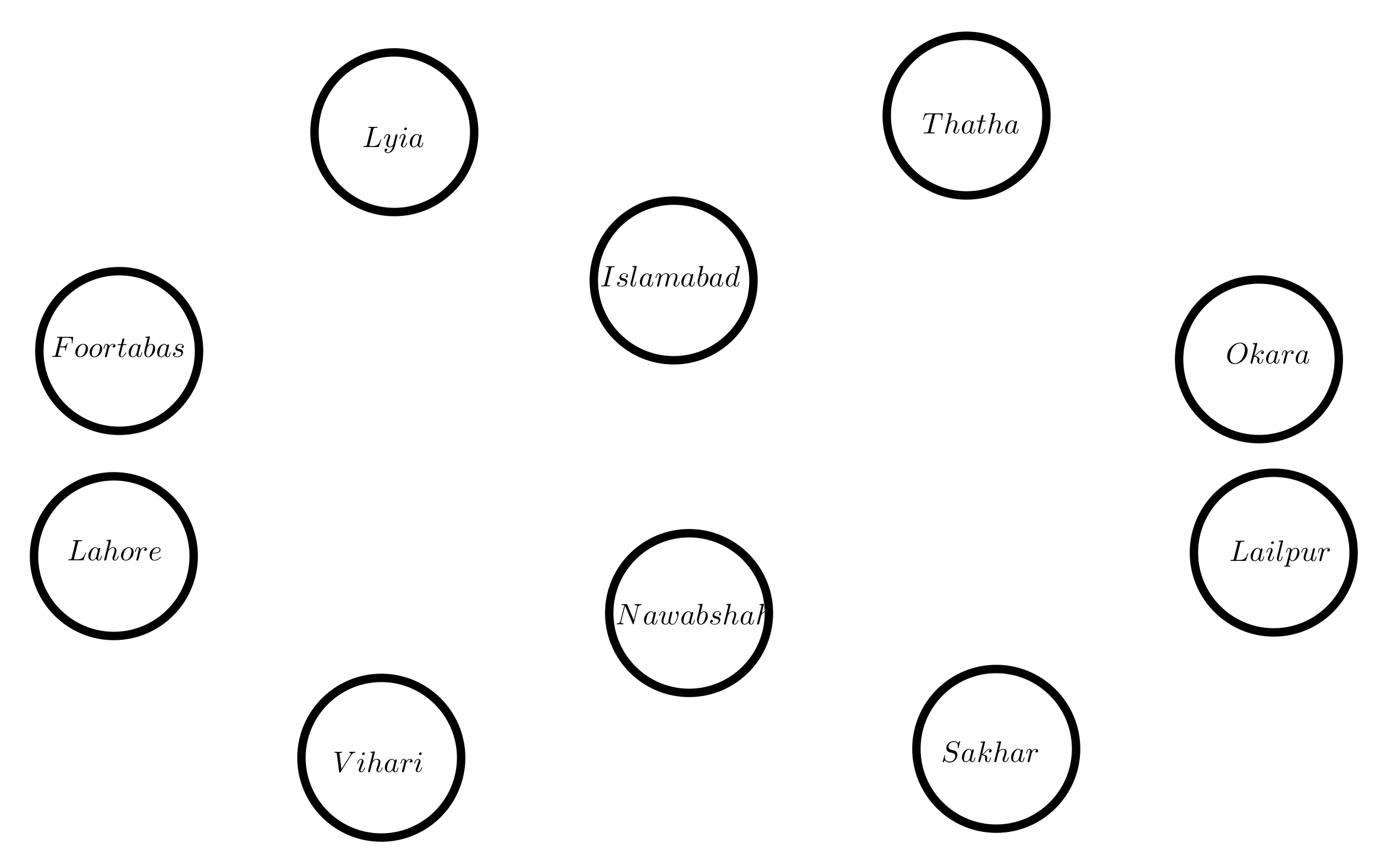
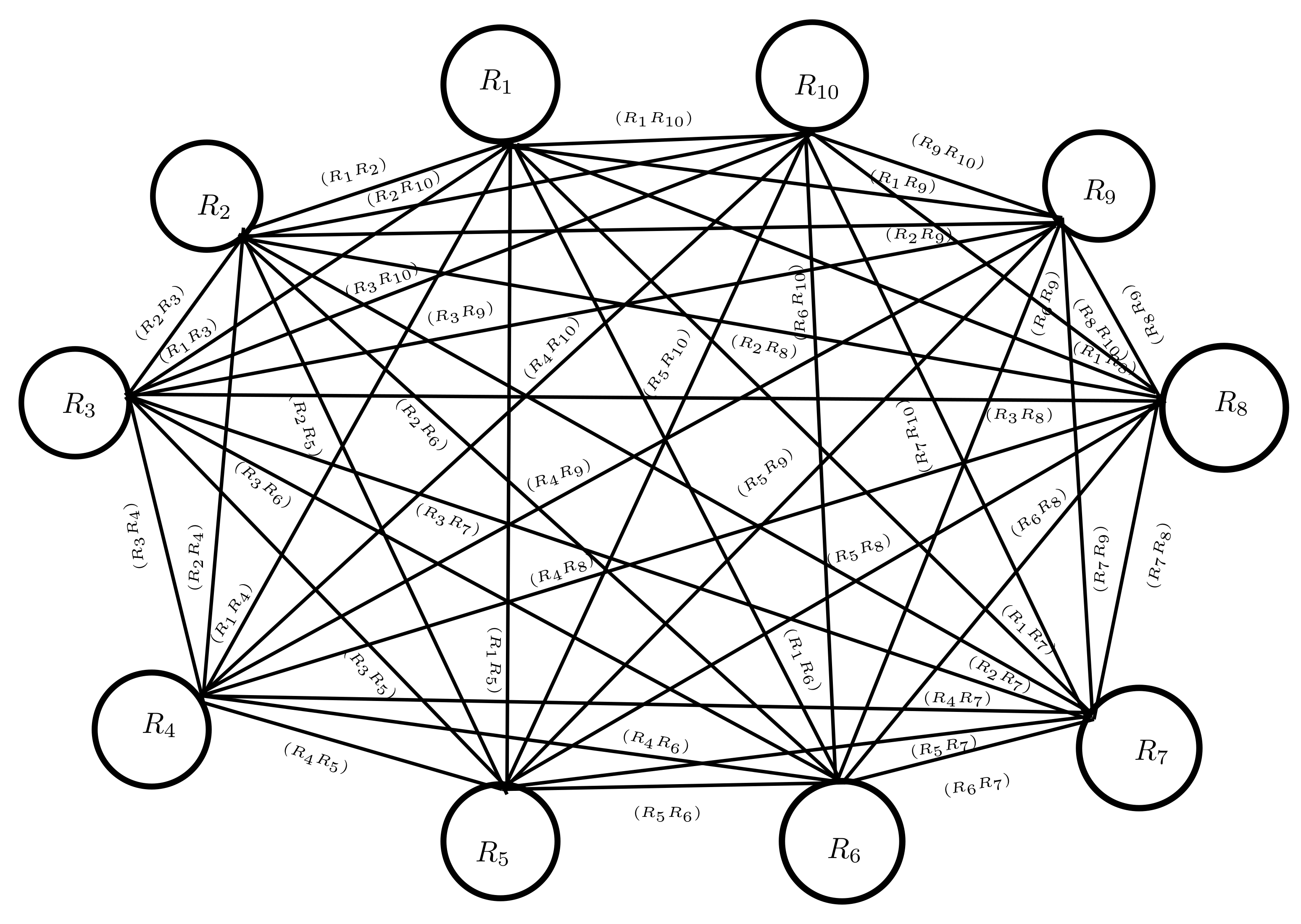
CFGs play a great role in fuzzy decision making and image segmentation. We presented a few factors in the application which will help in a physical way. For this, the government of Pakistan wants to construct COVID-19 Designated Tertiary Hospitals in any district that has a plan to make the minimum number of COVID-19 Designated Tertiary Hospitals in the district so that many people can benefit from this project. For this purpose, the following are some parameters taken into account: (1) a good place to build a COVID-19 Tertiary Hospital; (2) patients; (3) an urban location; (4) access to the facility; (5) security and safety; and (6) cost and efficiency. Assume that members of a team select 10 areas where they are engaged in the established COVID-19 Designated Tertiary Hospitals so that they may assist more patients for their treatment purposes. They see the following two scenarios: Constructing a COVID-19 Designated Tertiary Hospital in 1 of the 10 approved locations.

Constructing a COVID-19 Designated Tertiary Hospital between any 2 of the selected 10 places. Suppose that P = {Islamabad, Thatha, Okara, Lailpur, Sakhar, Nawabshah, Vihari, Lahore, Foortabas, Layia} is the set of locations where the team wishes to construct the COVID-19 Designated Tertiary Hospital as a node set. Assume that, after carefully analyzing the various characteristics, 80 percent of the specialists on the panel agree that Islamabad will have a COVID-19 Designated Tertiary Hospital. As a result, we can determine the term of membership. The phase term, which defines the time, must be computed for this. Twenty percent of professionals believe that Islamabad always manages a large number of patients. We will make a model of this information as $0.8e^{0.2\pi i}>$. Hence, it is their final argument. The team now wished to travel to Thatha. Assume that 70 percent of the team’s specialists feel that Thatha will have a COVID-19 Designated Tertiary Hospital after thoroughly analyzing the various factors. As a result, we may determine the terms of the membership functions. The phase term, which defines the period, must be computed for this. According to 50 percent of professionals, Thatha led a large number of patients at one point in time. We make a model of this information as $<0.7e^{0.5\pi i}>$. After this, they visit Okara for their valuable mission. Suppose the model information about Okara is $<0.4e^{0.3\pi i}>$. This means that 40 percent of the population prefers this location. However, 30 percent of those polled are opposed to it. In a similar way, they go to every place and collect all the information as follows:

$<Lailpur:0.8e^{0.4\pi i}>$, $<Sakhar:0.1e^{0.5\pi i}>$, $<Nawabshah:0.2e^{0.5\pi i}>$, $<Vihari:0.2e^{0.5\pi i}>$, $<Lahore:0.3e^{0.6\pi i}>$, $<Foortabas:0.5e^{0.6\pi i}>$, $<Lyia:0.5e^{0.4\pi i}>$. We can denote this model as

$$B=\left\{\begin{array}{c}<Islamabad:0.8e^{0.2\pi i}>\hfill \\ <Thatha:0.7e^{0.5\pi i}>\hfill \\ <Okara:0.3e^{0.2\pi i}>\hfill \\ <Lailpur:0.8e^{0.4\pi i}>\hfill \\ <Sakhar:0.1e^{0.5\pi i}>\hfill \\ <Nawabshah:0.2e^{0.5\pi i}>\hfill \\ <Vihari:0.2e^{0.5\pi i}>\hfill \\ <Lahore:0.3e^{0.6\pi i}>\hfill \\ <Foortabas:0.5e^{0.6\pi i}>\hfill \\ <Lyia:0.5e^{0.4\pi i}>\hfill \end{array}\right.$$

The complex membership of the nodes represents the positive characteristics of a specific parameter for choosing a city for the COVID-19 Designated Tertiary Hospital. Now, we have truth membership function

Islamabad = 0.8,

Thatha = 0.7,

Okara = 0.3,

Lailpur = 0.8,

Sakhar = 0.1,

Nawabshah = 0.2,

Vihari = 0.2,

Lahore = 0.3,

Foortabas = 0.5,

Lyia = 0.5,

To determine the optimal choice, we see 10 truth membership functions. The value of Islamabad and Lailpur are the same. Now we add tradition and phase terms, for Islamabad, 0.8 + 0.2 = 1 and for Lailpur, 0.8 + 0.4 = 1.2. Lailpur city is the best choice for the COVID-19 Designated Tertiary Hospital. This is the application of CFG where it has no edge between vertices. CFG with no edge is shown in Figure 19.

Take P = {Islamabad, Thatha, Okara, Lailpur, Sakhar, Nawabshah, Vihari, Lahore, Foortabas, Lyia} = $\{R_1,R_2,R_3,R_4,R_5,R_6,R_7,R_8,R_9,R_{10}\}$.

Now the team goes to look at situation two as follows: we find other edges according to the condition of the team.

$$F=\left\{\begin{array}{c}<R_1{R}_2:0.7e^{0.3\pi i}>\hfill \\ <R_1{R}_3:0.4e^{0.2\pi i}>\hfill \\ <R_1{R}_4:0.6e^{0.3\pi i}>\hfill \\ <R_1{R}_5:0.2e^{0.3\pi i}>\hfill \\ <R_1{R}_6:0.3e^{0.3\pi i}>\hfill \\ <R_1{R}_7:0.1e^{0.3\pi i}>\hfill \\ <R_1{R}_8:0.6e^{0.3\pi i}>\hfill \\ <R_1{R}_9:0.7e^{0.3\pi i}>\hfill \\ <R_1{R}_{10}:0.5e^{0.3\pi i}>\hfill \\ <R_2{R}_3:0.4e^{0.2\pi i}>\hfill \\ <R_2{R}_4:0.3e^{0.4\pi i}>\hfill \\ <R_2{R}_5:0.2e^{0.4\pi i}>\hfill \\ <R_2{R}_6:0.3e^{0.4\pi i}>\hfill \\ <R_2{R}_7:0.1e^{0.4\pi i}>\hfill \\ <R_2{R}_8:0.8e^{0.4\pi i}>\hfill \\ <R_2{R}_9:0.7e^{0.3\pi i}>\hfill \\ <R_2{R}_{10}:0.5e^{0.4\pi i}>\hfill \\ <R_3{R}_4:0.4e^{0.2\pi i}>\hfill \\ <R_3{R}_5:0.2e^{0.2\pi i}>\hfill \\ <R_3{R}_6:0.3e^{0.2\pi i}>\hfill \\ <R_3{R}_7:0.1e^{0.2\pi i}>\hfill \\ <R_3{R}_8:0.4e^{0.2\pi i}>\hfill \\ <R_3{R}_9:0.2e^{0.2\pi i}>\hfill \\ <R_3{R}_{10}:0.4e^{0.2\pi i}>\hfill \\ <R_4{R}_5:0.2e^{0.4\pi i}>\hfill \\ <R_4{R}_6:0.3e^{0.4\pi i}>\hfill \\ <R_4{R}_7:0.1e^{0.4\pi i}>\hfill \\ <R_4{R}_8:0.6e^{0.4\pi i}>\hfill \\ <R_4{R}_9:0.3e^{0.3\pi i}>\hfill \\ <R_4{R}_{10}:0.6e^{0.4\pi i}>\hfill \\ <R_5{R}_6:0.4e^{0.5\pi i}>\hfill \\ <R_5{R}_7:0.1e^{0.4\pi i}>\hfill \\ <R_5{R}_8:0.2e^{0.5\pi i}>\hfill \\ <R_5{R}_9:0.2e^{0.3\pi i}>\hfill \\ <R_5{R}_{10}:0.2e^{0.4\pi i}>\hfill \\ <R_6{R}_7:0.1e^{0.4\pi i}>\hfill \\ <R_6{R}_8:0.3e^{0.6\pi i}>\hfill \\ <R_6{R}_9:0.3e^{0.3\pi i}>\hfill \\ <R_6{R}_{10}:0.3e^{0.4\pi i}>\hfill \\ <R_7{R}_8:0.1e^{0.4\pi i}>\hfill \\ <R_7{R}_9:0.1e^{0.3\pi i}>\hfill \\ <R_7{R}_{10}:0.1e^{0.4\pi i}>\hfill \\ <R_8{R}_9:0.3e^{0.3\pi i}>\hfill \\ <R_8{R}_{10}:0.6e^{0.4\pi i}>\hfill \\ <R_9{R}_{10}:0.4e^{0.3\pi i}>\hfill \end{array}\right.$$

traditional membership values of edges are given

$R_1{R}_2=0.7$, $R_1{R}_3=0.4$, $R_1{R}_4=0.6$, $R_1{R}_5=0.2$, $R_1{R}_6=0.3$,

$R_1{R}_7=0.1$, $R_1{R}_8=0.6$, $R_1{R}_9=0.7$, $R_1{R}_{10}=0.5$, $R_2{R}_3=0.4$,

$R_2{R}_4=0.3$, $R_2{R}_5=0.2$, $R_2{R}_6=0.3$, $R_2{R}_7=0.1$, $R_2{R}_8=0.8$,

$R_2{R}_9=0.7$, $R_2{R}_{10}=0.5$, $R_3{R}_4=0.4$, $R_3{R}_5=0.2$, $R_3{R}_6=0.3$,

$R_3{R}_7=0.1$, $R_3{R}_8=0.4$, $R_3{R}_9=0.2$, $R_3{R}_{10}=0.4$, $R_4{R}_5=0.2$,

$R_4{R}_6=0.3$. $R_4{R}_7=0.1$, $R_4{R}_8=0.6$, $R_4{R}_9=0.3$, $R_4{R}_{10}=0.6$,

$R_5{R}_6=0.4$, $R_5{R}_7=0.1$, $R_5{R}_8=0.2$, $R_5{R}_9=0.2$, $R_5{R}_{10}=0.2$,

$R_6{R}_7=0.1$, $R_6{R}_8=0.3$, $R_6{R}_9=0.3$, $R_6{R}_{10}=0.3$, $R_7{R}_8=0.1$,

$R_7{R}_9=0.1$, $R_7{R}_{10}=0.1$, $R_8{R}_9=0.3$, $R_8{R}_{10}=0.6$, $R_9{R}_{10}=0.4$

$S\left(R_2{R}_8\right)$ is the largest value and therefore more suitable for making the COVID-19 Designated Tertiary Hospital. CFG with an edge is shown in Figure 20.

5. Conclusions

Complex fuzzy models have greater flexibility and comparability than fuzzy models. The CFG is a FG extension. Each vertex and edge in a complex fuzzy graphical model has only one complex membership grade. To improve the approximation, CFG can be employed. Different sorts of degrees of vertices were employed in this project. Only the overall contribution of the amplitude in the system is determined by the degree of vertices in FG. The overall information and contribution of the amplitude and phase components are given by the degree of vertices in CFG. This article looked at the communication between a few hospitals. The CFGs and their associated network systems were the exclusive focus of this study. This strategy can only be used if one-directed thinking occurs in a linked, complex fuzzy graphical system. Obtaining accurate data is not always easy. We defined the order and size of the CFG. We determined the operations on CFG, including union, intersection, and join of CFG. We discussed the degree and total degree of vertex of the CFG. Finally, we described how CFG can be used to solve decision-making problems in the COVID-19 environment. The maximal product and symmetric difference of CFG are discussed. In the future, our aim is to introduce (1) bipolar-CFG and (2) rejection of CFG.