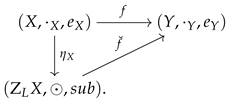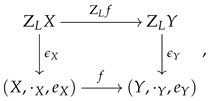Z_L-Completions for Z_L-Semigroups

Abstract

In this paper, we generalize a common completion pattern of ordered semigroups to the fuzzy setting. Based on a standard L-completion $Z_L$, we introduce the notion of a $Z_L$-semigroup as a generalization of an L-ordered semigroup, where L is a complete residuated lattice. For this asymmetric mathematical structure, we define a $Z_L$-completion of it to be a complete residuated L-ordered semigroup together with a join-dense L-ordered semigroup embedding satisfying the universal property. We prove that: (1) For every compositive $Z_L$, the category ${\mathbf{CS}}_L$ of complete residuated L-ordered semigroups is a reflective subcategory of the category ${\mathbf{S}}_{Z_L}$ of $Z_L$-semigroups; (2) for an arbitrary $Z_L$, there is an adjunction between ${\mathbf{S}}_{Z_L}$ and the category ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$ of weakly $Z_L$-continuous L-ordered semigroup embeddings of $Z_L$-semigroups. By appropriate specialization of $Z_L$, the results can be applied to the DM${}_L$-completion, certain completions associated with fuzzy subset systems, etc.

1. Introduction

Complete residuated lattices are important symmetric algebraic structures for fuzzy logic, probabilistic logic and linear logic. As the table of truth values, it has been extensively applied to fuzzy order (or L-order, $\mathcal{Q}$-order) theory originated by Zadeh [1]. A fuzzy order is a kind of fuzzy relation with reflexivity, transitivity and asymmetry. Now, fuzzy order theory has been widely used in various branches of mathematics and computer sciences. For crisp order structures as models in theoretical computer science, some form of completeness should be required, such as the DM-completion, the ideal completion, the join-completion, the $Z_{\mathrm{\Gamma }}$-completion, and so on (see [2,3,4,5,6,7,8,9,10,11,12,13]).

The fruitful results about completions of crisp order structures have inspired some scholars to study the completions in the fuzzy setting. Wagner [14], Bĕlohlávek [15,16] and Xie [17] generalized the DM-completion to the multi-valued framework from different perspectives. The interesting thing is that the DM-completions above are exactly the same when $\Omega =L$ is a frame. Subsequently, Wang and Zhao [18] obtained a category characterization of the DM-completion of fuzzy posets by constructing the join-completion of fuzzy posets. Moreover, they also solved the problem of whether the join-completions of fuzzy posets are entirely determined by the consistent fuzzy closure operators. Based on the work of [18], Su and Li [19] constructed the ${\Delta }_1$-completion and discussed how it relates to formal L-contexts over fuzzy posets. In general, the completion of fuzzy posets can be composed of some special fuzzy subset selection. Ma [20], Rao [21] and Zhao [22] systematically studied the fuzzy subset system and used it to construct the $Z_L$-continuity and $Z_L$-algebra of fuzzy posets. Following this line, Su et al. [23] established the $Z_L$-completions of fuzzy posets and then constructed a minimum $Z_L$-completion.

In order to enhance the applicability of ordered semigroups as mathematical tools, the combination of a fuzzy order and an algebraic system has appeared in recent years. Šešlja [24], Hao [25], Wang [26] and Borzooei [27] fused fuzzy order and algebraic structure in different ways and put forward new concepts such as fuzzy ordered group, fuzzy ordered semigroup and fuzzy lattice ordered group. Most of the above studies focus on the discussion of fuzzy order structure, in which algebraic structure only plays a secondary role. Then, Huang et al. [28] established various fuzzy ideals on fuzzy ordered semigroups from the perspective of algebraic structure as the main and fuzzy order structure as the auxiliary. In addition, they also established the category characterization of fuzzy ordered semigroups, which further improved fuzzy set theory of ordered algebra. Following this viewpoint, Su et al. [29] constructed an organic combination of fuzzy poset and semihypergroup, which is called an L-ordered L-semihypergroup. Then, they established three types of L-hyperideals and intra-regularity on it.

Motivated by studies for fuzzy ordered semigroups and completions of fuzzy posets, Zhao et al. [30] proposed the concept of L-quantale as a generalization of a crisp quantale. For each fuzzy ordered semigroup, they defined the L-quantale completion to be an L-quantale together with a special embedding. In particular, they discussed the relationship between fuzzy ordered semigroups and L-quantales from the categorical perspective. Following this line, Xia and Zhao [31] further studied the L-quantale completion and obtained the minimum L-quantale completion of every fuzzy ordered semigroup.

In the crisp setting, Erné and Reichman [32] introduced $\mathcal{Y}$-semigroups with ordered semigroups as a special case, and established a standard completion $\mathcal{Y}$ for a $\mathcal{Y}$-semigroup. This completion provided the common pattern for various completions of ordered semigroups. It is then natural to ask whether one can extend the theory of standard completions to the setting of L-ordered semigroups. In this paper, we answer this question by defining a new completion for fuzzy ordered semigroups, called $Z_L$-completion. It turns out that many kinds of completions, such as the DM-completion and L-quantale completion, are a special case of the $Z_L$-completion.

This paper is organized as follows: Section 2 lists some notions and results in [16,25,26,30,33,34,35,36,37,38]. In Section 3, based on an L-subset selection, a standard L-completion $Z_L$ of an L-ordered semigroup and (weakly) $Z_L$-continuous mapping preserving structures are introduced. In particular, some examples of compositive standard completions are presented. In Section 4, a $Z_L$-semigroup and its $Z_L$-completion with the university property are built. Moreover, it is shown that for every $Z_L$-semigroup, the standard L-completion $Z_L$ with a join-dense L-ordered semigroup embedding is a $Z_L$-completion. In Section 5, for different cases of $Z_L$, the corresponding categorical characterization of a $Z_L$-completion is established. Finally, we present conclusions in Section 6.

2. Preliminaries

This section reviews some basic concepts and results on fuzzy posets (see [16,33,34,35,36,37,38]). Throughout this paper, L denotes a complete residuated lattice $(L,\wedge ,\vee ,*,\to ,0,1)$ [39], where L is a complete lattice with the bottom 0 and the top 1, and $\ast :L\times L⟶L$ is a commutative, associative binary operator such that (1) ∗ is monotone on each argument; (2) ∗ has a right adjoint →, that is, $a\ast b\le c\iff a\le b\to c$ for all $a,b,c\in L$; (3) $1\ast a=a$ for all $a\in L$. Such a symmetry algebraic structure is significant in the narrow sense of fuzzy logic (see [15,39]).

An L-subset of X is a mapping from X to L; write $L^X$ for the set $\left\{A\right|AisanL-subsetofX\}$. For $A,B\in L^X$, define $A\subseteq B$ as $A\left(x\right)\le B\left(x\right),\forall x\in X$. We never distinguish between an element $b\in L$ and the constant function $\overline{b}:X⟶L$ satisfying $\forall x\in X,b\left(x\right)=b$, such as $(b\ast B)\left(x\right)=b\ast B\left(x\right)$ and $(b\to B)\left(x\right)=b\to B\left(x\right),\forall x\in X$.

Definition 1

([16,34]). A fuzzy order (or an L-order) e on a set X is an L-relation such that

(1) 

$\forall x\in X$, $e(x,x)=1$ (reflexivity);

(2) 

$\forall x,y,z\in X$, $e(x,y)\ast e(y,z)\le e(x,z)$ (transitivity);

(3) 

$\forall x,y\in X$, $e(x,y)=e(y,x)=1\Rightarrow x=y$ (asymmetry).

The pair $(X,e)$ is called a fuzzy poset (or an L-ordered set).

For an L-ordered set $(X,e)$, define a crisp order ${\le }_e$ on X as follows: $x{\le }_{e}y$ iff $e(x,y)=1$, and so $(X,{\le }_e)$ is a poset.

For a nonempty set X, $(L^X,sub)$ is an L-ordered set, where the inclusion L-order $sub$ [15] defined by $sub(A,B)={\bigwedge }_{x\in X}A\left(x\right)\to B\left(x\right),\forall A,B\in L^X$.

Proposition 1

([16,33]). $\mathcal{T}\subseteq L^X$ is an L-closure system (or a fuzzy closure system) on X iff

(1) 

$\forall \mathcal{A}\subseteq \mathcal{T},\bigwedge \mathcal{A}\in \mathcal{T}$;

(2) 

$\forall a\in L,A\in \mathcal{T},a\to A\in \mathcal{T}$.

For an L-closure operator C on X and an L-closure system $\mathcal{T}$ on X, ${\mathcal{T}}_C=\{A\in L^X:C\left(A\right)=A\}$ is an L-closure system on X and $C_{\mathcal{T}}$ is an L-closure operator on X given by $\forall A\in L^X,x\in X,C_{\mathcal{T}}\left(A\right)\left(x\right)={\bigwedge }_{B\in \mathcal{T}}sub(A,B)\to B\left(x\right)$. Moreover, $C=C_{{\mathcal{T}}_C}$ and $\mathcal{T}={\mathcal{T}}_{C_{\mathcal{T}}}$. In particular, $\forall A\in L^X,B\in \mathcal{T},sub(A,B)=sub(C\left(A\right),B)$.

Definition 2

([36,38]). Let $(X,e)$ be an L-ordered set. $x_0\in X$ is called a join $(resp.,meet)$ of A denoted by $x_0=\bigsqcup A$ $(resp.,x_0=\sqcap A)$, iff

(1) 

$\forall x\in X,A\left(x\right)\le e(x,x_0)(resp.,A\left(x\right)\le e(x_0,x))$;

(2) 

${\displaystyle \forall y\in X,\underset{x\in X}{\bigwedge }A\left(x\right)\to e(x,y)\le e(x_0,y)(resp.,\underset{x\in X}{\bigwedge }A\left(x\right)\to e(y,x)\le e(y,x_0))}$.

An L-ordered set $(X,e)$ is a complete L-lattice iff $\forall A\in L^X,\bigsqcup A$ exists. $A\in L^X$ is called a lower L-subset if $\forall x,y\in X,A\left(x\right)\ast e(y,x)\le A\left(y\right)$ and $\downarrow A\in L^X$ is defined by $\downarrow A\left(x\right)={\bigvee }_{x^{\prime }\in X}A\left(x^{\prime }\right)\ast e(x,x^{\prime }),\forall x\in X$. As usually, the set of all lower L-subsets of X is denoted by ${\mathrm{A}}_{L}X$ and $A\in {\mathrm{A}}_{L}X$ iff $A=\downarrow A$. Obviously, ${\mathrm{A}}_{L}X=\{\downarrow A|A\in L^X\}$ is an L-closure system and so $({\mathrm{A}}_{L}X,su{b}_X)$ is a complete L-lattice. $A\in L^X$ is called a directed L-subset if ${\bigvee }_{x\in X}A\left(x\right)=1$ and $A\left(x\right)\ast A\left(y\right)\le {\bigvee }_{z\in X}A\left(z\right)\ast e(x,z)\ast e(y,z),\forall x,y\in X$. Let ${\mathrm{D}}_{L}X$ denote the set of all directed L-subsets of X. For $x\in X$, a mapping ${\iota }_x:X⟶L$ defined by $\forall y\in X,{\iota }_x\left(y\right)=e(y,x)$ is called a principal L-ideal of X. Then ${\mathrm{M}}_{L}X=\left\{{\iota }_x\right|x\in X\}\subseteq {\mathrm{A}}_{L}X$. Similarly, for $A\in L^X$, we can obtain a mapping ${\iota }_A:L^X⟶L$ defined by ${\iota }_A\left(B\right)=sub(B,A),\forall B\in L^X$.

For each mapping $f:X\to Y$, we can define $f^{\to }:L^X\to L^Y$ and $f^{\leftarrow }:L^Y\to L^X$ (see [15,35]) as

$$f^{\to }\left(A\right)\left(y\right)=\underset{f\left(x\right)=y}{\bigvee }A\left(x\right),f^{\leftarrow }\left(B\right)\left(x\right)=B\left(f\left(x\right)\right),\forall x\in X,y\in Y.$$

Definition 3

([37,38]). A mapping $f:(X,e_X)\to (Y,e_Y)$ is called

(1) 

L-order preserving if $e_X(x,y)\le e_Y(f\left(x\right),f\left(y\right)),\forall x,y\in X$;

(2) 

L-order embedding if $e_X(x,y)=e_Y(f\left(x\right),f\left(y\right)),\forall x,y\in X$;

(3) 

join-preserving if $f(\bigsqcup A)=\bigsqcup f^{\to }\left(A\right),\forall A\in L^X$ with $\bigsqcup A$ existing;

(4) 

join-dense if $y=\bigsqcup f^{\to }\left(f^{\leftarrow }\left({\iota }_y\right)\right),\forall y\in Y$.

For an L-ordered set $(X,e)$, $X^{\prime }\subseteq X$ is said to be join-dense in X iff for every $x\in X$, there is $A\in L^{X^{\prime }}$ such that $x=\bigsqcup i_{X^{\prime },X}^{\to }\left(A\right)$ iff $x=\bigsqcup ({\iota }_x\wedge {\chi }_{X^{\prime }}),\forall x\in X$. Therefore, a mapping $f:X\to Y$ is join-dense iff $f\left(X\right)$ is join-dense in Y.

Definition 4

([35,37]). If two L-order preserving mappings $f:(X,e_X)\to (Y,e_Y),g:(Y,e_Y)\to (X,e_X)$ satisfy $\forall x\in X,y\in Y,e_Y(f\left(x\right),y)=e_X(x,g\left(y\right))$, then $(f,g)$ is called an L-adjunction between X and Y, where f is called the left L-adjoint of g and dually g the right L-adjoint of f. In this case, a left L-adjoint is also called a residuated mapping and its right L-adjoint a residual mapping.

Obviously, for each mapping $f:X\to Y$, the pair $(f^{\to },f^{\leftarrow })$ is an L-adjunction between $L^X$ and $L^Y$.

Theorem 1

([35,37]). Let $f:(X,e_X)\to (Y,e_Y),g:(Y,e_Y)\to (X,e_X)$ be two mappings.

(1) 

If $(X,e_X)$ is complete, then f has a right L-adjoint iff $f(\bigsqcup A)=\bigsqcup f^{\to }\left(A\right),\forall A\in L^X$;

(2) 

If $(Y,e_Y)$ is complete, then g has a left L-adjoint iff $g(\sqcap B)=\sqcap g^{\to }\left(B\right),\forall B\in L^Y$.

Clearly, a mapping between complete L-lattices is join-preserving iff it is residuated.

For an L-ordered set $(X,e)$ and $A\in L^X$, $A^u,A^l\in L^X$ are defined as follows:

$$A^u\left(x\right)=\underset{x^{\prime }\in X}{\bigwedge }A\left(x^{\prime }\right)\to e(x^{\prime },x),A^l\left(x\right)=\underset{x^{\prime }\in X}{\bigwedge }A\left(x^{\prime }\right)\to e(x,x^{\prime }),\forall x\in X.$$

The cut operator ${(-)}^{\delta }:L^X⟶L^X$ is defined by $A^{\delta }=A^{ul}$. A is called a cut if $A=A^{\delta }$. Obviously, every cut is always a lower L-subset and the cut operator is an L-closure operator on X. Moreover, ${\mathrm{DM}}_{L}X=\{A\in L^X:A=A^{\delta }\}$ is the Dedekind–MacNeille completion.

Definition 5

([25,26,30]). A triple $(X,·,e)$ is called an L-ordered semigroup (L-OS for short) provided that

(1) 

$(X,e)$ is an L-ordered set;

(2) 

$(X,·)$ is a semigroup;

(3) 

$e(x,y)\le e(z·x,z·y)$ and $e(x,y)\le e(x·z,y·z),\forall x,y,z\in X$.

Remark 1.

(1) 

The condition (3) is equivalent to all left translations ${\ell }_x:X⟶X,x^{\prime }\mapsto x·x^{\prime }$ and all right translations ${\hslash }_x:X⟶X,x^{\prime }\mapsto x^{\prime }·x$ are L-order preserving.

(2) 

An L-OS is called residuated if all left and right translations are residuated.

A mapping $f:(X,{·}_X)⟶(X,{·}_Y)$ is called a semigroup homomorphism if $f\left(x{·}_X{x}^{\prime }\right)=f\left(x\right){·}_{Y}f\left(x^{\prime }\right),\forall x,x^{\prime }\in X$. Moreover, a semigroup homomorphism $f:(X,{·}_X,e_X)⟶(X,{·}_Y,e_Y)$ is called (1) an L-OS homomorphism if it is L-ordered preserving; (2) an L-OS embedding if it is an L-ordered embedding. Then L-OSs with L-OS homomorphisms as morphisms form a category, denoted by L-OSG.

A complete L-OS $(X,·,e)$ means $\bigsqcup A$ exists for all $A\in L^X$. Let $(X,·,e)$ be an L-OS and $A,B\in L^X$, define a binary operator $·:L^X\times L^X⟶L^X$, as follows: $(A·B)\left(x\right)={\bigvee }_{x^{\prime }·x^{\prime \prime }=x}A\left(x^{\prime }\right)\ast B\left(x^{\prime \prime }\right),\forall x\in X$. Then we can check that $(L^X,·,su{b}_X)$ is a complete L-OS and $\bigsqcup \mathcal{A}={\bigvee }_{A\in L^X}\mathcal{A}\left(A\right)\ast A,\forall \mathcal{A}\in L^{L^X}$.

3. Standard $L$-Completions for $L$-Ordered Semigroups

In the crisp setting, a systematic analysis of standard completions for ordered semigroups has been developed in [32]. In this section, let us discuss such completions under a fuzzy framework.

An L-subset selection (or a fuzzy subset selection) $Z_L$ denotes a function which assigns to every L-OS $(X,·,e)$ a set $Z_{L}X$ of L-subsets of X, and $Z_L$ is called (1) a standard L-completion if ${\mathrm{M}}_{L}X\subseteq Z_{L}X\subseteq {\mathrm{A}}_{L}X$ and $Z_{L}X$ is an L-closure system; (2) an L-subset system if for each L-ordered preserving mapping $f:X⟶X^{\prime }$ and each $A\in Z_{L}X$, $f^{\to }\left(A\right)\in Z_L\left(X^{\prime }\right)$. Clearly, there is no implication relationship between the two L-subset selections.

$(X,·,e)$ is called $Z_L$-complete if $\bigsqcup D$ exists for all $D\in Z_{L}X$. It is noteworthy that for any standard L-completion $Z_L$, $(X,·,e)$ is $Z_L$-complete iff $(X,e)$ is complete. Moreover, for every $\mathfrak{X}\subseteq L^X$, we may form the system $Z_L\mathfrak{X}$ and call $\mathfrak{X}$$Z_L$-union complete if $\bigcup \mathcal{A}={\bigvee }_{A\in \mathfrak{X}}\mathcal{A}\left(A\right)\ast A\in \mathfrak{X}$ for all $\mathcal{A}\in Z_L\mathfrak{X}$. Of course, for any $Z_L\mathfrak{X}$, $Z_L$-union completeness entails $Z_L$-completeness, but not conversely. $P\subseteq X$ is called a $Z_L$-complete subsemigroup if $(P,·)$ is a subsemigroup of $(X,·)$ and $\bigsqcup i_{P,X}^{\to }\left(D\right)\in P$ for all $D\in Z_L\left(P\right)$. To simplify the description, $Z_L$ and $Z_{L}X$ are referred to as a standard L-completion without distinction.

Example 1.

Each of the following listed L-subset selection is a standard L-completion:

(1) 

the Alexandroff completion ${\mathrm{A}}_{L}X$;

(2) 

the Dedekind–MacNeille completion ${\mathrm{DM}}_{L}X$;

(3) 

the L-Frink ideal completion ${\mathrm{F}}_L^{\delta }X$ defined by

$${\mathrm{F}}_L^{\delta }X=\{A\in {\mathrm{A}}_{L}X|sub(F,A)\le sub(F^{\delta },A)forallfiniteL-subsetsFofX\},$$

where finite L-subset F means that $\{x\in X:F(x)\ne 0\}$ is finite;

(4) 

the ⊔-ideal completion ${\mathrm{J}}_{L}X$ given by

$${\mathrm{J}}_{L}X=\{A\in {\mathrm{A}}_{L}X|sub(D,A)\le A(\bigsqcup D)forallD\in L^{X}with\bigsqcup Dexisting\};$$

(5) 

the Scott completion ${\mathrm{D}}_L^{\delta }X$ defined by

$${\mathrm{D}}_L^{\delta }X=\{A\in {\mathrm{A}}_{L}X|sub(D,A)\le sub(D^{\delta },A)foralldirectedL-subsetsDofX\};$$

(6) 

the Scott join-completion ${\mathrm{D}}_L^{\bigsqcup }X$ given by

$${\mathrm{D}}_L^{\bigsqcup }X=\{A\in {\mathrm{A}}_{L}X|sub(D,A)\le A(\bigsqcup D)foralldirectedL-subsetsDwith\bigsqcup Dexisting\}.$$

In fact, it obtained from (4) by admitting directed L-subsets D only;

(7) 

the ${\Gamma }_{★}$-completion defined by ${\Gamma }_{★}X=\left\{A^{★}\right|A\in L^X\}$ (See [31]);

(8) 

Any L-subset selection $Z_L$ gives rise to the following standard L-completions:

$$Z_L^{\bigsqcup }X=\{A=\downarrow A|sub(D,A)\le A(\bigsqcup D)forallD\in Z_{L}Xwith\bigsqcup Dexisting\}$$

and

$$Z_L^{\delta }X=\{A=\downarrow A|sub(D,A)\le sub(D^{\delta },A)forallD\in Z_{L}X\}.$$

Obviously, $Z_L^{\delta }X\subseteq Z_L^{\bigsqcup }X$ and for every $Z_L$-complete L-ordered semigroup $(X,·,e)$, $Z_L^{\delta }X=Z_L^{\bigsqcup }X$.

Through simple calculation we get the following conclusion:

Proposition 2.

For an L-OS $(X,·,e)$, ${\mathrm{A}}_{L}X$ is the greatest standard L-completion and ${\mathrm{DM}}_{L}X$ is the least one.

Proof. 

It is obviously true that ${\mathrm{A}}_{L}X$ is the greatest standard L-completion. So we only need to show that ${\mathrm{DM}}_{L}X$ is the least standard L-completion. In fact, for any $x\in X$ and any standard L-completion $Z_L$ with $Z_{L}X\subseteq {\mathrm{DM}}_{L}X$, then $A^{\delta }\left(x\right)={\bigwedge }_{s\in X}sub(A,{\iota }_s)\to {\iota }_s\left(x\right)\ge {\bigwedge }_{B\in Z_{L}X}sub(A,B)\to B\left(x\right)=C\left(A\right)\left(x\right)$ and $A^{\delta }\left(x\right)={\bigwedge }_{B\in {\mathrm{DM}}_{L}X}sub(A,B)\to B\left(x\right)\le {\bigwedge }_{B\in Z_{L}X}sub(A,B)\to B\left(x\right)=C\left(A\right)\left(x\right)$ and so $A^{\delta }=C\left(A\right)$. This means that $Z_{L}X={\mathrm{DM}}_{L}X$. □

Obviously, for an arbitrary standard L-completion $Z_L$, $(Z_{L}X,\odot ,sub)$ is a complete L-OS by [30], where $\odot :L^X\times L^X⟶L^X$ is defined by $A\odot B=C(A·B)={\bigwedge }_{A^{\prime }\in Z_{L}X}sub(A·B,A^{\prime })\to A^{\prime }$.

Example 2.

For an L-OS $(X,·,e)$, ${\mathrm{D}}_{L}X$, ${\mathrm{A}}_{L}X$, and ${\mathrm{P}}_{L}X=L^X$ are L-subset selections and so ${\mathrm{D}}_L^{\bigsqcup }X$, ${\mathrm{A}}_L^{\bigsqcup }X$, ${\mathrm{P}}_L^{\bigsqcup }X$, ${\mathrm{D}}_L^{\delta }X$, ${\mathrm{A}}_L^{\delta }X$, ${\mathrm{P}}_L^{\delta }X$ are standard L-completions.

Given an arbitrary standard L-completion $Z_L$, we call a mapping $f:(X,{·}_X,e_X)⟶(Y,{·}_Y,e_Y)$ weakly $Z_L$-continuous if $f^{\leftarrow }\left({\iota }_y\right)\in Z_{L}X$ for all $y\in Y$, and we call f$Z_L$-continuous if $f^{\leftarrow }\left(B\right)\in Z_{L}X$ for all $B\in Z_{L}Y$. Then we can check that for a standard L-completion $Z_L$, f is $Z_L$-continuous iff $f^{\to }\left(C\left(A\right)\right)\subseteq C\left(f^{\to }\left(A\right)\right),\forall A\in L^X$.

Proposition 3.

Let $Z_L$ be an L-subset selection and consider the following conditions on a mapping $f:(X,{·}_X,e_X)⟶(X^{\prime },{·}_{X^{\prime }},e_{X^{\prime }})$:

(1a) 

f is $Z_L^{\delta }$-continuous;

(1b) 

f is weakly $Z_L^{\delta }$-continuous;

(1c) 

f is L-order preserving and $f^{\to }\left(D^{\delta }\right)\subseteq {\left(f^{\to }\left(D\right)\right)}^{\delta },\forall D\in Z_{L}X$;

(2a) 

f is $Z_L^{\bigsqcup }$-continuous;

(2b) 

f is weakly $Z_L^{\bigsqcup }$-continuous;

(2c) 

f is L-order preserving and $f(\bigsqcup D)=\bigsqcup f^{\to }\left(D\right)$ for all $D\in Z_{L}X$ with $\bigsqcup D$ existing.

Then

$$\begin{array}{cc}& \left(1a\right)\Rightarrow \left(1b\right)\iff \left(1c\right)\hfill \\ & \Downarrow \hfill \\ & \left(2a\right)\Rightarrow \left(2b\right)\iff \left(2c\right).\hfill \end{array}$$

If $Z_L$ is an L-subset system then $\left(Na\right)\iff \left(Nb\right)\iff \left(Nc\right)(N=1,2)$. If, in addition, $(X,{·}_X,e_X)$ is $Z_L$-complete then all six conditions are equivalent.

Proof. 

(1a)⇒(1b): It is obvious by ${\mathrm{M}}_L{X}^{\prime }\subseteq Z_L^{\delta }{X}^{\prime }$.

(1b)⇒(1c): Obviously, f is L-order preserving. Now we need to show that $f^{\to }\left(D^{\delta }\right)\subseteq {\left(f^{\to }\left(D\right)\right)}^{\delta },\forall D\in Z_{L}X$. In fact, for any $D\in Z_{L}X$ and any $x^{\prime }\in X^{\prime }$,

$$\begin{array}{cc}\hfill {\left(f^{\to }\left(D\right)\right)}^{\delta }\left(x^{\prime }\right)& =\underset{x^{\prime \prime }\in X^{\prime }}{\bigwedge }su{b}_{X^{\prime }}(f^{\to }\left(D\right),{\iota }_{x^{\prime \prime }})\to {\iota }_{x^{\prime \prime }}\left(x^{\prime }\right)\hfill \\ & =\underset{x^{\prime \prime }\in X^{\prime }}{\bigwedge }su{b}_X(D,f^{\leftarrow }\left({\iota }_{x^{\prime \prime }}\right))\to {\iota }_{x^{\prime \prime }}\left(x^{\prime }\right)\hfill \\ & \ge \underset{x^{\prime \prime }\in X^{\prime }}{\bigwedge }su{b}_X(D^{\delta },f^{\leftarrow }\left({\iota }_{x^{\prime \prime }}\right))\to {\iota }_{x^{\prime \prime }}\left(x^{\prime }\right)\hfill \\ & =\underset{x^{\prime \prime }\in X^{\prime }}{\bigwedge }su{b}_{X^{\prime }}(f^{\to }\left(D^{\delta }\right),{\iota }_{x^{\prime \prime }})\to {\iota }_{x^{\prime \prime }}\left(x^{\prime }\right)\hfill \\ & ={\left(f^{\to }\left(D^{\delta }\right)\right)}^{\delta }\left(x^{\prime }\right)\ge f^{\to }\left(D^{\delta }\right)\left(x^{\prime }\right).\hfill \end{array}$$

(1c)⇒(1b): Suppose that f is L-order preserving and $Z_L$-join preserving, then for any $x^{\prime }\in X^{\prime }$, $f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)$ is a lower L-subset. Moreover, for any $D\in Z_{L}X$,

$$\begin{array}{cc}\hfill su{b}_X(D,f^{\leftarrow }\left({\iota }_{x^{\prime }}\right))& =su{b}_{X^{\prime }}(f^{\to }\left(D\right),{\iota }_{x^{\prime }})\le su{b}_{X^{\prime }}({\left(f^{\to }\left(D\right)\right)}^{\delta },{\iota }_{x^{\prime }})\hfill \\ & \le su{b}_{X^{\prime }}(f^{\to }\left(D^{\delta }\right),{\iota }_{x^{\prime }})=su{b}_X(D^{\delta },f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)).\hfill \end{array}$$

Therefore $f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)\in Z_L^{\delta }X$.

If $Z_L$ is an L-subset system, then we have (1c)⇒(1a). In fact, for any $B\in Z_L^{\delta }X$ and any $D\in Z_{L}X$, $f^{\leftarrow }\left(B\right)$ is a lower L-subset and $f^{\to }\left(D\right)\in Z_L{X}^{\prime }$; moreover,

$$\begin{array}{cc}\hfill su{b}_X(D,f^{\leftarrow }\left(B\right))& =su{b}_{X^{\prime }}(f^{\to }\left(D\right),B)\le su{b}_{X^{\prime }}({\left(f^{\to }\left(D\right)\right)}^{\delta },B)\hfill \\ & \le su{b}_{X^{\prime }}(f^{\to }\left(D^{\delta }\right),B)=su{b}_X(D^{\delta },f^{\leftarrow }\left(B\right)).\hfill \end{array}$$

Therefore $f^{\leftarrow }\left(B\right)\in Z_L^{\delta }X$.

(1b)⇒(2b): It holds by $Z_L^{\delta }X\subseteq Z_L^{\bigsqcup }X$.

(2a)⇒(2b): It is obvious by ${\mathrm{M}}_L{X}^{\prime }\subseteq Z_L^{\bigsqcup }{X}^{\prime }$.

(2b)⇒(2c): Similar to (1b)⇒(1c), we only need to show that $f(\bigsqcup D)=\bigsqcup f^{\to }\left(D\right)$ for all $D\in Z_{L}X$ with $\bigsqcup D$ existing. In fact, for any $x^{\prime }\in X^{\prime }$ and any $D\in Z_{L}X$ with $\bigsqcup D$ existing, we have

$$\begin{array}{cc}\hfill e_{X^{\prime }}(f(\bigsqcup D),x^{\prime })& =f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)(\bigsqcup D)\ge su{b}_X(D,f^{\leftarrow }\left({\iota }_{x^{\prime }}\right))=su{b}_{X^{\prime }}(f^{\to }\left(D\right),{\iota }_{x^{\prime }})\hfill \\ & =\underset{x^{\prime \prime }\in X^{\prime }}{\bigwedge }{f}^{\to }\left(D\right)\left(x^{\prime \prime }\right)\to e_{X^{\prime }}(x^{\prime \prime },x^{\prime }).\hfill \end{array}$$

Moreover, for any $x\in X$ and any $x^{\prime }\in X^{\prime }$, we have $e_{X^{\prime }}(f\left(x\right),f(\bigsqcup D))\ge e_X(x,\bigsqcup D)\ge D\left(x\right)$, and so $f^{\to }\left(D\right)\left(x^{\prime }\right)={\bigvee }_{f\left(x\right)=x^{\prime }}D\left(x\right)\le e_{X^{\prime }}(x^{\prime },f(\bigsqcup D))$. Therefore, $f(\bigsqcup D)=\bigsqcup f^{\to }\left(D\right)$.

(2c)⇒(2b): For any $x^{\prime }\in X^{\prime }$ and any $D\in Z_{L}X$ with $\bigsqcup D$ existing, $f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)$ is a lower L-subset and $su{b}_X(D,f^{\leftarrow }\left({\iota }_{x^{\prime }}\right))=su{b}_{X^{\prime }}(f^{\to }\left(D\right),{\iota }_{x^{\prime }})=e_{X^{\prime }}(\bigsqcup f^{\to }\left(D\right),x^{\prime })=e_{X^{\prime }}(f(\bigsqcup D),x^{\prime })=f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)(\bigsqcup D)$. Therefore $f^{\leftarrow }\left({\iota }_{x^{\prime }}\right)\in Z_L^{\bigsqcup }{X}^{\prime }$ and thus f is weakly $Z_L^{\bigsqcup }$-continuous.

Suppose that $Z_L$ is an L-subset system, then (1c)⇒(1a). In fact, for any $B\in Z_L^{\delta }X$ and any $D\in Z_{L}X$, $f^{\leftarrow }\left(B\right)$ is a lower L-subset and $f^{\to }\left(D\right)\in Z_L{X}^{\prime }$; moreover,

$$\begin{array}{cc}\hfill su{b}_X(D,f^{\leftarrow }\left(B\right))& =su{b}_{X^{\prime }}(f^{\to }\left(D\right),B)\le B(\bigsqcup f^{\to }\left(D\right))=B(f(\bigsqcup D)=f^{\leftarrow }\left(B\right)(\bigsqcup D).\hfill \end{array}$$

Therefore, $f^{\leftarrow }\left(B\right)\in Z_L^{\bigsqcup }X$. Suppose that $(X^{\prime },{·}_{X^{\prime }},e_{X^{\prime }})$ is $Z_L$-complete, then $\left(1c\right)\iff \left(2c\right)$. In fact, for any $D\in Z_{L}X$, $\bigsqcup D$ and $\bigsqcup f^{\to }\left(D\right)$ exist. Moreover, $e_{X^{\prime }}(\bigsqcup f^{\to }\left(D\right),f(\bigsqcup D))={\bigwedge }_{x\in X}D\left(x\right)\to e_{X^{\prime }}(f\left(x\right),f(\bigsqcup D))\ge {\bigwedge }_{x\in X}D\left(x\right)\to e_X(x,\bigsqcup D)=e_X(\bigsqcup D,\bigsqcup D)=1$ and

$$\begin{array}{cc}\hfill e_{X^{\prime }}(f(\bigsqcup D),\bigsqcup f^{\to }\left(D\right))& =su{b}_{X^{\prime }}({\iota }_{f(\bigsqcup D)},{\iota }_{\bigsqcup f^{\to }\left(D\right)})=su{b}_{X^{\prime }}({\iota }_{f(\bigsqcup D)},{\left(f^{\to }\left(D\right)\right)}^{\delta })\hfill \\ & \ge su{b}_{X^{\prime }}({\iota }_{f(\bigsqcup D)},f^{\to }\left(D^{\delta }\right))=su{b}_{X^{\prime }}({\iota }_{f(\bigsqcup D)},f^{\to }\left({\iota }_{\bigsqcup D}\right))\hfill \\ & =f^{\to }\left({\iota }_{\bigsqcup D}\right)\left(f(\bigsqcup D)\right)=\underset{f\left(x\right)=f(\bigsqcup D)}{\bigvee }{e}_X(x,\bigsqcup D)\hfill \\ & \ge e_X(\bigsqcup D,\bigsqcup D)=1.\hfill \end{array}$$

□

Clearly, all identity mappings are $Z_L$-continuous and the compositions of $Z_L$-continuous mappings are again $Z_L$-continuous. Thus all L-OSs with $Z_L$-continuous L-OS homomorphisms form a category denoted by L-OSG${}_{Z_L}$, and it is a subcategory of L-OSG. We call a standard L-completion $Z_L$ compositive if the class of all weakly $Z_L$-continuous mappings is closed under composition.

Lemma 1.

(1) 

The embedding ${\eta }_X:X⟶Z_{L}X,x\mapsto {\iota }_x$ is weakly $Z_L$-continuous, and so are all corestrictions ${\eta }_X:X⟶\mathfrak{X}$ with ${\mathrm{M}}_{L}X\subseteq \mathfrak{X}\subseteq Z_{L}X$; ${\eta }_X:X⟶\mathfrak{X}$ is $Z_L$-continuous iff $\bigcup \mathcal{A}\in \mathfrak{X}$ for all $\mathcal{A}\in Z_L\mathfrak{X}$.

(2) 

An arbitrary mapping $f:X⟶X^{\prime }$ is $Z_L$-continuous iff the composite mapping ${\eta }_{X^{\prime }}\circ f:X⟶Z_L{X}^{\prime }$ is weakly $Z_L$-continuous.

Proof. 

(1) For any $D\in Z_{L}X$ and any $x\in X$, ${\eta }_X^{\leftarrow }\left({\iota }_D\right)\left(x\right)={\iota }_D\left({\eta }_X\left(x\right)\right)=su{b}_X({\iota }_x,D)=D\left(x\right)\in Z_{L}X$, which implies that ${\eta }_X:X⟶Z_{L}X$ is weakly $Z_L$-continuous. Similarly, we can check that ${\eta }_X:X⟶\mathfrak{X}$ is also weakly $Z_L$-continuous. Note the following fact: $\forall \mathcal{A}\in Z_L\mathfrak{X},x\in X$, ${\eta }_X^{\leftarrow }\left(\mathcal{A}\right)\left(x\right)=\mathcal{A}\left({\iota }_x\right)={\bigvee }_{A\in \mathfrak{X}}\mathcal{A}\left(A\right)\ast su{b}_X({\iota }_x,A)={\bigvee }_{A\in \mathfrak{X}}\mathcal{A}\left(A\right)\ast A\left(x\right)=(\bigcup \mathcal{A})\left(x\right)$. Therefore, ${\eta }_X:X⟶\mathfrak{X}$ is $Z_L$-continuous iff $\bigcup \mathcal{A}\in \mathfrak{X}$ for all $\mathcal{A}\in Z_L\mathfrak{X}$.

(2) Suppose that $f:X⟶X^{\prime }$ is $Z_L$-continuous. By (1), we have that for any $D\in Z_L{X}^{\prime }$, ${\eta }_{X^{\prime }}^{\leftarrow }\left({\iota }_D\right)\in Z_L{X}^{\prime }$ and so ${({\eta }_{X^{\prime }}\circ f)}^{\leftarrow }\left({\iota }_D\right)=f^{\leftarrow }\left({\eta }_{X^{\prime }}^{\leftarrow }\left({\iota }_D\right)\right)\in Z_{L}X$. Therefore, ${\eta }_{X^{\prime }}\circ f$ is weakly $Z_L$-continuous. Conversely, suppose that ${\eta }_{X^{\prime }}\circ f$ is weakly $Z_L$-continuous, then for any $D\in Z_L{X}^{\prime }$ and any $x\in X$, ${({\eta }_{X^{\prime }}\circ f)}^{\leftarrow }\left({\iota }_D\right)\in Z_{L}X$ and $f^{\leftarrow }\left(D\right)\left(x\right)=D\left(f\left(x\right)\right)=su{b}_{X^{\prime }}({\iota }_{f\left(x\right)},D)={\iota }_D\left(({\eta }_{X^{\prime }}\circ f)\left(x\right)\right)={({\eta }_{X^{\prime }}\circ f)}^{\leftarrow }\left({\iota }_D\right)\left(x\right)$. Thus f is $Z_L$-continuous. □

According to Lemma 1 we immediately get the following characterization of $Z_L$-union completeness and compositeness.

Proposition 4.

(1) 

A standard L-completion $Z_L$ is compositive iff every weakly $Z_L$-continuous mapping is already $Z_L$-continuous.

(2) 

A standard L-completion $Z_L$ is $Z_L$-union complete iff for each L-OS $(X,·,e)$ the embedding ${\eta }_X$ is $Z_L$-continuous.

(3) 

Every compositive standard L-completion $Z_L$ is $Z_L$-union complete.

(4) 

For every compositive standard L-completion $Z_L$, every residuated mapping is $Z_L$-continuous.

Corollary 1.

For an L-subset system $Z_L$, the standard L-completions $Z_L^{\delta }$ and $Z_L^{\bigsqcup }$ are compositive.

From Proposition 4, it is easy to check the following relationships among mappings:

where “compositive" means the standard L-completion $Z_L$ is compositive.

4. $Z_L$-Completions for $Z_L$-Semigroups

In this section, we shall consider completions for $Z_L$-semigroups. In one special case, it is the $\mathcal{Q}$-quantale completion of the $\mathcal{Q}$-ordered semigroup constructed and characterized in [30,31].

Definition 6.

Let $Z_L$ be a standard L-completion, we call an L-OS a $Z_L$-semigroup if all left and right translations are $Z_L$-continuous.

Obviously, when $L=\{0,1\}$, a $Z_L$-semigroup is just the $\mathcal{Y}$-semigroup defined in [32].

Example 3.

(1) 

An L-OS is an ${\mathrm{A}}_L$-semigroup $(X,·,e)$ since $\forall x\in X,A\in {\mathrm{A}}_{L}X$, ${\ell }_x^{\leftarrow }\left(A\right)$ and ${\hslash }_x^{\leftarrow }\left(A\right)$ are still lower L-subsets.

(2) 

A ${\mathrm{J}}_L$-semigroup is characterized by the identities

$${\ell }_x(\bigsqcup A)=\bigsqcup {\ell }_x^{\to }\left(A\right)and{\hslash }_x(\bigsqcup A)={\hslash }_x^{\to }\left(A\right)(\ast )$$

for all L-subsets $A\in L^X$ with $\bigsqcup A$ existing. Moreover, we can check that the equation (*) is equivalent to $\bigsqcup A·\bigsqcup B=\bigsqcup (A·B)$ for any $A,B\in L^X$ with $\bigsqcup A,\bigsqcup B$ existing.

(3) 

The example (2) can be generalized in an obvious way. Given an arbitrary L-subset system $Z_L$, it is easy to check that the $Z_L^{\bigsqcup }$-semigroups are those in which the identities (*) are valid for any L-subset $A\in Z_{L}X$ with $\bigsqcup A$ existing.

(4) 

Let $(X,e)$ be a meet L-semilattice (i.e., each finite L-subset has a meet), then $(X,{\le }_e)$ is a meet-semilattice and so $(X,\wedge ,e)$ is an L-OS, where ∧ is the meet operation on $(X,{\le }_e)$. In this case, $(X,\wedge ,e)$ is a $D_L^{\bigsqcup }$-semigroup characterized by ${\wedge }_x(\bigsqcup D)=\bigsqcup {\wedge }_x^{\to }\left(D\right)$ for all $x\in X$ and all L-ideals D possessing a join. This means that $(X,\wedge ,e)$ is $D_L^{\bigsqcup }$-semigroup iff $(X,e)$ is meet-continuous (See [40]).

(5) 

Every residuated L-OS is a $Z_L$-semigroup for compositive $Z_L$.

(6) 

$(X^{\prime },·,e)$ is a $Z_L$-subsemigroup of $(X,·,e)$ iff it is an L-ordered subsemigroup of $(X,·,e)$ and a $Z_L$-semigroup with respect to the induced L-order.

Proposition 5.

Let $(X,·,e)$ be a $Z_L$-semigroup and $A,B\in L^X$. Then

(1) 

$A·C\left(B\right)\subseteq A\odot B$ and $C\left(A\right)·B\subseteq A\odot B$;

(2) 

$A\odot B=A\odot C\left(B\right)=C\left(A\right)\odot B=C\left(A\right)\odot C\left(B\right)$; in particular, $A\odot (B\odot D)=A\odot (B·D)=(A·B)\odot D=(A\odot B)\odot D$;

(3) 

$(Z_{L}X,\odot ,sub)$ is a complete residuated L-OS;

(4) 

The natural embedding ${\eta }_X:X⟶Z_{L}X,x\mapsto {\iota }_x$ is a join-dense and weakly $Z_L$-continuous semigroup homomorphism.

Proof. 

(1) Let $x\in X$ and $B\in L^X$, ${\ell }_x^{\to }\left(C\left(B\right)\right)\subseteq C\left({\ell }_x^{\to }\left(B\right)\right)$ by the $Z_L$-continuity of translations. Then for any $A,B\in L^X$,

$$\begin{array}{cc}\hfill sub(A·C(B),C(A·B\left)\right)& =\underset{x\in X}{\bigwedge }(\underset{s·t=x}{\bigvee }A\left(s\right)\ast C\left(B\right)\left(t\right))\to C(A·B)\left(x\right)\hfill \\ & =\underset{s\in X}{\bigwedge }A\left(s\right)\to sub({\ell }_s^{\to }\left(C\left(B\right)\right),C(A·B))\hfill \\ & \ge \underset{s\in X}{\bigwedge }A\left(s\right)\to sub(C\left({\ell }_s^{\to }\left(B\right)\right),C(A·B))\hfill \\ & \ge \underset{s\in X}{\bigwedge }A\left(s\right)\to sub(B,{\ell }_s^{\leftarrow }(A·B))\hfill \\ & =\underset{s\in X}{\bigwedge }A\left(s\right)\to (\underset{t\in X}{\bigwedge }B\left(t\right)\to (\underset{s^{\prime }·t^{\prime }=s·t}{\bigvee }A\left(s^{\prime }\right)\ast B\left(t^{\prime }\right)))\hfill \\ & \ge \underset{s\in X}{\bigwedge }A\left(s\right)\to (\underset{t\in X}{\bigwedge }B\left(t\right)\to A\left(s\right)\ast B\left(t\right))=1,\hfill \end{array}$$

which implies $A·C\left(B\right)\subseteq C(A·B)$. Similarly, we have $C\left(A\right)·B\subseteq A\odot B$.

(2) By (1), it is easy to check.

(3) It only needs to show that $(Z_{L}X,\odot ,sub)$ is residuated. For $x\in X$ and any $A,B\in Z_{L}X$, ${\ell }_x^{\leftarrow }\left(B\right)\in Z_{L}X$ and so ${\bigwedge }_{x\in X}A\left(x\right)\to {\ell }_x^{\leftarrow }\left(B\right)\in Z_{L}X$ by Proposition 1. Now, we can define two mappings ${\ell }_A:Z_{L}X⟶Z_{L}X$ and ${\overline{\ell }}_A:Z_{L}X⟶Z_{L}X$ as follows: $B\mapsto A\odot B$ and $B\mapsto {\bigwedge }_{x\in X}A\left(x\right)\to {\ell }_x^{\leftarrow }\left(B\right)$, respectively. Then we have

$$\begin{array}{cc}\hfill sub(A\odot B,D)& =sub(A·B,D)=\underset{x\in X}{\bigwedge }(\underset{s·t=x}{\bigvee }A\left(s\right)\ast B\left(t\right))\to D\left(x\right)\hfill \\ & =\underset{s,t\in X}{\bigwedge }A\left(s\right)\ast B\left(t\right)\to D\left(st\right)=\underset{s,t\in X}{\bigwedge }A\left(s\right)\ast B\left(t\right)\to {\ell }_s^{\leftarrow }\left(D\right)\left(t\right)\hfill \\ & =\underset{s,t\in X}{\bigwedge }B\left(t\right)\to (\underset{s\in X}{\bigwedge }A\left(s\right)\to {\ell }_s^{\leftarrow }\left(D\right)\left(t\right))\hfill \\ & =\underset{s,t\in X}{\bigwedge }B\left(t\right)\to {\overline{\ell }}_A\left(D\right)\left(t\right)=sub(B,{\overline{\ell }}_A\left(D\right)).\hfill \end{array}$$

This implies that ${\ell }_A$ is a residuated mapping. Similarly, ${\hslash }_A$ is residuated. Therefore, $(Z_{L}X,\odot ,sub)$ is residuated.

(4) Obviously, ${\eta }_X$ is weakly $Z_L$-continuous by Lemma 1 (1). Moreover, for all $A\in Z_{L}X$ and all $x\in X$,

$$\begin{array}{cc}\hfill \bigsqcup i_{{\mathrm{M}}_{L}X,L^X}^{\to }\left(i_{{\mathrm{M}}_{L}X,Z_{L}X}^{\leftarrow }\left({\iota }_A\right)\right)\left(x\right)& =\underset{B\in L^X}{\bigvee }{i}_{{\mathrm{M}}_{L}X,L^X}^{\to }\left(i_{{\mathrm{M}}_{L}X,Z_{L}X}^{\leftarrow }\left({\iota }_A\right)\right)\left(B\right)\ast B\left(x\right)\hfill \\ & =\underset{B\in L^X}{\bigvee }\underset{i_{{\mathrm{M}}_{L}X,L^X}\left(B^{\prime }\right)=B}{\bigvee }{i}_{{\mathrm{M}}_{L}X,Z_{L}X}^{\leftarrow }\left({\iota }_A\right)\left(B^{\prime }\right)\ast B\left(x\right)\hfill \\ & =\underset{x^{\prime }\in X}{\bigvee }{\iota }_A\left({\iota }_{x^{\prime }}\right)\ast {\iota }_{x^{\prime }}\left(x\right)=A\left(x\right),\hfill \end{array}$$

which implies that $A=\bigsqcup i_{{\mathrm{M}}_{L}X,Z_{L}X}^{\to }\left(i_{{\mathrm{M}}_{L}X,Z_{L}X}^{\leftarrow }\left({\iota }_A\right)\right)$. Therefore, ${\eta }_X$ is join-dense. Next, we show that ${\eta }_X$ is a semigroup homomorphism. In fact, for any $x,x^{\prime }\in X$,

$$\begin{array}{cc}\hfill sub({\eta }_X\left(x\right)\odot {\eta }_X\left(x^{\prime }\right),{\eta }_X(x·x^{\prime }))& =\underset{s,t\in X}{\bigwedge }{\iota }_x\left(s\right)\ast {\iota }_{x^{\prime }}\left(t\right)\to {\iota }_{x·x^{\prime }}(s·t)\hfill \\ & \ge \underset{s,t\in X}{\bigwedge }e(s·x^{\prime },x·x^{\prime })\ast e(s·t,s·x^{\prime })\to e(s·t,x·x^{\prime })\hfill \\ & \ge \underset{s,t\in X}{\bigwedge }e(s·t,x·x^{\prime })\to e(s·t,x·x^{\prime })=1\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill sub({\eta }_X(x·x^{\prime }),{\eta }_X\left(x\right)\odot {\eta }_X\left(x^{\prime }\right))& =C({\eta }_X\left(x\right)·{\eta }_X\left(x^{\prime }\right))(x·x^{\prime })\hfill \\ & =\underset{B\in Z_{L}X}{\bigwedge }sub({\eta }_X\left(x\right)·{\eta }_X\left(x^{\prime }\right),B)\to B(x·x^{\prime })\hfill \\ & =\underset{B\in Z_{L}X}{\bigwedge }(\underset{s,t\in X}{\bigwedge }e(s,x)\ast e(t,x^{\prime })\to B(s·t))\to B(x·x^{\prime })\hfill \\ & \ge \underset{B\in Z_{L}X}{\bigwedge }B(x·x^{\prime })\to B(x·x^{\prime })=1.\hfill \end{array}$$

Hence ${\eta }_X\left(x\right)\odot {\eta }_X\left(x^{\prime }\right)={\eta }_X(x·x^{\prime })$. □

Remark 2.

(1) 

If $(X,·,e)$ is an L-ordered monoid then so is $(Z_{L}X,\odot ,sub)$. In fact, let $s_0\in X$ be a unit element and $A\in Z_{L}X$ then $sub({\iota }_{s_0}\odot A,A)={\bigwedge }_{s\in X}A\left(s\right)\to {\hslash }_s^{\leftarrow }\left(A\right)\left(s_0\right)={\bigwedge }_{s\in X}A\left(s\right)\to A(s_0·s)={\bigwedge }_{s\in X}A\left(s\right)\to A\left(s\right)=1$ and $sub(A,{\iota }_{s_0}\odot A)={\bigwedge }_{s\in X}A\left(s\right)\to ({\bigvee }_{t·x=s}{\iota }_{s_0}\left(t\right)\ast A\left(x\right))\ge {\bigwedge }_{s\in X}A\left(s\right)\to ({\iota }_{s_0}\left(s_0\right)\ast A\left(s\right))=1$. Thus it follows that ${\iota }_{s_0}\odot A=A$ and $A\odot {\iota }_{s_0}=A$ similarly.

(2) 

$(Z_{L}X,\odot ,sub)$ of commutative $Z_L$-semigroup $(X,·,e)$ is again commutative. From $(A·B)\left(x\right)={\bigvee }_{s·t=x}A\left(s\right)\ast B\left(t\right)={\bigvee }_{t·s=x}B\left(t\right)\ast A\left(s\right)=(B·A)\left(x\right)$ for any $A,B\in Z_{L}X$, we have $A\odot B=B\odot A$.

(3) 

For every standard L-completion $Z_L$, ${\mathrm{M}}_{L}X$ is join-dense in $Z_{L}X$.

(4) 

Every residuated L-OS is a ${\mathrm{J}}_L$-semigroup.

Definition 7.

Let $(X,{·}_X,e_X)$ be a $Z_L$-semigroup. A complete residuated L-OS $(Y,{·}_Y,e_Y)$ together with a join-dense L-OS embedding ${\eta }_X:X⟶Y$ is called a $Z_L$-completion of $(X,{·}_X,e_X)$ if ${\eta }_X:X⟶Y$ has the following universal property: For any weakly $Z_L$-continuous semigroup homomorphism $f:X⟶X^{\prime }$ mapping into a complete residuated L-OS $(X^{\prime },{·}_{X^{\prime }},e_{X^{\prime }})$, there exists a unique join-preserving L-OS homomorphism $\breve{f}:Y⟶X^{\prime }$ such that $f=\breve{f}\circ {\eta }_X$.

Clearly, a complete residuated L-OS is a $Z_L$-completion of itself.

Lemma 2.

Let $f,g:X⟶Y$ be join-preserving mappings between two $Z_L$-semigroups $(X,{·}_X,e_X)$ and $(Y,{·}_Y,e_Y)$ and $X^{\prime }$ join-dense in X.

(1) 

If $f\left(x\right)=g\left(x\right)$ for all $x\in X^{\prime }$, then $f\left(x\right)=g\left(x\right),\forall x\in X$;

(2) 

In the case that $(X,{·}_X,e_X)$ and $(Y,{·}_Y,e_Y)$ are ${\mathrm{J}}_L$-semigroups, f is a semigroup homomorphism if $f\left(s{·}_{X}t\right)=f\left(s\right){·}_{Y}f\left(t\right),\forall s,t\in X^{\prime }$.

Proof. 

(1) Let $x\in X$, then for any $y\in Y$,

$$\begin{array}{cc}\hfill e_Y(f\left(x\right),y)& =e_Y(f(\bigsqcup {\iota }_x\wedge {\chi }_{X^{\prime }}),y)=e_Y(\bigsqcup f^{\to }({\iota }_x\wedge {\chi }_{X^{\prime }}),y)\hfill \\ & =\underset{y^{\prime }\in Y}{\bigvee }{f}^{\to }({\iota }_x\wedge {\chi }_{X^{\prime }})\left(y^{\prime }\right)\to e_{(}{y}^{\prime },y)=\underset{x^{\prime }\in X^{\prime }}{\bigvee }{\iota }_x\left(x^{\prime }\right)\to e_Y(f\left(x^{\prime }\right),y)\hfill \\ & =\underset{x^{\prime }\in X^{\prime }}{\bigvee }{\iota }_x\left(x^{\prime }\right)\to e_Y(g\left(x^{\prime }\right),y)=e_Y(g\left(x\right),y),\hfill \end{array}$$

which implies that $f\left(x\right)=g\left(x\right)$ for all $x\in X$.

(2) For $s,t\in X$, let $A={\iota }_s\wedge {\chi }_{X^{\prime }}$ and $B={\iota }_t\wedge {\chi }_{X^{\prime }}$. Then $s=\bigsqcup A$, $t=\bigsqcup B$, and

$$\begin{array}{cc}\hfill (f^{\to }\left(A\right)·f^{\to }\left(B\right))\left(y\right)& =\underset{y_1{·}_Y{y}_2=y}{\bigvee }{f}^{\to }\left(A\right)\left(y_1\right)\ast f^{\to }\left(B\right)\left(y_2\right)\hfill \\ & =\underset{y_1{·}_Y{y}_2=y}{\bigvee }\left(\underset{f\left(x_1\right)=y_1}{\bigvee }A\left(x_1\right)\right)\ast \left(\underset{f\left(x_2\right)=y_2}{\bigvee }B\left(x_2\right)\right)\hfill \\ & =\underset{f\left(x_1\right){·}_{Y}f\left(x_2\right)=y}{\bigvee }A\left(x_1\right)\ast B\left(x_2\right)\hfill \\ & =\underset{f\left(x_1{·}_X{x}_2\right)=y}{\bigvee }A\left(x_1\right)\ast B\left(x_2\right)=f^{\to }\left(A{·}_{X}B\right)\left(y\right).\hfill \end{array}$$

Hence $f\left(s{·}_{X}t\right)=f(\bigsqcup A{·}_X\bigsqcup B)=f(\bigsqcup (A·B))=\bigsqcup f^{\to }(A·B)=\bigsqcup f^{\to }\left(A\right){·}_Y\bigsqcup f^{\to }\left(B\right)=f(\bigsqcup A){·}_{Y}f(\bigsqcup B)=f\left(s\right){·}_{Y}f\left(t\right)$. □

Theorem 2.

For each $Z_L$-semigroup $(X,{·}_X,e_X)$, $(Z_{L}X,\odot ,sub)$ is a $Z_L$-completion of $(X,{·}_X,e_X)$.

Proof. 

By Proposition 5 (3) and (4), we only need to show that ${\eta }_X:X⟶Z_{L}X$ has the universal property. Let $f:X⟶Y$ be a weakly $Z_L$-continuous semigroup homomorphism from $(X,{·}_X,e_X)$ to a complete residuated L-OS $(Y,{·}_Y,e_Y)$, then for any $A\in Z_{L}X$ and $y\in Y$, $\bigsqcup f^{\to }\left(A\right)$ exists and $f^{\leftarrow }\left({\iota }_y\right)\in Z_{L}X$. Define $\breve{f}:Z_{L}X⟶Y$ as $\breve{f}\left(A\right)=\bigsqcup f^{\to }\left(A\right)$. Then $e_Y(\breve{f}\left(A\right),y)=e_Y(\bigsqcup f^{\to }\left(A\right),y)=su{b}_Y(f^{\to }\left(A\right),{\iota }_y)=su{b}_X(A,f^{\leftarrow }\left({\iota }_y\right))$. This implies that the mapping $\overline{f}:Y⟶Z_{L}X,y\mapsto f^{\leftarrow }\left({\iota }_y\right)$ is a right adjoint of $\breve{f}$ and so $\breve{f}$ is residuated. Moreover, for any $x\in X$, $e_Y(\breve{f}\circ {\eta }_X\left(x\right),f\left(x\right))=e_Y(\breve{f}\left({\iota }_x\right),f\left(x\right))=su{b}_X({\iota }_x,f^{\leftarrow }\left({\iota }_{f\left(x\right)}\right))=f^{\leftarrow }\left({\iota }_{f\left(x\right)}\right))\left(x\right)=1$ and $e_Y(f\left(x\right),\breve{f}\circ {\eta }_X\left(x\right))=e_Y(f\left(x\right),\bigsqcup f^{\to }\left({\iota }_x\right))\ge f^{\to }\left({\iota }_x\right)(f\left(x\right)={\bigvee }_{f\left(x_1\right)=f\left(x\right)}{e}_X(x_1,x)\ge e_X(x,x)=1$; thus $\breve{f}\circ {\eta }_X\left(x\right)=f\left(x\right)$. The uniqueness of $\breve{f}$ can be obtained by Lemma 2 and Remark 2 (3). □

Remark 3.

(1) 

In the case of $Z_L=D{M}_L$, the $Z_L$-completion of a $Z_L$-semigroup is the Dedekind–MacNeille completion.

(2) 

In the case of $Z_L={\mathrm{A}}_L$, the $Z_L$-completion of a $Z_L$-semigroup is the Q-quantale completion defined in [31]. Therefore, the Q-quantale completion has the universal property and the $Z_L$-completion can be as a generalization of the Q-quantale completion.

From the proof of Theorem 2, we can directly reach the following conclusion:

Proposition 6.

We call a weakly $Z_L$-continuous mapping $f:X⟶Y$ between two L-OSs $(X,{·}_X,e_X)$ and $(Y,{·}_Y,e_Y)$ a $Z_L$-arrow if for every $A\in Z_{L}X$, $\bigsqcup f^{\to }\left(A\right)$ exists. Then a mapping $f:X⟶Y$ between L-OSs $(X,{·}_X,e_X)$ and $(Y,{·}_Y,e_Y)$ is a $Z_L$-arrow iff there exists a unique residuated mapping $\breve{f}:Z_{L}X⟶Y$ with $f=\breve{f}\circ {\eta }_X$, viz. $\breve{f}\left(A\right)=\bigsqcup f^{\to }\left(A\right)$, i.e., the following commutative diagram:

5. A Category Characterization of the $Z_L$-Completion

The $Z_L$-semigroups together with $Z_L$-continuous semigroup homomorphisms form a category ${\mathbf{S}}_{Z_L}$. For example, ${\mathbf{S}}_{{\mathrm{A}}_L}$ is the category of L-OSs and L-OS homomorphisms. Moreover, denote by ${\mathbf{CS}}_L$ the category of complete residuated L-ordered semigroups together with join-preserving L-OS homomorphisms. Obviously, ${\mathbf{CS}}_L=Q$-Quant, defined in [31]. In this section, we describe the $Z_L$-completion of a $Z_L$-semigroup from the perspective of category. Next, we first discuss whether an arbitrary $Z_L$-continuous semigroup homomorphism $f:X⟶Y$ may be lifted to a join-preserving semigroup homomorphism between the $Z_L$-completions $(Z_{L}X,\odot ,su{b}_X)$ and $(Z_{L}Y,\odot ,su{b}_Y)$.

Lemma 3.

For every $Z_L$-continuous semigroup homomorphism $f:X⟶Y$, the mapping $Z_{L}f:Z_{L}X⟶Z_{L}Y,A\mapsto C\left(f^{\to }\left(A\right)\right)$ is a join-preserving semigroup homomorphism.

Proof. 

Since $f:X⟶Y$ is $Z_L$-continuous, $f^{\leftarrow }\left(B^{\prime }\right)\in Z_{L}X$ for any $B^{\prime }\in Z_{L}Y$. So we obtain a mapping $Z_L^{\ast }f:Z_{L}Y⟶Z_{L}X,B^{\prime }\mapsto f^{\leftarrow }\left(B^{\prime }\right)$. Then for any $A\in Z_{L}X$ and any $B^{\prime }\in Z_{L}Y$,

$$su{b}_X(A,Z_L^{\ast }f\left(B^{\prime }\right))=su{b}_Y(f^{\to }\left(A\right),B^{\prime })=su{b}_Y(C\left(f^{\to }\left(A\right)\right),B^{\prime })=su{b}_Y\left(Z_{L}f\left(A\right)\right),B^{\prime }).$$

Hence $Z_{L}f$ is residuated and thus is join-preserving by Theorem 1. Moreover, for any $A,B\in Z_{L}X$, $Z_{L}f\left(A\right)\odot Z_{L}f\left(B\right)=C\left(f^{\to }\left(A\right)\right)\odot C\left(f^{\to }\left(B\right)\right)=f^{\to }\left(A\right)\odot f^{\to }\left(B\right)=C(f^{\to }\left(A\right)·f^{\to }\left(B\right))=C\left(f^{\to }(A·B)\right)$ and so $Z_{L}f\left(A\right)\odot Z_{L}f\left(B\right)\subseteq C\left(f^{\to }(A\odot B)\right)=Z_{L}f(A\odot B)$. On the other hand, for all $y\in Y$,

$$\begin{array}{cc}\hfill Z_{L}f(A\odot B)\left(y\right)& =C\left(f^{\to }(A\odot B)\right)\left(y\right)=\underset{D\in Z_{L}Y}{\bigwedge }su{b}_Y(f^{\to }(A\odot B),D)\to D\left(y\right)\hfill \\ & =\underset{D\in Z_{L}Y}{\bigwedge }su{b}_X(A\odot B,f^{\leftarrow }\left(D\right))\to D\left(y\right)\hfill \\ & =\underset{D\in Z_{L}Y}{\bigwedge }su{b}_X(C(A·B),C\left(f^{\leftarrow }\left(D\right)\right))\to D\left(y\right)\hfill \\ & \le \underset{D\in Z_{L}Y}{\bigwedge }su{b}_X(A·B,f^{\leftarrow }\left(D\right))\to D\left(y\right)\hfill \\ & =\underset{D\in Z_{L}Y}{\bigwedge }su{b}_Y(f^{\to }(A·B),D)\to D\left(y\right)=C\left(f^{\to }(A·B)\right).\hfill \end{array}$$

Hence $Z_{L}f\left(A\right)\odot Z_{L}f\left(B\right)=Z_{L}f(A\odot B)$. This means $Z_{L}f$ is a semigroup homomorphism. To sum up, we have that $Z_{L}f$ is a join-preserving semigroup homomorphism. □

From this lemma, the following conclusion can be drawn directly:

Corollary 2.

Every standard L-completion $Z_L$ gives rise to a functor between ${\mathbf{S}}_{Z_L}$ and ${\mathbf{CS}}_L$.

However, it should be pointed out that for a $Z_L$-continuous mapping f the lifted mapping $Z_{L}f$ need not be $Z_L$-continuous. See the following example:

Example 4.

Define a standard L-completion $Z_L$ by

$$Z_{L}X=\left\{\begin{array}{cc}D{M}_{L}X\hfill & (X,{\le }_e)isafourelementsBooleanlattice\hfill \\ D{M}_{L}X\bigcup \left\{0_X\right\}\hfill & otherwise.\hfill \end{array}\right.$$

Let $X=\{x_1,x_2\}$, $Y=\{y_1,y_2\}$ and $L=\{0,1\}$, define $e_X:X\times X⟶L$, $e_Y:Y\times Y⟶L$, ${·}_X:X\times X⟶X$ and ${·}_Y:Y\times Y⟶Y$ as follows, respectively:

$$\begin{array}{ccc}\hfill & & \\ \hfill e_X& x_1& x_2\hfill \\ \hfill x_1& 1& 0\hfill \\ \hfill x_2& 0& 1\hfill \\ \hfill \end{array},\begin{array}{ccc}\hfill & & \\ \hfill e_Y& y_1& y_2\hfill \\ \hfill y_1& 1& 1\hfill \\ \hfill y_2& 0& 1\hfill \\ \hfill \end{array},\begin{array}{ccc}\hfill & & \\ \hfill {·}_X& x_1& x_2\hfill \\ \hfill x_1& x_1& x_2\hfill \\ \hfill x_2& x_2& x_2\hfill \\ \hfill \end{array},\begin{array}{ccc}\hfill & & \\ \hfill {·}_Y& y_1& y_2\hfill \\ \hfill y_1& y_1& y_2\hfill \\ \hfill y_2& y_2& y_2\hfill \\ \hfill \end{array}.$$

Then $L^X=\{A_1,A_2,A_3,A_4\},L^Y=\{B_1,B_2,B_3,B_4\}$, where $A_1=(1,0),A_2=(0,1),A_3=(1,1),A_4=(0,0)=0_X,B_1=(1,0),B_2=(0,1),B_3=(1,1),B_4=(0,0)=0_Y$. It is easy to check that $Z_{L}X=L^X$ and $Z_{L}Y=\{B_1,B_3,B_4\}$. By simple calculations, $(X,{·}_X,e_X)$ and $(Y,{·}_Y,e_Y)$ are $Z_L$-semigroups. Moreover, $(Z_{L}X,{\le }_{su{b}_X})$ is a four element Boolean lattice and $(Z_{L}Y,{\le }_{su{b}_Y})$ is a three element Boolean lattice and so $Z_L{Z}_{L}X=D{M}_L{Z}_{L}X$ and $Z_L{Z}_{L}Y=D{M}_L{Z}_{L}Y\bigcup \left\{0_{Z_{L}Y}\right\}$. Now, a mapping $f:X⟶Y$ is defined by $f\left(x_1\right)=y_2,f\left(x_2\right)=y_1$, then f is obviously $Z_L$-continuous and $Z_{L}f$ is residuated. Note that $0_{Z_{L}Y}\in Z_L{Z}_{L}Y$, while ${\left(Z_{L}f\right)}^{\leftarrow }\left(0_{Z_{L}Y}\right)=0_{Z_{L}X}\notin Z_L{Z}_{L}X$

Example 4 implies that the functor $Z_L$ does not necessarily induce an endofunctor of ${\mathbf{S}}_{Z_L}$.

Lemma 4

([41]). Let the category $\mathcal{C}$ be the full subcategory of the category $\mathcal{D}$ and $\mathcal{C}$ the reflective subcategory of $\mathcal{D}$, then the inclusion functor $I:\mathcal{C}⟶\mathcal{D}$ is monadic.

Proposition 7.

(1) 

Every CS${}_L$-morphism $f:X⟶Y$ satisfies the following commutative diagram:

where ${ϵ}_X:Z_{L}X⟶X$ is defined by ${ϵ}_X\left(A\right)=\bigsqcup A$ for all $A\in Z_{L}X$.

(2) 

${\mathbf{CS}}_L$ is the full subcategory of the category L-OSG${}_R$ of L-OSs and residuated semigroup homomorphisms.

(3) 

${\mathbf{CS}}_L$ is the reflective subcategory of L-OSG${}_R$; moreover, the inclusion functor I from ${\mathbf{CS}}_L$ to L-OSG${}_R$ is monadic.

Proof. 

(1) Let $f:X⟶Y$ be a ${\mathbf{CS}}_L$-morphism and $A\in Z_{L}X$, then $f(\bigsqcup A)=\bigsqcup f^{\to }\left(A\right)$ and so

$$\begin{array}{cc}\hfill (f\circ {ϵ}_X)\left(A\right)& =f(\bigsqcup A)=\bigsqcup f^{\to }\left(A\right)=\bigsqcup C\left(f^{\to }\left(A\right)\right)\left(byproofofLemma3\right)\hfill \\ & ={ϵ}_Y\left(C\left(f^{\to }\left(A\right)\right)\right)={ϵ}_Y\left(Z_{L}f\left(A\right)\right)=({ϵ}_Y\circ Z_{L}f)\left(A\right).\hfill \end{array}$$

(2) Clearly, Obj(${\mathbf{CS}}_L$)⊆Obj(L-OSG${}_R$). Moreover, for any $(X,e_X),(Y,e_Y)\in$Obj(${\mathbf{CS}}_L$), $f:X⟶Y\in$Hom(L-OSG${}_R$) iff $f\in$Hom(${\mathbf{CS}}_L$) by Theorem 1. Therefore, ${\mathbf{CS}}_L$ is the full subcategory of L-OSG${}_R$.

(3) By Definition 4.16 of reflective subcategory in [42] and Theorem 2, ${\mathbf{CS}}_L$ is the reflective subcategory of L-OSG${}_R$ and so the inclusion functor I from ${\mathbf{CS}}_L$ to L-OSG${}_R$ is monadic by Lemma 4. □

Remark 4.

Obviously, L-OSG${}_R$ is a subcategory of L-OSG as Obj(L-OSG ${}_R$)=Obj(L-OSG) and Hom(L-OSG ${}_R$)⊆ Hom(L-OSG). Then we have that ${\mathbf{CS}}_L$ is also a reflective subcategory of L-OSG. This is just Proposition 6.19 in [31].

Theorem 3.

For any standard L-completion $Z_L$, if every $Z_L$-arrow into a complete L-OS is $Z_L$-continuous, then ${\mathbf{CS}}_L$ is a reflective subcategory of ${\mathbf{S}}_{Z_L}$ with reflection mappings ${\eta }_X$. In this case, the inclusion functor $I:{\mathbf{CS}}_L⟶{\mathbf{S}}_{Z_L}$ is the right adjoint of the functor $Z_L:{\mathbf{S}}_{Z_L}⟶{\mathbf{CS}}_L$ defined by $Z_L\left((X,·,e)\right)=(Z_{L}X,\odot ,sub)$ for any $(X,·,e)\in$Obj$\left({\mathbf{S}}_{Z_L}\right)$ and $Z_L\left(f\right)=Z_{L}f$ for any $f\in$Hom$\left({\mathbf{S}}_{Z_L}\right)$.

Proof. 

Hypothesis and Corollary 2 ensure that ${\mathbf{CS}}_L$ is a reflective subcategory of ${\mathbf{S}}_{Z_L}$ with reflection mappings ${\eta }_X$. □

By Proposition 4 and Theorem 3, for every compositive standard L-completion $Z_L$, ${\mathbf{CS}}_L$ is a reflective subcategory of ${\mathbf{S}}_{Z_L}$, but not vice versa. See the following:

Proposition 8.

Let $Z_L$ be an arbitrary standard L-completion such that $Z_{L}Y=D{M}_{L}Y$ for every complete L-OS $(Y,{·}_Y,e_Y)$. Then ${\mathbf{CS}}_L$ is a reflective subcategory of ${\mathbf{S}}_{Z_L}$. However, if $0_X\in Z_{L}X$ for at least one $Z_L$-semigroup $(X,{·}_X,e_X)$ possessing a least element 0 (i.e., $e_X(0,x)=1,\forall x\in X$) then $Z_L$ is not compositive.

Proof. 

Notice that for a complete L-OS $(Y,{·}_Y,e_Y)$, ${\eta }_Y:Y⟶Z_{L}Y=D{M}_{L}Y$ is $Z_L$-continuous, i.e., $\bigsqcup (\bigcup \mathcal{A})\in D{M}_{L}Y$ for any $\mathcal{A}\in D{M}_{L}D{M}_{L}Y$. In fact, $\forall y\in Y$,

$$\begin{array}{cc}\hfill C(\bigsqcup (\bigcup \mathcal{A}\left)\right)\left(y\right)& =\underset{A\in D{M}_{L}X}{\bigwedge }sub(\bigsqcup (\bigcup \mathcal{A}),A)\to A\left(y\right)\hfill \\ & =\underset{A\in D{M}_{L}X}{\bigwedge }(\underset{A^{\prime }\in D{M}_{L}X}{\bigwedge }\mathcal{A}\left(A^{\prime }\right)\to sub(A^{\prime },A))\to sub({\iota }_y,A)\hfill \\ & ={\mathcal{A}}^{\delta }\left({\iota }_y\right)=\mathcal{A}\left({\iota }_y\right)=\underset{A\in D{M}_{L}X}{\bigvee }\mathcal{A}\left(A\right)\ast sub({\iota }_y,A)\hfill \\ & =\underset{A\in D{M}_{L}X}{\bigvee }\mathcal{A}\left(A\right)\ast A\left(y\right)=\bigsqcup (\bigcup \mathcal{A})\left(y\right).\hfill \end{array}$$

Then for every $Z_L$-arrow f into a complete L-OS $(Y,{·}_Y,e_Y)$, ${\eta }_Y\circ f$ is weakly $Z_L$-continuous and so f is $Z_L$-continuous by Lemma 1 (2). Therefore, ${\mathbf{CS}}_L$ is a reflective subcategory of ${\mathbf{S}}_{Z_L}$. However, if $(X,{·}_X,e_X)$ has a least element 0 and $0_X\in Z_{L}X$ then the inclusion mapping $i:\left\{0\right\}⟶X$ is weakly $Z_L$-continuous but not $Z_L$-continuous since $i^{\leftarrow }\left(0_X\right)=0_{\left\{0\right\}}\notin Z_L\left\{0\right\}$. □

Lemma 5.

Let $f:X⟶Y$ be a weakly $Z_L$-continuous L-OS embedding between an L-OS $(X,{·}_X,e_X)$ and a complete residuated L-OS $(Y,{·}_Y,e_Y)$. Then the following three conditions are equivalent:

(1) 

f is join-dense;

(2) 

$\breve{f}:Z_{L}Y⟶Y,B\mapsto \bigsqcup f^{\to }\left(B\right)$ is surjective;

(3) 

There is a (unique) surjective ${\mathbf{CS}}_L$-morphism $g:Z_{L}X⟶Y$ with $f=g\circ {\eta }_X$.

Proof. 

(1)⇒(2): For any $y\in Y$, we have $B=f^{\leftarrow }\left({\iota }_y\right)\in Z_{L}Y$ and so $y=\bigsqcup f^{\to }\left(f^{\leftarrow }\left({\iota }_y\right)\right)=\breve{f}\left(B\right)$. Hence $\breve{f}$ is surjective.

(2)⇒(3): Obviously.

(3)⇒(1): For any $y\in Y$, there is $A\in Z_{L}X$ with $y=g\left(A\right)=g(\bigsqcup {\eta }_X^{\to }\left(A\right))=\bigsqcup g^{\to }\left({\eta }_X^{\to }\left(A\right)\right)=\bigsqcup {(g\circ {\eta }_X)}^{\to }\left(A\right))=\bigsqcup f^{\to }\left(A\right)$. Let $B\left(y\right)=f^{\to }\left(A\right)\left(y\right),\forall y\in f\left(X\right)$, then $B\in L^{f\left(X\right)}$ and $i^{\to }\left(B\right)\left(y^{\prime }\right)=f^{\to }\left(A\right)\left(y^{\prime }\right),\forall y^{\prime }\in Y$. Hence $y=\bigsqcup i^{\to }\left(B\right)$. This means that f is join-dense. □

The category ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$ of weakly $Z_L$-continuous L-OS embeddings of $Z_L$-semigroups is defined as follows: The objects of ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$ are weakly $Z_L$-continuous L-OS embeddings of $Z_L$-semigroups into complete residuated L-OSs and the morphisms of ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$ are join-preserving semigroup homomorphisms between two weakly $Z_L$-continuous L-OS embeddings, that is, a morphism between two weakly $Z_L$-continuous L-OS embeddings $f:X⟶Y$ and $f^{\prime }:X^{\prime }⟶Y^{\prime }$ is a join-preserving semigroup homomorphism $h:Y⟶Y^{\prime }$ such that there is a $Z_L$-continuous mapping $h_0:X⟶X^{\prime }$ satisfying $h\circ f=f^{\prime }\circ h_0$. The objects of a full subcategory ${\mathbf{S}}_{Z_L}^{\to }\mathbf{C}$ of ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$ are the weakly $Z_L$-continuous and join-dense L-OS embeddings. Then for an arbitrary standard L-completion $Z_L$, we can define a functor $\overleftarrow{\mathbb{P}}:{\mathbf{S}}_{Z_L}^{\to }\mathbf{E}⟶{\mathbf{S}}_{Z_L}$ with $\overleftarrow{\mathbb{P}}f=$ domain of f for a ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$-object f and $\overleftarrow{\mathbb{P}}h=h_0$ for a ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$-morphism h.

Theorem 4.

Let $Z_L$ be an arbitrary standard L-completion.

(1) 

$\overleftarrow{\mathbb{P}}$ has a left adjoint $\overrightarrow{Z_L}:{\mathbf{S}}_{Z_L}⟶{\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$ with $\overrightarrow{Z_L}X={\eta }_X$ for a ${\mathbf{S}}_{Z_L}$-object X and $\overrightarrow{Z_L}f=Z_{L}f$ for a ${\mathbf{S}}_{Z_L}$-morphism f.

(2) 

$\overleftarrow{\mathbb{P}}$ restricts to a forgetful (i.e., faithful) functor from ${\mathbf{S}}_{Z_L}^{\to }\mathbf{C}$ to ${\mathbf{S}}_{Z_L}$ which is a right adjoint to the corestriction of the functor $\overrightarrow{Z_L}$ to ${\mathbf{S}}_{Z_L}^{\to }\mathbf{C}$.

(3) 

In each of these adjunctions, the counit ϵ is given by ${ϵ}_f:Z_{L}X⟶Y,Y\mapsto \bigsqcup f^{\to }\left(A\right)$ for all weakly $Z_L$-continuous L-OS embeddings $f:X⟶Y$.

Proof. 

Let $f:X⟶X^{\prime }$ be a ${\mathbf{S}}_{Z_L}$-morphism and $g:X^{\prime }⟶Y^{\prime }$ a weakly $Z_L$-continuous L-OS embedding. Then $g\circ f$ is weakly $Z_L$-continuous, and the mapping $\breve{(g\circ f)}$ is the unique ${\mathbf{S}}_{Z_L}^{\to }\mathbf{E}$-morphism $h:{\eta }_X⟶g$ with $h_0=f$ by Proposition 6. This means that the functor $\overleftarrow{\mathbb{P}}$ has a left adjoint $\overrightarrow{Z_L}$. Therefore, (1) holds and thus (2) and (3) hold. □

6. Conclusions

In order to provide a common completion pattern for L-OSs, we introduced the notion of standard L-completion $Z_L$ as a generalization of various completions, such as the Dedekind–MacNeille completion, the Alexandroff completion, ect. For L-OSs, the basic notions about (weakly) $Z_L$-continuous mappings arose naturally. In addition, we built $Z_L$-semigroups and their $Z_L$-completion with the universal property. We also present the categorical characterization of $Z_L$-completion under different cases of $Z_L$. The work is an extension of the crisp case and an attempt to further study asymmetric fuzzy algebraic structures.