Approximating Fixed Points of Relatively Nonexpansive Mappings via Thakur Iteration

Abstract

The study of symmetry is a major tool in the nonlinear analysis. The symmetricity of distance function in a metric space plays important role in proving the existence of a fixed point for a self mapping. In this work, we approximate a fixed point of noncyclic relatively nonexpansive mappings by using a three-step Thakur iterative scheme in uniformly convex Banach spaces. We also provide a numerical example where the Thakur iterative scheme is faster than some well known iterative schemes such as Picard, Mann, and Ishikawa iteration. Finally, we provide a stronger version of our proposed theorem via von Neumann sequences.

1. Introduction

Approximating fixed points for different kinds of mappings is an important tool to solve many problems in the theory of nonlinear analysis. In this view, Picard iteration is an important starting point for the development of other new iterative schemes. However, Picard iteration does not converge to a fixed point for a large class of mappings, for example, the class of nonexpansive mappings. This was proved by Krasnoselskii [1]. Let K be a nonempty subset of a Banach space X. The map F:K → K is nonexpansive if $\Vert Fw-Fz\Vert \le \Vert w-z\Vert$ for all $w,z\in K$. In 1967, Browder [2] introduced the iterative process to fixed points of nonexpansive self maps on closed and convex subsets of a Hilbert space. Mann [3] constructed the iterative process to approximate the fixed points of a nonexpansive mapping, it is defined by the following method: for a starting point $w_0\in K,$

$$w_{n+1}=(1-{\eta }_n)w_n+{\eta }_{n}F{w}_n,$$

(1)

where $\left\{{\eta }_n\right\}$ is a sequence in $[0,1].$

Later, the Ishikawa [4] iteration is a two step iterative process that helps to approximate fixed points of nonexpansive mappings; for a starting point $w_0\in K,$ this iterative scheme is defined by:

$$\left\{\begin{array}{c}{w}_{n+1}=(1-{\eta }_n)w_n+{\eta }_{n}F{u}_n,\hfill \\ u_n=(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n,\hfill \end{array}\right.$$

(2)

where $\left\{{\eta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $[0,1].$

Agarwal et al. [5] introduced a two step iterative process in 2007: for an arbitrary $w_0\in K,$ define:

$$\left\{\begin{array}{c}{w}_{n+1}=(1-{\eta }_n)F{w}_n+{\eta }_{n}F{u}_n,\hfill \\ u_n=(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n,\hfill \end{array}\right.$$

(3)

where $\left\{{\eta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $[0,1].$

In 2000, Noor [6] introduced the following iteration scheme: starting with $w_0\in K,$ define $\left\{w_n\right\}$ iteratively by:

$$\left\{\begin{array}{c}{w}_{n+1}=(1-{\eta }_n)w_n+{\eta }_{n}F{v}_n,\hfill \\ v_n=(1-{\delta }_n)w_n+{\delta }_{n}F{u}_n,\hfill \\ u_n=(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n,\hfill \end{array}\right.$$

(4)

where $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $[0,1].$

In the sequel, we will consider the following iterative process defined by Thakur et al. in [7]: for an arbitrary chosen element $w_0\in K,$ the sequence $\left\{w_n\right\}$ is generated by:

$$\left\{\begin{array}{c}{w}_{n+1}=(1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n,\hfill \\ v_n=(1-{\delta }_n)u_n+{\delta }_{n}F{u}_n,\hfill \\ u_n=(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n,\hfill \end{array}\right.$$

(5)

where $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are sequences in $[0,1]$ satisfying one of the following conditions:

(Q)

$0<ϵ\le {\eta }_n\le 1,0<ϵ\le {\delta }_n(1-{\delta }_n)$ and ${\gamma }_n\to 0$ as $n\to \infty$,

(R)

$0<ϵ\le {\gamma }_n(1-{\gamma }_n).$

Recently, Anthony Eldred et al. [8] approximated fixed points in uniformly convex Banach space using the Mann iterative process $w_{n+1}=(1-{\eta }_n)w_n+{\eta }_{n}F{w}_n,{\eta }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ to a relatively nonexpansive map of the type $F:M\cup N\to M\cup N,$ which satisfies $\left(i\right)F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N$ and $\left(ii\right)∥Fw-Fz∥\le ∥w-z∥,\forall w\in M,z\in N.$ One can note that relatively nonexpansive mappings need not be continuous in general. Gopi et al. [9] also approximated the common fixed point via Ishikawa iterative process. Pragadeeswarar et al. [10] approximated the common best proximity point for a pair of mean nonexpansive mappings. In 2020, Gabeleh et al. [11] introduced a geometric notion of proximal Opial’s condition on a nonempty, closed and convex pair of subsets of strictly convex Banach spaces and proved the strong and weak convergence of the Ishikawa iterative scheme for noncyclic relatively nonexpansive mappings in uniformly convex Banach spaces.

In 2019, Gabriela et al. [12] proved the convergence of Thakur et al.’s iteration method for Suzuki-type nonexpansive mappings. This class of mappings properly contains the class of nonexpansive mappings. At this moment, it is natural to think that one can approximate a fixed point for relatively nonexpansive mappings using the Thakur iterative process.

Motivated by the work of Gabeleh et al. and Gabriela et al., we approximate a fixed point for noncyclic relatively nonexpansive mappings in uniformly convex Banach space through the Thakur iterative process. We also provide a strong convergence result of the Thakur iterative process and we compare the Thakur iterative process to some well known iterations. Finally, we propose a numerical example to show that the Thakur iterative process converges more effectively than the Picard iterative process, Mann iterative process and Ishikawa iterative process.

2. Preliminaries

Let M and N be nonempty subsets of a Banach space X. The following notations are used subsequently:

$$\begin{array}{ccc}& & d(w,N)=inf\{∥w-z∥:z\in N\};\hfill \\ & & d(M,N)=inf\{∥w-z∥:w\in M,z\in N\};\hfill \\ & & P_M\left(w\right)=\{z\in M:∥w-z∥=d(w,M)\};\hfill \\ & & M_0=\{w\in M:∥w-z^{\prime }∥=d(M,N)\mathrm{for}\mathrm{some}{z}^{\prime }\in N\};\hfill \\ & & N_0=\{z\in N:∥w^{\prime }-z∥=d(M,N)\mathrm{for}\mathrm{some}{w}^{\prime }\in M\}.\hfill \end{array}$$

If M is a convex, closed subset of a reflexive and strictly convex space, then $P_M\left(w\right)$ contains one element and if M and N are convex, closed subsets of a reflexive space, with either M or N being bounded, then $M_0\ne Ø.$ It can be pointed out that the relevance of the subsequent study to symmetry is obvious since distances between points and between sets are symmetry. For instance, in the above equations, $d(M,N)=d(N,M)$ is a symmetry property for the distance between the sets M and N.

The following definitions and theorems are very useful to our results:

Definition 1.

Let M and N be nonempty subsets of a metric space $(X,d)$. An element $w\in M$ is said to be a best proximity point of the nonself-mapping $F:M\to N$ if it satisfies the condition that:

$$\begin{array}{c}\hfill d(w,Fw)=d(M,N).\end{array}$$

Definition 2.

Let M and N be nonempty subsets of a Banach space X. A mapping $F:M\cup N\to M\cup N$ is relatively nonexpansive if:

$$\begin{array}{c}\hfill ∥Fw-Fz∥\le ∥w-z∥,forallw\in M,z\in N.\end{array}$$

Theorem 1

([13]). Let M and N be nonempty closed bounded convex subsets of a uniformly convex Banach space. Let $F:M\cup N\to M\cup N$ satisfy:

1. 

$F\left(M\right)\subseteq N$ and $F\left(N\right)\subseteq M;$ and

2. 

$∥Fw-Fz∥\le ∥w-z∥$ for $w\in M,z\in N.$

Then there exist $(w,z)\in M\times N$ such that $∥w-Fw∥=∥z-Fz∥=d(M,N).$

Theorem 2

([13]). Let M and N be nonempty closed bounded convex subsets of a uniformly convex Banach space. Let $F:M\cup N\to M\cup N$ satisfy:

1. 

$F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N;$ and

2. 

$∥Fw-Fz∥\le ∥w-z∥$ for $w\in M,z\in N.$

Then there exist $w_0\in M$ and $z_0\in N$ such that $F{w}_0=w_0,F{z}_0=z_0,$ and $∥w_0-z_0∥=d(M,N).$

Theorem 3

([14]). Let X be a uniformly convex Banach space, and F be a nonexpansive mapping of the closed convex bounded subset K of X into K. Then F has a fixed point in K.

Proposition 1

([15]). If X is a uniformly convex space and $\eta \in (0,1)$ and $ϵ>0,$ then for any $d>0,$ if $w,z\in X$ are such that $∥w∥\le d,∥z∥\le d,∥w-z∥\ge ϵ,$ then there exists $\delta =\delta \left(\frac{ϵ}{d}\right)>0$ such that $∥\eta w+(1-\eta )z∥\le \left(1-2\delta \left(\frac{ϵ}{d}\right)min(\eta ,1-\eta )\right)d.$

Definition 3

([16]). Let C be a nonempty subset of a Banach space X and T be a selfmap on C. T is said to satisfy condition $\left(C\right)$ if $\parallel Tx-Ty\parallel \le \parallel x-y\parallel ,$ whenever $\frac{1}{2}\parallel x-Tx\parallel \le \parallel x-y\parallel$ for all $x,y\in C$. Such mappings are often called generalized nonexpansive mappings or Suzuki mappings.

Theorem 4

([12]). Let C be a nonempty, closed and convex subset of a uniformly convex Banach space $X$, and let $T:C\to C$ be a mapping satisfying condition (C). For an arbitrarily chosen $x_0\in C$, let the sequence $\left\{x_n\right\}$ be generated by (1) for all $n\ge 0,$ where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\}\in (0,1),\left\{{\gamma }_n\right\}$ bounded away from 0 and 1. Then $F\left(T\right)=\{x\in C:T(x)=x\}\ne Ø$ if and only if $\left\{x_n\right\}$ is bounded and ${lim}_{n\to \infty }\parallel T{x}_n-x_n\parallel =0$.

Theorem 5

([12]). Let C be a nonempty, compact and convex subset of a uniformly convex Banach space X and let T and $\left\{x_n\right\}$ be as in Theorem 4. Then $\left\{x_n\right\}$ converges strongly to a fixed point of $T$.

Let M be a convex closed subset of a Hilbert Space X. Then for $w\in X,$ we know that $P_M\left(w\right)$ is the nearest to w and unique point of M. $P_M$ is nonexpansive and distinguished by the Kolmogorov’s criterion:

• $〈w-P_{M}w,P_{M}w-a〉\ge 0,$ for all $w\in X$ and $a\in M.$

Let M and N be two convex closed subsets of $X.$ Define:

$$\begin{array}{c}\hfill P\left(w\right)=P_M\left(P_N\left(w\right)\right)\mathrm{for}\mathrm{each}w\in X.\end{array}$$

Then, $\left\{P^n\left(w\right)\right\}\subset M$ and $\left\{P_N\left(P^n\left(w\right)\right)\right\}\subset N.$ When M and N are closed, the convergence of these sequences in norm were proved by von Neumann [17]. The sequences $\left\{P^n\left(w\right)\right\}$ and $\left\{P_N\left(P^n\left(w\right)\right)\right\}$ are called von Neumann sequences or the alternating projection algorithm for two sets.

Theorem 6

([8]). Let M and N be nonempty bounded closed convex subsets of a uniformly convex Banach space and suppose that $F:M\cup N\to M\cup N$ satisfies:

1. 

$F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N;$ and

2. 

$\Vert Fw-Fz\Vert \le \Vert w-z\Vert$ for $w\in M,z\in N.$

Let $w_0\in M,$ and define $w_{n+1}=P^n\left((1-{\eta }_n)w_n+{\eta }_{n}F{w}_n\right),{\eta }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ and $n=0,1,2,\dots$ Then $li{m}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0.$ Moreover, if $F\left(M\right)$ lies in a compact set, then $\left\{w_n\right\}$ converges to a fixed point of F.

Definition 4

([18]). Let M and N be nonempty closed convex subsets of a Hilbert space X. We say that $(M,N)$ is boundedly regular if for each bounded subset S of X and for each $ϵ>0$ there exists $\delta >0$ such that:

$$\begin{array}{c}\hfill max\left\{d\right(w,M),d(w,N-v\left)\right\}\le \delta \Rightarrow d(w,N)\le ϵ,\forall w\in X,\end{array}$$

(6)

where $v=P_{\overline{N-M}}\left(0\right)$ is the displacement vector from M to N. $(v$ is the unique vector satisfying $\Vert v\Vert =d(M,N))$.

Theorem 7

([18]). If $(M,N)$ is boundedly regular, then the von Neumann sequences converges in norm.

Theorem 8

([18]). If M or N is boundedly compact, then $(M,N)$ is boundedly regular.

Lemma 1

([19]). Let M be a nonempty closed and convex subset and N be a nonempty closed subset of a uniformly convex Banach space. Let $\left\{w_n\right\}$ and $\left\{a_n\right\}$ be sequences in M and $\left\{z_n\right\}$ be a sequence in N satisfying:

1. 

$\Vert w_n-z_n\Vert \to d(M,N),$

2. 

$\Vert a_n-z_n\Vert \to d(M,N).$

Then $\Vert w_n-a_n\Vert$ converges to zero.

Corollary 1

([19]). Let M be a nonempty closed convex subset and N be a nonempty closed subset of uniformly convex Banach space. Let $\left\{w_n\right\}$ be a sequence in M and $z_0\in N$ such that $\Vert w_n-z_0\Vert \to d(M,N).$ Then $\left\{w_n\right\}$ converges to $P_M\left(z_0\right).$

Proposition 2

([13]). Let M and N be two closed and convex subsets of a Hilbert space X. Then $P_N\left(M\right)\subseteq N,P_M\left(N\right)\subseteq M$, and $\Vert P_{N}w-P_{M}z\Vert \le \Vert w-z\Vert$ for $w\in M$ and $z\in N$.

Lemma 2

([8]). Let M and N be two closed and convex subsets of a Hilbert space X. For each $w\in X,$

$$\begin{array}{c}\hfill \Vert P^{n+1}\left(w\right)-a\Vert \le \Vert P^n\left(w\right)-a\Vert , foreacha\in M_0\cup N_0.\end{array}$$

Lemma 3

([20]). Let $(M,N)$ be a nonempty, bounded, closed and convex pair in a reflexive and strictly convex Banach space X. Define $\mathcal{P}:M_0\cup N_0\to M_0\cup N_0$ as:

$$\begin{array}{c}\hfill \mathcal{P}\left(x\right)=\left\{\begin{array}{c}{\mathcal{P}}_{M_0}\left(x\right)ifx\in N_0,\hfill \\ {\mathcal{P}}_{N_0}\left(x\right)ifx\in M_0.\hfill \end{array}\right.\end{array}$$

(7)

Then the following statements hold.

1. 

$\parallel x-\mathcal{P}x\parallel =d(M,N)$ for any $x\in M_0\cup N_0$ and $\mathcal{P}\left(M_0\right)\subseteq N_0,\mathcal{P}\left(N_0\right)\subseteq M_0.$

2. 

$\mathcal{P}$ is an isometry, that is, $\parallel \mathcal{P}x-\mathcal{P}y\parallel =\parallel x-y\parallel$ for all $(x,y)\in M_0\times N_0.$

3. 

$\mathcal{P}$ is affine.

Definition 5

([21]). If $M_0\ne Ø$ then the pair $(M,N)$ is said to have P-property if for any $u_1,u_2\in M_0$ and $v_1,v_2\in N_0$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}d(u_1,v_1)=d(M,N)\hfill \\ d(u_2,v_2)=d(M,N)\hfill \end{array}\right.\Rightarrow d(u_1,u_2)=d(v_1,v_2).\end{array}$$

Lemma 4

([22]). Every, nonempty, bounded, closed and convex pair in a uniformly convex Banach space X has the P-property.

Lemma 5

([23]). Let $(M,N)$ be a nonempty, closed and convex pair in a uniformly convex Banach space $X$. Then for the projection mapping $\mathcal{P}:M_0\cup N_0\to M_0\cup N_0$ defined in (7) we have both ${\mathcal{P}|}_{M_0}$ and ${\mathcal{P}|}_{N_0}$ are continuous. For more results on approximation for fixed points, one can refer [24,25,26,27,28,29,30,31,32].

3. Main Results

Theorem 9.

Let M and N be nonempty bounded closed convex subsets of a uniformly convex Banach space and suppose that $F:M\cup N\to M\cup N$ satisfies:

1. 

$F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N;$ and

2. 

$\Vert Fw-Fz\Vert \le \Vert w-z\Vert$ for $w\in M,z\in N.$

For an arbitrary chosen $w_0\in M,$ let the sequence $\left\{w_n\right\}$ be generated by (5) where ${\eta }_n,{\delta }_n,{\gamma }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ and $n=0,1,2,\dots$ Suppose $d(w_n,M_0)\to 0,$ then $li{m}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0$. Moreover, if $F\left(M\right)$ lies in a compact set then $\left\{w_n\right\}$ converges to a fixed point of F.

Proof. 

If $d(M,N)=0,$ then $M_0=N_0=M\cap N$ and by Theorems 4 and 5 we can prove the result from the truth that $F:M\cap N\to M\cap N$ is nonexpansive. Therefore let us take that $d(M,N)>0.$ By Theorem 2, there exists $z\in N_0$ such that $Fz=z.$ Now, from (5), we have:

$$\begin{array}{ccc}\hfill \parallel u_n-z\parallel & =& \parallel (1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n-z\parallel \hfill \\ & =& \parallel (1-{\gamma }_n)(w_n-z)+{\gamma }_n(F{w}_n-z)\parallel \hfill \\ & \le & (1-{\gamma }_n)\parallel w_n-z\parallel +{\gamma }_n\parallel F{w}_n-z\parallel \hfill \\ & \le & (1-{\gamma }_n)\parallel w_n-z\parallel +{\gamma }_n\parallel w_n-z\parallel \hfill \\ & =& \parallel w_n-z\parallel .\hfill \end{array}$$

(8)

In the same way, we can obtain:

$$\begin{array}{ccc}\hfill \parallel v_n-z\parallel & =& \parallel (1-{\delta }_n)u_n+{\delta }_{n}F{u}_n-z\parallel \hfill \\ & =& \parallel (1-{\delta }_n)(u_n-z)+{\delta }_n(F{u}_n-z)\parallel \hfill \\ & \le & (1-{\delta }_n)\parallel u_n-z\parallel +{\delta }_n\parallel F{u}_n-z\parallel \hfill \\ & \le & (1-{\delta }_n)\parallel u_n-z\parallel +{\delta }_n\parallel u_n-z\parallel \hfill \\ & =& \parallel u_n-z\parallel .\hfill \end{array}$$

Now, using inequality (8), one gets:

$$\begin{array}{c}\hfill \parallel v_n-z\parallel \le \parallel w_n-z\parallel .\end{array}$$

(9)

Therefore, by (8) and (9), we obtain:

$$\begin{array}{ccc}\hfill \Vert w_{n+1}-z\Vert & =& \Vert (1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n-z\Vert \hfill \\ & =& \parallel (1-{\eta }_n)(F{u}_n-z)+{\eta }_n(F{v}_n-z)\parallel \hfill \\ & \le & (1-{\eta }_n)\parallel u_n-z\parallel +{\eta }_n\parallel v_n-z\parallel \hfill \\ & \le & (1-{\eta }_n)\parallel w_n-z\parallel +{\eta }_n\parallel w_n-z\parallel \hfill \\ & =& \parallel w_n-z\parallel .\hfill \end{array}$$

This implies that the sequence $\{\Vert w_n-z\Vert \}$ is non increasing. Then we can find $d>0$ such that ${lim}_{n\to \infty }\Vert w_n-z\Vert =d.$

Suppose there exists a subsequence $\left\{w_{n_k}\right\}$ of $\left\{w_n\right\}$ and an $ϵ>0$ such that $\Vert w_{n_k}-F{w}_{n_k}\Vert \ge ϵ>0$ for all k.

Since the modulus of convexity of $\delta$ of X is continuous and increasing function we choose $\xi >0$ as small that $\left(1-c\delta (\frac{ϵ}{d+\xi })\right)(d+\xi )<d,$ where $c>0.$

Now we choose k, such that $\Vert w_{n_k}-z\Vert \le d+\xi .$ Now we have:

$$\begin{array}{ccc}\hfill \Vert z-w_{n_k+1}\Vert & =& \Vert z-\left((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k}\right)\Vert \hfill \\ & =& \Vert (1-{\eta }_{n_k})z+{\eta }_{n_k}z-\left((1-{\eta }_{n_k})F\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)+{\eta }_{n_k}F{v}_{n_k}\right)\Vert \hfill \\ & \le & (1-{\eta }_{n_k})\Vert z-F\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)\Vert +{\eta }_{n_k}\Vert Fz-F{v}_{n_k}\Vert \hfill \\ & \le & (1-{\eta }_{n_k})\Vert z-\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)\Vert +{\eta }_{n_k}\Vert z-v_{n_k}\Vert .\hfill \end{array}$$

(10)

Now, by Proposition 1, we can obtain:

$$\begin{array}{ccc}\hfill \Vert z-\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)\Vert & =& \Vert (1-{\gamma }_{n_k})(z-w_{n_k})+{\gamma }_{n_k}(z-F{w}_{n_k})\Vert \hfill \\ & \le & \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi ).\hfill \end{array}$$

(11)

Additionally, using (11), we get:

$$\begin{array}{ccc}\hfill \Vert z-v_{n_k}\Vert & =& \Vert z-\left((1-{\delta }_{n_k})u_{n_k}+{\delta }_{n_k}F{u}_{n_k}\right)\Vert \hfill \\ & =& \Vert (1-{\delta }_{n_k})(z-u_{n_k})+{\delta }_{n_k}(z-F{u}_{n_k})\Vert \hfill \\ & \le & (1-{\delta }_{n_k})\Vert z-u_{n_k}\Vert +{\delta }_{n_k}\Vert z-F{u}_{n_k}\Vert \hfill \\ & \le & (1-{\delta }_{n_k})\Vert z-u_{n_k}\Vert +{\delta }_{n_k}\Vert z-u_{n_k}\Vert \hfill \\ & =& \Vert z-u_{n_k}\Vert \hfill \\ & \le & \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi ).\hfill \end{array}$$

Therefore, the Equation (10) becomes:

$$\begin{array}{ccc}\hfill \Vert z-w_{n_k+1}\Vert & \le & \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi ).\hfill \end{array}$$

Since there exists $l>0$ such that $2\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\ge l,$

$$\begin{array}{c}\hfill \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi )\le \left(1-l\delta \left(\frac{ϵ}{d+\xi }\right)\right)(d+\xi ).\end{array}$$

Suppose that we choose very small $\xi >0$, we have $\left(1-l\delta \left(\frac{ϵ}{d+\xi }\right)\right)(d+\xi )<d$, which is a contradiction. This implies that ${lim}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0.$ Since $F\left(M\right)$ is contained in a compact set, $\left\{F{w}_n\right\}$ has a subsequence $\left\{F{w}_{n_k}\right\}$ that converges to a point $a\in M.$ Also $\left\{w_{n_k}\right\}$ converges to a. Since $d(w_n,M_0)\to 0,$ there exists $\left\{a_n\right\}\subseteq M_0$ such that $\Vert w_n-a_n\Vert \to 0.$ Therefore, $a_{n_k}\to a,$ which gives that $a\in M_0.$

Let $D=d(M,N)$ and choose $b\in N_0$ such that $\Vert a-b\Vert =D$.

We have $\Vert w_{n_k}-b\Vert \to \Vert a-b\Vert =D$, and $\Vert w_{n_k}-b\Vert \ge \Vert F{w}_{n_k}-Fb\Vert \to \Vert a-Fb\Vert$. So $\Vert a-Fb\Vert =D$. By strict convexity of the norm, $Fb=b$. It follows that $Fa=a$.

Let $x\in M_0$. Then we have

$$\parallel Fx-F\mathcal{P}x\parallel \le \parallel x-\mathcal{P}x\parallel =d(M,N).$$

Therefore, $\parallel Fx-F\mathcal{P}x\parallel =d(M,N)=\parallel Fx-\mathcal{P}Fx\parallel$. By Lemma 4, we get $F\mathcal{P}x=\mathcal{P}Fx$. In particular, $F\mathcal{P}a=\mathcal{P}Fa$. So $F\left(\mathcal{P}a\right)=\mathcal{P}a.$ Since $\mathcal{P}a\in N_0$, we can obtain that ${lim}_{n\to \infty }\Vert w_n-\mathcal{P}a\Vert$ exists. Therefore,

$$\underset{n\to \infty }{lim}\parallel w_n-\mathcal{P}a\parallel =\underset{k\to \infty }{lim}\parallel w_{n_k}-\mathcal{P}a\parallel =\parallel a-\mathcal{P}a\parallel =d(M,N).$$

This implies $w_n\to a.$ □

Corollary 2.

Let M and N be nonempty bounded closed convex subsets of a uniformly convex Banach space and suppose that $F:M\cup N\to M\cup N$ satisfies:

1. 

$F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N;$ and

2. 

$\Vert Fw-Fz\Vert \le \Vert w-z\Vert$ for $w\in M,z\in N.$

For an arbitrary chosen $w_0\in M_0,$ let the sequence $\left\{w_n\right\}$ be generated by (5), where ${\eta }_n,{\delta }_n,{\gamma }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ and $n=0,1,2,\dots ,$ then $li{m}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0.$ Moreover, if $F\left(M\right)$ lies in a compact set then $\left\{w_n\right\}$ converges to a fixed point of F.

Corollary 3.

Let M and N be nonempty bounded closed convex subsets of a Hilbert space and let F be as in Theorem 2. Let $w_0\in M_0,$ and define $w_{n+1}=P^n\left((1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n\right),$ where $v_n=(1-{\delta }_n)u_n+{\delta }_{n}F{u}_n,u_n=(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n,{\eta }_n,{\delta }_n,{\gamma }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ and $n=0,1,2,\dots$ then $li{m}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0$. Moreover, if $F\left(M\right)$ is mapped into a compact subset of N then $\left\{w_n\right\}$ converges to a fixed point of F.

Proof. 

One can note that $P^n\left((1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n\right)=(1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n$. By Theorem 9, the result follows. □

Example 1.

Let $X={\mathbb{R}}^3,$

$$\begin{array}{c}\hfill M=\left\{\right(w,x,y):-4\le w\le -3,-1\le x\le 1,-1\le y\le 1\}and\\ \hfill N=\left\{\right(w,x,y):3\le w\le 4,-1\le x\le 1,-1\le y\le 1\}.\end{array}$$

Define

$$\begin{array}{c}\hfill F:M\to M\mathrm{by}F(w,x,y)=\left(\frac{w-3}{2},x,y\right),\\ \hfill F:N\to N\mathrm{by}F(w,x,y)=\left(\frac{w+3}{2},x,y\right).\end{array}$$

Let $(w,x,y)\in M,(w^{\prime },x,y)\in N$. Then,

$$\begin{array}{ccc}\hfill \Vert F(w,x,y)-F(w^{\prime },x,y)\Vert & =& \Vert \left(\frac{w-3}{2},x,y\right)-\left(\frac{w^{\prime }+3}{2},x,y\right)\Vert \hfill \\ & =& \Vert \left(\frac{w-w^{\prime }-6}{2},0,0\right)\Vert \hfill \\ & =& \sqrt{{\left(\frac{w-w^{\prime }-6}{2}\right)}^2+0}\hfill \\ & \le & \sqrt{{(w-w^{\prime })}^2}.\hfill \end{array}$$

Hence F is a relatively nonexpansive mapping.

Let $(w_0,x_0,y_0)=(-3.5,1,-1)$. First the Thakur et al. iteration method becomes with ${\eta }_n={\delta }_n={\gamma }_n=0.999$:

$$\begin{array}{ccc}\hfill (u_n,1,-1)& =& (1-0.999)(w_n,1,-1)+0.999\left(\frac{w_n-3}{2},1,-1\right)\hfill \\ & =& 0.001(w_n,1,-1)+(0.4995w_n-1.4985,0.999,-0.999)\hfill \\ & =& (0.5005w_n-1.4985,1,-1),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (v_n,1,-1)& =& 0.001(0.5005w_n-1.4985,1,-1)+0.999F(u_n,1,-1)\hfill \\ & =& (0.0005005w_n-0.0014985,0.001,0.001)+0.999F(u_n,1,-1).\hfill \end{array}$$

Now, we derive:

$$\begin{array}{ccc}\hfill F(u_n,1,-1)& =& \left(\frac{u_n-3}{2},1,-1\right)\hfill \\ & =& \left(\frac{0.5005w_n-1.4985-3}{2},1,-1\right)\hfill \\ & =& (0.25025w_n-2.24925,1,-1).\hfill \end{array}$$

So,

$$\begin{array}{ccc}\hfill (v_n,1,-1)& =& (0.0005005w_n-0.0014985,0.001,0.001)+0.999(0.25025w_n-2.24925,1,-1)\hfill \\ & =& (0.25050025w_n-2.24849925,1,-1)\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill F(v_n,1,-1)& =& \left(\frac{v_n-3}{2},1,-1\right)\hfill \\ & =& \left(\frac{0.25050025w_n-2.24849925-3}{2},1,-1\right)\hfill \\ & =& (0.125250125w_n-2.624249625,1,-1).\hfill \end{array}$$

Finally, we can obtain:

$$\begin{array}{ccc}\hfill (w_{n+1},1,-1)& =& (0.125375124875w_n-2.623874625375,1,-1).\hfill \end{array}$$

For the Ishikawa iteration, set $(w_{n+1},1,-1)=(1-{\eta }_n)(w_n,1,-1)+{\eta }_{n}F\left((1-{\delta }_n)(w_n,1,-1)+{\delta }_{n}F(w_n,1,-1)\right)$ with ${\eta }_n={\delta }_n=0.999$. We have $F(w,1,-1)=\left(\frac{w-3}{2},1,-1\right)$. Then,

$$\begin{array}{ccc}\hfill (w_{n+1},1,-1)& =& (1-0.999)(w_n,1,-1)+0.999F\left((1-0.999)(w_n,1,-1)+0.999\left(\frac{w_n-3}{2},1,-1\right)\right)\hfill \\ & =& 0.001(w_n,1,-1)+0.999F\left(0.001(w_n,1,-1)+(0.4995w_n-1.4985,0.999,0.999)\right)\hfill \\ & =& 0.001(w_n,1,-1)+0.999F(0.5005w_n-1.4985,1,-1)\hfill \\ & =& 0.001(w_n,1,-1)+0.999\left(\frac{0.5005w_n-1.4985-3}{2},1,-1\right)\hfill \\ & =& (0.001w_n,0.001,0.001)+(0.24999975w_n-2.24700075,0.999,0.999)\hfill \\ & =& (0.25099975w_n-2.24700075,1,-1).\hfill \end{array}$$

In Picard iteration we have $(w_{n+1},1,-1)=F(w_n,1,-1)=\left(\frac{w_n-3}{2},1,-1\right)$, and Mann with ${\eta }_n=0.999$ or Krasnoselskij iteration, we have:

$$\begin{array}{ccc}\hfill (w_{n+1},1,-1)& =& (1-{\eta }_n)(w_n,1,-1)+{\eta }_{n}F(w_n,1,-1)\hfill \\ & =& (1-0.999)(w_n,1,-1)+0.999\left(\frac{w_n-3}{2},1,-1\right)\hfill \\ & =& (0.001w_n,0.001,0.001)+(0.4995w_n-1.4985,0.999,0.999)\hfill \\ & =& (0.5005w_n-1.4985,1,-1).\hfill \end{array}$$

Using Matlab coding we give the comparison table for approaching a fixed point in these four iteration processes.

The

Table 1. Comparison result of Thakur et al.’s iteration method with Picard, Mann and Ishikawa iterations via Matlab coding.

n	Picard Iteration	Mann Iteration	Ishikawa Iteration	Thakur et al. Iteration Method
12	(−3.0001220703125,1,−1)	(−3.000123543239806,1,−1)	(−3.000000031264355,1,−1)	(−3.000000000007542,1,−1)
13	(−3.00006103515625,1,−1)	(−3.000061833391523,1,−1)	(−3.000000007847345,1,−1)	(−3.000000000000945,1,−1)
14	(−3.000030517578125,1,−1)	(−3.000030947612457,1,−1)	(−3.000000001969682,1,−1)	(−3.000000000000119,1,−1)
15	(−3.000015258789062,1,−1)	(−3.000015489280035,1,−1)	(−3.00000000049439,1,−1)	(−3.000000000000000,1,−1)
⋮	⋮	⋮	⋮	⋮
20	(−3.000000476837158,1,−1)	(−3.000000486465046,1,−1)	(−3.000000000000493,1,−1)
21	(−3.000000238418579,1,−1)	(−3.000000243475755,1,−1)	(−3.000000000000124,1,−1)
22	(−3.00000011920929,1,−1)	(−3.000000121859615,1,−1)	(−3.000000000000000,1,−1)
⋮	⋮	⋮	⋮	⋮
41	(−3.000000000000227,1,−1)	(−3.000000000000236,1,−1)
42	(−3.000000000000114,1,−1)	(−3.000000000000118,1,−1)
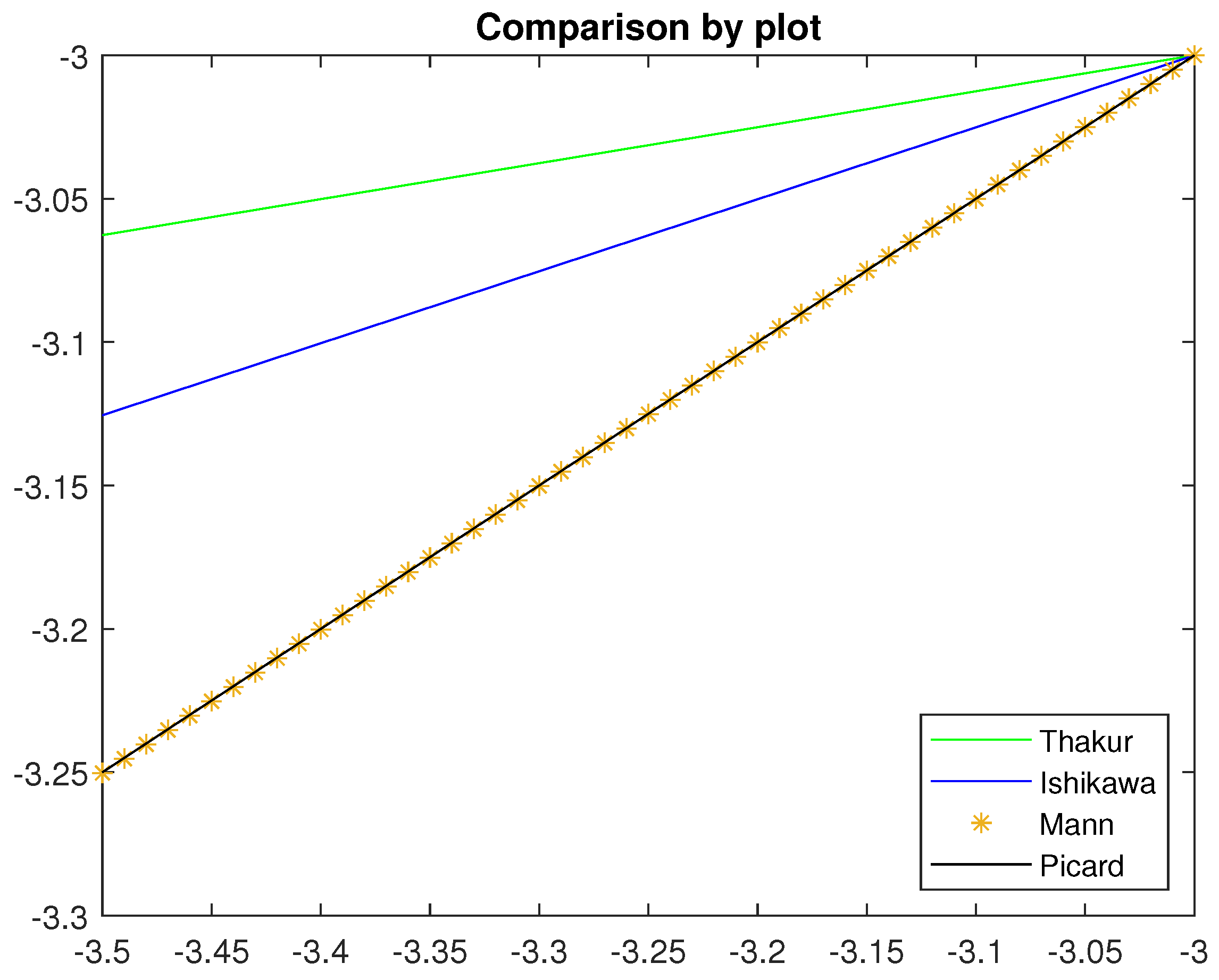
43	(−3.000000000000000,1,−1)	(−3.000000000000000,1,−1)

shows that the Thakur iteration attains the fixed point at the fifteenth iterative step. However, the other iterations take more than fifteen iterative steps to reach the fixed point. This reveals that the Thakur iteration is faster than the other iterative processes.

The Figure 1 shows a comparison of Thakur et al.’s iteration method with Picard, Mann and Ishikawa iterations by using the continuous data points from −3.5 to −3.

Now we relax the assumptions on constants $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\},\left\{{\gamma }_n\right\}$ and $d(w_n,M_0)\to 0$ in the above theorem and we prove the following theorem by using the conditions (Q) or (R) on constants $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\}$ and $\left\{{\gamma }_n\right\}.$

Lemma 6

([11]). A Banach space X is uniformly convex if and only if for each fixed number $r>0,$ there exists a continuous strictly increasing function $\varphi :[0,\infty )\to [0,\infty ),\varphi \left(t\right)=0$ iff $t=0,$ such that

$${\parallel \lambda x+(1-\lambda )y\parallel }^2\le {\lambda \parallel x\parallel }^2+{(1-\lambda )\parallel y\parallel }^2-\lambda (1-\lambda )\varphi (\parallel x-y\parallel ),$$

for all $\lambda \in [0,1]$ and all $x,y\in X$ such that $\parallel x\parallel \le r$ and $\parallel y\parallel \le r.$

Lemma 7

([11]). Consider a strictly increasing function $\varphi :[0,\infty )\to [0,\infty )$ with $\varphi \left(0\right)=0.$ If a sequence $\left\{r_n\right\}$ in $[0,\infty )$ satisfies ${lim}_{n\to \infty }\varphi \left(r_n\right)=0,$ then ${lim}_{n\to \infty }{r}_n=0.$

Lemma 8

([11]). Let $(A,B)$ be a nonempty and closed pair in a uniformly convex Banach space X such that A is convex. Let $\left\{x_n\right\}$ and $\left\{z_n\right\}$ be sequences in A and $\left\{y_n\right\}$ be a sequence in B such that ${lim}_{n\to \infty }\parallel x_n-y_n\parallel =d(A,B)$ and ${lim}_{n\to \infty }\parallel z_n-y_n\parallel =d(A,B);$ then we have ${lim}_{n\to \infty }\parallel x_n-z_n\parallel =0.$

Theorem 10.

Let M and N be nonempty bounded closed convex subsets of a uniformly convex Banach space and suppose that $F:M\cup N\to M\cup N$ satisfies:

1. 

$F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N;$ and

2. 

$\Vert Fw-Fz\Vert \le \Vert w-z\Vert$ for $w\in M,z\in N.$

For an arbitrarily chosen $w_0\in M_0,$ let the sequence $\left\{w_n\right\}$ be generated by (5) where $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\},\left\{{\gamma }_n\right\}$ satisfy either (Q) or (R) and $n=0,1,2,\dots$ Then $li{m}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0.$ Moreover, if $F\left(M\right)$ lies in a compact set then $\left\{w_n\right\}$ converges to a fixed point of F.

Proof. 

By Theorem 2, we can find $z\in N_0$ such that $Fz=z$. Then from Lemma 6 there exists a continuous strictly increasing function $\varphi :[0,\infty )\to [0,\infty )$ such that:

$$\begin{array}{ccc}\hfill \parallel w_{n+1}{-z\parallel }^2& =& \parallel (1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n{-z\parallel }^2\hfill \\ & =& \parallel {\eta }_n(F{v}_n-z)+(1-{\eta }_n)(F{u}_n-z){\parallel }^2\hfill \\ & \le & {\eta }_n\parallel F{v}_n{-z\parallel }^2+(1-{\eta }_n)\parallel F{u}_n{-z\parallel }^2-{\eta }_n(1-{\eta }_n)\varphi (\parallel F{v}_n-F{u}_n\parallel )\hfill \\ & \le & {\eta }_n\parallel v_n{-z\parallel }^2+(1-{\eta }_n){\parallel u_n-z\parallel }^2\hfill \\ & =& {\eta }_n\parallel (1-{\delta }_n)u_n+{\delta }_{n}F{u}_n{-z\parallel }^2+(1-{\eta }_n){\parallel (1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n-z\parallel }^2\hfill \\ & =& {\eta }_n{\parallel {\delta }_n(F{u}_n-z)+(1-{\delta }_n)(u_n-z)\parallel }^2\hfill \\ & & +(1-{\eta }_n){\parallel {\gamma }_n(F{w}_n-z)+(1-{\gamma }_n)(w_n-z)\parallel }^2\hfill \\ & \le & {\eta }_n{\delta }_n\parallel F{u}_n{-z\parallel }^2+{\eta }_n(1-{\delta }_n)\parallel u_n{-z\parallel }^2-{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )\hfill \\ & & +(1-{\eta }_n){\gamma }_n\parallel F{w}_n-z\parallel +(1-{\eta }_n)(1-{\gamma }_n){\parallel w_n-z\parallel }^2\hfill \\ & & -(1-{\eta }_n){\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & \le & {\eta }_n{\delta }_n\parallel u_n{-z\parallel }^2+{\eta }_n(1-{\delta }_n)\parallel u_n{-z\parallel }^2-{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )\hfill \\ & & +(1-{\eta }_n){\gamma }_n\parallel w_n-z\parallel +(1-{\eta }_n)(1-{\gamma }_n){\parallel w_n-z\parallel }^2\hfill \\ & & -(1-{\eta }_n){\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & \le & {\eta }_n\parallel u_n{-z\parallel }^2-{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )+(1-{\eta }_n){\parallel w_n-z\parallel }^2\hfill \\ & & -(1-{\eta }_n){\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & =& {\eta }_n\parallel (1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n{-z\parallel }^2-{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )\hfill \\ & & +(1-{\eta }_n)\parallel w_n{-z\parallel }^2-(1-{\eta }_n){\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & =& {\eta }_n\parallel {\gamma }_n(F{w}_n-z)+(1-{\gamma }_n)(w_n-z){\parallel }^2-{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )\hfill \\ & & +(1-{\eta }_n)\parallel w_n{-z\parallel }^2-(1-{\eta }_n){\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & \le & {\eta }_n{\gamma }_n\parallel F{w}_n-z\parallel +{\eta }_n(1-{\gamma }_n)\parallel w_n{-z\parallel }^2-{\eta }_n{\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & & -{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )+(1-{\eta }_n){\parallel w_n-z\parallel }^2\hfill \\ & & -(1-{\eta }_n){\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\hfill \\ & \le & \parallel w_n{-z\parallel }^2-{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )-{\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel ).\hfill \end{array}$$

Therefore, we can deduce the following inequalities:

$$\begin{array}{c}\hfill {\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )\le \parallel w_n{-z\parallel }^2-{\parallel w_{n+1}-z\parallel }^2,\end{array}$$

(12)

$$\begin{array}{c}\hfill {\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\le \parallel w_n{-z\parallel }^2-{\parallel w_{n+1}-z\parallel }^2.\end{array}$$

(13)

Now, we proceed the following two cases:

Case 1: 

Suppose that $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ satisfy (Q). From (12), we get

$$\sum _{n=1}^m{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )\le \parallel w_1{-z\parallel }^2-{\parallel w_{m+1}-z\parallel }^2.$$

As $m\to \infty$, we get ${\sum }_{n=1}^{\infty }{\eta }_n{\delta }_n(1-{\delta }_n)\varphi (\parallel F{u}_n-u_n\parallel )<\infty .$ Since ${\eta }_n{\delta }_n(1-{\delta }_n)\ge {ϵ}^2,$ implies $\varphi (\parallel F{u}_n-u_n\parallel )\to 0,$ so $\parallel F{u}_n-u_n\parallel \to 0.$ Since $\mathcal{P}$ is affine and isometry and $\mathcal{P}F=F\mathcal{P}$ on $M_0\cup N_0,$

$$\begin{array}{ccc}\hfill \parallel F{w}_n-\mathcal{P}{w}_n\parallel & \le & \parallel F{w}_n-\mathcal{P}F{u}_n\parallel +\parallel \mathcal{P}F{u}_n-\mathcal{P}{w}_n\parallel \hfill \\ & =& \parallel F{w}_n-F\mathcal{P}{u}_n\parallel +\parallel F{u}_n-w_n\parallel \hfill \\ & \le & \parallel w_n-\mathcal{P}{u}_n\parallel +\parallel F{u}_n-u_n\parallel +\parallel u_n-w_n\parallel \hfill \\ & =& \parallel w_n-\mathcal{P}{u}_n\parallel +\parallel F{u}_n-u_n\parallel +{\gamma }_n\parallel F{w}_n-w_n\parallel .\hfill \end{array}$$

(14)

Now,

$$\begin{array}{ccc}\hfill \parallel w_n-\mathcal{P}{u}_n\parallel & =& \parallel w_n-\mathcal{P}\{(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n\}\parallel \hfill \\ & =& \parallel w_n-\mathcal{P}{w}_n+{\gamma }_n(\mathcal{P}{w}_n-\mathcal{P}F{w}_n)\parallel \hfill \\ & \le & \parallel w_n-\mathcal{P}{w}_n\parallel +{\gamma }_n\parallel \mathcal{P}{w}_n-\mathcal{P}F{w}_n\parallel \hfill \\ & =& \parallel w_n-\mathcal{P}{w}_n\parallel +{\gamma }_n\parallel w_n-F{w}_n\parallel .\hfill \end{array}$$

Therefore, the inequality reduces to

$$\parallel F{w}_n-\mathcal{P}{w}_n\parallel \le \parallel w_n-\mathcal{P}{w}_n\parallel + {\gamma }_n\parallel w_n-F{w}_n\parallel + \parallel F{u}_n-u_n\parallel + {\gamma }_n\parallel F{w}_n-w_n\parallel .$$

Letting $n\to \infty ,$ we obtain ${lim}_{n\to \infty }\parallel F{w}_n-\mathcal{P}{w}_n\parallel \le {lim}_{n\to \infty }\parallel w_n-\mathcal{P}{w}_n\parallel =d(M,N).$

Therefore, by Lemma 8, it is implied that $\parallel F{w}_n-w_n\parallel \to 0.$

Case 2: 

Suppose that $\left\{{\eta }_n\right\},\left\{{\delta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ satisfy (R). From (13), we get

$$\sum _{n=1}^m{\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )\le \parallel w_1{-z\parallel }^2-{\parallel w_{m+1}-z\parallel }^2.$$

As $m\to \infty$, we get ${\sum }_{n=1}^{\infty }{\gamma }_n(1-{\gamma }_n)\varphi (\parallel F{w}_n-w_n\parallel )<\infty .$ In view of the fact that ${\gamma }_n(1-{\gamma }_n)\ge ϵ$, it implies $\varphi (\parallel F{w}_n-w_n\parallel )\to 0,$ so $\parallel F{w}_n-w_n\parallel \to 0.$

Therefore, $\parallel F{w}_n-w_n\parallel \to 0$ in both the cases. Now, since $F\left(M\right)$ lies in a compact subset then $\left\{F{w}_n\right\}$ has a convergent subsequence $\left\{F{w}_{n_k}\right\}$, converging to some point $u\in M_0$. We also have $w_{n_k}\to u.$ Additionally, from $F\left(\mathcal{P}u\right)=\mathcal{P}\left(Fu\right),$ we have

$$\parallel F{w}_{n_k}-\mathcal{P}\left(Fu\right)\parallel =\parallel F{w}_{n_k}-F\left(\mathcal{P}u\right)\parallel \le \parallel w_{n_k}-\mathcal{P}u\parallel \to d(M,N).$$

So one can obtain, by Lemma 8, $F{w}_{n_k}\to Fu.$ By uniqueness of limit, $Fu=u.$ So $F\left(\mathcal{P}u\right)=\mathcal{P}\left(Fu\right)=\mathcal{P}u.$ Therefore, we get that ${lim}_{n\to \infty }\parallel w_n-\mathcal{P}u\parallel$ exists. So

$$\underset{n\to \infty }{lim}\parallel w_n-\mathcal{P}u\parallel =\underset{k\to \infty }{lim}\parallel w_{n_k}-\mathcal{P}u\parallel =\parallel u-\mathcal{P}u\parallel =d(M,N),$$

which gives $w_n\to u.$ □

In the next result, we provide a stronger version to iterate the fixed point via von Neumann sequences.

Theorem 11.

Let M and N be nonempty bounded closed convex subsets of a Hilbert space and suppose that $F:M\cup N\to M\cup N$ satisfies

1. 

$F\left(M\right)\subseteq M$ and $F\left(N\right)\subseteq N;$ and

2. 

$\Vert Fw-Fz\Vert \le \Vert w-z\Vert$ for $w\in M,z\in N.$

Let $w_0\in M,$ and define $w_{n+1}=P^n\left((1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n\right),$ where $v_n=(1-{\delta }_n)u_n+{\delta }_{n}F{u}_n,u_n=(1-{\gamma }_n)w_n+{\gamma }_{n}F{w}_n,{\eta }_n,{\delta }_n,{\gamma }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ and $n=0,1,2,\dots$, then $li{m}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0.$ Moreover, if $F\left(M\right)$ lies in a compact set and $\Vert u_n-F{u}_n\Vert \to 0,\Vert v_n-F{v}_n\Vert \to 0$ then $\left\{w_n\right\}$ converges to a fixed point of F.

Proof. 

If $d(M,N)=0,$ then $M_0=N_0=M\cap N$ and $F:M\cap N\to M\cap N$ is nonexpansive with $w_{n+1}=P^n\left((1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n\right)=(1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n,$ the usual Thakur et al. iteration method. So let us take that $d(M,N)>0.$ By Theorem 2, we can find $z\in N_0$ such that $Fz=z.$ Now, by (8) and (9), we obtain:

$$\begin{array}{ccc}\hfill \Vert w_{n+1}-z\Vert & =& \Vert P^n\left((1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n\right)-z\Vert \hfill \\ & \le & \Vert (1-{\eta }_n)F{u}_n+{\eta }_{n}F{v}_n-z\Vert \hfill \\ & =& \parallel (1-{\eta }_n)(F{u}_n-z)+{\eta }_n(F{v}_n-z)\parallel \hfill \\ & \le & (1-{\eta }_n)\parallel u_n-z\parallel +{\eta }_n\parallel v_n-z\parallel \hfill \\ & \le & (1-{\eta }_n)\parallel w_n-z\parallel +{\eta }_n\parallel w_n-z\parallel \hfill \\ & =& \parallel w_n-z\parallel .\hfill \end{array}$$

This implies that the sequence $\{\Vert w_n-z\Vert \}$ is non increasing. Then we can find $d>0$ such that ${lim}_{n\to \infty }\Vert w_n-z\Vert =d.$

Suppose there exists a subsequence $\left\{w_{n_k}\right\}$ of $\left\{w_n\right\}$ and an $ϵ>0$ such that

$\Vert w_{n_k}-F{w}_{n_k}\Vert \ge ϵ>0$ for all k.

Since the modulus of convexity of $\delta$ of X is a continuous and increasing function we choose $\xi >0$ to be small such that $\left(1-c\delta (\frac{ϵ}{d+\xi })\right)(d+\xi )<d,$ where $c>0.$

Now we choose k, such that $\Vert w_{n_k}-z\Vert \le d+\xi .$ Now we have:

$$\begin{array}{ccc}\hfill \Vert z-w_{n_k+1}\Vert & =& \Vert z-P^{n_k}\left((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k}\right)\Vert \hfill \\ & \le & \Vert z-\left((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k}\right)\Vert \hfill \\ & =& \Vert (1-{\eta }_{n_k})z+{\eta }_{n_k}z-\left((1-{\eta }_{n_k})F\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)+{\eta }_{n_k}F{v}_{n_k}\right)\Vert \hfill \\ & \le & (1-{\eta }_{n_k})\Vert z-F\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)\Vert +{\eta }_{n_k}\Vert Fz-F{v}_{n_k}\Vert \hfill \\ & \le & (1-{\eta }_{n_k})\Vert z-\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)\Vert +{\eta }_{n_k}\Vert z-v_{n_k}\Vert .\hfill \end{array}$$

(15)

Now,

$$\begin{array}{ccc}\hfill \Vert z-\left((1-{\gamma }_{n_k})w_{n_k}+{\gamma }_{n_k}F{w}_{n_k}\right)\Vert & =& \Vert (1-{\gamma }_{n_k})(z-w_{n_k})+{\gamma }_{n_k}(z-F{w}_{n_k})\Vert \hfill \\ & \le & \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi ).\hfill \end{array}$$

(16)

Additionally, using (16), we get:

$$\begin{array}{ccc}\hfill \Vert z-v_{n_k}\Vert & =& \Vert z-\left((1-{\delta }_{n_k})u_{n_k}+{\delta }_{n_k}F{u}_{n_k}\right)\Vert \hfill \\ & =& \Vert (1-{\delta }_{n_k})(z-u_{n_k})+{\delta }_{n_k}(z-F{u}_{n_k})\Vert \hfill \\ & \le & (1-{\delta }_{n_k})\Vert z-u_{n_k}\Vert +{\delta }_{n_k}\Vert z-F{u}_{n_k}\Vert \hfill \\ & \le & (1-{\delta }_{n_k})\Vert z-u_{n_k}\Vert +{\delta }_{n_k}\Vert z-u_{n_k}\Vert \hfill \\ & =& \Vert z-u_{n_k}\Vert \hfill \\ & \le & \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi ).\hfill \end{array}$$

Therefore, the Equation (15) becomes:

$$\begin{array}{ccc}\hfill \Vert z-w_{n_k+1}\Vert & \le & \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi ).\hfill \end{array}$$

Since there exists $l>0$ such that $2\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\ge l,$

$$\begin{array}{c}\hfill \left(1-2\delta \left(\frac{ϵ}{d+\xi }\right)\min \{{\gamma }_{n_k},1-{\gamma }_{n_k}\}\right)(d+\xi )\le \left(1-l\delta \left(\frac{ϵ}{d+\xi }\right)\right)(d+\xi ).\end{array}$$

Suppose that we choose very small $\xi >0$, we have $\left(1-l\delta \left(\frac{ϵ}{d+\xi }\right)\right)(d+\xi )<d$, which is a contradiction. This implies that ${lim}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0.$ Now we prove that $\parallel w_{n+1}-w_n\Vert \to 0.$ From the Thakur et al. iteration method, we get $\parallel u_n-w_n\parallel ={\gamma }_n\parallel F{w}_n-w_n\parallel .$ Since ${lim}_{n\to \infty }\Vert w_n-F{w}_n\Vert =0$ we obtain $\parallel u_n-w_n\parallel \to 0.$

Since $F\left(M\right)$ is contained in a compact set, $\left\{F{w}_n\right\}$ has a subsequence $\left\{F{w}_{n_k}\right\}$ that converges to a point $v_0\in M.$$\left\{w_{n_k}\right\}$ also converges to $v_0$. From the given sequence, we obtain:

$$\begin{array}{ccc}\hfill \Vert w_{n_k+1}-w_{n_k}\Vert & =& \Vert P^{n_k}\left((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k}\right)-w_{n_k}\Vert \hfill \\ & \le & \Vert (1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k}-w_{n_k}\Vert \hfill \\ & =& \parallel F{u}_{n_k}-w_{n_k}\parallel +{\eta }_{n_k}\Vert F{u}_{n_k}-F{v}_{n_k}\Vert \hfill \\ & \le & \parallel F{u}_{n_k}-u_{n_k}\parallel +\parallel u_{n_k}-w_{n_k}\parallel \hfill \\ & & +{\eta }_{n_k}\left(\Vert F{u}_{n_k}-u_{n_k}\Vert +\Vert u_{n_k}-v_{n_k}\Vert +\Vert v_{n_k}-F{v}_{n_k}\Vert \right).\hfill \end{array}$$

Since $\Vert F{u}_{n_k}-u_{n_k}\Vert \to 0$ implies $\Vert u_{n_k}-v_{n_k}\Vert \to 0.$ Then $\Vert w_{n_k+1}-w_{n_k}\Vert \to 0.$ Therefore, $w_{n_k+1}\to v_0,$ which implies that $w_n\to v_0.$ We also have $F{z}_{n_k}\to v_0$ as $k\to \infty .$

Now, $\Vert F{w}_{n_k}-F\left(P_N\left(v_0\right)\right)\Vert \le \Vert w_{n_k}-P_N\left(v_0\right)\Vert$, which gives that $\Vert v_0-F\left(P_N\left(v_0\right)\right)\Vert \le \Vert v_0-P_N\left(v_0\right)\Vert .$ Therefore, $F\left(P_N\left(v_0\right)\right)=P_N\left(v_0\right)$.

Additionally, $\Vert F\left(P\left(v_0\right)\right)-P_N\left(v_0\right)\Vert =\Vert F\left(P\left(v_0\right)\right)-F\left(P_N\left(v_0\right)\right)\Vert \le \Vert P\left(v_0\right)-P_N\left(v_0\right)\Vert .$ So $F\left(P\left(v_0\right)\right)=P\left(v_0\right)$.

Now, $\Vert F{P}_N\left(P\left(v_0\right)\right)-P\left(v_0\right)\Vert =\Vert F{P}_N\left(P\left(v_0\right)\right)-F\left(P\left(v_0\right)\right)\Vert \le \Vert P_N\left(P\left(v_0\right)\right)-P\left(v_0\right)\Vert$. Thus $F{P}_N\left(P\left(v_0\right)\right)=P_N\left(P\left(v_0\right)\right)$.

For any $n,F\left(P^n\left(v_0\right)\right)=P^n\left(v_0\right)$ and $F{P}_N\left(P^n\left(v_0\right)\right)=P_N\left(P^n\left(v_0\right)\right).$ By Theorem 7, for each $x\in M$ the sequence $\left\{P^n\left(x\right)\right\}$ converges to some $u\left(x\right)\in M_0.$ Now,

$$\begin{array}{ccc}\hfill \Vert F\left(u\left(v_0\right)\right)-P_N\left(u\left(v_0\right)\right)\Vert & \le & \underset{n\to \infty }{lim}\Vert F\left(u\left(v_0\right)\right)-P_N\left(P^n\left(v_0\right)\right)\Vert \hfill \\ & =& \underset{n\to \infty }{lim}\Vert F\left(u\left(v_0\right)\right)-F\left(P_N\left(P^n\left(v_0\right)\right)\right)\Vert \hfill \\ & \le & \underset{n\to \infty }{lim}\Vert u\left(v_0\right)-P_N\left(P^n\left(v_0\right)\right)\Vert \hfill \\ & =& \Vert u\left(v_0\right)-P_N\left(u\left(v_0\right)\right)\Vert .\hfill \end{array}$$

So $\Vert F\left(u\left(v_0\right)\right)-P_N\left(u\left(v_0\right)\right)\Vert \le \Vert u\left(v_0\right)-P_N\left(u\left(v_0\right)\right)\Vert$. Therefore, $F\left(u\left(v_0\right)\right)=u\left(v_0\right)$ and similarly $F{P}_N\left(u\left(v_0\right)\right)=P_N\left(u\left(v_0\right)\right).$

Now we define $g_n:M\to \mathbb{R}$ by $g_n\left(x\right)=\Vert P^n\left(x\right)-u\left(x\right)\Vert$. Since $\Vert u\left(x\right)-u\left(y\right)\Vert ={lim}_{n\to \infty }\Vert P^n\left(x\right)-P^n\left(y\right)\Vert \le \Vert x-y\Vert ,$ we conclude that u is continuous. Therefore, $g_n\left(w\right)$ is continuous and converges pointwise to zero. Since $u\left(x\right)\in M_0,$ by Lemma 2, we obtain $g_{n+1}\le g_n.$ Therefore $g_n$ converges uniformly on the compact set

$$S=\{(1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k}\}\cup \left\{v_0\right\}.$$

Therefore

$$\underset{k\to \infty }{lim}\Vert P^{n_k}((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k})-u((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k})\Vert =0.$$

Since $u((1-{\eta }_{n_k})F{u}_{n_k}+{\eta }_{n_k}F{v}_{n_k})\to u\left(v_0\right),$ we get $w_{n_k+1}\to u\left(v_0\right),$ which gives that $u\left(v_0\right)=v_0.$

Therefore $F{v}_0=F\left(u\left(v_0\right)\right)=u\left(v_0\right)=v_0$, which completes the proof. □

Suppose X is a Hilbert space and let F be as in Theorem 1. Consider $P_{M}F:M\to M$ and $P_{N}F:N\to N$. From Proposition 2, $\Vert P_{M}F\left(w\right)-P_{N}F\left(z\right)\Vert \le \Vert w-z\Vert$ for $w\in M$ and $z\in N;$ by Theorems 9 and 11 we give the following results on convergence of best proximity points.

Corollary 4.

Let M and N be nonempty, closed, bounded and convex subsets of a Hilbert space X. Let F be as in Theorem 1. If M is mapped into a compact subset of N, then for any $w_0\in M_0$ the sequence defined by $w_{n+1}=(1-{\eta }_n)P_{M}F{u}_n+{\eta }_n{P}_{M}F{v}_n,$ where $v_n=(1-{\delta }_n)u_n+{\delta }_n{P}_{M}F{u}_n,u_n=(1-{\gamma }_n)w_n+{\gamma }_n{P}_{M}F{w}_n,$ converges to w in $M_0$ such that $\Vert w-Fw\Vert =d(M,N).$

Corollary 5.

Let M and N be nonempty, closed, bounded and convex subsets of a Hilbert space X. Let F be as in Theorem 1. If M is mapped into a compact subset of N, then for any $w_0\in M$ the sequence is defined by $w_{n+1}=(1-{\eta }_n)P_{M}F{u}_n+{\eta }_n{P}_M{v}_n,$ where $v_n=(1-{\delta }_n)u_n+{\delta }_n{P}_{M}F{u}_n,u_n=(1-{\gamma }_n)w_n+{\gamma }_n{P}_{M}F{w}_n$ converges to w in $M_0$ such that $\Vert w-Fw\Vert =d(M,N),$ provided $d(w_n,M_0)\to 0.$

Corollary 6.

Let M and N be nonempty, closed, bounded and convex subsets of a Hilbert space X. Let F be as in Theorem 1. If M is mapped into a compact subset of N, then for any $w_0\in M_0$ the sequence is defined by $w_{n+1}=P^n\left((1-{\eta }_n)P_{M}F{u}_n+{\eta }_n{P}_{M}F{v}_n\right),$ where $v_n=(1-{\delta }_n)u_n+{\delta }_n{P}_{M}F{u}_n,u_n=(1-{\gamma }_n)w_n+{\gamma }_n{P}_{M}F{w}_n$ converges to w in $M_0$ such that $\Vert w-Fw\Vert =d(M,N).$

Proof. 

The result follows from Corollary 4. □

Corollary 7.

Let M and N be nonempty, closed, bounded and convex subsets of a Hilbert space X. Let F be as in Theorem 1. Let $w_0\in M,$ and define $w_{n+1}=P^n\left((1-{\eta }_n)P_{M}F{u}_n+{\eta }_n{P}_{M}F{v}_n\right),$ where $v_n=(1-{\delta }_n)u_n+{\delta }_n{P}_{M}F{u}_n,u_n=(1-{\delta }_n)w_n+{\delta }_n{P}_{M}F{w}_n,{\eta }_n,{\delta }_n\in (ϵ,1-ϵ),$ where $ϵ\in (0,1/2)$ and $n=0,1,2,\dots$. If M is mapped into a compact subset of N and $\Vert u_n-P_{M}F{u}_n\Vert \to 0,\Vert v_n-P_{M}F{v}_n\Vert \to 0$, then $\left\{w_n\right\}$ converges to w in $M_0$ such that $\Vert w-Fw\Vert =d(M,N).$

Proof. 

The result follows from Theorem 11. □

4. Conclusions

The fixed point theorems help to provide sufficient conditions to ensure the existence of a solution for many nonlinear problems. On the other hand, the fixed point theorems give the solution of equations of the form $Tx=x,$ where T is self mapping. In the literature, there is a large number of research works dealing with the existence of fixed points and also the convergence results for fixed points of different kinds of mappings via some basic iterative procedures. Here, we approximate a fixed point of noncyclic relatively nonexpansive mappings by using a three-step Thakur iterative scheme in uniformly convex Banach spaces. We also provide a numerical example where the Thakur iterative scheme is faster than some well known iterative schemes such as Picard, Mann, and Ishikawa iterations. Finally, we provide a stronger version of our proposed theorem via von Neumann sequences.