A Novel DEMATEL Approach by Considering Normalization and Invertibility

Abstract

DEMATEL is a popular approach in multi-criteria decision making (MCDM) to understand the influence relationship between elements. In addition, the result of DEMATEL is used as the input in other approaches to explore further applications. However, DEMATEL may fail to derive the reasonable total influence matrix, i.e., all positive elements. Hence, DEMATEL uses a special normalization method to avoid that situation. It has been reported that selecting the normalization method plays a critical role after we determine the research method. This paper compares different normalization methods in DEMATEL and proposes a novel formula to derive the total influence matrix when the conventional DEMATEL cannot obtain a correct result. The numerical examples demonstrate how different normalization methods generate contradicted results of DEMATEL and the proposed approach ensures a reasonable result. In addition, we also shed light on further applications based on this paper.

1. Introduction

Decision-making trial and evaluation laboratory (DEMATEL) was developed to understand the problem or structure of the problem in the 1970s [1,2,3]. The basic idea of DEMATEL comes from Leontief’s input and output model [4]. The purpose of DEMATEL is to derive the influential relationship between elements within the problem.

Recently, DEMATEL has received much attention in the exploration of various applications, such as combining conflicting evidence [5], analyzing barriers to green lean practices [6], and safety management decision making [7]. In addition, DEMATEL was also used to integrate with other methods for further applications, such as grey theory [8], TOPSIS (technique for order of preference by similarity to ideal solution) [9], and ANFIS (adaptive network-based fuzzy inference system) [10]. However, papers seldom discuss the mathematical properties of DEMATEL. Therefore, the motivation of this paper is to fill the gap between the theory and practice of DEMATEL to discuss the infeasible situation of DEMATEL via the perspectives of normalization and invertibility.

Normalization is a common skill in the field of multi-criteria decision making (MCDM) to normalize raw data into a specific range, usually between zero and one, to avoid possible problems from different scales and units. The conventional normalization methods include vector normalization [11], max normalization [12], sum normalization [13], logarithmic normalization [14], and minmax normalization [15], and the corresponding formulas of the normalization methods can refer to [16]. It has been reported that researchers often underestimate the importance of the proper selection of data normalization [17]. Ref [16] also revealed that once we determine the analytic method in our research, the corresponding normalization method plays a crucial role in the final result. Although several papers compared the influence of different normalization methods on various MCDM models, e.g., TOPSIS, VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje) [18], and SAW (sample additive weighting), the situation of DEMATEL is not reported so far. Hence, the appropriate normalization method of DEMATEL is the first concern in this paper.

Furthermore, the infeasible situation of DEMATEL is another concern here to uncover the reason why DEMATEL cannot derive the result and propose a novel method to handle that situation. Although plenty of papers have used DEMATEL to consider various MCDM problems, no paper reports the infeasible situation of DEMATEL so far. However, the infeasible solution of DEMATEL may come from different normalization methods or incorporating the feedback effect.

Hence, the purpose of this paper is two-fold. First, we will explain what conditions of DEMATEL suffer the problem of the infeasible situation from the perspectives of the normalization method and feedback effect. Second, we will propose a novel method to derive and ensure the feasible solution of DEMATEL under any situation, i.e., considering different normalization methods and the feedback effect. The proposed method enables DEMATEL to handle more complicated problems without worrying about the possible infeasible situation.

2. DEMATEL Description

DEMATEL was developed by the Science and Human Affairs Program of the Battelle Memorial Institute of Geneva between 1972 and 1976 to be a structural method to solve complicated and intertwined problems [1,2,3]. Since DEMATEL has been used widely in past papers, we focus on discussing the mathematical property of DEMATEL as follows.

First, an expert is asked to use the scale [0,4] to indicate the influence level between elements, namely, the direct-influence matrix, where zero to four denotes no influence to extreme influence. Then, the normalized direct-influence matrix D can be obtained by normalizing the direct-influence matrix $\mathit{X}=[x_{ij}]$, in which all principal diagonal elements are equal to zero such that

$$\mathit{D}=s\cdot \mathit{X},s>0$$

(1)

where

$$s=min\left(1/\underset{1\le i\le n}{\max }{\displaystyle \sum _{j=1}^{\mathrm{n}}\left|x_{ij}\right|},1/\underset{1\le j\le n}{\max }{\displaystyle \sum _{i=1}^{\mathrm{n}}\left|x_{ij}\right|}\right)$$

(2)

is nothing but the normalization of the direct-influence matrix, which ensures the condition of strictly diagonally dominant matrices.

Then, the full direct/indirect-influence matrix F can be obtained by

$$\mathit{F}={\displaystyle \sum _{i=1}^{\infty }{\mathit{D}}^i}=\mathit{D}{\left(\mathit{I}-\mathit{D}\right)}^{-1}$$

(3)

Example 2.

Next, we can give a numerical example to show how the conventional DEMATEL processes. We first assume the direct-influence matrix, which is provided by an expert as:

$$\mathit{X}=\left[\begin{array}{rrrr}\hfill 0& \hfill 4& \hfill 3& \hfill 0\\ \hfill 4& \hfill 0& \hfill 4& \hfill 2\\ \hfill 2& \hfill 0& \hfill 1& \hfill 4\\ \hfill 0& \hfill 1& \hfill 2& \hfill 0\end{array}\right].$$

Then, we use Equation (2) to derive the normalized direct-influence matrix as

$$\mathit{D}=\left[\begin{array}{rrrr}\hfill 0.0& \hfill 0.4& \hfill 0.3& \hfill 0.0\\ \hfill 0.4& \hfill 0.0& \hfill 0.4& \hfill 0.2\\ \hfill 0.2& \hfill 0.0& \hfill 0.1& \hfill 0.4\\ \hfill 0.0& \hfill 0.1& \hfill 0.2& \hfill 0.0\end{array}\right],$$

such that the maximum column/row sum is equal to one.

Finally, we can calculate the direct- and indirect-influence matrix F as

$$\mathit{F}=\mathit{D}{(\mathit{I}-\mathit{D})}^{-1}=\left[\begin{array}{rrrr}\hfill 0.4137& \hfill 0.6115& \hfill 0.8453& \hfill 0.4604\\ \hfill 0.7482& \hfill 0.3669& \hfill 1.0072& \hfill 0.6763\\ \hfill 0.3813& \hfill 0.2158& \hfill 0.4748& \hfill 0.6331\\ \hfill 0.1511& \hfill 0.1799& \hfill 0.3957& \hfill 0.1942\end{array}\right]$$

to understand the total influence between elements.

However, Equation (2) is only one kind of normalization, and if we normalized the direct-influence matrix by dividing the maximum elements within the matrix, i.e., the max normalization method, we could obtain:

$$\mathit{D}=\left[\begin{array}{rrrr}\hfill 0& \hfill 1& \hfill 0.75& \hfill 0\\ \hfill 1& \hfill 0& \hfill 1& \hfill 0.5\\ \hfill 0.5& \hfill 0& \hfill 0.25& \hfill 1\\ \hfill 0& \hfill 0.25& \hfill 0.5& \hfill 0\end{array}\right]$$

and

$$(\mathit{I}-\mathit{D})=\left[\begin{array}{rrrr}\hfill 1& \hfill -1& \hfill -0.75& \hfill 0\\ \hfill -1& \hfill 1& \hfill -1& \hfill -0.5\\ \hfill -0.5& \hfill 0& \hfill 0.75& \hfill -1\\ \hfill 0& \hfill -0.25& \hfill -0.5& \hfill 1\end{array}\right].$$

respectively.

Clearly, the matrix $(\mathit{I}-\mathit{D})$ is against the strictly diagonally dominant matrix and is not invertible here, i.e., we cannot derive ${(\mathit{I}-\mathit{D})}^{-1}$. Note that the invertibility of $(\mathit{I}-\mathit{D})$ is a necessary condition for DEMATEL to derive the result. Hence, Equation (2) is solely used to meet the convergent condition of the matrix, despite the fact that the max normalization should be another consideration.

3. Invertibility of DEMATEL

DEMATEL uses a specific normalization and ignores the feedback effect to ensure the existence of the solution. However, it hinders the possible applications in dealing with practical problems. Here, we release the feedback effect in DEMATEL to consider a more realistic situation as follows:

Example 2.

Assume the direct-influence matrix between elements can be represented as

$$\mathit{X}=\left[\begin{array}{rrrr}\hfill 0& \hfill 2& \hfill 3& \hfill 4\\ \hfill 3& \hfill 4& \hfill 0& \hfill 2\\ \hfill 2& \hfill 3& \hfill 4& \hfill 0\\ \hfill 4& \hfill 0& \hfill 2& \hfill 3\end{array}\right],$$

and the corresponding normalized direct-influence matrix can be derived by Equation (2) as:

$$\mathit{D}=\left[\begin{array}{rrrr}\hfill 0& \hfill 2/9& \hfill 3/9& \hfill 4/9\\ \hfill 3/9& \hfill 4/9& \hfill 0& \hfill 2/9\\ \hfill 2/9& \hfill 3/9& \hfill 4/9& \hfill 0\\ \hfill 4/9& \hfill 0& \hfill 2/9& \hfill 3/9\end{array}\right].$$

Then, we can calculate ($\mathit{I}-\mathit{D}$) as:

$$\mathit{I}-\mathit{D}=\left[\begin{array}{rrrr}\hfill 1& \hfill -2/9& \hfill -3/9& \hfill -4/9\\ \hfill -3/9& \hfill 5/9& \hfill 0& \hfill -2/9\\ \hfill -2/9& \hfill -3/9& \hfill 5/9& \hfill 0\\ \hfill -4/9& \hfill 0& \hfill -2/9& \hfill 6/9\end{array}\right].$$

Clearly, ($\mathit{I}-\mathit{D}$) is not satisfied with the condition of diagonally dominant matrices and is not invertible here.

The above direct-influence matrix in Example 2 seems an easy and common problem in DEMATEL, but the result of this problem is undefined (i.e., it produces an infinite matrix) because the matrix ($\mathit{I}-\mathit{D}$) is singular.

Definition 1.

If A is a real$n\times n$matrix and can be written in the form$\mathit{A}=s\mathit{I}-\mathit{B}$where$\mathit{B}\ge 0$and$s=\rho (\mathit{B})$, then A is a singular matrix.

If $\mathit{I}-\mathit{D}$ is singular, ${(\mathit{I}-\mathit{D})}^{-1}$ does not exist. That is, DEMATEL cannot work when dealing with this situation because of the mathematical problem. To release the above restriction, our concern here is transformed into finding a generalized method to calculate the inverse of a singular matrix. Traditionally, the Moore–Penrose inverse is widely used to find the unique matrix for any matrix.

Definition 2

[19]. Let A be a real $n\times n$ matrix. A matrix ${\mathit{A}}^{+}\in {ℝ}^{n\times n}$ is said to be the Moore–Penrose inverse if

$$\mathit{A}{\mathit{A}}^{+}\mathit{A}=\mathit{A},{\mathit{A}}^{+}\mathit{A}{\mathit{A}}^{+}={\mathit{A}}^{+},(\mathit{A}{\mathit{A}}^{+}{)}^{\prime }=\mathit{A}{\mathit{A}}^{+},\mathrm{and}({\mathit{A}}^{+}\mathit{A}{)}^{\prime }={\mathit{A}}^{+}\mathit{A}$$

(4)

where ${\mathit{A}}^{\prime }$ is the conjugate matrix of $\mathit{A}$.

Note that Moore–Penrose’s method can ensure that ${\mathit{A}}^{+}$ always exists and is unique. According to the definition of the Moore–Penrose’s inverse, we can have

$$(\mathit{I}-\mathit{D})(\mathit{I}+\mathit{D}+{\mathit{D}}^2+\dots )(\mathit{I}-\mathit{D})=(\mathit{I}-\mathit{D})$$

(5)

and ensure that

$${(\mathit{I}-\mathit{D})}^{+}=(\mathit{I}+\mathit{D}+{\mathit{D}}^2+\dots )$$

(6)

Therefore, we can apply Moore–Penrose’s inverse, ${(\mathit{I}-\mathit{D})}^{+}$, to DEMATEL.

Let us re-consider the direct-influence matrix in Example 2 and find ${(\mathit{I}-\mathit{D})}^{-1}$ by the Moore–Penrose inverse as follows:

$${(\mathit{I}-\mathit{D})}^{+}={\left(\left[\begin{array}{rrrr}\hfill 1& \hfill -2/9& \hfill -3/9& \hfill -4/9\\ \hfill -3/9& \hfill 5/9& \hfill 0& \hfill -2/9\\ \hfill -2/9& \hfill -3/9& \hfill 5/9& \hfill 0\\ \hfill -4/9& \hfill 0& \hfill -2/9& \hfill 6/9\end{array}\right]\right)}^{+}$$

$$=\left[\begin{array}{rrrr}\hfill 0.5666& \hfill -0.3139& \hfill -0.1508& \hfill -0.1019\\ \hfill -0.1508& \hfill 0.9253& \hfill -0.6073& \hfill -0.1671\\ \hfill -0.3139& \hfill -0.0204& \hfill 0.9253& \hfill -0.5910\\ \hfill -0.1019& \hfill -0.5910& \hfill -0.1671& \hfill 0.8601\end{array}\right]$$

The result of the Moore–Penrose inverse seems helpful and useful when dealing with any singular matrix in DEMATEL. However, the Moore–Penrose inverse cannot guarantee that the inverse matrix is positive, which is a necessary condition of DEMATEL.

In fact, the Moore–Penrose inverse can only ensure that the inverse of a singular matrix is positive under some conditions. For example, [20] showed that the Moore–Penrose inverse could obtain a positive result when the symmetric singular tridiagonal M-matrix is considered. Next, we employ another method to derive the inverse of a matrix that ensures the positive matrix.

Definition 3.

Let A be a real $n\times n$matrix. The index of A,$Ind(\mathit{A})$, is the smallest nonnegative integer k such that$Rank({\mathit{A}}^{k+1})=Rank({\mathit{A}}^k)$. The Drazin inverse of A, i.e.,${\mathit{A}}^{\mathit{D}}$, is the unique solution of the equation of${\mathit{A}}^{k+1}\mathit{X}={\mathit{A}}^k$,$\mathit{X}\mathit{A}\mathit{X}=\mathit{X}$, and$\mathit{A}\mathit{X}=\mathit{X}\mathit{A}$where$k=Ind(\mathit{A})$.

Lemma 1

[21]. Let A be a real $n\times n$ matrix in standard form,

$$\mathit{A}={\mathit{P}}^{\prime }\left[\begin{array}{cccc}{\mathit{A}}_{11}& {\mathit{A}}_{11}& \cdots & {\mathit{A}}_{11}\\ 0& {\mathit{A}}_{11}& \cdots & {\mathit{A}}_{11}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\mathit{A}}_{11}\end{array}\right]\mathit{P}$$

where  $\mathit{P}$ denotes the permutation matrix and $c>0$  be a number such that  ${(\mathit{A}+t\mathit{I})}^{-1}$exists for all$t\in (0,c)$. If B(t) is the block diagonal matrix which can be presented as

$$\mathit{B}(t)=\left[\begin{array}{cccc}{({\mathit{A}}_{11}+t\mathit{I})}^{-1}& 0& \cdots & 0\\ 0& {({\mathit{A}}_{22}+t\mathit{I})}^{-1}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {({\mathit{A}}_{mm}+t\mathit{I})}^{-1}\end{array}\right]$$

and C is the nilpotent matrix which can be represented as

$$\mathit{C}=\left[\begin{array}{cccc}0& -{\mathit{A}}_{12}& \cdots & -{\mathit{A}}_{1m}\\ 0& 0& \cdots & ⋮\\ ⋮& ⋮& \ddots & -{\mathit{A}}_{m-1,m}\\ 0& 0& \cdots & 0\end{array}\right],$$

then

$${(\mathit{A}+t\mathit{I})}^{-1}={\displaystyle \sum _{k=0}^{m-1}{(\mathit{B}(t)\mathit{C})}^k\mathit{B}(t)}\mathrm{on}(0,c).$$

(7)

If A is an M-matrix, then

$$\mathit{C}\ge 0\mathrm{and}\mathit{B}(t)\ge 0\mathrm{on}(0,c),$$

(8)

$${(\mathit{A}+t\mathit{I})}^{-1}\mathit{B}{(t)}^{-1}\ge 0\mathrm{and}{(\mathit{A}+t\mathit{I})}^{-1}\ge 0\mathrm{on}(0,c),$$

(9)

and

$${(\mathit{A}+t\mathit{I})}^{-1}\ge \frac{1}{m}{(\mathit{A}+t\mathit{I})}^{-1}\mathit{B}{(t)}^{-1}{(\mathit{A}+t\mathit{I})}^{-1}\mathrm{on}(0,c).$$

(10)

Theorem 1.

If A is an M-matrix, then there is a number $c>0$such that${(\mathit{A}+t\mathit{I})}^{-1}(\mathit{I}-t{\mathit{A}}^{\mathit{D}})$is positive when$t\in (0,c)$.

Proof. 

First, we can calculate

$${(\mathit{A}+t\mathit{I})}^{-1}(\mathit{I}-t{\mathit{A}}^{\mathit{D}})={(\mathit{A}+t\mathit{I})}^{-1}+t{(\mathit{A}+t\mathit{I})}^{-1}{\mathit{A}}^{\mathit{D}}$$

$$\ge \frac{1}{m}{(\mathit{A}+t\mathit{I})}^{-1}\mathit{B}{(t)}^{-1}{(\mathit{A}+t\mathit{I})}^{-1}+t{(\mathit{A}+t\mathit{I})}^{-1}{\mathit{A}}^{\mathit{D}}(\mathrm{Lemma}1)$$

$$={(\mathit{A}+t\mathit{I})}^{-1}\mathit{B}{(t)}^{-1}\left[\frac{1}{m}{(\mathit{A}+t\mathit{I})}^{-1}+t\mathit{B}(t){\mathit{A}}^{\mathit{D}}\right].$$

Since ${(\mathit{A}+t\mathit{I})}^{-1}\mathit{B}{(t)}^{-1}\ge 0$ (from Lemma 1), we only need to prove $\left[\frac{1}{m}{(\mathit{A}+t\mathit{I})}^{-1}+t\mathit{B}(t){\mathit{A}}^{\mathit{D}}\right]\ge 0$. Then, we can obtain

${\left[\frac{1}{m}{(\mathit{A}+t\mathit{I})}^{-1}+t\mathit{B}{\mathit{A}}^{\mathit{D}}\right]}_{ij}=\frac{1}{m}{\left[{(\mathit{A}+t\mathit{I})}^{-1}\right]}_{ij}$ when ${\left[{\mathit{A}}^{\mathit{D}}\right]}_{ij}=0$.

If ${\left[{\mathit{A}}^{\mathit{D}}\right]}_{ij}\ne 0$, then we can consider the following equation

$$t^{r(i)}{\left[\frac{1}{m}{(\mathit{A}+t\mathit{I})}^{-1}+t\mathit{B}{\mathit{A}}^{\mathit{D}}\right]}_{ij}=\frac{1}{m}{t}^{r(i)}{\left[{(\mathit{A}+t\mathit{I})}^{-1}\right]}_{ij}+t^{r(i)+1}{({\mathit{A}}_{ii}+t\mathit{I})}^{-1}{\left[{\mathit{A}}^{\mathit{D}}\right]}_{ij}.$$

As $t\to 0^{+}$, it guarantees that

$$t^{r(i)+1}{({\mathit{A}}_{ii}+t\mathit{I})}^{-1}{\left[{\mathit{A}}^{\mathit{D}}\right]}_{ij}\to 0$$

and

$$\underset{}{\lim }\frac{1}{m}{t}^{r(i)}{\left[{(\mathit{A}+t\mathit{I})}^{-1}\right]}_{ij}>0$$

Thus, we can obtain ${(\mathit{A}+t\mathit{I})}^{-1}(\mathit{I}-t{\mathit{A}}^{\mathit{D}})\ge 0$. Q.E.D. □

According to the result of Theorem 1, we can directly derive Theorems 2 and 3.

Theorem 2.

If A is an M-matrix, then for every $t>0$,$\mathit{G}(t)={(\mathit{A}+t\mathit{I})}^{-1}(\mathit{I}-t{\mathit{A}}^{\mathit{D}})={\mathit{A}}^{\mathit{D}}+{(\mathit{A}+t\mathit{I})}^{-1}(\mathit{I}-\mathit{A}{\mathit{A}}^{\mathit{D}})$is nonsingular. Furthermore, a number exists$c>0$such that$\mathit{G}(t)\ge 0$when$t\in (0,c)$.

Theorem 3.

If A is an M-matrix, then there is a number $c>0$such that$\mathit{A}+t(\mathit{I}-\mathit{A}{\mathit{A}}^{\mathit{D}})$is inverse positive when$t\in (0,c)$.

Although for every M-matrix, the matrix $\mathit{A}+t(\mathit{I}-\mathit{A}{\mathit{A}}^{\mathit{D}})$ is inverse positive for some interval $(0,c)$, an expression for the maximal value for c is unknown. However, when the condition $Ind(\mathit{A})=1$ is satisfied, the maximal c is equal to the largest t for which $(\mathit{I}-\mathit{A}{\mathit{A}}^{\mathit{D}})\ge -t{\mathit{A}}^{\mathit{D}}$ [8].

Let us resolve the problem of Example 2 by using Theorem 1 to derive the positive inverse of the singular M-matrix as follows.

According to Theorem 3, which indicates that ${\mathit{A}}^{-1}={\left[\mathit{A}+t(\mathit{I}-\mathit{A}{\mathit{A}}^{\mathit{D}})\right]}^{-1}$ approximately holds and the result of [8], we can derive the following equation

$${(\mathit{I}-\mathit{D})}^{-1}={\left[(\mathit{I}-\mathit{D})+t(\mathit{I}-(\mathit{I}-\mathit{D}){(\mathit{I}-\mathit{D})}^{\mathit{D}})\right]}^{-1}$$

(11)

to ensure the positive matrix.

Next, we used Equation (11) to conduct Example 3 and derive the result of ${(\mathit{I}-\mathit{D})}^{-1}$ as:

$${(\mathit{I}-\mathit{D})}^{-1}=\left[\begin{array}{rrrr}\hfill 1.3166& \hfill 0.4361& \hfill 0.5992& \hfill 0.6481\\ \hfill 0.5992& \hfill 1.6753& \hfill 0.1427& \hfill 0.5829\\ \hfill 0.4361& \hfill 0.7296& \hfill 1.6753& \hfill 0.1590\\ \hfill 0.6481& \hfill 0.1590& \hfill 0.5829& \hfill 1.6101\end{array}\right],t=1/3.$$

Then, the result of F can be calculated as:

$$\mathit{F}=\left[\begin{array}{rrrr}\hfill 0.5666& \hfill 0.6861& \hfill 0.8492& \hfill 0.8981\\ \hfill 0.8492& \hfill 0.9253& \hfill 0.3927& \hfill 0.8329\\ \hfill 0.6861& \hfill 0.9796& \hfill 0.9253& \hfill 0.4090\\ \hfill 0.8981& \hfill 0.4090& \hfill 0.8329& \hfill 0.8601\end{array}\right].$$

Note that the value t is set to one first. If the matrix ${(\mathit{I}-\mathit{D})}^{-1}$ is negative, we can follow the Fibonacci number to set t = 1/2, 1/3, 1/5,…, successively to ensure the positive inverse in practice.

Moreover, we can employ another normalization to the direct-influence matrix by dividing the maximum element of the matrix such that:

$$\mathit{D}=\left[\begin{array}{rrrr}\hfill 0& \hfill 2/4& \hfill 3/4& \hfill 4/4\\ \hfill 3/4& \hfill 4/4& \hfill 0& \hfill 2/4\\ \hfill 2/4& \hfill 3/4& \hfill 4/4& \hfill 0\\ \hfill 4/4& \hfill 0& \hfill 2/4& \hfill 3/4\end{array}\right].$$

Since the above matrix is still not invertible, we can use the proposed method to derive the inverse matrix of $(\mathit{I}-\mathit{D})$ as:

$${(\mathit{I}-\mathit{D})}^{-1}={\left[(\mathit{I}-\mathit{D})+t(\mathit{I}-(\mathit{I}-\mathit{D}){(\mathit{I}-\mathit{D})}^{\mathit{D}})\right]}^{-1}$$

$$=\left[\begin{array}{rrrr}\hfill 1.2691& \hfill 0.4568& \hfill 0.6627& \hfill 0.6114\\ \hfill 0.6627& \hfill 1.4314& \hfill 0.1185& \hfill 0.7874\\ \hfill 0.4568& \hfill 0.9565& \hfill 1.4314& \hfill 0.1553\\ \hfill 0.6114& \hfill 0.1553& \hfill 0.7874& \hfill 1.4459\end{array}\right],t=1/3.$$

The above result indicates that the elements of ${(\mathit{I}-\mathit{D})}^{-1}$ are all positive and overcome the infeasible problem of conventional DEMATEL by using Equation (2). Finally, the result of the total influence matrix can be calculated as:

$$\mathit{F}=\left[\begin{array}{rrrr}\hfill 0.5713& \hfill 0.7059& \hfill 0.8534& \hfill 0.8694\\ \hfill 0.8534& \hfill 0.8229& \hfill 0.4486& \hfill 0.8751\\ \hfill 0.7059& \hfill 1.0038& \hfill 0.8229& \hfill 0.4673\\ \hfill 0.8694& \hfill 0.4673& \hfill 0.8751& \hfill 0.7882\end{array}\right]$$

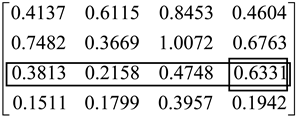
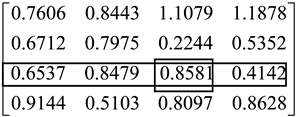
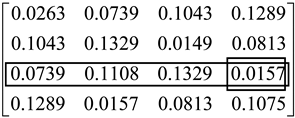
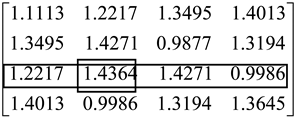
Next, let us re-consider Example 1 and derive the result by the different normalization methods as shown in

Table 1. Comparisons among different normalization methods in DEMATEL.

Conventional DEMATEL	DEMATEL with max normalization (t = 1/3)
DEMATEL with sum normalization	DEMATEL with vector normalization

. Here, we use three different normalization methods, i.e., max, sum, and vector methods, to derive the results of DEMATEL. In addition, DEMATEL with the max normalization method needs to use the proposed method to obtain the convergent solution.

From the above results, it can be seen that the different normalizations also result in the different results of DEMATEL. For example, we compare the influence of the third element on other elements. The conventional DEMATEL approach indicates that the third element has the most influence on the fourth element. However, DEMATEL with the max and vector normalization methods shows different results. Hence, we should use different normalization methods carefully because the result of DEMATEL may be used as the input in other methods, e.g., D-ANP (DEMATEL-based analytic network process). The proposed method extended DEMATEL to incorporate different normalizations and the feedback effect without worrying about the invertible issue of $(\mathit{I}-\mathit{D})$.

4. Discussion

DEMATEL is a popular method to understand the structure and influence relationship between elements. In addition, the result of DEMATEL is also used as the input in other methods for further applications. However, the conventional DEMATEL uses a particular normalization method to normalize the initial direct matrix for obtaining the positive total influence matrix. However, our numerical examples show that different normalization methods may derive inconsistent results. This result is not surprising and conforms with the results of past papers that the normalization methods play a vital role in the result.

Next, our paper also describes how different normalizations and the feedback effect may result in the infeasible solution of DEMATEL, which has not been reported so far. To reflect the infeasible solution, we propose a novel method, based on the Drazin inverse, to ensure a fair result, i.e., all elements are positive, of DEMATEL. Hence, we can extend the conventional DEMATEL by considering different normalization methods and the feedback effect for more sophisticated applications without worrying about obtaining the wrong result.

In addition, we also shed some light on future applications as follows. Firstly, since many papers used the total influence matrix of DEMATEL as the input in other approaches, e.g., ANP, the compromise may be the linear combination of different normalization methods. This concept can correspond to the managerial strategy of risk aversion. However, determining the weights of varying influence matrices should be another essential issue for future research.

5. Conclusions

This paper considers the issues of normalization and invertibility of DEMATEL and shows how the conventional DEMATEL fails when considering the max normalization and the feedback effect. This paper extends conventional DEMATEL to consider the more complicated situation with sound mathematical properties. The numerical examples indicate that different normalization methods may obtain opposite results, and some of them may result in unreasonable results of DEMATEL. Hence, we provide a new formula for DEMATEL to calculate the total influence matrix, based on the Drazin inverse, to guarantee a feasible solution under the above situations.