Analytical Solutions of Nonlocal Thermoelastic Interaction on Semi-Infinite Mediums Induced by Ramp-Type Heating
Abstract
:1. Introduction
2. Mathematical Model
- (i)
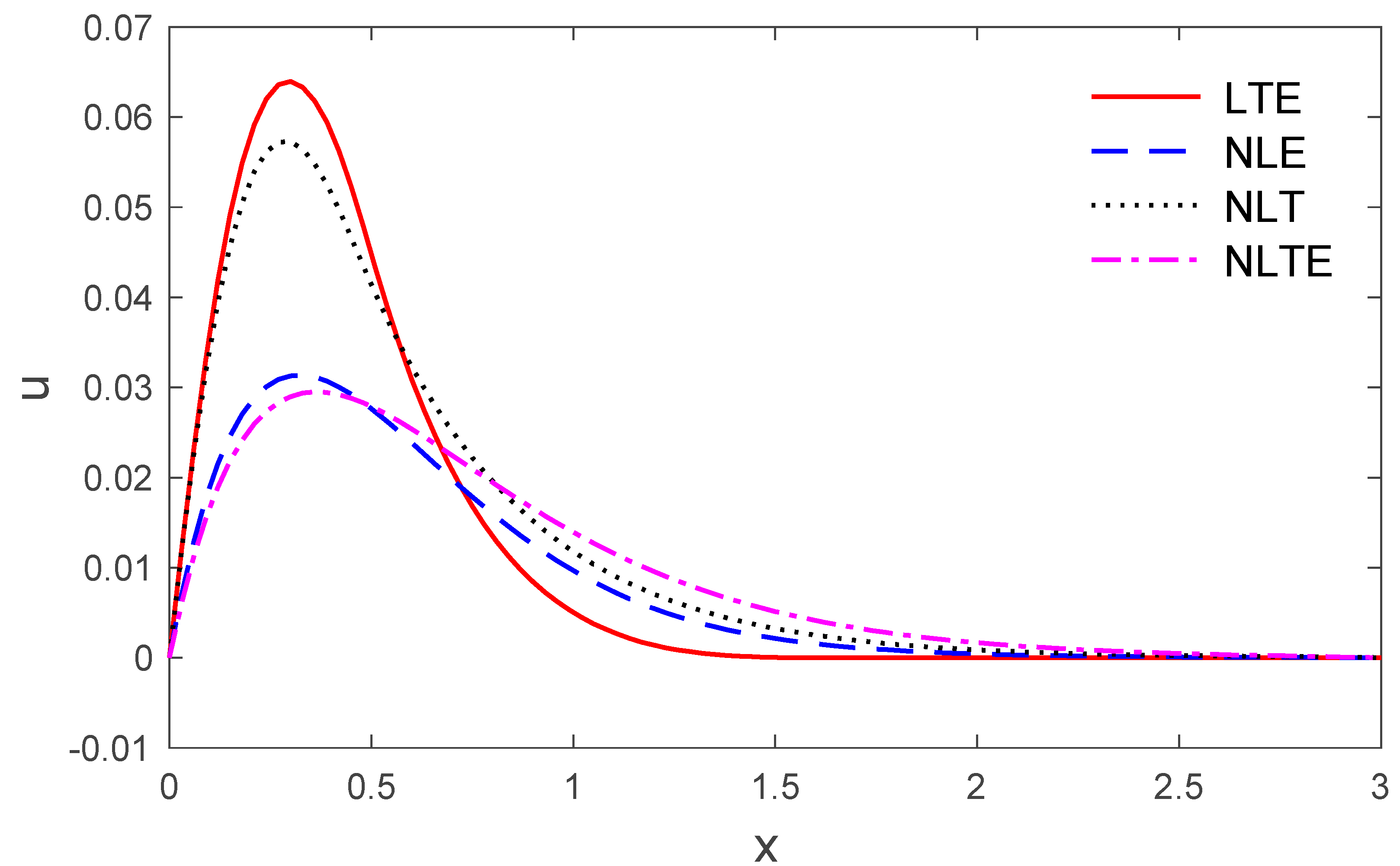
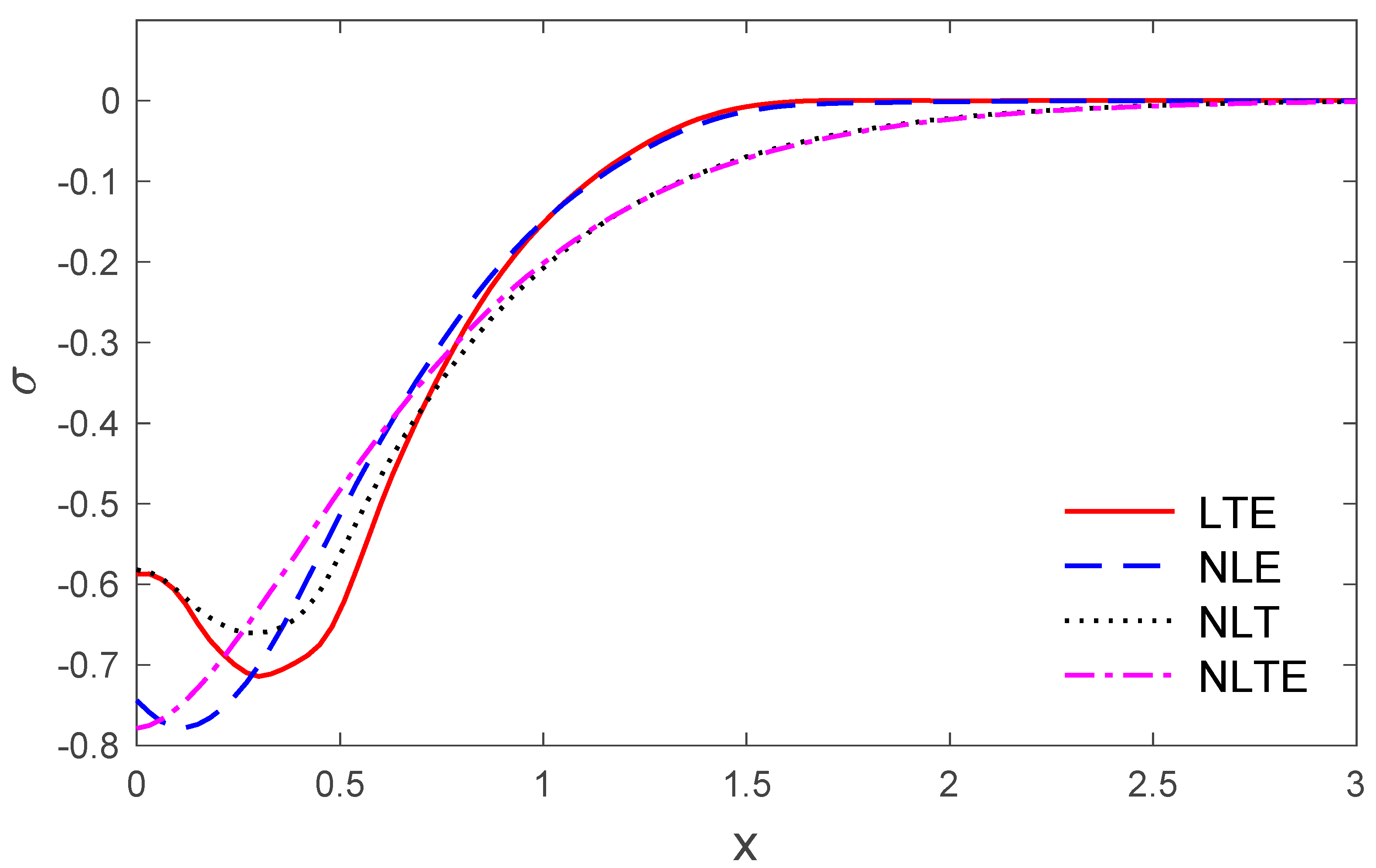
- NTE refers to the nonlocal thermoelastic model
- (ii)
- NT refers to the nonlocal thermal model
- (iii)
- NE refers to the nonlocal elastic model
- (iv)
- LTE refers to the local thermoelastic model
3. Application
4. Results and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the time | |
| the displacements | |
| , | the temperature variations |
| the reference temperature | |
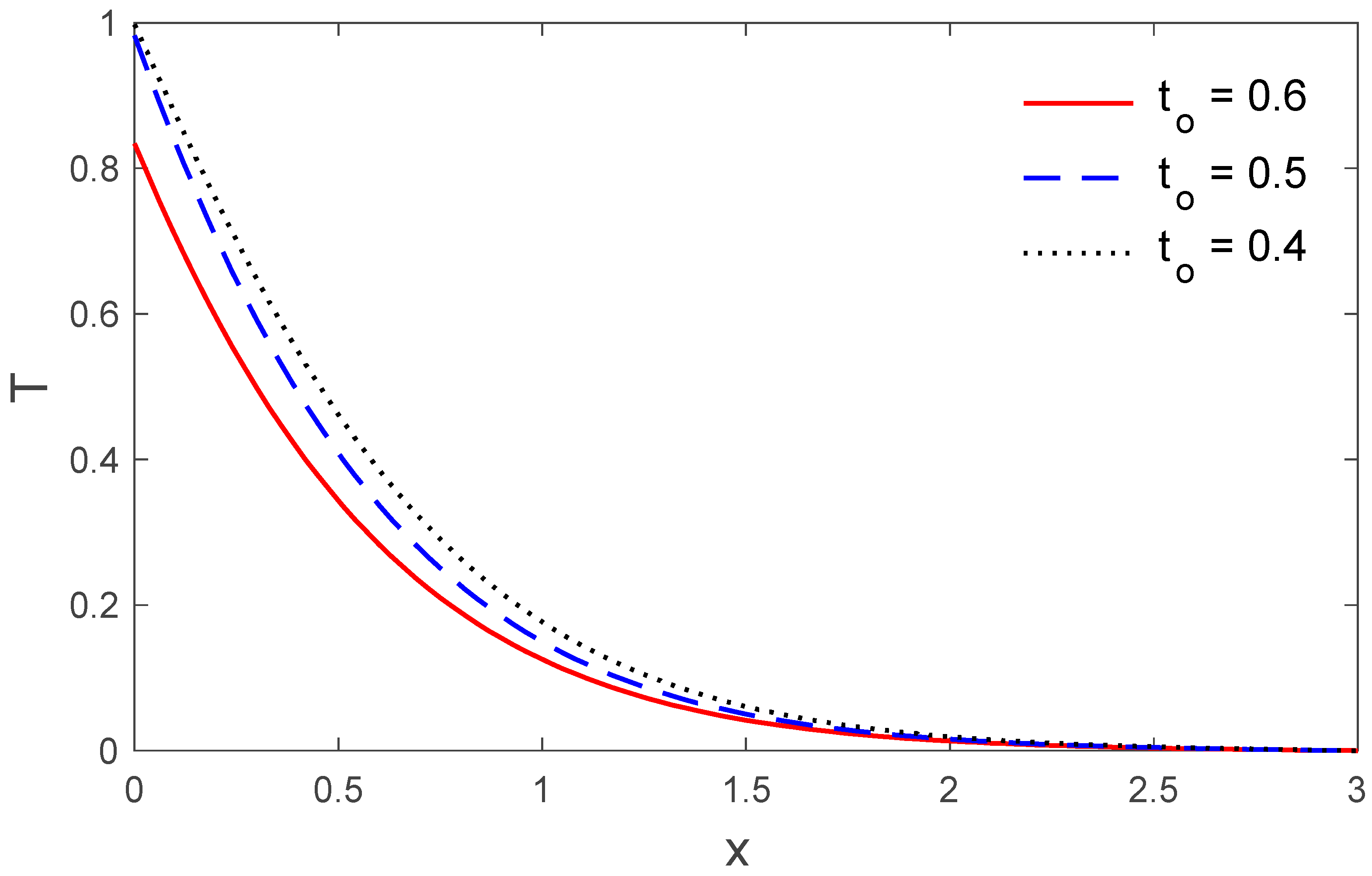
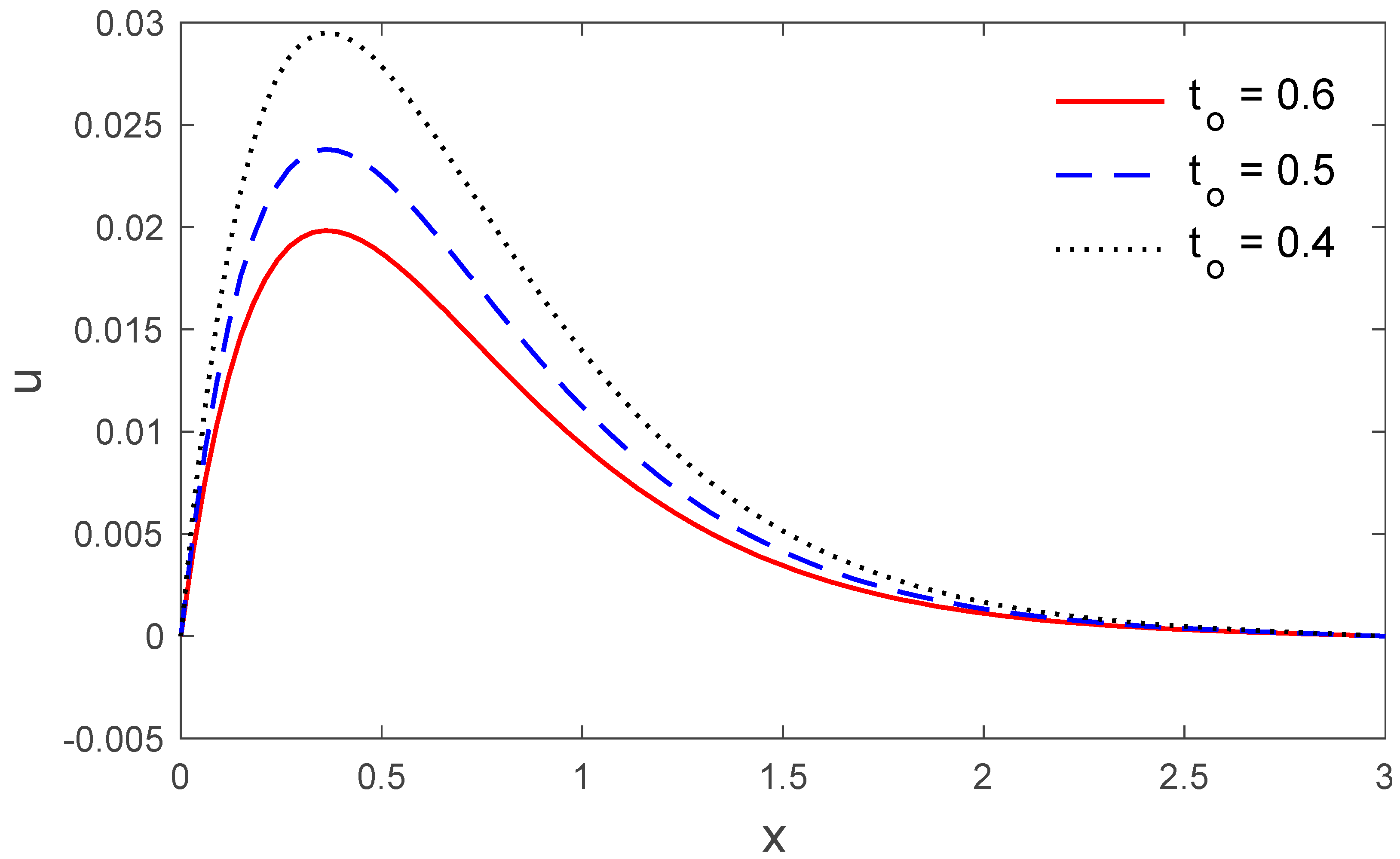
| the ramp type heating parameter | |
| the thermal relaxation time | |
| the specific heat at constant strain | |
| the density of material | |
| the coefficient of linear thermal expansion | |
| the stresses components | |
| the heat conductivity | |
| the Lame’s constants |
References
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of nonlocal thermoelasticity. Int. J. Eng. Sci. 1974, 12, 1063–1077. [Google Scholar] [CrossRef]
- Altan, B. Uniqueness in the linear theory of nonlocal elasticity. Bull. Tech. Univ. Istanb. 1984, 37, 373–385. [Google Scholar]
- Dhaliwal, J.W.R.S. Uniqueness in generalized nonlocal thermoelasticity. J. Therm. Stresses 1993, 16, 71–77. [Google Scholar] [CrossRef]
- Eringen, A.C. Memory-dependent nonlocal electromagnetic elastic solids and superconductivity. J. Math. Phys. 1991, 32, 787–796. [Google Scholar] [CrossRef]
- Povstenko, Y.Z. The nonlocal theory of elasticity and its applications to the description of defects in solid bodies. J. Math. Sci. 1999, 97, 3840–3845. [Google Scholar] [CrossRef]
- Eringen, A.C.; Wegner, J. Nonlocal continuum field theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Narendar, S.; Gopalakrishnan, S. Nonlocal scale effects on ultrasonic wave characteristics of nanorods. Phys. E Low-Dimens. Syst. Nanostructures 2010, 42, 1601–1604. [Google Scholar] [CrossRef]
- Yu, Y.J.; Tian, X.-G.; Liu, X.-R. Size-dependent generalized thermoelasticity using Eringen's nonlocal model. Eur. J. Mech. A/Solids 2015, 51, 96–106. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abouelregal, A.E. Nonlocal thermoelastic vibrations for variable thermal conductivity nanobeams due to harmonically varying heat. J. Vibroengineering 2014, 16, 3665–3678. [Google Scholar]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Eringen, A.C. Mechanics of micromorphic materials. In Applied Mechanics; Springer: Berlin/Heidelberg, Germany, 1966; pp. 131–138. [Google Scholar]
- Eringen, A.C. Theory of micromorphic materials with memory. Int. J. Eng. Sci. 1972, 10, 623–641. [Google Scholar] [CrossRef]
- He, J.-H. A generalized variational principle in micromorphic thermoelasticity. Mech. Res. Commun. 2005, 32, 93–98. [Google Scholar] [CrossRef]
- Abbas, I.A. Analytical solution for a free vibration of a thermoelastic hollow sphere. Mech. Based Des. Struct. Mach. 2015, 43, 265–276. [Google Scholar] [CrossRef]
- Abo-Dahab, S.; Abbas, I.A. LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Appl. Math. Model. 2011, 35, 3759–3768. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Magneto-thermoelastic response of an infinite functionally graded cylinder using the finite element method. J. Vib. Control. 2014, 20, 1907–1919. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, T.; He, C.-H.; Tian, D. Thermal oscillation arising in a heat shock of a porous hierarchy and its application. Facta Univ. Ser. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- He, J.-H.; Abd Elazem, N.Y. Insights into Partial Slips and Temperature Jumps of a Nanofluid Flow over a Stretched or Shrinking Surface. Energies 2021, 14, 6691. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I.A. Analytical solutions of photo-thermo-elastic waves in a non-homogenous semiconducting material. Results in Physics 2018, 10, 385–390. [Google Scholar] [CrossRef]
- Sharma, D.K.; Thakur, P.C.; Sarkar, N. Effect of dual-phase-lag model on free vibrations of isotropic homogenous nonlocal thermoelastic hollow sphere with voids. Mech. Based Des. Struct. Mach. 2020, 1–17. [Google Scholar] [CrossRef]
- Zhang, P.; He, T. A generalized thermoelastic problem with nonlocal effect and memory-dependent derivative when subjected to a moving heat source. Waves Random Complex Media 2020, 30, 142–156. [Google Scholar] [CrossRef]
- Yu, Y.J.; Tian, X.-G.; Xiong, Q.-L. Nonlocal thermoelasticity based on nonlocal heat conduction and nonlocal elasticity. Eur. J. Mech. A/Solids 2016, 60, 238–253. [Google Scholar] [CrossRef]
- Bachher, M.; Sarkar, N. Nonlocal theory of thermoelastic materials with voids and fractional derivative heat transfer. Waves Random Complex Media 2019, 29, 595–613. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Faghidian, S.A.; Shirazi, A.H. Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Univ. Ser. Mech. Eng. 2021, 19, 633–656. [Google Scholar] [CrossRef]
- Sarkar, N. Wave propagation in an initially stressed elastic half-space solids under time-fractional order two-temperature magneto-thermoelasticity. Eur. Phys. J. Plus 2017, 132, 154. [Google Scholar] [CrossRef]
- Ezzat, M.; El-Karamany, A.; El-Bary, A. Modeling of memory-dependent derivative in generalized thermoelasticity. Eur. Phys. J. Plus 2016, 131, 372. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I.; Marin, M. A gl model on thermo-elastic interaction in a poroelastic material using finite element method. Symmetry 2020, 12, 488. [Google Scholar] [CrossRef] [Green Version]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. Aip Adv. 2015, 5, 037113. [Google Scholar] [CrossRef] [Green Version]
- Marin, M. An evolutionary equation in thermoelasticity of dipolar bodies. J. Math. Phys. 1999, 40, 1391–1399. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Shaw, S.; Mukhopadhyay, B. Theory of fractional-ordered thermoelastic diffusion. Eur. Phys. J. Plus 2016, 131, 183. [Google Scholar] [CrossRef]
- Abbas, I.A.; Alzahrani, F.S.; Elaiw, A. A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 2019, 29, 328–343. [Google Scholar] [CrossRef]
- Abbas, I.A.; El-Amin, M.; Salama, A. Effect of thermal dispersion on free convection in a fluid saturated porous medium. Int. J. Heat Fluid Flow 2009, 30, 229–236. [Google Scholar] [CrossRef]
- Sharma, D.K.; Thakur, D.; Sarkar, N. Effect of dual-phase-lag model on the vibration analysis of nonlocal generalized thermoelastic diffusive hollow sphere. Waves Random Complex Media 2020, 18. [Google Scholar] [CrossRef]
- Sarkar, N.; Mondal, S.; Othman, M.I.A. L–S theory for the propagation of the photo-thermal waves in a semiconducting nonlocal elastic medium. Waves Random Complex Media 2020, 14. [Google Scholar] [CrossRef]
- Sharma, D.K.; Bachher, M.; Sharma, M.K.; Sarkar, N. On the Analysis of Free Vibrations of Nonlocal Elastic Sphere of FGM Type in Generalized Thermoelasticity. J. Vib. Eng. Technol. 2021, 9, 149–160. [Google Scholar] [CrossRef]
- Sharma, D.K.; Thakur, P.C.; Sarkar, N.; Bachher, M. Vibrations of a nonlocal thermoelastic cylinder with void. Acta Mech. 2020, 231, 2931–2945. [Google Scholar] [CrossRef]
- Marin, M.; Othman, M.I.A.; Abbas, I.A. An extension of the domain of influence theorem for generalized thermoelasticity of anisotropic material with voids. J. Comput. Theor. Nanosci. 2015, 12, 1594–1598. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Marin, M. Harmonic vibrations in thermoelasticity of microstretch materials. J. Vib. Acoust. Trans. ASME 2010, 132, 0445011–0445016. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Said, S.; Marin, M. A novel model of plane waves of two-temperature fiber-reinforced thermoelastic medium under the effect of gravity with three-phase-lag model. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4788–4806. [Google Scholar] [CrossRef]
- Eringen, A.C. Plane waves in nonlocal micropolar elasticity. Int. J. Eng. Sci. 1984, 22, 1113–1121. [Google Scholar] [CrossRef]
- Eringen, A.C. Microcontinuum Field Theories: I. Foundations and Solids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; Chapman and Hall/CRC: London, UK, 2016. [Google Scholar]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Abbas, I.A. Eigenvalue approach in a three-dimensional generalized thermoelastic interactions with temperature-dependent material properties. Comput. Math. Appl. 2014, 68, 2036–2056. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach for an unbounded medium with a spherical cavity based upon two-temperature generalized thermoelastic theory. J. Mech. Sci. Technol. 2014, 28, 4193–4198. [Google Scholar] [CrossRef]
- Abbas, I.A. A dual phase lag model on thermoelastic interaction in an infinite fiber-reinforced anisotropic medium with a circular hole. Mech. Based Des. Struct. Mach. 2015, 43, 501–513. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Lahiri, A.; Das, B.; Sarkar, S. Eigenvalue approach to thermoelastic interactions in an unbounded body with a spherical cavity. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010; pp. 1881–1886. [Google Scholar]
- Hobiny, A.D.; Abbas, I.A. A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech. Time-Depend. Mater. 2017, 21, 61–72. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abdalla, A.-E.-N.N.; Alzahrani, F.S.; Spagnuolo, M. Wave propagation in a generalized thermoelastic plate using eigenvalue approach. J. Therm. Stresses 2016, 39, 1367–1377. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Alzahrani, F.S.; Abbas, I.A. Photo-thermal interactions in a semiconducting media with a spherical cavity under hyperbolic two-temperature model. Mathematics 2020, 8, 585. [Google Scholar] [CrossRef] [Green Version]
- Bayones, F.S.; Mondal, S.; Abo-Dahab, S.M.; Kilany, A.A. Effect of moving heat source on a magneto-thermoelastic rod in the context of Eringen’s nonlocal theory under three-phase lag with a memory dependent derivative. Mech. Based Des. Struct. Mach. 2021, 1–17. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Abbas, I.; Alshehri, H.; Marin, M. Analytical Solutions of Nonlocal Thermoelastic Interaction on Semi-Infinite Mediums Induced by Ramp-Type Heating. Symmetry 2022, 14, 864. https://doi.org/10.3390/sym14050864
Hobiny A, Abbas I, Alshehri H, Marin M. Analytical Solutions of Nonlocal Thermoelastic Interaction on Semi-Infinite Mediums Induced by Ramp-Type Heating. Symmetry. 2022; 14(5):864. https://doi.org/10.3390/sym14050864
Chicago/Turabian StyleHobiny, Aatef, Ibrahim Abbas, Hashim Alshehri, and Marin Marin. 2022. "Analytical Solutions of Nonlocal Thermoelastic Interaction on Semi-Infinite Mediums Induced by Ramp-Type Heating" Symmetry 14, no. 5: 864. https://doi.org/10.3390/sym14050864
APA StyleHobiny, A., Abbas, I., Alshehri, H., & Marin, M. (2022). Analytical Solutions of Nonlocal Thermoelastic Interaction on Semi-Infinite Mediums Induced by Ramp-Type Heating. Symmetry, 14(5), 864. https://doi.org/10.3390/sym14050864






