An Optimized Neural Network Acoustic Model for Porous Hemp Plastic Composite Sound-Absorbing Board
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
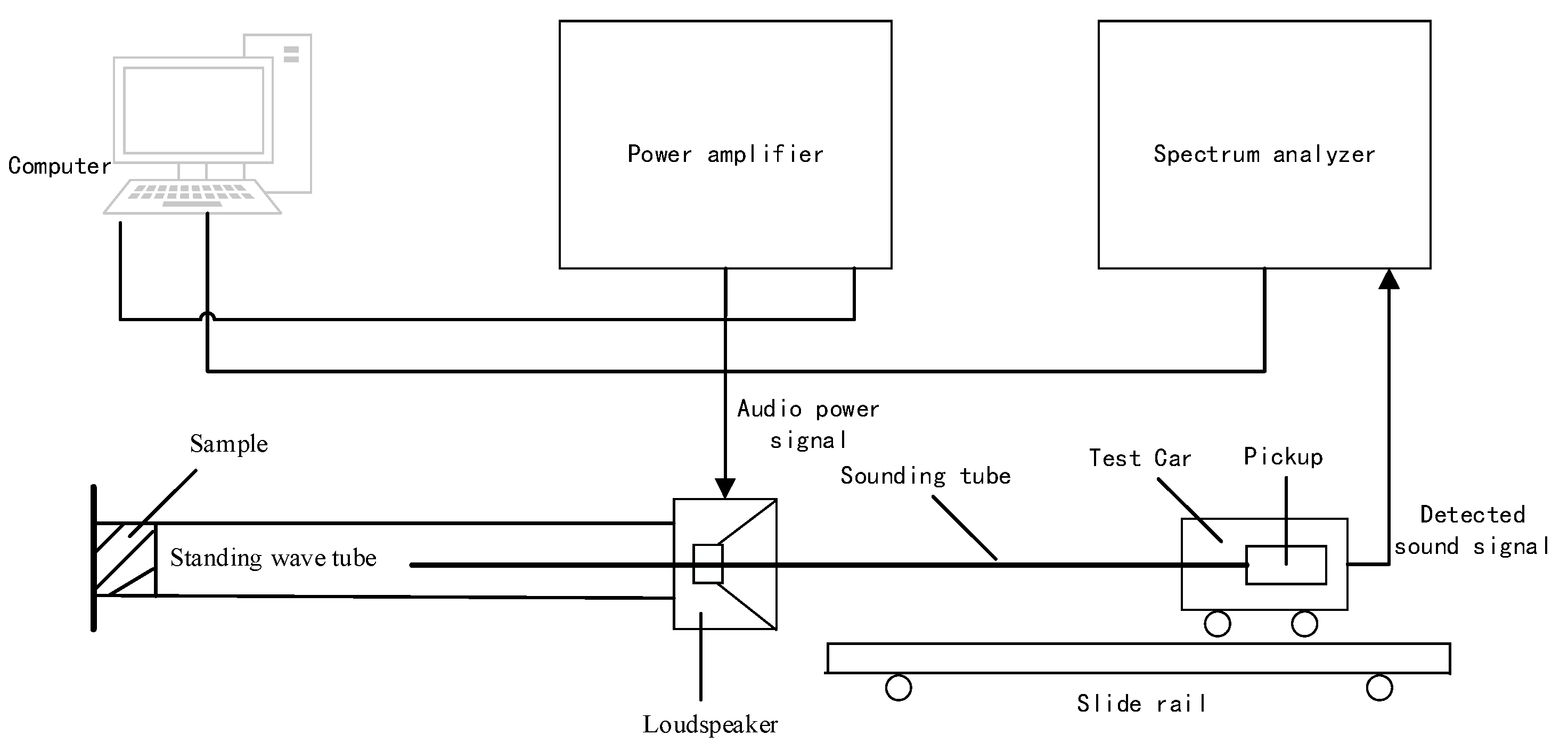
3.1. Obtaining Data
3.2. Proposed Model
3.2.1. Design of the Neural Network Structure
3.2.2. Data Processing
3.2.3. Improved Genetic Algorithm
- (1)
- Initialization and Encoding
- (2)
- Fitness function design
- (3)
- Selection operator
- (4)
- Crossover operator
- (5)
- Mutation operator
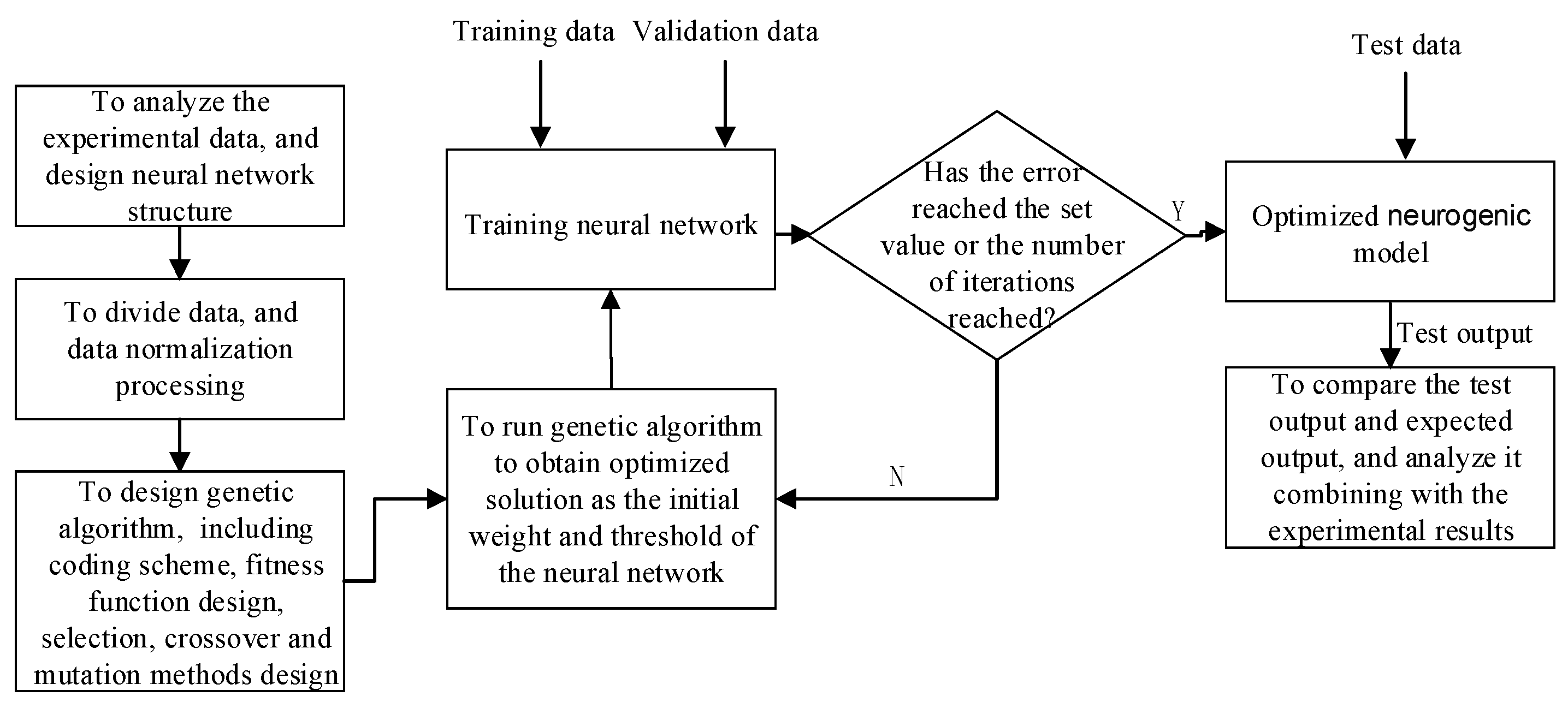
3.2.4. Training of the Neural Network Model
- (1)
- Set the allowable training error , damping constant , number of iterations , initial value = , and let . Then input the weight and threshold obtained by the genetic algorithm into the network, together with the training data, as the initialized weight and threshold vector.
- (2)
- Calculate the network output and error. The error function is shown in Equation (14), where the mean squared error (MSE) is adopted. represents the ideal network output in the formula, , the actual network output, p, the number of specimens, , the vector composed of the weight and threshold of iteration , and , the error generated by specimen .
- (3)
- Calculate the Jacobian matrix according to Equation (15).
- (4)
- Calculate the increment of weight and threshold using the method shown in Equation (16), where represents the unit matrix, is the error matrix of all the specimens, and is the Jacobian matrix.
- (5)
- If is smaller than , the set error value, end the training. If not, continue to step (6).
- (6)
- Update the weight and threshold vector according to Equation (17), calculate the error according to Equation (14), and if , update and according to Equations (18) and (19), respectively, and continue to step (2). Otherwise, update and according to Equations (18) and (20), and then progress to step (4).
3.2.5. Model Testing
4. Experiment Results and Discussion
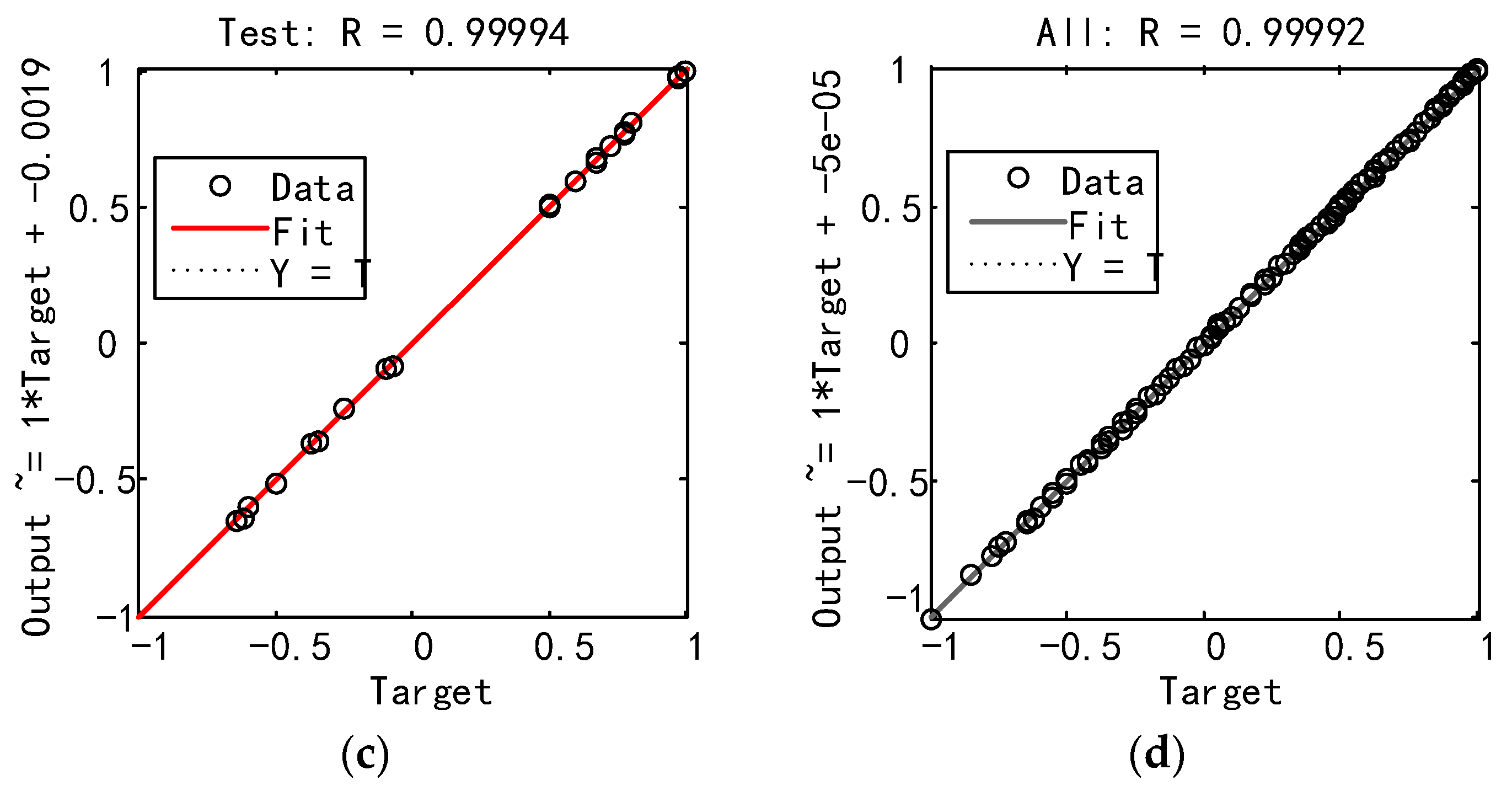
4.1. Test Output Results
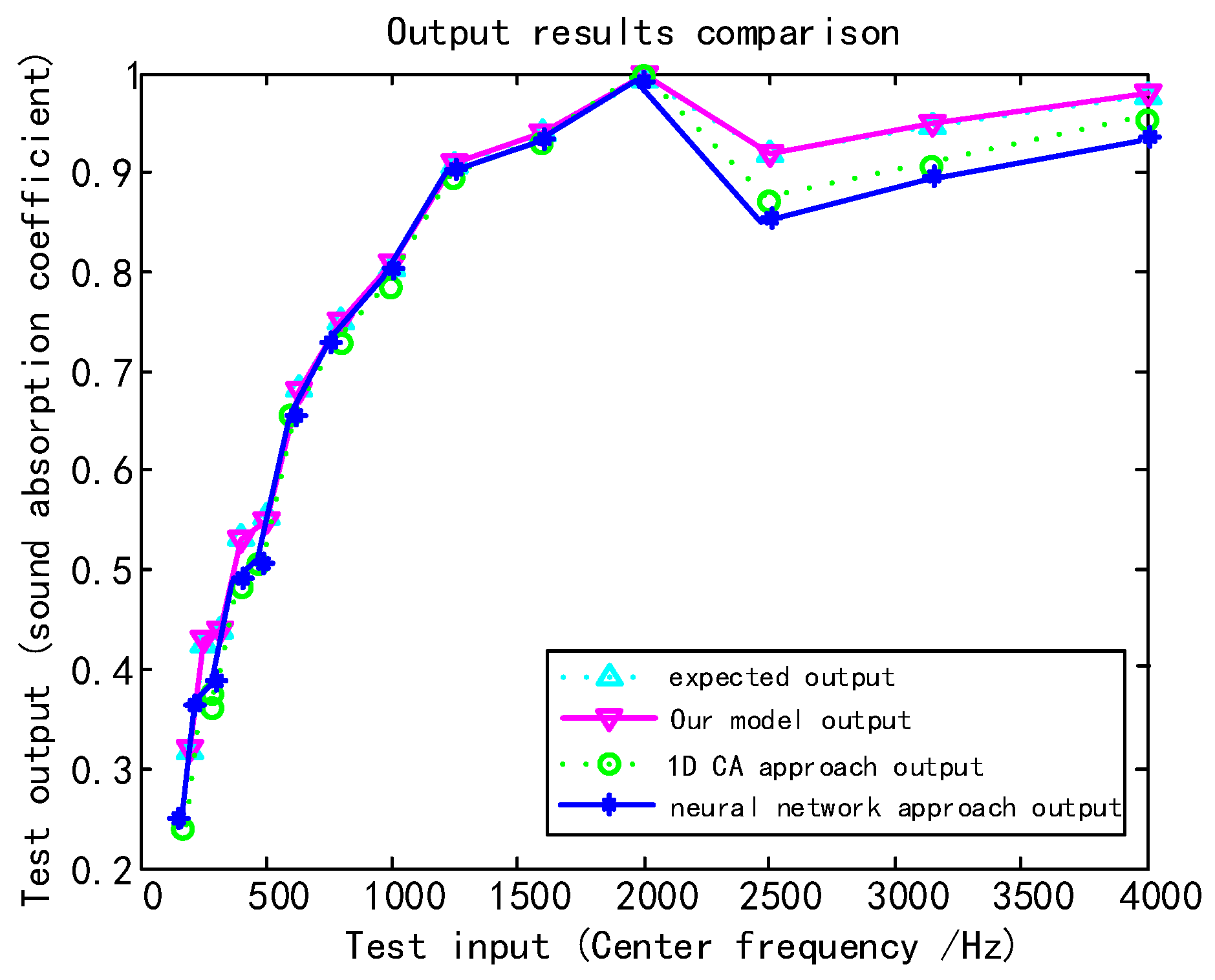
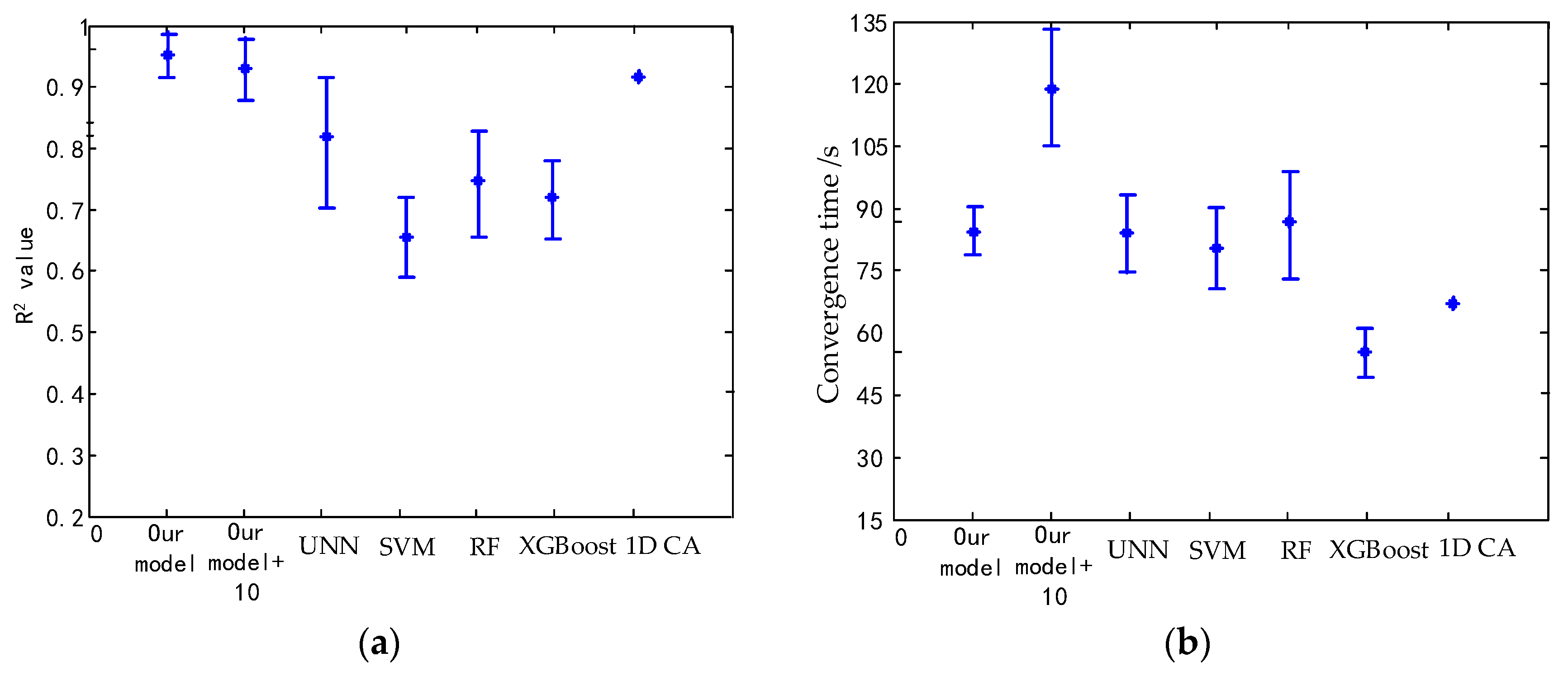
4.2. Comparison of Output Results
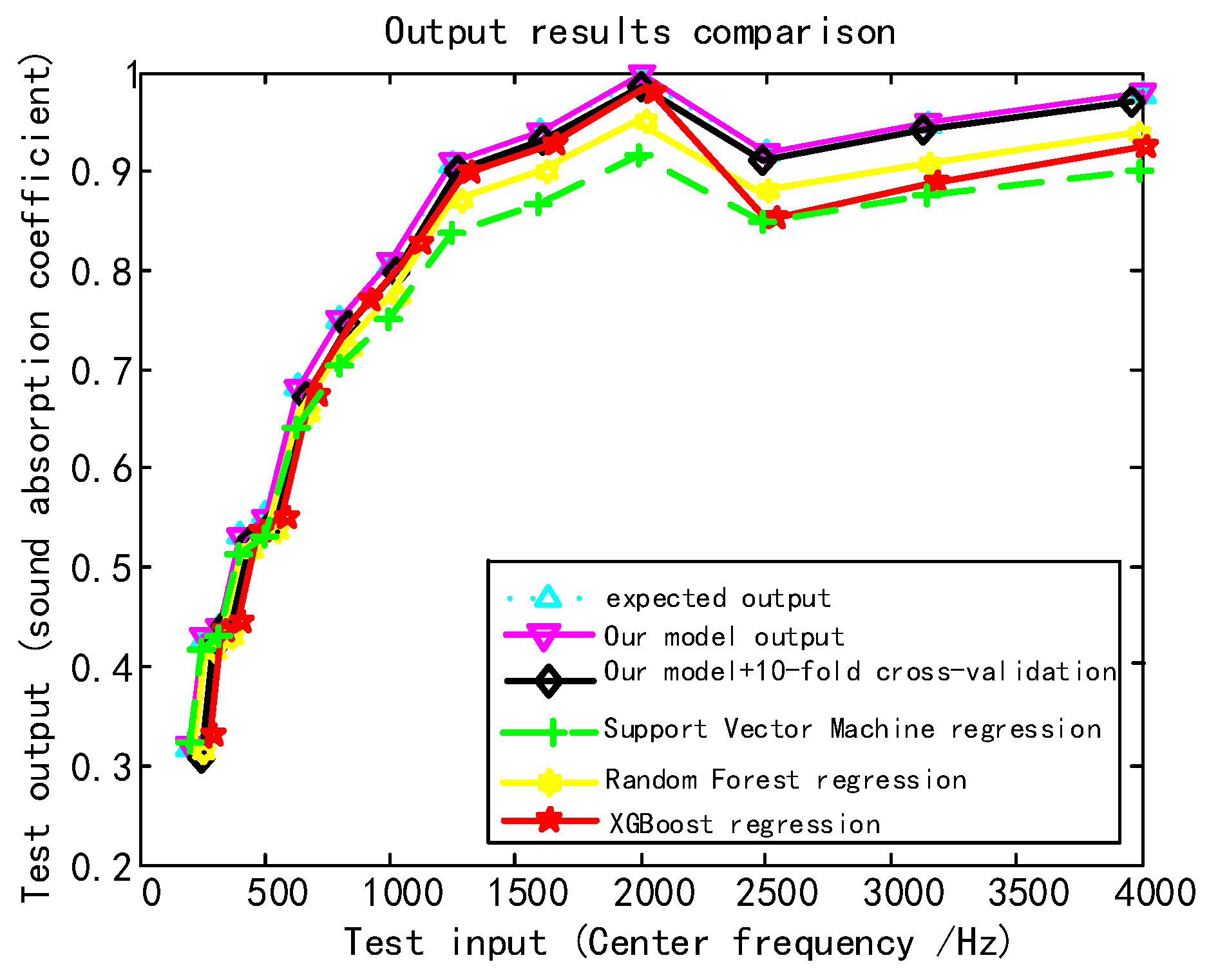
4.3. Validating Efficacy
4.4. Performance Analysis of the Proposed Model
4.4.1. Enhanced Solution Generation
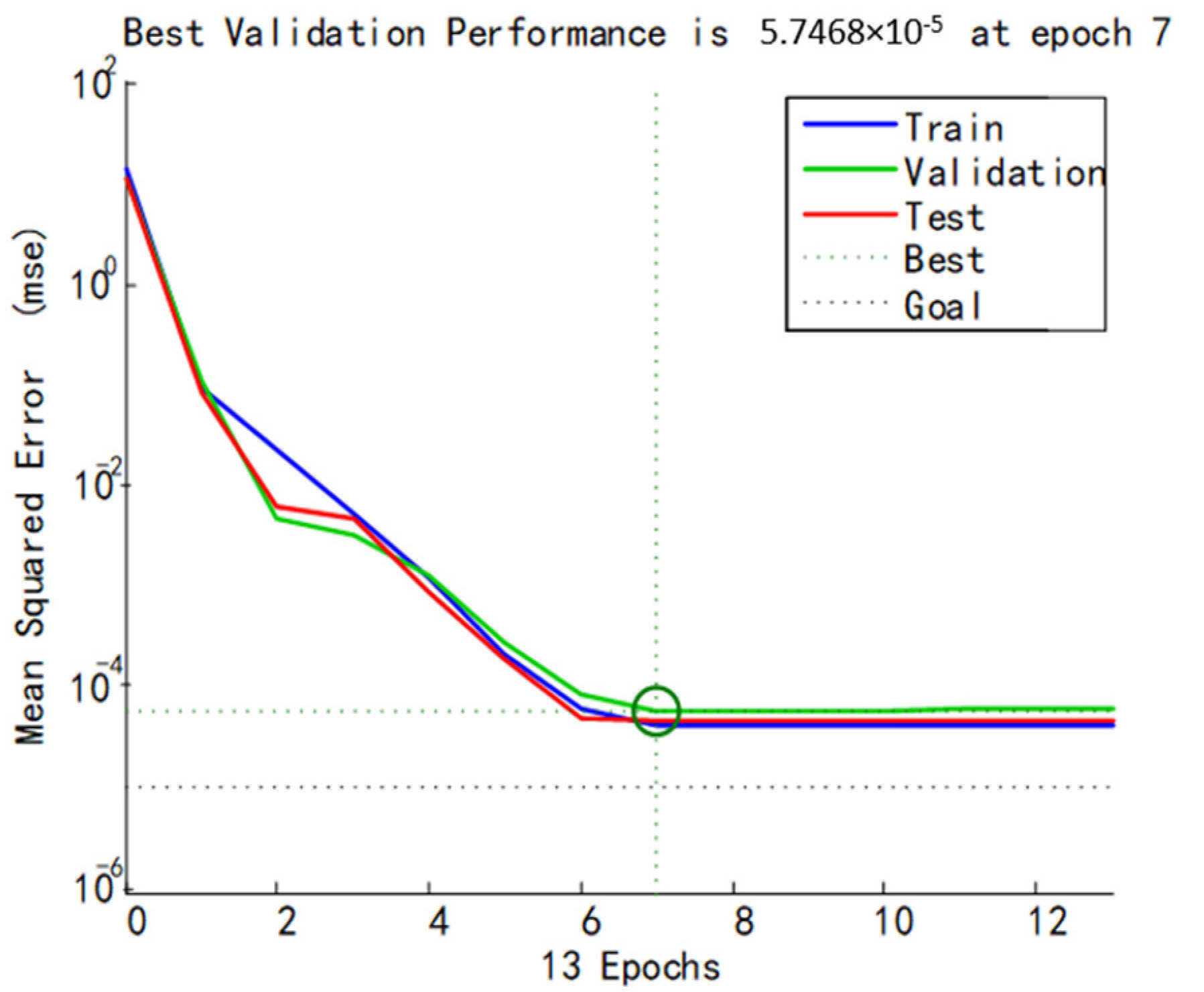
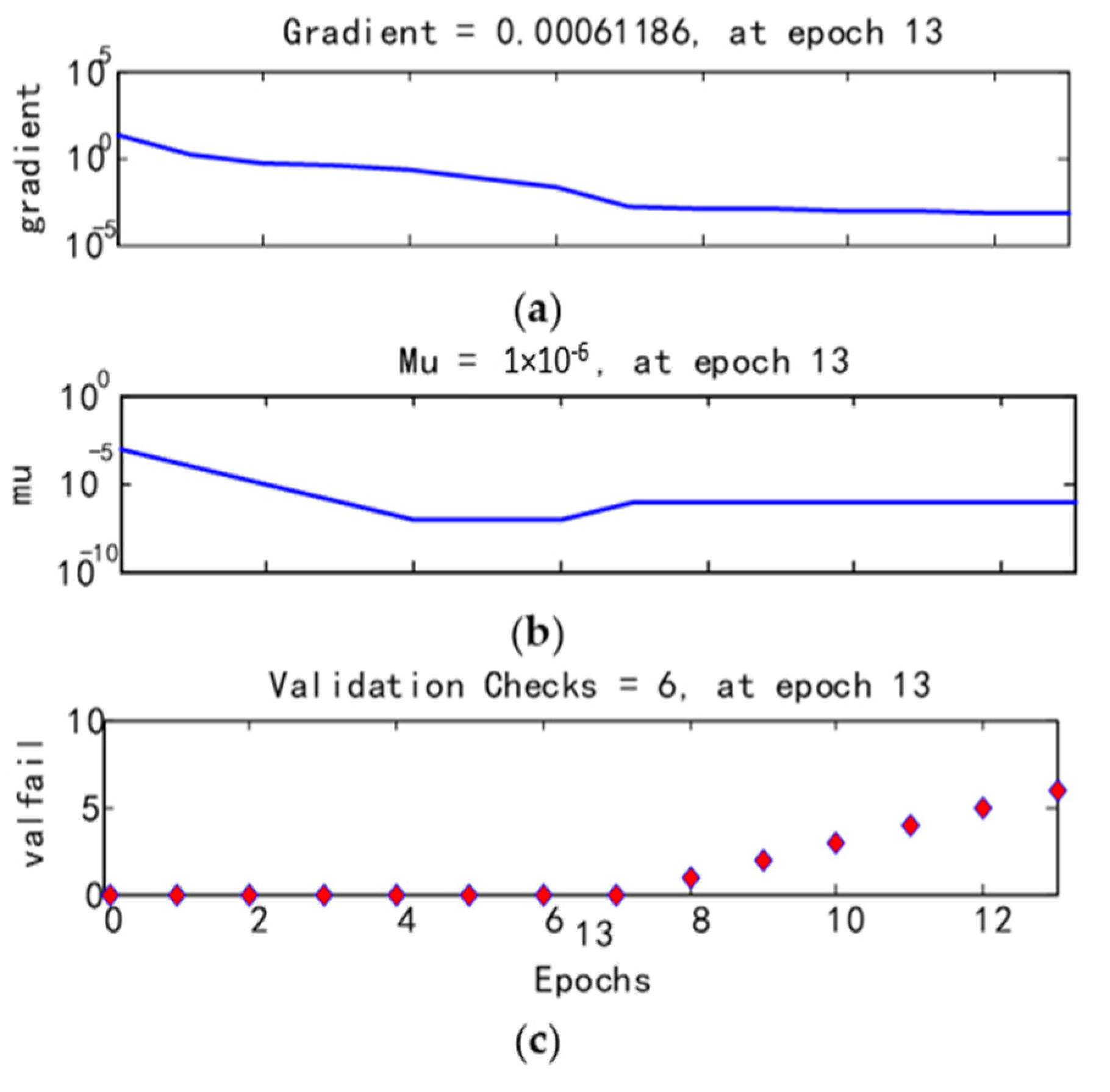
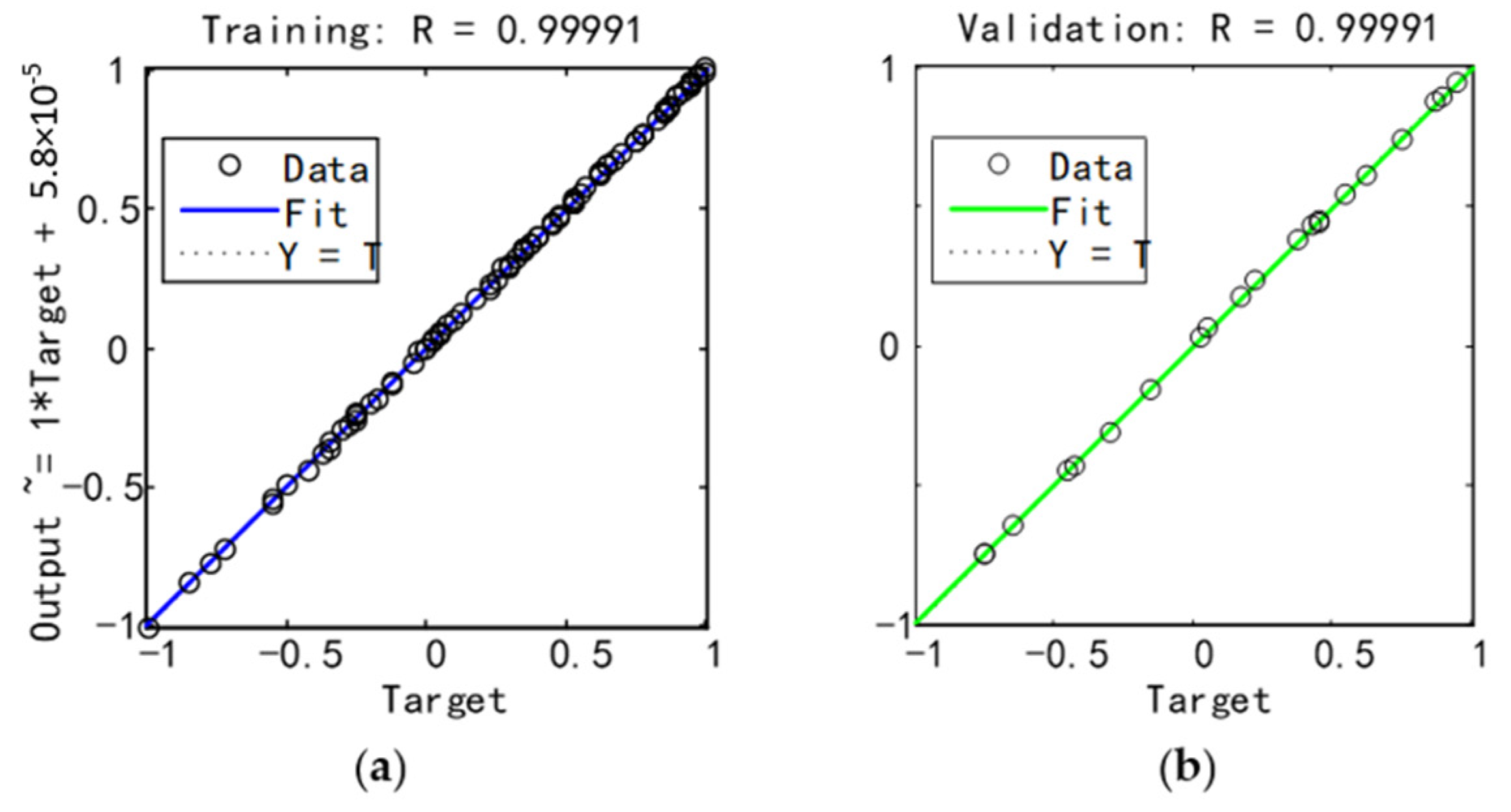
4.4.2. Performance Analysis of Trained Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, J.; Ketzel, M.; Kakosimos, k.; Mette, S.; Jensena, S.S. Road traffic air and noise pollution exposure assessment: A review of tools and techniques. Sci. Total Environ. 2018, 634, 661–676. [Google Scholar] [CrossRef] [PubMed]
- Sordello, R.; Ratel, O.; Flamerie, F.; Léger, C. Evidence of the impact of noise pollution on biodiversity: A systematic map. Environ. Evid. 2020, 9, 20. [Google Scholar] [CrossRef]
- Nazneen, S. Effects of noise pollution on the health of exposed population and its threshold levels. J. Med. Sci. 2017, 25, 366–372. [Google Scholar]
- Peplow, A.; Thomas, J.; Alshehhi, A. Noise Annoyance in the UAE: A Twitter Case Study via a Data-Mining Approach. Int. J. Environ. Res. Public Health 2021, 18, 2198. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zeng, S.; Chen, N.; Shang, D.W. Research progress of ammonia adsorption materials. Chin. J. Process Eng. 2019, 19, 14–24. [Google Scholar]
- Yu, Y.; He, H.L.; Wang, W.Q.; Lu, T.C. The ability of porous brittle materials to absorb and withstand high energy density pulse. Acta Phys. Sin. 2015, 64, 124302. [Google Scholar]
- Luo, J.J. Influence of Polymeric Sand Porous Material on the Aerodynamic Effect when a High-Speed Train is Entering into a Tunnel. J. Residuals Sci. Technol. 2017, 14, S93–S103. [Google Scholar]
- Das, J.; Roy, M.D. A Study of Sound Absorption Properties of Jute Felt Mattress. J. Inst. Eng. 2021, 102, 369–375. [Google Scholar] [CrossRef]
- Ramamoorthy, V.T.; Zcan, E.A.; Parkes, J.; Parkes, A.J.; Jaouen, L. Metaheuristic optimisation of sound absorption performance of multilayered porous materials. In Proceedings of the 23rd International Congress on Acoustics, Aachen, Germany, 9–13 September 2019. [Google Scholar]
- Bai, C.; Shen, M. Sound absorption characteristics of layered composite material with melamine porous material. J. Appl. Acoust. 2019, 38, 76–84. [Google Scholar]
- Mareze, P.H.; Brandao, E.; Fonseca, W.D.; Olavo, M.S.; Lenzi, A. Modeling of acoustic porous material absorber using rigid multiple micro-ducts network: Validation of the proposed model. J. Sound Vib. 2019, 443, 376–396. [Google Scholar] [CrossRef]
- Sun, F.S.; Li, L.J.; Gang, X.Y.; Jiao, X.J.; Dai, X.J. Equivalent model of spatial random array vibration system on sound-absorbing computing for porous material. Appl. Acoust. 2020, 165, 107299. [Google Scholar]
- Gao, N.; Zhang, Z.C.; Tang, L.L.; Hou, H.; Chen, K. Optimal design of broadband quasi-perfect sound absorption of composite hybrid porous metamaterial using TLBO algorithm. Appl. Acoust. 2021, 183, 108296. [Google Scholar] [CrossRef]
- Lee, J.; Jung, I. Tuning sound absorbing properties of open cell polyurethane foam by impregnating graphene oxide. Appl. Acoust. 2019, 151, 10–21. [Google Scholar] [CrossRef]
- Pereira, M.; Mareze, P.H.; Godinho, L.; Amado-Mendes, L.P.; Ramis, J. Proposal of numerical models to predict the diffuse field sound absorption of finite sized porous materials -BEM and FEM approaches. Appl. Acoust. 2021, 180, 108092. [Google Scholar] [CrossRef]
- Liu, Y.J. On the BEM for acoustic wave problems. Eng. Anal. Bound. Elem. 2019, 107, 53–62. [Google Scholar] [CrossRef]
- Gao, N.S.; Tang, L.L.; Deng, J.; Lu, K.; Hou, H.; Chen, K. Design, fabrication and sound absorption test of composite porous metamaterial with embedding I-plates into porous polyurethane sponge. Appl. Acoust. 2021, 175, 107845. [Google Scholar] [CrossRef]
- Hassani, P.; Soltani, P.; Ghane, M.; Zarrebini, M. Porous resin-bonded recycled denim composite as an efficient sound-absorbing material. Appl. Acoust. 2021, 173, 107710. [Google Scholar] [CrossRef]
- Semeniuk, B.P.; Lundberg, E.; Gransson, P. Acoustics modelling of open-cell foam materials from microstructure and constitutive properties. J. Acoust. Soc. Am. 2021, 149, 2016–2026. [Google Scholar] [CrossRef]
- Aniszewska, D.; Rybaczuk, M. Modelling highly porous brittle materials with the movable cellular automata method. In Proceedings of the Central European Symposium on Thermophysics 2019, Rhodes, Greece, 24 July 2019. [Google Scholar]
- Luo, K.; Wang, Z.G. Acellular automata method for acoustic problem. J. Vib. Shock 2021, 40, 69–74. [Google Scholar]
- Plyushchenkov, B.D.; Turchaninov, V.I.; Nikitin, A.A. Modeling of seismic-acoustic fields in axially symmetric absorbing mediums. Problem statement. Mat. Modelirovanie 2017, 29, 62–76. [Google Scholar]
- Bucurica, M.; Dogaru, I.; Dogaru, R. A low complexity method for analyzing acoustic echo signals in the framework of a cellular automata virtual environment. UPB Sci. Bull. Ser. C 2018, 80, 121–132. [Google Scholar]
- Nishawala, V.V.; Ostoja-starzewski, M.M.; Leamy, J.; Demmine, P.N. Simulation of elastic wave propagation using cellular automata and peridynamics, and comparison with experiments. Wave Motion 2016, 60, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Faris, H.; Mirjalili, S.; Aljarah, I. Automatic selection of hidden neurons and weights in neural networks using grey wolf optimizer based on a hybrid encoding scheme. Int. J. Mach. Learn. Cybern. 2019, 10, 2901–2920. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S. An efficient hybrid multilayer perceptron neural network with grasshopper optimization. Soft Comput.—Fusion Found. Methodol. Appl. 2019, 23, 7941–7958. [Google Scholar] [CrossRef]
- Xu, Y.; He, M. Improved artificial neural network based on intelligent optimization algorithm. Neural Netw. World 2018, 28, 345–360. [Google Scholar] [CrossRef] [Green Version]
- Zakaria, A.; Mohamed, A.E.; Ahmed, A.E.; Ye, H.Y.; Zhang, J.H. Forecasting gold price fluctuations using improved multilayer perceptron neural network and whale optimization algorithm. Resour. Policy 2019, 61, 250–260. [Google Scholar]
- Poonguzhali, V.; Deepan, T.; Umar, M.; Sathiya, P. Application of ANN Modelling and GA Optimization for Improved Creep and Corrosion Properties of Spin-Arc Welded AA5083-H111 Alloy. Russ. J. Non-Ferr. Met. 2020, 61, 188–198. [Google Scholar] [CrossRef]
- Badhwar, P.; Kumar, A.; Yadav, A.; Kumar, P.; Siwach, R.; Chhabra, D.; Dubey, K.K. Improved Pullulan Production and Process Optimization Using Novel GA–ANN and GA–ANFIS Hybrid Statistical Tools. Biomolecules 2020, 10, 124. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.Y.; Huang, F.L.; Li, L.; Zhang, C.Y. Optimization of wastewater anaerobic digestion treatment based on GA-BP neural network. Desalination Water Treat. 2018, 122, 30–35. [Google Scholar] [CrossRef]
- Shi, T.Y.; Lai, J.H.; Gu, R.P.; Wei, Z.Q. An Improved Artificial Neural Network Model for Flights Delay Prediction. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2159027. [Google Scholar] [CrossRef]
- Tu, J.S.; Liu, Y.Z.; Zhou, M.; Li, R.X. Prediction and analysis of compressive strength of recycled aggregate thermal insulation concrete based on GA-BP optimization network. J. Eng. Des. Technol. 2020, 19, 412–422. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R. Red deer algorithm (RDA): A new nature-inspired meta-heuristic. Soft Comput. 2020, 24, 14637–14665. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Azari, M.N.; Hajiaghaei-Keshteli, M. An Improved Red Deer Algorithm to Address a Direct Current Brushless Motor Design Problem. Sci. Iran. 2019, 28, 1750–1764. [Google Scholar] [CrossRef] [Green Version]
- Unnisa, N.; Tatineni, M. Adaptive Deep Learning Strategy with Red Deer Algorithm for Sparse Channel Estimation and Hybrid Precoding in Millimeter Wave Massive MIMO-OFDM systems. Wirel. Pers. Commun. 2022, 122, 3019–3051. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R. The Social Engineering Optimizer (SEO). Eng. Appl. Artif. Intell. 2018, 72, 267–293. [Google Scholar] [CrossRef]
- Zhang, C.; Fathollahi-Fard, A.M.; Li, J.Y.; Tian, G.D. Disassembly Sequence Planning for Intelligent Manufacturing Using Social Engineering Optimizer. Symmetry 2021, 13, 663. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Ranjbar-Bourani, M.; Cheikhrouhou, N.; Hajiaghaei-Keshtelib, M. Novel modifications of social engineering optimizer to solve a truck scheduling problem in a cross-docking system. Comput. Ind. Eng. 2019, 137, 106103. [Google Scholar] [CrossRef]
- Wang, X.B. The Cellular Automata Acoustic Modeling of the Porous Material and the Research of Acoustic Performance of the Material Under the Intensive of the High Sound Pressure. Master’s Thesis, Ningxia University, Yinchuan, China, 27 May 2016. [Google Scholar]
- Shafiullah, M.; Rana, M.J.; Shahriar, M.S.; Al-Sulaiman, F.A.; Ahmed, S.D.; Amjad, A. Extreme learning machine for real-time damping of LFO in power system networks. Electr. Eng. 2021, 103, 279–292. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.A.; Al-Mohammed, A.H. Power System Fault Diagnosis: A Wide Area Measurement Based Intelligent Approach, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 397–410. [Google Scholar]









| Center Frequency/Hz | Maximum Sound Pressure/dB | Minimum Sound Pressure/dB |
|---|---|---|
| 200 | 96.9 | 71.8 |
| 250 | 100.7 | 79.8 |
| 315 | 109.6 | 88.3 |
| 400 | 106 | 85.4 |
| 500 | 105 | 85.4 |
| 630 | 90.8 | 73.5 |
| 800 | 90.8 | 74.2 |
| 1000 | 87 | 72.3 |
| 1250 | 73.8 | 61.6 |
| 1600 | 74.5 | 62.1 |
| 2000 | 63.5 | 52.6 |
| 2500 | 54 | 39.8 |
| 3150 | 49.6 | 37.2 |
| 4000 | 47.4 | 37.4 |
| Evolutional Epochs | Population Size | Crossover Probability | Mutation Probability |
|---|---|---|---|
| 100 | 30 | 0.3 | 0.1 |
| Evaluation Index | Our Model | Our Model +10-fold Cross-Validation | 1D CA | Unoptimized Neural Network | Support Vector | Random Forest | XGBoost |
|---|---|---|---|---|---|---|---|
| RMSE | (1.1728 ± 0.312) × 10−6 | (1.1366 ± 0.543) × 10−6 | 2.1846 × 10−4 | (8.691 ± 1.136) × 10−3 | (8.783 ± 1.826) × 10−3 | (5.2765 ± 2.138) × 10−3 | (7.1863 ± 0.768) × 10−3 |
| R2 | 0.95 ± 0.046 | 0.94 ± 0.041 | 0.91 | 0.82 ± 0.06 | 0.65 ± 0.06 | 0.75 ± 0.07 | 0.72 ± 0.06 |
| Convergence time/s | 85 + 6.25 | 121 ± 10.95 | 65.1 | 85 ± 10.9 | 78 ± 7.5 | 83 ± 10.8 | 55 ± 4.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, H.; Lian, Z.; Tan, B.; Zheng, Y.; E, E. An Optimized Neural Network Acoustic Model for Porous Hemp Plastic Composite Sound-Absorbing Board. Symmetry 2022, 14, 863. https://doi.org/10.3390/sym14050863
Wang H, Zhao H, Lian Z, Tan B, Zheng Y, E E. An Optimized Neural Network Acoustic Model for Porous Hemp Plastic Composite Sound-Absorbing Board. Symmetry. 2022; 14(5):863. https://doi.org/10.3390/sym14050863
Chicago/Turabian StyleWang, Haizhen, Hong Zhao, Zuozheng Lian, Bin Tan, Yongjie Zheng, and Erdun E. 2022. "An Optimized Neural Network Acoustic Model for Porous Hemp Plastic Composite Sound-Absorbing Board" Symmetry 14, no. 5: 863. https://doi.org/10.3390/sym14050863
APA StyleWang, H., Zhao, H., Lian, Z., Tan, B., Zheng, Y., & E, E. (2022). An Optimized Neural Network Acoustic Model for Porous Hemp Plastic Composite Sound-Absorbing Board. Symmetry, 14(5), 863. https://doi.org/10.3390/sym14050863





