Reliability Estimation for Stress-Strength Model Based on Unit-Half-Normal Distribution

Abstract

Many lifetime distribution models have successfully served as population models for risk analysis and reliability mechanisms. We propose a novel estimation procedure of stress–strength reliability in the case of two independent unit-half-normal distributions can fit asymmetrical data with either positive or negative skew, with different shape parameters. We obtain the maximum likelihood estimator of the reliability, its asymptotic distribution, and exact and asymptotic confidence intervals. In addition, confidence intervals of model parameters are constructed by using bootstrap techniques. We study the performance of the estimators based on Monte Carlo simulations, the mean squared error, average bias and length, and coverage probabilities. Finally, we apply the proposed reliability model in data analysis of burr measurements on the iron sheets.

1. Introduction

Recently, ref. [1] introduced a new distribution defined on the unit interval with one parameter and simple structure based on the half normal distribution, called the unit-half-normal distribution, as a good alternative to the Topp–Leone distribution [2], Kumaraswamy distribution [3], unit-logistic distribution [4], beta distribution of two parameters (or the Pearson type IV distribution) [5], unit-Birnbaum–Saunders distribution [6], and unit-Lindley distribution [7], among others. The probability density function (PDF) of the unit-half-normal distribution is as follows

$$f_X(x;\eta )=\frac{2}{\eta {(1-x)}^2}\varphi \left(\frac{x}{\eta (1-x)}\right),0\le x<1,$$

(1)

where $\eta >0$ is a scale parameter and $\varphi (·)$ is the PDF of the standard normal distribution. From now on, a random variable X with PDF defined in (1) will be denoted by $UHN\left(\eta \right)$. The corresponding cumulative distribution function (CDF) is

$$F_X(x;\eta )=2\Phi \left(\frac{x}{\eta (1-x)}\right)-1,$$

(2)

where $\Phi (·)$ is the CDF of the standard normal distribution. Figure 1 and Figure 2 illustrate some of the possible shape of the unit-half-normal distribution for selected values of the parameter $\eta$. From these figures, we observed that, the PDF shapes are unimodal and asymmetric (left and right skewed). As showed by [1], the unit-half-normal distribution belongs the exponential family of probability distributions.

Figure 1. Plot of density function of UHN distribution for $0<\eta <1$.

Figure 2. Plot of density function of UHN distribution for $\eta >1$.

The literature demonstrates that estimation of the stress–strength model, $R=P(Y<X)$, has already been performed assuming that X and Y are independent random variables with positive support and different degrees of skewness and kurtosis described by the same kind of probability distribution. We refer the reader to [8] for a review and the references therein for more information on this claim. Much less attention is given when X and Y take values in a limited range, such as proportions, percentages and fractions. The main goal of this work is to develop the inferential procedure of the stress–strength parameter R, when X and Y are independent $UHN\left(\eta \right)$ and $UHN\left(\lambda \right)$, respectively. We can note the important role in the reliability analysis played the stress–strength parameter. Let X and Y denote, respectively, the stress and the strength. We say that the system is failed if the used stress is greater than its strength, in one active system.

The rest of the paper is structured as follows. The next section presents the entropy and mean residual life of a random variable with $UHN$ distribution. Then, we present an expression for the stress–strength reliability (R), MLE of R, its exact distribution and some properties, and three algorithms to simulate random variables from R. In the subsequent section, confidence intervals for R are developed by means of exact, asymptotic and bootstrap approaches. Next, the computational simulations are presented to evaluate the performance of the MLE and exact, asymptotic and bootstrap confidence intervals, followed by the section containing an application in the context burr measurements on the iron sheets. Finally, some concluding remarks are presented in the last section.

2. Entropy and Mean Residual Life

In this section, we present the entropy and mean residual life for a random variable with $UHN$ distribution.

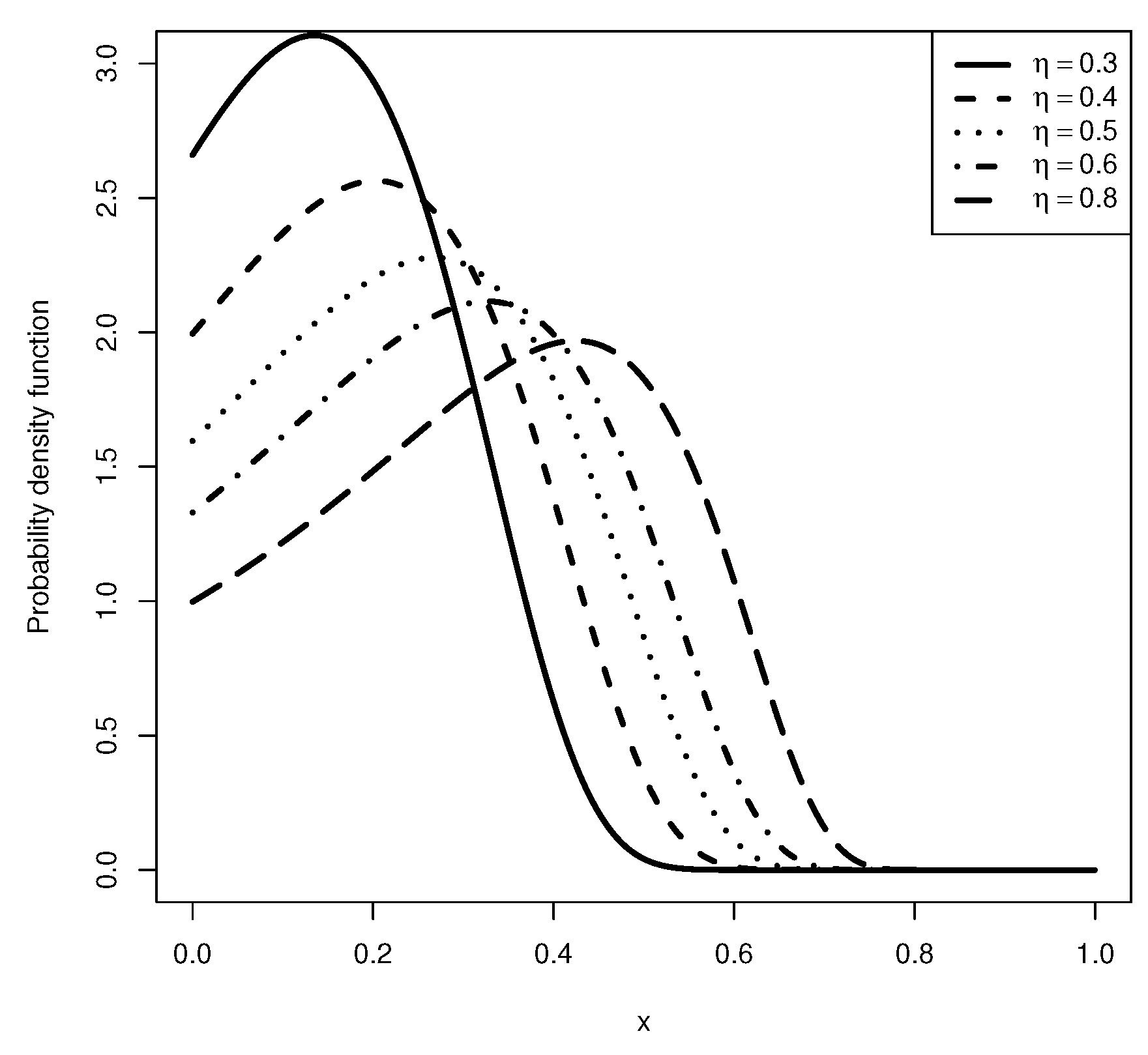
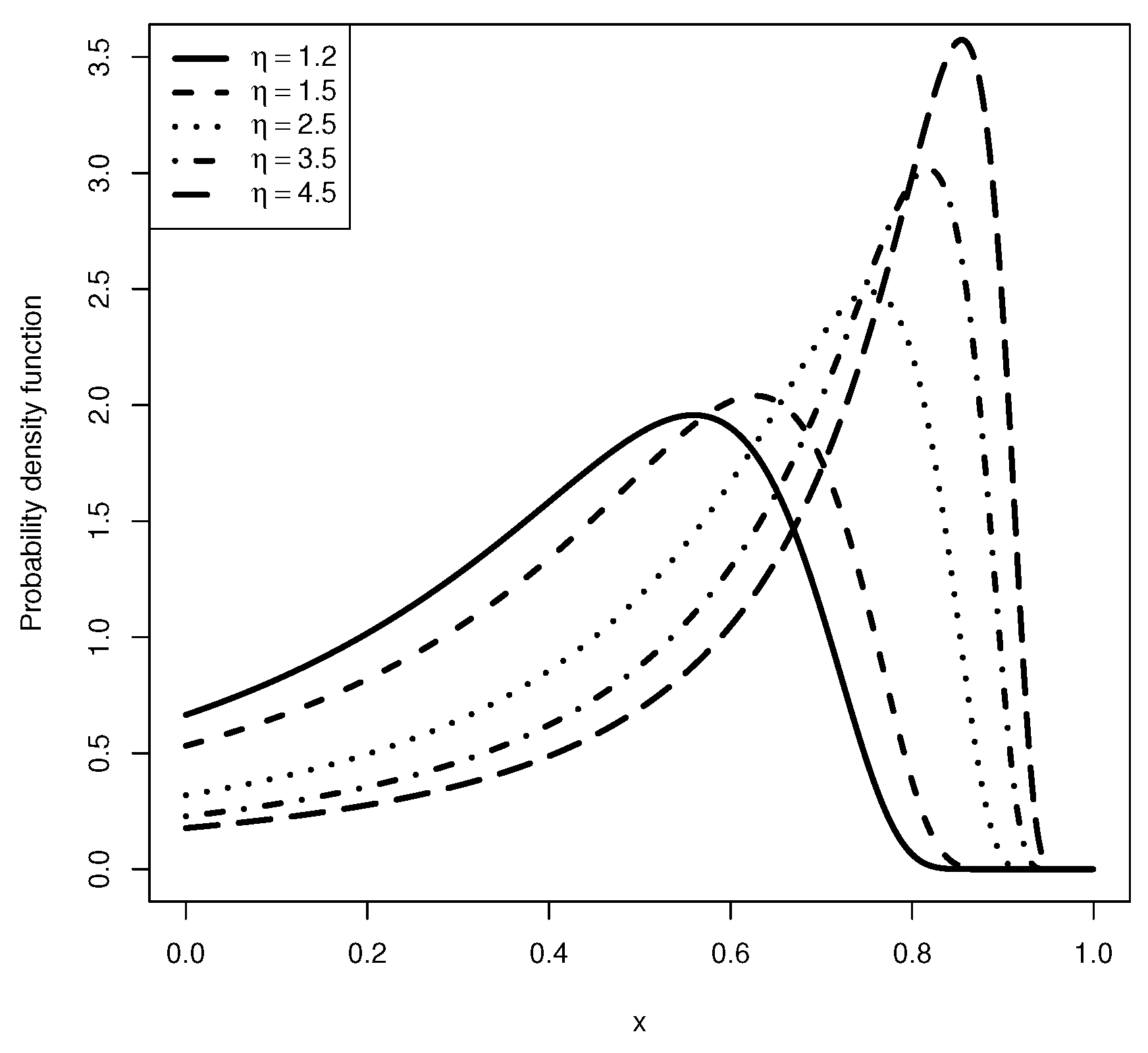
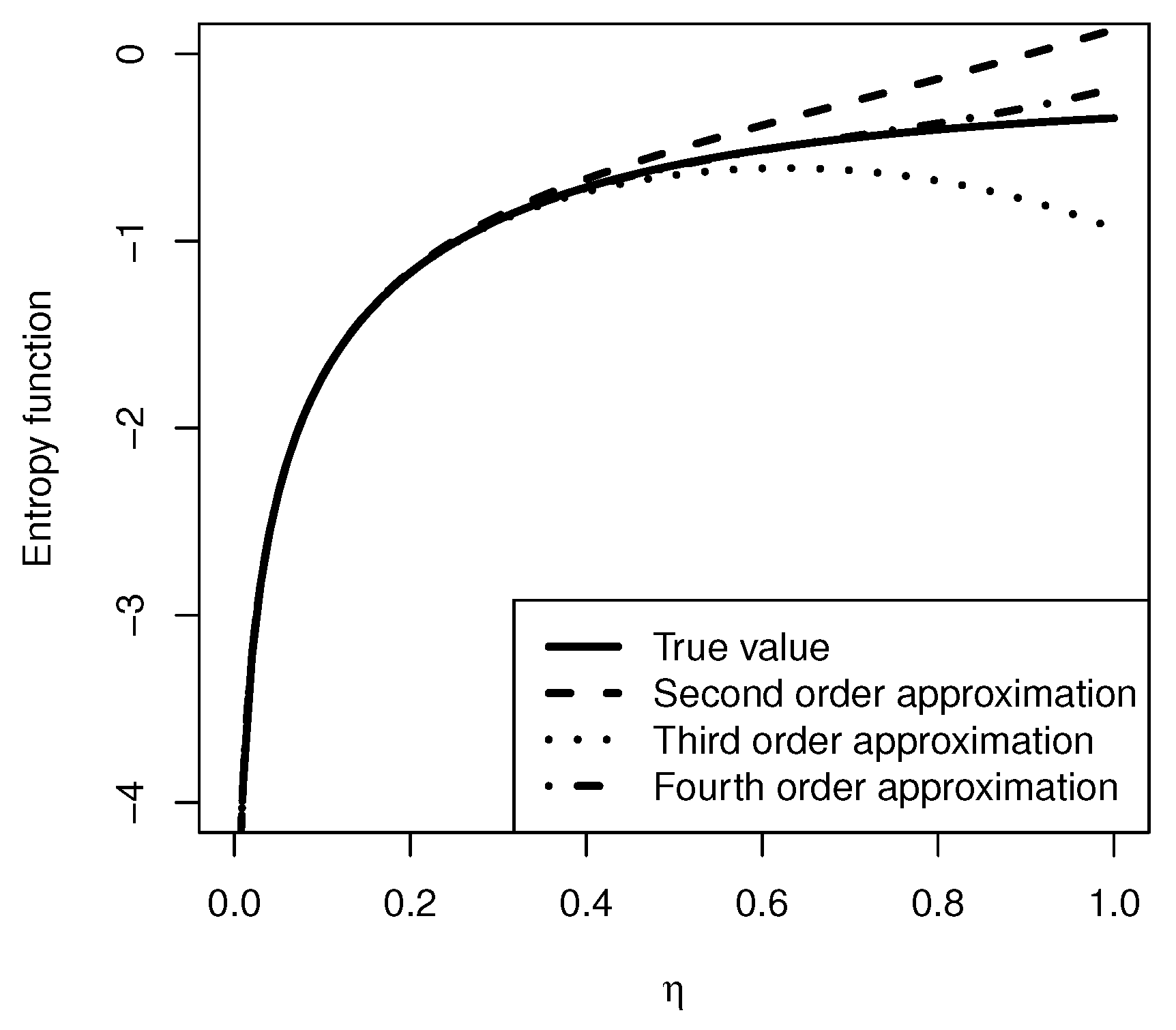
2.1. Entropy

The entropy of a random variable X with PDF (1) is a measure of variation of the uncertainty. A large value of entropy indicate the grater uncertainty in the data. Using $U=\frac{X}{\eta (1-X)}$ and numerical integration, it is possible to calculate the entropy as a function of the scale parameter $\eta$. Then the Shannon entropy [9], defined by $\mathbb{E}(-log{f}_X\left(x\right))$, is equal to

$$\begin{array}{cc}\hfill \xi :=\mathbb{E}(-log{f}_X\left(x\right))& =\frac{1}{2}+\frac{1}{2}log\left(\frac{\pi {\eta }^2}{2}\right)\hfill \\ \hfill & -4{\int }_0^{\infty }log(1+\eta u)\varphi \left(u\right)du.\hfill \end{array}$$

Using the Taylor expansion for $log(1+x)$ around zero, but instead of x, we have $0<\eta u<1$.

$$\xi =\frac{1}{2}+\frac{1}{2}log\left(\frac{\pi {\eta }^2}{2}\right)-4{\int }_0^{\infty }\varphi \left(u\right)\sum _{k=1}^{\infty }\frac{{(-1)}^{k+1}}{k}{\eta }^k{u}^{k}du.$$

Thus, by interchanging the order of the summation and the integration, the final form of the entropy is given by

$$\xi \simeq \frac{1}{2}+\frac{1}{2}log\left(\frac{\pi {\eta }^2}{2}\right)-\frac{1}{\sqrt{\pi }}\sum _{k=1}^{\infty }\frac{{(-1)}^{k+1}{2}^{1+\frac{k}{2}}}{k}{\eta }^k\Gamma \left(\frac{1+k}{2}\right).$$

(3)

Figure 3 shows the value of (3) for true value for $\eta$ from zero to one. The real value was computed by numerical integration. The software R [10] provides this option with the function integrate.

Figure 3. Entropy values for a range of values of $\eta$.

We can note that the second and third order approximation is not as good as the fourth order ones. However, all approximations are good especially for values of $0<\eta <1/2$.

2.2. Mean Residual Life

The mean residual life or life expectancy is an important characteristic of the model. It gives the expected additional lifetime given that a component has survived until time t. For a non-negative continuous random variable $X\sim UHN\left(\eta \right)$ the mean residual life function is defined as

$$\mathbb{E}(X-t|X>t)=\mathbb{E}(X|X>t)-t,$$

where $t\in (0,1)$. The above conditional expectation is given by

$$\begin{array}{cc}\hfill \mathbb{E}\left(X\right|X>t)& ={\int }_t^1\frac{x{f}_X\left(x\right)}{P(X>t)}dx\hfill \\ \hfill & ={\int }_t^1\frac{x{f}_X\left(x\right)}{1-F_X\left(t\right)}dx.\hfill \end{array}$$

(4)

Calculation of the numerator is done in the same way as the calculation of the mean. Thus

$$\begin{array}{ccc}\hfill {\int }_t^{1}x{f}_X\left(x\right)dx& =& 2{\int }_t^1\frac{x}{\eta {(1-x)}^2}\varphi \left(\frac{x}{\eta (1-x)}\right)dx\hfill \\ & =& 2{\int }_{\frac{t}{\eta (1-t)}}^{\infty }\frac{\eta u}{1+\eta u}\varphi \left(u\right)du,\hfill \end{array}$$

where $\eta u=x/(1-x)$.

Finally, Equation (4) can be written as

$$\mathbb{E}(X-t|X>t)=\frac{{\int }_{\frac{t}{\eta (1-t)}}^{\infty }\frac{\eta u}{1+\eta u}\varphi \left(u\right)du}{\Phi \left(\frac{t}{\eta (t-1)}\right)}-t.$$

The integral of the numerator can be calculated with numerical methods. More on mean residual life, we refer our readers to [11], among others

3. Stress–Strength Reliability Model

An expression for the stress–strength reliability R is given by the following theorem.

Theorem 1.

Suppose X and Y are random variables independently distributed as $X\sim UHN\left(\eta \right)$ and $Y\sim UHN\left(\lambda \right)$, the reliability of the system with stress variable (Y) and strength variable (X) is given by

$$R=P(Y<X)=\frac{2}{\pi }arctan\left(\frac{\eta }{\lambda }\right),\eta >0,\lambda >0.$$

(5)

Proof of Theorem 1.

Using the Equations (1) and (2) with $x/(1-x)=\eta u$ we have

$$\begin{array}{cc}\hfill P(Y<X)& ={\int }_0^1{F}_Y\left(x\right)f_X\left(x\right)dx\hfill \\ \hfill & ={\int }_0^1\left[2\Phi \left(\frac{x}{\lambda (1-x)}\right)-1\right]\hfill \\ \hfill & \times \frac{2}{\eta {(1-x)}^2}\varphi \left(\frac{x}{\eta (1-x)}\right)dx\hfill \\ \hfill & =2{\int }_0^1\frac{2}{\eta {(1-x)}^2}\varphi \left(\frac{x}{\eta (1-x)}\right)\hfill \\ \hfill & \times \Phi \left(\frac{x}{\lambda (1-x)}\right)dx-1\hfill \\ \hfill & =2{\int }_0^{\infty }2\varphi \left(u\right)\Phi \left(\frac{\eta }{\lambda }u\right)du-1\hfill \\ \hfill & =\frac{2}{\pi }arctan\left(\frac{\eta }{\lambda }\right).\hfill \end{array}$$

   □

Since $\eta \ge \lambda$ ($\eta \le \lambda$) then $P(Y>X)\ge 0.5$ ($P(Y>X)\le 0.5$). We can note that $P(Y>X)$ can be computed by Equation (5) when $\eta$ and $\lambda$ are known. We then focus on estimating $\eta$ and $\lambda$.

3.1. Maximum Likelihood Estimation of R

Before we move on to calculate the maximum likelihood estimation of R, some results are necessary.

Lemma 1.

If $X\sim UHN\left(\eta \right)$ then $\frac{X}{1-X}\sim HN\left(\eta \right)$.

Proof of Lemma 1.

See [1].    □

Corollary 1.

If $\frac{X}{1-X}\sim HN\left(\eta \right)$ then $\frac{1}{{\eta }^2}{\left(\frac{X}{1-X}\right)}^2\sim {\chi }_{\left(1\right)}^2$, where ${\chi }_{\left(1\right)}^2$ denotes the chi-squared distribution with 1 degree of freedom.

Proof of Corollary 1.

Let $Z=\frac{1}{{\eta }^2}{\left(\frac{X}{1-X}\right)}^2$

$$\begin{array}{cc}\hfill P(Z\le z)& =P\left({\left(\frac{X}{1-X}\right)}^2\le {\eta }^{2}z\right)=P\left(\frac{X}{1-X}\le \eta \sqrt{z}\right)\hfill \\ \hfill & =2\Phi \left(\sqrt{z}\right)-1.\hfill \end{array}$$

The derivative of $P(Z\le z)$ gives the PDF of ${\chi }_{\left(1\right)}^2$.    □

Corollary 2.

If $U_i=\frac{X_i}{1-X_i}\sim HN\left(\eta \right)$, $i=1,\dots ,n$, and $V_j=\frac{Y_j}{1-Y_j}\sim HN\left(\lambda \right)$, $j=1,\dots ,m$, with $U_i$ independent of $V_i$, then

1.

${\sum }_{i=1}^n{\left(\frac{U_i}{\eta }\right)}^2\sim {\chi }_{\left(n\right)}^2$ and ${\sum }_{j=1}^m{\left(\frac{V_j}{\lambda }\right)}^2\sim {\chi }_{\left(m\right)}^2$

2.

$\mathbb{E}\left({\widehat{\eta }}^2\right)={\eta }^2$ and $\mathbb{E}\left({\widehat{\lambda }}^2\right)={\lambda }^2$

3.

${\left(\frac{\widehat{\eta }}{\widehat{\lambda }}\right)}^2{\left(\frac{\lambda }{\eta }\right)}^2\sim F_{(n,m)}$

4.

$\mathbb{E}\left(\frac{{\widehat{\eta }}^2}{{\widehat{\lambda }}^2}\right)=\frac{m}{m-2}\left(\frac{{\eta }^2}{{\lambda }^2}\right),m>2$.

Now, suppose ${(X_1,X_2,\dots ,X_n)}^{\prime }$ is a random sample of size n from $UHN\left(\eta \right)$ and ${(Y_1,Y_2,\dots ,Y_m)}^{\prime }$ is a independent random sample of size m from $UHN\left(\lambda \right)$ with $\eta >0$ and $\lambda >0$. The log-likelihood is given by

$$\begin{array}{cc}\hfill l(\eta ,\lambda )& =\sum _{i=1}^{n}log{f}_X(x_i;\eta )+\sum _{j=1}^{n}log{f}_Y(y_j;\lambda )\hfill \\ \hfill & =-nlog\eta -mlog\lambda -2\sum _{i=1}^{n}log(1-x_i)\hfill \\ & -2\sum _{j=1}^{m}log(1-y_j)-\frac{1}{2{\eta }^2}\sum _{i=1}^n{\left(\frac{x_i}{1-x_i}\right)}^2\hfill \\ \hfill & -\frac{1}{2{\lambda }^2}\sum _{j=1}^m{\left(\frac{y_j}{1-y_j}\right)}^2.\hfill \end{array}$$

The maximum likelihood estimators (MLEs) $\widehat{\eta }$ and $\widehat{\lambda }$ of $\eta$ and $\lambda$, respectively, are the solutions of the following system of linear equations:

$$\begin{array}{cc}\hfill \frac{\partial l(\eta ,\lambda )}{\partial \eta }& =\frac{-n}{\eta }+\frac{1}{{\eta }^3}\sum _{i=1}^n{\left(\frac{x_i}{1-x_i}\right)}^2=0\hfill \\ \hfill \frac{\partial l(\eta ,\lambda )}{\partial \lambda }& =\frac{-m}{\lambda }+\frac{1}{{\lambda }^3}\sum _{j=1}^m{\left(\frac{y_j}{1-y_j}\right)}^2=0.\hfill \end{array}$$

The solution to the system of equations is

$$\begin{array}{cc}\hfill \widehat{\eta }& ={\left\{\frac{1}{n}\sum _{i=1}^n{\left(\frac{x_i}{1-x_i}\right)}^2\right\}}^{1/2}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \widehat{\lambda }& ={\left\{\frac{1}{m}\sum _{j=1}^m{\left(\frac{y_j}{1-y_j}\right)}^2\right\}}^{1/2}.\hfill \end{array}$$

(7)

Therefore, under the invariance property of the MLE [12] and Equation (5), the MLE of R becomes

$$\widehat{R}=\frac{2}{\pi }arctan\left(\frac{\widehat{\eta }}{\widehat{\lambda }}\right).$$

(8)

Corollary 3.

If$U_i=\frac{X_i}{1-X_i}\sim HN\left(\eta \right)$, $i=1,\dots ,n$, and$V_j=\frac{Y_j}{1-Y_j}\sim HN\left(\lambda \right)$, $j=1,\dots ,m$, with$U_i$independent of$V_i$, then

1.

${\chi }_{\eta }=\frac{\sqrt{n}}{\eta }\widehat{\eta }\sim {\chi }_{\left(n\right)}$, then$\mathbb{E}\left({\chi }_{\eta }\right)=\sqrt{2}\frac{\Gamma \left(\right(n+1)/2)}{\Gamma (n/2)}$and$Var\left({\chi }_{\eta }\right)=n-{\mathbb{E}}^2\left({\chi }_{\eta }\right)$.

2.

${\chi }_{\lambda }=\frac{\sqrt{m}}{\lambda }\widehat{\lambda }\sim {\chi }_{\left(m\right)}$, then$\mathbb{E}\left({\chi }_{\lambda }\right)=\sqrt{2}\frac{\Gamma \left(\right(m+1)/2)}{\Gamma (m/2)}$and$Var\left({\chi }_{\lambda }\right)=m-{\mathbb{E}}^2\left({\chi }_{\lambda }\right)$,

where ${\chi }_{\left(s\right)}$ denotes the chi-distribution with s degrees of freedom.

Remark 1.

From Corollary 3 we have $\mathbb{E}\left(\widehat{\eta }\right)=\frac{\eta }{\sqrt{n}}\frac{\sqrt{2}\Gamma ((n+1)/2)}{\Gamma (n/2)}$ and $\mathbb{E}\left(\widehat{\lambda }\right)=\frac{\lambda }{\sqrt{m}}\frac{\sqrt{2}\Gamma ((m+1)/2)}{\Gamma (m/2)}$. Therefore, both $\widehat{\eta }$ and $\widehat{\lambda }$ are biased estimators of η and λ, respectively.

3.2. Confidence Intervals for $\eta$ and $\lambda$

Let $X_1,\dots ,X_n$ and $Y_1,\dots ,Y_m$ be random samples from $UHN\left(\eta \right)$ and $UHN\left(\lambda \right)$, respectively. In addition, let the two samples be independent. From Corollary 3, we have ${\chi }_{\eta }^2=\frac{n}{{\eta }^2}{\widehat{\eta }}^2\sim {\chi }_{\left(n\right)}^2$ and ${\chi }_{\lambda }^2=\frac{m}{{\lambda }^2}{\widehat{\lambda }}^2\sim {\chi }_{\left(m\right)}^2$. Taking ${\chi }_{\eta }^2$ and ${\chi }_{\lambda }^2$ as two pivotal quantities, the $100(1-\alpha )\%$ confidence intervals for $\eta$ and $\lambda$ are given by $\left(\widehat{\eta }\sqrt{\frac{n}{{\chi }_{(1-\alpha /2,n)}^2}},\widehat{\eta }\sqrt{\frac{n}{{\chi }_{(\alpha /2,n)}^2}}\right)$ and $\left(\widehat{\lambda }\sqrt{\frac{m}{{\chi }_{(1-\alpha /2,m)}^2}},\widehat{\lambda }\sqrt{\frac{m}{{\chi }_{(\alpha /2,m)}^2}}\right)$, respectively, where ${\chi }_{(\alpha /2,a)}^2$ and ${\chi }_{(1-\alpha /2,a)}^2$ are the lower and upper $(\alpha /2)$th percentiles of a chi-square distribution with a degrees of freedom.

3.3. Exact PDF for R

Lemma 2.

Let $W\sim F_{(n,m)}$ then the PDF of $Z=\widehat{\eta }/\widehat{\lambda }$ is given by

$$\begin{array}{cc}\hfill f_Z(z;n,m,\eta ,\lambda )& =2\frac{{\lambda }^2}{{\eta }^2}z{f}_W\left(\frac{{\lambda }^2}{{\eta }^2}{z}^2\right)\hfill \\ \hfill & =2\frac{{\left(\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}\right)}^{\frac{n}{2}}}{B(\frac{n}{2},\frac{m}{2})}\frac{z^{n-1}}{{(1+\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}{z}^2)}^{\frac{n}{2}+\frac{m}{2}}},\hfill \end{array}$$

(9)

for $0<z<\infty$, where $n,m>0$, $\eta ,\lambda >0$ and $B(n/2,m/2)=\Gamma (n/2)\Gamma (m/2)/\Gamma \left(\right(n+m)/2)$.

Proof. 

Using the Corollary 2, let $W=Z^2{\left(\frac{\lambda }{\eta }\right)}^2\sim F_{(n,m)}$ then

$$P\left(Z\le z\right)=P\left(\eta W^{1/2}\le \lambda z\right)=P\left(W\le \frac{{\lambda }^2}{{\eta }^2}{z}^2\right)=F_W\left(\frac{{\lambda }^2}{{\eta }^2}{z}^2\right)$$

The derivative of $P(Z\le z)$ gives the PDF in Equation (9).    □

Remark 2.

Note that the random variable $\frac{\widehat{\eta }}{\widehat{\lambda }}$ is a ratio of independent generalized gamma random variables, since we can write $\frac{\widehat{\eta }}{\widehat{\lambda }}=\frac{Z_1}{Z_2}$ with $Z_1\sim \mathcal{G}\Gamma (2,n,\eta \sqrt{2/n})$ and $Z_2\sim \mathcal{G}\Gamma (2,m,\lambda \sqrt{2/m})$, where $\mathcal{G}\Gamma (p,d,a)$ denotes a generalized gamma distribution. Following [13] the ratio of independent generalized gamma random variables has a generalized F distribution.

Proposition 1.

A random variable R follows a $f_R$ distribution, denoted as $R\sim f_R(\eta ,\lambda ,n,m)$, if its PDF is given by

$$\begin{array}{cc}\hfill f_R(r;\eta ,\lambda ,n,m)& =\frac{\pi {\left(\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}\right)}^{\frac{n}{2}}}{B\left(\frac{n}{2},\frac{m}{2}\right)}\hfill \\ \hfill & \times \frac{{sec}^2\left(\frac{\pi }{2}r\right){(tan\left(\frac{\pi }{2}r\right))}^{n-1}}{{\left(1+\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}{tan}^2\left(\frac{\pi }{2}r\right)\right)}^{\frac{n+m}{2}}},\hfill \end{array}$$

(10)

for $0<r<1$, where $\eta ,\lambda >0$ and $n,m>0$.

Proof of Proposition 1.

Using Lemma 2 and Equation (8) we have the result.    □

With a little algebraic handling and the help of Maple or Mathematica software, it can be proved that the expectation of R is given by

$$\begin{array}{cc}\hfill \mathbb{E}\left(R\right)& =\frac{\pi csc\left(\frac{\pi }{2}n\right)}{\Gamma \left(\frac{n}{2}\right)\Gamma (1-\frac{n}{2})}-\frac{2}{n}{\left(\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}\right)}^{\frac{n}{2}}\frac{sec\left(\frac{\pi }{2}n\right)}{B(\frac{n}{2},\frac{m}{2})}\hfill \\ \hfill & \times {}_2{F}_1\left(\left[\frac{n}{2},\frac{n+m}{2}\right],\left[1+\frac{n}{2}\right],\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}\right)\hfill \\ \hfill & -\frac{2}{\pi }{\left(\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}\right)}^{\frac{1}{2}}\frac{\Gamma \left(\frac{n-1}{2}\right)\Gamma \left(\frac{m+1}{2}\right)}{\Gamma \left(\frac{n}{2}\right)\Gamma \left(\frac{m}{2}\right)}\hfill \\ \hfill & \times {}_3{F}_2\left(\left[\frac{1}{2},1,\frac{m+1}{2}\right],\left[\frac{3}{2},\frac{3-n}{2}\right],\frac{n}{m}\frac{{\lambda }^2}{{\eta }^2}\right),\hfill \end{array}$$

where ${}_p{F}_q$ is the hypergeometric function such that

$${}_p{F}_q([a_1,\dots ,a_p],[b_1,\dots ,b_q],z)=\sum _{k=0}^{\infty }\frac{{\left(a_1\right)}_k\dots {\left(a_p\right)}_k}{{\left(b_1\right)}_k\dots {\left(b_q\right)}_k}\frac{z^k}{k!}$$

and ${\left(a\right)}_k$ is the Pochhammer symbol or ascending factorial. It is defined by ${\left(a\right)}_0=1$ for $k=0$, and by ${\left(a\right)}_k=a(a+1)...(a+k-1)$ for $k\ge 1$. However, for all integer k, we write simply

$${\left(a\right)}_k=\frac{\Gamma (a+k)}{\Gamma \left(a\right)}.$$

We may generate values of R using different procedures. Next, we describe Algorithms 1–3.

Algorithm 1: Algorithm to generate observations from $R\sim f_R(\eta ,\lambda ,n,m)$.

Require Initialize the algorithm fixing $\eta$, $\lambda$, n and m 1. Generate $Z_1$ from $\Gamma (n/2,2{\eta }^2/n)$ 2. Generate $Z_2$ from $\Gamma (m/2,2{\lambda }^2/m)$ 3. Compute $$R=\frac{2}{\pi }arctan\left(\sqrt{\frac{Z_1}{Z_2}}\right).$$ 4. Repeat steps 1 to 3 N times to get a sample of size N 5. return${(R_1,\dots ,R_N)}^{\prime }$.

Algorithm 2: Algorithm to generate observations from $R\sim f_R(\eta ,\lambda ,n,m)$.

Require Initialize the algorithm fixing $\eta$, $\lambda$, n and m 1. Generate $Z_1$ from ${\chi }_{\left(n\right)}^2$ 2. Generate $Z_2$ from ${\chi }_{\left(m\right)}^2$ 3. Compute $$R=\frac{2}{\pi }arctan\left(\frac{\eta }{\lambda }\sqrt{\frac{m}{n}\frac{Z_1}{Z_2}}\right).$$ 4. Repeat steps 1 to 3 N times to get a sample of size N 5. return${(R_1,\dots ,R_N)}^{\prime }$.

Algorithm 3: Algorithm to generate observations from $R\sim f_R(\eta ,\lambda ,n,m)$.

Require Initialize the algorithm fixing $\eta$, $\lambda$, n and m 1. Generate F from $F_{(n,m)}$ 2. Compute $$R=\frac{2}{\pi }arctan\left(\frac{\eta }{\lambda }\sqrt{F}\right).$$ 3. Repeat steps 1 and 2 N times to get a sample of size N 4. return${(R_1,\dots ,R_N)}^{\prime }$.

4. Interval Estimation of $\mathit{R}$

In this section, we consider the interval estimation of R based on exact, asymptotic and bootstrap methods.

4.1. Exact Confidence Interval

Let us assume that $X\sim UHN\left(\eta \right)$ and $Y\sim UHN\left(\lambda \right)$, and we have a sample $X_1,\dots ,X_n$ from the distribution of X and a sample $Y_1,\dots ,Y_m$ from the distribution of Y. In addition, let the two samples be independent. From Corollary 1, we have $F=\frac{{\lambda }^2}{{\eta }^2}\frac{{\widehat{\eta }}^2}{{\widehat{\lambda }}^2}\sim F_{(n,m)}$ then $F^{★}=\frac{{\eta }^2}{{\lambda }^2}\frac{{\widehat{\lambda }}^2}{{\widehat{\eta }}^2}\sim F_{(m,n)}$. Taking $F^{★}$ as a pivotal quantity, a $100(1-\alpha )\%$ confidence interval for R is given by

$$\left(\frac{2}{\pi }arctan\left(\frac{\widehat{\eta }}{\widehat{\lambda }}{F}_{(\alpha /2,m,n)}^{1/2}\right),\frac{2}{\pi }arctan\left(\frac{\widehat{\eta }}{\widehat{\lambda }}{F}_{(1-\alpha /2,m,n)}^{1/2}\right)\right),$$

(11)

where $F_{(\alpha /2,m,n)}$ and $F_{(1-\alpha /2,m,n)}$ denote, respectively, the lower and upper $(\alpha /2)$th percentiles of F distribution with m and n degrees of freedom.

4.2. Asymptotic Distribution and Confidence Interval

In this subsection, at first, we compute the asymptotic distribution of $\widehat{\theta }=(\widehat{\eta },\widehat{\lambda })$ and after this, we study the asymptotic distribution of $\widehat{R}$. From the asymptotic distribution of $\widehat{R}$, we get the asymptotic confidence interval of R.

Let $J\left(\theta \right)=(J_{ij}\left(\theta \right),i,j=1,2)$ be the expected Fisher’s information matrix of $\theta =(\eta ,\lambda )$. The elements of the expected Fisher’s information matrix are

$$\begin{array}{cc}\hfill J_{11}& =\mathbb{E}\left(-\frac{{\partial }^{2}l(\eta ,\lambda )}{\partial {\eta }^2}\right)=\frac{2n}{{\eta }^2}\hfill \\ \hfill J_{22}& =\mathbb{E}\left(-\frac{{\partial }^{2}l(\eta ,\lambda )}{\partial {\lambda }^2}\right)=\frac{2m}{{\lambda }^2}\hfill \\ \hfill J_{21}& =J_{12}=0.\hfill \end{array}$$

Under some regularity conditions, we have

$$\left[\begin{array}{c}\sqrt{n}(\widehat{\eta }-\eta )\\ \sqrt{m}(\widehat{\lambda }-\lambda )\end{array}\right]\stackrel{d}{\to }{N}_2\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}\frac{{\eta }^2}{2}& 0\\ 0& \frac{{\lambda }^2}{2}\end{array}\right]\right).$$

The point estimator of R is $\widehat{R}=R(\widehat{\eta },\widehat{\lambda })$. We obtain the asymptotic confidence interval for R following this procedure (see [14])

$$\begin{array}{cc}\hfill d_1(\eta ,\lambda )& =\frac{\partial R}{\partial \eta }=\frac{2\lambda }{\pi ({\eta }^2+{\lambda }^2)},\mathrm{and}\hfill \\ \hfill d_2(\eta ,\lambda )& =\frac{\partial R}{\partial \lambda }=-\frac{2\eta }{\pi ({\eta }^2+{\lambda }^2)}.\hfill \end{array}$$

This gives

$$\begin{array}{cc}\hfill \mathrm{Var}\left(\widehat{R}\right)& =\mathrm{Var}\left(\widehat{\eta }\right)d_1^2(\eta ,\lambda )+\mathrm{Var}\left(\widehat{\lambda }\right)d_2^2(\eta ,\lambda )\hfill \\ \hfill & =\frac{2{\eta }^2{\lambda }^2}{{\pi }^2{({\eta }^2+{\lambda }^2)}^2}\left[\frac{1}{n}+\frac{1}{m}\right].\hfill \end{array}$$

Thus, we obtain the following result

$$Z_R=\frac{\widehat{R}-R}{\frac{\sqrt{2}\widehat{\eta }\widehat{\lambda }}{\pi ({\widehat{\eta }}^2+{\widehat{\lambda }}^2)}{\left[\frac{1}{n}+\frac{1}{m}\right]}^{1/2}}\stackrel{d}{\to }N(0,1).$$

Hence, the asymptotic $100(1-\alpha )\%$ confidence interval for R is given by

$$\widehat{R}\pm Z_{(1-\alpha /2)}\frac{\sqrt{2}\widehat{\eta }\widehat{\lambda }}{\pi ({\widehat{\eta }}^2+{\widehat{\lambda }}^2)}{\left[\frac{1}{n}+\frac{1}{m}\right]}^{1/2},$$

(12)

where $Z_{(1-\alpha /2)}$ is the $(1-\alpha /2)$th percentile of the standard normal distribution and $\widehat{R}$ is given by (8).

4.3. Bootstrap Confidence Intervals

MLE is a typical statistical method. However, in many practical situations since the sample size is not large, so the large-sample based inference such as MLE-based asymptotic estimates may not be suitable and may even be misleading sometimes. In this subsection, parametric and nonparametric bootstrap confidence intervals are constructed for unknown parameters; see [15,16] for details.

4.3.1. Parametric Bootstrap Sampling Algorithm

Next, to generate parametric bootstrap samples, as suggested by [16], of $\eta$, $\lambda$ and R, from the given independent random samples, we use the following method $X_1,\dots ,X_n$ and $Y_1,\dots ,Y_m$ obtained from $UHN\left(\eta \right)$ and $UHN\left(\lambda \right)$, respectively.

• Stage 1 Compute MLE of $\eta$ and $\lambda$, say $\widehat{\eta }$ and $\widehat{\lambda }$, based on data $X={(X_1,\dots ,X_n)}^{\prime }$ and $Y={(Y_1,\dots ,Y_m)}^{\prime }$.
• Stage 2 Based on $\widehat{\eta }$ and $\widehat{\lambda }$, generates samples $X^{★}={(X_1^{★},\dots ,X_n^{★})}^{\prime }$ from $UHN\left(\widehat{\eta }\right)$ and $Y^{★}={(Y_1^{★},\dots ,Y_m^{★})}^{\prime }$ from $UHN\left(\widehat{\lambda }\right)$ with

  $$\begin{array}{cc}\hfill X_i^{★}& =\frac{\widehat{\eta }{\Phi }^{-1}\left(\frac{U_{i1}+1}{2}\right)}{1+\widehat{\eta }{\Phi }^{-1}\left(\frac{U_{i1}+1}{2}\right)}\hfill \\ \hfill Y_i^{★}& =\frac{\widehat{\lambda }{\Phi }^{-1}\left(\frac{U_{i2}+1}{2}\right)}{1+\widehat{\lambda }{\Phi }^{-1}\left(\frac{U_{i2}+1}{2}\right)}\hfill \end{array}$$

  where for $j=1,2$, $U_{ij}$ is generated independent observations from the uniform distribution $U(0,1)$ of sample size n and m, respectively.
• Stage 3 Compute MLE of $\eta$ and $\lambda$, say ${\widehat{\eta }}^{★}$ and ${\widehat{\lambda }}^{★}$, based on data $X^{★}$ and $Y^{★}$, respectively.
• Stage 4 Compute MLE of R, say ${\widehat{R}}^{★}$, based on ${\widehat{\eta }}^{★}$ and ${\widehat{\lambda }}^{★}$.
• Stage 5 Repeat Steps 2 to 4 B times and generate B bootstrap estimates of $\eta$, $\lambda$ and R.

4.3.2. Nonparametric Bootstrap Sampling Algorithm

Next, we describe the steps to obtain nonparametric bootstrap samples of $\eta$, $\lambda$ and R.

• Stage 1 Draw random samples with replacement $X^{★}={(X_1^{★},\dots ,X_n^{★})}^{\prime }$ and $Y^{★}={(Y_1^{★},\dots ,Y_m^{★})}^{\prime }$ from the original data $X={(X_1,\dots ,X_n)}^{\prime }$ and $Y={(Y_1,\dots ,Y_m)}^{\prime }$, respectively.
• Stage 2 Compute the bootstrap estimates $\eta$ and $\lambda$, say ${\widehat{\eta }}^{★}$ and ${\widehat{\lambda }}^{★}$, based on data $X^{★}$ and $Y^{★}$, respectively.
• Stage 3 Using ${\widehat{\eta }}^{★}$ and ${\widehat{\lambda }}^{★}$ and Equation (8), compute the bootstrap estimate of R, say ${\widehat{R}}^{★}$.
• Stage 4 Repeat Steps 1 and 3 B times and generate B bootstrap estimates of $\eta$, $\lambda$ and R.

Now, we propose different types of bootstrap confidence intervals for the parameter R using the parametric and nonparametric bootstrap samples. Identically to R, we compute the confidence intervals of $\eta$ and $\lambda$. For $b=1,\dots ,B$, we denote $\left\{{\widehat{R}}_b^{★}\right\}$ the set of bootstrap estimates of R. We also denote the MLE obtained from the original real dataset as $\widehat{R}$ and we assumed that the confidence level is $100(1-\alpha )\%$.

Bootstrap-t confidence interval. The bootstrap-t confidence interval reproduces the way of constructing the standard-t confidence interval. The t-like critical value and the standard error of $\widehat{R}$ are computed based on the bootstrap estimates $\left\{{\widehat{R}}_b^{★}\right\}$. We obtain the bootstrap standard error as follows

$$s{e}^{★}\left(\widehat{R}\right)=\sqrt{\frac{{\sum }_{b=1}^B{({\widehat{R}}_b^{★}-{\widehat{R}}^{★})}^2}{B}},\mathrm{where}{\widehat{R}}^{★}=\sum _{b=1}^B\frac{{\widehat{R}}_b^{★}}{B}.$$

To find the t-like critical value, denoted by ${\widehat{t}}^{★\alpha }$, we standardize $\left\{{\widehat{R}}_b^{★}\right\}$$(b=1,\dots ,B)$ by using

$$z_b^{★}\left(R\right)=\frac{{\widehat{R}}_b^{★}-\widehat{R}}{s{e}^{★}\left(\widehat{R}\right)}.$$

Then, we obtain ${\widehat{t}}^{★\alpha }$ from the bootstrap estimate:

$$\frac{\#\left\{z_b^{★}\left(R\right)\le {\widehat{t}}^{★\alpha }\right\}}{B}=\alpha .$$

Then, we obtain the $100(1-\alpha )\%$ bootstrap-t confidence interval

$$\left(\widehat{R}-{\widehat{t}}^{★(1-\alpha /2)}·s{e}^{★}\left(\widehat{R}\right),\widehat{R}+{\widehat{t}}^{★(\alpha /2)}·s{e}^{★}\left(\widehat{R}\right)\right).$$

Bootstrap percentile confidence interval. To obtain bootstrap percentile confidence interval [17] of R, we simply find the $\alpha /2$ and $1-\alpha /2$ percentiles, denoted by ${\widehat{R}}^{★(\alpha /2)}$ and ${\widehat{R}}^{★(1-\alpha /2)}$, based on the set of bootstrap estimates of R. The simple $100(1-\alpha )\%$ bootstrap percentile confidence interval is defined to be $({\widehat{R}}^{★(\alpha /2)},{\widehat{R}}^{★(1-\alpha /2)})$.

Bias-Corrected and Accelerated Bootstrap (BCa) Method. To overcome the overcoverage issues in percentile bootstrap CIs, the BCa method corrects for both bias and skewness of the bootstrap parameter estimates by incorporating a bias-correction factor and an acceleration factor (see [17,18]). The bias-correction factor $z_0$ is estimated as the proportion of the bootstrap estimates less than the original parameter estimate $\widehat{\theta }$,

$$z_0={\Phi }^{-1}\left(\frac{\#\{{\widehat{R}}^{★}-\widehat{R}\}}{B}\right)$$

where ${\Phi }^{-1}$ is the inverse CDF of a standard normal distribution. We can estimate the acceleration factor a through jackknife or leave-one-out resampling, which involves generating n replicates of the original sample, where n is the number of observations in the sample. The first jackknife replicate is obtained by leaving out the first case ($i=1$) of the original sample, the second by leaving out the second case ($i=2$), and so on, until n samples of size $n-1$ are obtained. For each of the jackknife resamples, ${\widehat{R}}_{(-i)}$ is obtained. The average of these estimates is,

$${\widehat{R}}_{(·)}=\frac{1}{n}\sum _{i=1}^n{\widehat{R}}_{\left(i\right)}.$$

Then, the acceleration factor $\widehat{a}$ is calculated as follows

$$\widehat{a}=\frac{{\sum }_{i=1}^n{({\widehat{R}}_{(·)}-{\widehat{R}}_{\left(i\right)})}^3}{6{\left\{{\sum }_{i=1}^n{({\widehat{R}}_{(·)}-{\widehat{R}}_{\left(i\right)})}^2\right\}}^{3/2}}.$$

With the values of $z_0$ and $\widehat{a}$, the values $a_1$ and $a_2$ are calculated

$$\begin{array}{cc}\hfill a_1& =\Phi \left(z_0+\frac{z_0+z^{(\alpha /2)}}{1+\widehat{a}\left(z_0+z^{(\alpha /2)}\right)}\right)\hfill \\ \hfill a_2& =\Phi \left(z_0+\frac{z_0+z^{(1-\alpha /2)}}{1+\widehat{a}\left(z_0+z^{(1-\alpha /2)}\right)}\right).\hfill \end{array}$$

Here, $z^{(\alpha /2)}$ is the $100\left(\alpha /2\right)$th percentile point of a standard normal distribution. Then, a $100(1-\alpha )\%$ BCa confidence interval of R is given by $\left({\widehat{R}}^{★\left(a_1\right)},{\widehat{R}}^{★\left(a_2\right)}\right)$. For more on different types of confidence intervals, see [19], among others.

5. Simulation Study

In this section, we present a small Monte Carlo simulation study in order to illustrate the behavior of different estimates for different sample sizes. The simulation studies were conducted using 10,000 samples from $UHN\left(\eta \right)$ and $UHN\left(\lambda \right)$. The sample sizes were combinations of n and m, with n = 15, 20, 30, 50, 100 and m = 15, 20, 30, 50, 100. In all cases, we take $\eta =0.3$ and $\lambda =0.2$, with those values we get $R=0.63$. In [1], the reader can find a simulation study for different values of the shape parameter including values greater than 1. From the sample, we estimate $\eta$ and $\lambda$ using MLE Equations (6) and (7). Once $\eta$ and $\lambda$ are estimated, we compute the MLE of R using (8). We also compute the average biases and mean squared errors (MSEs) using MLE and parametric and nonparametric bootstrap estimates (Par.Boot/Npar.Boot) of $\eta$, $\lambda$ and R in Table 1 over the 10,000 replications. We obtain the 95% confidence intervals based on the exact and asymptotic distributions of $\eta$, $\lambda$ and R. We also obtain the 95% confidence intervals based on parametric and nonparametric bootstrap methods for $\eta$, $\lambda$ and R. Based on exact and asymptotic distribution of $\eta$, $\lambda$ and R, and parametric and nonparametric bootstrap methods of $\eta$, $\lambda$ and R, we reported the average confidence lengths and coverage probabilities for 95% confidence intervals in Table 2. For the bootstrap methods, estimates and confidence interval was computed based on $B=500$ replications. Some of the points are quite clear from this simulation. Even for small sample sizes, the performance of the MLEs and bootstrap methods are quite satisfactory in terms of biases and MSEs. In addition for all methods when sample sizes n, m increases then the average bias and MSEs decreases. It verifies the consistency property of the MLE of $\eta$, $\lambda$ and R. It is observed that the bootstrap methods behave almost in a similar way both with respect to biases and MSEs.

Table 1. Average biases and MSE values (within bracket) for parameters at $\eta =0.3$, $\lambda =0.2$ and $R=0.63$.

$(\mathit{n},\mathit{m})$	Method	$\mathit{\eta }$	$\mathit{\lambda }$	R
$(15,20)$	MLE	−0.0044(0.0029)	−0.0025(0.0010)	−0.0052(0.0051)
	Npar.Boot	−0.0086(0.0029)	−0.0046(0.0010)	−0.0098(0.0051)
	Par.Boot	−0.0093(0.0029)	−0.0049(0.0010)	−0.0105(0.0050)
$(20,15)$	MLE	−0.0039(0.0022)	−0.0029(0.0013)	−0.0014(0.0049)
	Npar.Boot	−0.0072(0.0022)	−0.0057(0.0013)	−0.0022(0.0048)
	Par.Boot	−0.0076(0.0022)	−0.0062(0.0013)	−0.0021(0.0047)
$(20,20)$	MLE	−0.0032(0.0022)	−0.0029(0.0010)	−0.0017(0.0044)
	Npar.Boot	−0.0065(0.0022)	−0.0051(0.0010)	−0.0040(0.0043)
	Par.Boot	−0.0069(0.0022)	−0.0053(0.0010)	−0.0043(0.0043)
$(20,30)$	MLE	−0.0033(0.0022)	−0.0017(0.0007)	−0.0042(0.0038)
	Npar.Boot	−0.0065(0.0022)	−0.0032(0.0007)	−0.0081(0.0037)
	Par.Boot	−0.0070(0.0022)	−0.0034(0.0007)	−0.0088(0.0037)
$(30,20)$	MLE	−0.0020(0.0015)	−0.0021(0.0010)	$3.6\times {10}^{-5}\left(0.0036\right)$
	Npar.Boot	−0.0043(0.0015)	−0.0043(0.0010)	$-3.2\times {10}^{-6}\left(0.0035\right)$
	Par.Boot	−0.0045(0.0015)	−0.0045(0.0010)	0.0002(0.0035)
$(30,30)$	MLE	−0.0024(0.0015)	−0.0016(0.0007)	−0.0019(0.0030)
	Npar.Boot	−0.0047(0.0015)	−0.0031(0.0007)	−0.0036(0.0030)
	Par.Boot	−0.0049(0.0015)	−0.0033(0.0007)	−0.0036(0.0030)
$(30,50)$	MLE	−0.0027(0.0015)	−0.0011(0.0004)	−0.0036(0.0024)
	Npar.Boot	−0.0050(0.0015)	−0.0021(0.0004)	−0.0066(0.0024)
	Par.Boot	−0.0052(0.0015)	−0.0021(0.0004)	−0.0069(0.0024)
$(50,30)$	MLE	−0.0016(0.0009)	−0.0013(0.0007)	−0.0002(0.0022)
	Npar.Boot	−0.0030(0.0009)	−0.0028(0.0007)	0.0002(0.0022)
	Par.Boot	−0.0031(0.0009)	−0.0029(0.0007)	0.0003(0.0022)
$(50,50)$	MLE	−0.0011(0.0009)	−0.0010(0.0004)	−0.0007(0.0018)
	Npar.Boot	−0.0025(0.0009)	−0.0019(0.0004)	−0.0018(0.0017)
	Par.Boot	−0.0026(0.0009)	−0.0020(0.0004)	−0.0018(0.0017)
$(100,100)$	MLE	−0.0005(0.0004)	−0.0002(0.0002)	−0.0007(0.0009)
	Npar.Boot	−0.0013(0.0004)	−0.0007(0.0002)	−0.0013(0.0009)
	Par.Boot	−0.0013(0.0004)	−0.0007(0.0002)	−0.0013(0.0009)

Table 2. Average confidence length and coverage probabilities of confidence intervals using exact, asymptotic and various parametric and non-parametric bootstrap methods.

$(\mathit{n},\mathit{m})$	Method		$\mathit{\eta }$	$\mathit{\lambda }$	R
$(15,20)$	Exact		0.2383(0.950)	0.1163(0.943)	0.2766(0.944)
	Asympt.		0.2108(0.944)	0.1225(0.934)	0.2732(0.941)
	Non-par	t	0.2402(0.949)	0.1187(0.941)	0.2768(0.942)
	Boot	q	0.1671(0.945)	0.1101(0.942)	0.2769(0.943)
	CIs	$BCa$	0.1720(0.943)	0.1105(0.943)	0.2744(0.942)
	Par	t	0.2394(0.942)	0.1174(0.943)	0.2801(0.945)
	Boot	q	0.2384(0.951)	0.1161(0.942)	0.2765(0.943)
	CIs	$BCa$	0.2382(0.949)	0.1164(0.942)	0.2750(0.947)
$(20,15)$	Exact		0.2018(0.947)	0.1838(0.943)	0.2719(0.951)
	Asympt.		0.1842(0.946)	0.1408(0.941)	0.2713(0.947)
	Non-par	t	0.2201(0.950)	0.1123(0.945)	0.2718(0.948)
	Boot	q	0.1834(0.949)	0.1089(0.946)	0.2617(0.947)
	CIs	$BCa$	0.1923(0.948)	0.1166(0.947)	0.2742(0.953)
	Par	t	0.2386(0.947)	0.1812(0.947)	0.2760(0.949)
	Boot	q	0.2381(0.948)	0.1705(0.946)	0.2748(0.951)
	CIs	$BCa$	0.2385(0.949)	0.1877(0.945)	0.2742(0.958)
$(20,20)$	Exact		0.2013(0.945)	0.1349(0.952)	0.2542(0.947)
	Asympt.		0.1838(0.942)	0.1223(0.949)	0.2527(0.942)
	Non-par	t	0.2206(0.949)	0.1125(0.947)	0.2721(0.943)
	Boot	q	0.1832(0.949)	0.1087(0.947)	0.2611(0.948)
	CIs	$BCa$	0.1920(0.947)	0.1169(0.948)	0.2557(0.946)
	Par	t	0.2249(0.948)	0.1311(0.948)	0.2758(0.947)
	Boot	q	0.2245(0.947)	0.1201(0.949)	0.2751(0.946)
	CIs	$BCa$	0.2249(0.948)	0.1308(0.947)	0.2556(0.945)
$(20,30)$	Exact		0.2017(0.947)	0.1271(0.943)	0.2346(0.945)
	Asympt.		0.1841(0.946)	0.1004(0.944)	0.2320(0.944)
	Non-par	t	0.1918(0.949)	0.1169(0.945)	0.2232(0.945)
	Boot	q	0.1799(0.948)	0.1001(0.946)	0.2311(0.946)
	CIs	$BCa$	0.1801(0.949)	0.1007(0.947)	0.2301(0.951)
	Par	t	0.2116(0.946)	0.1315(0.947)	0.2351(0.946)
	Boot	q	0.2011(0.947)	0.1316(0.948)	0.2313(0.947)
	CIs	$BCa$	0.2007(0.948)	0.1318(0.949)	0.2332(0.955)
$(30,20)$	Exact		0.1596(0.951)	0.1643(0.941)	0.2311(0.953)
	Asympt.		0.1503(0.945)	0.1224(0.942)	0.2311(0.949)
	Non-par	t	0.1501(0.949)	0.1568(0.946)	0.2278(0.945)
	Boot	q	0.1424(0.947)	0.1502(0.947)	0.2199(0.946)
	CIs	$BCa$	0.1425(0.947)	0.1507(0.948)	0.2121(0.946)
	Par	t	0.1602(0.947)	0.1677(0.943)	0.2401(0.948)
	Boot	q	0.1599(0.948)	0.1601(0.947)	0.2397(0.946)
	CIs	$BCa$	0.1566(0.947)	0.1609(0.947)	0.2320(0.945)
$(30,30)$	Exact		0.1597(0.949)	0.1065(0.952)	0.2086(0.948)
	Asympt.		0.1504(0.942)	0.1003(0.943)	0.2078(0.946)
	Non-par	t	0.1495(0.951)	0.1044(0.953)	0.2084(0.951)
	Boot	q	0.1485(0.948)	0.0979(0.951)	0.1999(0.947)
	CIs	$BCa$	0.1486(0.945)	0.0977(0.949)	0.2082(0.943)
	Par	t	0.1604(0.949)	0.1071(0.950)	0.2117(0.948)
	Boot	q	0.1601(0.948)	0.1063(0.951)	0.2085(0.945)
	CIs	$BCa$	0.1598(0.948)	0.1065(0.948)	0.2080(0.944)
$(30,50)$	Exact		0.1604(0.949)	0.1026(0.935)	0.1881(0.949)
	Asympt.		0.1510(0.934)	0.1080(0.938)	0.1865(0.945)
	Non-par	t	0.1485(0.950)	0.0998(0.938)	0.1856(0.946)
	Boot	q	0.1449(0.948)	0.0904(0.937)	0.1855(0.947)
	CIs	$BCa$	0.1451(0.951)	0.0911(0.938)	0.1870(0.945)
	Par	t	0.1649(0.946)	0.1087(0.939)	0.1882(0.942)
	Boot	q	0.1601(0.949)	0.1023(0.940)	0.1876(0.944)
	CIs	$BCa$	0.1604(0.947)	0.1024(0.941)	0.1875(0.935)
$(50,30)$	Exact		0.1211(0.951)	0.1372(0.937)	0.1855(0.951)
	Asympt.		0.1169(0.941)	0.1000(0.932)	0.1856(0.940)
	Non-par	t	0.1171(0.943)	0.0989(0.942)	0.1823(0.942)
	Boot	q	0.1078(0.948)	0.0942(0.940)	0.1799(0.946)
	CIs	$BCa$	0.1081(0.947)	0.0943(0.941)	0.1854(0.946)
	Par	t	0.1285(0.946)	0.1389(0.945)	0.1899(0.948)
	Boot	q	0.1203(0.945)	0.1367(0.946)	0.1862(0.945)
	CIs	$BCa$	0.1213(0.949)	0.1369(0.945)	0.1860(0.944)
$(50,50)$	Exact		0.1215(0.951)	0.0810(0.954)	0.1621(0.950)
	Asympt.		0.1172(0.940)	0.0781(0.942)	0.1617(0.944)
	Non-par	t	0.1149(0.944)	0.0751(0.945)	0.1602(0.948)
	Boot	q	0.1102(0.943)	0.0733(0.943)	0.1599(0.950)
	CIs	$BCa$	0.1101(0.942)	0.0731(0.944)	0.1625(0.949)
	Par	t	0.1201(0.942)	0.0791(0.942)	0.1672(0.947)
	Boot	q	0.1172(0.941)	0.0773(0.941)	0.1624(0.943)
	CIs	$BCa$	0.1199(0.941)	0.0785(0.940)	0.1623(0.950)
$(100,100)$	Exact		0.0845(0.948)	0.0563(0.946)	0.1149(0.943)
	Asympt.		0.0830(0.945)	0.0553(0.944)	0.1147(0.942)
	Non-par	t	0.0865(0.942)	0.0571(0.943)	0.1153(0.944)
	Boot	q	0.0818(0.944)	0.0498(0.947)	0.1001(0.944)
	CIs	$BCa$	0.0830(0.943)	0.5341(0.941)	0.1154(0.953)
	Par	t	0.0838(0.942)	0.0862(0.951)	0.1162(0.945)
	Boot	q	0.0834(0.941)	0.0856(0.952)	0.1049(0.943)
	CIs	$BCa$	0.0836(0.943)	0.0861(0.951)	0.1150(0.954)

We also compute the confidence intervals and the corresponding coverage probabilities by different methods. For R, the exact confidence interval was computed using (11), the asymptotic confidence interval was computed using (12). For $\eta$ and $\lambda$, we compute the confidence intervals using the formulae of Section 3.2 for the exact confidence interval, for the asymptotic confidence intervals we use the formulae in [1]. For the bootstrap methods, the confidence intervals are computed using the formulae of Section 4.3. In this case, all the eight confidence intervals behave very similarly in the sense of average confidence lengths and coverage probabilities.

The confidence intervals based on asymptotic confidence interval provides the shortest length in comparison with the exact confidence interval, whereas in coverage probability, using exact confidence interval shows better performance than the asymptotic confidence interval. On the contrary, among the bootstrap methods considered here, bootstrap-p method performed well as compared with bootstrap-t and bootstrap-$BCa$ methods.

6. An Illustrative Example

Cutting processes are those where a great enough force is applied to a piece of raw metal, usually sheet metal to cause the material to fail. One of the most common cutting processes is shearing and it is performed by applying a shearing force on the metal sheets [20]. In this section, we propose the use of our procedure on two real-life data sets to illustrate the implementation of our methods. The two data sets were firstly introduced and studied by [21] for burr measurements on the iron sheets. For the first data set of 50 observations on burr (in the unit of millimeter), the hole diameter is 12 mm and the sheet thickness is 3.15 mm. We shall refer to this as data set 1 and is given in Table 3. For the second data set of 50 observations, hole diameter and sheet thickness are 9 mm and 2 mm, respectively. We shall refer to this as data set 2 and is given in Table 4. Hole diameter readings are taken on jobs with respect to one hole, selected and fixed as per a predetermined orientation. The two data sets relate to two different machines under comparison [21]. One may see [21] about the technical details of the data sets’ measurements.

Table 3. Data set 1.

0.04, 0.02, 0.06, 0.12, 0.14, 0.08, 0.22, 0.12, 0.08, 0.26,

0.24, 0.04, 0.14, 0.16, 0.08, 0.26, 0.32, 0.28, 0.14, 0.16,

0.24, 0.22, 0.12, 0.18, 0.24, 0.32, 0.16, 0.14, 0.08, 0.16,

0.24, 0.16, 0.32, 0.18, 0.24, 0.22, 0.16, 0.12, 0.24, 0.06,

0.02, 0.18, 0.22, 0.14, 0.06, 0.04, 0.14, 0.26, 0.18, 0.16

Table 4. Data set 2.

0.06, 0.12, 0.14, 0.04, 0.14, 0.16, 0.08, 0.26, 0.32, 0.22,

0.16, 0.12, 0.24, 0.06, 0.02, 0.18, 0.22, 0.14, 0.22, 0.16,

0.12, 0.24, 0.06, 0.02, 0.18, 0.22, 0.14, 0.02, 0.18, 0.22,

0.14, 0.06, 0.04, 0.14, 0.22, 0.14, 0.06, 0.04, 0.16, 0.24,

0.16, 0.32, 0.18, 0.24, 0.22, 0.04, 0.14, 0.26, 0.18, 0.16

First of all, we conduct a one sample Kolmogorov–Smirnov (K-S) goodness-of-fit test on $UHN$ distribution based on the two data sets. We report the MLEs and estimates using parametric and nonparametric bootstrap methods and its corresponding standard errors (S.E.) of model parameters as well as the p-value (pval) and the test statistic (D) of K-S goodness-of-fit test for both data sets (K-S${}^i$, for data set $i=1,2$) in Table 5. The K-S statistic (based on the MLE of the parameter $\widehat{\eta }=0.238$) is $0.080$ and the corresponding p-value is $0.726$ for data set 1. The K-S statistic (based on the MLE of the parameter $\widehat{\lambda }=0.219$) is $0.1$ and the corresponding p-value is $0.607$ for data set 2. Therefore, the two data sets are reasonably fitted for the unit-half-normal distribution. Point estimates of $\eta$, $\lambda$ and R are similar in all methods considered, but the standard errors of the nonparametric bootstrap estimates are smaller than the MLEs and the parametric bootstrap estimates. The confidence intervals for $\eta$, $\lambda$ and R at 95% confidence level are reported in Table 6. Noticed that length of exact confidence interval is larger than that of asymptotic as we expected. In addition, the confidence intervals of the parametric bootstrap methods are larger than that of nonparametric bootstrap methods.

Table 5. Maximum likelihood (MLE), parametric (Par.Boot) and non-parametric bootstrap (Npar.Boot) estimates (s.e.), statistics (D) and the p-values (pval) of K-S test of goodness-of-fit of the two distributions in both data sets.

	$\widehat{\mathit{\eta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{R}}$
MLE	${0.238}_{\left(0.024\right)}$	${0.219}_{\left(0.022\right)}$	${0.526}_{\left(0.045\right)}$
Npar.Boot	${0.237}_{\left(0.017\right)}$	${0.219}_{\left(0.016\right)}$	${0.526}_{\left(0.031\right)}$
Par.Boot	${0.235}_{\left(0.024\right)}$	${0.218}_{\left(0.023\right)}$	${0.524}_{\left(0.045\right)}$
K-S${}^1$:	$D=0.080$	pval = 0.726
K-S${}^2$:	$D=0.100$	pval = 0.607

Table 6. The exact, asymptotic and various parametric and non-parametric bootstrap confidence intervals of $\eta$, $\lambda$ and R at 95% confidence level.

		$\mathit{\eta }$	$\mathit{\lambda }$	R
Exact		(0.199, 0.296)	(0.184, 0.273)	(0.437, 0.613)
Asympt.		(0.191, 0.285)	(0.176, 0.262)	(0.438, 0.614)
Non-par	t	(0.205, 0.277)	(0.190, 0.257)	(0.455, 0.586)
Boot	q	(0.204, 0.271)	(0.188, 0.250)	(0.463, 0.586)
CIs	$BCa$	(0.207, 0.274)	(0.191, 0.254)	(0.460, 0.584)
Par	t	(0.196, 0.302)	(0.183, 0.276)	(0.425, 0.628)
Boot	q	(0.188, 0.287)	(0.175, 0.262)	(0.431, 0.615)
CIs	$BCa$	(0.199, 0.296)	(0.184, 0.273)	(0.437, 0.612)

7. Concluding Remarks

In this work, we study different estimators of $R=P(Y<X)$ considering that both random variables X and Y follow a unit-half-normal distribution, with different shape parameters. A MLE procedure to obtain the MLEs of the unknown shape parameters is presented. Moreover, the MLE and the exact and asymptotic distribution of R are deduced. This allows us to compute the exact and asymptotic confidence intervals (CI). Additionally, based on parametric and nonparametric bootstrap methods, we are able to compute estimates of R and its respective CI. The simulation study shows that the performance of the MLEs, in terms of biases and MSEs, is quite satisfactory. We observe, also, a decrease in the average bias and MSEs as the sample size increases. From the point of view of biases and MSEs, we noticed similar performances using the MLEs and bootstrap methods. We studied, using different methods, the CI and the corresponding coverage percentages. We observe similar performances in terms of average confidence lengths and coverage probabilities for all the eight CI consider in this work. Based on the CI of R develop in this work, the best preference is using the nonparametric bootstrap method.

It was observed that the MLE of the shape parameter of the UHN distribution is biased. Although, the MLE possesses a number of attractive limiting properties: asymptotically unbiased, consistent, and asymptotically normal, many of these properties depend on an extremely large sample sizes. Those properties, such as unbiasedness, may not be valid for small or even moderate sample sizes, see [22], which are more practical in real data applications. Some bias-corrected techniques for the MLEs are desired in practice, especially when the sample size is small, see, for example, refs. [23,24,25,26,27] and references therein. Bias correction is an important topic in the UHN distribution, but is outside the scope of this article.