Abstract
The classical logit and probit models allow to explain a dichotomous dependent variable as a function of factors or covariates which can influence the response variable. This paper introduces a new skew-logit link for item response theory by considering the arctan transformation over the scobit logit model, yielding a very flexible link function from a new class of generalized distribution. This approach assumes an asymmetric model, which reduces to the standard logit model for a special case of the parameters that control the distribution’s symmetry. The model proposed is simple and allows us to estimate the parameters without using Bayesian methods, which requires implementing Markov Chain Monte Carlo methods. Furthermore, no special function appears in the formulation of the model. We compared the proposed model with the classical logit specification using three datasets. The first one deals with the well-known data collection widely studied in the statistical literature, concerning with mortality of adult beetle after exposure to gaseous carbon disulphide, the second one considers an automobile insurance portfolio. Finally, the third dataset examines touristic data related to tourist expenditure. For these examples, the results illustrate that the new model changes the significance level of some explanatory variables and the marginal effects. For the latter example, we have also modified the definition of the intercept in the linear predictor to prevent confounding.
1. Introduction
In many applications of statistical principles and procedures, the practitioners finds observations that take two possible values. This binary values are often measured with explanatory variables or covariates, either continuous or discrete, or even categorical. The relation between the response and the covariates is usually modeled by assuming that the probability of one response, after a suitable transformation, is typically linear in the covariates.
The logit model, which is based on the logistic distribution, examines in insurance settings the explanatory variables that explain why the insured do or do not claim in an insurance portfolio. Nevertheless, individual responses are often much more frequent with one of the values taken by the dependent variable than with the other one or vice versa; i.e., there is a clear asymmetry between the two responses. This issue is crucial when the model determines certain factors as statistically significant, thus this could imply uncertain consequences in the decisions taken by the economic agents’ decisions. From the practical experience, this is a frequent situation. Particularly, for the one of the examples considered in this work, many more policyholders do not claim to the insurance company.
Hence, the requirements based on an asymmetric logit model is preferable than the logit one, which assumes symmetry between the two values taken by the dependent variable. The work of [1] was the pioneering work attending to the asymmetric case in logit and probit model specification. This work was used for estimating dose response and requires fitting two additional parameters to the data to describe the distribution, rather than only one. Since this work, numerous models that generalize discrete-choice ones have been proposed in the statistical bibliography. Based on ideas in [1], in [2] the the scobit model was firstly introduced. This model was useful in situations where the practitioner wants to use a skew-logit (skew-probit) to explain the data. Due to the advances in computational calculations, more asymmetric alternative to the classical logit and probit models were included in the statistical literature. See, for instance [3,4,5,6]. On the other hand, Refs. [7,8] applied Bayesian procedures via a skewed link in their examination of binary responses when one dependent variable is much more frequent than the other one. This methodology is difficult to implement because it is required Markov Chain Monte Carlo (MCMC) to obtain the parameter estimates. Nevertheless, recently [9] have implemented a similar model where it is not required the MCMC methodology to obtain Bayesian approximation. Ref. [10] presented a new skew-probit link for item responses by considering an aggregated skew-normal distribution. Ref. [11] consider a widened class of parametric link functions that includes, as special cases, both symmetric as well as asymmetric links when binary responses are considered. Ref. [12] extents the asymmetry logit model introducing Weibull link (skewed) distribution for categorical data arising from binomial and multinomial model. Some papers discussing these issues are given next. Ref. [13] considered skewed logit link to estimate the fraudulent conduct reflected in a Spanish database of insurance claims. Ref. [14] examined the risk variables underlying automobile insurance claims having into account the asymmetry of the database. Ref. [15] compared the binary logistic and skewed logistic (Scobit) regression models in the context of injury costs in motor vehicle collisions. Ref. [16] analyzed logistic regression when some of the explanatory variables have skewed cell probabilities and lastly [17] considered the logistic model proposed by [1] to examine correlated infant morbidity data. More recently, Ref. [18] derived a new class of the logistic model which was used to explain unimodal data that include some level of skewness and Ref. [19] introduced a skew logit distribution which was based on the use of the alpha skew logistic model. In [20], new distributions for analyzing categorical data which contain binary case as special one are considered.
The formal aspects of the classical logistic and probit regression models are shown in Section 2. The skewed models introduced here are developed in Section 3. Three numerical examples together with the description of the second and third database are shown in Section 4. Finally, Section 5 concludes.
2. Methodological Background
In order to make this article self-contained, we proceed to briefly explain the logistic specification. Let the variable Y denotes a dichotomic dependent variable that can take the values , corresponding to the case where the event under study occurs, or when the event does not occur. Let x be a vector of predictors. Our purpose is to fit a binary regression model to describe the variable Y as a function of the observed values in x. We focus, particularly, on the logistic regression model. See Refs. [21,22] for more details.
Let be a random variable related to an event for an individual i that is specified as , where is a vector of regressors, which represents the effect of each variable in the model to be estimated and is a vector of explanatory variables, which can include an intercept, for the individual i. The disturbance term is a random variable. Note that is unobserved and continuous. We now assume that
Therefore,
where is the cumulative distribution function of the random variable . In addition, the marginal effect on due to changes in is , where is the probability density function of .
If we assume that is the standard normal cumulative distribution function (cdf), , we obtain the probit model, and if we assume the logistic distribution, the logistic regression model that will be considered in this work is obtained. Then, for the individual i in a sample of size n, we have that
and . Remind that the density of the standard logistic distribution is symmetric about 0. To sum up, the logit model takes the following form:
Therefore, the likelihood is provided by
where the regression parameters are estimated via maximum likelihood. Therefore, the model gives the probability of each individual to take the event. The logit (frequentist approach) model is implemented in most of the standard statistical software packages such as Mathematica (Champaign, IL, USA), STATA (Texas, TX, USA), and R (Vienna, Austria), among others. We have estimated the basic logit model by using WinRats econometric software (see [23]).
3. Asymmetric Logistic Specification
In this work, a novel procedure to include an additional parameter to a family of probability distributions is presented after completing a change of variable in the truncated Cauchy distribution. Consequently, we obtain a class of probabilistic families that incorporates an extra scale parameter and the inverse of the circular tangent function () in its analytical expression. The density function of the half-Cauchy distribution [24] truncated at is given by
In this expression, is the inverse of the circular tangent function. Let us now consider the transformation , where is the cdf of a random variable X with support in and where a and b can be either finite or non-finite. Then, the corresponding probability density function of the random variable X derived from (2) is
for and . The cdf of X, which is derived from (3) by integration, is provided by
Moreover, it is easy to check that (3) and (4) are genuine probability density function and cdf, respectively, when the support of the parameter is extended to except for zero. Here, we have that . Additionally, by taking in (4) the limit when the parameter approaches to zero and applying L’Hospital’s rule, it is simple to see that the parent cdf, , is obtained as a particular case, that is, when . Therefore, this procedure can be considered as a method to add a scale parameter to a parent cdf and, consequently, a method to derive a more flexible cdf. Particularly, the case where is replaced by the cdf of the classical Pareto distribution was considered in [25,26] and the case where the parent cdf is the classical exponential distribution was studied in [27].
Specific Model
Let us consider the cdf given in (1) to obtain a generalization of the same by introducing this distribution (4). The resulting distribution, logistic arctan distribution (LAT in advance), can be arranged by some stochastic orders depending on the value of the parameter via the likelihood ratio order, that is defined as follows (see [28]).
Definition 1.
Let and be continuous random variables with density functions and , respectively, such that
is non-decreasing over the union of the supports of and . Then, is said to be smaller than in the likelihood ratio order (denoted by ).
Some stochastic orders can order many parametric families of distributions depending on the value of their parameters. We prove now that the LAT distribution can be arranged via the likelihood ratio order, which is defined below (see [29]). Likelihood ratio order is a powerful tool in parametric models. See, for instance, Section1.C of [28] where many of its properties are explained. Some examples of distributions ordered by the likelihood ratio order are the normal and exponential distributions among others. Now, we have the next result.
Theorem 1.
Let and be two random variables with density functions and respectively. If then
Proof.
Note that for the ratio provided in (5) we have that
is positive for and . Here, gives the hyperbolic cosine of z. Thus, is non-decreasing and then the result holds. □
The likelihood ratio order is stronger than the hazard rate order and the usual stochastic order, which are defined as follows:
Definition 2.
Let and be two random variables with respective distribution functions provided by and and hazard rates and respectively. Then:
- (i)
- is said to be stochastically smaller than denoted by if for all x;
- (ii)
- is said to be smaller than in the hazard rate order, denoted by if for all x.
Now, the following corollary is presented.
Corollary 1.
Let and be two LAT random variables with respective pdf’s and and hazard rates and respectively. If then and .
Proof.
It is well-known (see [28]) that
Then, this result follows directly from Theorem 1 and (6). □
The examination of stochastic ordering is appropriate in many scenarios of applied statistics. For example, in binary regression, this ordering would provide that the approximation of p to 1 is faster than the one obtained via the logistic distribution. In contrast, the approximation to zero would be slower. However, sometimes the reverse would be required. The approximation of p to 1 was slower than the approximation to zero or a combination of both. The approach to 1 was slower and the approach to zero faster. This can be achieved by applying the arctan transformation to the distribution with cdf
The cdf provided in (7) is one of the several proposed by [30]. It is a max-stable (maximum of several random variables) distribution, which is also related to extreme value theory and also referred to in the literature as Lehmann’s alternative or exponentiated distribution of the form , where and is a continuous cumulative distribution function. For details about this family of distributions, see [31]. Furthermore, this distribution is the cdf used in the skewed logit model proposed by [1] and known as scobit model.
Thus, we focus now on the distribution obtained when (7) is implemented in (4), providing a distribution, say which is much more flexible and with cdf given by
Henceforward, we will denote this distribution as the SAT distribution, highlighting the fact that is the arc transformation of the Scobit model.
For the resulting random variable, it is not straightforward to prove that , however we can prove that by using in Definition 2. Therefore, for a random variable with cdf for any and and , we have that . This is corroborated below in Figure 1 where the cdf for special values of parameters and are shown. It is observed that as the parameter is closed to zero and (corresponds to the symmetric case, i.e., the classical logit specification), the shape of the curve varies.
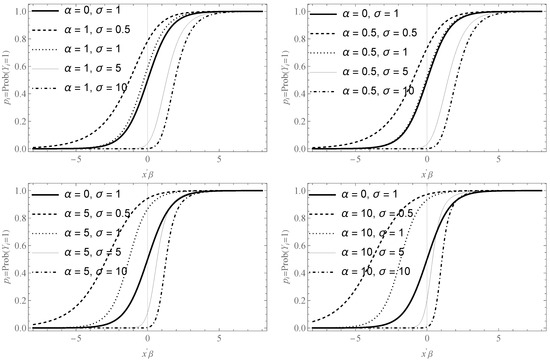
Figure 1.
Cumulative distribution function (logistic kernel mean function) of the skewed logit model for special values of skewness parameters and . The case , corresponds to the classical logistic specification.
Changes in the marginal effect against , for specific parameter values of and are displayed in Figure 2. This graph shows the relationship between and the marginal effect for a continuous covariate (). Its maximum value varies from (symmetry case with and ) to the left or right, respectively, as these parameters decrease or increase. As it is observed, the marginal effects take on their maximum values at different probability levels depending on the values of these parameters.
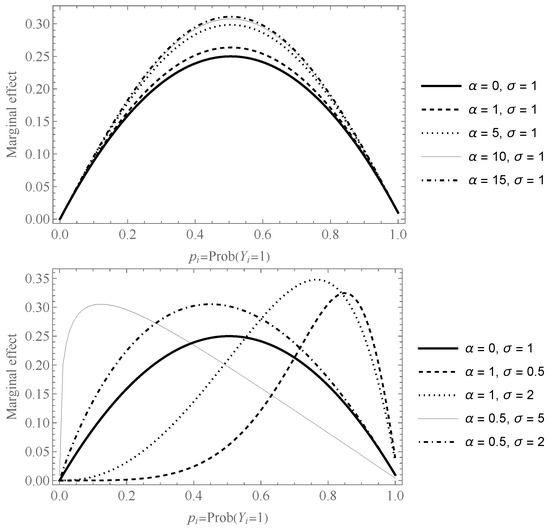
Figure 2.
Marginal effect of the skewed logit model with different values of skewness parameters and . The case , corresponds to the classical logistic specification.
4. Empirical Application
In order to apply and illustrate our methodology, we consider three datasets. The first deals with a well-known data collection widely examined in the statistical literature. It deals with mortality of adult beetle after five hours of exposure to gaseous carbon disulphide. The original dataset appeared in [32] and it has been discussed in many papers, such as [1]. We also reproduce them in Table 1 together with the fitted data values via maximum likelihood estimation. As in [1], we have added a location parameter and a scale parameter to the logistic distribution given in (1). The estimated parameters are and with the standard errors in brackets. Observe that the parameter is not significant at the usual statistical levels. The negative value of the maximum of the log-likelihood function (NLL) is 3.116. The estimation with the arc transformation of this logistic distribution, expression is given in (4), yielded the same estimates of the parameters because the parameter collapsed to zero. Nevertheless, for the general scobit model (the arc tan transformation of the scobit model provided in (7) and with cdf given by

Table 1.
Data taken from [32] dealing with mortality of adult beetle after five hours exposure to gaseous carbon disulphide.
The parameter estimates are as follows: , , , with a NLL value of 3.048. This Table also shows the contribution of every observation to Pearson’s chi-squared test statistics.
The second dataset is concerning with automobile insurance portfolio. This dataset is available at the website of the Faculty of Business and Economics, Macquarie University (Sydney, Australia), see also [33].
4.1. Brief Description of the Automobile Database
The dataset considered here is well-known in the actuarial literature. It is based on one-year vehicle insurance policies in 2004 or 2005. There are n = 67,856 policies for which the binary dependent variable is expressed as a collection of ones and zeros, with one representing the occurrence of at least one claim. A pictorial representation of this dependent variable is shown in Figure 3. A significant imbalance in the two categories of outcome considered can be observed. In this case, the portfolio contains 4624 (6.8%) of policyholders who had at least one claim. The description of the explanatory variables associated with the claims considered in this work is as follows:
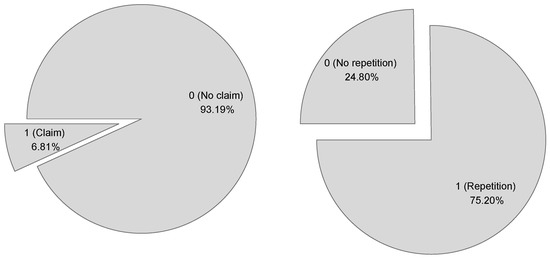
Figure 3.
A pictorial representation of the dependent variable. Second example on the left and third example on the right.
- Vehicle’s value (VAGE) in USD 10,000;
- The body of the vehicle, coded as, Bus (BUS), Convertible (CONVT), Coupe (COUPE), Utility (UTE), and Hatchback (HBACK);
- Area: driver’s area of residence: A, B, C, D, E (the reference variable is the driver’s area of residence F);
- Age (AGE): driver’s age category: 1 (youngest), 2, 3, 4, 5, 6 (older);
4.2. Third Database and Brief Description
The third dataset is concerned with tourism. The database was obtained from the 2017 Canary Islands Tourist Expenditure Survey, carried out by the Canary Islands Institute of Statistics (ISTAC). This study corresponds to personal interviews with tourists from mainland Spain on departure and provides quarterly information about their total expenditure in the Canaries. The sample includes both package and non-package tourists, staying for at least one and no more than 30 consecutive nights (representing around 99% of the sample). After excluding observation data with missing values and non-response, 10,000 observations remained in the sample.
- Length of stay (LS) (trip duration or number of nights) in the Canaries;
- INCOME. This is an ordered categorical variable. It takes the following values: =1, from €12,001 to €24,000; =2, from €24,001 to €36,000; =3, from €36,001 to €48,000; =4, from €48,001 to €60,000; =5, from €60,001 to €72,000; =6, from €72,001 to €84,000; and =7, higher than €84,001;
- Type of accommodation. Three types of variable are considered. First, an indicator which takes the value 1 if the tourist accommodation is a 5-star hotel/aparthotel, and the value 0 otherwise (STARSUP). Second, an indicator which takes the value 1 for a 4-star hotel/aparthotel (STAR45), and 0 otherwise. Finally, a binary variable which takes the value 1 if the accommodation is a 1, 2, or 3-star hotel/aparthotel, and 0 otherwise (STAR3). The reference category represents other types of accommodation, such as the tourists’ own property, friends or family property, or campsites or apartments;
- REPETITION. A dichotomic variable which takes the value 1 if the tourist has visited the Canaries previously, and 0 otherwise. This corresponds to the dependent variable;
- JOB. This variable contains the following categories: business owner, self employed, liberal profession, upper management employee, middle management employee, auxiliary level employee, other employee, student, retired, homemaker, and unemployed. Three dummy variables are considered. Business owner takes the value 1 if the tourist is a business owner, and 0 otherwise. Self employed takes the value 1 if the tourist is self employed or has a liberal profession and 0 otherwise. Salaried worker takes the value 1 if the tourist works for a salary and 0 otherwise. The reference category is student, retired, homemaker, and unemployed;
- LOW COST. This is an indicator that takes the value one if the tourist has travelled in a low-cost airline and 0 otherwise.
4.3. Estimation Results and Discussion
Table 1 summarizes the estimation results for the three models examined, logistic, scobit, and general scobit, they are given by
respectively.
Parameter estimates, standard error (in brackets) and marginal effects (ME) for standard logistic and skewed logistic models: Scobit and SAT are displayed in Table 2 for the second example (automobile dataset). Overall, the three models similarly fit the data, as judged by the NLL and the chi-square value. Nevertheless, the model with more significant variables is the SAT. Qualitatively, all the models yielded similar results, with coefficient estimates showing the same signs for all variables. It is interesting to note that the parameters which control the skewness in the Scobit model () and the SAT model ( and ) are highly significant. Thus, as judged by their values and significance, we cannot reject the assumption of asymmetry of the dependent variable. However, it is noticeable substantial differences in the magnitude of estimated coefficients for several explanatory variables, affecting the marginal effects. The marginal effect on on a change on , for a continuous variable, can be calculated as

Table 2.
Parameter estimates, standard error (in brackets) and marginal effects (ME) for standard logistic and skewed logistic models: Scobit and SAT.
For dichotomous variables, taking values 0 and 1, the marginal effect for the variable is given by , where for , the kth explanatory variable takes the value 1 and for the value 0, remaining the rest of the explanatory variables constant. Since there is a marginal effect for each individual in the sample and some variables are continuous and other are binary variables, we computed the marginal effect for all the individuals and took their mean value, i.e., average marginal effect. It should be noted that some of the marginal effects obtained were slightly different between the logit, Scobit, and general Scobit. In this regard, as illustrated in this Table, for the explanatory variable Vehicle’s value (VAGE), the marginal effect under the logit model is 0.005, this is intuitively interpreted as an increase of USD 10,000 in the vehicle’s value, increases the probability of occurrence of at least one claim in 0.5%. The increase in that probability for the scobit model is 0.1% whereas for the general Scobit is 0.7%. Similarly, the marginal effect for the variable AGE is —0.007 for the logit model, which is interpreted as an increase of one in the driver’s age category year would decrease the probability of occurrence of at least one claim by 0.7%, holding the other variables fixed. The decrease in the probability under the scobit model is 0.2% where under the general scobit model is 1%, which is not negligible.
Below in Table 3 parameter estimates together with standard errors (in brackets) and marginal effects for standard logistic and skewed logistic models: Scobit, LAT, and SAT for the third example are provided. No important differences are observed between the four regression models in terms of the marginal effects and significance level of the explanatory variables considered. Nevertheless, both the NLL and the chi-square statistics are reduced under the SAT regression model. The response variable is repetition of holidays destination (:=1).

Table 3.
Parameter estimates, standard error (in brackets) for standard logistic and skewed logistic models: Scobit, LAT, and SAT.
Figure 4 displays the cdf of the three models considered by using the parameter estimates exhibited in Table 2 and Table 3. It can be seen that for the scobit and SAT models, the approximation of p to 0 is faster than the one for the logit model, as expected. In contrast, the approximation to the value 1 is slower.
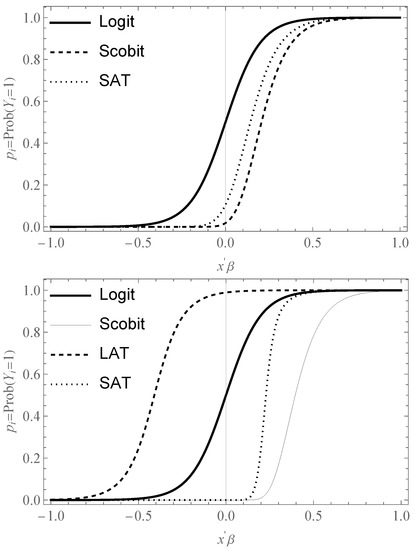
Figure 4.
CDF of the classical logit, scobit, LAT, and SAT obtained from the estimated parameters. Second example above and third example below.
Furthermore, as a Reviewer has pointed out, when the link function is skewed, then the definition of the intercept needs to be changed to prevent confounding. This matter which has been neglected in the literature is dealt in deep in [9] for the skew probit model. Following the latter paper, we can redefine the intercept as where q is the quantile level. Then, we have that the expression for the intercept for the Scobit and SAT regression models are given by
respectively.
Below in Table 4 are displayed the parameter estimates, standard error (in brackets) for Scobit and SAT regression models when the intercept has been redefined to prevent confounding. The LAT regression model has not been incorporated into this Table because the parameter is insignificant. The estimate of the quantile level q is significant at the 1% level for both models. Nevertheless, for the other explanatory variables, there are no essential differences concerning the models with an intercept to the significant covariates with the exemption of JOB, which is statistically significant at the 10% significant level under both models.

Table 4.
Parameter estimates, standard error (in brackets) for Scobit and SAT models with redefined intercept.
5. Final Comments
We have introduced a binary skewed model starting first with the classical logistic specification and followed next, by the scobit specification. This new model performs well when there exists a pronounced imbalance in the distribution of the response variable. The significant difference between the classical model and the new one is mainly based on the slight differences in the resulting marginal effects. In summary, for the dataset considered in the empirical application section of this work, no substantial differences were found in the three models examined when the NLL was considered as a measure of model selection. However, relevant differences in the significance level and marginal effects for some of the explanatory variables were observed in the general logistic model introduced in this work that were not observed in the other two models.
Following the ideas provided in [9] when we perform a skew logit or probit model, the new link functions need to be scaled and centered bringing the results into the same scale and estimates, and, thus, they could be compared. This is obviously more important in the Bayesian context, which is not the case discussed here, for obvious reasons.
Finally, by replacing the cdf of the standard normal (i.e., ) distribution in (4) , expressions of the type , are obtained, that is, generalizations of the probit model. Alternatively, generalizations of the binomial proportion generalized linear models can be also simply derived by modifying the cauchit, log-log and complementary log-log link functions accordingly. These issues can be studied in future works.
Author Contributions
Conceptualization, E.G.-D., E.C.-O. and H.W.G.; Formal analysis, E.G.-D., E.C.-O. and H.W.G.; Investigation, E.G.-D., E.C.-O. and H.W.G.; Methodology, E.G.-D., E.C.-O. and H.W.G.; Software, E.G.-D., E.C.-O. and H.W.G.; Supervision, E.G.-D., E.C.-O. and H.W.G.; Validation, E.G.-D., E.C.-O. and H.W.G. All of the authors contributed significantly to this research article. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank to the Ministerio de Economía y Competitividad, Spain (project ECO2017-85577-P, EGD. The research of H.W. Gómez was supported by PUENTE-UA project, Chile.
Data Availability Statement
Second dataset is available in a publicly accessible repository. The data presented in this study are openly available at the website of the Faculty of Business and Economics, Macquarie University (Sydney, Australia). Third dataset presented in this study are available on request from the corresponding authors. The data are not publicly available due to legal issues.
Acknowledgments
We thank the two anonymous reviewers for their valuable comments and suggestions, which have greatly helped us improve the original manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prentice, R.L. A generalization of the probit and logit methods for dose-response curves. Biometrika 1976, 32, 761–768. [Google Scholar] [CrossRef]
- Nagler, J. Scobit: An alternative estimator to logit and probit. Am. J. Polit. Sci. 1994, 38, 230–255. [Google Scholar] [CrossRef]
- Aranda-Ordaz, F.J. On two families of transformations to additivity for Binary Response data. Biometrika 1981, 68, 357–363. [Google Scholar] [CrossRef]
- Guerrero, V.M.; Johnson, R. Use of the Box-Cox transformation with Binary Response models. Biometrika 1982, 69, 309–314. [Google Scholar] [CrossRef]
- Albert, J.; Chib, S. Bayesian residual analysis for binary response regression models. Biometrika 1995, 82, 747–769. [Google Scholar] [CrossRef]
- Stukel, T.A. Generalized logistic models. J. Am. Stat. Assoc. 1988, 83, 426–431. [Google Scholar] [CrossRef]
- Chen, M.; Dey, D. Bayesian modeling of correlated binary responses via scales mixture of multivariate normal link models. Sankhȳa Ser. A Indian J. Stat. Spec. Issue Bayesian Anal. 1998, 60, 322–343. [Google Scholar]
- Chen, M.; Dey, D.; Shao, Q. A new skewed link model for dichotomous quantal response data. J. Am. Stat. Assoc. 1999, 94, 1172–1186. [Google Scholar] [CrossRef]
- van Niekerk, J.; Rue, H. Skewed probit regression-identifiability, contraction and reformulation. REVSTAT–Stat. J. 2021, 19, 1–22. [Google Scholar]
- Bazán, J.L.; Branco, M.S.; Bolfarine, H. A skew item response model. Bayesian Anal. 2006, 1, 861–892. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Bazán, J.L. New links for binary regression: An application to coca cultivation in Peru. Test 2006, 27, 597–617. [Google Scholar] [CrossRef]
- Caron, R.; Sinha, D.; Dey, D.K.; Polpo, A. Categorical data analysis using a skewed Weibull regression model. Entropy 2018, 20, 176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bermúdez, L.; Pérez-Sánchez, J.; Ayuso, M.; Gómez-Déniz, E.; Vázquez-Polo, F. A bayesian dichotomous model with asymmetric link for fraud in insurance. Insur. Math. Econ. 2008, 42, 779–786. [Google Scholar] [CrossRef]
- Pérez-Sánchez, J.; Negrín-Hernández, M.; García-García, C.; Gómez-Déniz, E. Bayesian asymmetric logit model for detecting risk factors in motor ratemaking. ASTIN Bull. 2014, 44, 445–457. [Google Scholar] [CrossRef]
- Tay, R. Comparison of the binary logistic and skewed logistic (Scobit) models of injury severity in motor vehicle collisions. Accid. Anal. Prev. 2016, 88, 52–55. [Google Scholar] [CrossRef]
- Alkhalaf, A.; Zumbo, B.D. The impact of predictor variable(s) with skewed cell probabilities on Wald tests in binary logistic regression. J. Mod. Appl. Stat. Methods 2017, 16, 40–80. [Google Scholar] [CrossRef]
- Mwenda, N.; Nduati, R.; Kosgei, M.; Kerich, G. Skewed logit model for analyzing correlated infant morbidity. PLoS ONE 2021, 16, e0246269. [Google Scholar] [CrossRef]
- Mirzadeh, S.; Iranmanesh, A. A new class of skew-logistic distribution. Math. Sci. 2019, 13, 375–385. [Google Scholar] [CrossRef] [Green Version]
- Esmaeili, H.; Lak, F.; Alizadeh, M.; Dehghan, M. The Alpha-Beta Skew Logistic Distribution: Properties and Applications. Stat. Optim. Inf. Comput. 2020, 8, 304–317. [Google Scholar] [CrossRef]
- Liu, M.; Zhu, F.; Zhu, K. Modeling normalcy-dominant ordinal time series: An application to air quality level. J. Time Ser. Anal. 2022; forthcoming. [Google Scholar] [CrossRef]
- O’Connell, A. Logistic Regression Models for Ordinal Response Variables; Quantitative Applications in Social Sciences Series; SAGE Publications: Thousand Oaks, CA, USA, 2001. [Google Scholar]
- Cramer, J.S. Logit Models from Economics and Other Fields; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Brooks, C. RATS Handbook to Accompany Introductory Econometrics for Finance; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Jacob, E.; Jayakumar, K. On half-Cauchy distribution and process. Int. J. Stat. Math. 2012, 3, 77–81. [Google Scholar]
- Gómez-Déniz, E.; Calderín, E. On the use of the Pareto ArcTan distribution for describing city size in Australia and New Zealand. Phys. A—Stat. Mech. Its Appl. 2015, 436, 821–832. [Google Scholar] [CrossRef]
- Gómez-Déniz, E. A family of arctan Lorenz curves. Empir. Econ. 2016, 51, 1215–1233. [Google Scholar] [CrossRef]
- Calderín-Ojeda, E.; Azpitarte, F.; Gómez-Déniz, E. Modelling income data using two extensions of the exponential distribution. Phys. A—Stat. Mech. Its Appl. 2016, 461, 756–766. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ross, S.M. Stochastic Processes, 2nd ed.; Wiley Series in Probability; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Burr, I.W. Cumulative frequency functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Sarabia, J.; Castillo, E. About a class of max-stable families with applications to income distributions. METRON 2005, LXIII, 505–527. [Google Scholar]
- Bliss, C.I. The calculation of the dosage-mortality curve. Ann. Appl. Biol. 1935, 22, 134–167. [Google Scholar] [CrossRef]
- de Jong, P.; Heller, G. Generalized Linear Models for Insurance Data; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).