Mean Remaining Strength Estimation of Multi-State System Based on Nonparametric Bayesian Method

Abstract

In a stress-strength system, the mean remaining strength is the key to deciding the safety threshold for the system continuing to operate. In this study, a multi-state stress-strength system composed of two-state components is discussed, and the mean remaining strength of the system is studied. Applying a multidimensional signature, the dynamic signature form is established, and the mean remaining strength of the system in different states is deduced. Moreover, the nonparametric Bayesian method is used to estimate the mean remaining strength of the system. The results of Monte Carlo simulation show that the nonparametric Bayesian method can reasonably estimate the mean remaining strength of a multi-state system, and its estimation effect is better than that of the nonparametric estimation method. A practical case based on a fiber strength dataset is presented as an application of the proposed methodology.

1. Introduction

In the case of a stress-strength setting, the reliability estimation and residual strength analysis of the component and the system are the focus of reliability theory research. The stress-strength reliability (SSR) of a system or component generally refers to the probability that it will fully carry out a specific function under certain environmental conditions. The component’s strength is Y and the stresses X applied to it by the working environment are regarded as random variables in the stress-strength setting. When the strength is less than stress, the system will not work. Birnbaum et al. [1] introduced the definition of the SSR as $R=P(X<Y)$. The mean remaining strength (MRS) can provide guidance for determining mean safety threshold and reliability at the current stress, assuming that the strength of the system is T, and the stress is X. When the system does not fail at the strength level t, Bairamov et al. [2] defined the MRS of the system by $E(T-X-t|T-X>t)$.

Recently, more researchers have analyzed the parameter estimation when the stress and strength obey different distributions. Bi et al. [3] investigated the Bayesian and approximate maximum likelihood estimation of SSR when stress and strength obey the inverse Weibull. Dey et al. [4] discussed Bayesian and non-Bayesian estimates of component reliability, assuming stress and strength both obey the Kumaraswamy distribution. Agiwal et al. [5] developed a Bayesian estimation program to estimate the reliability when both stress and strength are the inverse Chen random variables. Chen et al. [6] proposed prediction limits based on a gamma distribution and applied it to SSR estimation. Kayal et al. [7] obtained the point estimate and interval estimate of SSR for a multi-component system by using classical and Bayesian methods. In the literature mentioned above, the system is assumed to be binary.

For a binary system, there are two possible states: the working or failure state. However, the system may be in an intermediate state in some cases, which means that it probably has more performance levels. From the actual situation, a multi-state system under a stress-strength setting has been widely discussed. Eryilmaz et al. [8] used the value of $X-Y$ to classify the multiple states of the system, and estimated the state probability of the system. Eryılmaz et al. [9] considered using the number of components whose strength was higher or lower than multiple stress components to define the various states of the system, and analyzed the SSR of this system. Qin et al. [10] classified the different states of the system by using the ratio of strength and stress values. In all the aforementioned literature, the component states are defined as multi-state in the study of multi-state systems under the stress-strength setting. However, it is complicated to obtain multiple states of components in practice, so a multi-state system composed of two-state components can be considered. In the study of this multi-state system, the system signature is used to establish the relationship between the component and the system.

System signature has become a practical tool for the research and comparison of complex systems. Samaniego et al. [11] firstly proposed system signature based on independent and identically distributed (IID) components. On this basis, Marichal et al. [12] extended the signature definition to a three-state system composed of two-state components. He et al. [13] generalized three-state to multi-state, and the definition of a multi-state system signature was given. Recently, many scholars have applied signature theory, which can simplify the calculation to the reliability research of the stress-strength system. Pakdaman et al. [14] developed the strength system signature for a stress-strength model, and assessed the SSR. Liu et al. [15] investigated the reliability estimation of stress-strength of a multitype component system, which considered the survival signature of the extended form of the system signature. System signature is widely used in the estimation problem of SSR under a stress-strength setting. In the analysis of another problem in the stress-strength model, there is less literature and the system signature is rarely used.

In practical applications, the remaining useful lifetime is widely used in product prediction and maintenance [16]. Under the stress-strength model, it is also necessary to estimate the MRS of the product based on the stress condition. Gürler et al. [17] firstly studied the MRS of components in a stress-strength setting, and presented the MRS model of some simple systems composed of n independent components. Based on this model, Bairamov et al. [2] deduced the expression for the MRS in some simple systems with exchangeable components. This expression is used to estimate the parameter of MRS. Gurler et al. [18] considered the two-component parallel system and presented the maximum likelihood estimation (MLE) of its MRS. Kizilaslan et al. [19] studied the MLE and Bayesian estimation of the MRS in a parallel system. In addition, some scholars have analyzed the stress-strength system from other novel perspectives. Manuel et al. [20] used the square root of the ratio of maximum principal stress and the minimum principal stress to determine the maximum and minimum lifetime in a Weibull analysis, and obtained the base lifetime. Manuel et al. [21] defined the safety factor of a Weibull distribution as the evaluation index of system reliability, and gave a detailed solution process considering the same and different shaped parameters. However, these two methods and the above estimates of MRS are both parameter estimations under the given distribution assumption. Parameter estimation relies on restrictive assumptions about a particular family of parameters of the distribution, which are often not easy to select. This leads to the emergence of nonparametric estimation, which combines Bayesian rules and develops into nonparametric Bayesian methods that take into account prior information and data.

Recently, nonparametric Bayesian methods have been considered by numerous researchers in reliability analysis. The prior distribution used in these methods usually has an asymmetric distribution, such as Dirichlet distribution, gamma distribution, and beta distribution. Polpo et al. [22] performed nonparametric Bayesian estimation of the reliability function of a component in a parallel system. For the series-parallel and parallel-series systems, Polpo et al. [23] gave the nonparametric Bayesian estimation of a system reliability function. Liu et al. [24] considered a nonparametric Bayesian method to evaluate the reliability of a hybrid system, which can simplify the hybrid system into parallel-series and series-parallel systems in an accelerated lifetime test. However, currently, there is little research on the nonparametric Bayesian methods in a stress-strength setting. Therefore, this method is considered to analyze the stress and strength data.

In this paper, a multi-state system composed of two-state components is studied under the stress-strength setting. In terms of the multidimensional system signature, the system dynamic signature at the strength level t is deduced. Furthermore, the expression of the MRS of the multi-state strength system is obtained. The nonparametric Bayesian method is employed to estimate the MRS, and an example of an asymmetric structure system is considered in a Monte Carlo simulation. In addition, to prove the applicability of the proposed method, a practical case based on datasets is given.

This paper is organized as follows. In Section 2, the signature and some hypotheses of the multi-state strength system are introduced, and the dynamic signature and its calculation are discussed. In Section 3, the MRS of the multi-state strength system is deduced. In Section 4, based on the a priori Dirichlet process, the posterior distribution of the stress and strength distribution function is obtained. Then, in order to illustrate the feasibility of the nonparametric Bayesian method, the results of the Monte Carlo simulation are provided in Section 5. In addition, a real dataset is analyzed in Section 6. Finally, we give some concluding remarks and discuss scope for future research in Section 7.

2. The Multi-State Strength System Signature

We consider a multi-state strength system composed of m two-state components with $n+1$ system states. Assuming that the components are independent of each other, each component has two variables; one is the strength of the component, the other is the external force borne by all components (we call this stress). The component strength follows the absolute continuous distribution F, and the stress is subject to the absolute continuous distribution G.

The state vector of each component is represented by $y=(y_1,y_2,\dots ,y_m)$, where $y_i\in (0,1)$$(i=1,\dots ,m)$ is the state of the component i. The state $y_i=1$ means component i is working; that is, the component strength is greater than the stress, and state $y_i=0$ means component i is failing. The state of the strength system is denoted as h, where $h\in S=\{0,1,\dots ,n-1,n\}$. The perfect working state is denoted by n, the complete failure state is denoted by 0, and the different degrees of ordered degradation of the system correspond to intermediate states $1,2,\dots ,n-1$. The structure function of a multi-state strength system is defined as $\phi :{(0,1)}^m\to S$. Suppose that each argument in $\phi \left(h\right)$ increases monotonically and $\phi \left(0\right)=0$, $\phi \left(1\right)=1$, where $0=(0,0,\dots ,0)$ and $1=(1,1,\dots ,1)$.

Next, we introduce some assumptions about this system.

(1)

The state of the system at the strength level $t\ge 0$ is completely dependent on the states of each component.

(2)

All the components of system are independent of each other and their distributions are unknown.

(3)

The performance of the component and the system drop from perfect to failure. All of the components are in their best state at the very beginning of their lifetime.

Next, we give the signature of the multi-state strength system and its calculation content in detail.

2.1. The Signature of the Stress-Strength System

Zarezadeh et al. [25] studied the signature of a three-state network structure composed of three states: prefect, partially functioning, and failure. Then they extended the signature to the $n-dimensional$ signature. The signature of a multi-state system is given in [13], which is defined as follows.

Definition 1.

Let system strength $T_k$$(k=1,2,\dots ,n)$ be the degenerated strength of a multi-state strength system from state n to state $n-k$. We assume that the component strengths $Y_i$$(i=1,\dots ,m)$ are IID random variables, and obey absolutely continuous distribution $F\left(y\right)$, $y\ge 0$. Then, the signature of the system is

$$s=\left(s_{i_1,i_2,\dots ,i_n},1\le i_1,i_2,\dots ,i_n\le m\right),$$

where $Y_{i_1:m},\dots ,Y_{i_n:m}$ are the $i_1\mathrm{th},\dots ,i_n\mathrm{th}$ order statistics of $Y_1,\dots ,Y_m$, respectively, and $s_{i_1,i_2,\dots ,i_n}=P\{T_1=Y_{i_1:m},T_2=Y_{i_2:m},\dots ,T_n=Y_{i_n:m}\}$.

For more information, one can refer to He et al. [13].

2.2. The Calculation of Signature

Let $T_k$ be the system strength. The signature of the system is a high-dimensional probability matrix, called S, with elements whose spatial coordinates are $(i_1,i_2,\dots ,i_n)$, which can be given by the following formula:

$$s_{i_1,i_2,\dots ,i_n}=P\{T_1=Y_{i_1:m},T_2=Y_{i_2:m},\dots ,T_n=Y_{i_n:m}\}$$

Considering the multi-state system from the perspective of arrangement and combination, let ${\Pi }_n$ be the set of different permutations of component set $\left\{1,2,\dots ,n\right\}$, with arbitrary arrangement $({\pi }_1,{\pi }_2,\dots ,{\pi }_n)\in {\Pi }_n$, $i_k=i_k\left(\pi \right)$ indicating that the system state is $n-k+1$ before the failure of the $i_k\mathrm{th}$ component, and the system state changing to $n-k$ after the failure of the $i_k\mathrm{th}$ component. This is expressed by the structure function as follows: for $k=1,2,\dots ,n$.

$$\varphi \left(0_{{\pi }_1},\dots ,0_{{\pi }_{i_k-1}},1_{{\pi }_{i_k}},1_{{\pi }_{i_k+1}},\dots ,1_{{\pi }_m}\right)=n-k+1,$$

$$\varphi \left(0_{{\pi }_1},\dots ,0_{{\pi }_{i_k-1}},0_{{\pi }_{i_k}},1_{{\pi }_{i_k+1}},\dots ,1_{{\pi }_m}\right)=n-k.$$

Thus, $A_n\left(\pi \right)=\{i_1\left(\pi \right),i_2\left(\pi \right),\dots ,i_n\left(\pi \right)\}$ is the element in arrangement ${\Pi }_n$. For example, $A_{i_1,i_2,\dots ,i_n}=\{{\Pi }_n:i_1\left(\pi \right)=i_1,i_2\left(\pi \right)=i_2,\dots ,i_n\left(\pi \right)=i_n\}$. This can also be written as $A_{i_1,i_2,\dots ,i_n}=\{{\Pi }_n:T_1=Y_{i_1:m},T_2=Y_{i_2:m},\dots ,T_n=Y_{i_n:m}\}$.

Then, the calculation formula of the signature is

$$s_{i_1,i_2,\dots ,i_n}=\frac{|A_{i_1,i_2,\dots ,i_n}|}{m!},$$

where $|A_{i_1,i_2,\dots ,i_n}|$ is the number of elements in the set $A_{i_1,i_2,\dots ,i_n}=\{{\Pi }_n:T_1=Y_{i_1:m},T_2=Y_{i_2:m},\dots ,T_n=Y_{i_n:m}\}$, and ${\Pi }_n$ is the set of all permutations of $\{1,\dots ,n\}$.

In addition, Da et al. [26] gave the definition of a two-dimensional marginal signature, and similarly obtained a multi-state marginal signature, which is expressed as ${\overline{s}}_{i_1,i_2,\dots ,i_n}$, then

$$\begin{array}{cc}\hfill & {\overline{s}}_{i_1,i_2,\dots ,i_n}=P(T_1>Y_{i_1:m},T_2>Y_{i_2:m},\dots ,T_n>Y_{i_n:m})\hfill \\ \hfill & ={\sum }_{l_1=i_1+1}^{m-n+1}{\sum }_{l_2=max(l_1+1,i_2+1)}^{m-n+2}\cdots {\sum }_{l_n=max(l_{n-1}+1,i_n+1)}^m·P(T_1=Y_{l_1:m},\hfill \\ \hfill & T_2=Y_{l_2:m},\dots ,T_n=Y_{l_n:m})\hfill \\ \hfill & ={\sum }_{l_1=i_1+1}^{m-n+1}{\sum }_{l_2=max(l_1+1,i_2+1)}^{m-n+2}\cdots {\sum }_{l_n=max(l_{n-1}+1,i_n+1)}^m{s}_{l_1,l_2,\dots ,l_n},\hfill \end{array}$$

where $l_k$ is the number of component failures before exiting state $n-i_k$ to state $n-i_{k+1}$, so $l_{k+1}\ge l_k+1$, $i_{k+1}=i_k+1$.

2.3. The Dynamic Signature

In some cases, the system is in the intermediate state if there are failure components. At this point, we need to evaluate the reliability of the dynamic system. Xu et al. [27] and Luo et al. [28] have established the evaluation model of the dynamic system reliability. Based on the reliability block diagram, dynamic signature is a practical and simple method. Suppose that at the strength level t, the system has $k\left(t\right)(i_{l\left(t\right)}<k\left(t\right)<i_{l\left(t\right)+1})$ component failures, the system state is $h\left(t\right)$, and the degradation order of the system is $l\left(t\right)$, such that $h\left(t\right)=n-l\left(t\right)$. Let the events $E_{k\left(t\right)}=\{Y_{k\left(t\right):m}\le t\le Y_{k\left(t\right)+1:m}\}$, which means that at the strength level t, the $k\left(t\right)\mathrm{th}$ component is failing and the $\left(k\right(t)+1)\mathrm{th}$ component is alive. Suppose that $F_{l\left(t\right)+1}=\{T_1<t,\cdots ,T_{l\left(t\right)}<t,T_{l\left(t\right)+1}>t,\cdots ,T_n>t\}$, this means that the system has degenerated, the system strength $T_1,T_2,\dots ,T_{l\left(t\right)}$ has degraded from n to $n-1,\dots ,n-l\left(t\right)$, which is less than the strength level t, and system strength $T_{l\left(t\right)+1},\dots ,T_n$ is more than the strength level t. Therefore, the current system needs to take into account the condition $E_{k\left(t\right)}\cap F_{l\left(t\right)+1}$. Then, the system signature is a high-dimensional matrix of ${[m-k(t\left)\right]}^{h\left(t\right)}$, represented as

$$\begin{array}{cc}\hfill & s_{i_1,i_2,\dots ,i_n}(m-k\left(t\right))\hfill \\ \hfill & =\frac{s_{i_1,i_2,\dots ,i_n}}{{\sum }_{i_1=1}^{m-n+1}\cdots {\sum }_{i_{l\left(t\right)+1}=k\left(t\right)+1}^{m-n+l\left(t\right)+1}{\sum }_{i_{l\left(t\right)+2}=i_{l\left(t\right)+1}+1}^{m-n+l\left(t\right)+2}\cdots {\sum }_{i_n=i_{n-1}+1}^m{s}_{i_1,i_2,\dots ,i_n}}\hfill \\ \hfill & =\frac{s_{i_1,i_2,\dots ,i_n}}{s_{i_1,i_2,\dots ,i_n}^{*}},\hfill \end{array}$$

where $s_{i_1,i_2,\dots ,i_n}^{*}={\sum }_{i_1=1}^{m-n+1}\cdots {\sum }_{i_{l\left(t\right)+1}=k\left(t\right)+1}^{m-n+l\left(t\right)+1}\cdots {\sum }_{i_n=i_{n-1}+1}^m{s}_{i_1,i_2,\dots ,i_n}$, and $i_{l\left(t\right)}\ge k\left(t\right)+1$,

$i_{l\left(t\right)+2}\ge i_{l\left(t\right)+1}+1,\dots ,i_n\ge i_{n-1}+1$.

The derivation of system signature $S\left(m-k\left(t\right)\right)$ is shown in Appendix A.

3. The Remaining Strength

Consider the $n+1$$(n\ge 2)$ states strength system composed of m two-state components. The strength of the system components is IID and has the same continuous distribution function $F\left(y\right)$. The stress obeys the continuous distribution $G\left(x\right)$, and the stress at the strength level t is X. The MRS of the system, represented by ${\Phi }_{Y|X}$, can be represented as the expected residual strength under stress X. The definition of MRS is given by Bairamov et al. [2] as ${\Phi }_{Y|X}\left(t\right)=E(T-X-t|T-X>t),$$t>0$.

The MRS can indicate the average safe time of a component or system under the current stress X and strength level t. At the strength level t, the number of component failures can be obtained, and the dynamic signature can be used to establish the relationship between the system and component, so the MRS of the system can be deduced. The expression for MRS is shown in Theorem 1.

Theorem 1.

Let high-dimensional matrix S be a system of multi-dimensional signature. The original state of the system is n, and the final state of the system is 0, so the system strength is $T=T_n$. If $Y_1,Y_2,\dots ,Y_m$ are component strengths, the number of component failures is $k\left(t\right)$, the state order of system degradation is $l\left(t\right)$, and ${\overline{E}}_{k\left(t\right)}=\{Y_{k\left(t\right):m}-X\le t<Y_{k\left(t\right)+1:m}-X\}$, ${\overline{F}}_{l\left(t\right)+1}=\{T_1-X<t,\cdots ,T_{l\left(t\right)}-X\le t,T_{l\left(t\right)+1}-X>t,\cdots ,T_n-X>t\}$.

The MRS of the system at the strength level t and under the current stress X is given by

$$\begin{array}{cc}\hfill & {\Phi }_{Y|X}\left(t\right)\hfill \\ \hfill & =E\left(P(T-X-t|{\overline{E}}_{k\left(t\right)}\cap {\overline{F}}_{l\left(t\right)+1})\right)\hfill \\ \hfill & ={\int }_0^{\infty }P\left(T-X-t>z|{\overline{E}}_{k\left(t\right)}\cap {\overline{F}}_{l\left(t\right)+1}\right)dz\hfill \\ \hfill & ={\sum }_{i_1=1}^{m-n+1}\cdots {\sum }_{i_{l\left(t\right)+1}=k\left(t\right)+1}^{m-n+l\left(t\right)+1}\cdots {\sum }_{i_n=i_{n-1}+1}^m{s}_{i_1,i_2,\dots ,i_n}\left(m-k\left(t\right)\right)\hfill \\ \hfill & ·\frac{{\int }_0^{\infty }{\int }_0^{\infty }\left(\begin{array}{c}m\\ i_n\end{array}\right){\left[F(x+z+t)-F(x+t)\right]}^{i_n}{\left[1-F(x+z+t)\right]}^{m-i_n}dG\left(x\right)dz}{{\int }_0^{\infty }{\int }_0^{\infty }{[1-F(x+t\left)\right]}^{m}dG\left(x\right)dz}.\hfill \end{array}$$

(1)

The proof of Theorem 1 is given in Appendix B.

4. Nonparametric Bayesian Inference

The most widely used prior in nonparametric Bayesian analysis is the Dirichlet process. For a detailed description of the Dirichlet process see Ferguson et al. [29]. More recently, Maceachern et al. [30] outlined the nonparametric Bayesian approach.

4.1. Dirichlet Process

We assume that $\chi$ is a completely separable metric space and $\mathsf{Y}$ is the corresponding $\sigma -\mathrm{field}$ of subset of $\chi$. For all measurable partitions $(r_1,r_2,\dots ,r_k)$, the random probability P on measurable space $(\chi ,\mathsf{Y})$ can be expressed by the joint distribution $\left(P\left(r_1\right),P\left(r_2\right),\dots ,P\left(r_k\right)\right)$. We say $(r_1,r_2,\dots ,r_k)$ is a measurable partition of $\chi$, if $r_i\cap r_j=⌀$, $i\ne j$, ${\cup }_{j=1}^k{r}_j=\chi$, where $r_i,r_j\in \mathsf{Y}$, for $i,j=1,2,\dots ,k$.

Definition 2.

Let δ be a positive real number and $G_0$ be a finite nonnegative measure on $(\chi ,\mathsf{Y})$. This is a random process $P\left(r\right),r\in \mathsf{Y}$, which is a Dirichlet process with parameter $\delta G_0$ on $(\chi ,\mathsf{{\rm Y}})$, if the random vector $\left(P\left(r_1\right),\dots ,P\left(r_k\right)\right)$ is Dirichlet distribution $D\left(\delta G_0\left(r_1\right),\dots ,\delta G_0\left(r_k\right)\right)$, where $(r_1,\dots ,r_k)$ is the measurable partition of Υ, $\forall k=1,2,\dots$.

The nonparametric Bayesian estimation of the distribution function $F\left(y\right)$ of total samples Y is discussed in detail by Ferguson et al. [29]. Then, a posterior estimate of the distribution function is given.

If Y is a random variable representing the strength of a component, its cumulative distribution function (CDF) is $F\left(y\right)=P(Y\le y)$. It is known that the Dirichlet process is defined by the mean value (also known as the base measure), which is expressed as $F_0\left(y\right)$, and the precision parameter $\delta \ge 0$ controls the change of Dirichlet process near $F_0\left(y\right)$. The Dirichlet process can be described as a distribution of CDF. The Dirichlet process is defined by precision $\delta$ and the base measure $F_0\left(y\right)$ as $DP(\delta ,F_0)$. The Bayesian estimation of $F\left(y\right)\sim DP(\delta ,F_0)$ with a quadratic loss function is $E\left[F\left(y\right)\right]=F_0\left(y\right)$.

For an estimate ${\widehat{F}}_{SE}$ of F, its quality will be measured via the squared error loss function

$$L(F,{\widehat{F}}_{SE})=\int {\left(F\left(y\right)-{\widehat{F}}_{SE}\left(y\right)\right)}^{2}dw\left(y\right),$$

where w is a finite measure. Based on this loss function, the Bayes estimator of F is given by the posterior mean of F, which minimizes the Bayes risk; that is, $E\left[F\left(y\right)\right]=F_0\left(y\right)$.

If $P\in DP\left(\delta ,F_0\left(y\right)\right)$, the induced prior for $F\left(y\right)$ is given by

$$F\left(y\right)\sim beta\left(\delta \left((-\infty ,y]\right),\delta \left((y,\infty )\right)\right),y>0,$$

where $beta\left(a,b\right)$ is the beta distribution with parameters a and b. The Bayes rule for no data sample can be expressed as $\widehat{F}\left(y\right)=E\left(F\left(y\right)\right)=F_0\left(y\right)=\frac{\delta (-\infty ,y]}{\delta (-\infty ,y]+\delta (y,\infty )}=\frac{\delta \left((-\infty ,y]\right)}{\delta \left(\chi \right)},$ where $\chi$ is real number space, and $\delta \left((-\infty ,y]\right)+\delta \left((y,\infty )\right)=\delta \left(\chi \right)$.

To make the concept of the Dirichlet process more concrete, we demonstrate how to utilize the Dirichlet process to estimate CDF given some data. Suppose that $y_1,y_2,\dots ,y_m$ represent a random sample from $F\left(y\right)$, $y_1,y_2,\dots ,y_m|F\sim F$, where $F\sim DP(\delta ,F_0)$.

The prior information is contained in $F_0$ and $\delta$, the posterior of distribution F is also a Dirichlet process, and the posterior distribution is $F|y_1,y_2,\dots ,y_m\sim DP\left(\delta +m,\frac{\delta \left(\chi \right)F_0+m\widehat{F}\left(y\right)}{\delta \left(\chi \right)+m}\right)$.

$$\begin{array}{cc}\hfill {\widehat{F}}_{SE}\left(y\right|y_1,y_2,\dots ,y_m)& =\frac{\delta \left((-\infty ,t]\right)+{\sum }_{i=1}^m{\varsigma }_{(Y_i\le y)}}{\delta \left(\chi \right)+m}\hfill \\ \hfill & =\frac{\delta \left(\chi \right)}{\delta \left(\chi \right)+m}{F}_0+\frac{m}{\delta \left(\chi \right)+m}\widehat{F}\left(y\right|y_1,y_2,\dots ,y_m)\hfill \end{array}$$

where $\widehat{F}\left(y\right)=\frac{{\sum }_{i=1}^m{\varsigma }_{(Y_i\le y)}}{m}$ is empirical CDF based on the sample, and ${\varsigma }_{(Y_i\le y)}$ is the indicator function. Obviously, if $\delta$ is equal to 0, that means there is no prior information, and $F_0$ has no effect on the posterior estimate.

4.2. The Nonparametric Bayesian Estimation of Mean Remaining Strength

According to Theorem 1, combined with dynamic signature, we derived the nonparametric Bayesian estimator of MRS. Then the nonparametric Bayesian estimation of ${\Phi }_{Y|X}\left(t\right)$, denoted by ${\widehat{\Phi }}_{Y|X}\left(t\right)$ is

$$\begin{array}{cc}\hfill & {\widehat{\Phi }}_{Y|X}\left(t\right)\hfill \\ \hfill & ={\sum }_{i_1=1}^{m-n+1}\cdots {\sum }_{i_{l\left(t\right)+1}=k\left(t\right)+1}^{m-n+l\left(t\right)+1}\cdots {\sum }_{i_n=i_{n-1}+1}^m{s}_{i_1,i_2,\dots ,i_n}\left(m-k\left(t\right)\right)\hfill \\ \hfill & ·{\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}m\\ i_n\end{array}\right){\left({\phi }_1\right)}^{i_n}{\left({\phi }_2\right)}^{m-i_n}\Delta \widehat{G}\left(x\right)}{{\int }_0^{\infty }{\left[1-{\widehat{F}}_{SE}(x+t)\right]}^m\Delta \widehat{G}\left(x\right)}dz.\hfill \end{array}$$

(2)

where ${\phi }_1={\widehat{F}}_{SE}(x+z+t)-{\widehat{F}}_{SE}(x+t)$, ${\phi }_2=1-{\widehat{F}}_{SE}(x+z+t)$, and $\Delta \widehat{G}\left(x\right)={\displaystyle \underset{\Delta x\to 0}{lim}}\frac{(\widehat{G}(x+\Delta x)-\widehat{G}\left(x\right))}{\Delta x}$. ${\widehat{F}}_{SE}\left(y\right)$ is the nonparametric Bayesian estimation of strength distribution function $F\left(y\right)$. Similarly, $\widehat{G}\left(x\right)$ is the nonparametric Bayesian estimation of stress distribution function $G\left(x\right)$.

5. Simulation Analysis

In this section, the simulation analysis of MRS is discussed. Although the estimation of SSR for different systems has been widely researched, there is little literature on MRS estimation. In order to evaluate the performance of the nonparametric Bayesian method, Monte Carlo simulation is conducted with a simple five-component system.

We consider three different sample sizes: 50, 100, and 200. For the different parameter settings, the simulation is repeated 1000 times for each sample size. Suppose that the strength and stress data of the five components are generated by a Weibull distribution, in which strength and stress have different parameters. The shape parameters ${\alpha }_1$ and ${\alpha }_2$ are 1.5 and 2, respectively. Assuming that the scale parameter of strength is ${\eta }_{y_1}=10$, the scale parameter of stress is ${\eta }_{x_1}=5$. The CDF of the Weibull distribution is $F(y,\alpha ,\eta )=1-exp\left[-{\left(y/\eta \right)}^{\alpha }\right]$.

The root-mean-square error (RMSE) and relative bias (RB) are obtained by Equations (3) and (4), which are used to evaluate the simulation performance of MRS. In addition, the confidence interval for MRS estimation uses the nonparametric bootstrap method, known as BCI. For more details, please refer to the nonparametric bootstrap part in Ukoumunne et al. [31].

$$RMSE\left({\Phi }_{Y|X}\right)=\frac{1}{n}\sqrt{\sum _{q=1}^n{\left({\overline{\Phi }}_{Y|X}^q-{\overline{\Phi }}_{Y|X}\right)}^2}.$$

(3)

$$RB=\frac{1}{n}\sum _{q=1}^n\left(\left({\overline{\Phi }}_{Y|X}^q-{\Phi }_{Y|X}\right)/{\overline{\Phi }}_{Y|X}\right).$$

(4)

where n represents the number of simulations, ${\overline{\Phi }}_{Y|X}^q$ is the simulation estimate of MRS, and ${\overline{\Phi }}_{Y|X}$ is the real value of MRS.

A four-state system composed of five two-state components is analyzed, in which the component strengths $y_1,y_2,\dots ,y_5$ are IID, and obey continuous function $F\left(y\right)$. The reliability block diagram of the system is given in Figure 1.

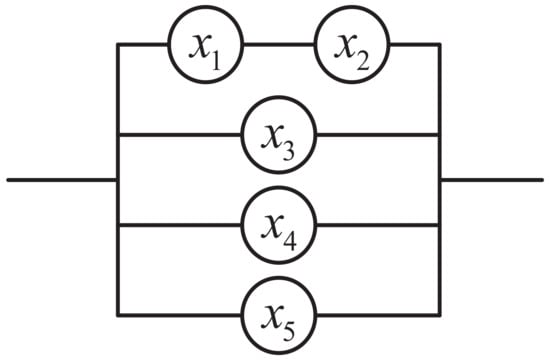
Figure 1. The reliability block diagram of the system.

When all four links of the system are working, the system is in a perfect state, and there is $h=3$; if only one link of the system fails, the system is in partial working perfect state, and there is $h=2$. When the number of live branches of the system is two, there is $h=1$; in the last case, if the working branches of the system do not exceed one, the system is in failure state, and $h=0$.

The system consists of five components; if the system state is three, the signature of the system is a three-dimensional matrix of $5^3$. According to the operation rules of the multi-dimensional signature, the arrangement and calculation of signature are shown in Table 1.

Table 1. Signature arrangement and calculation.

i	${\mathit{i}}_1$	${\mathit{i}}_2$	${\mathit{i}}_3$	The Number of Failure Sequences
State Changes	$3\to 2$	$2\to 1$	$1\to 0$
	1	2	3	84
	1	2	4	24
The corresponding	1	2	5	0
number of failed	1	3	4	12
components	1	3, 4	5	0
	2	3	4, 5	0
	2, 3	4	5	0

The system signature is a three-dimensional matrix with different values. The elements of the three-dimensional matrix are given by

$$s_{1,2,3}=\frac{84}{5!}=\frac{7}{10},s_{1,2,4}=\frac{24}{5!}=\frac{1}{5},s_{1,3,4}=\frac{12}{5!}=\frac{1}{10},$$

$$s_{1,2,5}=s_{1,3,5}=s_{1,4,5}=s_{2,3,4}=s_{2,3,5}=s_{2,4,5}=s_{3,4,5}=0.$$

The following two different system states are analyzed, and then the MRS of the system is estimated.

Assuming that at the strength level $t_1$, the system state is two, and exactly one component fails in the system; that is, $h\left(t_1\right)=2$, $k\left(t_1\right)=1$. Then, the dynamic signature of this system is a three-dimensional vector, whose elements are

$$s_{1,2,3}\left(4\right)=\frac{s_{1,2,3}}{{\sum }_{i_2=2}^4{\sum }_{i_3=3}^5{s}_{1,i_2,i_3}}=\frac{7/10}{7/10+1/5+1/10+0+0+0}=\frac{7}{10},$$

$$s_{1,2,4}\left(4\right)=\frac{s_{1,2,4}}{{\sum }_{i_2=2}^4{\sum }_{i_3=3}^5{s}_{1,i_2,i_3}}=\frac{1/5}{7/10+1/5+1/10+0+0+0}=\frac{1}{5},$$

$$s_{1,2,5}\left(4\right)=\frac{s_{1,2,5}}{{\sum }_{i_2=2}^4{\sum }_{i_3=3}^5{s}_{1,i_2,i_3}}=0,$$

$$s_{1,3,4}\left(4\right)=\frac{s_{1,3,4}}{{\sum }_{i_2=2}^4{\sum }_{i_3=3}^5{s}_{1,i_2,i_3}}=\frac{1/10}{7/10+1/5+1/10+0+0+0}=\frac{1}{10},$$

$$s_{1,3,5}\left(4\right)=\frac{s_{1,3,5}}{{\sum }_{i_2=2}^4{\sum }_{i_3=3}^5{s}_{1,i_2,i_3}}=0,$$

$$s_{1,4,5}\left(4\right)=\frac{s_{1,4,5}}{{\sum }_{i_2=2}^4{\sum }_{i_3=3}^5{s}_{1,i_2,i_3}}=0,$$

The stress on the system is $X\left(t_1\right)=x_1$. By using the Theorem 1 and Equation (2), the nonparametric Bayesian estimation of the system MRS is as follows:

$$\begin{array}{cc}\hfill & {\widehat{\Phi }}_{Y|X}=s_{1,2,3}\left(4\right){\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 3\end{array}\right){\left[{\phi }_1\left(t_1\right)\right]}^3{\left[{\phi }_2\left(t_1\right)\right]}^2\Delta \widehat{G}\left(x_1\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_1+t_1)]}^5\Delta \widehat{G}\left(x_1\right)}dz\hfill \\ \hfill & +s_{1,2,4}\left(4\right){\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 4\end{array}\right){\left[{\phi }_1\left(t_1\right)\right]}^4{\left[{\phi }_2\left(t_1\right)\right]}^1\Delta \widehat{G}\left(x_1\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_1+t_1)]}^5\Delta \widehat{G}\left(x_1\right)}dz\hfill \\ \hfill & +s_{1,3,4}\left(4\right){\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 4\end{array}\right){\left[{\phi }_1\left(t_1\right)\right]}^4{\left[{\phi }_2\left(t_1\right)\right]}^1\Delta \widehat{G}\left(x_1\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_1+t_1)]}^5\Delta \widehat{G}\left(x_1\right)}dz\hfill \\ \hfill & =\frac{7}{10}·{\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 3\end{array}\right){\left[{\phi }_1\left(t_1\right)\right]}^3{\left[{\phi }_2\left(t_1\right)\right]}^2\Delta \widehat{G}\left(x_1\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_1+t_1)]}^5\Delta \widehat{G}\left(x_1\right)}dz\hfill \\ \hfill & +\frac{3}{10}{\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 4\end{array}\right){\left[{\phi }_1\left(t_1\right)\right]}^4{\left[{\phi }_2\left(t_1\right)\right]}^1\Delta \widehat{G}\left(x_1\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_1+t_1)]}^5\Delta \widehat{G}\left(x_1\right)}dz,\hfill \end{array}$$

where ${\phi }_1\left(t_1\right)={\widehat{F}}_{SE}(x_1+z+t_1)-{\widehat{F}}_{SE}(x_1+t_1)$, ${\phi }_2\left(t_1\right)=1-{\widehat{F}}_{SE}(x_1+z+t_1)$.

For the strength level $t_1$ of this system, it is assumed to be the average value obtained after 1000 simulations of the maximum value in the first 20% of strength samples. The nonparametric estimation is a method to estimate the total distribution by using the empirical distribution function of data without considering the prior information. We present the nonparametric Bayesian estimation and nonparametric estimation results of MRS in this case.

As shown in Table 2 and Table 3, the MRS is obtained according to the determined parameters of simulated distribution, called the truth value, denoted by ${\overline{\Phi }}_{Y|X}$. The truth values of different parameters are marked in the notes of the corresponding table. In different sample sizes, the mean nonparametric Bayesian estimators and nonparametric estimators of MRS are presented after 1000 simulations, denoted as ${\widehat{\Phi }}_{Y|X}$ and ${{\Phi }^{*}}_{Y|X}$, respectively. The RB, RMSE, and 95% confidence interval of the two estimation methods for different sample sizes are given.

Table 2. In the first case $\left(h\left(t_1\right)=2,k\left(t_1\right)=1\right)$, data simulation with parameters ${\alpha }_1=1.5$, ${\eta }_{y_1}=10$, ${\eta }_{x_1}=5$.

Method	${\widehat{\mathbf{\Phi }}}_{\mathit{Y}|\mathit{X}}$			${{\mathbf{\Phi }}^{*}}_{\mathit{Y}|\mathit{X}}$
	RB	RMSE	BCI	RB	RMSE	BCI
50	−0.000351	0.038915	(3.453789, 3.547434)	−0.009267	1.025831	(3.337739, 3.612112)
100	−0.000178	0.019721	(3.468511, 3.532281)	−0.003696	0.409144	(3.390772, 3.581690)
200	0.000137	0.015179	(3.474462, 3.527438)	−0.002949	0.326449	(3.417412, 3.560427)

Notes: In this case, the true value is ${\overline{\Phi }}_{Y|X}=3.500482$.

Table 3. In the first case $\left(h\left(t_1\right)=2,k\left(t_1\right)=1\right)$, data simulation with parameters ${\alpha }_2=2$, ${\eta }_{y_1}=10$, ${\eta }_{x_1}=5$.

Method	${\widehat{\mathbf{\Phi }}}_{\mathit{Y}|\mathit{X}}$			${{\mathbf{\Phi }}^{*}}_{\mathit{Y}|\mathit{X}}$
	RB	RMSE	BCI	RB	RMSE	BCI
50	−0.001237	0.091625	(2.313369, 2.366051)	−0.003040	0.801361	(2.241631, 2.442657)
100	−0.000352	0.026075	(2.321894, 2.362433)	−0.001549	0.501322	(2.264925, 1.411483)
200	−0.000017	0.001279	(2.325878, 2.359606)	0.000438	0.274305	(2.292188, 2.395047)

Notes: In this case, the true value is ${\overline{\Phi }}_{Y|X}=2.342903$.

For the second consideration, suppose the strength level is $t_2$, the system state is 1, and the failure number of components is 2; that is, $h\left(t_2\right)=1,k\left(t_2\right)=2$. The elements of the signature matrix are

$$s_{1,2,3}\left(3\right)=\frac{s_{1,2,3}}{{\sum }_{i_3=3}^5{s}_{1,2,i_3}}=\frac{7/10}{7/10+1/5+0}=\frac{7}{9},$$

$$s_{1,2,4}\left(3\right)=\frac{s_{1,2,4}}{{\sum }_{i_3=3}^5{s}_{1,2,i_3}}=\frac{1/5}{7/10+1/5+0}=\frac{2}{9},$$

$$s_{1,2,5}\left(3\right)=\frac{s_{1,2,5}}{{\sum }_{i_3=3}^5{s}_{1,2,i_3}}=0.$$

The stress on the system is $X_2=x_2$; the strength level $t_2$ is assumed to be the average value of the maximum value in the first 40% of strength samples after 1000 simulations. Similarly, the nonparametric Bayesian estimation of MRS is

$$\begin{array}{cc}\hfill & {\widehat{\Phi }}_{Y|X}\left(t_2\right)=\frac{7}{9}·{\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 3\end{array}\right){\left[{\phi }_1\left(t_2\right)\right]}^3{\left[{\phi }_2\left(t_2\right)\right]}^2\Delta \widehat{G}\left(x_2\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_2+t_2)]}^5\Delta \widehat{G}\left(x_2\right)}dz\hfill \\ \hfill & +\frac{2}{9}·{\int }_0^{\infty }\frac{{\int }_0^{\infty }\left(\begin{array}{c}5\\ 4\end{array}\right){\left[{\phi }_1\left(t_2\right)\right]}^4{\left[{\phi }_2\left(t_2\right)\right]}^1\Delta \widehat{G}\left(x_2\right)}{{\int }_0^{\infty }{[1-{\widehat{F}}_{SE}(x_2+t_2)]}^5\Delta \widehat{G}\left(x_2\right)}dz,\hfill \end{array}$$

where ${\phi }_1\left(t_2\right)={\widehat{F}}_{SE}(x_2+z+t_2)-{\widehat{F}}_{SE}(x_2+t_2)$,${\phi }_2\left(t_2\right)=1-{\widehat{F}}_{SE}(x_2+z+t_2)$. The results of the two estimation methods are shown in Table 4 and Table 5.

Table 4. In the second case $\left(h\left(t_2\right)=1,k\left(t_2\right)=2\right)$, data simulation with parameters ${\alpha }_1=1.5$, ${\eta }_{y_1}=10$, ${\eta }_{x_1}=5$.

Method	${\widehat{\mathbf{\Phi }}}_{\mathit{Y}|\mathit{X}}$			${{\mathbf{\Phi }}^{*}}_{\mathit{Y}|\mathit{X}}$
	RB	RMSE	BCI	RB	RMSE	BCI
50	−0.001100	0.061824	(3.161819, 3.231117)	−0.001603	0.161954	(3.053035, 3.340022)
100	0.000794	0.080122	(3.169057, 3.226699)	−0.001210	0.122307	(3.092817, 3.290774)
200	0.000319	0.032267	(3.170345, 3.216967)	0.000918	0.092792	(3.123799, 3.277338)

Notes: In this case, the true value is ${\overline{\Phi }}_{Y|X}=3.19513$.

Table 5. In the second case $\left(h\left(t_2\right)=1,k\left(t_2\right)=2\right)$, data simulation with parameters ${\alpha }_2=2$, ${\eta }_{y_1}=10$, ${\eta }_{x_1}=5$.

Method	${\widehat{\mathbf{\Phi }}}_{\mathit{Y}|\mathit{X}}$			${{\mathbf{\Phi }}^{*}}_{\mathit{Y}|\mathit{X}}$
	RB	RMSE	BCI	RB	RMSE	BCI
50	−0.000717	0.047200	(2.051986, 2.111535)	−0.081337	0.535545	(1.962603, 2.174293)
100	−0.000665	0.043804	(2.058941, 2.102717)	−0.001065	0.070153	(2.003463, 2.157305)
200	0.000046	0.003061	(2.064393, 2.100238)	0.000944	0.062181	(2.025504, 2.137185)

Notes: In this case, the true value is ${\overline{\Phi }}_{Y|X}=2.082105$.

The following can be seen from Table 2 and Table 3:

(a)

Under the same parameters, the absolute value of RB is relatively small; that is, the estimated value is not far from the true value. Compared with RB in Table 2, RB of the nonparametric Bayesian estimator is one order of magnitude lower than RB of the nonparametric estimator. In Table 3, except that the RB data of the first row are not significantly different, the other two rows also have the same results. This is likely to be due to a small sample size.

(b)

With the increase in the sample size, the evaluation indexes RB and RMSE decreased gradually. For the same sample size, the RB and RMSE of the nonparametric Bayesian estimation are both smaller than that of the nonparametric estimation.

(c)

For the confidence interval, the confidence interval length of the nonparametric Bayesian estimation is significantly smaller than that of the nonparametric estimation under the same sample size. With the increases in sample size, the confidence interval lengths of both estimation methods decrease.

(d)

By comparing the confidence interval of the nonparametric estimator with the sample size of 200 and the nonparametric Bayesian estimator with the sample size of 50, we find that the confidence interval length of the latter is smaller than that of the former. This indicates that the discretization degree of the results of the nonparametric Bayesian estimation is obviously smaller than that of the nonparametric estimation.

(e)

For the same scale parameters and different shape parameters, the larger the shape parameters, the smaller the value of MRS. This result is consistent with the consideration in [17].

By comparing Table 2 and Table 4, it can be concluded that under the different system states, when the system state is low, its MRS value is also small, which is consistent with the actual situation. Even when considering different system states, in the same sample size, the RB, RMSE, and confidence interval lengths of the nonparametric Bayesian estimation are still significantly smaller than that of the nonparametric estimation.

From Table 2, Table 3, Table 4 and Table 5, it is readily seen that in the MRS estimation, the nonparametric Bayesian method can be used to estimate MRS. When the sample size is small, the estimation effect is good, and the estimation effect is better than that of the nonparametric estimation method. Nonparametric Bayesian methods have the advantage of not requiring a distribution hypothesis. This advantage is of great value in determining the reliability of a new product, because the lifetime distribution of the new product may be different from that of existing products.

6. Application Based on Real Data

In this section, we analyze two real datasets and demonstrate the applicability of the above method in practice. The datasets are as follows.

Data 1:

$$Y=\left[\begin{array}{cc}& 693.73,704.66,323.83,778.17,123.06,637.66,383.43,151.48,108.94,50.16,\hfill \\ & 671.49,183.16,727.23,257.44,291.27,101.15,376.42,163.40,141.38,700.74,\hfill \\ & 262.90,353.24,422.11,43.93,590.48,212.13,303.90,506.60,530.55,177.25.\hfill \end{array}\right]$$

Data 2:

$$X=\left[\begin{array}{cc}& 71.46,419.02,284.64,585.57,456.60,688.16,662.66,113.85,187.85,45.58,\hfill \\ & 578.62,756.70,594.29,166.49,707.36,99.72,765.14,187.13,145.96,350.70,\hfill \\ & 547.44,116.99,375.81,119.86,581.60,48.01,200.16,36.75,244.53,83.55.\hfill \end{array}\right]$$

Data 1 and data 2 comprise the break strength of fiber under different gauge lengths. Saracoglu et al. [32] analyzed the two datasets by fitting an exponential distribution and estimated the reliability of stress-strength. Hassan et al. [33] used the Kolmogorov–Smirnov goodness-of-fit test with the Weibull distribution for fitting the datasets. Bai et al. [34] also considered this datasets in the example analysis.

Consider the multi-state system mentioned in Section 5. Regard data 1 as strength data, and regard data 2 as stress data. In order to facilitate calculation, the two datasets are divided by 100. The quintile of data 1 is $\left(1.6686,3.1387,3.6573,5.7550,7.7817\right)$, and in turn, we assume that it is the failure strength of five components. According to the discussion of Weibull distribution in [33], the prior measure of the distribution function is presented by $DP\left(\delta ,F_0\left(y\right)\right)$ with parameters $\delta (y,\infty )={\sigma }_0{e}^{-{\lambda }_{0}y},{\lambda }_0=1$. Combined with the prior information, we use the nonparametric Bayesian method and theorem 1 to estimate the MRS of ${\widehat{\Phi }}_{Y|X}^1\left(t_1\right)$ and ${\widehat{\Phi }}_{Y|X}^2\left(t_2\right)$ in different states. ${\widehat{\Phi }}_{Y|X}^1\left(t_1\right)$ is the MRS estimator when the system state is 2, and there is exactly one component failure of the system; assuming that a component fails when $t_1=1.6686$ is observed, then we can obtain ${\widehat{\Phi }}_{Y|X}^1\left(t_1\right)=2.4866$. This means that when the system stress and system level $t_1$ increase by more than 2.4866, the system will fail. ${\widehat{\Phi }}_{Y|X}^2\left(t_2\right)$ is the MRS estimator when the failure number of the component is 2, and the system state is 1. Suppose that when $t_2=3.1387$, there are two component failures, it can be calculated that ${\widehat{\Phi }}_{Y|X}^2\left(t_2\right)=1.0121$. This shows that the system will fail if the system stress and system level $t_2$ increase by 1.0121. It can be seen that the nonparametric Bayesian method can evaluate the MRS in practical problems.

7. Conclusions and Prospects

In this study, we discussed the MRS of a multi-state system consisting of two-state components under the stress-strength setting. On the basis of multi-dimensional system signature, the dynamic signature of the multi-state system at the strength level t was considered. The MRS expression of the multi-state strength system was obtained. The nonparametric Bayesian method was used to estimate MRS and was compared with the nonparametric method. In the simulation, the RB, RMSE, and confidence interval were used as evaluation indicators. The results show that the nonparametric Bayesian method is more effective than the nonparametric estimation method. In addition, real datasets were analyzed to prove the applicability of the nonparametric Bayesian method.

In future research, we will discuss the MRS of a system with component strength dependence. At the same time, we can also consider the case where components are repairable or replaceable. In addition, for the censored data, the effectiveness and superiority of the nonparametric Bayesian estimation method are more obvious. We will analyze the right censored data and interval censored data, and estimate the SSR or MRS of the complex system using a nonparametric Bayesian method.