Relativistic Magnetized Astrophysical Plasma Outflows in Black-Hole Microquasars
Abstract
1. Introduction
2. Radiation Field Density and Transport Equation in Microquasar Jets
2.1. Microquasar Jet Mechanisms Leading to Neutrino and Gamma-Ray Production
2.2. Solution of the Transfer Equation
3. Interaction Frequency and Particle Emission through p- Mechanism
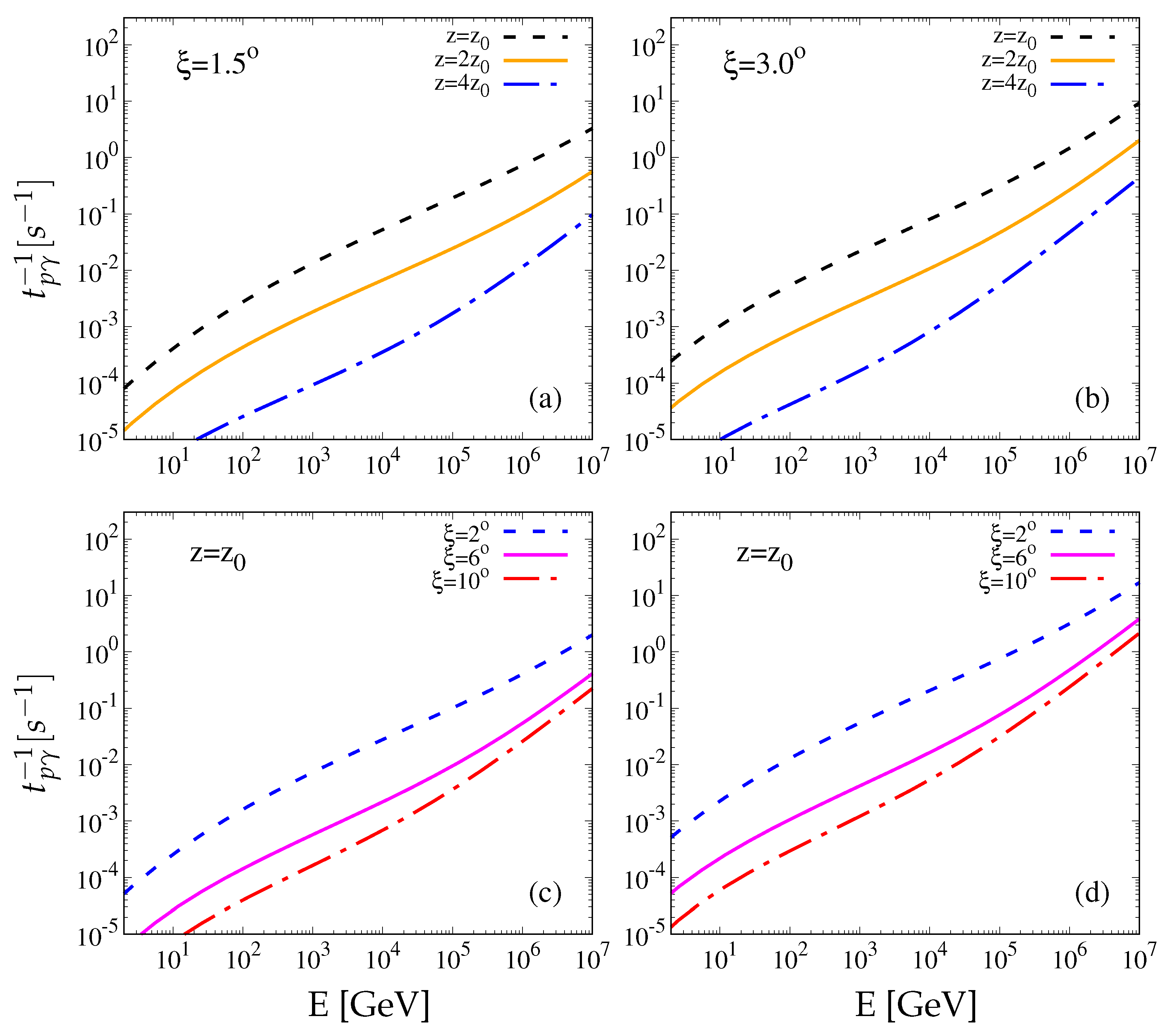
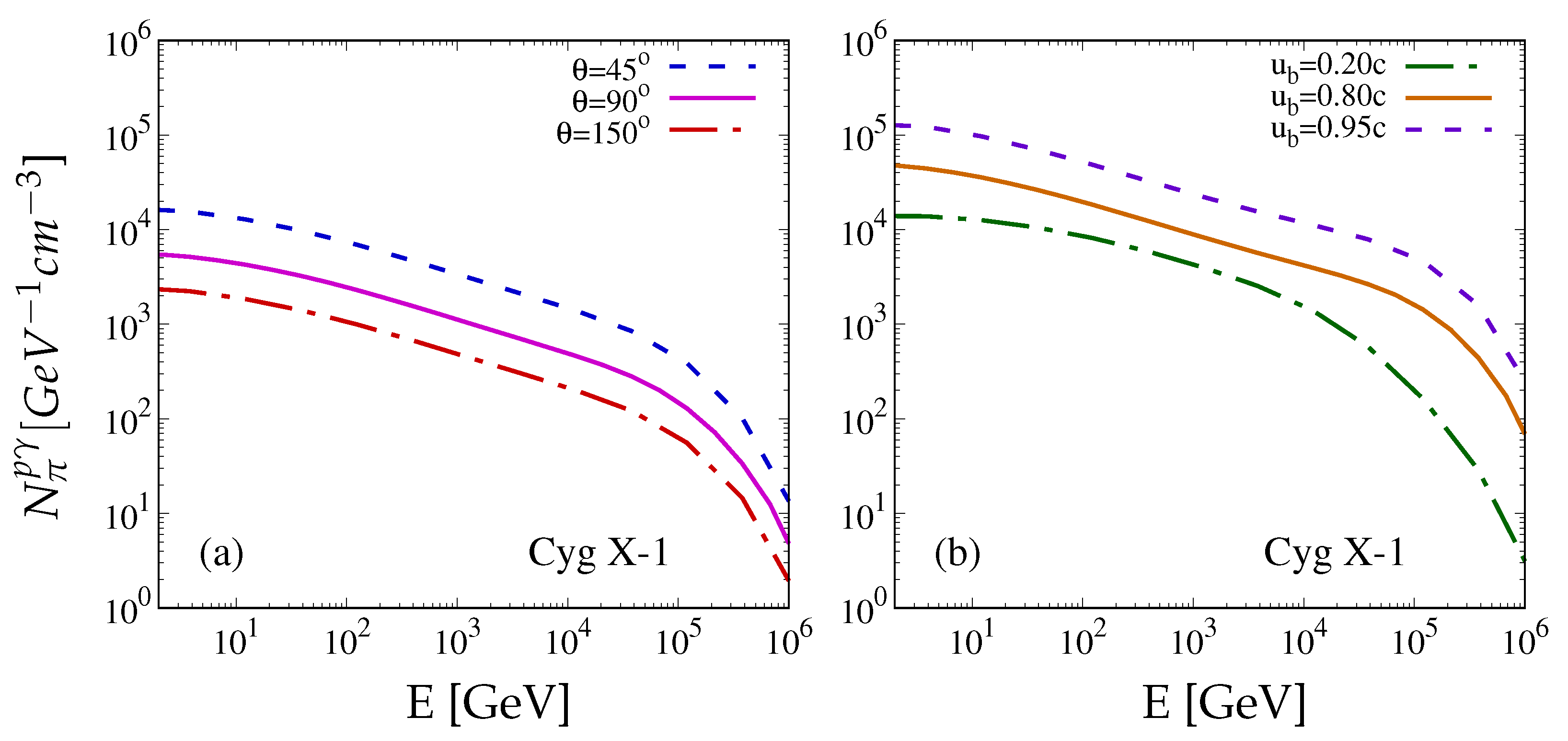
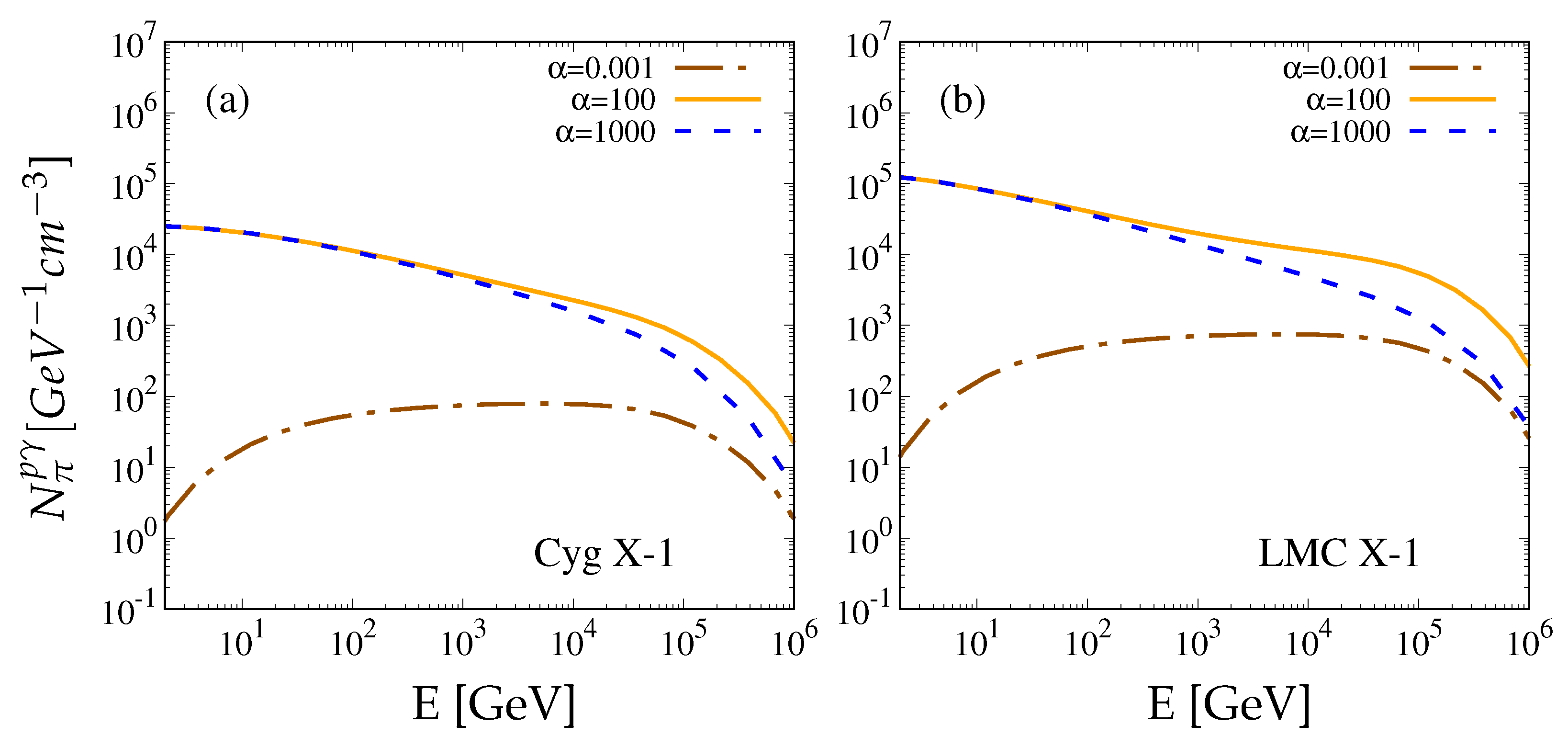
4. Results and Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Synchrotron Power Radiation by Particle Distributions
Appendix A.2. Injection Function in Observer’s Reference Frame
References
- Heinz, S.; Sunyaev, R. Cosmic rays from microquasars: A narrow component to the CR spectrum? Astron. Astrophys. 2002, 390, 751–766. [Google Scholar] [CrossRef]
- Fabrika, S. The jets and supercritical accretion disk in SS433. Astrophys. Space Phys. Rev. 2004, 12, 1–152. [Google Scholar]
- Aharonian, F.; Akhperjanian, A.G.; Aye, K.M.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Berghaus, P.; Bernlöhr, K.; Boisson, C.; et al. Discovery of Very High Energy Gamma Rays Associated with an X-ray Binary. Science 2005, 309, 746–749. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Asensio, M.; Baixeras, C.; Barrio, J.A.; Bartelt, M.; Bartko, H.; et al. Variable Very-High-Energy Gamma-Ray Emission from the Microquasar LS I +61 303. Science 2006, 312, 1771–1773. [Google Scholar] [CrossRef] [PubMed]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Very High Energy Gamma-Ray Radiation from the Stellar Mass Black Hole Binary Cygnus X–1. Astrophys. J. 2007, 665, L51–L54. [Google Scholar] [CrossRef]
- Falcke, H.; Biermann, P. The jet-disk symbiosis. 1. Radio to X-ray emission models for quasars. Astron. Astrophys. 1994, 293, 665–682. [Google Scholar]
- Papavasileiou, T.V.; Kosmas, O.T.; Sinatkas, J. Simulations of Neutrino and Gamma-Ray Production from Relativistic Black-Hole Microquasar Jets. Galaxies 2021, 9, 67. [Google Scholar] [CrossRef]
- Körding, E.G.; Fender, R.P.; Migliari, S. Jet-dominated advective systems: Radio and X-ray luminosity dependence on the accretion rate. Mon. Not. R. Astron. Soc. 2006, 369, 1451–1458. [Google Scholar] [CrossRef]
- Smponias, T.; Kosmas, O. High Energy Neutrino Emission from Astrophysical Jets in the Galaxy. Adv. High Energy Phys. 2015, 921757. [Google Scholar] [CrossRef]
- Smponias, T.; Kosmas, O. Neutrino Emission from Magnetized Microquasar Jets. Adv. High Energy Phys. 2017, 2017, 496274. [Google Scholar] [CrossRef]
- Kosmas, O.T.; Smponias, T. Simulations of Gamma-Ray Emission from Magnetized Microquasar Jets. Adv. High Energy Phys. 2018, 2018, 960296. [Google Scholar] [CrossRef]
- Aartsen, M.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147–151. [Google Scholar]
- Romero, G.E.; Boettcher, M.; Markoff, S.; Tavecchio, F. Relativistic Jets in Active Galactic Nuclei and Microquasars. Space Sci. Rev. 2017, 207, 5–61. [Google Scholar] [CrossRef]
- Vieyro, F.L.; Romero, G.E. Particle transport in magnetized media around black holes and associated radiation. Astron. Astrophys. 2012, 542, A7. [Google Scholar] [CrossRef]
- Romero, G.E.; Vila, G.S. The proton low-mass microquasar: High-energy emission. Astron. Astrophys. 2008, 485, 623–631. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Rodríguez, L.F. Sources of Relativistic Jets in the Galaxy. Annu. Rev. Astron. Astrophys. 1999, 37, 409–443. [Google Scholar] [CrossRef]
- Beall, J.H. A Review of Astrophysical Jets. PoS Proc. Sci. 2015, 246, 58–70. [Google Scholar] [CrossRef]
- Reynoso, M.M.; Romero, G.E.; Christiansen, H.R. Production of gamma rays and neutrinos in the dark jets of the microquasar SS433. Mon. Not. R. Astron. Soc. 2008, 387, 1745–1754. [Google Scholar] [CrossRef][Green Version]
- Reynoso, M.M.; Romero, G.E. Magnetic field effects on neutrino production in microquasars. Astron. Astrophys. 2009, 493, 1–11. [Google Scholar] [CrossRef]
- Bosch-Ramon, V.; Romero, G.E.; Paredes, J.M. A broadband leptonic model for gamma-ray emitting microquasars. Astron. Astrophys. 2006, 447, 263–276. [Google Scholar] [CrossRef]
- Begelman, M.C.; Rudak, B.; Sikora, M. Consequences of Relativistic Proton Injection in Active Galactic Nuclei. Astrophys. J. 1990, 362, 38. [Google Scholar] [CrossRef]
- Berezhko, E.G.; Ellison, D.C. A Simple Model of Nonlinear Diffusive Shock Acceleration. Astrophys. J. 1999, 526, 385–399. [Google Scholar] [CrossRef]
- Gallant, Y.A.; Achterberg, A. Ultra-high-energy cosmic ray acceleration by relativistic blast waves. Mon. Not. R. Astron. Soc. 1999, 305, L6–L10. [Google Scholar] [CrossRef]
- Kirk, J.G.; Guthmann, A.W.; Gallant, Y.A.; Achterberg, A. Particle Acceleration at Ultrarelativistic Shocks: An Eigenfunction Method. Astrophys. J. 2000, 542, 235–242. [Google Scholar] [CrossRef]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Not. R. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Romero, G.E.; Torres, D.F.; Kaufman Bernadó, M.M.; Mirabel, I.F. Hadronic gamma-ray emission from windy microquasars. Astron. Astrophys. 2003, 410, L1–L4. [Google Scholar] [CrossRef]
- Romero, G.E.; Okazaki, A.T.; Orellana, M.; Owocki, S.P. Accretion vs. colliding wind models for the gamma-ray binary LS I +61 303: An assessment. Astron. Astrophys. 2007, 474, 15–22. [Google Scholar] [CrossRef]
- Friend, D.B.; Castor, J.I. Radiation driven winds in X-ray binaries. Astrophys. J. 1982, 261, 293–300. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
- Papavasileiou, T.V.; Papadopoulos, D.A.; Kosmas, T.S. Astrophysical magnetohydrodynamical outflows in the extragalactic binary system LMC X-1. J. Phys. Conf. Ser. 2020, 1730, 012138. [Google Scholar] [CrossRef]
- Papadopoulos, D.A.; Papavasileiou, T.V.; Kosmas, T.S. High energy neutrino and gamma-ray emissions from the jets of M33 X-7 microquasar. J. Phys. Conf. Ser. 2021, 1730, 012137. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; de Almeida, U.B.; Barrio, J.A.; González, J.B.; et al. Search for very high-energy gamma-ray emission from the microquasar Cygnus X-1 with the MAGIC telescopes. Mon. Not. R. Astron. Soc. 2017, 472, 3474–3485. [Google Scholar]
- Hyde, E.A.; Russell, D.M.; Ritter, A.; Filipovic, M.D.; Kaper, L.; Grieve, K.; O’Brien, A.N. LMC X-1: A New Spectral Analysis of the O-star in the Binary and Surrounding Nebula. Astron. Soc. Pac. 2017, 129, 094201. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Searches for Sterile Neutrinos with the IceCube Detector. Phys. Rev. Lett. 2016, 117, 071801. [Google Scholar] [CrossRef] [PubMed]
- Adrián-Martínez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Albert, A.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G Nucl. Part Phys. 2016, 43, 084001. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M.; Sunyaev, R.A.; Fabrika, S.N.; Postnov, K.A.; Molkov, S.V.; Barsukova, E.A.; Antokhina, E.A.; Irsmambetova, T.R.; Panchenko, I.E.; Seifina, E.V.; et al. INTEGRAL observations of SS433: Results of a coordinated campaign. Astron. Astrophys. 2005, 437, 561–573. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 1970, 42, 237–271. [Google Scholar] [CrossRef]
- Khangulyan, D.; Hnatic, S.; Aharonian, F.; Bogovalov, S. TeV light curve of PSR B1259–63/SS2883. Mon. Not. R. Astron. Soc. 2007, 380, 320–330. [Google Scholar] [CrossRef][Green Version]
- Atoyan, A.M.; Dermer, C.D. Neutral Beams from Blazar Jets. Astrophys. J. 2003, 586, 79. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A. Energy spectra of gamma rays, electrons, and neutrinos produced at interactions of relativistic protons with low energy radiation. Phys. Rev. D 2008, 78, 034013. [Google Scholar] [CrossRef]
- Orosz, J.A.; McClintock, J.E.; Aufdenberg, J.P.; Remillard, R.A.; Reid, M.J.; Narayan, R.; Gou, L. The mass of the black hole in cygnus X-1. Astrophys. J. 2011, 742, 84. [Google Scholar] [CrossRef]
- Orosz, J.A.; Steeghs, D.; McClintock, J.E.; Torres, M.A.P.; Bochkov, I.; Gou, L.; Narayan, R.; Blaschak, M.; Levine, A.M.; Remillard, R.A.; et al. A new dynamical model for the black hole binary lmc X-1. Astrophys. J. 2009, 697, 573–591. [Google Scholar] [CrossRef]
- Stirling, A.; Spencer, R.; de La Force, C.; Garrett, M.; Fender, R.; Ogley, R. A relativistic jet from Cygnus X-1 in the low/hard X-ray state. Mon. Not. R. Astron. Soc. 2001, 327, 1273–1278. [Google Scholar] [CrossRef]
- Torres, D.F.; Reimer, A. Hadronic beam models for quasars and microquasars. Astron. Astrophys. 2011, 528, L2. [Google Scholar] [CrossRef]
| Description | Parameter | Cygnus X-1 | LMC X-1 |
|---|---|---|---|
| Jet’s base | (cm) | ||
| Acceleration zone limit | (cm) | ||
| Mass of compact object | 14.8 [41] | 10.91 [42] | |
| Angle to the line-of-sight | () | 27.1 [41] | 36.38 [42] |
| Jet’s half-opening angle | () | 1.5 [43] | 3 * |
| Jet’s bulk velocity | 0.6c [43] | 0.92c * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papavasileiou, T.; Kosmas, O.; Sinatkas, I. Relativistic Magnetized Astrophysical Plasma Outflows in Black-Hole Microquasars. Symmetry 2022, 14, 485. https://doi.org/10.3390/sym14030485
Papavasileiou T, Kosmas O, Sinatkas I. Relativistic Magnetized Astrophysical Plasma Outflows in Black-Hole Microquasars. Symmetry. 2022; 14(3):485. https://doi.org/10.3390/sym14030485
Chicago/Turabian StylePapavasileiou, Theodora, Odysseas Kosmas, and Ioannis Sinatkas. 2022. "Relativistic Magnetized Astrophysical Plasma Outflows in Black-Hole Microquasars" Symmetry 14, no. 3: 485. https://doi.org/10.3390/sym14030485
APA StylePapavasileiou, T., Kosmas, O., & Sinatkas, I. (2022). Relativistic Magnetized Astrophysical Plasma Outflows in Black-Hole Microquasars. Symmetry, 14(3), 485. https://doi.org/10.3390/sym14030485







