Uniqueness of the Inflationary Higgs Scalar for Neutron Stars and Failure of Non-Inflationary Approximations
Abstract
:1. Introduction
2. Non-Inflationary Higgs Scalar-Tensor Gravity in the Einstein Frame and Static NSs Phenomenology
3. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Smith, T.L.; Caldwell, R. LISA for Cosmologists: Calculating the Signal-to-Noise Ratio for Stochastic and Deterministic Sources. Phys. Rev. D 2019, 100, 104055. [Google Scholar] [CrossRef] [Green Version]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. Prog. Theor. Exp. Phys. 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron stars 1: Equation of state and structure, Astrophys. Space Sci. Libr. 2007, 326, 1–619. [Google Scholar]
- Friedman, J.L.; Stergioulas, N. Rotating Relativistic Stars; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef] [Green Version]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lattimer, J.M.; Prakash, M. The physics of neutron stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef] [Green Version]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Stellar structure models in modified theories of gravity: Lessons and challenges. Phys. Rept. 2020, 876, 1–75. [Google Scholar] [CrossRef]
- Lattimer, J.M. The nuclear equation of state and neutron star masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef] [Green Version]
- Steiner, A.W.; Gandolfi, S. Connecting Neutron Star Observations to Three-Body Forces in Neutron Matter and to the Nuclear Symmetry Energy. Phys. Rev. Lett. 2012, 108, 081102. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Perez-Garcia, M.A.; Berry, D.K.; Piekarewicz, J. Dynamical response of the nuclear ’pasta’ in neutron star crusts. Phys. Rev. C 2005, 72, 35801. [Google Scholar]
- Watanabe, G.; Iida, K.; Sato, K. Thermodynamic properties of nuclear ’pasta’ in neutron star crusts. Nucl. Phys. A 2003, 676, 455–473. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435–450. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Chen, L.W.; Li, B.A.; Ma, H.R. Nuclear constraints on properties of neutron star crusts. Astrophys. J. 2009, 697, 1549–1568. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef] [Green Version]
- de Jesús Mendoza-Temis, J.; Wu, M.R.; Martínez-Pinedo, G.; Langanke, K.; Bauswein, A.; Janka, H.T. Nuclear robustness of the r process in neutron-star mergers. Phys. Rev. C 2015, 92, 55805. [Google Scholar] [CrossRef] [Green Version]
- Ho, W.C.G.; Elshamouty, K.G.; Heinke, C.O.; Potekhin, A.Y. Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 2015, 91, 15806. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Probing the nuclear equation of state from the existence of a ~2.6 M⊙ neutron star: The GW190814 puzzle. Symmetry 2021, 13, 183. [Google Scholar] [CrossRef]
- Buschmann, M.; Co, R.T.; Dessert, C.; Safdi, B.R. X-ray Search for Axions from Nearby Isolated Neutron Stars. Phys. Rev. Lett. 2021, 126, 21102. [Google Scholar] [CrossRef]
- Safdi, B.R.; Sun, Z.; Chen, A.Y. Detecting Axion Dark Matter with Radio Lines from Neutron Star Populations. Phys. Rev. D 2019, 99, 123021. [Google Scholar] [CrossRef] [Green Version]
- Hook, A.; Kahn, Y.; Safdi, B.R.; Sun, Z. Radio Signals from Axion Dark Matter Conversion in Neutron Star Magnetospheres. Phys. Rev. Lett. 2018, 121, 241102. [Google Scholar] [CrossRef] [Green Version]
- Edwards, T.D.P.; Kavanagh, B.J.; Visinelli, L.; Weniger, C. Transient Radio Signatures from Neutron Star Encounters with QCD Axion Miniclusters. Phys. Rev. Lett. 2021, 127, 131103. [Google Scholar] [CrossRef] [PubMed]
- Nurmi, S.; Schiappacasse, E.D.; Yanagida, T.T. Radio signatures from encounters between Neutron Stars and QCD-Axion Minihalos around Primordial Black Holes. arXiv 2021, arXiv:2102.05680. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended Gravity Description for the GW190814 Supermassive Neutron Star. Phys. Lett. B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Farinelli, R.; Odintsov, S.D. Mass-radius relation for neutron stars in f(R) gravity. Phys. Rev. D 2016, 93, 23501. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Extreme neutron stars from Extended Theories of Gravity. JCAP 2015, 2015, 1. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Maximal neutron star mass and the resolution of the hyperon puzzle in modified gravity. Phys. Rev. D 2014, 89, 103509. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Further stable neutron star models from f(R) gravity. JCAP 2013, 2013, 40. [Google Scholar] [CrossRef] [Green Version]
- Arapoglu, A.S.; Deliduman, C.; Eksi, K.Y. Constraints on Perturbative f(R) Gravity via Neutron Stars. JCAP 2011, 2011, 20. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Odintsov, S.D. Rotating Neutron Stars in F(R) Gravity with Axions. Mon. Not. Roy. Astron. Soc. 2020, 498, 3616. [Google Scholar] [CrossRef]
- Lobato, R.V.; Carvalho, G.A.; Bertulani, C.A. Neutron stars in f(R,Lm) gravity with realistic equations of state: Joint-constrains with GW170817, massive pulsars, and the PSR J0030+0451 mass-radius from NICER data. Eur. Phys. J. C 2021, 81, 1013. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Universal inflationary attractors implications on static neutron stars. Class. Quant. Grav. 2021, 38, 175005. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Neutron Stars in Scalar-tensor Gravity with Higgs Scalar Potential. arXiv 2021, arXiv:2104.01982. [Google Scholar]
- Odintsov, S.D.; Oikonomou, V.K. Neutron stars phenomenology with scalar–tensor inflationary attractors. Phys. Dark Univ. 2021, 32, 100805. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Causal limit of neutron star maximum mass in f(R) gravity in view of GW190814. Phys. Lett. B 2021, 816, 136222. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Novel stellar astrophysics from extended gravity. EPL 2021, 134, 59001. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion cooling of neutron stars. Phys. Rev. D 2016, 93, 65044. [Google Scholar] [CrossRef] [Green Version]
- Khadkikar, S.; Raduta, A.R.; Oertel, M.; Sedrakian, A. Maximum mass of compact stars from gravitational wave events with finite-temperature equations of state. Phys. Rev. C 2021, 103, 55811. [Google Scholar] [CrossRef]
- Sedrakian, D.M.; Hayrapetyan, M.V.; Shahabasyan, M.K. Gravitational radiation of slowly rotating neutron stars. Astrophysics 2006, 49, 194–200. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion cooling of neutron stars. II. Beyond hadronic axions. Phys. Rev. D 2019, 99, 43011. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Guo, G.; Lien, J.H.; Lin, Y.H.; Wu, M.R. Compact Dark Objects in Neutron Star Mergers. arXiv 2020, arXiv:2012.11908. [Google Scholar]
- Vretinaris, S.; Stergioulas, N.; Bauswein, A. Empirical relations for gravitational-wave asteroseismology of binary neutron star mergers. Phys. Rev. D 2020, 101, 84039. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Blacker, S.; Vijayan, V.; Stergioulas, N.; Chatziioannou, K.; Clark, J.A.; Bastian, N.U.F.; Blaschke, D.B.; Cierniak, M.; Fischer, T. Equation of state constraints from the threshold binary mass for prompt collapse of neutron star mergers. Phys. Rev. Lett. 2020, 125, 141103. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef] [Green Version]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [Green Version]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Nathanail, A.; Most, E.R.; Rezzolla, L. GW170817 and GW190814: Tension on the maximum mass. Astrophys. J. Lett. 2021, 908, L28. [Google Scholar] [CrossRef]
- Köppel, S.; Bovard, L.; Rezzolla, L. A General-relativistic Determination of the Threshold Mass to Prompt Collapse in Binary Neutron Star Mergers. Astrophys. J. Lett. 2019, 872, L16. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167. [Google Scholar] [CrossRef] [Green Version]
- Faraoni, V.; Capozziello, S. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer: Dordrecht, The Netherland, 2010; p. 170. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef] [Green Version]
- de la Cruz-Dombriz, A.; Saez-Gomez, D. Black holes, cosmological solutions, future singularities, and their thermodynamical properties in modified gravity theories. Entropy 2012, 14, 1717. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef] [Green Version]
- Dimopoulos, K. Introduction to Cosmic Inflation and Dark Energy; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Pani, P.; Berti, E. Slowly rotating neutron stars in scalar-tensor theories. Phys. Rev. D 2014, 90, 24025. [Google Scholar] [CrossRef] [Green Version]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. Slowly rotating neutron and strange stars in R2 gravity. JCAP 2014, 2014, 6. [Google Scholar] [CrossRef] [Green Version]
- Horbatsch, M.; Silva, H.O.; Gerosa, D.; Pani, P.; Berti, E.; Gualtieri, L.; Sperhake, U. Tensor-multi-scalar theories: Relativistic stars and 3 + 1 decomposition. Class. Quant. Grav. 2015, 32, 204001. [Google Scholar] [CrossRef]
- Silva, H.O.; Macedo, C.F.B.; Berti, E.; Crispino, L.C.B. Slowly rotating anisotropic neutron stars in general relativity and scalar–tensor theory. Class. Quant. Grav. 2015, 32, 145008. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S.; Stergioulas, N.; Kokkotas, K.D. Rapidly rotating neutron stars in scalar-tensor theories of gravity. Phys. Rev. D 2013, 88, 84060. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Gao, Y.; Shao, L. Strong-field effects in massive scalar-tensor gravity for slowly spinning neutron stars and application to X-ray pulsar pulse profiles. Phys. Rev. D 2020, 102, 64057. [Google Scholar] [CrossRef]
- Salgado, M.; Sudarsky, D.; Nucamendi, U. On spontaneous scalarization. Phys. Rev. D 1998, 58, 124003. [Google Scholar] [CrossRef] [Green Version]
- Shibata, M.; Taniguchi, K.; Okawa, H.; Buonanno, A. Coalescence of binary neutron stars in a scalar-tensor theory of gravity. Phys. Rev. D 2014, 89, 84005. [Google Scholar] [CrossRef] [Green Version]
- Savaş Arapoğlu, A.; Yavuz Ekşi, K.; Emrah Yükselci, A. Neutron star structure in the presence of nonminimally coupled scalar fields. Phys. Rev. D 2019, 99, 64055. [Google Scholar] [CrossRef] [Green Version]
- Ramazanoğlu, F.M.; Pretorius, F. Spontaneous Scalarization with Massive Fields. Phys. Rev. D 2016, 93, 64005. [Google Scholar] [CrossRef] [Green Version]
- Altaha Motahar, Z.; Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Axial quasinormal modes of scalarized neutron stars with massive self-interacting scalar field. Phys. Rev. D 2019, 99, 104006. [Google Scholar] [CrossRef] [Green Version]
- Chew, X.Y.; Dzhunushaliev, V.; Folomeev, V.; Kleihaus, B.; Kunz, J. Rotating wormhole solutions with a complex phantom scalar field. Phys. Rev. D 2019, 100, 44019. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Scen Khoo, F.; Kunz, J. Ultra-long-lived quasi-normal modes of neutron stars in massive scalar-tensor gravity. EPL 2020, 130, 50002. [Google Scholar] [CrossRef]
- Altaha Motahar, Z.; Blázquez-Salcedo, J.L.; Kleihaus, B.; Kunz, J. Scalarization of neutron stars with realistic equations of state. Phys. Rev. D 2017, 96, 64046. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.; Shaposhnikov, M. Higgs inflation at the critical point. Phys. Lett. B 2014, 734, 249–254. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Rubio, J.; Shaposhnikov, M.; Zenhausern, D. Higgs-Dilaton Cosmology: From the Early to the Late Universe. Phys. Rev. D 2011, 84, 123504. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.; Magnin, A.; Shaposhnikov, M.; Sibiryakov, S. Higgs inflation: Consistency and generalisations. JHEP 2011, 2011, 16. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.L.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. B 2008, 659, 703–706. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.S.; Sahni, V.; Toporensky, A.V. Initial conditions for Inflation in an FRW Universe. Phys. Rev. D 2018, 98, 83538. [Google Scholar] [CrossRef] [Green Version]
- Steinwachs, C.F.; Kamenshchik, A.Y. Non-minimal Higgs Inflation and Frame Dependence in Cosmology. AIP Conf. Proc. 2013, 1514, 161–164. [Google Scholar]
- Rubio, J. Higgs inflation. Front. Astron. Space Sci. 2019, 5, 50. [Google Scholar] [CrossRef]
- Kaiser, D.I. Primordial spectral indices from generalized Einstein theories. Phys. Rev. D 1995, 52, 4295–4306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gundhi, A.; Steinwachs, C.F. Scalaron-Higgs inflation. Nucl. Phys. B 2020, 954, 114989. [Google Scholar] [CrossRef]
- Cervantes-Cota, J.L.; Dehnen, H. Induced gravity inflation in the standard model of particle physics. Nucl. Phys. B 1995, 442, 391–412. [Google Scholar] [CrossRef] [Green Version]
- Kamada, K.; Kobayashi, T.; Takahashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized Higgs inflation. Phys. Rev. D 2012, 86, 23504. [Google Scholar] [CrossRef] [Green Version]
- Schlogel, S.; Rinaldi, M.; Staelens, F.; Fuzfa, A. Particlelike solutions in modified gravity: The Higgs monopole. Phys. Rev. D 2014, 90, 44056. [Google Scholar] [CrossRef] [Green Version]
- Füzfa, A.; Rinaldi, M.; Schlögel, S. Particlelike distributions of the Higgs field nonminimally coupled to gravity. Phys. Rev. Lett. 2013, 111, 121103. [Google Scholar] [CrossRef] [Green Version]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef] [Green Version]
- Read, J.S.; Markakis, C.; Shibata, M.; Uryu, K.; Creighton, J.D.E.; Friedman, J.L. Measuring the neutron star equation of state with gravitational wave observations. Phys. Rev. D 2009, 79, 124033. [Google Scholar] [CrossRef]
- Faraoni, V. Cosmology in Scalar-Tensor Gravity; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Faraoni, V. Conformally coupled inflation. Galaxies 2013, 1, 96–106. [Google Scholar] [CrossRef] [Green Version]
- Buck, M.; Fairbairn, M.; Sakellariadou, M. Inflation in models with Conformally Coupled Scalar fields: An application to the Noncommutative Spectral Action. Phys. Rev. D. 2010, 82, 43509. [Google Scholar] [CrossRef] [Green Version]
- Faraoni, V.; Gunzig, E.; Nardone, P. Conformal transformations in classical gravitational theories and in cosmology. Fund. Cosmic Phys. 1999, 20, 121. [Google Scholar]
- Nikolaos Stergioulas. Available online: https://github.com/niksterg (accessed on 14 January 2021).
- Wiringa, R.B.; Fiks, V.; Fabrocini, A. Equation of state for dense nucleon matter. Phys. Rev. C. 1988, 38, 1010–1037. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef] [Green Version]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. The Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels–Montreal functionals—I. Role of symmetry energy. Mon. Not. Roy. Astron. Soc. 2019, 481, 2994–3026. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef] [Green Version]
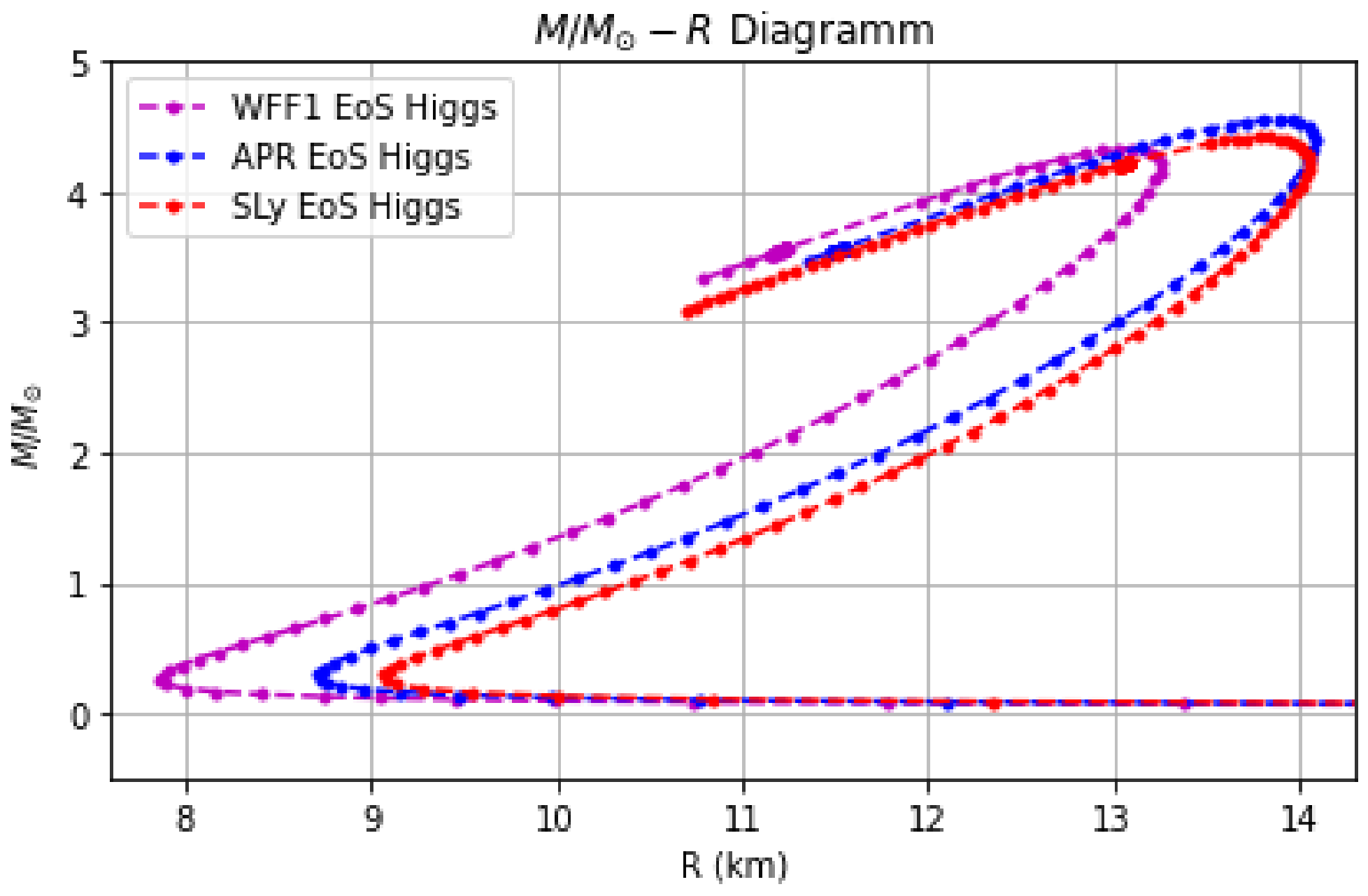
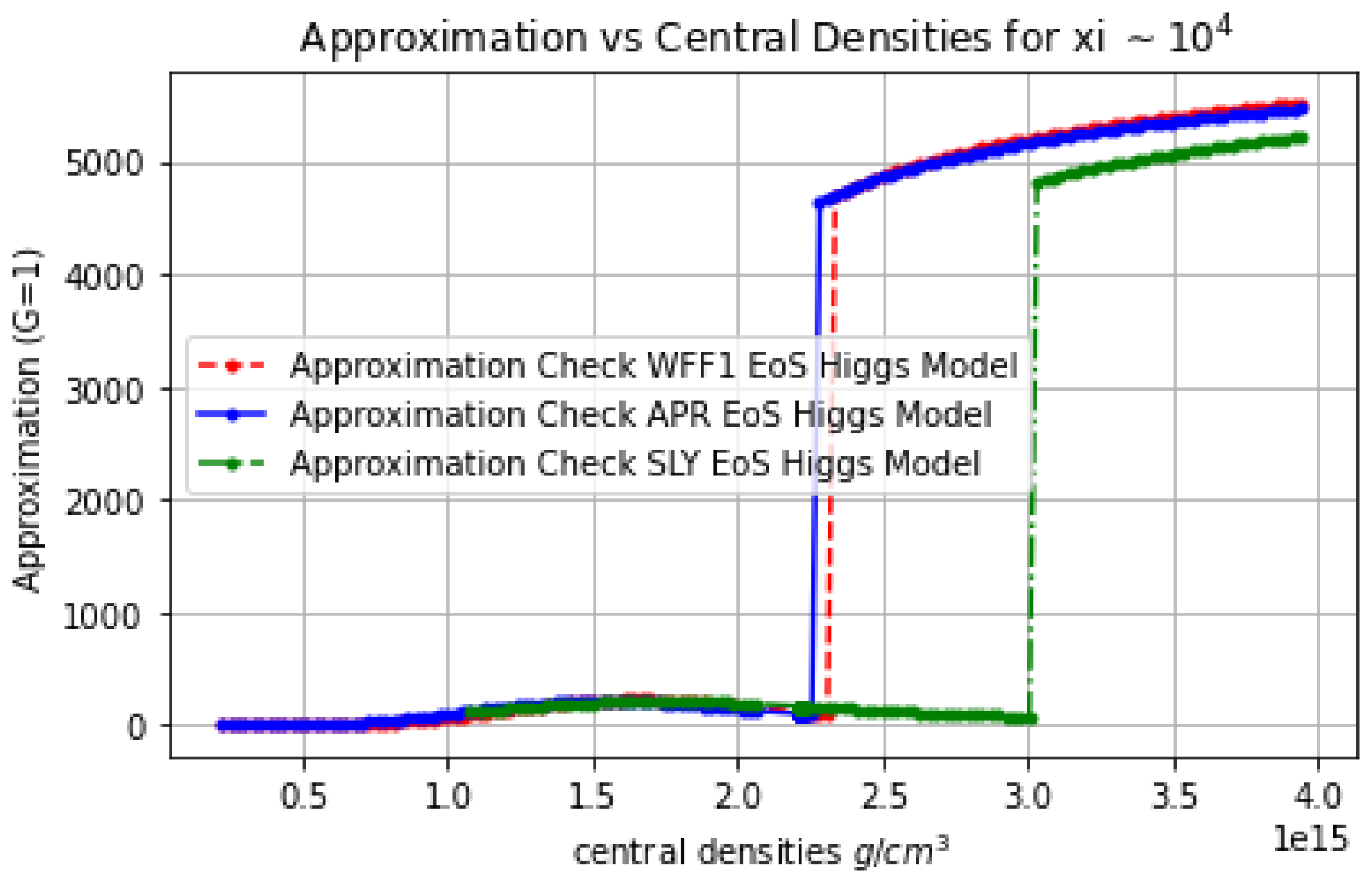
| Model | APR EoS | SLy EoS | WFF1 EoS |
|---|---|---|---|
| GR | |||
| Alternative Higgs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oikonomou, V.K. Uniqueness of the Inflationary Higgs Scalar for Neutron Stars and Failure of Non-Inflationary Approximations. Symmetry 2022, 14, 32. https://doi.org/10.3390/sym14010032
Oikonomou VK. Uniqueness of the Inflationary Higgs Scalar for Neutron Stars and Failure of Non-Inflationary Approximations. Symmetry. 2022; 14(1):32. https://doi.org/10.3390/sym14010032
Chicago/Turabian StyleOikonomou, Vasilis K. 2022. "Uniqueness of the Inflationary Higgs Scalar for Neutron Stars and Failure of Non-Inflationary Approximations" Symmetry 14, no. 1: 32. https://doi.org/10.3390/sym14010032
APA StyleOikonomou, V. K. (2022). Uniqueness of the Inflationary Higgs Scalar for Neutron Stars and Failure of Non-Inflationary Approximations. Symmetry, 14(1), 32. https://doi.org/10.3390/sym14010032






