Prioritized Aggregation Operators for Intuitionistic Fuzzy Information Based on Aczel–Alsina T-Norm and T-Conorm and Their Applications in Group Decision-Making
Abstract
1. Introduction
- (1)
- To propose prioritized AOs for IF information based on the Aczel–Alsina TN and TCN, i.e., IFPAAA and IFPAAG operators, to overcome shortcomings.
- (2)
- To study the importance of the proposed IFPAAA and IFPAAG operators.
- (3)
- To study some properties of the proposed prioritized AOs.
- (4)
- To apply the IFPAAA and IFPAAG operators in a MAGDM problem.
- (5)
- To compare the results obtained using the proposed prioritized AOs of IFVs with other existing AOs.
2. Preliminaries
- (1)
- If, then has less preference than.
- (2)
- If, then andare the same.
- (3)
- If, then has less preference than.
- (4)
- If, then andare the same.
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- ,
3. Intuitionistic Fuzzy Prioritized Aczel–Alsina Averaging Aggregation Operators
- (I)
- For , using Aczel–Alsina operations of IFVs, we obtain
- (II)
- Assume that Equation (3) is true for , then we have
- (I)
- For , using Aczel–Alsina operations of IFVs, we obtain
- (II)
- If Equation (4) holds true for , then we have
4. MAGDM Methods Using Investigated Operators Based on IFVs
5. Practical Example
6. Comparative Study
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Tang, Y.M.; Zhang, L.; Bao, G.Q.; Ren, F.J.; Pedrycz, W. Symmetric Implicational Algorithm Derived from Intuitionistic Fuzzy Entropy. Iran. J. Fuzzy Syst. 2022, 19, 27–44. [Google Scholar]
- Reddy K., S.; Panwar, L.K.; Panigrahi, B.K.; Kumar, R. Computational Intelligence for Demand Response Exchange Considering Temporal Characteristics of Load Profile via Adaptive Fuzzy Inference System. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 235–245. [Google Scholar] [CrossRef]
- Deschrijver, G.; Cornelis, C.; Kerre, E.E. On the Representation of Intuitionistic Fuzzy T-Norms and t-Conorms. IEEE Trans. Fuzzy Syst. 2004, 12, 45–61. [Google Scholar] [CrossRef]
- Garg, H. Generalized Pythagorean Fuzzy Geometric Aggregation Operators Using Einstein T-Norm and t-Conorm for Multicriteria Decision-Making Process. Int. J. Intell. Syst. 2017, 32, 597–630. [Google Scholar] [CrossRef]
- Gál, L.; Lovassy, R.; Rudas, I.J.; Kóczy, L.T. Learning the Optimal Parameter of the Hamacher T-Norm Applied for Fuzzy-Rule-Based Model Extraction. Neural Comput. Applic 2014, 24, 133–142. [Google Scholar] [CrossRef]
- De Baets, B.; De Meyer, H.E. The Frank T-Norm Family in Fuzzy Similarity Measurement. In Proceedings of the EUSFLAT Conference, Leicester, UK, 5–7 September 2001; pp. 249–252. [Google Scholar]
- Dombi, J. A General Class of Fuzzy Operators, the DeMorgan Class of Fuzzy Operators and Fuzziness Measures Induced by Fuzzy Operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Aczél, J.; Alsina, C. Characterizations of Some Classes of Quasilinear Functions with Applications to Triangular Norms and to Synthesizing Judgements. Aequ. Math. 1982, 25, 313–315. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Xu, Z.; Yager, R.R. Some Geometric Aggregation Operators Based on Intuitionistic Fuzzy Sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Intuitionistic Fuzzy Geometric Aggregation Operators Based on Einstein Operations. Int. J. Intell. Syst. 2011, 26, 1049–1075. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Intuitionistic Fuzzy Information Aggregation Using Einstein Operations. IEEE Trans. Fuzzy Syst. 2012, 20, 923–938. [Google Scholar] [CrossRef]
- Huang, J.-Y. Intuitionistic Fuzzy Hamacher Aggregation Operators and Their Application to Multiple Attribute Decision Making. J. Intell. Fuzzy Syst. 2014, 27, 505–513. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Wang, Y. Multiple Attribute Group Decision Making Methods Based on Intuitionistic Fuzzy Frank Power Aggregation Operators. J. Intell. Fuzzy Syst. 2015, 29, 2235–2246. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Yager, R.R. Aczel–Alsina Aggregation Operators and Their Application to Intuitionistic Fuzzy Multiple Attribute Decision Making. Int. J. Intell. Syst. 2022, 37, 1529–1551. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Alshahrani, M.N.; Yang, M.-S.; Pamucar, D. Novel Aczel–Alsina Operators for Pythagorean Fuzzy Sets with Application in Multi-Attribute Decision Making. Symmetry 2022, 14, 940. [Google Scholar] [CrossRef]
- Khan, M.R.; Wang, H.; Ullah, K.; Karamti, H. Construction Material Selection by Using Multi-Attribute Decision Making Based on q-Rung Orthopair Fuzzy Aczel–Alsina Aggregation Operators. Appl. Sci. 2022, 12, 8537. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Yang, M.-S.; Pamucar, D. Aczel-Alsina Aggregation Operators on T-Spherical Fuzzy (TSF) Information with Application to TSF Multi-Attribute Decision Making. IEEE Access 2022, 10, 26011–26023. [Google Scholar] [CrossRef]
- Senapati, T. Approaches to Multi-Attribute Decision-Making Based on Picture Fuzzy Aczel–Alsina Average Aggregation Operators. Comput. Appl. Math. 2022, 41, 1–19. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Mesiar, R.; Yager, R.R. Novel Aczel–Alsina Operations-Based Interval-Valued Intuitionistic Fuzzy Aggregation Operators and Their Applications in Multiple Attribute Decision-Making Process. Int. J. Intell. Syst. 2021, 37, 5059–5081. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Mesiar, R.; Yager, R.R.; Saha, A. Novel Aczel–Alsina Operations-Based Hesitant Fuzzy Aggregation Operators and Their Applications in Cyclone Disaster Assessment. Int. J. Gen. Syst. 2022, 51, 511–546. [Google Scholar] [CrossRef]
- Ullah, K. Picture Fuzzy Maclaurin Symmetric Mean Operators and Their Applications in Solving Multiattribute Decision-Making Problems. Math. Probl. Eng. 2021, 2021, 1098631. [Google Scholar] [CrossRef]
- Khan, Q.; Mahmood, T.; Ullah, K. Applications of Improved Spherical Fuzzy Dombi Aggregation Operators in Decision Support System. Soft Comput. 2021, 25, 9097–9119. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized Aggregation Operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized OWA Aggregation. Fuzzy Optim. Decis. Mak. 2009, 8, 245–262. [Google Scholar] [CrossRef]
- Yan, H.-B.; Huynh, V.-N.; Nakamori, Y.; Murai, T. On Prioritized Weighted Aggregation in Multi-Criteria Decision Making. Expert Syst. Appl. 2011, 38, 812–823. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Z. Prioritized Intuitionistic Fuzzy Aggregation Operators. Inf. Fusion 2013, 14, 108–116. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Aslam, M.; Chinram, R. Another View of Complex Intuitionistic Fuzzy Soft Sets Based on Prioritized Aggregation Operators and Their Applications to Multiattribute Decision Making. Mathematics 2021, 9, 1922. [Google Scholar] [CrossRef]
- Arora, R.; Garg, H. Group Decision-Making Method Based on Prioritized Linguistic Intuitionistic Fuzzy Aggregation Operators and Its Fundamental Properties. Comp. Appl. Math. 2019, 38, 36. [Google Scholar] [CrossRef]
- Arora, R.; Garg, H. Prioritized Averaging/Geometric Aggregation Operators under the Intuitionistic Fuzzy Soft Set Environment. Sci. Iran. 2017, 25, 466–482. [Google Scholar] [CrossRef]
- Chen, T.-Y. A Prioritized Aggregation Operator-Based Approach to Multiple Criteria Decision Making Using Interval-Valued Intuitionistic Fuzzy Sets: A Comparative Perspective. Inf. Sci. 2014, 281, 97–112. [Google Scholar] [CrossRef]
- Gao, H. Pythagorean Fuzzy Hamacher Prioritized Aggregation Operators in Multiple Attribute Decision Making. J. Intell. Fuzzy Syst. 2018, 35, 2229–2245. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M.; Wang, J. Bipolar Fuzzy Dombi Prioritized Aggregation Operators in Multiple Attribute Decision Making. Soft. Comput. 2020, 24, 3631–3646. [Google Scholar] [CrossRef]
- Riaz, M.; Pamucar, D.; Athar Farid, H.M.; Hashmi, M.R. Q-Rung Orthopair Fuzzy Prioritized Aggregation Operators and Their Application towards Green Supplier Chain Management. Symmetry 2020, 12, 976. [Google Scholar] [CrossRef]
- Gao, H.; Wei, G.; Huang, Y. Dual Hesitant Bipolar Fuzzy Hamacher Prioritized Aggregation Operators in Multiple Attribute Decision Making. IEEE Access 2018, 6, 11508–11522. [Google Scholar] [CrossRef]
- Liu, P.; Akram, M.; Sattar, A. Extensions of Prioritized Weighted Aggregation Operators for Decision-Making under Complex q-Rung Orthopair Fuzzy Information. J. Intell. Fuzzy Syst. 2020, 39, 7469–7493. [Google Scholar] [CrossRef]
- Wei, G. Hesitant Fuzzy Prioritized Operators and Their Application to Multiple Attribute Decision Making. Knowl.-Based Syst. 2012, 31, 176–182. [Google Scholar] [CrossRef]
- Mahmood, T.; Ali, Z. Prioritized Muirhead Mean Aggregation Operators under the Complex Single-Valued Neutrosophic Settings and Their Application in Multi-Attribute Decision Making. J. Comput. Cogn. Eng. 2022, 1, 104. [Google Scholar] [CrossRef]
- Mahmood, T.; Warraich, M.S.; Ali, Z.; Pamucar, D. Generalized MULTIMOORA Method and Dombi Prioritized Weighted Aggregation Operators Based on T-Spherical Fuzzy Sets and Their Applications. Int. J. Intell. Syst. 2021, 36, 4659–4692. [Google Scholar] [CrossRef]
- Mahmood, T. A Novel Approach towards Bipolar Soft Sets and Their Applications. J. Math. 2020, 2020, 4690808. [Google Scholar] [CrossRef]
- Farahbod, F.; Eftekhari, M. Comparison of Different T-Norm Operators in Classification Problems. Int. J. Fuzzy Log. Syst. 2012, 2, 33–39. [Google Scholar] [CrossRef]
- Seikh, M.R.; Mandal, U. Intuitionistic Fuzzy Dombi Aggregation Operators and Their Application to Multiple Attribute Decision-Making. Granul. Comput. 2021, 6, 473–488. [Google Scholar] [CrossRef]
- Waqar, M.; Ullah, K.; Pamucar, D.; Jovanov, G.; Vranješ, Ð. An Approach for the Analysis of Energy Resource Selection Based on Attributes by Using Dombi T-Norm Based Aggregation Operators. Energies 2022, 15, 3939. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Ullah, K.; Pamucar, D.; Cirovic, G. Power Aggregation Operators Based on T-Norm and t-Conorm under the Complex Intuitionistic Fuzzy Soft Settings and Their Application in Multi-Attribute Decision Making. Symmetry 2021, 13, 1986. [Google Scholar] [CrossRef]
- Wang, L.; Peng, X. An Approach to Decision Making with Interval-Valued Complex Pythagorean Fuzzy Model for Evaluating Personal Risk of Mental Patients. J. Intell. Fuzzy Syst. 2021, 41, 1461–1486. [Google Scholar] [CrossRef]
- Liu, P.; Mahmood, T.; Ali, Z. Complex Q-Rung Orthopair Fuzzy Aggregation Operators and Their Applications in Multi-Attribute Group Decision Making. Information 2020, 11, 5. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An Approach toward Decision-Making and Medical Diagnosis Problems Using the Concept of Spherical Fuzzy Sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Akram, M.; Ullah, K.; Pamucar, D. Performance Evaluation of Solar Energy Cells Using the Interval-Valued T-Spherical Fuzzy Bonferroni Mean Operators. Energies 2022, 15, 292. [Google Scholar] [CrossRef]
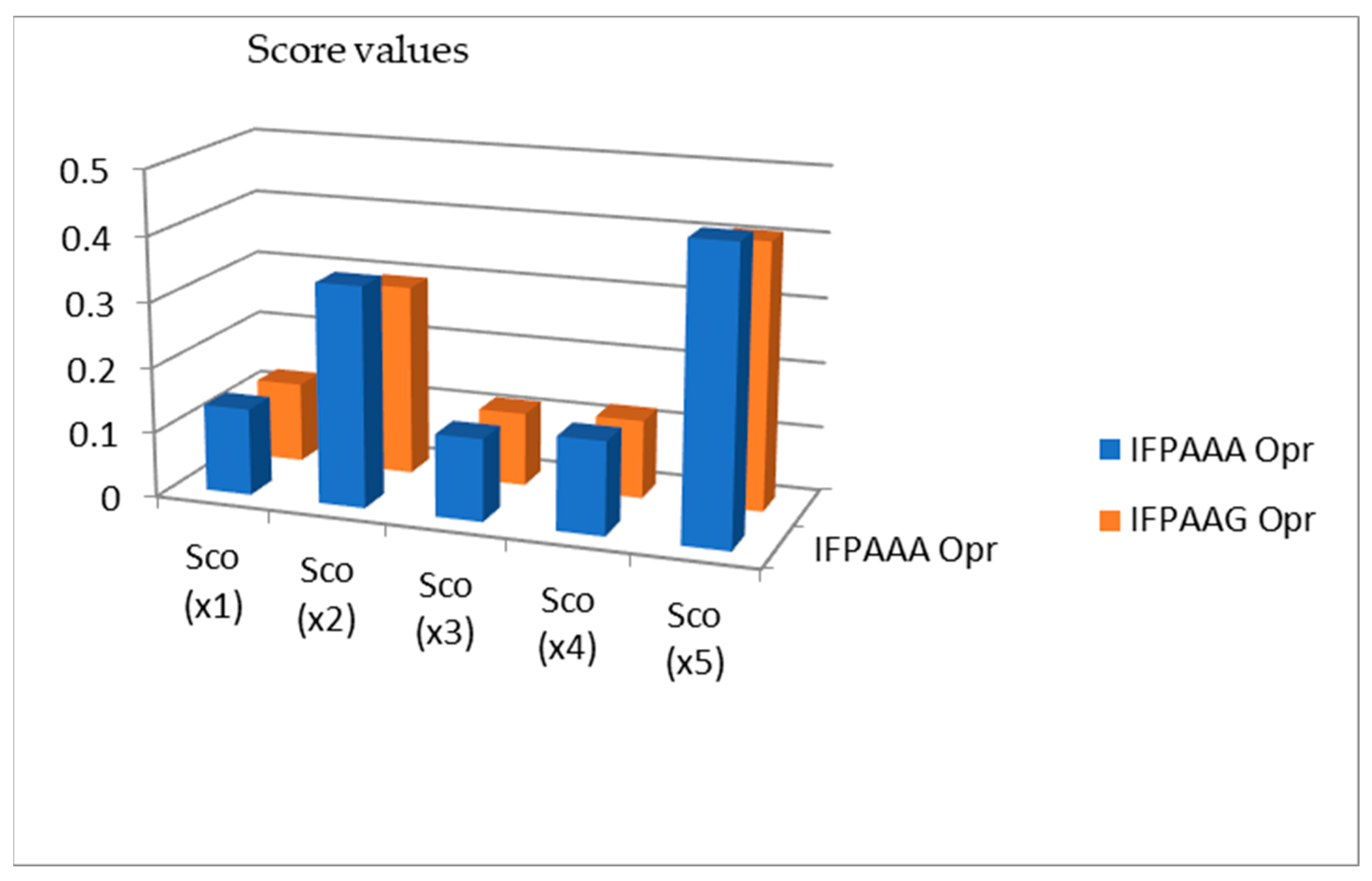
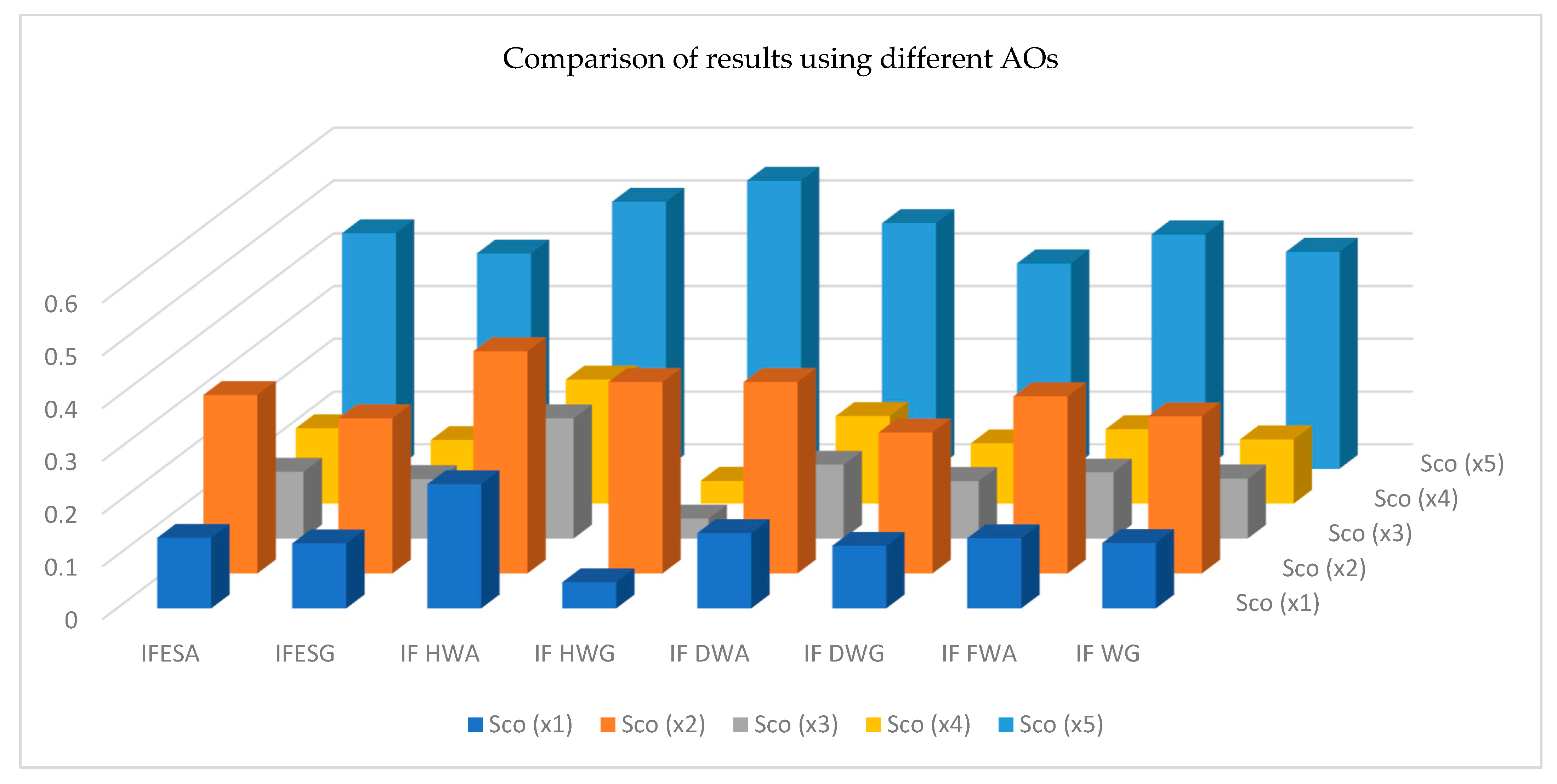
| 0.5 | 0.2 | 0.22 | 0.21 | 0.5 | 0.3 | 0.41 | 0.1 | |
| 0.6 | 0.3 | 0.3 | 0.11 | 0.3 | 0.21 | 0.21 | 0.2 | |
| 0.4 | 0.2 | 0.7 | 0.2 | 0.6 | 0.34 | 0.4 | 0.3 | |
| 0.4 | 0.1 | 0.6 | 0.3 | 0.4 | 0.22 | 0.32 | 0.3 | |
| 0.6 | 0.1 | 0.5 | 0.4 | 0.6 | 0.12 | 0.12 | 0.1 | |
| 0.5 | 0.3 | 0.6 | 0.4 | 0.4 | 0.2 | 0.3 | 0.2 | |
| 0.4 | 0.3 | 0.3 | 0.1 | 0.6 | 0.1 | 0.3 | 0.1 | |
| 0.3 | 0.1 | 0.3 | 0.1 | 0.4 | 0.3 | 0.41 | 0.4 | |
| 0.6 | 0.1 | 0.2 | 0.1 | 0.4 | 0.3 | 0.6 | 0.2 | |
| 0.5 | 0.2 | 0.3 | 0.21 | 0.4 | 0.1 | 0.1 | 0.1 | |
| 0.4124 | 0.2894 | 0.4618 | 0.2829 | 0.3403 | 0.1221 | 0.5364 | 0.1667 | |
| 0.5870 | 0.2298 | 0.5365 | 0.2295 | 0.2140 | 0.1069 | 0.5679 | 0.1296 | |
| 0.3984 | 0.2837 | 0.5147 | 0.3545 | 0.5890 | 0.2512 | 0.5494 | 0.2429 | |
| 0.4064 | 0.2644 | 0.3315 | 0.2035 | 0.2239 | 0.1092 | 0.3046 | 0.1203 | |
| 0.5870 | 0.1104 | 0.6365 | 0.2505 | 0.5168 | 0.1047 | 0.3597 | 0.1778 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarfraz, M.; Ullah, K.; Akram, M.; Pamucar, D.; Božanić, D. Prioritized Aggregation Operators for Intuitionistic Fuzzy Information Based on Aczel–Alsina T-Norm and T-Conorm and Their Applications in Group Decision-Making. Symmetry 2022, 14, 2655. https://doi.org/10.3390/sym14122655
Sarfraz M, Ullah K, Akram M, Pamucar D, Božanić D. Prioritized Aggregation Operators for Intuitionistic Fuzzy Information Based on Aczel–Alsina T-Norm and T-Conorm and Their Applications in Group Decision-Making. Symmetry. 2022; 14(12):2655. https://doi.org/10.3390/sym14122655
Chicago/Turabian StyleSarfraz, Mehwish, Kifayat Ullah, Maria Akram, Dragan Pamucar, and Darko Božanić. 2022. "Prioritized Aggregation Operators for Intuitionistic Fuzzy Information Based on Aczel–Alsina T-Norm and T-Conorm and Their Applications in Group Decision-Making" Symmetry 14, no. 12: 2655. https://doi.org/10.3390/sym14122655
APA StyleSarfraz, M., Ullah, K., Akram, M., Pamucar, D., & Božanić, D. (2022). Prioritized Aggregation Operators for Intuitionistic Fuzzy Information Based on Aczel–Alsina T-Norm and T-Conorm and Their Applications in Group Decision-Making. Symmetry, 14(12), 2655. https://doi.org/10.3390/sym14122655








