Optical Imaging and Analytical Design of Localized Topological Structures in Chiral Liquid Crystals
Abstract
1. Introduction
2. Materials and Methods
2.1. Frank Free Energy
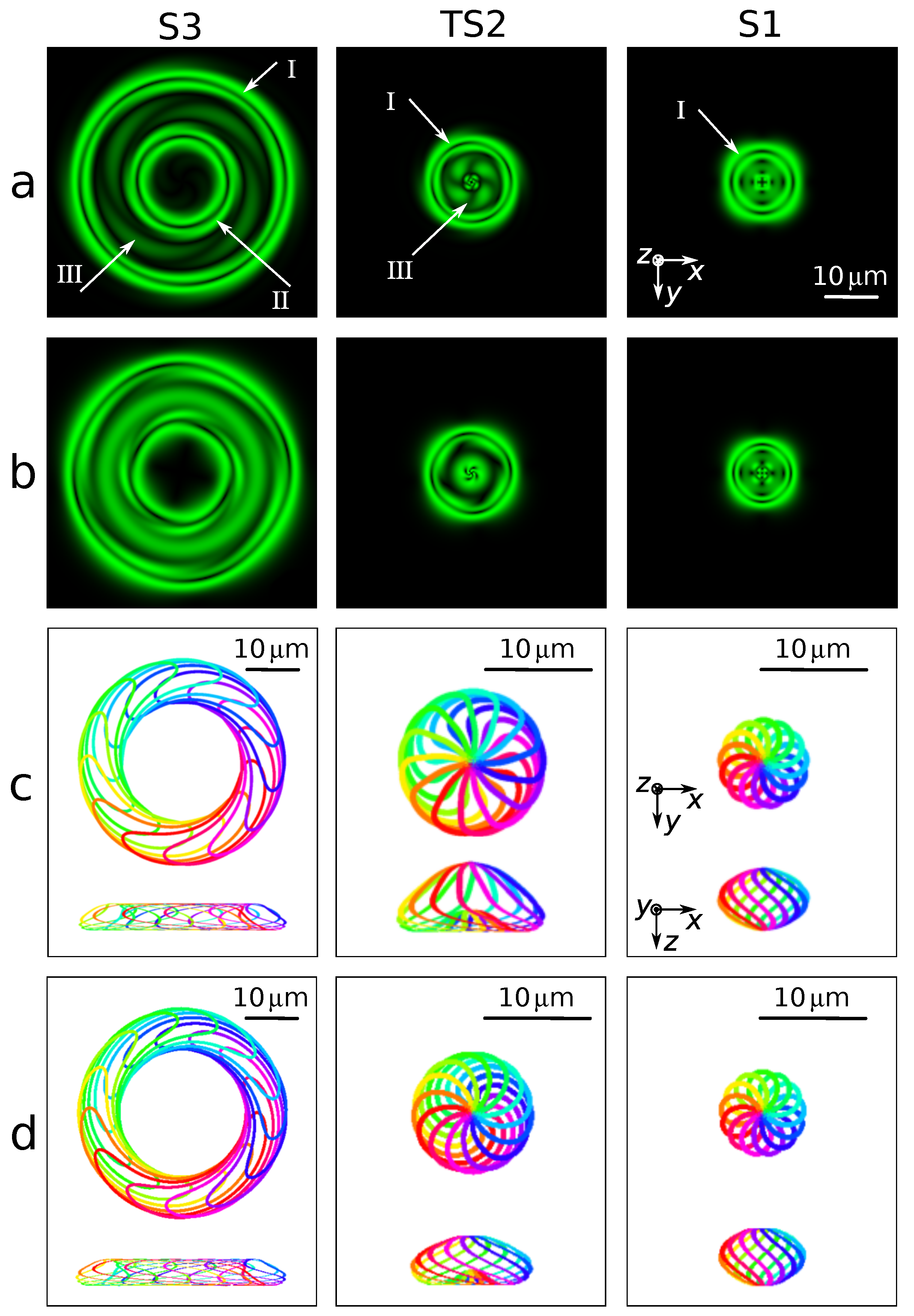
2.2. Optical Imaging of Localized Topological Structures
3. Results
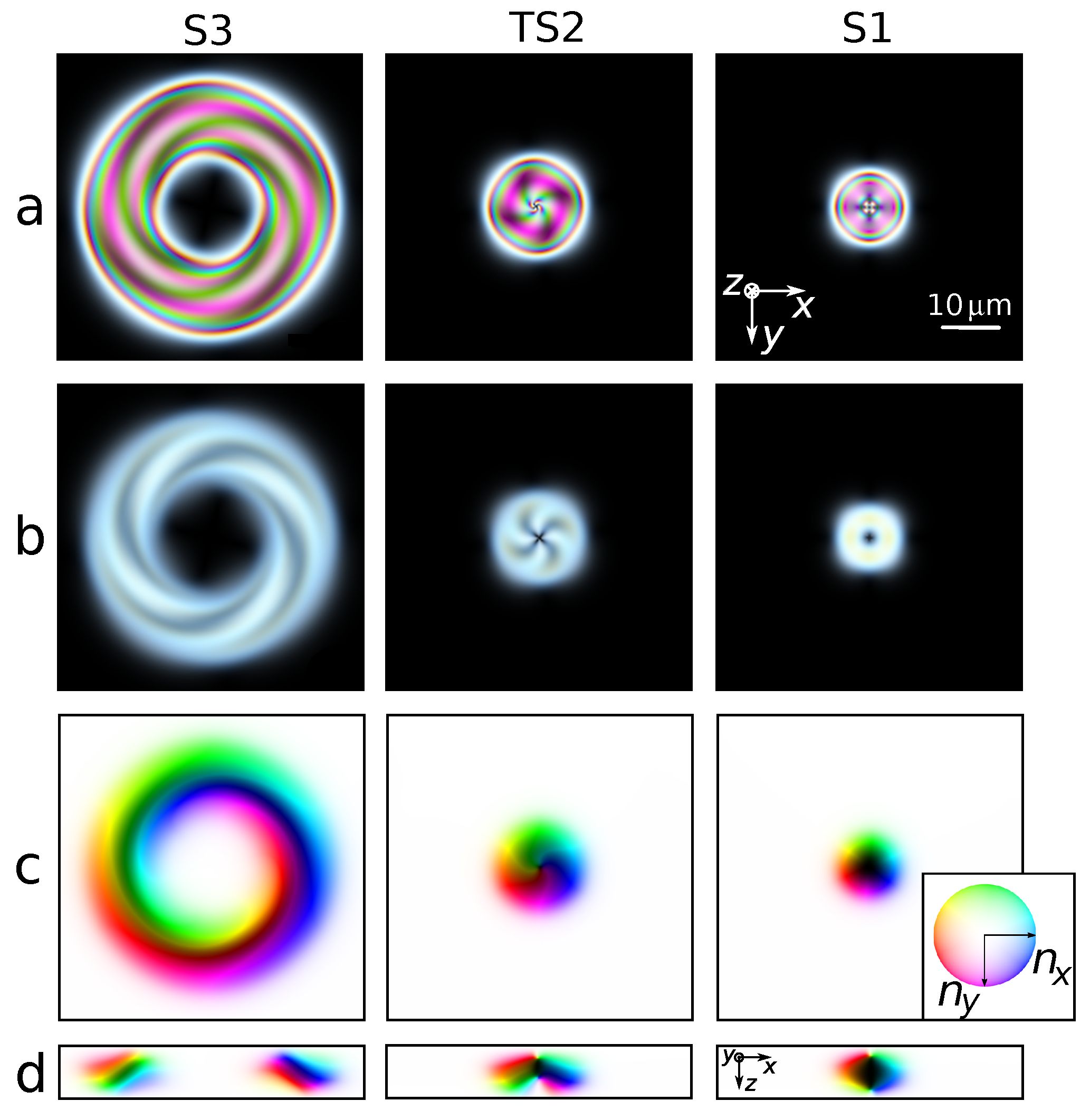
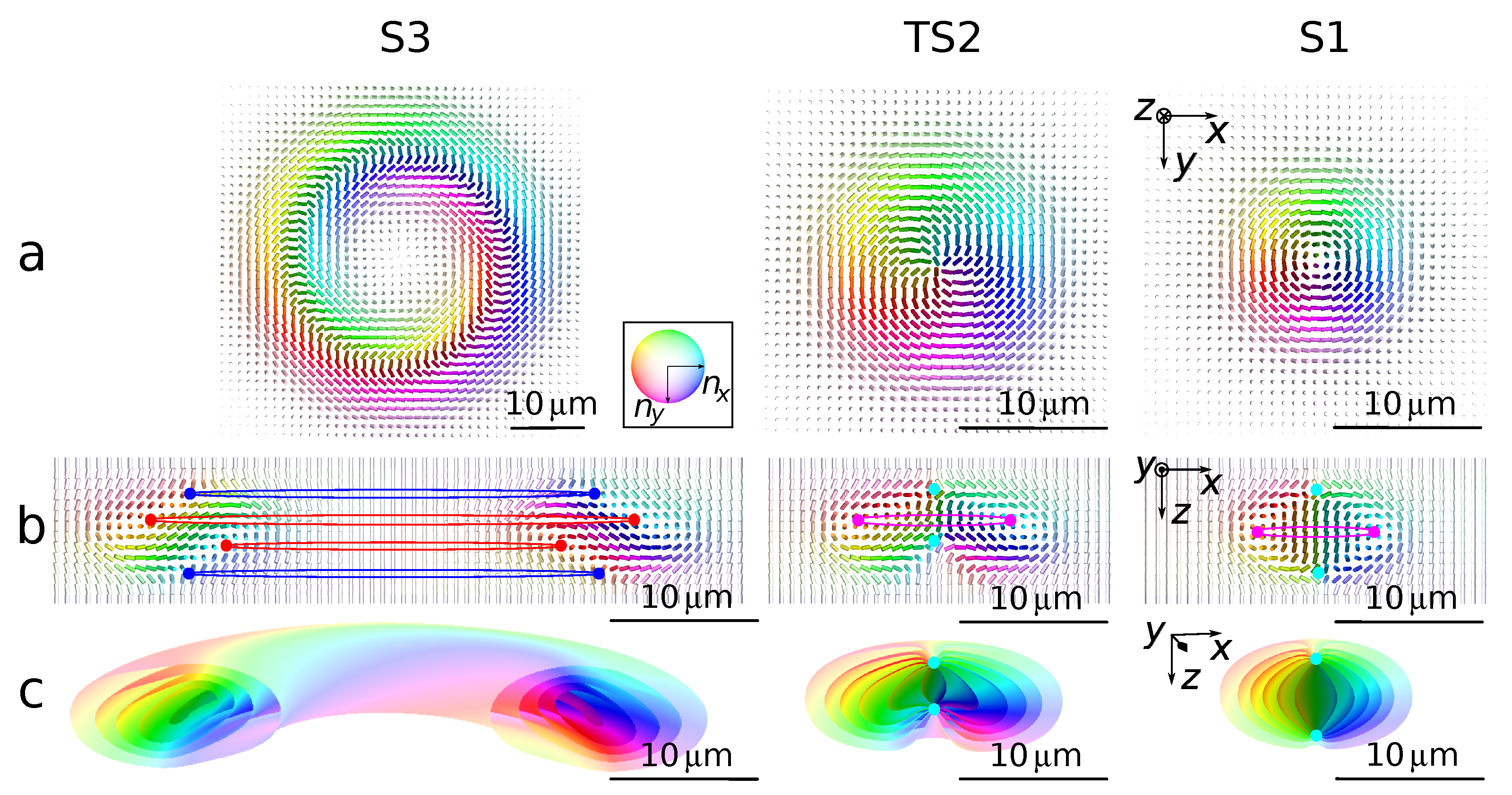
3.1. Simulated Structures
3.2. Analytical Design of Localized Topological Structures
3.3. Approximated Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Haas, W.E.L.; Adams, J.E. Electrically variable diffraction in spherulitic liquid crystals. Appl. Phys. Lett. 1974, 25, 263–264. [Google Scholar] [CrossRef]
- Kawachi, M.; Osamu Kogure, O.; Kato, Y. Bubble domain texture of a liquid crystal. Jpn. J. Appl. Phys. 1974, 13, 1457. [Google Scholar] [CrossRef]
- Hamdi, R.; Petriashvili, G.; Lombardo, G.; De Santo, M.P.; Barberi, R. Liquid crystal bubbles forming a tunable micro-lenses array. J. Appl. Phys. 2011, 110, 074902. [Google Scholar] [CrossRef]
- Yang, B.; Brasselet, E. Arbitrary vortex arrays realized from optical winding of frustrated chiral liquid crystals. J. Opt. 2013, 15, 044021. [Google Scholar] [CrossRef]
- Hess, A.J.; Poy, G.; Tai, J.S.B.; Žumer, S.; Smalyukh, I.I. Control of Light by Topological Solitons in Soft Chiral Birefringent Media. Phys. Rev. X 2020, 10, 031042. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Qi, Z.; Smalyukh, I.I. Optical generation of crystalline, quasicrystalline, and arbitrary arrays of torons in confined cholesteric liquid crystals for patterning of optical vortices in laser beams. Phys. Rev. E 2012, 86, 021703. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Mundoor, H.; Smalyukh, I.I.; Van De Lagemaat, J. Plasmon–Exciton Interactions Probed Using Spatial Coentrapment of Nanoparticles by Topological Singularities. ACS Nano 2015, 9, 1239–12400. [Google Scholar] [CrossRef]
- Evans, J.S.; Ackerman, P.J.; Broer, D.J.; van de Lagemaat, J.; Smalyukh, I.I. Optical generation, templating, and polymerization of three-dimensional arrays of liquid-crystal defects decorated by plasmonic nanoparticles. Phys. Rev. E 2013, 87, 032503. [Google Scholar] [CrossRef]
- Saberi-Pouya, S.; Conti, S.; Perali, A.; Croxall, A.F.; Hamilton, A.R.; Peeters, F.M.; Neilson, D. Experimental conditions for the observation of electron-hole superfluidity in GaAs heterostructures. Phys. Rev. B 2020, 101, 140501. [Google Scholar] [CrossRef]
- Ribiere, P.; Pirkl, S.; Oswald, P. Electric-field-induced phase transitions in frustrated cholesteric liquid crystals of negative dielectric anisotropy. Phys. Rev. A 1991, 44, 8198. [Google Scholar] [CrossRef]
- Oswald, P.; Baudry, J.; Pirkl, S. Static and dynamic properties of cholesteric fingers in electric field. Phys. Rep. 2000, 337, 67–96. [Google Scholar] [CrossRef]
- Afghah, S.; Selinger, J.V. Theory of helicoids and skyrmions in confined cholesteric liquid crystals. Phys. Rev. E 2017, 96, 012708. [Google Scholar] [CrossRef]
- Durey, G.; Sohn, H.R.O.; Ackerman, P.J.; Brasselet, E.; Smalyukh, I.I.; Lopez-Leon, T. Topological solitons, cholesteric fingers and singular defect lines in Janus liquid crystal shells. Soft Matter 2020, 16, 2669. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Smalyukh, I.I. Diversity of Knot Solitons in Liquid Crystals Manifested by Linking of Preimages in Torons and Hopfions. Phys. Rev. X 2017, 7, 011006. [Google Scholar] [CrossRef]
- Smalyukh, I.I.; Lansac, Y.; Clark, N.A.; Trivedi, R.P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 2010, 9, 139–145. [Google Scholar] [CrossRef]
- Loussert, C.; Brasselet, E. Multiple chiral topological states in liquid crystals from unstructured light beams. Appl. Phys. Lett. 2014, 104, 051911. [Google Scholar] [CrossRef]
- Shvetsov, S.; Orlova, T.; Emelyanenko, A.V.; Zolot’ko, A. Thermo-Optical Generation of Particle-Like Structures in Frustrated Chiral Nematic Film. Crystals 2019, 9, 574. [Google Scholar] [CrossRef]
- Loussert, C.; Iamsaard, S.; Katsonis, N.; Brasselet, E. Subnanowatt Opto-Molecular Generation of Localized Defects in Chiral Liquid Crystals. Adv. Mater. 2014, 26, 4242–4246. [Google Scholar] [CrossRef]
- Orlova, T.; Lancia, F.; Loussert, C.; Iamsaard, S.; Katsonis, N.; Brasselet, E. Revolving supramolecular chiral structures powered by light in nanomotor-doped liquid crystals. Nat. Nanotechnol. 2018, 13, 304–308. [Google Scholar] [CrossRef]
- Orlova, T.; Iegorov, R.; Kiselev, A.D. Light-induced pitch transitions in photosensitive cholesteric liquid crystals: Effects of anchoring energy. Phys. Rev. E 2014, 89, 012503. [Google Scholar] [CrossRef]
- Chen, B.G.G.; Ackerman, P.J.; Alexander, G.P.; Kamien, R.D.; Smalyukh, I.I. Generating the Hopf Fibration Experimentally in Nematic Liquid Crystals. Phys. Rev. Lett. 2013, 110, 237801. [Google Scholar] [CrossRef]
- Trivedi, R.P.; Lee, T.; Bertness, K.A.; Smalyukh, I.I. Three dimensional optical manipulation and structural imaging of soft materials by use of laser tweezers and multimodal nonlinear microscopy. Opt. Express 2010, 18, 27658–27669. [Google Scholar] [CrossRef]
- Pirkl, S.; Ribiere, P.; Oswald, P. Forming process and stability of bubble domains in dielectrically positive cholesteric liquid crystals. Liq. Cryst. 1993, 13, 413–425. [Google Scholar] [CrossRef]
- Shen, Y.; Dierking, I. Electrically driven formation and dynamics of skyrmionic solitons in chiral nematics. Phys. Rev. Appl. 2021, 15, 054023. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Trivedi, R.P.; Senyuk, B.; van de Lagemaat, J.; Smalyukh, I.I. Two-dimensional skyrmions and other solitonic structures in confinement-frustrated chiral nematics. Phys. Rev. E 2014, 90, 012505. [Google Scholar] [CrossRef]
- Smalyukh, I.I.; Zribi, O.V.; Butler, J.C.; Lavrentovich, O.D.; Wong, G.C. Structure and Dynamics of Liquid Crystalline Pattern Formation in Drying Droplets of DNA. Phys. Rev. Lett. 2006, 96, 177801. [Google Scholar] [CrossRef]
- Posnjak, G.; Čopar, S.; Muševič, I. Hidden topological constellations and polyvalent charges in chiral nematic droplets. Nat. Commun. 2017, 8, 14594. [Google Scholar] [CrossRef]
- Fernandez-Nieves, A.; Puertas, A.M. Fluids, Colloids and Soft Materials: An Introduction to Soft Matter Physics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 165–186. [Google Scholar]
- Wu, J.-S.; Smalyukh, I.I. Hopfions, heliknotons, skyrmions, torons and both abelian and nonabelian vortices in chiral liquid crystals. Liq. Cryst. Rev. 2022, 1–35. [Google Scholar] [CrossRef]
- Smalyukh, I.I. Review: Knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 2020, 83, 106601. [Google Scholar] [CrossRef]
- Kougo, J.; Araoka, F.; Haba, O.; Yonetake, K.; Aya, S. Photo-reconfigurable twisting structure in chiral liquid crystals triggered by photoresponsive surface. J. Chem. Phys. 2021, 155, 061101. [Google Scholar] [CrossRef]
- de Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Tambovtsev, I.M.; Leonov, A.O.; Lobanov, I.S.; Kiselev, A.D.; Uzdin, V.M. Topological structures in chiral media: Effects of confined geometry. Phys. Rev. E 2022, 105, 034701. [Google Scholar] [CrossRef]
- Lobanov, I.; Uzdin, V. The lifetime of micron scale topological chiral magnetic states with atomic resolution. Comput. Phys. Commun. 2021, 269, 108136. [Google Scholar] [CrossRef]
- Lobanov, I.; Potkina, M.; Uzdin, V. Stability and lifetimes of magnetic states of nano- and microstructures (Brief Review). JETP Lett. 2021, 113, 801. [Google Scholar] [CrossRef]
- Trabi, C.L.; Brown, C.V.; Smith, A.A.T.; Mottram, N.J. Interferometric method for determining the sum of the flexoelectric coefficients (e1+e3) in an ionic nematic material. Appl. Phys. Lett. 2008, 92, 223509. [Google Scholar] [CrossRef]
- Strömer, J.F.; Raynes, E.P. Study of elastic constant ratios in nematic liquid crystals. Appl. Phys. Lett. 2006, 88, 051915. [Google Scholar] [CrossRef]
- Raynes, E.P.; Brown, C.V.; Strömer, J.F. Method for the measurement of the K22 nematic elastic constant. Appl. Phys. Lett. 2003, 82, 13–15. [Google Scholar] [CrossRef]
- Wang, H.; Wu, T.X.; Gauza, S.; Wu, J.R.; Wu, S.T. A method to estimate the Leslie coefficients of liquid crystals based on MBBA data. Liquid Cryst. 2006, 33, 91–98. [Google Scholar] [CrossRef]
- Yeh, P.; Gu, C. Optics of Liquid Crystal Displays; Wiley: New York, NY, USA, 1999; p. 438. [Google Scholar]
- Ellis, P.W.; Pairam, E.; Fernández-Nieves, A. Simulating optical polarizing microscopy textures using Jones calculus: A review exemplified with nematic liquid crystal tori. J. Phys. D Appl. Phys. 2019, 52, 213001. [Google Scholar] [CrossRef]
- Baudry, J.; Pirkl, S.; Oswald, P. Topological properties of singular fingers in frustrated cholesteric liquid crystals. Phys. Rev. E 1998, 57, 3038. [Google Scholar] [CrossRef]
- Smalyukh, I.I.; Senyuk, B.I.; Palffy-Muhoray, P.; Lavrentovich, O.D.; Huang, H.; Gartland, E.C.; Bodnar, V.H.; Kosa, T.; Taheri, B. Electric-field-induced nematic-cholesteric transition and three-dimensional director structures in homeotropic cells. Phys. Rev. E 2005, 72, 061707. [Google Scholar] [CrossRef]
- Li, J.; Wen, C.H.; Gauza, S.; Lu, R.; Wu, S.T. Refractive indices of liquid crystals for display applications. J. Disp. Technol. 2005, 1, 51–61. [Google Scholar] [CrossRef]
- Gil, L.; Gilli, J.M. Surprising dynamics of some cholesteric liquid crystal patterns. Phys. Rev. Lett. 1998, 80, 5742. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobanov, I.; Aksenova, E.; Orlova, T.; Darmoroz, D.; Uzdin, V.; Kiselev, A.D. Optical Imaging and Analytical Design of Localized Topological Structures in Chiral Liquid Crystals. Symmetry 2022, 14, 2476. https://doi.org/10.3390/sym14122476
Lobanov I, Aksenova E, Orlova T, Darmoroz D, Uzdin V, Kiselev AD. Optical Imaging and Analytical Design of Localized Topological Structures in Chiral Liquid Crystals. Symmetry. 2022; 14(12):2476. https://doi.org/10.3390/sym14122476
Chicago/Turabian StyleLobanov, Igor, Elena Aksenova, Tetiana Orlova, Darina Darmoroz, Valery Uzdin, and Alexei D. Kiselev. 2022. "Optical Imaging and Analytical Design of Localized Topological Structures in Chiral Liquid Crystals" Symmetry 14, no. 12: 2476. https://doi.org/10.3390/sym14122476
APA StyleLobanov, I., Aksenova, E., Orlova, T., Darmoroz, D., Uzdin, V., & Kiselev, A. D. (2022). Optical Imaging and Analytical Design of Localized Topological Structures in Chiral Liquid Crystals. Symmetry, 14(12), 2476. https://doi.org/10.3390/sym14122476





