Cross-Gramian-Based Model Reduction for Descriptor Systems
Abstract
1. Introduction
2. Model Reduction Based on Gramians
2.1. Preliminaries
- (a)
- the descriptor system is completely controllable;
- (b)
- for all and ;
- (c)
- for all and ;
- (d)
- and .
- (a)
- the descriptor system is completely observable;
- (b)
- for all and ;
- (c)
- for all and ;
- (d)
- and .
- the proper Hankel singular values are defined as the square roots of the largest eigenvalues of .
- the improper Hankel singular values are defined as the square roots of the largest eigenvalues of .
2.2. Model Reduction Based on Gramians for Descriptor Systems
| Algorithm 1The BFSR method based on Gramians |
|
| Algorithm 2LR-ADI for PGCTLE |
|
| Algorithm 3LR-Smith for PGDTLE |
|
3. Model Reduction Based on Cross Gramians
3.1. Cross-Gramian-Based Balanced Realization
3.2. Cross-Gramian-Based Model Reduction
| Algorithm 4The BFSR method based on cross Gramians |
|
3.3. Low-Rank Iterative Methods for PGCTSE and PGDTSE
| Algorithm 5LR-ADI for PGCTSE |
|
| Algorithm 6LR-Smith for PGDTSE |
|
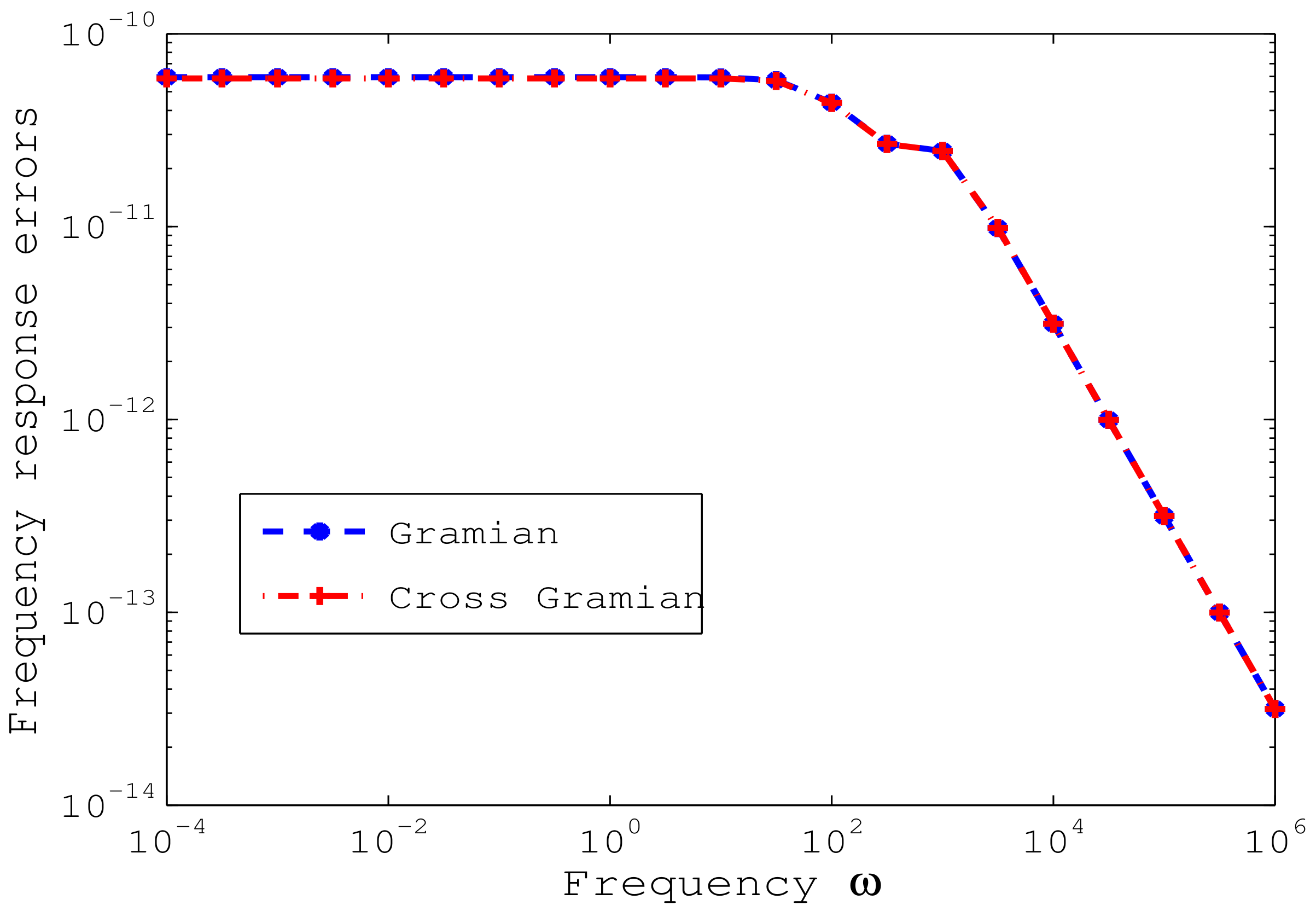
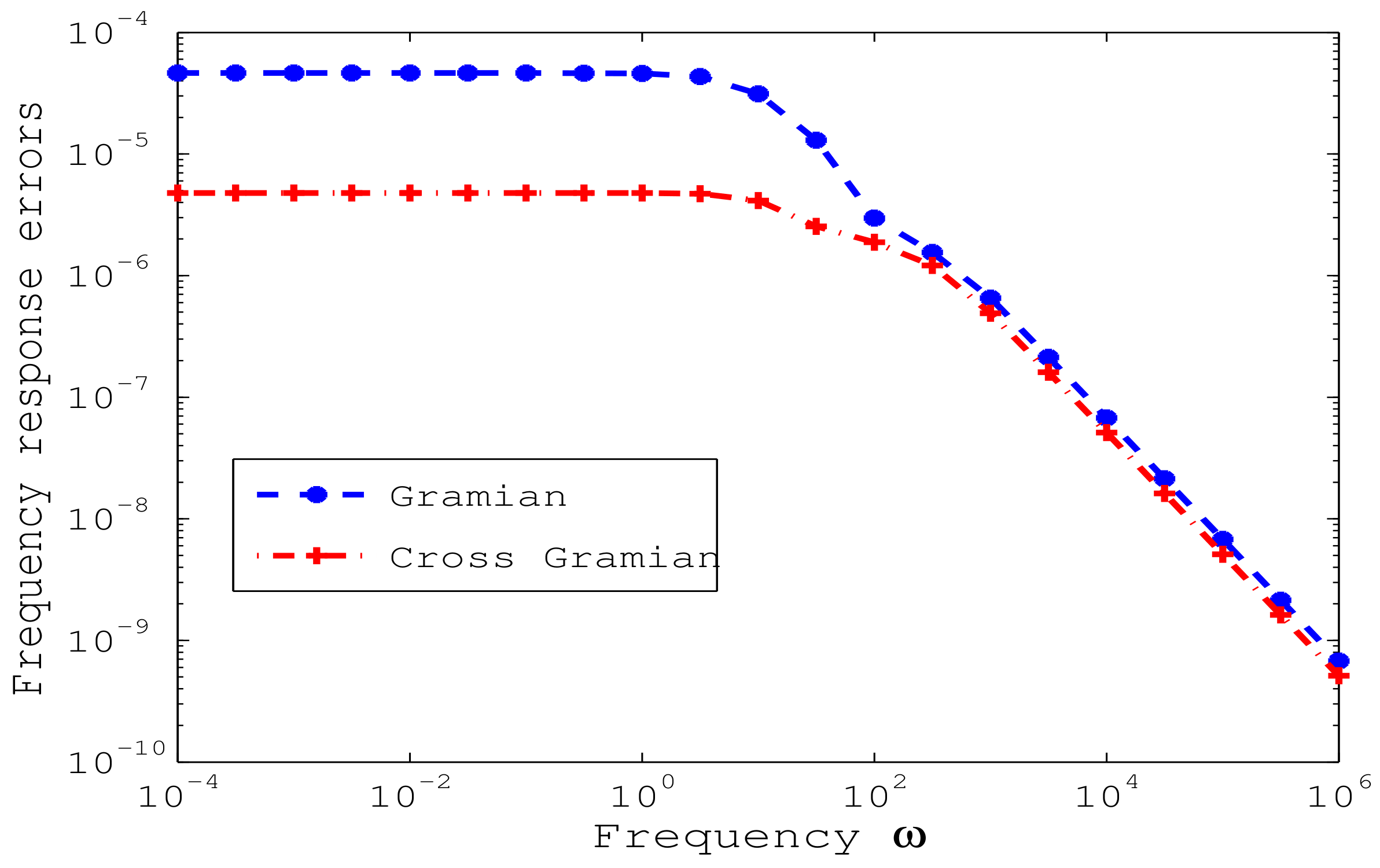
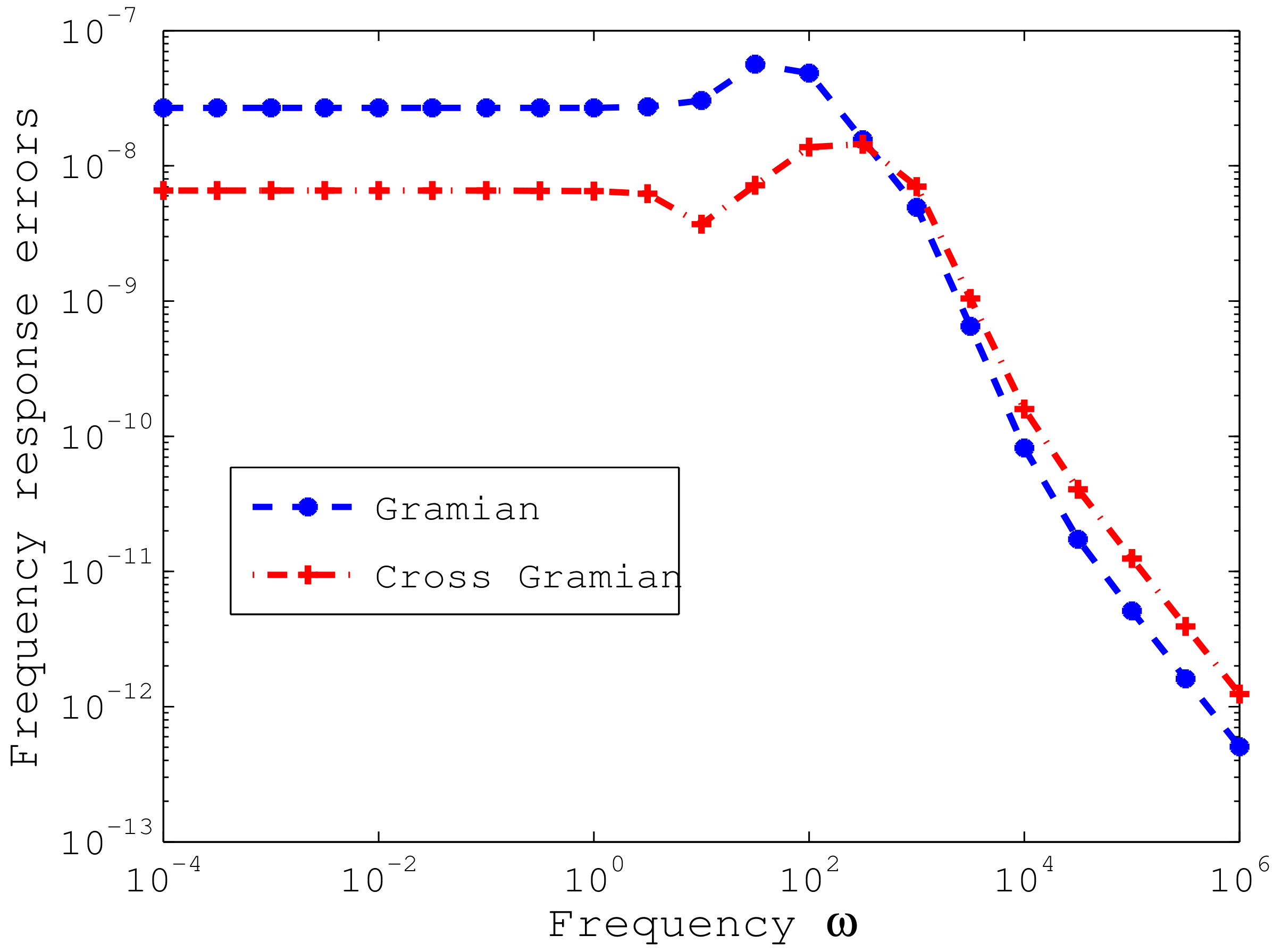
4. Numerical Experiments
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alfke, D.; Feng, L.; Lombardi, L.; Antonini, G.; Benner, P. Model order reduction for delay systems by iterative interpolation. Int. J. Numer. Methods Eng. 2020, 122, 684–706. [Google Scholar]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar]
- Lu, K.; Yu, H.; Chen, Y.; Cao, Q.; Hou, L. A modified nonlinear POD method for order reduction based on transient time series. Nonlinear Dyn. 2015, 79, 1195–1206. [Google Scholar]
- Lu, K. Statistical moment analysis of multi-degree of freedom dynamic system based on polynomial dimensional decomposition method. Nonlinear Dyn. 2018, 93, 2003–2018. [Google Scholar]
- Allen, J.J. Micro Electro Mechanical System Design; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Günther, M.; Feldmann, U. CAD-based electric-circuit modeling in industry. i. mathematical structure and index of network equations. Surv. Math. Ind. 1999, 8, 97–129. [Google Scholar]
- Dai, L. Singular Control Systems; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 1989; Volume 118. [Google Scholar]
- Moore, B.C. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Automat. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Liu, Y.; Anderson, B.D.O. Singular perturbation approximation of balanced systems. Int. J. Control 1989, 50, 1379–1405. [Google Scholar]
- Glover, K. All optimal Hankel-norm approximations of linear multivariable systems and their l∞-errors bounds. Int. J. Control 1984, 39, 1115–1193. [Google Scholar] [CrossRef]
- Benner, P.; Mehrmann, V.; Sorensen, D.C. (Eds.) Dimension Reduction of Large-Scale Systems; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2005; Volume 45. [Google Scholar]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Antoulas, A.C.; Sorensen, D.C.; Gugercin, S. A survey of model reduction methods for large-scale systems. Contemp. Math. 2001, 280, 193–219. [Google Scholar]
- Bai, Z. Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems. Appl. Numer. Math. 2002, 43, 9–44. [Google Scholar]
- Freund, R.W. Model reduction methods based on krylov susbspace. Acta Numer. 2003, 12, 267–319. [Google Scholar]
- Baur, U.; Benner, P. Cross-gramian based model reduction for data-sparse systems. Electr. Trans. Numer. Anal. 2008, 31, 256–270. [Google Scholar]
- Sorensen, D.C.; Antoulas, A.C. The sylvester equation and approximate balanced reduction. Linear Algebra Appl. 2002, 352, 671–700. [Google Scholar] [CrossRef]
- Stykel, T. Gramian-based model reduction for descriptor systems. Math. Control Signals Systems 2004, 16, 297–319. [Google Scholar] [CrossRef]
- Low-rank iterative methods for projected generalized Lyapunov equations. Elect. Trans. Numer. Anal. 2008, 30, 187–202.
- Varga, A. Efficient minimal realization procedure based on balancing. In Proceedings of the IMACS/IFAC Symposium on Modelling and Control of Technological Systems, Lille, France, 7–10 May 1991; Volume 2, pp. 42–47. [Google Scholar]
- Stykel, T. Analysis and Numerical Solution of Generalized Lyapunov Equations. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2002. [Google Scholar]
- Gantmacher, F. Theory of Matrices; Chelsea: New York, NY, USA, 1959. [Google Scholar]
- Cobb, D. Controllability, observability, and duality in singular systems. IEEE Trans. Automat. Control 1984, 29, 1076–1082. [Google Scholar]
- Yip, E.L.; Sincovec, R.F. Solvability, controllability and observability of continuous descriptor systems. IEEE Trans. Automat. Control 1981, 26, 702–707. [Google Scholar]
- Golub, G.H.; Loan, C.F.V. Matrix Computations, 3rd ed.; Johns Hoplins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Mehrmann, V.; Stykel, T. Balanced truncation model reduction for large-scale systems in descriptor form. In Dimension Reduction of Large-Scale Systems; Benner, P., Mehrmann, V., Sorensen, D., Eds.; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2005; Volume 45, pp. 83–115. [Google Scholar]
- Li, J.; White, J. Low rank solution of lyapunov equations. SIAM J. Matrix Anal. Appl. 2002, 24, 260–280. [Google Scholar]
- Penzl, T. A cyclic low-rank smith method for large sparse lyapunov equations. SIAM J. Sci. Comput. 2000, 21, 1401–1418. [Google Scholar]
- Fernando, K.; Nicholson, H. On the structure of balanced and other principal representations of SISO systems. IEEE Trans. Automat. Control 1983, 28, 228–231. [Google Scholar]
- Benner, P.; Li, R.; Truhar, N. On the ADI method for Sylvester equations. J. Comput. Appl. Math. 2009, 233, 1035–1045. [Google Scholar]
- Stykel, T. Balanced truncation model reduction for semidiscretized Stokes equation. Linear Algebra Appl. 2006, 415, 262–289. [Google Scholar]
- Lin, Y.; Bao, L. The projected generalized Sylvester equations: Numerical solution and applications. WSEAS Trans. Math. 2016, 15, 83–95. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y. Cross-Gramian-Based Model Reduction for Descriptor Systems. Symmetry 2022, 14, 2400. https://doi.org/10.3390/sym14112400
Lin Y. Cross-Gramian-Based Model Reduction for Descriptor Systems. Symmetry. 2022; 14(11):2400. https://doi.org/10.3390/sym14112400
Chicago/Turabian StyleLin, Yiqin. 2022. "Cross-Gramian-Based Model Reduction for Descriptor Systems" Symmetry 14, no. 11: 2400. https://doi.org/10.3390/sym14112400
APA StyleLin, Y. (2022). Cross-Gramian-Based Model Reduction for Descriptor Systems. Symmetry, 14(11), 2400. https://doi.org/10.3390/sym14112400







