Numerical Investigation of the Two-Dimensional Fredholm Integral Equations of the Second Kind by Bernstein Operators
Abstract
:1. Introduction
2. Bernstein Polynomial Approximation Method
2.1. Two-Dimensional Bernstein Polynomial Approximation Method
2.2. Discretization of the Integral Equations by Bernstein’s Approximation
| Algorithm 1: Numerical solution of the two dimensional Fredholm integral equation of the second kind by using Bernstein polynomial approximation , is obtained as follows: |
STEP 1. Put the m and n values. STEP 3. Use STEP 1 and STEP 2 by Equation (11) to find matrix A. STEP 4. Calculate , . STEP 5. Solve the system (10) and denote the numerical solution by . STEP 6. Substitute in Equation (5) and compute . STEP 7. Calculate the error function . |
3. Numerical Results
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaswon, M.; Symm, G.T. Integral Equation Methods in Potential Theory and Elastostatics; Academic Press: London, UK, 1977. [Google Scholar]
- Daddi-Moussa-Ider, A.; Kaoui, B.; Löwen, H. Axisymmetric flow due to a Stokeslet near a finite-sized elastic membrane. J. Phys. Soc. Jpn. 2019, 88, 054401. [Google Scholar] [CrossRef] [Green Version]
- Daddi-Moussa-Ider, A. Asymmetric Stokes flow induced by a transverse point force acting near a finite-sized elastic membrane. J. Phys. Soc. Jpn. 2020, 89, 124401. [Google Scholar] [CrossRef]
- Honerkamp, J.; Weese, J.J. Tikhonovs regularization method for ill-posed problems. Contin. Mech. Thermodyn. 1990, 2, 17–30. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Abdou, M.A. Boundary and Initial Value Problems and Integral Operator. Adv. Differ. Equ. Control Process. 2018, 19, 391–404. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, H.; Zheng, G. Mathematical analysis of Plasmon Resonances for Curved Nanorods. J. Math. Pures Appl. 2021, 153, 248–280. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, D.; Guo, Y. A Reference Ball Based Iterative Algorithm for Imaging Acoustic Obstacle from Phaseless Far-field Data. Inverse Probl. Imaging 2019, 13, 177C195. [Google Scholar] [CrossRef] [Green Version]
- Yin, W.; Yang, W.; Liu, H. A Neural Network Scheme for Recovering Scattering Obstacles with Limited Phaseless Far-field Data. J. Comput. Phys. 2020, 417, 109594. [Google Scholar] [CrossRef]
- Yilmaz, B.; Cetin, Y. Numerical Solutions of the Fredholm Integral Equations of The Second Type. New Trends Math. 2017, 5, 284–292. [Google Scholar] [CrossRef]
- Maleknejad, K.; Hashemizadeh, E.; Ezzati, R. A new Approach to the Numerical Solution of Volterra Integral Equations by using Bernstein’s Approximation. Commun. Nonlinear Sci. Numer. Simulat 2011, 16, 647–655. [Google Scholar] [CrossRef]
- Donatella, O.; Russo, M.G. Bivariate Generated Bernstein Operators and Their Application To Fredholm Integral Equations. Publications de l’Institude Mathématique Nouvelle Série Tome 2016, 100, 114–162. [Google Scholar]
- Mustafa, M.M.; Ghanim, I.N. Numerical Solution of Linear Volterra-Fredholm Integral Equations Using Lagrange Polynomials. Math. Theory Model. 2014, 4, 137–146. [Google Scholar]
- Liu, H.; Pan, J.H.Y. Numerical Solution of Two Dimensional Fredholm Integral Equations of the Second Kind by The Barycentric Lagrange Fuction. J. Appl. Math. Phys. 2017, 5, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Amiri, S.; Hajipour, M.; Baleanu, D. On Accurate Solution of The Fredholm Integral Equations of The Second Kind. Appl. Numer. Math. 2020, 150, 478–490. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, Z.; Huang, Y. Numerical Solutions for Fredholm Integral Equations of The Second Kind with Singular Kernel Using Spectral Collacation Method. Appl. Math. Comput. 2019, 349, 314–324. [Google Scholar]
- Buranay, S.C.; Ozarslan, M.A.; Falahhesar, S.S. Numerical Solution of The Fredholm and Volterra Integral Equations by Modified Bernstein-Kantorovich Operators. Mathematics 2021, 9, 1193. [Google Scholar] [CrossRef]
- Dahaghin, M.S.; Eskandari, S. Solving Two-dimensional Volterra-Fredholm Integral Equations of The Second Kind by Using Bernstein Polynomials. Appl.-Math.-J. Chin. Univ. 2017, 32, 68–78. [Google Scholar] [CrossRef]
- Shekarabi, F.H.; Maleknejad, K.; Ezzati, R. Application of Two-dimensional Bernstein Polynomials for Solving Mixed Volterra-Fredholm Integral Equations. Afr. Mat. 2015, 26, 1237–1251. [Google Scholar] [CrossRef]
- Usta, F.; Akyiğit, M.; Say, F.; Ansari, K.J. Bernstein Operator Method for Approximate Solution of Singularly perturbed Volterra Integral Equations. J. Math. Anal. Appl. 2022, 507, 125828. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşi, Ş.; Ansari, K.J. Application of Vieta-Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity. Symmetry 2021, 13, 2370. [Google Scholar] [CrossRef]
- Özger, F.; Ansari, K.J. Statistical Convergence of Bivariate Generalized Bernstein Operators via Four-Dimensional Infinite Matrices. Filomat 2022, 36, 507–525. [Google Scholar] [CrossRef]
- Okumuş, F.T.; Akyiğit, M.; Ansari, K.J.; Usta, F. On Approximation of Bernstein-Chlodowsky-Gadjiev Type Operators that Fix e−2x. Adv. Contin. Discret. Model. 2022, 2022. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ansari, K.J.; Özger, F.; Ödemiş Özger, Z. A Link Between Approximation Theory and Summability Methods via Four-Dimensional Infinite Matrices. Mathematics 2021, 9, 1985. [Google Scholar] [CrossRef]
- Babaaghaie, A.; Maleknejad, K. A new approach for numerical solution of two-dimensional nonlinear Fredholm integral equationa in the most general kind of kernel, based on Bernstein polynomials and its convergence analysis. J. Comput. Appl. Math. 2018, 344, 484–494. [Google Scholar] [CrossRef]
- Asgari, M.; Ezzati, R. Using operational Matrix of two dimensional Bernstein polynomials for solving two-dimensional equations of fractional order. Appl. Math. Comput. 2017, 307, 290–298. [Google Scholar] [CrossRef]
- Buranay, S.C.; Iyikal, O.C. High Order Iterative Methods for Matrix Inversion and Regularized Solution of Fredholm Integral Equation of First Kind with Noisy Data. Third International Conference on Computational Mathematics and Engineering Sciences (CMES2018). ITM Web Conf. 2018, 22, 01002. [Google Scholar] [CrossRef] [Green Version]
- Buranay, S.C.; Iyikal, O.C. Approximate Schur-Block ILU Preconditioners for Regularized Solution of Discrete Ill-Posed Problems. Math. Probl. Eng. 2019, 2019, 1912535. [Google Scholar] [CrossRef] [Green Version]
- Buranay, S.C.; Iyikal, O.C. A predictor-corrector iterative method for solving linear least squares problems and perturbation error analysis. J. Inequalities Appl. 2019, 2019, 203. [Google Scholar] [CrossRef] [Green Version]
- Buranay, S.C.; Iyikal, O.C. Incomplete Block-Matrix Factorization of M-matrices Using Two-step Iterative Method for Matrix Inversion and Preconditioning. Math. Methods Appl. Sci. 2020, 44, 7634–7650. [Google Scholar] [CrossRef]
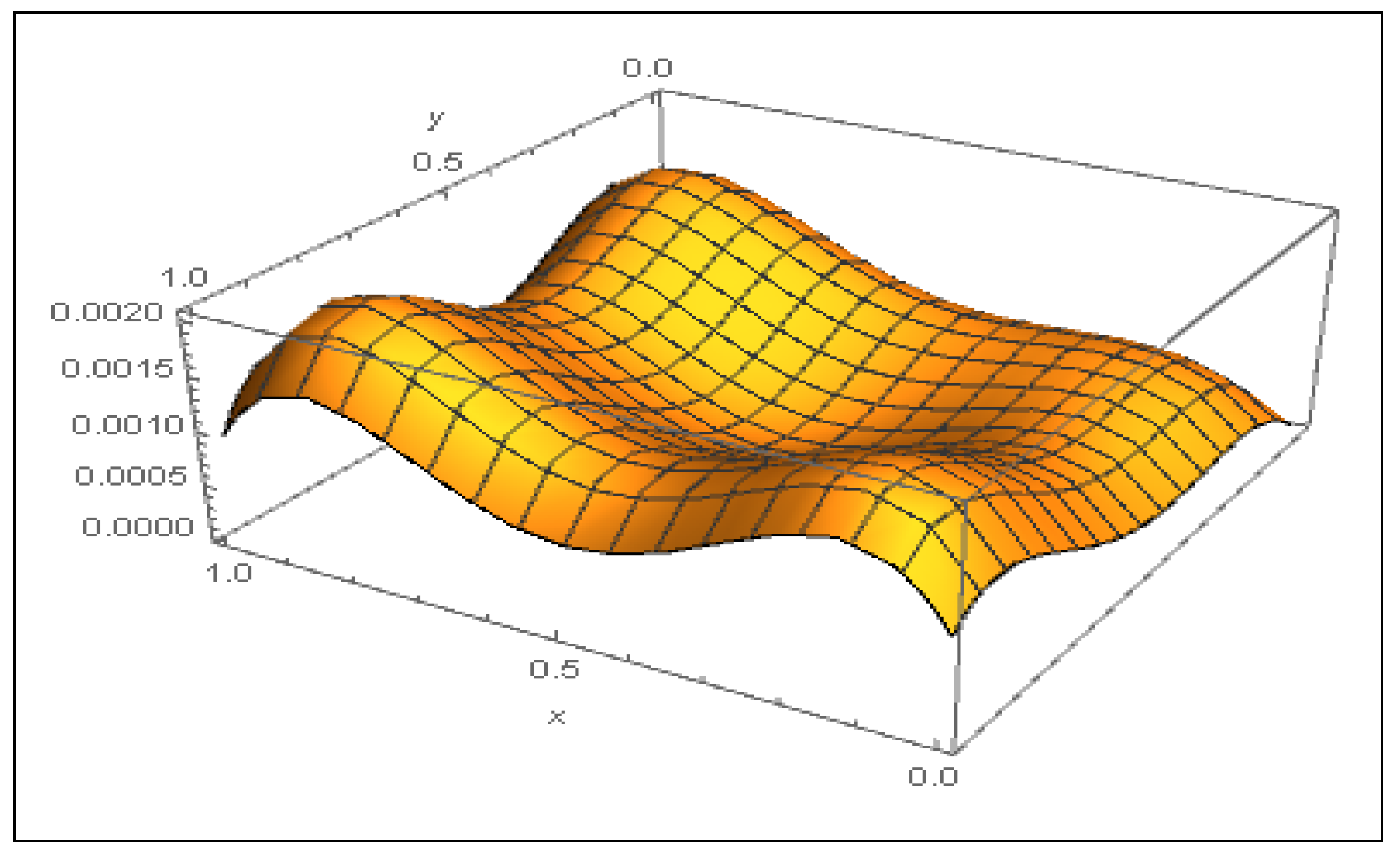
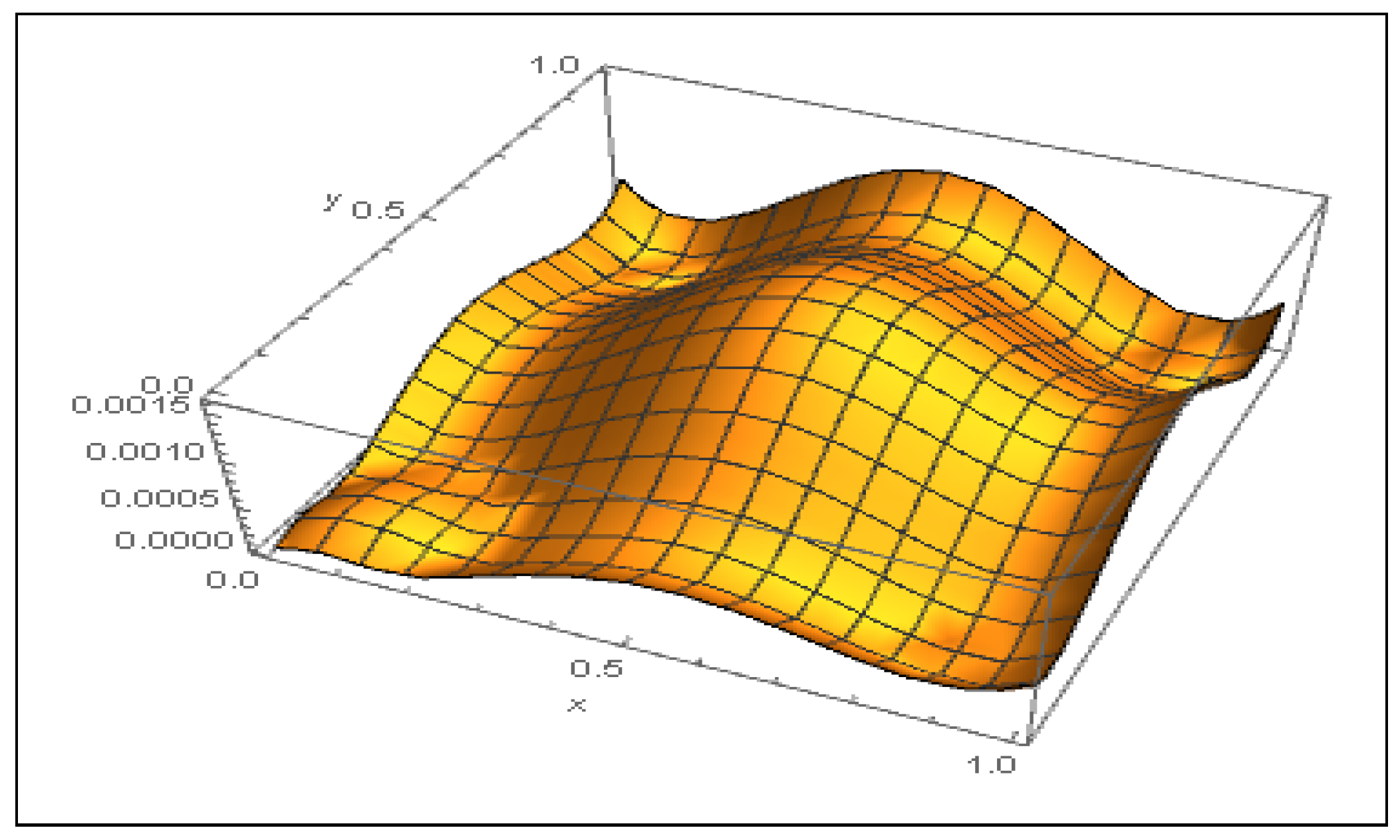
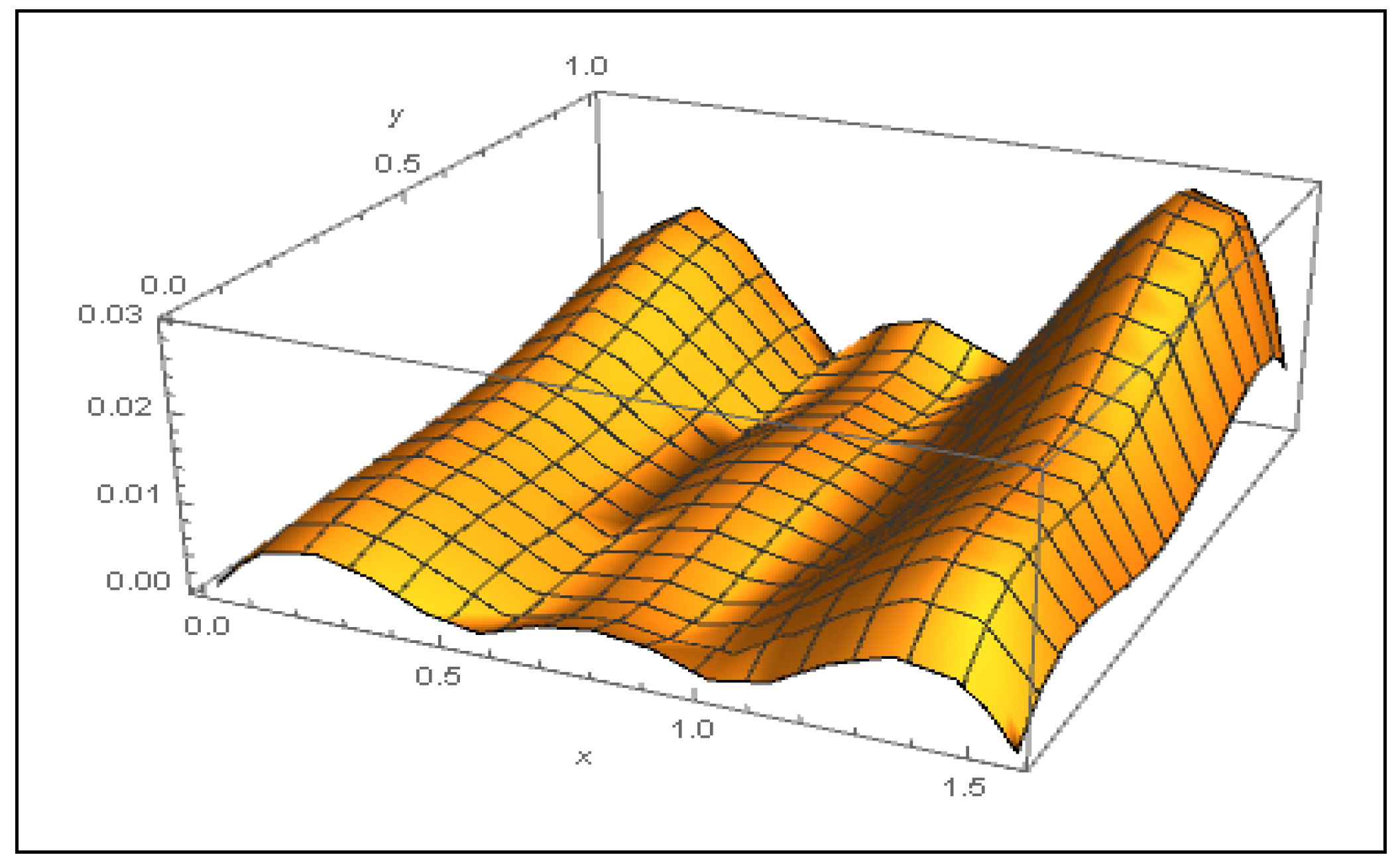
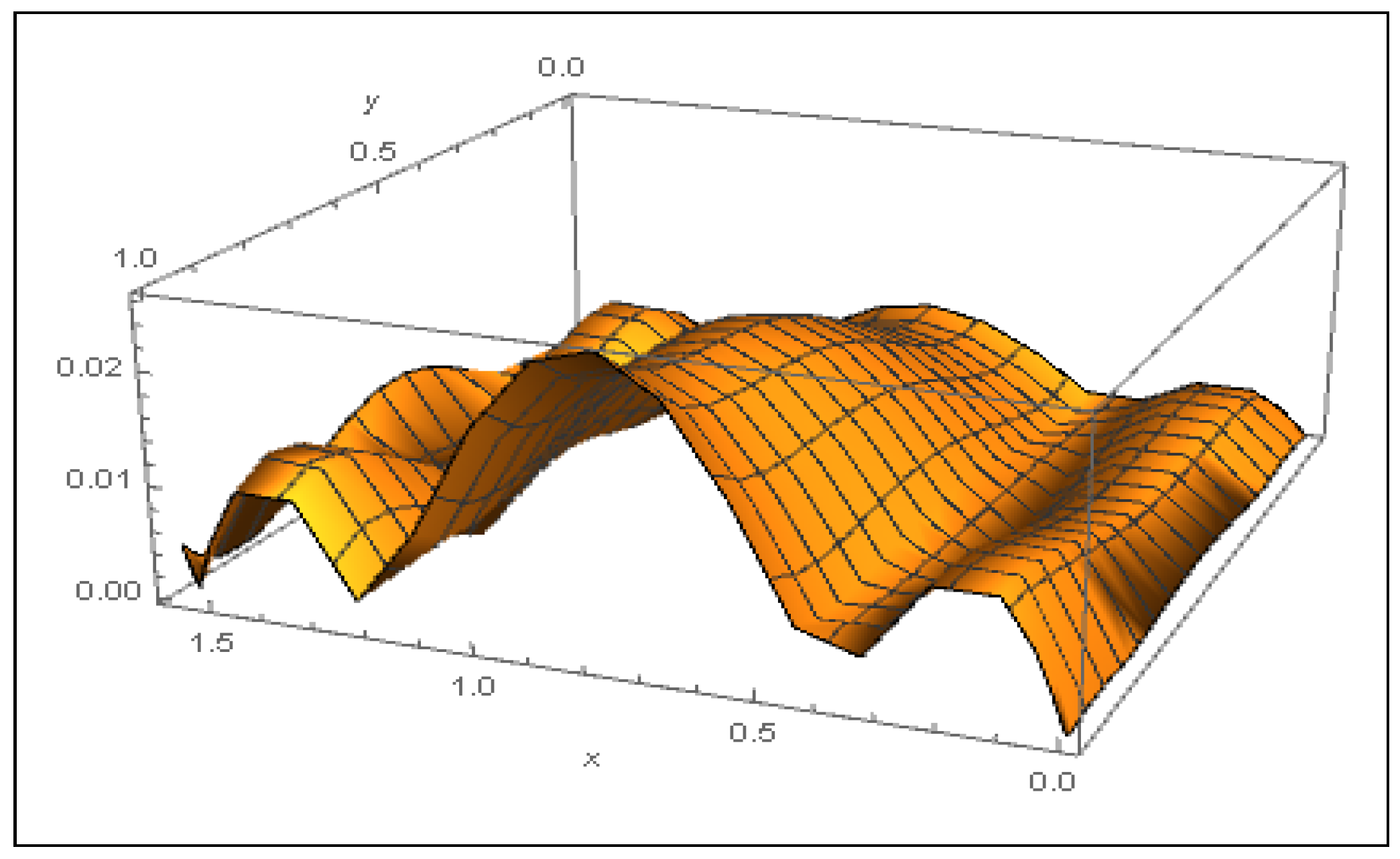
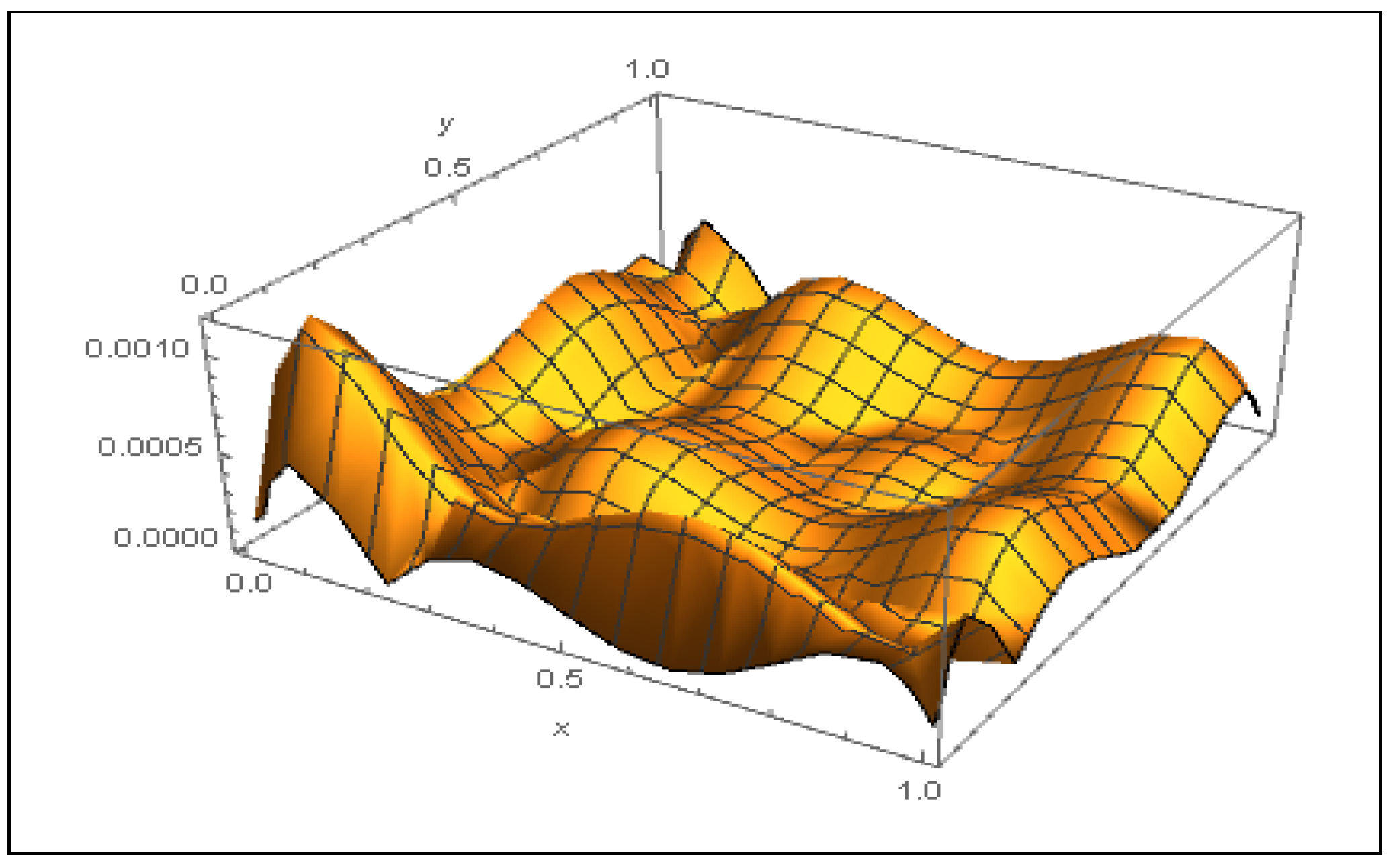
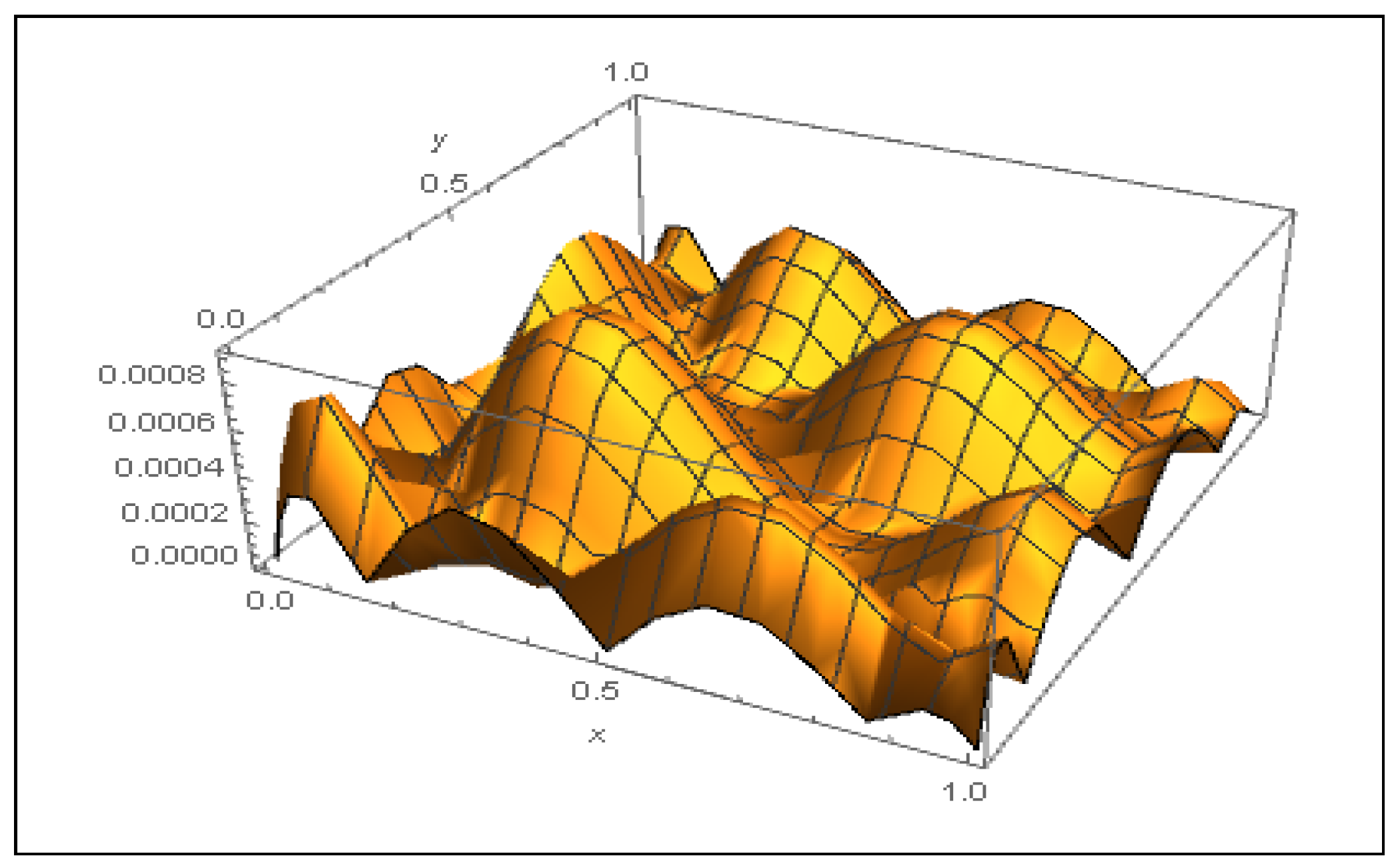
| RMSE | e | ||
|---|---|---|---|
| RMSE | e | ||
|---|---|---|---|
| 231,568 | |||
| RMSE | e | ||
|---|---|---|---|
| 370,059 | |||
| RMSE | e | ||
|---|---|---|---|
| RMSE | e | ||
|---|---|---|---|
| 405,765 | |||
| RMSE | e | ||
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iyikal, O.C. Numerical Investigation of the Two-Dimensional Fredholm Integral Equations of the Second Kind by Bernstein Operators. Symmetry 2022, 14, 625. https://doi.org/10.3390/sym14030625
Iyikal OC. Numerical Investigation of the Two-Dimensional Fredholm Integral Equations of the Second Kind by Bernstein Operators. Symmetry. 2022; 14(3):625. https://doi.org/10.3390/sym14030625
Chicago/Turabian StyleIyikal, Ovgu Cidar. 2022. "Numerical Investigation of the Two-Dimensional Fredholm Integral Equations of the Second Kind by Bernstein Operators" Symmetry 14, no. 3: 625. https://doi.org/10.3390/sym14030625
APA StyleIyikal, O. C. (2022). Numerical Investigation of the Two-Dimensional Fredholm Integral Equations of the Second Kind by Bernstein Operators. Symmetry, 14(3), 625. https://doi.org/10.3390/sym14030625






