Abstract
The energy efficiency of machines is nowadays an intensively studied problem. The efficiency of the induction motor is dominantly influenced by the rotor’s and stator winding’s temperature. The main goal of the research presented in this paper is to develop a methodology based on Computational Fluid Dynamics (CFD) analysis of internal and external aerodynamics, which is necessary for the optimisation of cooling of the induction motors. In this paper, the theoretical, as well as the numerical study of the internal and external aerodynamics of the induction motor, is described and verified by the experimental measurements. In the CFD-based numerical study, the Reynolds-averaged Navier–Stokes (RANS) turbulence modelling approach was applied to the flow field simulations inside and outside the induction motor. The complexity of the solved problem is increased not only by the geometric asymmetry but also by the flow’s asymmetric character caused by the fan’s rotation to cool the motor casing. This increases demand, especially on computational resources, as it is impossible to create a simplified numerical model incorporating symmetry. The volume flow of the cooling air and velocity between ribs was measured for the experimental study. Comparing the results of the Computational Fluid Dynamics (CFD) simulations and data obtained from the experimental measurement, we concluded that the results of CFD simulations are in good relationship with the results of experimental measurement and analytical approximations. An experimentally validated CFD model of the induction motor, the so-called digital twin, will be in the future used for virtual optimisation of the new designs concerning minimising losses and maximising efficiency, respectively.
1. Introduction
The latest technological progress in computing has significantly changed the concept of new product design, production control, or autonomous systems. In the last few years, we have witnessed many transitions to virtual prototyping and gradual pressure on integrating a large part of the industrial sector in the fourth industrial revolution, or Industry 4.0. In collaboration with Siemens, s.r.o. Works Elektromotory Frenstat has developed a complex methodology for creating a full virtual prototype of an induction motor for future use of this prototype as a part of a digital twin of an electric motor. An essential part of the design of rotating equipment, such as induction motors, is the determination of the magnitude of individual losses, such as electromagnetic losses, mechanical losses, etc.
2. Problem Statement
One of the critical parameters of electrical machines, such as induction motors, is the temperature of the rotor and stator. This is because the efficiency of induction motors is directly proportional to the temperature of the rotor and stator winding, which is caused by the electric resistivity of the material. For this reason, the total efficiency of the induction motor is dominantly influenced by effective cooling. Thus, the flow field surrounding the induction motor plays a dominant role in the cooling process. Precise analysis of the flow field is the first step to performing thermal analysis because the problem of effective cooling has become a dominant role in the design of electric machines [1]. The durability and reliability of modern machines are rather limited by the winding temperature rather than the acting of magnetic and electric loading. Aerodynamics and thermal analysis of electric machines has been underdeveloped compared to electromagnetic calculation till nowadays. Heat transfer is realised in two ways (1) natural convection and (2) forced convection. Both types of convection play a role during induction motor cooling, but forced convection is usually dominant and wanted. Forced convection is mostly generated by the fan installed on the shaft. The shaft is the momentum source that causes turbulent flow between the fins of the frame and other parts of the induction motor.
The turbulent flow between the fins of the induction motor frame, or, in other words, external aerodynamics, has been investigated by many authors, e.g., [2]. Still, the problem of flow induced by a fan of an induction motor is too complicated to use simplified equations of fluid mechanics. Some empirical formulas can be used to describe the velocity profile between fins; however, the validity of formulas is usually limited by many parameters, such as the design of the frame, nominal speed, etc. Therefore, generally valid empirical formulae describing external aerodynamics for every type of electric machine have not been discovered yet.
Internal aerodynamics is difficult to describe by empirical formulas due to the complexity of the flow field and the complicated shape of the internal cavities of the induction motor. So experimental studies which deal with complex 3D internal aerodynamics of electric machines do not exist, and the simplified empirical solution of the internal flow has not been developed yet, except for flow in the rotor-stator air gap. The air gap may be analysed as a concentric cylinder gap with a stationary external cylinder and rotating internal cylinder, and this flow is known as Taylor–Couette flow [3]. The flow regime and other parameters necessary for heat transfer can be estimated based on dimensionless numbers, namely Taylor and Reynolds numbers.
As mentioned above, the aerodynamics analysis of the induction motor is problematic; experimental measurement of the flow field is difficult, and for internal flow, almost impossible. The experimental measurement process is usually focused on determining mechanical loss, winding loss, and other losses. The experimental measurement is very important for evaluating and determining nominal motor parameters. So measurement plays an irreplaceable role in the manufacturing and design process, but there is an effort to minimise it due to time and cost consumption. Two ball bearings usually cause mechanical friction loss. This loss is important because it can be described as an additional heat source in a numeric model like Finite Element Modelling (FEM) or CFD. The measured winding loss is one of the important results which can be directly compared with the results of numerical simulation. The other losses, such as corrected rotor and stator winding loss, iron loss, and additional-load loss, were also measured, but they are unimportant for determining aerodynamic loss [4,5]. Generally speaking, the induction motor optimises significantly depending on a detailed flow field analysis. A CFD induction motor model has been established to analyse external and internal flow fields to implement virtual optimisation. This procedure is usually called the creation of a digital twin.
2.1. Model Description
In this paper, the induction motor with nominal power of 315 kW, operating rotational speed of 2987 rpm, and weight of approximately 1400 kg was investigated. The 3D geometric model was provided by Siemens, s.r.o. Works Elektromotory Frenstat. The original 3D model is shown in Figure 1. The CAD model contained up to 150 parts, excluding electrical windings, and slot liners. The motor’s main parts are cast iron, e.g., frame, end shields, terminal box, etc. Terminal box (D) consists of three parts connected by bolts, and it includes a terminal plate. The stator core (K) was connected to the motor frame (C) by an overlap fit. It is made up of hundreds of steel sheets. Technological processes formed a regular air gap pattern around the stator assembly perimeter. In total, 48 electrical winding packs (L) are embedded in the stator core, and they are separated from each other by slot liners. The rotor part consisted of the rotor core (M), shaft (Q), and aluminium rotor cage (N). The rotor core was made up of hundreds of steel sheets too. The rotor cage is cast, including straight blades. The two ball bearings (O) are mounted in the non-drive end-shield (G) and drive end-shield (B), and they are lubricated by grease. Both bearings are sealed with a bearing cover (P) and shaft sealing ring (R). Both shields are designed with internal and external cooling fins for better bearing heat transfer. Compared to the motor diameter, a small fan wheel (I) was designed to minimise noise levels and reduce mechanical loss. To do the bi-directional operation, it is designed with straight blades. It is covered by a fan cowl (J). The individual parts are marked in Figure 2.
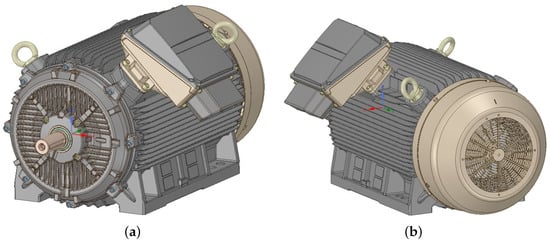
Figure 1.
A 3D model of the electric motor. (a) Front view; (b) Rear view.
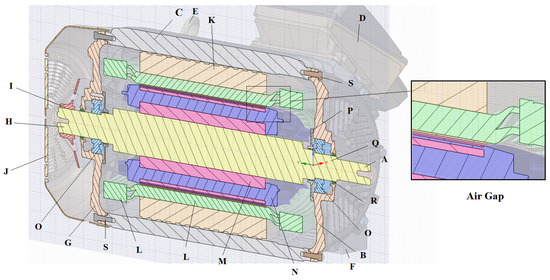
Figure 2.
Individual parts view inside of the motor under investigation.
The real geometry of the motor is too complicated to create a computational grid, so small gaps, holes, faces, etc., were modified. Modifications of geometry were generally insignificant with respect to its complexity. The bolt heads (S) were capped. The washers were united with bolts. The circlips were united with the shaft (Q). The electrical winding (L) was split into two parts. The first embedded part contained a parallel arrangement of individual wires. The second torus part contained a circular arrangement of individual wires. In both cases, individual wires were replaced by a solid domain. Slot liners consisting of polyethylene terephthalate (PET) film were neglected. The air gaps between the stator assembly (K) and the finned frame (C) were neglected. The air gap between the stator assembly (K) and rotor assembly (M) is relatively large, so it was included in a simulation. The individual parts were moulded together to achieve the correct contact interface. For this reason, access to the interior of the motor body was only possible through one small air hole drilled in the rear end shield. Assuming that it is neglected, it is possible to solve the internal/external airflow velocity independently of each other and, thus, also significantly reduce the time-consuming task.
3. Theoretical Background
3.1. External Air-Flow Velocity Profiles
A crucial parameter for the future adequate Finite Element Method (FEM) model for optimisation is the correct determination of the heat transfer coefficient (HTC) on the external surfaces of the induction motor. Analytic formulae exist for determining HTC, but some empirical constants are necessary to specify. The empirical constants can be evaluated by applying the computed fluid dynamics (CFD) model to external aerodynamics. If the HTC is specified correctly, then the FEM model can be used for the optimisation of the motor, e.g., material modification, without the time and money more consuming CFD model.
As was mentioned above, without the CFD approach, it is not easy to predict the airflow velocity profile around the motor fins. There are plenty of papers dealing with the thermal distribution in a specific motor, but fewer for those that generally deal with the airflow around the fins of the motor [6]. A lot of measurements are always needed for the determination of empirical formulas. In an electric motor, many fin channels outside the body are obstructed by terminal boxes, bolt lugs, and cables. Another deficiency of electric motors is the airflow leaks out of the open channels. Then the local air velocity is lower at the drive end shield without a fan cowl. The typical reduction of the velocity profile is shown in Figure 3.
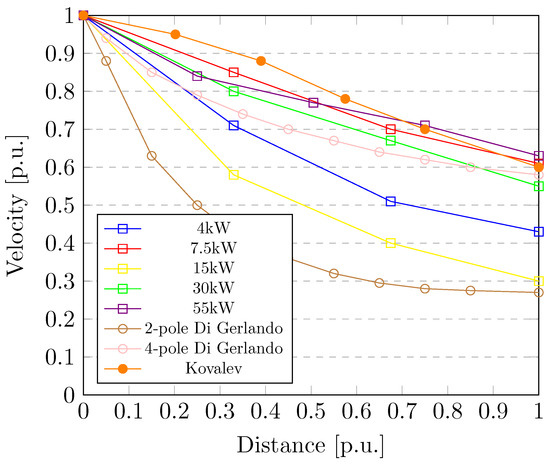
Figure 3.
Fin channel velocity reduction with distance from fan cowl.
One of the papers that deals with an empirical expression of the airflow velocity profile for the electric motor surface is Klimenta [2]. His equation is expressed in the form of a polynomial of fourth degree (1).
where the constant [−] is unknown dimensionless coefficients depends only on the airflow conditions, it defines the rate of deceleration of the air depending on the size and number of obstacles downstream of the fan cowl. For example, for = 1 in the calculation, the effect of the aerodynamic resistance is negligible, and vice versa for = 2/3 in the calculation, the effect of the aerodynamic resistance is significant. [m/s] is the initial velocity at the fan outlet. [m] is the average fin length, and y [m] is the longitudinal distance from the fan cowl. The length of fins/frame L5 is shown in Figure 4, where the parts of a standard induction motor are also presented. All exterior parts of the induction motor were described in Section 2.1.
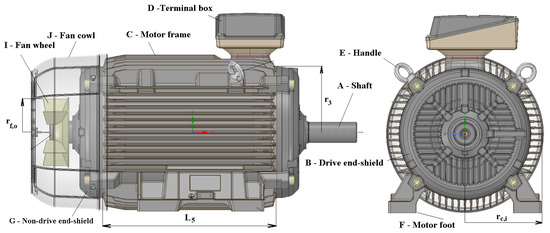
Figure 4.
Schematic motor.
is an unknown dimensionless coefficient. It is assumed that it depends on the ratio between the initial velocity at the fan outlet [m/s] and the peripheral velocity of the fan wheel [m/s]. is defined by theory-based and empirically established dependence (2).
where [m] height from the base to the centre of the shaft, p [−] number of poles, [rpm] rotational speed of the rotor, [−] constant depending on the number of poles and motor power rate P [W]. = 3 for p ≤ 4 and P ≤ 15 kW, = 2 for p ≤ 4 and P > 15 kW, and = 8/3 for p > 4 and P∀. [m · rpm] is experimentally determined constant.
According to [7,8,9,10], the ratio equations for steady, fully developed, laminar, and turbulent flows of a Newtonian fluid through the gap between the non-drive end-shield and the fan cowl can be written in the form (3) and (4).
where [m] is the maximum radius of the end shield, [m] is the minimum radius of the fan cowl and n [−] is the dimensionless constant given by (5). The values of the ratio are estimated by means of the one-seventh-power equation and the definition of the peripheral velocity of the fan wheel (6). The one-seventh-power equation is used to avoid the calculation of the exponent n and the Reynolds number in the cases of the absence of adequate geometric and heat transfer data.
where [m/s], [m] is the fan radius and [rpm]. The Reynolds number is expressed by (7), and the flow velocity versus flow type by (8) and (9).
Empirical Equation (4) is Nikuradse’s equation for turbulent velocity profile in a circular rough pipe. According to the theory [11,12], the flow in a circular pipe is laminar if the Reynolds number is less than 2320, and the resistance factor is the same for rough as for smooth pipes. Turbulent flow is greater than 4000, and the resistance factor is independent of the Reynolds number (quadratic law of resistance). The transitional zone is between laminar and turbulent flow regimes increasing the resistance factor. The thickness of the laminar layer is here of the same order of magnitude as that of the projections. It is also assumed that Equation (4) can be a good approximation to the transition velocity profile. In our case, it is acceptable because the fan wheel and its cowl create high turbulences before the passage of the cooling fins [13,14,15,16,17].
As was mentioned above, the velocity along the rib is defined by relation (1), which contains three empirical constants , , and . The effect of constants on velocity along the rib was estimated as a first. Four combinations of constants , , and were tested. The result of test calculations of the airflow velocity profile is shown in the graph, Figure 5. The black curve describes the airflow velocity profile as a function of the distance using the constants , , and according to the recommendation by Klimenta [2] for our investigated motor. To better clarify how constants affect the shape of the airflow velocity profile, these individual constants were tested. The blue curve describes the same situation as the red, but the constants and were changed. The solid red curve is similar to blue except that constant was modified only. The red dashed curve was changed by constant , and the remaining are the same as in the case of the red curve.
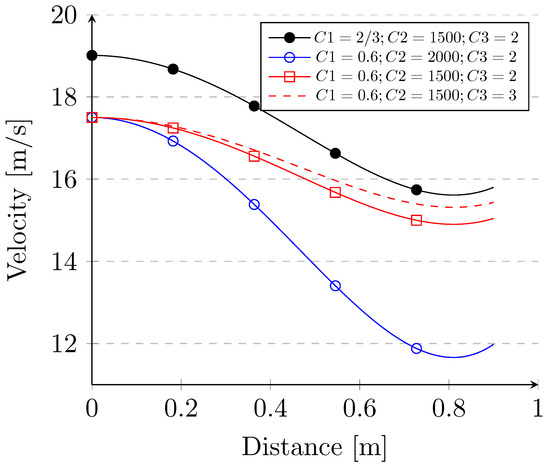
Figure 5.
Air-flow velocity profile.
It can be seen that the most problematic constant is , which determines the slope of the curve. Unfortunately, this can only be determined by experiment or by estimating it from another geometrically similar motor. Klimenta [2] formulated the expression for determining the airflow velocity profile, which is valid for small motors up to approximately 15 kW. Based on his comparisons, it was found that: (1) the coefficient amounts to 1500 [m·rpm], and (2) that the values of the coefficient are: = 3 for p ≤ 4 and P ≤ 15 kW, = 2 for p ≤ 4 and P > 15 kW and = 8/3 for p > 4 and P∀. This was in satisfactory agreement with most of the experimental data. The quantity P = 15 kW, which corresponds to the change in the value of the factor, also coincides with the fact that induction motors rated up to 15 kW usually have an aluminium frame. In comparison, motors rated above 15 kW have a frame made of cast iron [18]. The results show that the empirical formula is very flexible. The velocity profile along the fin can be fitted by an appropriate combination of , , and . Generally, all three constants can be determined by employing CFD and/or experimental measurement. Both methods are introduced in the following sections.
3.2. Internal Air-Flow
The exact determination of the drag moment due to air friction in the rotor-stator air gap and on the rotor blades is crucial for specifying the internal mechanical losses. It is generally known that if the air gap decreases, the friction moment increases, and the heat transfer between the stator and rotor decreases and vice versa. This phenomenon was investigated by Taylor [19,20], who derived relations for the so-called Taylor vortex development. On the basis of the Taylor number, it can be calculated the Nusselt number, which is necessary for the specification of the heat transfer coefficient (10). The Equation (11) expresses the dimensionless Taylor number as a function of the Reynolds number (12).
where [W/mK] is a heat transfer coefficient, [W/mK] is a thermal conductivity of an air, [m] is an air gap radial thickness, [m] is radius of a rotor, [1/s] is angular velocity of a rotor, [m/s] is a kinetic viscosity of air.
Three possible flow regimes in the concentric fluid gap have been identified by Taylor. If < 41, the flow regime is laminar, and heat transfer is only due to the thermal conduction of air. If 41 < < 100, there is a transitional flow region with enhanced heat transfer in the vortex form. And if > 100, the flow regime is turbulent and turbulent heat transfer dominates.
A more complex determination of convective cooling concerns the air space between the end shields and the rotor. Convection for all surfaces must be modelled, e.g., end-windings, rotor cooling blades, etc. Convection cooling depends on many factors, e.g., the shape of the end winding, added fanning effects due to wafters, and the shape of the end shield. Several authors have studied such cooling [18,21,22,23]. The formula for general use was defined in the form (13).
where v [m/s] is the speed of air around end-windings, characterizes natural convection, and characterize forced convection and [W/mK] is the average convective heat transfer coefficient. The value of individual coefficients, according to the authors, is given in Table 1.

Table 1.
Correlation coefficients of the convective cooling around end-winding.
Figure 6 shows randomly selected predictions of according to the authors. It can be seen that the heat transfer coefficient increases with the increasing velocity of the air, and all curves have the same slope.
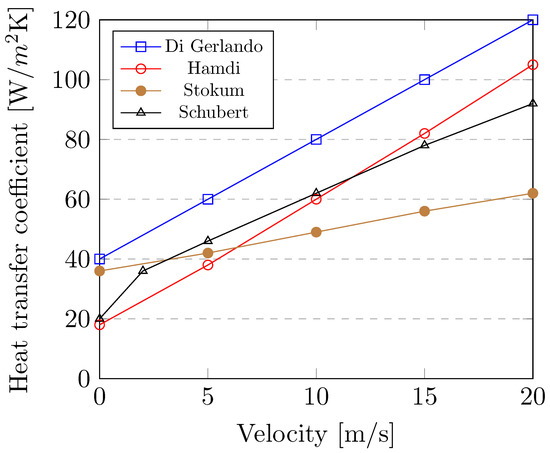
Figure 6.
Correlation coefficients of the convective cooling around end-winding.
However, because of the complicated geometry of the end shields and complex wire end-winding, Equation (13) is inadequate for a whole simulated air domain. The effective thermal conductivity approach can be applied here. In this case, the internal air domain was divided into several sections so that the temperature distribution corresponds to the simulated flow with the inclusion of the energy equation. This approach is explained in Section 7.
4. Experimental Measurements
Measurements of the motor under investigation were performed in a Siemens laboratory chamber equipped and tempered according to standards. Measuring and calculation of efficiency were in accordance with IEC/EN 60034-2-1:ED.2-14. Basic test conditions were: (1) the ambient temperature was 20.2 °C. (2) The load test condition was set to 100%, corresponding to 315 kW of motor power. (3) The rotational speed was 2987 [1/min]. (4) The motor’s operating temperature was reached. (5) The motor was mounted to the ground with four bolts.
Total mechanical losses (mechanical friction and windage) were 1870 W, including the external fan wheel and 1044 W without it. It means that the aerodynamic loss caused by the external fan is 826 W. Frictional losses of 360 W were estimated by the SKF calculator. SKF calculator included 8452 N radial force and 0 N axial force for drive end-shield ball bearing; 1007 N radial force and −1117 N axial force for non-drive end-shield ball bearing. It also included parameters, such as rotational speed (2987 [1/min]), the temperature of inner (70 °C) and outer (60 °C) rings, and the type of lubrication (grease). From the values obtained above, a simple calculation (14) will determine the internal losses are 684 W. Determining the internal losses in the same way as in the case of an external fan is impossible because the frame and end shields would have to be modified, and the probes inside the motor would influence the measured flow field. So measurement inside the motor is theoretically possible, but it cannot be performed practically. So numerical modelling is the real possible way to study the internal flow field.
In the second phase, the air velocity profile was measured at individual planes A, B, C, and D. Plane A is 100 mm downstream of the fan cowl, while the other planes are 210 mm from each other, Figure 7a. The representation of the individual measuring points is shown in Figure 7. For example, plane A contains a total of 40 measurement points. In total, 13 points were on the left side (L1–L13), 13 points were on the right side (R1–R13), and 14 points were on the top side (T1–T14). The air velocity was not measured at the bottom side due to insufficient space for the Prandtl tube. An illustrative location of the Prandtl tube between the fins is shown in Figure 8a.
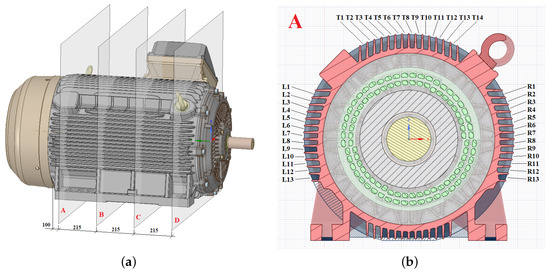
Figure 7.
Sketch of the experimental setup. (a) Measured planes A, B, C, D; (b) Marked an area at plane A of the motor.
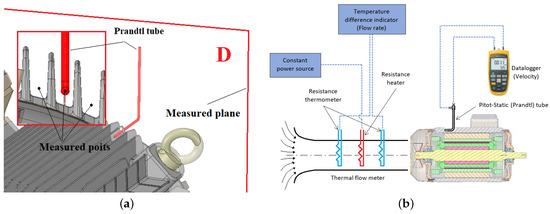
Figure 8.
Sketch of the experimental setup. (a) An illustrative location of the Prandtl tube; (b) Measurement of cooling air volume flow rate.
A Fluke 922 air-flow meter was used to measure air velocity between fins. It is a handheld instrument that measures differential pressure and calculates air velocity and airflow. Its specifications are shown in Table 2.

Table 2.
Specification of the Fluke 922.
The measuring tube was placed perpendicular to the wall of the motor body so that it was not in contact with any wall. However, obstructing lugs deflected the measuring tube at some points. The measured values oscillated in the interval m/s.
The airflow rate through a fan cowl was 37.4 [m/min]. The scheme of the measurement is shown in Figure 8b.
Type A and Type B uncertainty were evaluated for every measured variable based on methodology processed by Siemens laboratory. So the experimental measurement was checked and verified by a responsible person according to the experimental methodology by Siemens.
The results of the measurements are summarised and compared with CFD in Section 6.
5. Numerical Methods and Governing Equation
Experimental measurement is very important, but numerical simulation can quickly give more information about the studied problem, especially if the HPC is available. Numerical simulation is a very effective method to study phenomena, such as the flow of fluid, heat transfer, etc., nowadays. So in the numerical simulation, a RANS turbulence model was used to establish the induction motor model. The simulation includes two domains, which are the solid domains, e.g., stator, rotor, housing, and the fluid domains represented by external fluid, internal fluid, and air gap. Reynolds number outside and inside motor is generally greater than 2300, so the turbulence model is also required to describe the fluid flow. According to the CFD theory, the two-equation eddy-viscosity turbulence model SST k- is a good choice. This model combines k- approach near the wall and k- approach in a free stream. The main governing equations of the mathematical model presented in this paper can be found in books with CFD theory, e.g., [1,24,25,26]. Nevertheless, the fundamental equations are listed below, with brief information on the physical quantity calculated when solving a particular equation.
Reynolds’s form of continuity equation solves pressure only in fluids
Reynolds form of Navier-Stokes equation solves velocity vector only in fluids
where: effective viscosity is defined as .
Turbulent and effective viscosity is calculated to close a set of fundamental equations and is defined based on Reynolds averaged theory.
The model predicts turbulence by two partial differential equations for two variables, k, end , respectively. The first variable is the turbulence kinetic energy (k), the second () is the vorticity, and the third () is the specific rate of dissipation.
or
The following equation solves the total energy of the fluid. The total energy of the fluid is defined as
5.1. General Setup Description of Numerical Model
The complexity of internal end external fluid flow leads to a very large computational grid, especially if precise results of the simulation are expected. Using the HPC infrastructure available at IT4Innovations, CFD simulations can be performed for the complete induction motor without significant shape simplifications. According to the presented approach, experimental measurements can be partially replaced by a virtual numerical model. It allows acceleration of the process of fan section design, as well as an estimate of the impact of each modification on the parameters of the induction motor without the production of the physical prototype. Computational grid, CFD simulation, post-processing, and flow field visualisation were achieved by commercial software Ansys Meshing and Ansys CFX.
The total number of elements was 130 million for external analysis and 73 million for internal analysis. The final meshes (130 million and 70 million) were used after the independent test. The rough, medium, and fine mesh was created. The numerical simulation was performed at the same conditions for three meshes. Differences between medium and fine mesh were significantly less than between coarse and medium mesh. Thus the fine mesh was assessed as suitable for simulations. Figure 9 shows velocity results for the motor’s three types of meshes at plane A.
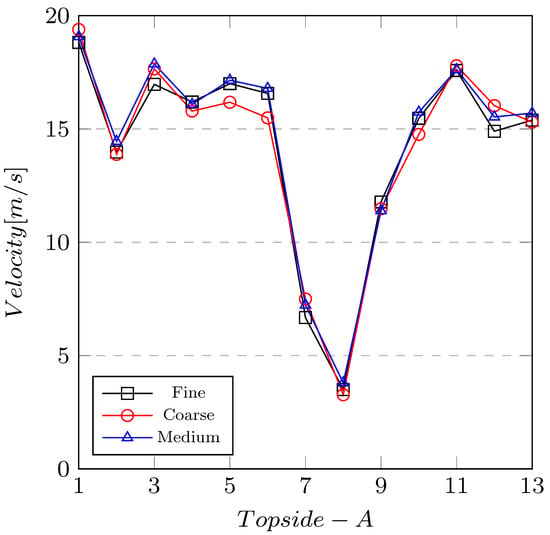
Figure 9.
Comparison of results at plane A on the top side of the motor.
The same procedure was used to create a mesh for the internal domains. The boundary layer contained 10–15 elements at 2–2.5 mm thickness for all fluid domains except the air gap between the rotor and stator. There are 25 elements in the radial direction of the air gap, and a mapped mesh was created. Figure 10 shows the fins and air gap cross-section of the computational mesh.
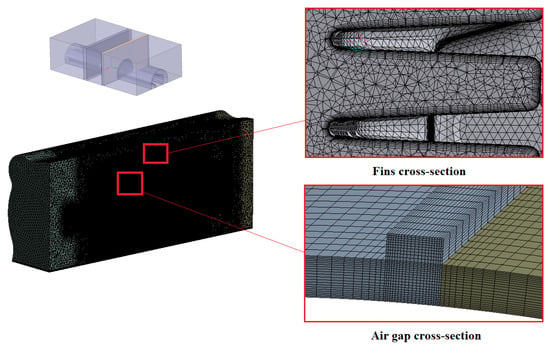
Figure 10.
A general view of the final computational grid.
The following pre-processing settings were chosen for both analyses, Table 3.

Table 3.
Pre-processing settings.
The transient time step was chosen based on the stability of the computations to achieve convergence criteria. Formula (23) was used to calculate the initial time step.
where [s] is the calculated estimated transient time step, [rad] is the estimated rotation in a one-time step, and [1/s] is the angular velocity of a rotor.
The following solver settings were chosen for both analyses, Table 4.

Table 4.
Solver settings.
5.2. Description, Setup, and Results of the External Domains
The numerical model contained one stationary and two rotating domains. The stationary domain consisted of multiple regions interconnected by a conformal mesh. The elements became smaller towards the motor, and the mesh grow ratio was 1.2. The dimensions of the stationary domain were modelled at a sufficient distance from the motor body: (1) 3 m in axial distance from the fan cowl and 4 m from the end of the drive shaft extension, (2) 2.5 m from the highest point of the motor body including the terminal box, (3) 3 m on each side of the motor mounting feet, and (4) the side of the motor mounting feet was collinear with a floor. The first rotating domain was created around the drive shaft extension, and the second one around the fan wheel, Figure 11. The external domain in the figure is simplified for better visualisation.
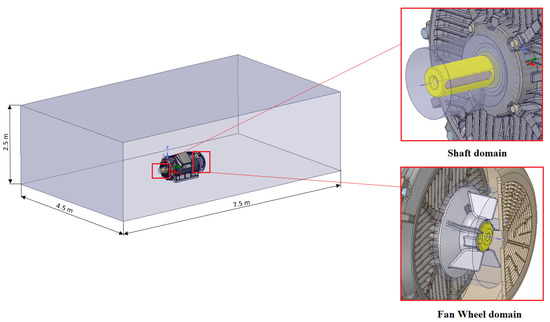
Figure 11.
Motor enclosing domains.
The open pressure boundary condition Opening Pressure and Direction = 0 Pa was applied at the outer walls of the stationary domain except for the bottom side. There was applied No Slip Wall condition. The Flow Direction was set to Normal to Boundary Condition. An assumption of an incompressible flow with constant air values at 20 °C was set.
Both steady-state and transient analyses were performed with the same boundary and initial conditions. The time step t = 0.0002 s of the transient analysis was calculated according to Formula (23).
External analysis was launched on 432 cores. The total computational time was 146 h (approx. six days). The steady-state model was used to solve the first initial simulation, which took 15 h. This simulation was used as initial conditions for transient simulation. The initialisation of transient simulation by steady solution saved the total time of the simulation because a steady-state simulation substituted the motor’s start-up. The transient simulation was not complete until the stable periodic flow was achieved, and it took 131 h.
The computational grid included four planes according to the arrangement of experimental measurement. Planes were perpendicular to the rotational axis and represented frame cross-section, Figure 12. The planes allowed calculating the average airflow velocity in the space between fins, and area-weighted average expression (areaAve) was used. For the steady-state simulation, the airflow velocity is calculated as the average of the last 200 iterations after reaching the steady-state. The airflow velocity was calculated for the transient simulation as the average of the last 15 fan revolutions after reaching the steady periodic flow.
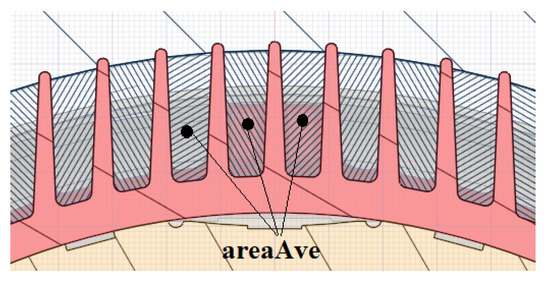
Figure 12.
AreaAve cross-section detail.
The velocity field results are shown in Figure 13. Isosurfaces show air runaround motor frame velocity at 5 m/s, 10 m/s, 20 m/s, and 30 m/s. It is obvious that due to the fan wheel’s rotation, the motor fins are periodically cooled by air. This is done so that air is partially moved from one fin to the other. The mounting lugs of the end shield are the barrier to flowing air, and insufficient cooling was identified between a few fins.
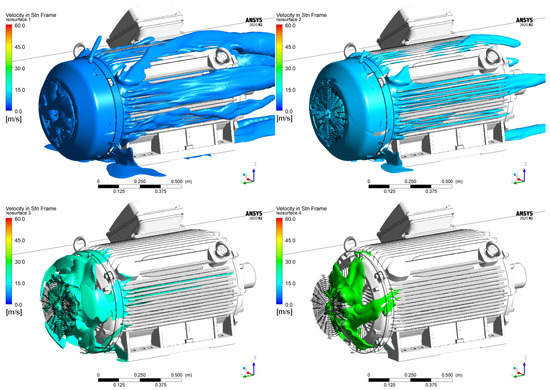
Figure 13.
Isosurfaces of the air velocity.
The airflow rate through a fan cowl was calculated at 37.4 [m/min]. It is also appropriate to mention the aerodynamic loss (23) and fan wheel efficiency (24).
where [kg/s] is an air mass flow, [Pa] is the total pressure at the fan cowl outlet, [Pa] is the total pressure at the fan cowl inlet and [kg/m] is the air density at 20 °C, [W] is mechanical loss of the fan wheel. For our investigated motor the = 150 W and = 16%.
5.3. Description, Setup, and Results of the Internal Domains
As mentioned above, theoretical analysis of flow inside the motor is practically unfeasible except for the air gap. The flow inside the motor is too complicated due to the geometry’s complexity and the high turbulence intensity. This analysis included five stationary domains (Main domains; Side Domain 1, 2; Air Gap) and three rotating domains (Bearing 1, 2; Rotating Domain), Figure 14. The air gap domain was static, but the rotating wall condition was set to the side of the rotor surface. A transient analysis was performed for two variants: (1) an incompressible airflow assumption and (2) a compressible airflow assumption. Both variants were simulated with constant air values at 60 °C. The inside air temperature was determined based on a motor and experimental measurement test. The grease inside the ball bearings was neglected. The time step of the transient analysis was set according to Formula (23), and it was slightly increased to t = 5 s.
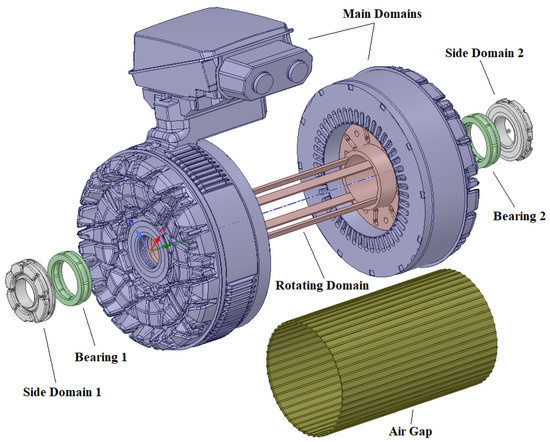
Figure 14.
Internal domains of electric motor.
Internal analysis was launched on 288 CPUs. The total computational time for the assumption of incompressible flow was 51 h. The steady-state model was performed for approximately 3 h. The total computational time for the compressible flow assumption was 228 h (approximately 9.5 days). The steady-state model was performed for approximately 8 h.
An Equation (26) was easily used to evaluate the power loss on the surfaces of the rotating parts.
where [Nm] is calculated CFD drag moment of individual surface, [1/s] is the rotor’s angular velocity. Figure 15 shows the surfaces of individual drag moments of the rotor. The calculated values of the individual drag moments of rotor parts are summarised in Table 5.
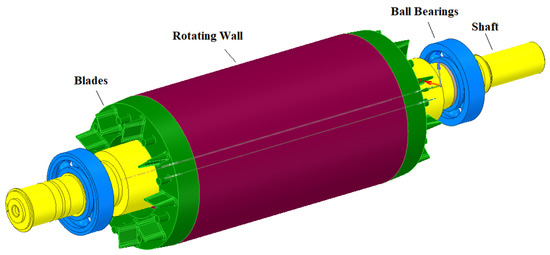
Figure 15.
Surfaces for calculation of drag moments.

Table 5.
Summary of the drag moments.
The assumption of incompressible flow is sufficient for calculating mechanical losses inside the motor, significantly reducing the time-consuming problem. The total loss consisting of the partial losses gave a value of approximately 670 W for compressible and incompressible airflow, respectively. Value oscillated in both simulations’ interval W.
Figure 16a shows the Taylor vortices in the air gap. According to (11), the flow regime is turbulent and turbulent heat transfer dominates. Figure 16b shows high turbulent flow inside the motor frame.
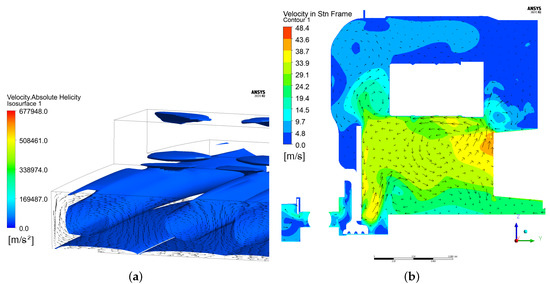
Figure 16.
Turbulent flow inside of the motor frame. (a) Taylor vortices inside the air gap; (b) Measurement of cooling air volume flow rate.
6. Comparison of Results and Discussion
The airflow velocity measurements in the space between the fins were compared with the CFD calculation in Figure 17. The figure compares results at plane C on the left side of the motor. All remaining results are shown in Figure 18. Figure 18 contains a total of twelve graphs. Each cross-section plane has three result graphs (left, right, and top side of the motor). The abbreviations in the legend mean: M—experimentally measured, S—steady state analysis, and T—transient analysis.
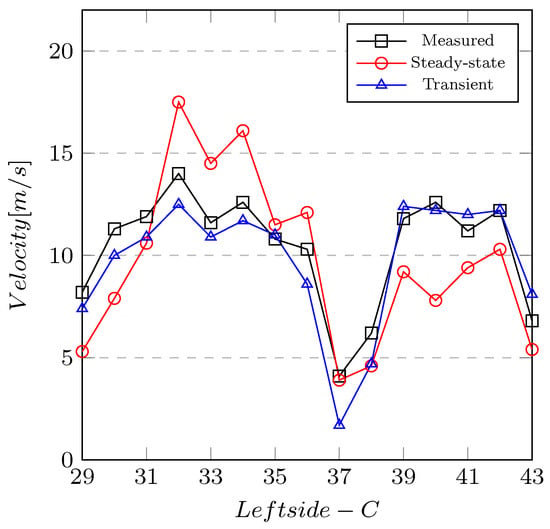
Figure 17.
Comparison of results at plane C on the left side of the motor.
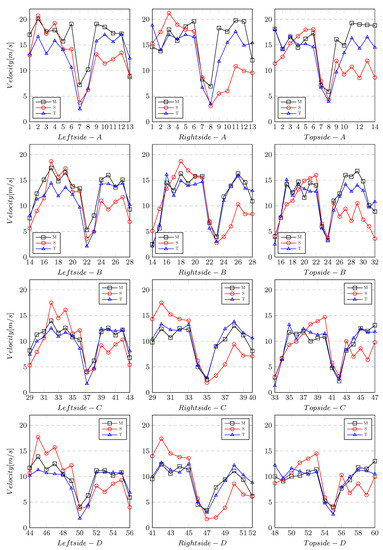
Figure 18.
Results at plane A, B, C, and D.
The following conclusions were summarised from the results. Transient analysis shows much higher agreement with measurements than steady-state analysis. This is a very important finding in the flow area because it primarily affects the heat transfer from the motor frame to the surrounding environment. The transient analysis does not show accurate results in the first two planes, as is the case for the C and D planes. There the trend is almost identical. There is a significant decrease in the air velocity in each graph. Lugs cause this phenomenon by bolting the bearing end shields. These lugs form block the free passage of air. Lugs can be seen in Figure 2 at the bolt locations (S). The shape of the curves changes from a higher value to a lower one, thus resembling a saw function. This is due to the different lengths of the fins. This trend did not appear with equally long fins in previous motor calculations.
We are aware that we have introduced some errors in the results from the CFD analysis by obtaining the airflow velocity from the area average. The most accurate results would be if we modelled a Prandtl tube at each space between fins. However, the goal of this project was to find a way to get the results accurate enough in a reasonable amount of time. Thus, our assumption is a compromise between accuracy and computation time.
In Section 3.1, the prediction of the airflow velocity profile using Klimenta expressions was explained. There are necessary using the constants , , and for expression (1). Klimenta expressed the expression for determining the airflow velocity profile, which is valid for small motors up to approximately 15 kW. Based on his comparisons, it was found: (1) that the coefficient amounts to 1500 m·rpm, and (2) that the values of the coefficient are: = 3 for p ≤ 4 and P ≤ 15 kW, = 2 for p ≤ 4 and P > 15 kW and = 8/3 for p > 4 and P∀. This was in satisfactory agreement with most of the experimental data. The main question was whether it applies to a higher-power motor and, if so, in which conditions it applies.
Comparison of curves shows that these relationships by Klimenta cannot be acceptably fitted to CFD or Experimental measurement, Figure 19. As was mentioned above, the Klimenta curve was derived for induction motors with a nominal load up to 15 kW. Thereby this discrepancy is explained. However, the “shape” of the curve representing CFD and the experiment are similar. The constants were determined on the base of the method of least squares, and the best approximation had the following values: = 0.6 [−], = 2000 [m·rpm] and = 2 [−].
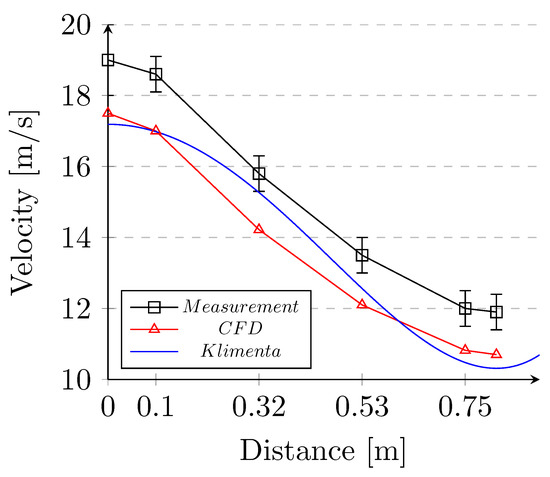
Figure 19.
Air-flow velocity profile.
The difference between the measured and calculated value was approximately 1.5 m/s. This was caused due to the error mentioned above in averaging the results in post-process. The trend was preserved.
The losses caused by the external fan and the blade cage were discussed in the next sections. Experimental measurement found that the total mechanical losses (windage and friction) reached 1870 W. The distribution of these losses was: The loss due to the external fan wheel was 826 W. The loss due to the internal drag moment was 684 W. The loss due to friction in the ball bearings was 360 W. On the other hand, the losses from CFD analyses were found to be as follows: The loss due to the external fan wheel was 908 W. The loss due to the internal drag moment was 670 W. The loss due to friction in the bearings was 360 W. A summary is shown in Table 6.

Table 6.
Summary of the mechanical losses.
The difference between the volumetric airflow rates was only 0.1 [m/min], which is a satisfactory agreement between measurement and CFD calculation.
7. Equivalent FEM Model
Determining the type of Taylor number in the air gap was crucial for determining the effective thermal conductivity for the FEM model. A thin air gap simulated by CFD (fluid material, ca. 10 layers of cells) was substituted by one layer of solid material in the FEM model with effective thermal conductivity. As a result, heat power transferred through a thin air gap is the same, and simulation is simpler. Turbulent thermal conductivity is an artificial increase in the thermal conductivity of the air due to turbulent flow inside the air gap. The Taylor number is 414 for investigated induction motor, with an air gap of 2.7 mm, which means the third relation shall be applied to determine the Nusselt number from Table 7. An example of the importance of determining effective thermal conductivity is shown in Figure 20.

Table 7.
Calculation of Nusselt number.
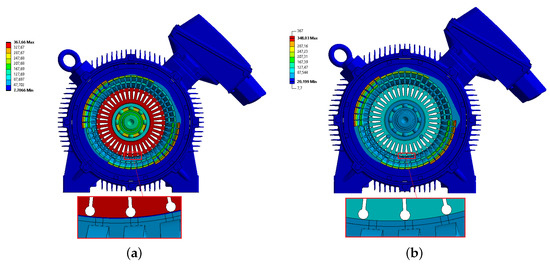
Figure 20.
Thermal conductivity’s of the air gap. (a) Thermal conductivity of the air gap; (b) The effective thermal conductivity of the air gap.
The FEM simulation setup for both cases was identical with an exception: (1) the figure on the left shows an example of the thermal conductivity of the air gap for about 60 °C with a value of 0.029 [W/mK]. (2) The right figure shows the temperature distribution result after setting the effective thermal conductivity of 0.24 [W/mK]. This value was obtained from a simple CFD simulation of the flow inside the gap, including heat transfer. It can be seen that the rotor temperature decreased significantly, and the stator temperature increased.
8. Summary and Outlook
The paper is focused on a detailed analysis of the flow surrounding the induction motor and the flow inside the motor. The first part deals with the theoretical analysis of flow according to generally known theories and formulas. Many authors have derived empirical formulas for describing the flow between ribs of induction motor frame with respect to length and distance from the leading edge. These formulae are always valid only for specific cases and types of induction motors, usually for power up to 15 kW, and they cannot be applied generally. The first step was to perform a CFD simulation for a high-power induction motor 315 kW and its comparison with experimental measurement and empirical formulas. The comparison focused on velocity between frame ribs, fan torque, and cooling air’s volume flow. Next, all types of losses were evaluated and compared with experimental measurement results. Next, the CFD simulation with heat transfer, inside and outside the induction motor, is scheduled. There is no relevant way to estimate the heat transfer coefficient on the outside and inside surfaces. The heat transfer coefficient can be simulated by CFD, including heat transfer or experimental measurement. Both are complicated and time-consuming. But the CFD can be performed virtually without special requests on experimental devices, and the CFD model is generally useful for virtual prototyping. Our main aim is the substitution of CFD for the FEM model, which needs fewer computational sources. The equivalent FEM model demands boundary conditions on internal and external surfaces, especially the heat transfer coefficient. It can be generally determined based on CFD simulation. If the motor optimisation does not significantly influence external and/or internal aerodynamics, then HTC is the same, and external and/or internal CFD is unnecessary. The CFD will be used to generalise the heat transfer coefficient and transport properties of air inside the induction motor. The heat transfer coefficient and transport properties will be generalised by empirical formulas, and then applied in FEM as boundary conditions. The methodology outlined in the paper will be used by the manufacturer of induction motors in the future design and prototyping improvement process.
Author Contributions
Conceptualization, M.G.; Formal analysis, T.B. (Tomáš Blejchař) and M.N.; Funding acquisition, T.B. (Tomáš Brzobohatý) and T.K.; Investigation, M.G., T.B. (Tomáš Blejchař) and M.N.; Methodology, M.G.; Project administration, T.B. (Tomáš Brzobohatý) and T.K.; Resources, M.N.; Supervision, T.K.; Validation, M.G. and M.N.; Writing—original draft, M.G.; Writing—review and editing, T.B. (Tomáš Blejchař). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Industry and Trade Czech Republic grant number CZ.01.1.02/0.0/0.0/17_176/0015651 and Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90140).
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Ministry of Industry and Trade Czech Republic (CZ.01.1.02/0.0/0.0/17_176/0015651) and Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90140).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries: Maharashtra, India, 2006; ISBN 978-1928729082. [Google Scholar]
- Klimenta, D.O.; Hannukainen, A. An Approximate Estimation of Velocity Profiles and Turbulence Factor; Thermal Science: Belgrade, Serbia, 2017; pp. 1515–1527. [Google Scholar] [CrossRef][Green Version]
- Staton, D.A.; Cavagnino, A. Convection Heat Transfer and Flow Calculations Suitable for Analytical Modelling of Electric Machines. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 4841–4846. [Google Scholar] [CrossRef]
- Pecinka, P.; Kocman, S.; Orsag, P.; Otýpka, J. Solutions to increase the efficiency of induction motors. In Proceedings of the 18th International Scientific Conference on Electric Power Engineering, Ostrava, Czech Republic, 17–19 May 2017. [Google Scholar] [CrossRef]
- Rehman, Z.; Seong, K. Three-D Numerical Thermal Analysis of Electric Motor with Cooling Jacket. Energies 2018, 11, 92. [Google Scholar] [CrossRef]
- Di Gerlando, A.; Vistoli, I. Improved Thermal Modelling of Induction Motors for Design Purposes. In Proceedings of the IET 6th International Conference on Electrical Machines and Drives, Oxford, UK, 8–10 September 1993; pp. 381–386. [Google Scholar]
- Hewitt, G.F.; Hall-Taylor, N.S. Annular Two-Phase Flow; Pergamon Press: Oxford, UK, 1970; ISBN 978-0-08-015797-9. [Google Scholar]
- Holland, F.A.; Bragg, R. Fluid Flow for Chemical Engineers, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1995; pp. 85–88. ISBN 978-0340610589. [Google Scholar]
- Balachandran, P. Engineering Fluid Mechanics; PHI Learning Private Limited: New Delhi, India, 2011; pp. 232–275. ISBN 978-8120340725. [Google Scholar]
- Webster, J.G.; Eren, H. Measurement, Instrumentation, and Sensors Handbook, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2014; pp. 57.6–57.8. ISBN 0-8493-2145-X. [Google Scholar]
- Gioia, G.; Chakraborty, P. Turbulent Friction in Rough Pipes and the Energy Spectrum of the Phenomenological Theory. Phys. Rev. Lett. 2006, 96, 044502. [Google Scholar] [CrossRef] [PubMed]
- Nikuradse, J. Stromungsgesetze in rauhen Rohren. Forschung auf dem Gebiete des Ingenieurwesens. In Forschungsheft; VDIVerlag: Berlin, Germany, 1933; p. 361, (English translation: Laws of flow in rough pipes, NACA TM 1292, 1950). [Google Scholar]
- Staton, D.A.; Cavagnino, A. Convection Heat Transfer and Flow Calculations Suitable for Electric Machines Thermal Models. IEEE Trans. Ind. Electron. 2008, 55, 3509–3516. [Google Scholar] [CrossRef]
- Valenzuela, M.A. Thermal Evaluation of TEFC Induction Motors Operating on Frequency-Controlled Variable-Speed Drives. IEEE Trans. Ind. Appl. 2004, 40, 692–698. [Google Scholar] [CrossRef]
- Valenzuela, M.A.; Tapia, J.A. Heat Transfer and Thermal Design of Finned Frames for TEFC Variable-Speed Motors. IEEE Trans. Ind. Electron. 2008, 55, 3500–3580. [Google Scholar] [CrossRef]
- Valenzuela, M.A.; Tapia, J.A. Heat Transfer and Thermal Design of Finned Frames for TEFC Variable Speed Motors. In Proceedings of the 32nd Annual Conference on IEEE Industrial Electronics—IECON 2006, Paris, France, 7–10 November 2006; pp. 4835–4840. [Google Scholar]
- Romo, J.L.; Adrian, M.B. Prediction of Internal Temperature in Three-Phase Induction Motors with Electronic Speed Control. Electr. Power Syst. Res. 1998, 45, 91–99. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D. Determination of Critical Parameters in Electrical Machine Thermal Models. IEEE Trans. Ind. Appl. 2008, 44, 1150–1159. [Google Scholar] [CrossRef]
- Anderson, K.R.; Lin, J.; Wong, A. Experimental and Numerical Study of Windage Losses in the Narrow Gap Region of a High-Speed Electric Motor. Fluids 2018, 3, 22. [Google Scholar] [CrossRef]
- Bousbaine, A. An Investigation into the Thermal Modelling of Induction Motors; Department of Electronic and Electrical Engineering, University of Sheffield: Sheffield, UK, 1993. [Google Scholar]
- Kovalev, E.B.; Burkovskii, A.N.; Tokarenko, A.T. Heat Release in Channels between Frame-Ribbing of Enclosed Asynchronous Motors. Elektrotekhnika 1965, 36, 27–29. [Google Scholar]
- Touhami, S.; Bertin, Y.; Lefèvre, Y.; Llibre, J.-F.; Hénaux, C.; Fénot, M. Lumped Parameter Thermal Model of Permanent Magnet Synchronous Machines; Electrimacs: Toulouse, France, 2017. [Google Scholar]
- Mellor, P.H.; Roberts, D.; Turner, D.R. Lumped parameter thermal model for electrical machines of TEFC design. IEE Proc. B 1991, 138, 205–218. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Computational Fluid Dynamics. The Basics with Applications; McGraw-Hill: New York, NY, USA, 1995; ISBN 0-07-001685-2. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1996; ISBN 3-540-59434-5. [Google Scholar]
- Xie, Y.; Guo, J.; Chen, P.; Li, Z. Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load. Energies 2018, 11, 2024. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).