Inclusive Charged-Particle Kinematic Distributions at LHC Energies: Data versus Theory
Abstract
1. Introduction
2. The Method and Formalism
2.1. PYTHIA8.3
2.2. Sibyll
2.3. EPOS
2.3.1. EPOS1.99
2.3.2. EPOS LHC
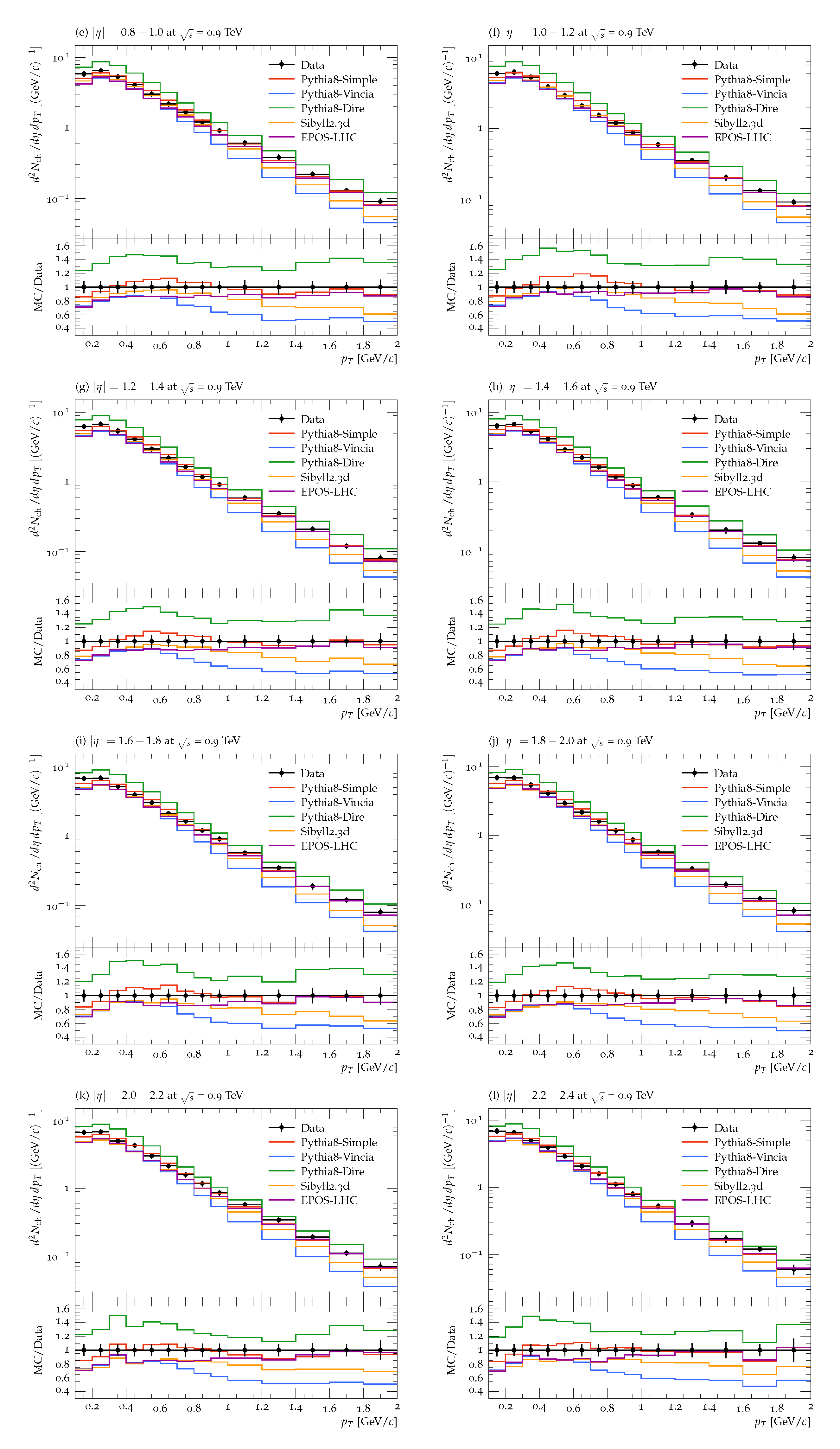
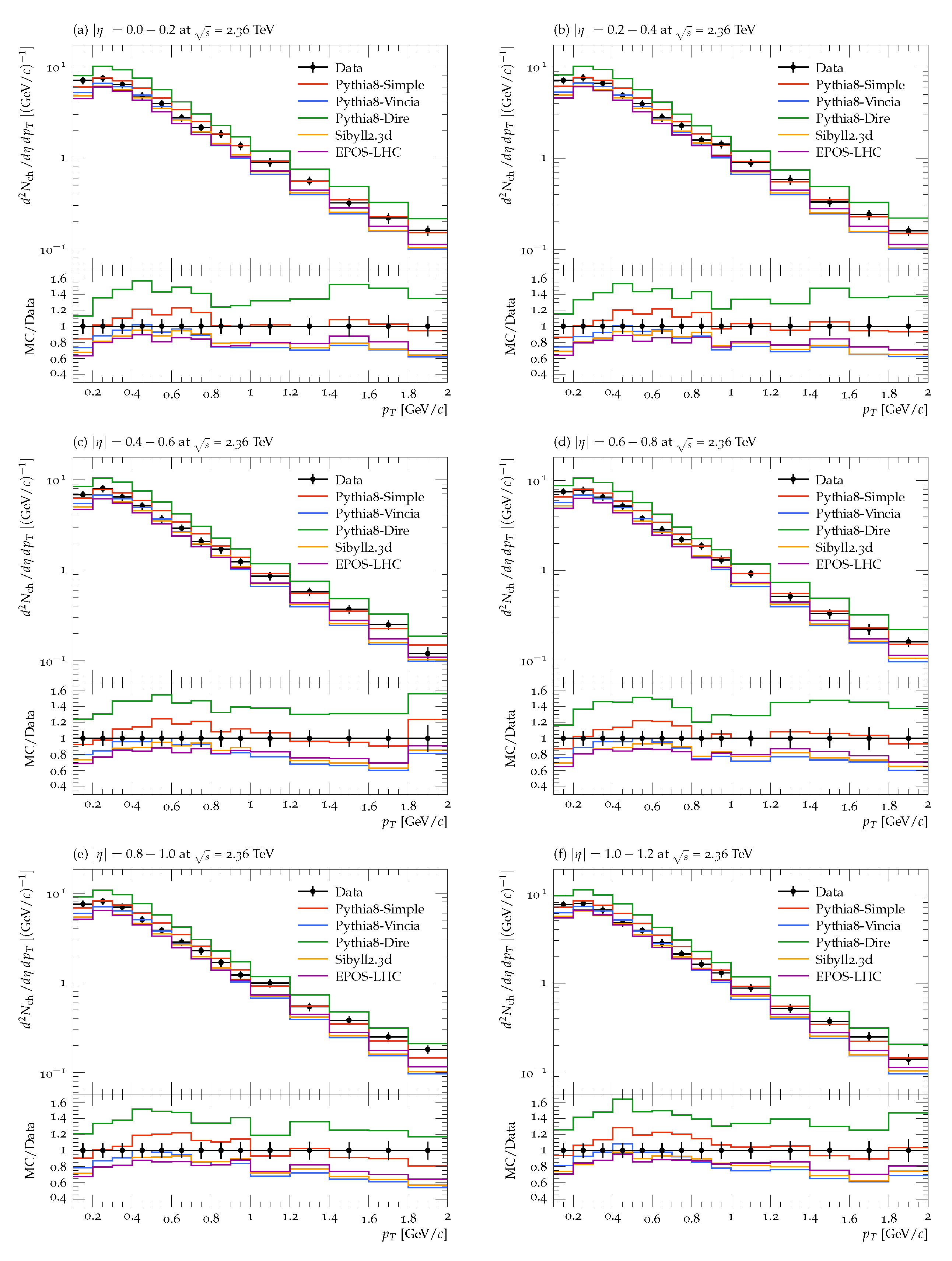
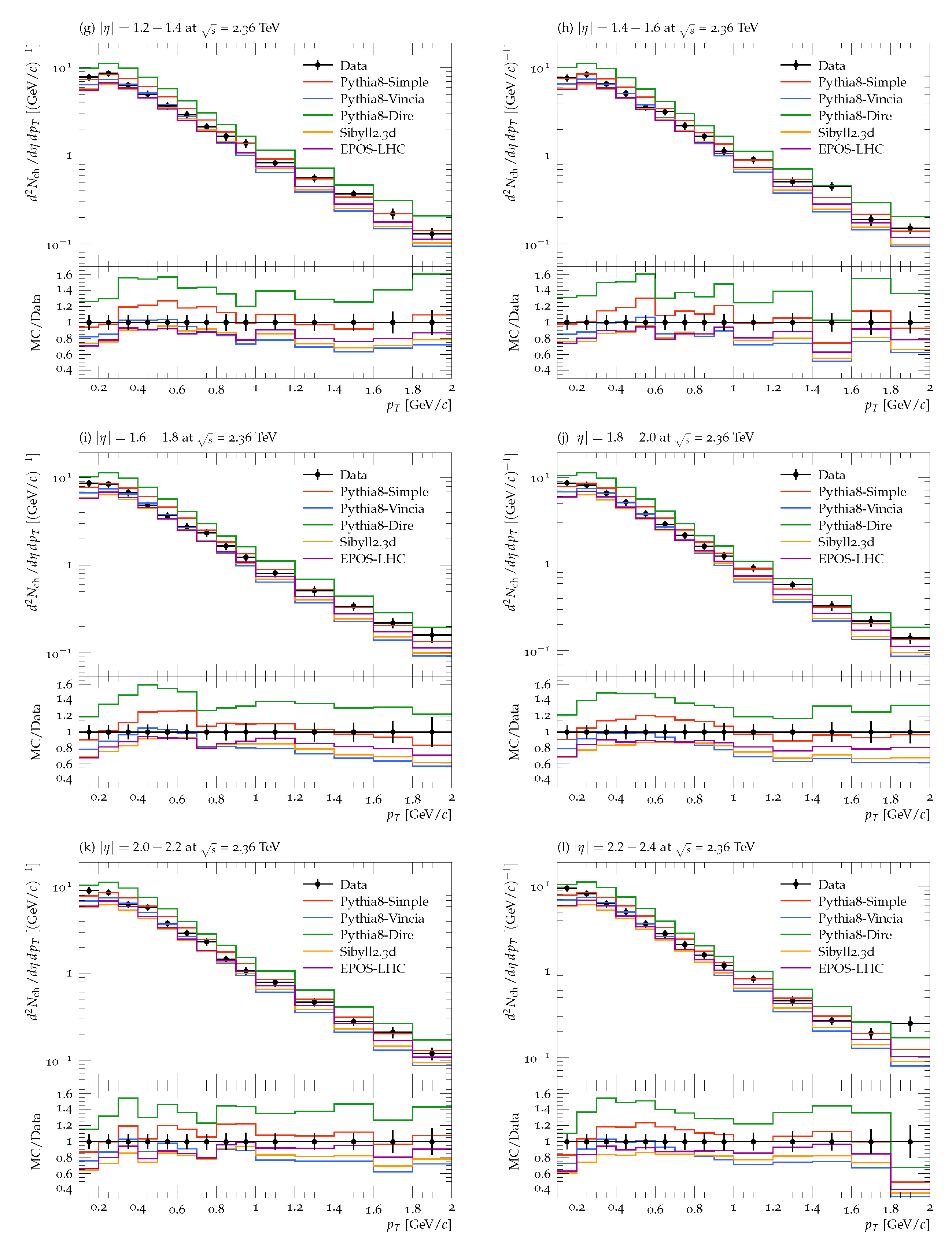
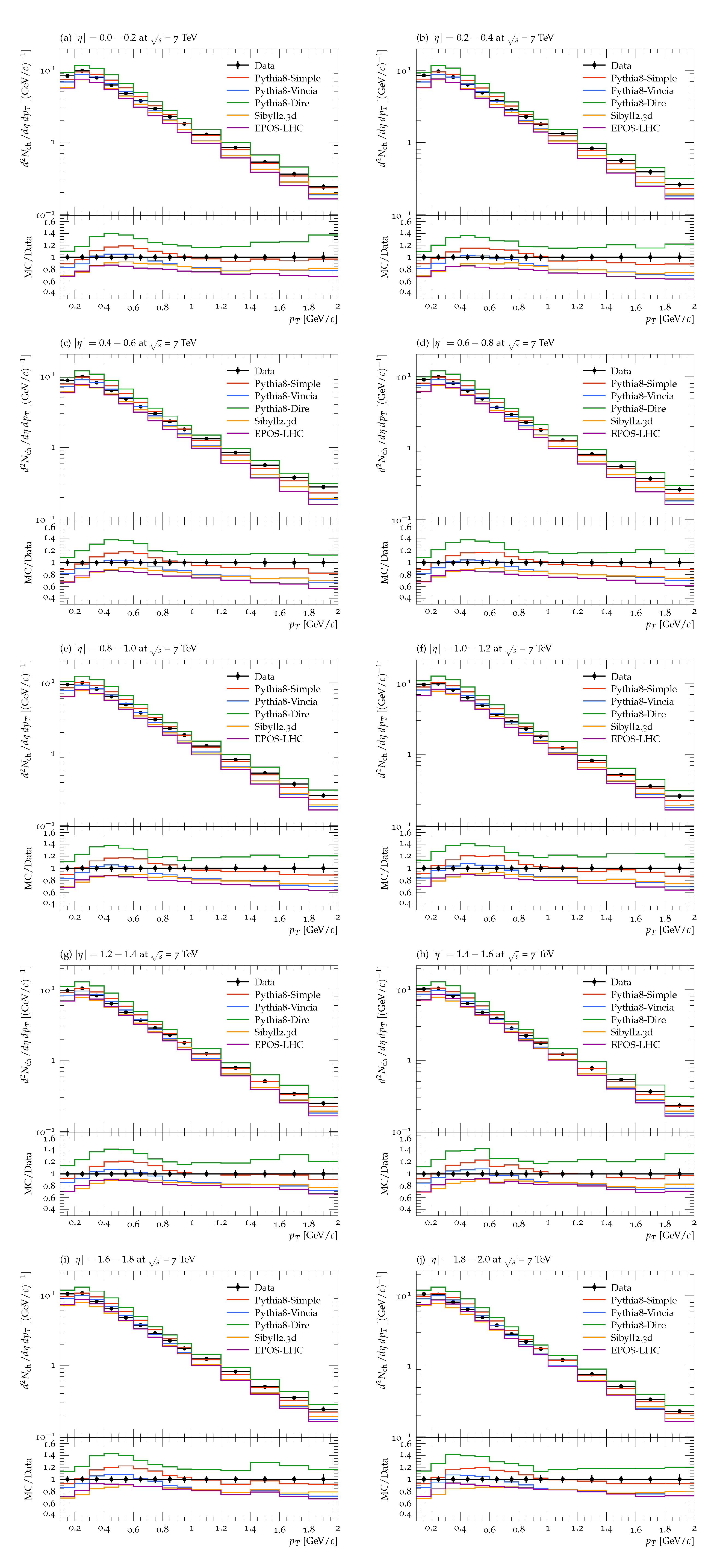
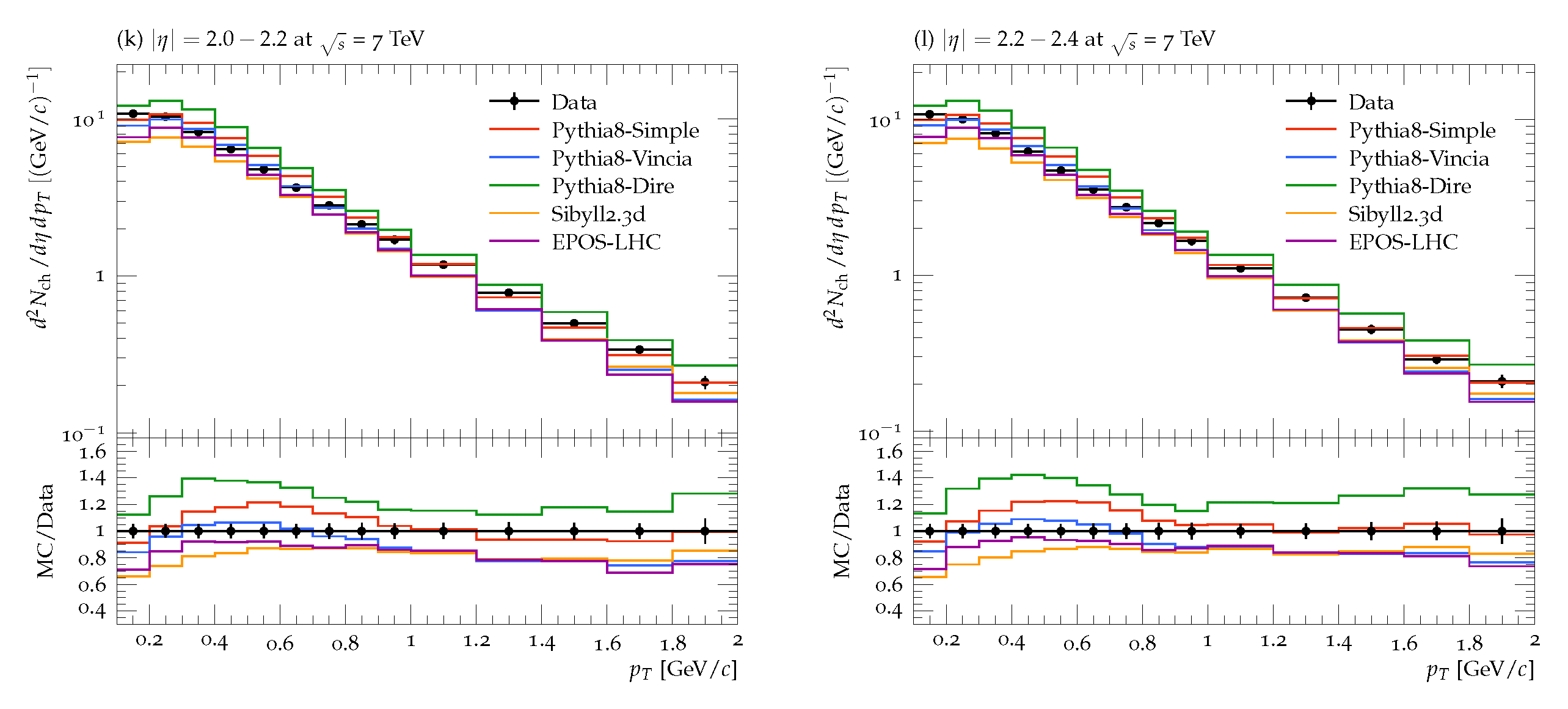
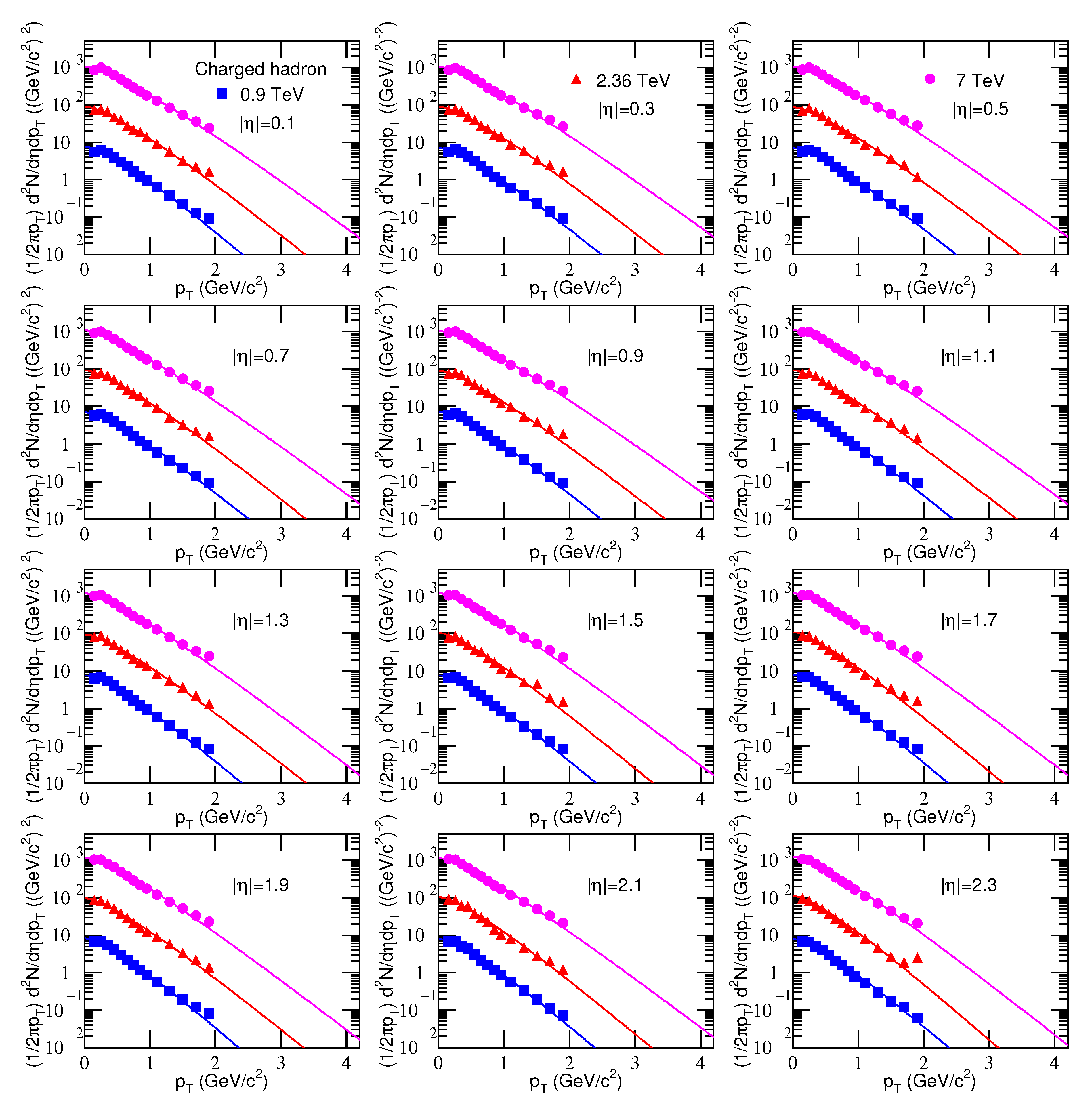
3. Results and Discussion
Comparison with the Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Compliance with Ethical Standards
References
- Biallas, A.; Bleszynski, M.; Czyz, W. Multiplicity distributions in nucleus-nucleus collisions at high energies. Nucl. Phys. B 1976, 111, 461–476. [Google Scholar]
- Bjorken, J.D. Highly relativistic nucleus-nucleus collisions: The central rapidity region. Phys. Rev. D 1983, 27, 140. [Google Scholar]
- Kharzeev, D.; Nardi, M. Hadron production in nuclear collisions at RHIC and high-density QCD. Phys. Lett. B 2001, 507, 121–128. [Google Scholar]
- Grosse-Oetringhaus, J.F.; Fiete, J.; Reygers, K. Charged-particle multiplicity in proton–proton collisions. J. Phys. G Nucl. Part. Phys. 2010, 37, 083001. [Google Scholar]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. Charged-particle multiplicity and pseudorapidity distributions measured with the PHOBOS detector in Au+ Au, Cu+ Cu, d+ Au, and p + p collisions at ultrarelativistic energies. Phys. Rev. C 2011, 83, 024913. [Google Scholar]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; Aparin, A.; et al. Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys. Rev. C 2017, 96, 044904. [Google Scholar]
- Toia, A. ALICE Collaboration. Bulk properties of Pb–Pb collisions at TeV measured by ALICE. J. Phys. G 2011, 38, 124007. [Google Scholar] [CrossRef]
- Sahoo, R.; Mishra, A.N.; Behera, N.K.; Nandi, B.K. Charged particle, photon multiplicity, and transverse energy production in high-energy heavy-ion collisions. Adv. High-Energy Phys. 2015, 2015, 612390. [Google Scholar]
- Sarkisyan, E.K.G.; Mishra, A.N.; Sahoo, R.; Sakharov, A.S. Multihadron production dynamics exploring the energy balance in hadronic and nuclear collisions. Phys. Rev. D 2016, 93, 054046. [Google Scholar]
- Basu, S.; Nayak, T.K.; Datta, K. Beam energy dependence of pseudorapidity distributions of charged particles produced in relativistic heavy-ion collisions. Phys. Rev. C 2016, 93, 064902. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Mrenna, S.; Skands, P. PYTHIA 6.4 physics and manual. J. High Energy Phys. 2006, 05, 026. [Google Scholar]
- Da Silva, A.V.; Bierlich, C.; Chinellato, D.D.; Takahashi, J. Studying the effect of the hadronic phase in nuclear collisions with PYTHIA and UrQMD. Springer Proc. Phys. 2020, 250, 319. [Google Scholar] [CrossRef]
- Fletcher, R.S.; Gaisser, T.K.; Lipari, P.; Stanev, T. SIBYLL: An Event generator for simulation of high-energy cosmic ray cascades. Phys. Rev. D 1994, 50, 5710–5731. [Google Scholar] [CrossRef]
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. EPOS LHC: Test of collective hadronization with data measured at the CERN Large Hadron Collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]
- Ostapchenko, S. Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: QGSJET-II model. Phys. Rev. D 2011, 83, 014018. [Google Scholar]
- Adams, J.; Aggarwal, M.; Ahammed, Z.; Amontee, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; STAR Collaboration; et al. Experimental and theoretical challenges in the search for the quark–gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102. [Google Scholar]
- Heinz, U.W.; Jacob, M. Evidence for a new state of matter: An assessment of the results from the CERN lead beam programme. arXiv 2000, arXiv:nucl-th/0002042. [Google Scholar]
- Khachatryan, V.; CMS Collaboration; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Friedl, M.; Frühwirth, R.; et al. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at = 0.9 and 2.36 TeV. J. High Energy Phys. 2010, 2010, 41. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Transverse-Momentum and Pseudorapidity Distributions of Charged Hadrons inppCollisions ats = 7 TeV. Phys. Rev. Lett. 2010, 105, 022002. [Google Scholar] [CrossRef]
- Yang, P.-P.; Duan, M.-Y.; Liu, F.-H.; Sahoo, R. Analysis of Identified Particle Transverse Momentum Spectra Produced in pp, p–Pb and Pb–Pb Collisions at the LHC Using TP-like Function. Symmetry 2022, 14, 1530. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D.S. Relativistic thermodynamics: Transverse momentum distributions in high-energy physics. Eur. Phys. J. A 2012, 48, 60. [Google Scholar]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; Averbeck, R.; et al. Identified charged particle spectra and yields in Au+Au collisions at = 200 GeV. Phys. Rev. 2004, 69, 034909. [Google Scholar]
- Koch, P.; Rafelski, J.; Greiner, W. Strange hadrons in hot nuclear matter. Phys. Lett. B 1983, 123, 151–154. [Google Scholar]
- Braun-Munzinger, P.; Magestro, D.; Redlich, K.; Stachel, J. Hadron production in Au-Au collisions at RHIC. Phys. Lett. 2001, 518, 41–46. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions. Acta Phys. Pol. B 2009, 40, 1005–1012. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. The horn, the hadron mass spectrum and the QCD phase diagram—The statistical model of hadron production in central nucleus-nucleus collisions. Nucl. Phys. A 2010, 834, 237c–240c. [Google Scholar]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Hadron production in central nucleus-nucleus collisions at chemical freeze-out. Nucl. Phys. A 2006, 772, 167–199. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar]
- Ajaz, M.; HajIsmail, A.A.K.; Ahmed, A.; Wazir, Z.; Shehzadi, R.; Younis, H.; Khan, G.; Khan, R.; Ali, S.; Waqas, M.; et al. Centrality dependence of dristibutions and nuclear modification factor of charged particles in Pb–Pb interactions at = 2.76 TeV. Results Phys. 2021, 30, 104790. [Google Scholar]
- Ajaz, M.; Waqas, M.; Peng, G.X.; Yasin, Z.; Younis, H.; Ismail, A.A.K.H. Study of pT spectra of light particles using modified Hagedorn function and cosmic rays Monte Carlo event generators in proton–proton collisions at s = 900 GeV. Eur. Phys. J. Plus 2022, 137, 52. [Google Scholar] [CrossRef]
- Ajaz, M.; Ismail, A.A.K.H.; Waqas, M.; Suleymanov, M.; AbdelKader, A.; Suleymanov, R. Pseudorapidity dependence of the bulk properties of hadronic medium in pp collisions at 7 TeV. Sci. Rep. 2022, 12, 8142. [Google Scholar] [CrossRef]
- Ullah, S.; Ajaz, M.; Wazir, Z.; Ali, Y.; Khan, K.H.; Younis, H. Hadron production models’ prediction for pT distribution of charged hadrons in pp interactions at 7 TeV. Sci. Rep. 2019, 9, 11811. [Google Scholar] [CrossRef]
- Tabassam, U.; Ali, Y.; Suleymanov, M.; Bhatti, A.S.; Ajaz, M. The production of π, K, p and in p-Pb collisions at sNN = 5.02 TeV. Mod. Phys. Lett. A 2018, 33, 1850094. [Google Scholar] [CrossRef]
- Ajaz, M.; Waqas, M.; Li, L.-L.; Ismail, A.A.K.H.; Tabassam, U.; Suleymanov, M. Bulk properties of the medium in comparison with models’ predictions in pp collisions at 13 TeV. Eur. Phys. J. Plus 2022, 137, 592. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.; Ajaz, M.; Khubrani, A.; Dawi, E.; Khan, M.A.; Tawfik, A. Pseudorapidity dependence of the transverse momentum distribution of charged particles in pp collisions at 0.9, 2.36, and 7 TeV. Res. Phys. 2022, 42, 105989. [Google Scholar] [CrossRef]
- Ajaz, M.; Khan, R.; Wazir, Z.; Khan, I.; Bibi, T. Model prediction of transverse momentum spectra of strange hadrons in pp collisions at = 200 GeV. Int. J. Theor. Phys. 2020, 59, 3338. [Google Scholar]
- Khan, R.; Ajaz, M. Model predictions of charge particle densities and multiplicities in the forward region at 7 TeV. Mod. Phys. Lett. A 2020, 35, 2050190. [Google Scholar] [CrossRef]
- Ajaz, M.; Tufail, M.; Ali, Y. Study of the Production of Strange Particles in Proton–Proton Collisions at = 0.9 TeV. Arab. J. Sci. Eng. 2020, 45, 411–416. [Google Scholar] [CrossRef]
- Yang, P.-P.; Ajaz, M.; Waqas, M.; Liu, F.-H.; Suleymanov, M.K. Pseudorapidity dependence of the p T spectra of charged hadrons in pp collisions at s = 0.9 and 2.36 TeV. J. Phys. G Nucl. Part. Phys. 2022, 49, 055110. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Sjöstrand, T. The Pythia event generator: Past, present and future. Comput. Phys. Commun. 2020, 246, 106910. [Google Scholar]
- Sjöstrand, T. A model for initial state parton showers. Phys. Lett. B 1985, 157, 321–325. [Google Scholar] [CrossRef]
- Bengtsson, M.; Sjöstrand, T. Coherent parton showers versus matrix elements—Implications of PETRA/PEP data. Phys. Lett. B 1987, 185, 435–440. [Google Scholar] [CrossRef]
- Bengtsson, M.; Sjöstrand, T. A comparative study of coherent and non-coherent parton shower evolution. Nucl. Phys. B 1987, 289, 810–846. [Google Scholar] [CrossRef]
- Norrbin, E.; Sjöstrand, T. QCD radiation off heavy particles. Nucl. Phys. B 2001, 603, 297–342. [Google Scholar] [CrossRef]
- Lönnblad, L. ARIADNE version 4: A Program for simulation of QCD cascades implementing the color dipole model. Comput. Phys. Commun. 1992, 71, 15. [Google Scholar] [CrossRef]
- Höche, S.; Reichelt, D.; Siegert, F. Momentum conservation and unitarity in parton showers and NLL resummation. J. High Energy Phys. 2018, 2018, 118. [Google Scholar] [CrossRef]
- Höche, S.; Prestel, S. The midpoint between dipole and parton showers. Eur. Phys. J. C 2015, 75, 461. [Google Scholar] [CrossRef]
- Höche, S.; Prestel, S. Triple collinear emissions in parton showers. Phys. Rev. D 2017, 96, 074017. [Google Scholar] [CrossRef]
- Höche, S.; Krauss, F.; Prestel, S. Implementing NLO DGLAP evolution in parton showers. J. High Energy Phys. 2017, 2017, 93. [Google Scholar] [CrossRef]
- Dulat, F.; Höche, S.; Prestel, S. Leading-color fully differential two-loop soft corrections to QCD dipole showers. Phys. Rev. D 2018, 98, 074013. [Google Scholar] [CrossRef]
- Prestel, S.; Spannowsky, M. HYTREES: Combining matrix elements and parton shower for hypothesis testing. Eur. Phys. J. C 2019, 79, 546. [Google Scholar] [CrossRef]
- Andersen, J.R.; Gütschow, C.; Maier, A.; Prestel, S. A Positive Resampler for Monte Carlo events with negative weights. Eur. Phys. J. C 2020, 80, 1007. [Google Scholar] [CrossRef]
- Gellersen, L.; Prestel, S.; Spannowsky, M. Coloring mixed QCD/QED evolution. SciPost Phys. 2022, 13, 034. [Google Scholar]
- Riehn, F.; Engel, R.; Fedynitch, A.; Gaisser, T.K.; Stanev, T. A new version of the event generator Sibyll. PoS ICRC 2016, 2015, 558. [Google Scholar]
- Ahn, E.-J.; Engel, R.; Gaisser, T.K.; Lipari, P.; Stanev, T. Cosmic ray interaction event generator SIBYLL 2.1. Phys. Rev. D 2009, 80, 094003. [Google Scholar]
- Gaisser, T.K.; Halzen, F. “Soft” Hard Scattering in the Teraelectronvolt Range. Phys. Rev. Lett. 1985, 54, 1754. [Google Scholar]
- Pancheri, G.; Srivastava, Y. Jets in Minimum Bias Physics. Conf. Proc. C 1985, 28, 850313. [Google Scholar]
- Durand, L.; Hong, P. QCD and rising cross sections. Phys. Rev. Lett. 1987, 58, 303. [Google Scholar]
- Bengtsson, H.-U.; Sjostrand, T. The Lund Monte Carlo for hadronic processes—PYTHIA version 4.8. Comput. Phys. Commun. 1987, 46, 43–82. [Google Scholar] [CrossRef]
- Sjostrand, T. Status of fragmentation models. Int. J. Mod. Phys. A 1988, 3, 751–823. [Google Scholar] [CrossRef]
- Drescher, H.J.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton-based gribov-regge theory. Phys. Rept. 2001, 350, 93–289. [Google Scholar] [CrossRef]
- Heck, D.; Knapp, J.; Capdevielle, J.N.; Schatz, G.; Thouw, T. CORSIKA: A Monte Carlo code to simulate extensive air showers. FZKA-6019. 1998. [Google Scholar]
- Pierog, T. LHC results and high energy cosmic ray interaction models. J. Phys. Conf. Ser. 2013, 409, 012008. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajaz, M.; Waqas, M.; Khan, R.; Adil Khan, M.; Li, L.-L.; Alrebdi, H.I.; Abdel-Aty, A.-H. Inclusive Charged-Particle Kinematic Distributions at LHC Energies: Data versus Theory. Symmetry 2022, 14, 2401. https://doi.org/10.3390/sym14112401
Ajaz M, Waqas M, Khan R, Adil Khan M, Li L-L, Alrebdi HI, Abdel-Aty A-H. Inclusive Charged-Particle Kinematic Distributions at LHC Energies: Data versus Theory. Symmetry. 2022; 14(11):2401. https://doi.org/10.3390/sym14112401
Chicago/Turabian StyleAjaz, Muhammad, Muhammad Waqas, Rashid Khan, Muhammad Adil Khan, Li-Li Li, Haifa I. Alrebdi, and Abdel-Haleem Abdel-Aty. 2022. "Inclusive Charged-Particle Kinematic Distributions at LHC Energies: Data versus Theory" Symmetry 14, no. 11: 2401. https://doi.org/10.3390/sym14112401
APA StyleAjaz, M., Waqas, M., Khan, R., Adil Khan, M., Li, L.-L., Alrebdi, H. I., & Abdel-Aty, A.-H. (2022). Inclusive Charged-Particle Kinematic Distributions at LHC Energies: Data versus Theory. Symmetry, 14(11), 2401. https://doi.org/10.3390/sym14112401








