Intelligent Bio-Latticed Cryptography: A Quantum-Proof Efficient Proposal
Abstract
1. Introduction
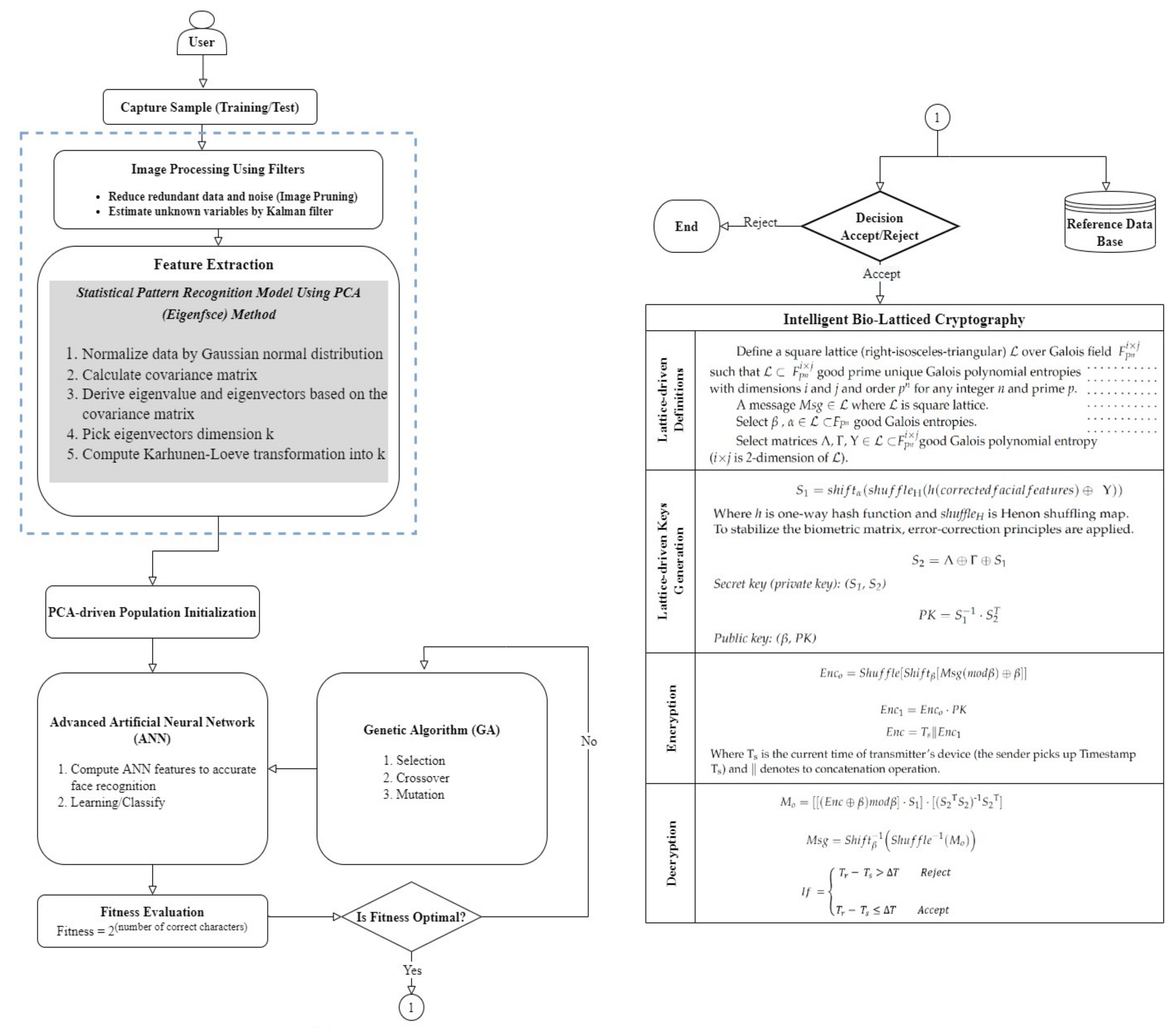
- Normalising data by Gaussian normal distribution. Gaussian distribution is a normal unique probability distribution that is preferred for describing random systems because numerous random processes that occur in nature act as normal distributions. The central limit theorem declares that for any distribution, the sum of random variables tends to fall within normal distribution under moderate circumstances. Thus, normal distribution has flexible mathematical attributes [7];
- Calculating a covariance matrix;
- Deriving eigenvalue and eigenvectors based on the covariance matrix;
- Picking eigenvector dimension k;
- Computing the Karhunen–Loève transformation into k.
- While humanity is benefitted by the information technology revolution, which derives its power from information to transfer knowledge and share resources, many exploit this revolution for malicious purposes such as attacking, eavesdropping, fraud, etc. According to PwC’s survey 2022 [17], cybercrimes have topped the list of external fraud threats faced by businesses worldwide. The survey included 1296 chief executive officers belonging to 53 countries in the world, and nearly half of these corporations () admitted that they had been subjected to cyber-attack, fraud, or financial crimes due to the high rate of cybercrimes and fraud around the world since the emergence of COVID-19. Moreover, Ref. [17] stated that cyber-attacks pose more risk to organisations than before, as fraud and cyber-attacks have become more sophisticated. One in five global businesses, whose revenues exceed $10 billion, have been exposed to a fraud case that cost more than $50 million. More than a third of corporations () with revenues of less than USD 100 million reported having experienced some form of cybercrime and of these corporations were affected by more than USD 1 million. Consequently, to counter this dangerous phenomenon, we propose intelligent performance-efficient lattice-driven cryptography using biometrics.
- The main benefit of combining lattice theory and biometrics is that doing so eliminates the need to save or send biometric templates, private keys, or any secret information, which solves some public key infrastructure problems, such as public keys distribution challenges and key expiration issues, thereby preserving privacy, improving cybersecurity in a post-quantum era, and minimising the risk of information leakage online or offline.
- The proposed cryptography resists quantum attacks such as Shor’s quantum algorithm. At the same time, it inherits neither the shortcomings of the quantum computer, such the large gap between the implementation of real devices and physical quantum theory, nor the defects of quantum cryptography, such as a vulnerability to side-channel attacks, source flaws, laser damage, Trojan horses, injection-locking lasers, and timing attacks. Since the first quantum cryptosystems—represented by quantum key distribution systems—were made available, many adversaries have attempted to hack them with unsettling success. Fierce attacks have focused on exploiting flaws in the equipment used to transmit quantum information. Consequently, adversaries have demonstrated that the equipment is not perfect, even though the laws of quantum physics imply perfect security and privacy. Furthermore, one of the most significant drawbacks of quantum computing and quantum cryptography is the limited distance that must be considered for transmitting photons, which often should not exceed tens of kilometres. This is due to the probability that the polarisation of photons may change or even disappear completely as a result of consecutive collisions with other particles while travelling long distances. However, this problem can be solved by adding spaced quantum repeaters at uniform intervals that amplify optical signals and maintain quantum randomness for thousands of kilometres.
- Enhancement of cybersecurity allows the private keys created from biometric encryption to be stronger, more complex, and less vulnerable to cybersecurity attacks. Traditional/classical biometric systems are susceptible to various attacks, such as manipulations, impersonation attacks, stolen verifier attacks, device compromise attacks, replay attacks, denial-of-service (DoS) attacks, distributed denial-of-service (DDoS) attacks, integrity threats, privacy threats, confidentiality concerns, and insider attacks. The use of the proposed advanced algorithm eliminates these vulnerabilities. It also enhances accuracy and performance by using artificial intelligence (AI), such as machine learning (artificial neural networks) and genetic algorithms.
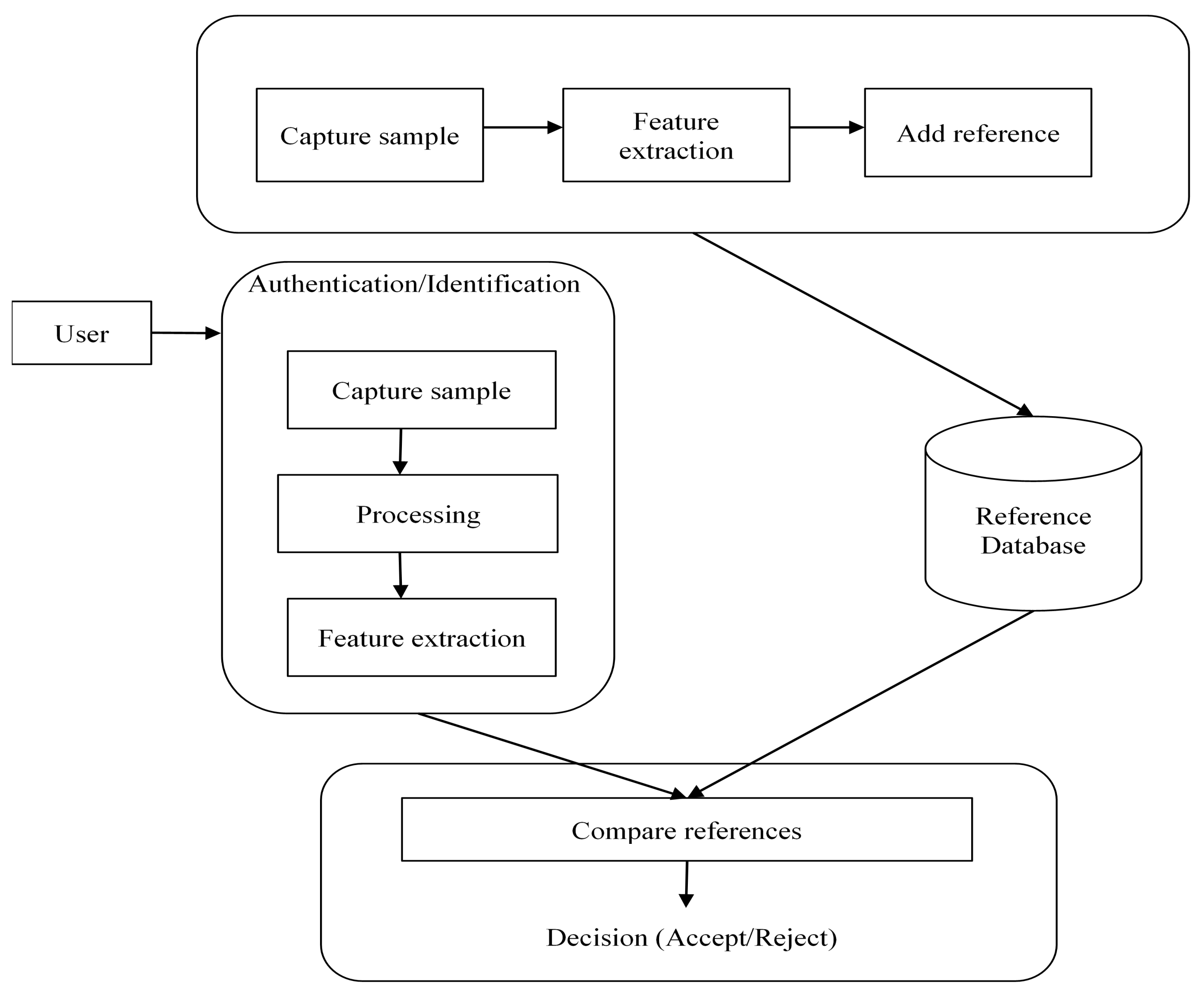
2. Biometrics
- An enrolment module acquires the data related to biometrics;
- A feature-extraction module extracts the required set of characteristics from the collected biometric data;
- A matching module compares the extracted features with the features in existing data;
- A decision-making module checks whether the identity of the user exists and whether it is accepted or rejected.
- Universality: each person must have it;
- Uniqueness: there should be sufficient and significant differences between the characteristics of any two persons;
- Longevity: it must be adequately invariant over a certain period.
3. Merits of Combining Biometrics and Asymmetric Encryption
3.1. Management of Public and Private Keys
3.2. No Storage of Biometric Data
3.3. Cancellation and Revocation in Biometric Systems
3.4. Security against Known Vulnerabilities in Biometric Systems
3.5. Security and Privacy of Personal Data
3.6. Public Acceptance Based on Embedded Privacy and Security
3.7. Making Biometric Systems Scalable
4. Lightweight Intelligent Bio-Latticed Cryptography
- Because biometric data is naturally changeable, while the symmetrical cryptography process requires exact data to operate properly, the representation of biometrics must be corrected symmetrically before it can be employed. To stabilise the biometric matrix, error-correction principles are symmetrically applied [30,40,41]. Further detailed information concerning the principles of the process of data correction can be found in [30,40,41].Secret key (private key): (S1, S2)where T refers to the matrix transpose operation.Public key: (β, PK)
- Encryption:where Ts is the current time of the transmitter’s device (the sender picks up timestamp Ts) and ∥ denotes a concatenation operation.
- Decryption:When the receiver obtains the encrypted message at time Tr, this message is decrypted via the secret key () and then tested for the timestamp freshness Ts. If (Tr − Ts) > T, the receiver will reject this message, since it is expired; i.e., it is significantly vulnerable to reply attack, where T indicates the expected time interval for the communication delay in the wireless networks. Conversely, if (Tr − Ts) ≤ T, the receiver will accept this message.

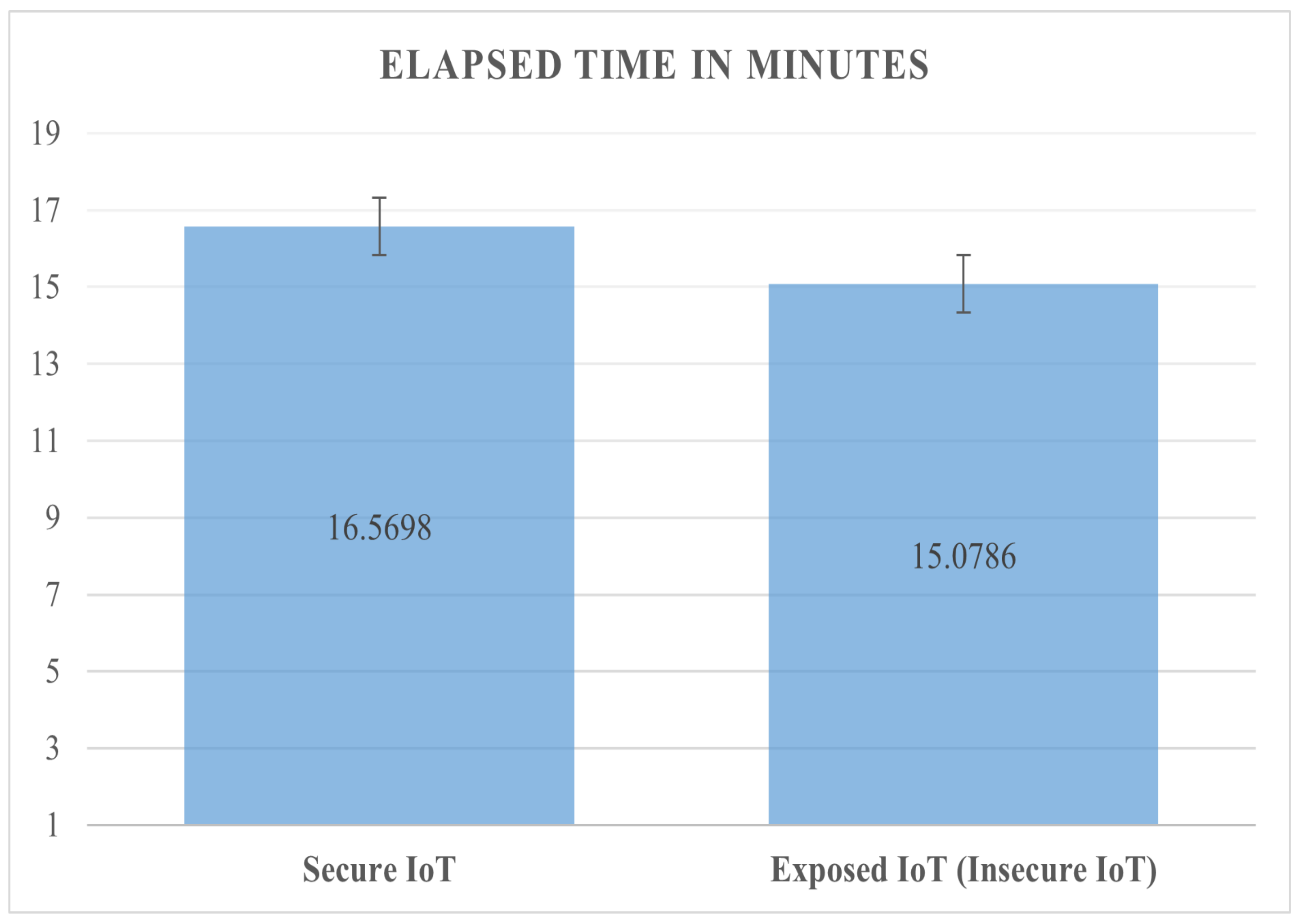
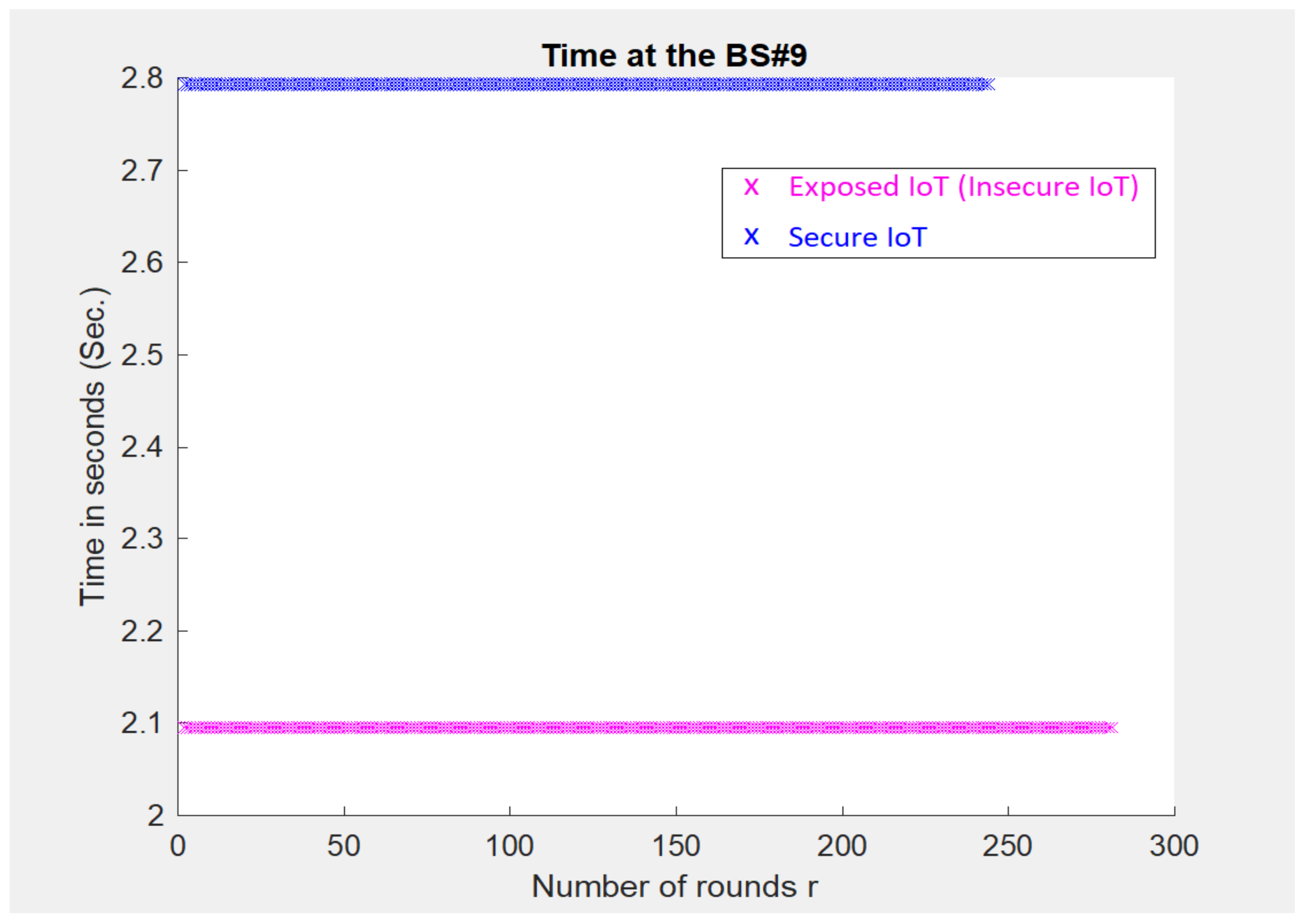
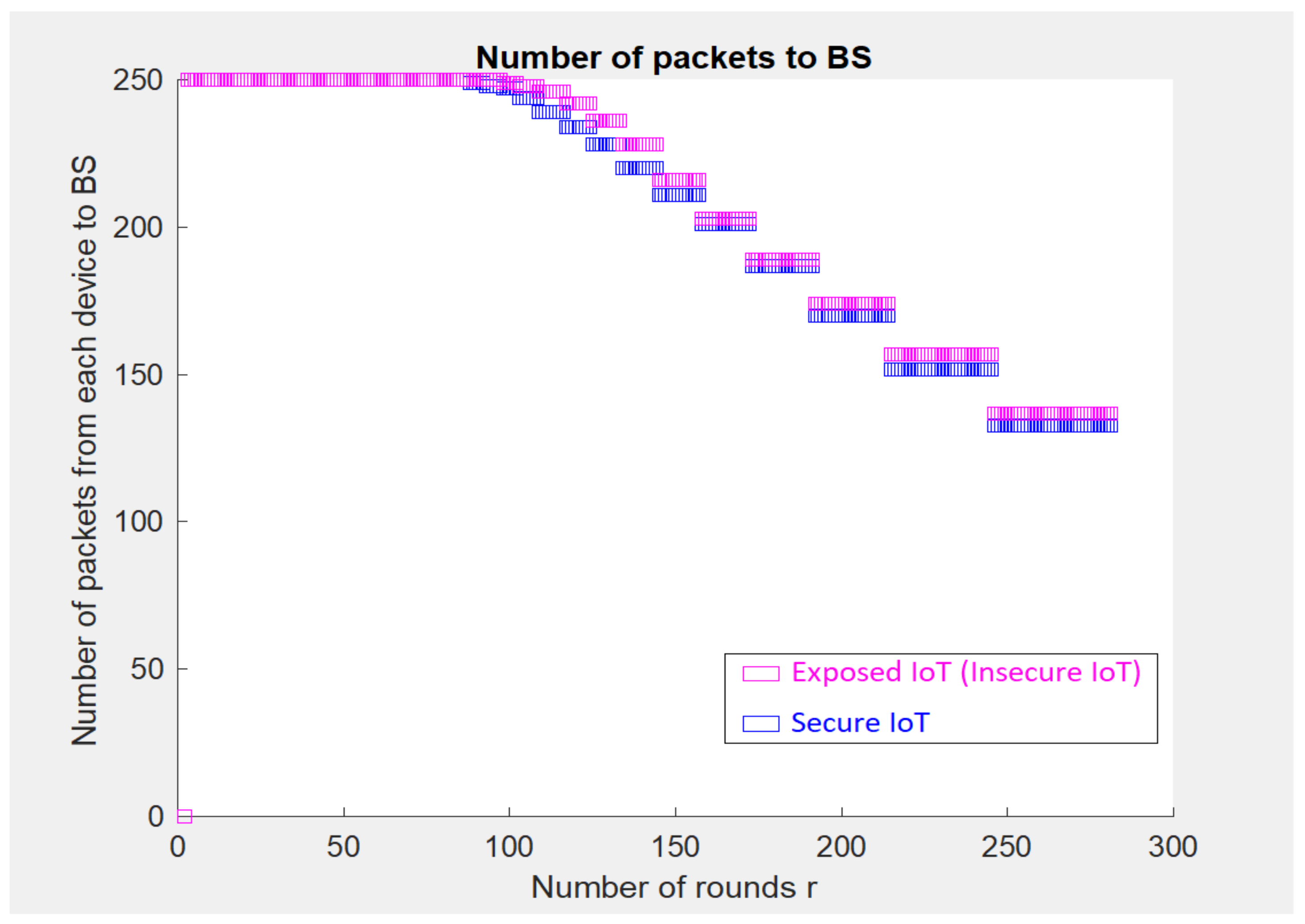
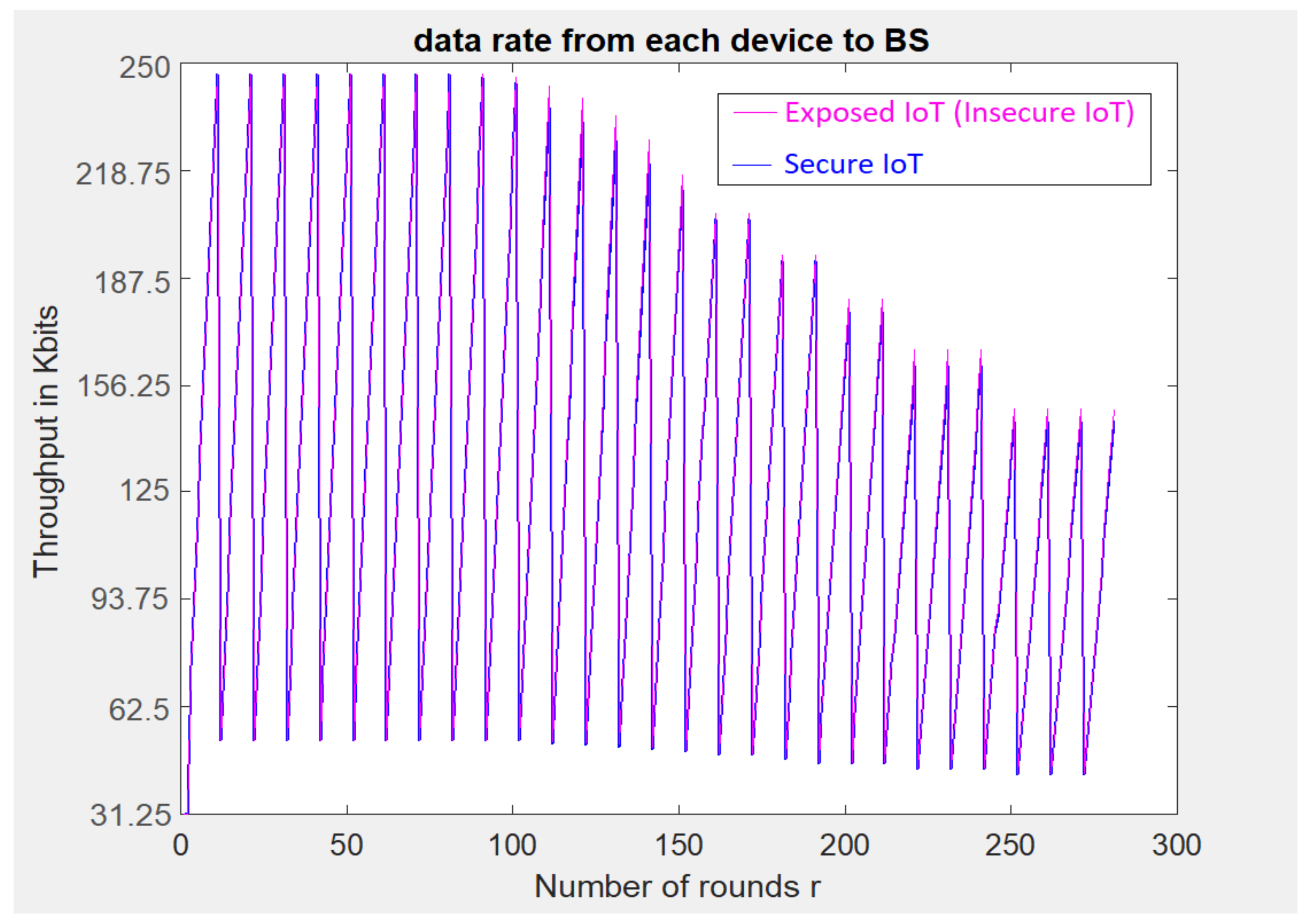
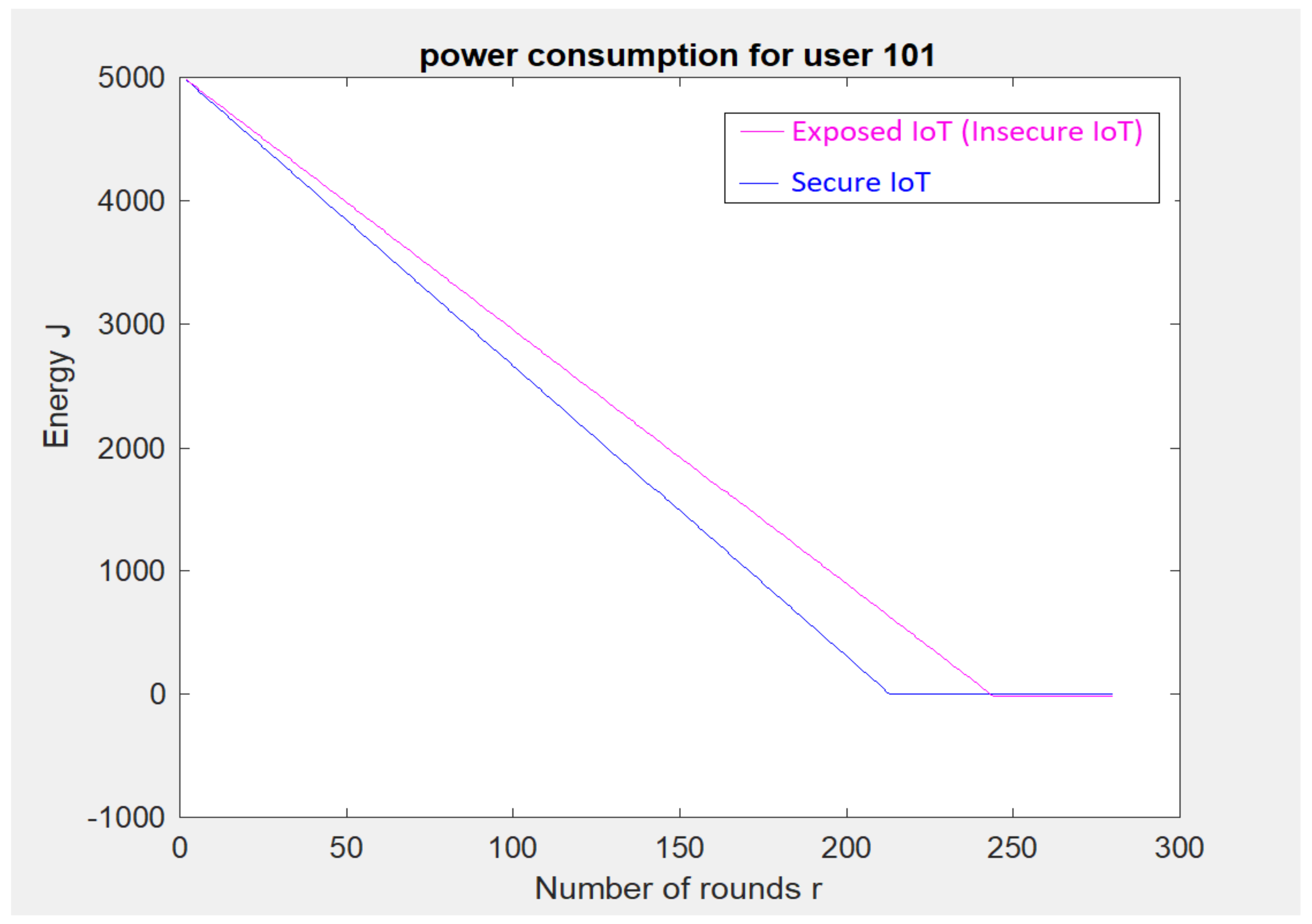
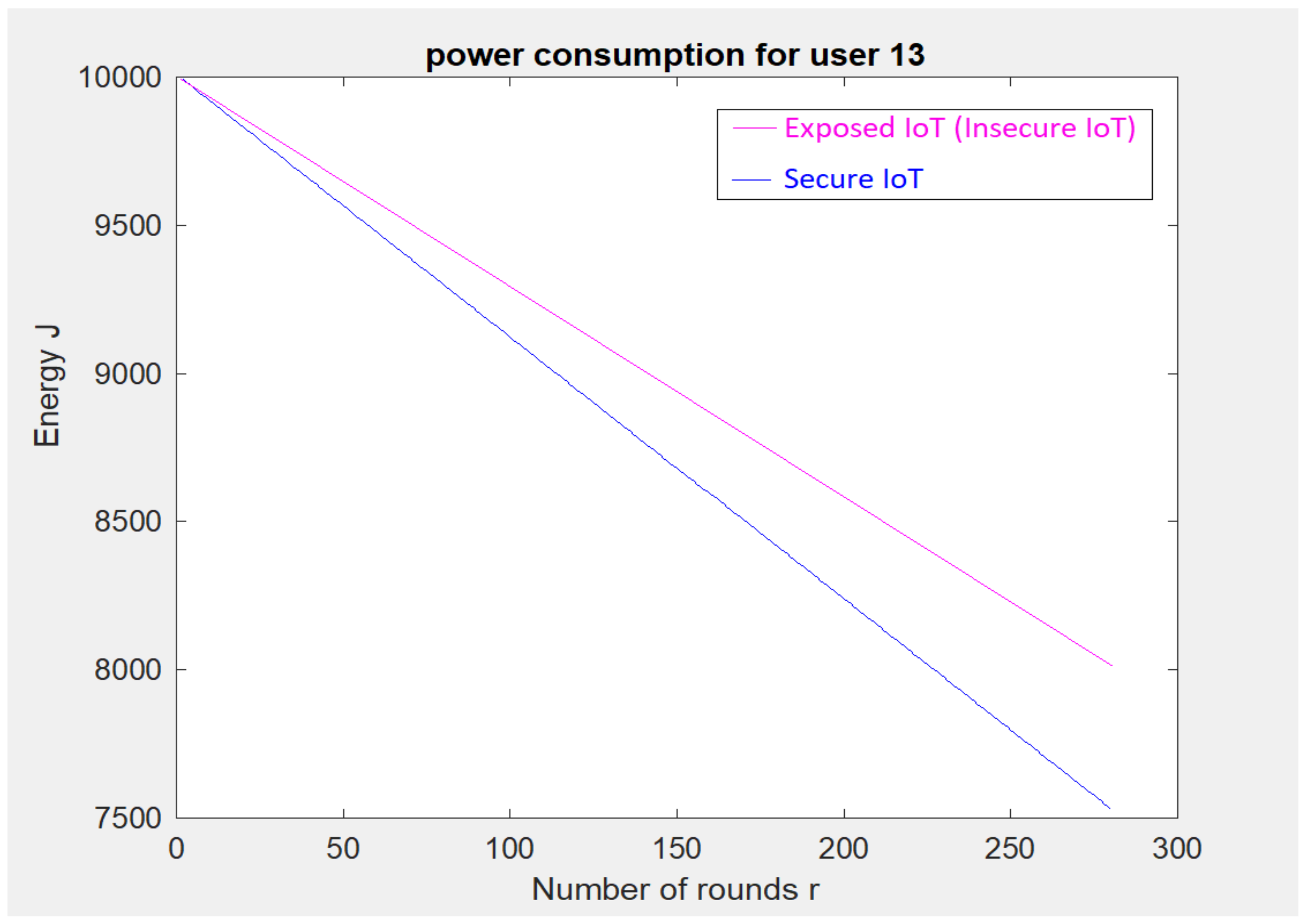
5. Implementation-Based Evaluation Results
- An 80 km2 classical attocell network topology in an urban macrocell scenario such as a smart city;
- Five cells; each cell () is 2 km;
- 24 Base Stations (BSs). is a hexagon bordered by BSs placed at the vertices, with another BS placed at the centre;
- The number of devices is 250, and these are positioned randomly in 2-dimensional space;
- In traditional cellular communications, all the devices transmit uplink/downlink requests at the same time to the BS. In other words, all transmissions between cellular devices must be accomplished through the BS without considering if Device-to-Device (D2D) communication is within two cellular devices’ reach;
- The initial energy for a cell device () is 5000–10,000 Joules.
6. Security Proof of the Proposed Lattice-Driven Encryption Scheme
- Biometric templates blended with encryption keys can improve online cybersecurity while simultaneously preserving users’ privacy.Proof. In the lightweight intelligent bio-latticed cryptosystem, the one-way hash function of a corrected facial image is XORed with matrix 2-dimension good Galois polynomial entropy to regenerate the private key (S1, S2) on-the-fly without transmitting or holding any secret data that may be compromised and breach the privacy of users. In biometric encryption, there is no requirement to memorise either facial images or templates of these images, which adresses the classic flaw of biometric methods. Additionally, an adversary cannot retrieve an encryption parameter , a facial image, or a facial template after binding them and then discarding them. This leads to the dramatic enhancement of security features, such as generating a robust biometric-based lattice private key (S1, S2) on-the-fly and at the same time maintaining the performance of restricted-resource devices, since this private key has more security than typical passwords and less storage space than biometric facial data. Additionally, the key generating process is characterised by its low computational requirements and lightweight operations.
- Lightweight intelligent bio-latticed cryptography and Galois field .Proof. A finite field, which is commonly referred to as a Galois field, is a set of numbers to perform mathematical operations such as addition, multiplication, subtraction, and division that always produces a result contained within the same set of numbers. Cryptography benefits from this, since a restricted set of very large numbers can be used [68]. The proposed bio-lattice cryptography uses Galois field theory, which has many applications in cryptography. Some of the main reasons for this are that it is possible for arithmetic operations to scramble data quickly and efficaciously when the data is represented as a vector in a Galois Field, and subtraction and multiplication in a Galois Field need extra operations/steps, unlike in Euclidean space [69].In the proposed bio-lattice cryptography, is used, since manipulating the bytes is required. has an array of elements that together represent all of the various potential values that may be assigned to a byte. Because the Galois field’s addition and multiplication operations are closed, it is easy to perform arithmetic operations on any two bytes to yield a new byte belonging to the array of that field, making it ideal for manipulating bytes [70]. Furthermore, multiplications in can be optimised securely for applications in cryptography when the is smaller than the bits of the device (i.e., < 64, on standard desktops or smartphones) [71].The National Institute of Standards and Technology (NIST) has issued a request for standardization of Post-Quantum Cryptography (PQC) [72] because of the growing awareness of the need for PQC in light of the impending arrival of quantum computing. According to Danger et al. [71], code-based encryption, along with multivariate and lattice-based cryptosystems, is one of the primary competitors for this challenge, because of its inherent resistance to quantum cyberattacks. Despite being nearly as age-old as RSA and Diffie–Hellman, the original McEliece cryptography has never been widely employed, mostly because of its large key sizes [71]. There are numerous cryptosystems defined on that were recognised as candidates for the first round of the NIST PQC competition [71].The carry-less feature of addition in makes arithmetic operations in this setting notably desirable. Consequently, many cryptographic approaches use it, since it provides efficiency in both hardware and software implementations because there is no carry and, thus, there are no lengthy delays [71]. In addition, Danger et al. [71] present a case study in which they assess several implementations of multiplication with regard to both their level of safety and how well they perform. They claim in their conclusion that their findings are applicable to accelerate and secure implementations of the other PQC outlined in their research, in addition to symmetric cyphers such as AES that operate on finite fields .Moreover, in the implementation of any cryptographic application, the size of the employed finite fields and the conditions imposed on the field parameters are determined by security concerns [73]. Therefore, the proposed intelligent bio-latticed cryptography devotes a square lattice (right-isosceles-triangular) over Galois field such that ⊂ good prime unique Galois polynomial entropies with dimensions i and j and order pn for any integer n and prime p.
- Entropic randomness, shifting, shuffling, XOR, and proposed lattice-driven cryptosystem.Proof. Random entropies are essential for assuring the security of sensitive information stored electronically [74,75]. Furthermore, a MATLAB-based shuffling package was developed to enhance a cryptosystem in [76]. This research paper included suggestions to enhance cryptography and make it invulnerable to data leaks using random shuffling. Hence, in the proposed cryptosystem, entropic randomness distribution, shifting, shuffling, and XORing are all used to make it difficult for an adversary without the appropriate private key to extrapolate anything valuable about the message (plaintext) from the encrypted message (corresponding ciphertext), strengthening proposed cryptosystem’s ability to resist data leaks and preserve privacy and making it more secure.Reyzin summarised essential entropy concepts used to study cryptographic architectures in [77], since the capability of assigning a random variable’s value in a single try is often used as a significant metric of its quality, especially in applications related to cybersecurity. Moreover, he defined this capability as follows:A random variable A has min-entropy b, indicated by , if .Extractors of randomness have been expressed in terms of their compatibility with any distribution having a min-entropy [77,78]. Furthermore, the outputs from robust extractors are almost uniform, regardless of the seed, and tend to maximal min-entropy, as these extractors are able to generate outputs with a high possibility over the seed selection [77].Similar to cryptography literature employing shuffling to prevent information leaks from encoded correspondences [76], Henon shuffling maps are used in the proposed lattice-driven cryptosystem. Using a random shuffling package, the researcher in [76] improved the security and efficacy of the Goldreich–Goldwasser–Halevi (GGH) public-key scheme. She proposed enhanced functions of GGH encryption and decryption principally relying on MATLAB- based shuffling to prevent sensitive information from leaking in images. In [32], public-key cryptography established on the closest vector problem was presented by Goldreich, Goldwasser, and Halevi to be an NP-hard lattice problem at the Crypto ’97 conference. Unfortunately, later at the Crypto ’99 conference, in [79], Phong Nguyen analysed the GGH cryptography and demonstrated that there are serious shortcomings including: any encrypted message can leak sensitive data concerning the plain message, and the difficulty of decryption can be reduced to a particular closest vector problem, which will significantly be easier than the general problem.
Reducing a Vector Module to a Lattice-Based Problem
| Algorithm 1: Reduction of the proposed lattice-based scheme |
INPUT: Basis of Hermite Normal Form, OUTPUT: Start for to 1 do for to 1 do end end return b End |
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PKI | Public Key Infrastructure |
| 6G | Sixth-generation Networks |
| NB-IoT | Narrowband-Internet of Things |
| IoT | Internet of Things |
| 5G PPP | European Infrastructure Public Private Partnership |
| LEACH | Low Energy Adaptive Clustering Hierarchy |
| BS | Base Station |
| Msg | Message |
| AI | Artificial Intelligence |
| DoS | Denial-of-Service attack |
| DDoS | Distributed Denial-of-Service attack |
| PCA | Principal Component Analysis |
| iIoT | Industrial Internet of Things |
| NP | Nondeterministic Polynomial-type |
| NP-hardness | Nondeterministic Polynomial-time hardness |
| SVP | Shortest Vector Problem |
| CVP | Closest Vector Problem |
| RP | Random Polynomial time |
| LLL | Lenstra–Lenstra–Lovász |
| BKZ | Block Korkine–Zolotarev |
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Cheng, C.; Lu, R.; Petzoldt, A.; Takagi, T. Securing the Internet of Things in a quantum world. IEEE Commun. Mag. 2017, 55, 116–120. [Google Scholar] [CrossRef]
- Liu, Z.; Choo, K.K.R.; Grossschadl, J. Securing edge devices in the post-quantum internet of things using lattice-based cryptography. IEEE Commun. Mag. 2018, 56, 158–162. [Google Scholar]
- Xu, R.; Cheng, C.; Qin, Y.; Jiang, T. Lighting the way to a smart world: Lattice-based cryptography for internet of things. arXiv 2018, arXiv:1805.04880. [Google Scholar]
- Althobaiti, O.S.; Dohler, M. Cybersecurity Challenges Associated with the Internet of Things in a Post-Quantum World. IEEE Access 2020, 8, 157356–157381. [Google Scholar]
- Guo, H.; Li, B.; Zhang, Y.; Zhang, Y.; Li, W.; Qiao, F.; Rong, X.; Zhou, S. Gait recognition based on the feature extraction of Gabor filter and linear discriminant analysis and improved local coupled extreme learning machine. Math. Probl. Eng. 2020, 2020, 5393058. [Google Scholar] [CrossRef]
- Bishop, G.; Welch, G. An introduction to the kalman filter. Proc. SIGGRAPH Course 2001, 8, 41. [Google Scholar]
- Fronckova, K.; Slaby, A. Kalman Filter Employment in Image Processing. In Proceedings of the International Conference on Computational Science and Its Applications (ICCSA 2020), Cagliari, Italy, 1–4 July 2020; Springer: Cham, Switzerland, 2020; pp. 833–844. [Google Scholar]
- Welch, G.F. Kalman filter. In Computer Vision; Ikeuchi, K., Ed.; Springer: Berlin, Germany, 2021; pp. 721–727. [Google Scholar]
- Rosa, L. Face Recognition Technology. Available online: http://www.facerecognition.it/ (accessed on 1 October 2021).
- Jalled, F. Face recognition machine vision system using Eigenfaces. arXiv 2017, arXiv:1705.02782. [Google Scholar]
- Tartakovsky, A.M.; Barajas-Solano, D.A.; He, Q. Physics-informed machine learning with conditional Karhunen-Loève expansions. J. Comput. Phys. 2021, 426, 109904. [Google Scholar]
- Lin, M.; Ji, R.; Li, S.; Wang, Y.; Wu, Y.; Huang, F.; Ye, Q. Network Pruning Using Adaptive Exemplar Filters. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Javadi, A.A.; Farmani, R.; Tan, T.P. A hybrid intelligent genetic algorithm. Adv. Eng. Inform. 2005, 19, 255–262. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Optimal sensor placement for health monitoring of high-rise structure based on genetic algorithm. Math. Probl. Eng. 2011, 2011, 395101. [Google Scholar] [CrossRef]
- Shiffman, D. The Nature of Code: Chapter 9. The Evolution of Code; Addison-Wesley: Boston, MA, USA, 2012; Available online: https://natureofcode.com/book/chapter-9-the-evolution-of-code/ (accessed on 29 January 2020).
- PwC. Protecting the Perimeter: The Rise of External Fraud. PwC’s Global Economic Crime and Fraud Survey 2022. 2022. Available online: https://www.pwc.com/gx/en/forensics/gecsm-2022/PwC-Global-Economic-Crime-and-Fraud-Survey-2022.pdf (accessed on 29 March 2022).
- Agbolade, O.; Nazri, A.; Yaakob, R.; Ghani, A.A.; Cheah, Y.K. Down Syndrome Face Recognition: A Review. Symmetry 2020, 12, 1182. [Google Scholar] [CrossRef]
- Sharifi, O.; Eskandari, M. Cosmetic Detection Framework for Face and Iris Biometrics. Symmetry 2018, 10, 122. [Google Scholar] [CrossRef]
- Zukarnain, Z.A.; Muneer, A.; Ab Aziz, M.K. Authentication Securing Methods for Mobile Identity: Issues, Solutions and Challenges. Symmetry 2022, 14, 821. [Google Scholar] [CrossRef]
- Militello, C.; Rundo, L.; Vitabile, S.; Conti, V. Fingerprint Classification Based on Deep Learning Approaches: Experimental Findings and Comparisons. Symmetry 2021, 13, 750. [Google Scholar] [CrossRef]
- Arsalan, M.; Hong, H.G.; Naqvi, R.A.; Lee, M.B.; Kim, M.C.; Kim, D.S.; Kim, C.S.; Park, K.R. Deep Learning-Based Iris Segmentation for Iris Recognition in Visible Light Environment. Symmetry 2017, 9, 263. [Google Scholar] [CrossRef]
- Wayman, J. Fundamentals of Biometric Authentication Technologies. Int. J. Image Graph. 2001, 1, 93–113. [Google Scholar] [CrossRef]
- Uludag, U.; Pankanti, S.; Prabhakar, S.; Jain, A. Biometric cryptosystems: Issues and challenges. Proc. IEEE 2004, 92, 948–960. [Google Scholar] [CrossRef]
- Delac, K.; Grgic, M. A survey of biometric recognition methods. In Proceedings of the 46th International Symposium, Zadar, Croatia, 18 June 2004; pp. 184–193. [Google Scholar]
- Jain, A.; Ross, A.; Prabhakar, S. An introduction to biometric recognition. IEEE Trans. Circuits Syst. Video Technol. 2004, 14, 4–20. [Google Scholar] [CrossRef]
- Cavoukian, A.; Stoianov, A.; Carter, F. Keynote Paper: Biometric Encryption: Technology for Strong Authentication, Security and Privacy. Policies Res. Identity Manag. Int. Fed. Inf. Process. 2007, 261, 57–77. [Google Scholar]
- Janbandhu, P.; Siyal, M. Novel biometric digital signatures for Internet-based applications. Inf. Manag. Comput. Secur. 2001, 9, 205–212. [Google Scholar] [CrossRef]
- Feng, H.; Wah, C. Private key generation from on-line handwritten signatures. Inf. Manag. Comput. Secur. 2002, 10, 4. [Google Scholar]
- Al-Hussain, A.; Al-Rassan, I. A biometric-based authentication system for web services mobile user. In Proceedings of the 8th International Conference on Advances in Mobile Computing and Multimedia, Paris, France, 8–10 November 2010; pp. 447–452. [Google Scholar]
- Mohammadi, S.; Abedi, S. ECC-Based Biometric Signature: A New Approach in Electronic Banking Security. In Proceedings of the 2008 International Symposium on Electronic Commerce and Security, Guangzhou, China, 3–5 August 2008; pp. 763–766. [Google Scholar]
- Goldreich, O.; Goldwasser, S.; Halevi, S. Public-key cryptosystems from lattice reduction problems. In Advances in Cryptology—CRYPTO ’97; Springer: Berlin, Germany, 1997; pp. 112–131. [Google Scholar]
- Althobaiti, O.S.; Dohler, M. Quantum-Resistant Cryptography for the Internet of Things Based on Location-Based Lattices. IEEE Access 2021, 9, 133185–133203. [Google Scholar] [CrossRef]
- Chen, C.; Hoffstein, J.; Whyte, W.; Zhang, Z. NIST PQ Submission: NTRUEncrypt A Lattice based Encryption Algorithm. NIST Post-Quantum Cryptography Standardization: Round 1 Submissions. 2018. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography/Round-1-Submissions (accessed on 29 March 2019).
- Bergami, F. Lattice-Based Cryptography. Master’s Thesis, Universita di Padova, Padova, Italy, 2016. [Google Scholar]
- Yuan, Y.; Cheng, C.M.; Kiyomoto, S.; Miyake, Y.; Takagi, T. Portable implementation of lattice-based cryptography using JavaScript. Int. J. Netw. Comput. 2016, 6, 309–327. [Google Scholar] [CrossRef]
- Ahmad, K.; Doja, M.; Udzir, N.I.; Singh, M.P. Emerging Security Algorithms and Techniques; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Proceedings of the International Algorithmic Number Theory Symposium; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar]
- Simon, J. DATA HASH—Hash for Matlab Array, Struct, Cell or File. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/31272-datahash (accessed on 1 January 2021.).
- Narayanan, G.; Haneef, N.; Narayanan, R. Matlab Implementation of “A Novel Approach to Improving Burst Errors Correction Capability of Hamming Code”. 2018. Available online: https://github.com/gurupunskill/novel-BEC (accessed on 29 March 2021).
- Afifi, M.; Derpanis, K.G.; Ommer, B.; Brown, M.S. Learning multi-scale photo exposure correction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9157–9167. Available online: https://github.com/mahmoudnafifi/Exposure_Correction (accessed on 29 December 2021).
- Boboc, A. Pattern Generator for MATLAB. MATLAB Central File Exchange. 2003. Available online: https://www.mathworks.com/matlabcentral/fileexchange/4024-pattern-generator-for-matlab (accessed on 17 October 2021).
- Althobaiti, O.S.; Dohler, M. Narrowband-internet of things device-to-device simulation: An open-sourced framework. Sensors 2021, 21, 1824. [Google Scholar] [CrossRef]
- Patel, P.; Ganatra, A. Investigate age invariant face recognition using PCA, LBP, Walsh Hadamard transform with neural network. In Proceedings of the International Conference on Signal and Speech Processing (ICSSP-14), Atlanta, GA, USA, 1 December 2014; pp. 266–274. Available online: https://github.com/Priyanka154/-Age-Invariant-Face-Recognition (accessed on 29 March 2021).
- Neerubai, S. Using PCA for Dimensionality Reduction of Facial Images. Available online: https://github.com/susmithaneerubai/Data-mining-project--Face-recognition (accessed on 1 March 2022).
- Nguyen, M.X.; Le, Q.M.; Pham, V.; Tran, T.; Le, B.H. Multi-scale sparse representation for robust face recognition. In Proceedings of the 2011 Third International Conference on Knowledge and Systems Engineering; 2011; pp. 195–199. Available online: https://github.com/tntrung/sparse_based_face_recognition (accessed on 29 March 2021).
- Cervantes, J.I. Face Recognition Written in MATLAB. 2014. Available online: https://github.com/JaimeIvanCervantes/FaceRecognition (accessed on 29 March 2020).
- Thomas. Face Recognition Neural Network Developed with MATLAB. 2015. Available online: https://github.com/tparadise/face-recognition (accessed on 29 March 2020).
- Aderohunmu, F.A. Energy Management Techniques in Wireless Sensor networks: Protocol Design and Evaluation. Ph.D. Thesis, University of Otago, Otago, New Zealand, 2010. [Google Scholar]
- Cai, J.; Nerurkar, A. Approximating the svp to within a factor (1-1/dim/sup/spl epsiv//) is np-hard under randomized conditions in Proceedings. In Proceedings of the Thirteenth Annual IEEE Conference on Comutational Complexity (Formerly: Structure in Complexity Theory Conference), Buffalo, NY, USA, 18 June 1998; pp. 46–55. [Google Scholar]
- Dinur, I. Approximating svp to within almost-polynomial factors is np-hard. Theor. Comput. Sci. 2002, 285, 55–71. [Google Scholar] [CrossRef]
- Dinur, I.; Kindler, G.; Safra, S. Approximating-CVP to within almost-polynomial factors is NP-hard. In Proceedings of the 39th Annual Symposium on Foundations of Computer Science (Cat. No. 98CB36280), Palo Alto, CA, USA, 8–11 November 1998; pp. 99–109. [Google Scholar]
- Buchmann, J.; Schmidt, P. Postquantum Cryptography. 2010. Available online: https://www-old.cdc.informatik.tu-darmstadt.de (accessed on 29 January 2018).
- Fortnow, L. The status of the p versus np problem. Commun. ACM 2009, 52, 78–86. [Google Scholar] [CrossRef]
- Baker, T.; Gill, J.; Solovay, R. Relativizations of the P=?NP question. SIAM J. Comput. 1975, 4, 431–442. [Google Scholar] [CrossRef]
- Vadhan, S.P. Computational Complexity. 2011. Available online: https://dash.harvard.edu/bitstream/handle/1/33907951/ComputationalComplexity-2ndEd-Vadhan.pdf?sequence=1 (accessed on 1 March 2018).
- Gorgui-Naguib, R.N. p-adic Number Theory and Its Applications in a Cryptographic Form. Ph.D. Thesis, University of London, London, UK, 1986. [Google Scholar]
- Woeginger, G.J. Exact algorithms for NP-hard problems: A survey. In Combinatorial Optimization—Eureka, You Shrink! Springer: Berlin/Heidelberg, Germany, 2003; pp. 185–207. [Google Scholar]
- Lagarias, J.C.; Lenstra, H.W., Jr.; Schnorr, C.P. Korkin-zolotarev bases and successive minima of a lattice and its reciprocal lattice. Combinatorica 1990, 10, 333–348. [Google Scholar] [CrossRef]
- Goldreich, O.; Goldwasser, S. On the limits of Nonapproximability of lattice problems. J. Comput. Syst. Sci. 2000, 60, 540–563. [Google Scholar] [CrossRef]
- Micciancio, D. The shortest vector in a lattice is hard to approximate to within some constant. SIAM J. Comput. 2001, 30, 2008–2035. [Google Scholar] [CrossRef]
- Khot, S. Hardness of approximating the shortest vector problem in lattices. J. ACM 2005, 52, 789–808. [Google Scholar] [CrossRef]
- Khot, S. Hardness of approximating the Shortest Vector Problem in high lp norms. J. Comput. Syst. Sci. 2006, 72, 206–219. [Google Scholar] [CrossRef]
- Van Emde Boas, P. Another NP-Complete Problem and the Complexity of Computing Short Vectors in a Lattice; Tecnical Report; Department of Mathmatics, University of Amsterdam: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Regev, O. New lattice-based cryptographic constructions. J. ACM 2004, 51, 899–942. [Google Scholar] [CrossRef]
- Aharonov, D.; Regev, O. Lattice problems in NP coNP. In Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, Rome, Italy, 17–19 October 2004; Volume 45, pp. 362–371. [Google Scholar]
- Islam, M.R.; Sayeed, M.S.; Samraj, A. Biometric template protection using watermarking with hidden password encryption. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; Volume 1, pp. 1–8. [Google Scholar]
- Bhowmik, A.; Menon, U. An adaptive cryptosystem on a Finite Field. PeerJ Comp. Sci. 2021, 7, e637. [Google Scholar] [CrossRef] [PubMed]
- Benvenuto, C.J. Galois Field in Cryptography; University of Washington: Washington, DC, USA, 2012; Volume 1, pp. 1–11. [Google Scholar]
- En, N.W. Why AES Is Secure. Available online: https://wei2912.github.io/posts/crypto/why-aes-is-secure.html (accessed on 1 July 2022).
- Danger, J.L.; El Housni, Y.; Facon, A.; Gueye, C.T.; Guilley, S.; Herbel, S.; Ndiaye, O.; Persichetti, E.; Schaub, A. On the Performance and Security of Multiplication in GF (2 N). Cryptography 2018, 2, 25. [Google Scholar] [CrossRef]
- NIST. Post-Quantum Cryptography PQC. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography (accessed on 1 May 2018).
- Guajardo, J.; Kumar, S.S.; Paar, C.; Pelzl, J. Efficient software-implementation of finite fields with applications to cryptography. Acta Appl. Math. 2006, 93, 3–32. [Google Scholar] [CrossRef]
- Simion, E. Entropy and randomness: From analogic to quantum world. IEEE Access 2020, 8, 74553–74561. [Google Scholar] [CrossRef]
- Teixeira, A.; Matos, A.; Antunes, L. Conditional rényi entropies. IEEE Trans. Inf. Theory 2012, 58, 4273–4277. [Google Scholar] [CrossRef]
- Dadheech, A. Preventing Information Leakage from Encoded Data in Lattice Based Cryptography. In Proceedings of the 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; pp. 1952–1955. [Google Scholar]
- Reyzin, L. Some notions of entropy for cryptography. In Proceedings of the 5th International Conference on Information Theoretic Security, Amsterdam, The Netherlands, 21–24 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 138–142. [Google Scholar]
- Nisan, N.; Zuckerman, D. Randomness is linear in space. J. Comput. Syst. Sci. 1996, 52, 43–52. [Google Scholar]
- Nguyen, P. Cryptanalysis of the Goldreich-Goldwasser-Halevi cryptosystem from crypto’97. In Advances in Cryptology- CRYPTO ’99: Proceedings of the 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 288–304. [Google Scholar]
- Rose, M. Lattice-Based Cryptography: A Practical Implementation. Master’s Thesis, University of Wollongong, Wollongong, Australia, 2011. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Althobaiti, O.S.; Mahmoodi, T.; Dohler, M. Intelligent Bio-Latticed Cryptography: A Quantum-Proof Efficient Proposal. Symmetry 2022, 14, 2351. https://doi.org/10.3390/sym14112351
Althobaiti OS, Mahmoodi T, Dohler M. Intelligent Bio-Latticed Cryptography: A Quantum-Proof Efficient Proposal. Symmetry. 2022; 14(11):2351. https://doi.org/10.3390/sym14112351
Chicago/Turabian StyleAlthobaiti, Ohood Saud, Toktam Mahmoodi, and Mischa Dohler. 2022. "Intelligent Bio-Latticed Cryptography: A Quantum-Proof Efficient Proposal" Symmetry 14, no. 11: 2351. https://doi.org/10.3390/sym14112351
APA StyleAlthobaiti, O. S., Mahmoodi, T., & Dohler, M. (2022). Intelligent Bio-Latticed Cryptography: A Quantum-Proof Efficient Proposal. Symmetry, 14(11), 2351. https://doi.org/10.3390/sym14112351





