A 3D Agent-Based Model of Lung Fibrosis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Framework and Implementation
- a MacBook Pro 2018 running macOS Big Sur on a 2.3 GHz Quad-Core Intel Core i5 processor with 8 GB RAM;
- a compute node of the Lichtenberg HPC system running CentOS 8.2 on 2x 2.3 GHz Intel Cascade-Lake AP 48-cores processor (96 total cores) with 384 GB RAM.
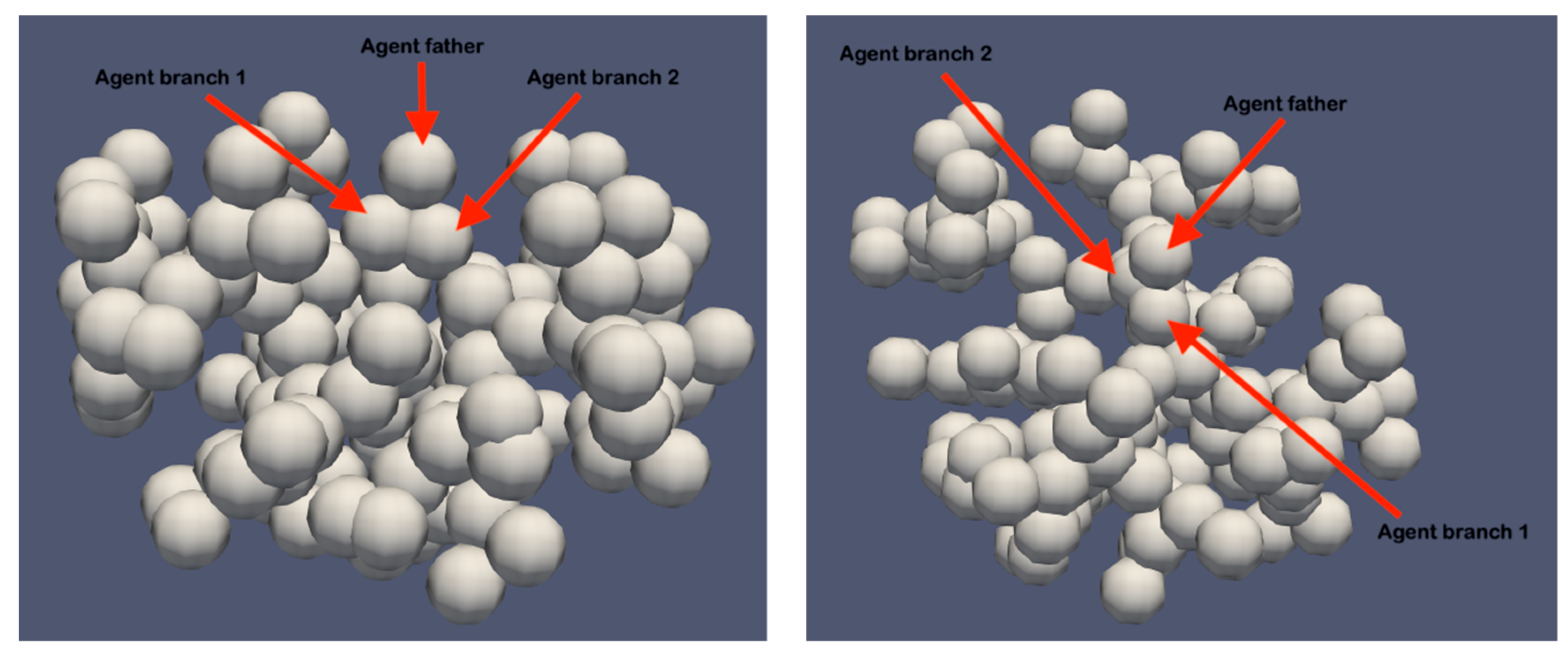
2.2. Building the Simulation Space
- Given the number of generations Ngen, define the number of segments as Nseg = 2Ngen − 1, the average segment length as avgSegLength, and the vector containing the coordinates of all the agents as Coords.
- Set the coordinates of the agent 0 (the first alveolar segment) to {0., 0., 0.} (i.e., the center of the simulation space), its unique index to 0, its origin to {0., 0., −avgSegLength/2}, and its end to {0., 0., avgSegLength/2}. Add {0., 0., 0.} to Coords.
- Loop (Nseg/2) times. At each step (starting from 1):
- a.
- Define the index of the father agent (i.e., the one from which branch 1 and branch 2 stem) as father = [(step + 1)/2] − 1.
- b.
- Project the coordinates of the father agent along its axis by avgSegLength.
- c.
- For each of the two new branches:
- i.
- Generate random polar and azimuthal angles θ and φ.
- ii.
- Rotate the projected father agent by θ and φ, keeping its origin fixed.
- iii.
- If the branch doesn’t overlap with the other agents already in the tree add its coordinates to Coords.
- iv.
- If the branch overlaps with any of the other agents already in the tree, go back to step i.
- Write Coords to a file, so that it can be used for multiple simulations.
2.3. Extracellular Mediators
- the function used to define substances at the beginning of a simulation so that both the depleting substance and the binding coefficient can be specified;
- the function that implements the central difference method by embedding the local depletion (i.e., , where is the binding coefficient and is the concentration of the depleting substance in the i-th box where the calculation is performed) into the decay term.
2.4. Hybrid Multi-Agent-Based Model
2.4.1. Secretion Behaviors
- PDGF/MMP/TIMP/IL13 secretion by M2, TNFα secretion by M1, TNFα/MCP1 secretion by active AEC2 (whose activation process is described in Section 2.4.4), and TGFβ secretion by fibroblasts have similar templates and depend on constant secretion rates.
- Both FGF2 secretion by active AEC2 and ECM secretion by myofibroblasts are increased by TGFβ. Similarly, TGFβ secretion by M2 is increased by IL13. In our model, these dynamic rates are expressed by
- As in [48], the constant secretion rate of ECM by fibroblasts is multiplied by the factor in Equation (6), where is the value at which the ECM saturates. When , secretion is stopped.
- Activated AEC2 cells transform the latent form of TGFβ secreted by fibroblasts into its active form. Within the same time step, they reduce the local concentration of TGFβi and increase that of TGFβa by the same amount given by Equation (7), where is a saturation constant.
2.4.2. Proliferation Behaviors
- The proliferation of AEC2 is governed by a constant rate that allows for the survival of both the AEC2 and AEC1 populations. To do so, at every time step, the AEC2 population increases by a constant fraction.
- Proliferation of fibroblasts depends on the number of healthy AEC2 in homeostasis and is further increased by damage-associated mediators such as FGF2, TGFβa, and IL13. To uncouple the two mechanisms, we implement (i) the F_addition behavior by which the number of fibroblasts is incremented according to a fixed fraction of AEC2 (represented by the parameter ), and (ii) the F_proliferate that computes the fraction of newborn fibroblasts using the rate in Equation (8).
2.4.3. Differentiation Behaviors
- In AEC21_Differentiation and M12_Differentiation, the phenotypes of constant fractions of AEC2 and M1 are changed so that the AEC1 and M2 populations in homeostasis can survive.
- M0 cells act as a reservoir for M1 cells (hence indirectly for M2 cells) both in homeostasis and in inflammatory conditions. In our model, we implement two different mechanisms within the same behavior to ensure that a minimum number of M1 is always maintained. We define a constant rate for the M0 to M1 differentiation and use this value only if the concentration of MCP1 is too low to provide the M1 cells’ baseline. As the inflammation develops and the MCP1 can sustain the growth of M1 cells, we use the differentiation rate in Equation (9), where the last factor ensures that M1 cells never exceed M0 cells, as described in [48]. As stated before, the principle of local information exchange is not violated since each alveolar duct agent records only its number of M0 and M1 cells. Therefore, may assume different values for different agents.
- Fibroblast to myofibroblast and M2 to M1 differentiation are implemented in F_MF_Differentiation and M21_Differentiation. Since both are triggered by extracellular mediators, their templates are similar, and the rates that describe the transitions are outlined in the following equations
2.4.4. Activation Behaviors
2.4.5. Apoptosis Behaviors
2.5. Initial Conditions and Input/Output System
- An operation runs through all the agents, collects the number of cells for each cell type, and stores the information in a vector.
- Another operation exploits the agents as probes: it gathers their position, uses these positions to get the local concentration of all the substances, computes the average concentration for each substance, and finally stores the information in a vector (note that there is no measurement within the diffusion grid boxes where agents are not localized).
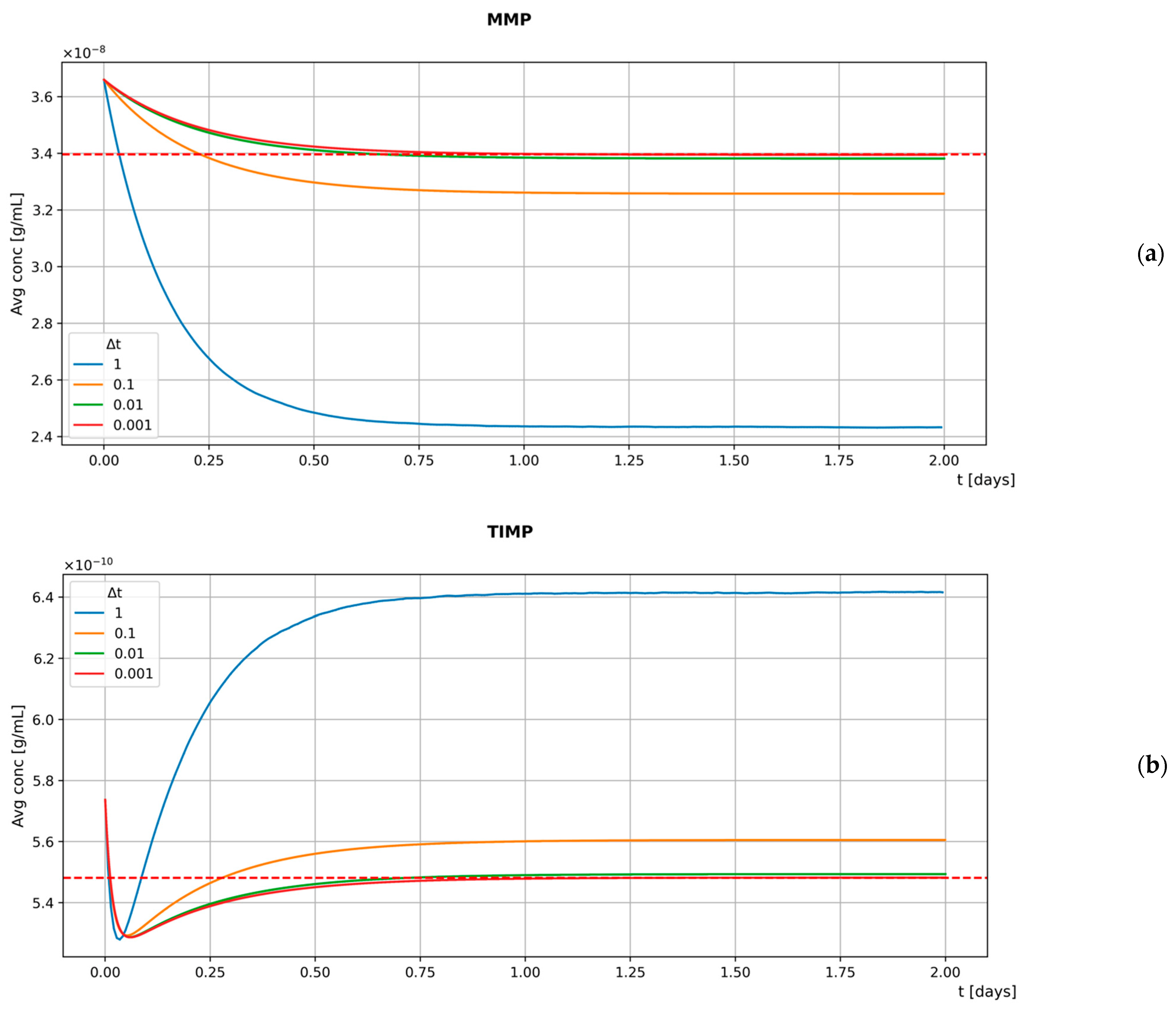
2.6. Sensitivity Analysis
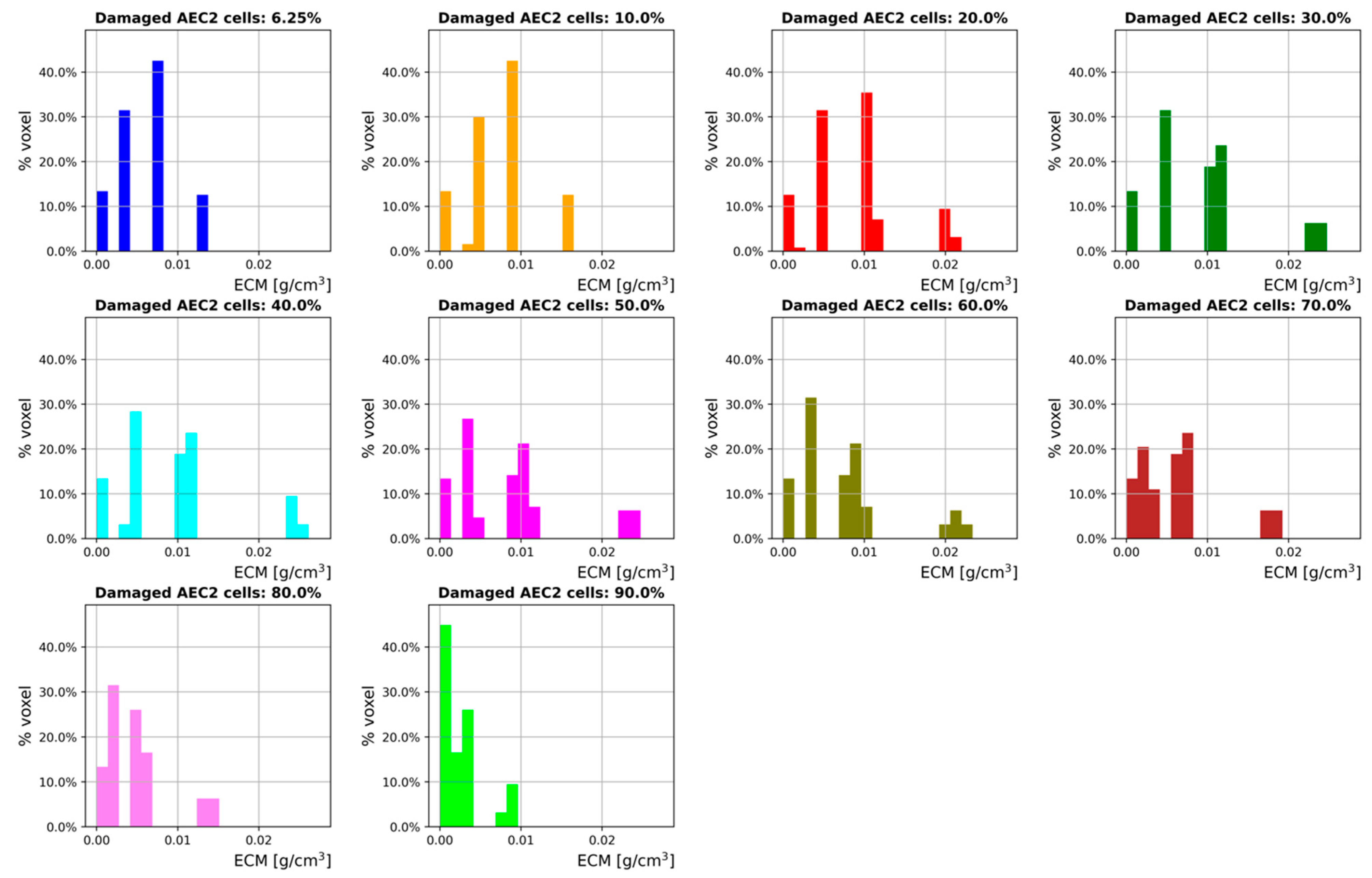
3. Results
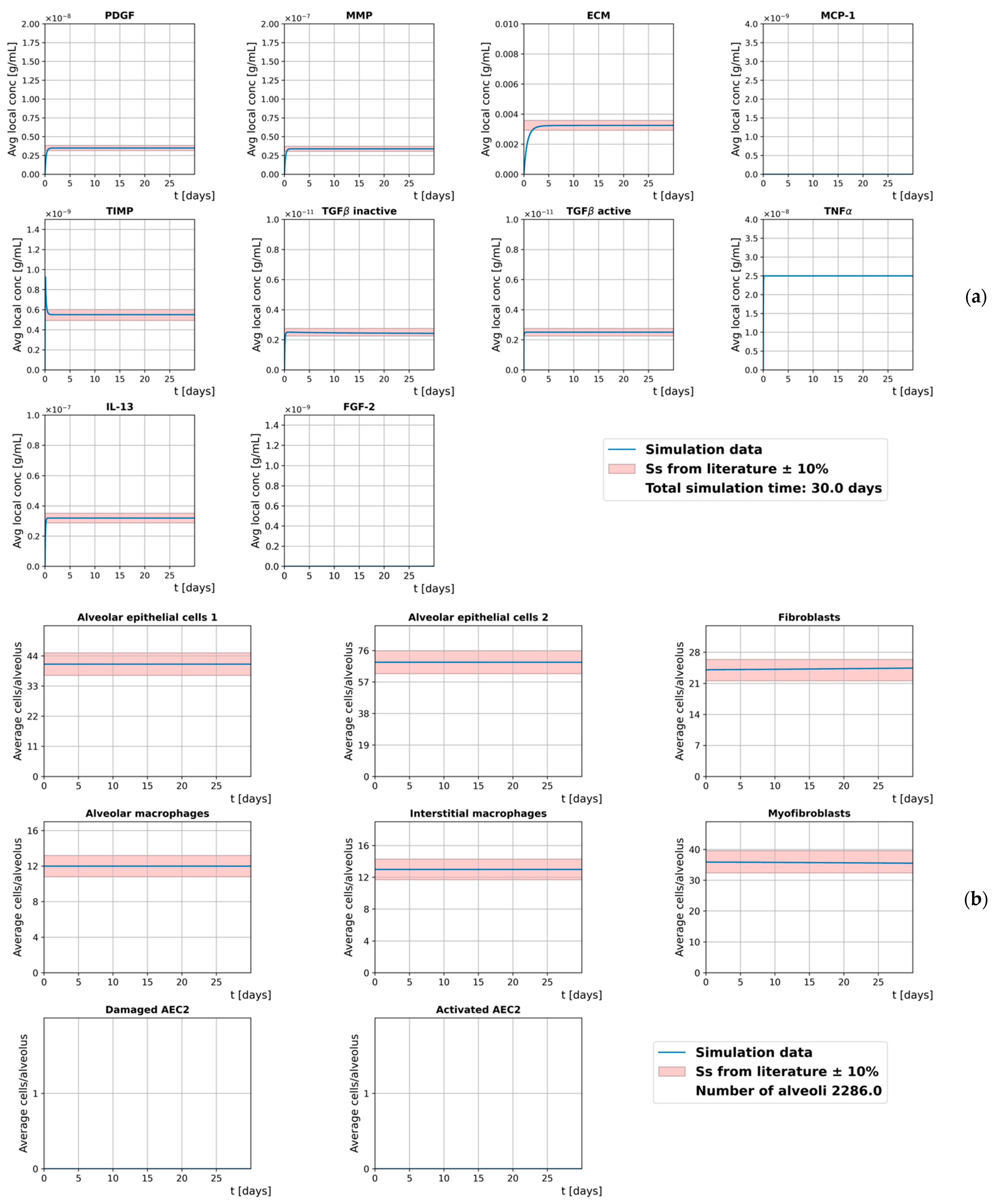
3.1. Homeostasis
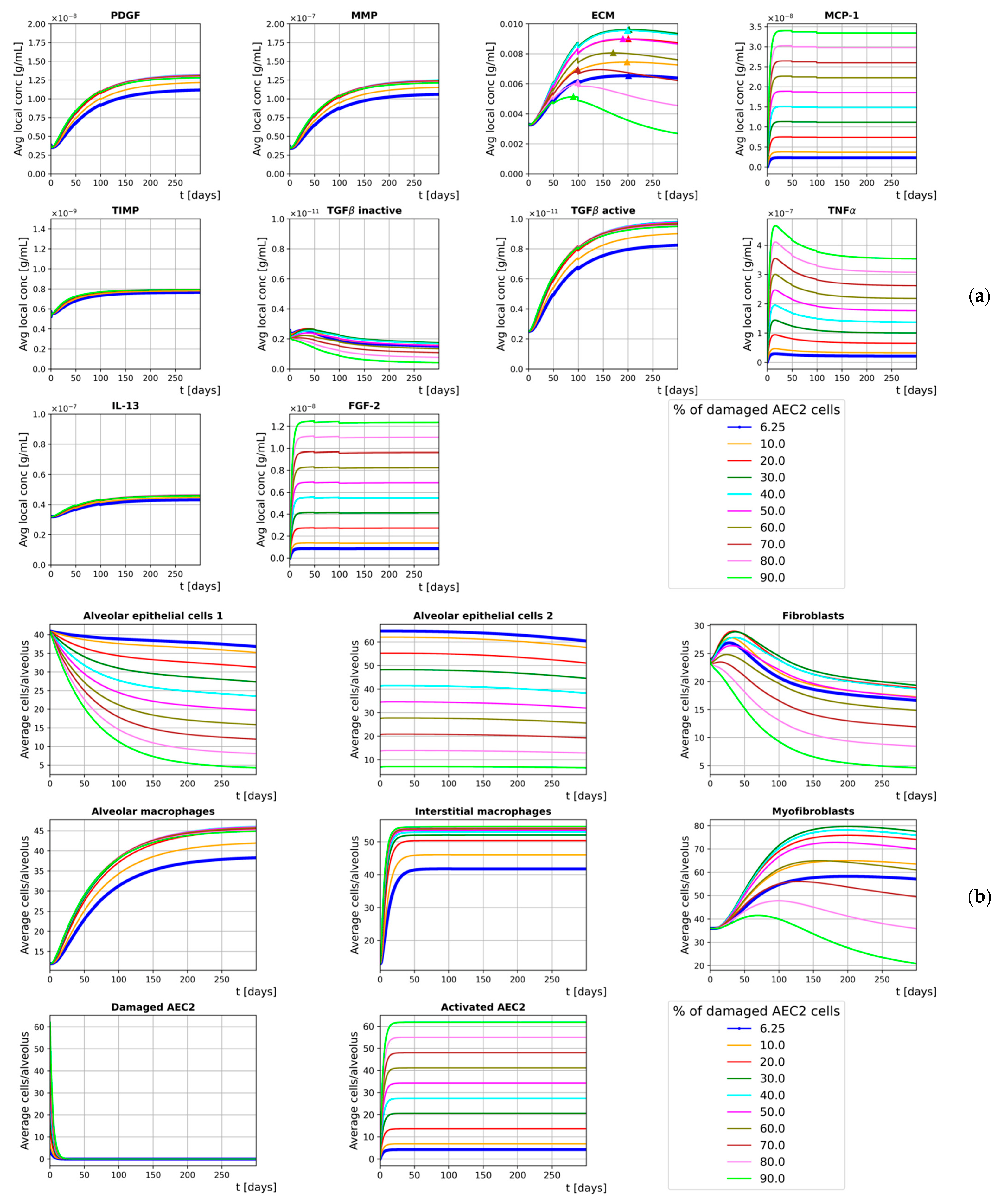
3.2. Inflammation
3.3. Sensitivity Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richeldi, L.; Collard, H.R.; Jones, M.G. Idiopathic pulmonary fibrosis. Lancet 2017, 389, 1941–1952. [Google Scholar] [CrossRef]
- Jin, H.; Yoo, Y.; Kim, Y.; Kim, Y.; Cho, J.; Lee, Y.S. Radiation-induced lung fibrosis: Preclinical animal models and therapeutic strategies. Cancers 2020, 12, 1561. [Google Scholar] [CrossRef] [PubMed]
- Türkkan, G.; Willems, Y.; Hendriks, L.E.L.; Mostard, R.; Conemans, L.; Gietema, H.A.; Mitea, C.; Peeters, S.; De Ruysscher, D. Idiopathic pulmonary fibrosis: Current knowledge, future perspectives and its importance in radiation oncology. Radiother. Oncol. 2021, 155, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R.; Sapoval, B.; Filoche, M. Design of peripheral airways for efficient gas exchange. Respir. Physiol. Neurobiol. 2005, 148, 3–21. [Google Scholar] [CrossRef] [PubMed]
- Martinez, F.J.; Collard, H.R.; Pardo, A.; Raghu, G.; Richeldi, L.; Selman, M.; Swigris, J.J.; Taniguchi, H.; Wells, A.U. Idiopathic pulmonary fibrosis. Nat. Rev. Dis. Prim. 2017, 3, 220. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R. Lung morphometry: The link between structure and function. Cell Tissue Res. 2017, 367, 413–426. [Google Scholar] [CrossRef]
- Sisson, T.H.; Mendez, M.; Choi, K.; Subbotina, N.; Courey, A.; Cunningham, A.; Dave, A.; Engelhardt, J.F.; Liu, X.; White, E.S.; et al. Targeted injury of type II alveolar epithelial cells induces pulmonary fibrosis. Am. J. Respir. Crit. Care Med. 2010, 181, 254–263. [Google Scholar] [CrossRef] [Green Version]
- Camelo, A.; Dunmore, R.; Sleeman, M.A.; Clarke, D.L. The epithelium in idiopathic pulmonary fibrosis: Breaking the barrier. Front. Pharmacol. 2014, 4, 111. [Google Scholar] [CrossRef] [Green Version]
- Selman, M.; Pardo, A. Role of epithelial cells in idiopathic pulmonary fibrosis: From innocent targets to serial killers. Proc. Am. Thorac. Soc. 2006, 3, 364–372. [Google Scholar] [CrossRef]
- Parimon, T.; Yao, C.; Stripp, B.R.; Noble, P.W.; Chen, P. Alveolar epithelial type II cells as drivers of lung fibrosis in idiopathic pulmonary fibrosis. Int. J. Mol. Sci. 2020, 21, 2269. [Google Scholar] [CrossRef] [Green Version]
- Yao, C.; Guan, X.; Carraro, G.; Parimon, T.; Liu, X.; Huang, G.; Mulay, A.; Soukiasian, H.J.; David, G.; Weigt, S.S.; et al. Senescence of Alveolar Type 2 Cells Drives Progressive Pulmonary Fibrosis. Am. J. Respir. Crit. Care Med. 2021, 203, 707–717. [Google Scholar] [CrossRef]
- Redente, E.F.; Keith, R.C.; Janssen, W.; Henson, P.M.; Ortiz, L.A.; Downey, G.P.; Bratton, D.L.; Riches, D.W.H. Tumor necrosis factor-α accelerates the resolution of established pulmonary fibrosis in mice by targeting profibrotic lung macrophages. Am. J. Respir. Cell Mol. Biol. 2014, 50, 825–837. [Google Scholar] [CrossRef] [Green Version]
- Broekelmann, T.J.; Limper, A.H.; Colby, T.V.; McDonald, J.A. Transforming growth factor β1 is present at sites of extracellular matrix gene expression in human pulmonary fibrosis. Proc. Natl. Acad. Sci. USA 1991, 88, 6642–6646. [Google Scholar] [CrossRef] [Green Version]
- Khalil, N.; Whitman, C.; Zuo, L.; Danielpour, D.; Greenberg, A. Regulation of alveolar macrophage transforming growth factor-β secretion by corticosteroids in bleomycin-induced pulmonary inflammation in the rat. J. Clin. Investig. 1993, 92, 1812–1818. [Google Scholar] [CrossRef] [Green Version]
- Nagaoka, I.; Trapnell, B.C.; Crystal, R.G. Upregulation of platelet-derived growth factor-A and -B gene expression in alveolar macrophages of individuals with idiopathic pulmonary fibrosis. J. Clin. Investig. 1990, 85, 2023–2027. [Google Scholar] [CrossRef] [Green Version]
- Hancock, A.; Armstrong, L.; Gama, R.; Millar, A. Production of interleukin 13 by alveolar macrophages from normal and fibrotic lung. Am. J. Respir. Cell Mol. Biol. 1998, 18, 60–65. [Google Scholar] [CrossRef]
- Selman, M.; Ruiz, V.; Cabrera, S.; Segura, L.; Ramírez, R.; Barrios, R.; Pardo, A. TIMP-1, -2, -3, and -4 in idiopathic pulmonary fibrosis. A prevailing nondegradative lung microenvironment? Am. J. Physiol. Cell. Mol. Physiol. 2000, 279, L562–L574. [Google Scholar] [CrossRef]
- Kelley, J.; Fabisiak, J.P.; Hawes, K.; Absher, M. Cytokine signaling in lung: Transforming growth factor-beta secretion by lung fibroblasts. Am. J. Physiol. 1991, 260, L123–L128. [Google Scholar] [CrossRef]
- Raghu, G.; Masta, S.; Meyers, D.; Narayanan, A.S. Collagen synthesis by normal and fibrotic human lung fibroblasts and the effect of transforming growth factor-beta. Am. Rev. Respir. Dis. 1989, 140, 95–100. [Google Scholar] [CrossRef]
- Lu, P.; Takai, K.; Weaver, V.M.; Werb, Z. Extracellular Matrix degradation and remodeling in development and disease. Cold Spring Harb. Perspect. Biol. 2011, 3, 124. [Google Scholar] [CrossRef]
- Morishima, Y.; Nomura, A.; Uchida, Y.; Noguchi, Y.; Sakamoto, T.; Ishii, Y.; Goto, Y.; Masuyama, K.; Zhang, M.J.; Hirano, K.; et al. Triggering the induction of myofibroblast and fibrogenesis by airway epithelial shedding. Am. J. Respir. Cell Mol. Biol. 2001, 24, 111. [Google Scholar] [CrossRef]
- Fichtner-Feigl, S.; Strober, W.; Kawakami, K.; Puri, R.K.; Kitani, A. IL-13 signaling through the IL-13α2 receptor is involved in induction of TGF-β1 production and fibrosis. Nat. Med. 2006, 12, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Hetzel, M.; Bachem, M.; Anders, D.; Trischler, G.; Faehling, M. Different effects of growth factors on proliferation and matrix production of normal and fibrotic human lung fibroblasts. Lung 2005, 183, 225–237. [Google Scholar] [CrossRef] [PubMed]
- Gu, L.; Zhu, Y.J.; Yang, X.; Guo, Z.J.; Xu, W.B.; Tian, X.L. Effect of TGF-β/Smad signaling pathway on lung myofibroblast differentiation. Acta Pharmacol. Sin. 2007, 28, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Hagimoto, N.; Kuwano, K.; Inoshima, I.; Yoshimi, M.; Nakamura, N.; Fujita, M.; Maeyama, T.; Hara, N. TGF-β1 as an Enhancer of Fas-Mediated Apoptosis of Lung Epithelial Cells. J. Immunol. 2002, 168, 6470–6478. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saito, A.; Okazaki, H.; Sugawara, I.; Yamamoto, K.; Takizawa, H. Potential action of IL-4 and IL-13 as fibrogenic factors on lung fibroblasts in vitro. Int. Arch. Allergy Immunol. 2003, 132, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L. TGF-beta 1 induced fibroblast proliferation is mediated by the FGF-2/ERK pathway. Front. Biosci. 2012, 17, 2667. [Google Scholar] [CrossRef] [Green Version]
- Li, C.M.; Khosla, J.; Pagan, I.; Hoyle, P.; Sannes, P.L. TGF-β1 and fibroblast growth factor-1 modify fibroblast growth factor-2 production in type II cells. Am. J. Physiol.-Lung Cell. Mol. Physiol. 2000, 279, 1038–1046. [Google Scholar] [CrossRef]
- Boström, H.; Willetts, K.; Pekny, M.; Levéen, P.; Lindahl, P.; Hedstrand, H.; Pekna, M.; Hellström, M.; Gebre-Medhin, S.; Schalling, M.; et al. PDGF-A signaling is a critical event in lung alveolar myofibroblast development and alveogenesis. Cell 1996, 85, 863–873. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Rekhter, M.D.; Gordon, D.; Phan, S.H. Myofibroblasts and their role in lung collagen gene expression during pulmonary fibrosis: A combined immunohistochemical and in situ hybridization study. Am. J. Pathol. 1994, 145, 114–125. [Google Scholar]
- Petrov, V.V.; Fagard, R.H.; Lijnen, P.J. Stimulation of collagen production by transforming growth factor-β1 during differentiation of cardiac fibroblasts to myofibroblasts. Hypertension 2002, 39, 258–263. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.K.; Kugler, M.C.; Wolters, P.J.; Robillard, L.; Galvez, M.G.; Brumwell, A.M.; Sheppard, D.; Chapman, H.A. Alveolar epithelial cell mesenchymal transition develops in vivo during pulmonary fibrosis and is regulated by the extracellular matrix. Proc. Natl. Acad. Sci. USA 2006, 103, 13180–13185. [Google Scholar] [CrossRef] [Green Version]
- Tashiro, J.; Rubio, G.A.; Limper, A.H.; Williams, K.; Elliot, S.J.; Ninou, I.; Aidinis, V.; Tzouvelekis, A.; Glassberg, M.K. Exploring animal models that resemble idiopathic pulmonary fibrosis. Front. Med. 2017, 4, 1211. [Google Scholar] [CrossRef] [Green Version]
- Brodland, G.W. How computational models can help unlock biological systems. Semin. Cell Dev. Biol. 2015, 47–48, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Winslow, R.L.; Trayanova, N.; Geman, D.; Miller, M.I. Computational medicine: Translating models to clinical care. Sci. Transl. Med. 2012, 4, 112. [Google Scholar] [CrossRef] [Green Version]
- Saha, A.; Saha, B. Novel coronavirus SARS-CoV-2 (Covid-19) dynamics inside the human body. Rev. Med. Virol. 2020, 30, 1411. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 Epidemic and Implementation of Population-Wide Interventions in Italy; Springer: Berlin/Heidelberg, Germany, 2020; Volume 26, ISBN 4159102008837. [Google Scholar]
- Van Dyke Parunak, H.; Savit, R.; Riolo, R.L. Agent-Based Modeling vs. Equation-Based Modeling: A Case Study and Users’ Guide; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1534, pp. 10–25. [Google Scholar]
- Murray, J.D. (Ed.) Mathematical Biology II. In Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 18, ISBN 978-0-387-95228-4. [Google Scholar]
- Murray, J.D. (Ed.) Mathematical Biology I. In Interdisciplinary Applied Mathematics, 3rd ed.; Springer: New York, NY, USA, 2002; Volume 17, ISBN 978-0-387-95223-9. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [Green Version]
- Cilfone, N.A.; Kirschner, D.E.; Linderman, J.J. Strategies for Efficient Numerical Implementation of Hybrid Multi-scale Agent-Based Models to Describe Biological Systems. Cell. Mol. Bioeng. 2015, 8, 119–136. [Google Scholar] [CrossRef] [Green Version]
- Breitwieser, L.; Hesam, A.; de Montigny, J.; Vavourakis, V.; Iosif, A.; Jennings, J.; Kaiser, M.; Manca, M.; Di Meglio, A.; Al-Ars, Z.; et al. BioDynaMo: A modular platform for high-performance agent-based simulation. Bioinformatics 2021, 19, 735. [Google Scholar] [CrossRef]
- Warsinske, H.C.; Wheaton, A.K.; Kim, K.K.; Linderman, J.J.; Moore, B.B.; Kirschner, D.E. Computational Modeling Predicts Simultaneous Targeting of Fibroblasts and Epithelial Cells Is Necessary for Treatment of Pulmonary Fibrosis. Front. Pharmacol. 2016, 7, 1452. [Google Scholar] [CrossRef] [Green Version]
- Rikard, S.M.; Athey, T.L.; Nelson, A.R.; Christiansen, S.L.M.; Lee, J.J.; Holmes, J.W.; Peirce, S.M.; Saucerman, J.J. Multiscale Coupling of an Agent-Based Model of Tissue Fibrosis and a Logic-Based Model of Intracellular Signaling. Front. Physiol. 2019, 10, 7566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, B.N.; Price, I.M.; Toapanta, F.R.; DeAlmeida, D.R.; Wiley, C.A.; Ross, T.M.; Oury, T.D.; Vodovotz, Y. An agent-based model of inflammation and fibrosis following particulate exposure in the lung. Math. Biosci. 2011, 231, 186–196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wellman, T.J.; Mondoñedo, J.R.; Davis, G.S.; Bates, J.H.T.; Suki, B. Topographic distribution of idiopathic pulmonary fibrosis: A hybrid physics- and agent-based model. Physiol. Meas. 2018, 39, 064007. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Marsh, C.; Friedman, A. A mathematical model of idiopathic pulmonary fibrosis. PLoS ONE 2015, 10, e0135097. [Google Scholar] [CrossRef] [Green Version]
- Haefeli-Bleuer, B.; Weibel, E.R. Morphometry of the human pulmonary acinus. Anat. Rec. 1988, 220, 401–414. [Google Scholar] [CrossRef]
- Paulin, G.A.; Ouriadov, A.; Lessard, E.; Sheikh, K.; McCormack, D.G.; Parraga, G. Noninvasive quantification of alveolar morphometry in elderly never- and ex-smokers. Physiol. Rep. 2015, 3, 113. [Google Scholar] [CrossRef]
- Hansen, J.E.; Ampaya, E.P. Human air space shapes, sizes, areas, and volumes. J. Appl. Physiol. 1975, 38, 990–995. [Google Scholar] [CrossRef]
- Weibel, E.R. Morphometry of the Human Lung; Springer: Berlin/Heidelberg, Germany, 1963; ISBN 9783642875557. [Google Scholar]
- Yablonskiy, D.A.; Sukstanskii, A.L.; Woods, J.C.; Gierada, D.S.; Quirk, J.D.; Hogg, J.C.; Cooper, J.D.; Conradi, M.S. Quantification of lung microstructure with hyperpolarized 3He diffusion MRI. J. Appl. Physiol. 2009, 107, 1258–1265. [Google Scholar] [CrossRef] [Green Version]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling; MIT Press: Cambridge, MA, USA, 2015; ISBN 978-0-262-73189-8. [Google Scholar]
- Dvorak, P.; Bednar, D.; Vanacek, P.; Balek, L.; Eiselleova, L.; Stepankova, V.; Sebestova, E.; Kunova Bosakova, M.; Konecna, Z.; Mazurenko, S.; et al. Computer-assisted engineering of hyperstable fibroblast growth factor 2. Biotechnol. Bioeng. 2018, 115, 850–862. [Google Scholar] [CrossRef]
- Kołodziej, M.; Sauer, D.G.; Beck, J.; Marek, W.K.; Hahn, R.; Jungbauer, A.; Dürauer, A.; Piątkowski, W.; Antos, D. Scale up of a chromatographic capture step for a clarified bacterial homogenate—Influence of mass transport limitation and competitive adsorption of impurities. J. Chromatogr. A 2020, 1618, 7253. [Google Scholar] [CrossRef]
- Stone, K.C.; Mercer, R.R.; Gehr, P.; Stockstill, B.; Crapo, J.D. Allometric relationships of cell numbers and size in the mammalian lung. Am. J. Respir. Cell Mol. Biol. 1992, 6, 235–243. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F. ROOT—An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Perez, J.R.; Lee, S.; Ybarra, N.; Maria, O.; Serban, M.; Jeyaseelan, K.; Wang, L.M.; Seuntjens, J.; Naqa, I. El A comparative analysis of longitudinal computed tomography and histopathology for evaluating the potential of mesenchymal stem cells in mitigating radiation-induced pulmonary fibrosis. Sci. Rep. 2017, 7, 110. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Moustafa, M.R.; Cao, L.; Kriegsmann, M.; Winter, M.; Schwager, C.; Jones, B.; Wang, S.; Bäuerle, T.; Zhou, P.K.; et al. Modeling and multiscale characterization of the quantitative imaging based fibrosis index reveals pathophysiological, transcriptome and proteomic correlates of lung fibrosis induced by fractionated irradiation. Int. J. Cancer 2019, 144, 3160–3173. [Google Scholar] [CrossRef] [Green Version]
- Mah, K.; Van Dyk, J. Quantitative measurement of changes in human lung density following irradiation. Radiother. Oncol. 1988, 11, 169–179. [Google Scholar] [CrossRef]
- Lehnert, S.; El-Khatib, E. The use of CT densitometry in the assessment of radiation-induced damage to the rat lung: A comparison with other endpoints. Int. J. Radiat. Oncol. Biol. Phys. 1989, 16, 117–124. [Google Scholar] [CrossRef]
- Du, F.; Liu, H.; Wang, W.; Zhang, Y.; Li, J. Correlation Between Lung Density Changes Under Different Dose Gradients and Radiation Pneumonitis—Based on an Analysis of Computed Tomography Scans During Esophageal Cancer Radiotherapy. Front. Oncol. 2021, 11, 19. [Google Scholar] [CrossRef]
- Schröder, C.; Engenhart-Cabillic, R.; Kirschner, S.; Blank, E.; Buchali, A. Changes of lung parenchyma density following high dose radiation therapy for thoracic carcinomas—An automated analysis of follow up CT scans. Radiat. Oncol. 2019, 14, 17. [Google Scholar] [CrossRef]
- Figueredo, G.P.; Siebers, P.O.; Owen, M.R.; Reps, J.; Aickelin, U. Comparing stochastic differential equations and agent-based modelling and simulation for early-stage cancer. PLoS ONE 2014, 9, e95150. [Google Scholar]
- Grazul-Bilska, A.T.; Luthra, G.; Reynolds, L.P.; Bilski, J.J.; Johnson, M.L.; Adbullah, S.A.; Redmer, D.A.; Abdullah, K.M. Effects of basic fibroblast growth factor (FGF-2) on proliferation of human skin fibroblasts in type II diabetes mellitus. Exp. Clin. Endocrinol. Diabetes 2002, 110, 176–181. [Google Scholar] [CrossRef]


| Extracellular Substance | Initial Concentration (g cm−3) | Diffusion Coefficient (cm2 day−1) | Decay Coefficient (day−1) | Source |
|---|---|---|---|---|
| TGFβa | 2.51 × 10−12 | 4.32 × 10−2 | 3.33 × 102 | [48] |
| TGFβi | 2.51 × 10−12 | 4.32 × 10−2 | 3.33 × 102 | Estimated |
| PDGF | 3.50 × 10−9 | 8.64 × 10−2 | 3.84 | [48] |
| FGF2 | 0 | 5.62 × 10−2 | 1.66 | [55,56] |
| TIMP | 5.74 × 10−10 | 4.32 × 10−2 | 21.60 | [48] |
| ECM | 3.26 × 10−3 | 0 | 0.37 | [48] |
| MMP | 3.66 × 10−8 | 4.32 × 10−2 | 4.32 | [48] |
| TNFα | 2.50 × 10−8 | 1.29 × 10−2 | 55.45 | [48] |
| IL13 | 3.20 × 10−8 | 1.08 × 10−2 | 12.47 | [48] |
| MCP1 | 0 | 1.73 × 10−1 | 1.73 | [48] |
| Cell Type | Cell Number per Alveolus 1 | Source |
|---|---|---|
| AEC 1 | 41 | [57] |
| AEC 2 | 69 | [57] |
| M1 | 13 | [57] |
| M2 | 12 | [57] |
| Fibroblasts | 24 | [48,57] |
| Myofibroblasts | 36 2 | [48,57] |
| M0 3 | 65 | [48,57] |
| Secretion | Proliferation | Differentiation | Activation | Apoptosis | |
|---|---|---|---|---|---|
| AEC2_TNFaSecretion | M2_PDGFSecretion | F_Proliferate | AEC21_Differentiation | AEC2_Activation | Apoptosis |
| AEC2_MCP1Secretion | M2_MMPSecretion | F_Addition | F_MF_Differentiation | ||
| AEC2_FGF2Secretion | M2_TIMPSecretion | AEC2_Proliferate | M01_Differentiation | ||
| AEC2_TGFbSecretion | M2_TGFbSecretion | M12_Differentiation | |||
| F_TGFbSecretion | M2_IL13Secretion | M21_Differentiation | |||
| F_ECMSecretion | M1_TNFaSecretion | ||||
| MF_ECMSecretion |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cogno, N.; Bauer, R.; Durante, M. A 3D Agent-Based Model of Lung Fibrosis. Symmetry 2022, 14, 90. https://doi.org/10.3390/sym14010090
Cogno N, Bauer R, Durante M. A 3D Agent-Based Model of Lung Fibrosis. Symmetry. 2022; 14(1):90. https://doi.org/10.3390/sym14010090
Chicago/Turabian StyleCogno, Nicolò, Roman Bauer, and Marco Durante. 2022. "A 3D Agent-Based Model of Lung Fibrosis" Symmetry 14, no. 1: 90. https://doi.org/10.3390/sym14010090
APA StyleCogno, N., Bauer, R., & Durante, M. (2022). A 3D Agent-Based Model of Lung Fibrosis. Symmetry, 14(1), 90. https://doi.org/10.3390/sym14010090








