Abstract
Many natural radial symmetrical shapes (e.g., sea stars) follow the Gielis equation (GE) or its twin equation (TGE). A supertriangle (three triangles arranged around a central polygon) represents such a shape, but no study has tested whether natural shapes can be represented as/are supertriangles or whether the GE or TGE can describe their shape. We collected 100 pieces of Koelreuteria paniculata fruit, which have a supertriangular shape, extracted the boundary coordinates for their vertical projections, and then fitted them with the GE and TGE. The adjusted root mean square errors (RMSEadj) of the two equations were always less than 0.08, and >70% were less than 0.05. For 57/100 fruit projections, the GE had a lower RMSEadj than the TGE, although overall differences in the goodness of fit were non-significant. However, the TGE produces more symmetrical shapes than the GE as the two parameters controlling the extent of symmetry in it are approximately equal. This work demonstrates that natural supertriangles exist, validates the use of the GE and TGE to model their shapes, and suggests that different complex radially symmetrical shapes can be generated by the same equation, implying that different types of biological symmetry may result from the same biophysical mechanisms.
1. Introduction
Gielis [1] proposed a polar coordinate equation to describe natural shapes, especially symmetrical shapes, as follows:
Here, r and φ are the polar radius and polar angle of a curve transcribing the outline of a shape, respectively; A, B, n1, n2, and n3 are parameters that need to be estimated; and m is a positive integer that determines the number of angles of the curve generated in [0, 2π). This equation can be rewritten [2,3] as:
where , , and . We refer to Equation (2) as the Gielis equation (GE) for convenience hereinafter. The GE is derived from the superellipse equation, which can generate diamonds, ellipses, rectangles, and transitional shapes between these classical geometries [4,5]. The GE has been demonstrated to reflect the natural shapes of bamboo leaves [6,7], cross sections of plant stems [5,8], avian eggs [9], and ginkgo seeds [3]. However, for radially symmetrical objects with a finite number of multiple axes of symmetry, such as some species of sea stars, the GE cannot validly describe their shapes. Thus, Shi et al. [2] proposed a generalized version of the GE as follows:
where f is a link function, and re is the elementary polar radius, defined as:
Given the above, the original GE can be regarded as a special case of the generalized GE of Shi et al. [2], in which a linear relationship between r and re on a log–log scale is assumed, i.e.,
where . To describe the shapes of sea stars, Shi et al. [2] proposed another special case of the GE (their equation 12) in which a hyperbolic relationship was assumed between r and re on a log–log scale, i.e.,
where a, b, and c are parameters that need to be estimated. We refer to the generalized GE with Equation (6) above as its link function as the twin Gielis equation (TGE) for convenience herein, with “twin” reflecting the fact that the TGE and GE are both special cases of the generalized GE. The TGE was found to better fit the shapes of some sea stars compared to the GE [2].
There are many complex triangular shapes in nature, but such shapes have so far rarely been studied using parametric models. Herein, we propose the term “supertriangle”, which is derived from the terms “supercircle” and “superellipse” [1,4], to describe such shapes. Special instances of Lamé curves [4] can be generalized by the GE and TGE to produce a wide variety of bilaterally and radially symmetrical shapes. This includes supertriangles, which are obtained in the GE and TGE when m = 3 and comprise three outward-pointing triangles linked at their bases to a central polygon. Simulated examples of supertriangles can be found in Matsuura’s work [10]. Considering that, similarly to sea stars, some of these shapes exhibit multiple, finite axes of complex radial symmetry (i.e., tri- or pentaradial symmetry), it would be worthwhile to test whether they follow the GE or TGE. There is also value in comparing the goodness of fit and the characteristics of symmetry modelled by the GE and TGE. In this study, we examined the vertical projections (from the fruit petiole to the fruit tip) of 100 pieces of fruit from the golden rain tree (Koelreuteria paniculata Laxmann, which belongs to the family Sapindaceae), an important urban landscape tree species that has fruit in the form of papery capsules, with a three-pointed shape when viewed from the petiole or tip. The shape of this tree’s fruit with a vertical view resembles a supertriangle, a shape that presumably could be modelled by the GE or TGE; although, importantly, no past study has investigated supertriangles in nature. Therefore, we fitted the outlines of the planar projections of these fruit to the GE and TGE to test: (i) whether the vertical projections of these fruit are supertriangles that follow the GE or TGE; (ii) whether the GE or TGE was better able to describe such a shape; and (iii) whether the GE or TGE generated a more symmetrical shape.
2. Materials and Methods
2.1. Fruit Sampling and Photography
Given that the conspecific morphological variation in plant organs (e.g., leaf shape) mainly results from genetic differences (between cultivars) rather than differences in the growing environment [11], we randomly sampled 100 fresh pieces of fruit from six adult golden rain trees (K. paniculata) of the same population growing on the Nanjing Forestry University campus (32°08′20″ N, 118°80′84″ E) from 8–9 October 2021. In China, the tree is naturally distributed in the lower reaches of the Yellow River and the Yangtze River, including the studied site. We chose to sample fruit in early October as the fruit was mature, and some had even fallen to the ground from the sampled trees. The collected fruit was then quickly brought back to the laboratory and photographed using the camera of an Apple iPhone 11 with 3024 × 4032 pixels. Each fruit was placed vertically in a round hole in a plastic test tube rack (27.8 cm × 23.0 cm × 7.5 cm, radius = 2 cm) to keep the vertical axis through the fruit petiole to the fruit tip approximately perpendicular to the horizontal surface of the rack (see Figure 1 for an example). To reduce measurement error, we photographed the fruit one at a time while arranging a transparent plastic ruler around each piece to measure its actual scale. The mean distance from the lens of the camera to the fruit averaged 15 cm.

Figure 1.
Side view (A) and top view (vertical projection) (B) of a K. paniculata fruit.
2.2. Image Processing and Outline Data Acquisition
We adjusted the image size to its actual size according to the scale of the ruler in the photo, and then saved the adjusted photos as BMP files at a resolution of 600 dpi. The m-file based on MATLAB (version ≥ 2009a) developed by Shi et al. [8,12] was used to extract the planar coordinates of the vertical projection of each fruit. The R script developed by Su et al. [13] was used to calculate the area of each fruit’s vertical projection; this was performed in R version 4.0.2 [14].
2.3. Models
Following the principle of Occam’s razor, we reduced the number of parameters in the tested models as much as possible to decrease model complexity. Simplified versions of the GE and TGE were used herein, rather than their original versions, as follows:
and
The two simplified equations were obtained by setting m = 3 and k = 1 in Equations (2) and (6). Thus, when we mention the GE and TGE hereinafter, we refer to Equations (7) and (8), respectively, and we do not refer to their original versions again.
2.4. Data Fitting Methods
For a standard curve generated by the GE or TGE in [0, 2π), the polar point is located at (0, 0) and the x-axis passes through the apex of an angle and the intersection of two other lobes of the circumcircle of the supertriangle, which is referred to as the major axis for convenience. However, for a scanned image, the polar point may not be the origin, and the major axis may not overlap with the x-axis. Thus, we needed to add three additional location parameters—x0, y0, and θ—to represent the planar coordinates of the polar point and the angle between the major axis and the x-axis. We estimated the location parameters and model parameters using the Nelder-Mead optimization method [15] by minimizing the target function of the residual sum of squares (RSS) between the observed polar radii from the polar point to the data points on the outline of the fruit’s vertical projection and those predicted by the GE or TGE as follows:
where and represent the i-th observed and predicted polar radii, respectively, and N represents the number of data points on the outline of the fruit’s vertical projection.
2.5. Comparison and Analysis of Models
To compare the goodness of fit to the data between the GE and TGE, the adjusted root mean square error (RMSEadj) was calculated [2,16] as:
Here, A represents the area of the fruit’s vertical projection. As the number of data points on the outline of a fruit projection image is fairly large (ranging from 2990 to 3000 for each of the 100 projections), it is almost meaningless to compare models by considering the influence of the number of model parameters on model structural complexity using, for example, Akaike’s Information Criterion or its corrected version [17,18]. However, the parameters n2 and n3 in the GE and TGE play important roles in determining whether a curve is more or less symmetrical, and thus can be used to evaluate the shapes produced by the two tested models. When the two parameters are equal, the GE or TGE can generate a perfect radially symmetrical shape with perfect bilateral symmetry along any one of the three major axes of a supertriangle. There is no evidence that the fruit of K. paniculata needs to deviate from a perfect triradially symmetrical shape. Thus, we hypothesized that the two parameters should be equal to maintain the radial symmetry of the fruit’s shape in vertical projection. To test whether this hypothesis held true, we performed a linear regression between the estimates of n3 and n2. If the 95% confidence interval (CI) of the slope included 1 and the intercept was not significant, we concluded that n3 was not significantly different from n2, which suggested that the shape produced had radial symmetry; otherwise, a deviation from perfect radial symmetry for the vertical projections of fruit was suggested.
Analysis of variance (ANOVA) at a 0.05 significance level was used to test whether there was a significant difference in the adjusted RMSE values between the GE and TGE. In addition, the mean and standard deviation of the 100 fruit projection areas were calculated for obtaining the coefficient of variation (=standard deviation/mean × 100%) of the samples. The statistical software R (version 4.0.2) [14] was used to carry out these calculations and statistical analyses.
3. Results
The mean and standard deviation of the 100 fruit vertical projection areas were 6.59 and 0.91 cm2, respectively. The coefficient of variation in the vertical projection size was equal to 13.86%.
Figure 2 shows the fitted results for four fruit vertical projections randomly sampled from the 100 studied projections. Although the shapes predicted by the GE and TGE did not overlap perfectly with the photographed outlines of fruit vertical projections, both equations basically generated shapes that approximated those of the actual projections. The adjusted RMSEs for the four samples shown in Figure 2 were all smaller than 0.05, which means that for each sample, the average absolute deviation between the observed and predicted radii from the polar point to the outline of the fruit’s vertical projection was less than 5% of the radius of a circle whose hypothetical area equals that of the projection.
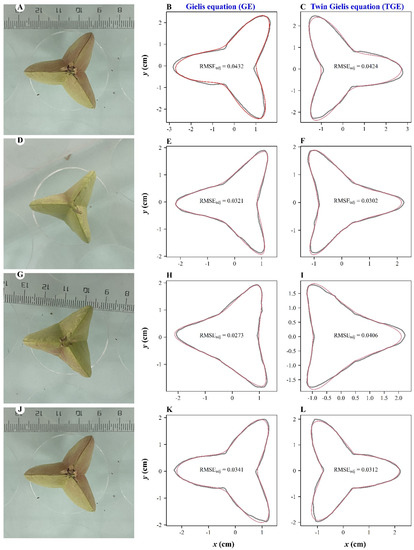
Figure 2.
Four sample vertical projections of K. paniculata fruit (A,D,G,J), and their fitted outlines predicted by the GE (B,E,H,K) and by the TGE (C,F,I,L). For the panels in the second and third columns from the left, the gray curves are the scanned outlines of fruit projections, and the red curves are the outlines predicted by the GE (second column) and by the TGE (third column).
The fitted results of the GE and TGE to the 100 fruit vertical projections were tabulated in Tables S1 and S2 in the online Supplementary Materials. For the GE, the adjusted RMSE values of 77 out of 100 fruit vertical projections were less than 0.05, while for the TGE 73 out of 100 fruit vertical projections had adjusted RMSE values less than 0.05. For the remaining projections, the adjusted RMSEs for both equations ranged from 0.05 to 0.072 (Figure 3). This demonstrates the validity of both the GE and TGE for use in describing the shapes of projections of K. paniculata fruit. The adjusted RMSE values of the GE were smaller than those of the TGE for 57 out of 100 fruit vertical projections. However, there was no significant overall difference in adjusted RMSEs between the GE and TGE (F1,198 = 0.97; p = 0.326). The estimates of n3 and n2 in the GE were not equal because the estimated intercept of the linear regression between these was significantly different from zero and the 95% CI of the slope was significantly different from one (Figure 4A). In contrast, the estimates of n3 and n2 in the TGE did not differ significantly—i.e., the regression intercept was not significantly different from zero and the 95% CI of the slope included one. Thus, we dropped the intercept from the regression of n3 vs. n2 for the TGE and redid the regression with the intercept set to zero. After doing this, the 95% CI of the proportionality coefficient (i.e., the slope) still included one (Figure 4B), so we then concluded that the n3 and n2 parameters in the TGE tended to be equal for the vertical projections of K. paniculata fruit. This suggested that the fitted curve of the TGE exhibits the characteristic radial symmetry of the fruit vertical projections. However, the GE predicted a certain amount of deviation from radial symmetry for the fruit projections.
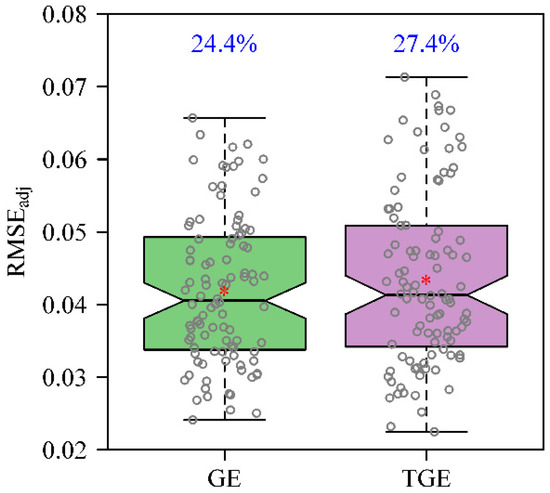
Figure 3.
Comparison of adjusted root mean square errors (RMSEadj) between the GE and TGE. The percentages above the uppermost whiskers represent the coefficients of variation of the RMSEadj values for each equation. The GE and TGE correspond to Equations (7) and (8), respectively, in the text.
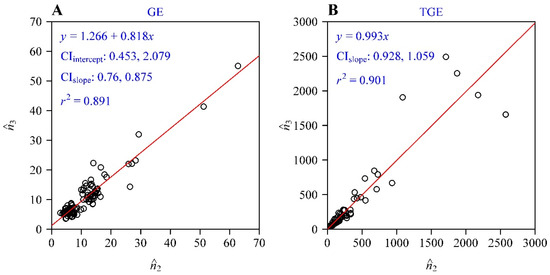
Figure 4.
Linear regressions of the estimate of n3 vs. that of n2 in the GE (A) and in the TGE (B). CI represents the 95% confidence interval. The number of data points plotted in each panel is 100.
4. Discussion
In this study, we photographed the vertical projections of fruit, rather than directly vertically scanning fruit to obtain their vertical projections, as the morphology of the fruit capsules made it difficult to maintain a consistent vertical view of the fruit using a photo scanner. We cannot exclude the possibility that artificial measurement errors were introduced when a smartphone was used to take the photos. Slight variations in the photographing distance and angle must inevitably have led to some errors [19]. In that case, even for a perfectly radially symmetrical object, some deformation from its original symmetry may have arisen when taking vertical photographs. In our calculations, there were relatively high adjusted RMSEs (>0.05) for a proportion (<30%) of fruit projections, which can be accounted for by such photographic errors to a great extent. The GE and TGE would have presumably been better able to describe the shapes of the fruit projections if photographic errors had been eliminated. Another source of errors is likely the individual variation in fruit morphology, as variation in fruit traits frequently exists within the same plant species [20]. If such variation does not change the radial symmetry of the fruit shape, it does not impact the validity of the GE and TGE in describing the shapes of fruit projections. However, some variation might have been caused by the physical compression of fruit by other fruit in close proximity as the studied fruit grew in clusters within the crown of the golden rain tree [21]. In addition to such physical compression through interactions between fruit, growth in clusters may also have led to heterogeneity in the light falling on different surfaces of the same fruit, potentially leading to deviation from the hypothesized radial symmetry of the fruit. The extreme physiological stress caused by low light has been demonstrated to increase the asymmetry of plant organs, especially of fruit [22]. Therefore, the asymmetry resulting from the physical compression of clustered fruit and physiological stress caused by light limitation may have decreased the goodness of fit to the data achieved by the GE and TGE.
There are many modern statistical approaches that can accurately describe or quantify the outlines of complex shapes (e.g., elliptic Fourier analysis, the square root velocity function and the Riemannian elastic metric, and comprehensive machine learning models) [23,24,25,26]. These methods allow one to extract and quantify the morphological traits of the outlines of objects and serve as a basis for classification and discrimination among different species or different individuals of the same species. However, these methods are not universal, and require very large sample sizes to accurately carry out such classification and discrimination, which is time-consuming. In practice, these approaches usually cannot quantify the extent of the asymmetry of an object and neglect to account for the scaling relationship or other functional relationships that exist between morphological dimensions that widely exist in biology and physics [27,28]. Relative to modern statistical methods, especially non-parametric data-fitting techniques, the GE and TGE have much simpler mathematical expressions, with four to five model parameters for describing supertriangles. Indeed, to describe sea star shapes, the GE and TGE only need three to four model parameters [2] as most sea star species have a lower extent of asymmetry than the fruit of the golden rain tree. It should also be noted that the GE and TGE can produce other shapes, such as avian eggs, bamboo leaves, ginkgo seeds, and the cross sections of some plant stems, in addition to sea stars [1,2,3,5,6,8,9,29]. This suggests that different types of shapes with natural symmetry can potentially be depicted by the same general geometric equation with different internal link functions, which deserves further investigation in the future.
In the GE and TGE, the parameters n2 and n3 control the extent of symmetry in the shapes produced. These two parameters differed significantly in the GE, and this indicates that the GE predicts asymmetrical projection shapes for the studied golden rain tree fruit; however, these two parameters did not differ significantly in the TGE, which suggests that the studied fruit projections tended to be radially symmetrical. Although the estimated n2 was proportional to the estimated n3 in the TGE, with the 95% CI of the slope including one, there were still some deviances between the two parameters, as reflected by the coefficient of determination of the regression being 0.901 (Figure 4B). This means that the TGE also reflects a certain degree of deviation from perfect radial symmetry for these fruit vertical projections, although the inequality between the parameters n2 and n3 in the TGE was less than in the GE. In other words, the GE might somewhat overfit the outlines of fruit vertical projections, while the TGE is somewhat conservative and less likely to reflect asymmetry. Considering model structure, the TGE is more complex than the GE as the TGE is based on the hypothesis of there being a hyperbolic relationship between the polar radius (r) and the elementary polar radius (re) of a shape on a log–log scale, whereas the GE hypothesizes a simpler linear relationship for these parameters on a log–log scale (see Equations (5) and (6)). However, there was no significant difference in goodness of fit between the GE and TGE. A shortcoming of the TGE is that it has five model parameters. Since n2 is not significantly different from n3, we set n2 = n3 to fit the outline data of the fruit projections. This setting limited the TGE from freely reflecting possible asymmetry during the data fitting, and thus decreased the ability of the TGE to describe actual fruit vertical projections. When n2 = n3 was set in the TGE, the mean adjusted RMSE was significantly higher than that of the GE and unconstrained TGE, although 52 out of 100 adjusted RMSEs of the simplified TGE (with n2 = n3) were still smaller than 0.05 and the remaining 48 adjusted RMSEs ranged from 0.05 to 0.10. Because of space limitations, we do not repeat these results in detail here. We do not recommend using this simplified TGE because it excessively limits the flexibility of model fitting without allowing for the existence of any asymmetry in the modelled shape. In addition, here we used the mature fruit. We did not attempt to provide “fixed” reference values of model parameters for the studied fruit. For immature fruit, the growth process may change the detailed numerical values of model parameters, but it should not change the conclusions that supertriangles exist in nature and that fruit vertical projections of K. paniculata can be described by GE or TGE.
We consider that the radial symmetrical structure for the vertical projections of K. paniculata fruit might be closely associated with a special function for seed emergence. The studied plant has fruit in the form of papery capsules. However, fresh fruit is not light, which implies that such a shape cannot facilitate the long-distance dispersal for seeds by themselves. The supertriangular cross section parallel to the ground is likely to reduce wind resistance and accelerate the speed of fruit falling. Thus, it can increase the impact of fruit falling on the ground to cause seeds to emerge from a cracked fruit.
5. Conclusions
The four-parameter Gielis equation with m = 3 (GE) and the five-parameter twin Gielis equation with m = 3 (TGE) can both describe the supertriangular shapes of the vertical projections of the studied golden rain tree fruit well. There was no significant difference in the goodness of fit (reflected by the adjusted root mean square errors) between the two equations. However, the GE tends to overfit asymmetrical shapes, and the TGE tends to produce more symmetrical shapes even when there should be a certain degree of asymmetry. The evidence obtained from the 100 studied fruit vertical projections shows that supertriangles described by the Gielis equation do exist in nature. The approximate radial symmetry of the three major axes of such shapes can be described by the GE and TGE, such as the five major axes of some sea star species in previous research. The present study shows that some radially symmetrical curves generated by the GE and TGE can correspond to actual natural shapes, and suggests that the natural symmetry of such shapes is likely to result from the same or similar development or growth mechanisms. Thus, the homology of natural symmetry can be expressed in mathematics. Additionally, it should be noted that, although in this study we focused on the fruit of Koelreuteria paniculata, supertriangular structures might exist in other organs of plants, e.g., flowers, in their early developmental stages [30], so this merits further investigation in the future.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/sym14010023/s1. Table S1: Fitted results for the outlines of 100 fruit vertical projections using the Gielis equation (GE); Table S2: Fitted results for the outlines of 100 fruit vertical projections using the twin Gielis equation (TGE).
Author Contributions
Fruit sampling and data acquisition, Y.L. (Yirong Li); formal analysis, B.K.Q. and P.S.; investigation, Y.L. (Yuping Li), B.K.Q., J.G., Y.L. (Yirong Li) and P.S.; writing—original draft preparation, Y.L. (Yuping Li) and P.S.; writing—review and editing, B.K.Q. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data can be found in Tables S1 and S2 in the online Supplementary Materials.
Acknowledgments
We thank Yabing Jiao and Kexin Yu for their valuable help in fruit sampling and data acquisition. We also thank the academic editor and three anonymous reviewers for their invaluable comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gielis, J. A general geometric transformation that unifies a wide range of natural and abstract shapes. Am. J. Bot. 2003, 90, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Ratkowsky, D.A.; Gielis, J. The generalized Gielis geometric equation and its application. Symmetry 2020, 12, 645. [Google Scholar] [CrossRef]
- Tian, F.; Wang, Y.; Sandhu, H.S.; Gielis, J.; Shi, P. Comparison of seed morphology of two ginkgo cultivars. J. Forest Res. 2020, 31, 751–758. [Google Scholar] [CrossRef]
- Lamé, G. Examen des Différentes Méthodes Employées Pour Résoudre les Problèmes de Géométrie; V. Courcier: Paris, France, 1818. [Google Scholar]
- Huang, W.; Li, Y.; Niklas, K.J.; Gielis, J.; Ding, Y.; Cao, L.; Shi, P. A superellipse with deformation and its application in describing the cross-sectional shapes of a square bamboo. Symmetry 2020, 12, 2073. [Google Scholar] [CrossRef]
- Shi, P.; Xu, Q.; Sandhu, H.S.; Gielis, J.; Ding, Y.; Li, H.; Dong, X. Comparison of dwarf bamboos (Indocalamus sp.) leaf parameters to determine relationship between spatial density of plants and total leaf area per plant. Ecol. Evol. 2015, 5, 4578–4589. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, L.; Reddy, G.V.P.; Hui, C.; Gielis, J.; Ding, Y.; Shi, P. A geometrical model for testing bilateral symmetry of bamboo leaf with a simplified Gielis equation. Ecol. Evol. 2016, 6, 6798–6806. [Google Scholar] [CrossRef]
- Shi, P.; Huang, J.; Hui, C.; Grissino-Mayer, H.D.; Tardif, J.; Zhai, L.; Wang, F.; Li, B. Capturing spiral radial growth of conifers using the superellipse to model tree-ring geometric shape. Front. Plant Sci. 2015, 6, 856. [Google Scholar] [CrossRef]
- Gielis, J.; Shi, P. Universal equations—A fresh perspective. Ann. N. Y. Acad. Sci. 2021; under review. [Google Scholar]
- Matsuura, M. Gielis’ superformula and regular polygons. J. Geom. 2015, 106, 383–403. [Google Scholar] [CrossRef]
- Koubouris, G.; Bouranis, D.; Vogiatzis, E.; Rezaei Nejad, A.; Giday, H.; Tsaniklidis, G.; Ligoxigakis, E.K.; Blazakis, K.; Kalaitzis, P.; Fanourakis, D. Leaf area estimation by considering leaf dimensions in olive tree. Sci. Hortic. 2018, 240, 440–445. [Google Scholar] [CrossRef]
- Shi, P.; Ratkowsky, D.A.; Li, Y.; Zhang, L.; Lin, S.; Gielis, J. General leaf-area geometric formula exists for plants—Evidence from the simplified Gielis equation. Forests 2018, 9, 714. [Google Scholar] [CrossRef]
- Su, J.; Niklas, K.J.; Huang, W.; Yu, X.; Yang, Y.; Shi, P. Lamina shape does not correlate with lamina surface area: An analysis based on the simplified Gielis equation. Glob. Ecol. Conserv. 2019, 19, e00666. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 1 July 2020).
- Nelder, J.A.; Mead, R. A simplex algorithm for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Wei, H.L.; Li, X.M.; Huang, H. Leaf shape simulation of castor bean and its application in nondestructive leaf area estimation. Int. J. Agric. Biol. Eng. 2019, 12, 135–140. [Google Scholar] [CrossRef]
- Shi, P.; Ge, F. A comparison of different thermal performance functions describing temperature-dependent development rates. J. Therm. Biol. 2010, 35, 225–231. [Google Scholar] [CrossRef]
- Spiess, A.-N.; Neumeyer, N. An evaluation of R squared as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual tree crown segmentation directly from UAV-Borne LiDAR data using the PointNet of deep learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Obeso, J.R.; Herrera, C.M. Inter- and intraspecific variation in fruit traits in co-occurring vertebrate-dispersed plants. Int. J. Plant Sci. 1994, 155, 382–387. [Google Scholar] [CrossRef]
- Wang, W.; Feng, X. Exploration on modeling and application of 3D digital model of landscape plants. Landsc. Archit. 2019, 26, 103–108. [Google Scholar] [CrossRef]
- Roy, B.A.; Stanton, M.L. Asymmetry of wild mustard, Sinapis arvensis (Brassicaceae), in response to severe physiological stresses. J. Evol. Biol. 1999, 12, 440–449. [Google Scholar] [CrossRef]
- Camargo Neto, J.; Meyer, G.E.; Jones, D.D.; Samal, A.K. Plant species identification using Elliptic Fourier leaf shape analysis. Comput. Electron. Agric. 2006, 50, 121–134. [Google Scholar] [CrossRef]
- Srivastava, A.; Klassen, E.; Joshi, S.H.; Jermyn, I.H. Shape analysis of elastic curves in Euclidean spaces. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1415–1428. [Google Scholar] [CrossRef] [PubMed]
- Laga, H.; Kurtek, S.; Srivastava, A.; Miklavcic, S.J. Landmark-free statistical analysis of the shape of plant leaves. J. Theor. Biol. 2014, 363, 41–502. [Google Scholar] [CrossRef] [PubMed]
- Teng, D.; Li, F.; Zhang, W. Using comprehensive machine-learning models to classify complex morphological characters. Ecol. Evol. 2021, 11, 10421–10431. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.W. On Growth and Form; Cambridge University Press: London, UK, 1917. [Google Scholar]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Gielis, J.; Caratelli, D.; Shi, P.; Ricci, P.E. A note on spirals and curvature. Growth Form 2020, 1, 1–8. [Google Scholar] [CrossRef][Green Version]
- Decraene, L.R.; Smets, E.; Clinckemaillie, D. Floral ontogeny and anatomy in Koelreuteria with special emphasis on monosymmetry and septal cavities. Plant Syst. Evol. 2000, 223, 91–107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).