Stability Analysis and Existence of Solutions for a Modified SIRD Model of COVID-19 with Fractional Derivatives

Abstract

This paper discusses and provides some analytical studies for a modified fractional-order SIRD mathematical model of the COVID-19 epidemic in the sense of the Caputo–Katugampola fractional derivative that allows treating of the biological models of infectious diseases and unifies the Hadamard and Caputo fractional derivatives into a single form. By considering the vaccine parameter of the suspected population, we compute and derive several stability results based on some symmetrical parameters that satisfy some conditions that prevent the pandemic. The paper also investigates the problem of the existence and uniqueness of solutions for the modified SIRD model. It does so by applying the properties of Schauder’s and Banach’s fixed point theorems.

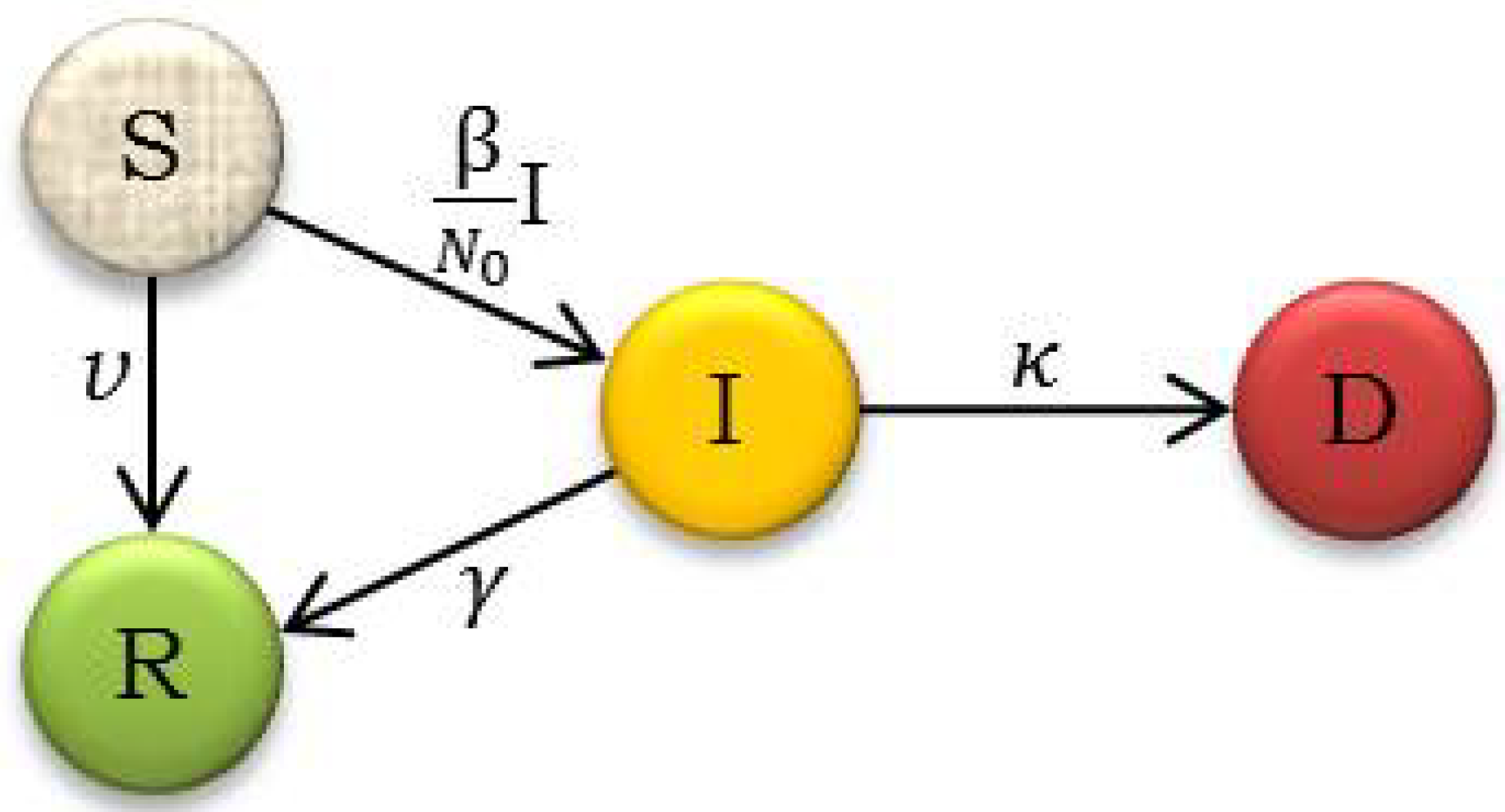
1. Introduction

The coronavirus pandemic was a major worldwide challenge in 2020. The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is the virus responsible for COVID-19 infection. The first cases were reported in Wuhan, China (see [1,2]); the virus spread throughout the rest of the world, leading to a pandemic outbreak that persisted throughout 2020 [3].

COVID-19 was declared to be a global threat, following its spread, and it affected 212 countries around the world. The available antivirals and vaccines at that point in time were ineffective against the new virus, while the new vaccines have reached the final stage of development and are being tested on larger populations.

A better understanding and evaluation of the existence, stability, and control of infectious diseases can be acquired through modeling them mathematically [4,5,6,7]. However, mathematical models’ classical approaches are not highly accurate in modeling such diseases; hence, the introduction of fractional differential equations for handling these problems becomes necessary. Of their various applications in applied fields, we mention optimization problems, artificial intelligence, medical diagnoses, etc. For further reading on the subject, readers can refer to the following works (Samko et al. 1993 [8], Podlubny 1999 [9], Kilbas et al. 2006 [10], Diethelm 2010 [11]).

The severity of this pandemic was a cause of concern for researchers throughout the world; this led some of them to study its origins, such as Hasan’s recent study et al. [12], which offered an insight into a novel COVID-19 compartmental SIRD model, whose representation is as follows:

$$\left\{\begin{array}{ccc}\frac{d}{dt}\mathfrak{S}\left(t\right)\hfill & =\hfill & -\beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{\mathcal{N}},\hfill \\ \frac{d}{dt}\mathfrak{I}\left(t\right)\hfill & =\hfill & \beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{\mathcal{N}}-\left(\gamma +\kappa \right)\mathfrak{I}\left(t\right),\hfill \\ \frac{d}{dt}\mathfrak{R}\left(t\right)\hfill & =\hfill & \gamma \mathfrak{I}\left(t\right),\hfill \\ \frac{d}{dt}\mathfrak{D}\left(t\right)\hfill & =\hfill & \kappa \mathfrak{I}\left(t\right).\hfill \end{array}\right.t\ge 0.$$

(1)

This model requires that the total population $\mathcal{N}$ be divided into the following epidemiological classes:

$$\mathfrak{S}:\mathrm{Susceptible}\mathrm{class},\mathfrak{I}:\mathrm{Infected}\mathrm{class},\mathfrak{R}:\mathrm{Recovered}\mathrm{class},\mathrm{and}\mathfrak{D}:\mathrm{Death}\mathrm{class}.$$

The parameters could be described as follows:

○

$\beta$ is the average number of contacts per person per time $t,$

○

$\gamma$ is the recovery rate,

○

$\kappa$ is the death rate.

Studying fractional calculus has been regarded as essential in the past few decades. It is considered to be an effective alternative to the integer-order models capable of describing and processing different structures’ properties of preservation and inheritance (see [8,10,13,14]).

Techniques of decomposition, homotopy, and variation were used to comprehensively analyze the mathematical models [15,16,17,18]. Currently, many methods such as the residual power series, symmetry, spectral, Fourier transform, similarity, and collocation methods are used to study and manage differential equations in both fractional and classical orders, along with their systems (for more details see [6,7,8,9,10,11,12,17,18,19,20,21,22,23,24,25,26,27,28,29]).

Furthermore, the most notable definitions among the fractional differential operators are those given by Riemann–Liouville, Caputo, and recently those given by Caputo–Katugampola. Each operator has different features that become apparent upon their use. The past two decades witnessed the adoption of Caputo derivatives to treat infectious diseases’ biological models. Therefore, we employ a fractional differential operator in order to signify that research proves the fractional derivatives’ efficiency in their description of acoustics, rheology, and polymeric chemistry among other scientific disciplines, in continuous-time modeling fields [30]. Deriving our inspiration from the aforementioned work, and by considering the positive vaccination factor $\upsilon$ as a parameter of the vaccine of the suspected population, we will study the ordinary model (1) under Caputo–Katugampola derivative. When $\rho >0$ and $0<\alpha <1,$

$$\left\{\begin{array}{ccc}{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\hfill & =\hfill & -\upsilon \mathfrak{S}\left(t\right)-\beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{{\mathcal{N}}_0},\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)\hfill & =\hfill & \beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{{\mathcal{N}}_0}-\left(\gamma +\kappa \right)\mathfrak{I}\left(t\right),\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R}\left(t\right)\hfill & =\hfill & \upsilon \mathfrak{S}\left(t\right)+\gamma \mathfrak{I}\left(t\right),\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\left(t\right)\hfill & =\hfill & \kappa \mathfrak{I}\left(t\right).\hfill \end{array}\right.$$

(2)

along with the positive initial conditions

$$\mathfrak{S}\left(0\right)={\mathfrak{S}}_0,\mathfrak{I}\left(0\right)={\mathfrak{I}}_0,\mathfrak{R}\left(0\right)={\mathfrak{R}}_0,\mathfrak{D}\left(0\right)={\mathfrak{D}}_0,$$

(3)

where $\beta ,$$\gamma$ and $\kappa$ are positive parameters could be described in the models (1), and $\upsilon$ is the vaccine of suspected population, ${\mathcal{N}}_0>0$ is the initial total population at the moment $t=0,$ with $0\le t\le T<\infty .$ The changes that occur in each human population in COVID-19 transmission for the modified SIRD model (2) can be interpreted by Figure 1;

It is essential to find the solution of (2) with an efficient technique. Considering this point, our main goal in this work is to determine the main symmetrical properties of the solution for the system of nonlinear fractional differential equation (2). First, checking the considered model’s stability necessitates establishing some existing results, determining the boundedness, and computing disease-free equilibrium points. Then, we provide the necessary conditions for obtaining at least one solution or its uniqueness using the fixed point theorems.

2. Preliminary and Necessary Definitions

The essential definitions from the fractional calculus theory are introduced in this section. Banach space of continuous functions from $\left[0,T\right]$ into $\mathbb{R}$ is denoted by $C\left(\left[0,T\right],\mathbb{R}\right),$ with the norm:

$${∥\phi ∥}_{\infty }=\underset{t\in \left[0,T\right]}{sup}\left|\phi \left(t\right)\right|.$$

Recently, Katugampola proposed a generalized derivative in [26,31,32]; moreover, he demonstrated the existence of solutions for Caputo–Katugampola fractional differential equations in [26]. It reads

$${}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\phi \left(t\right)={\mathcal{I}}_{0^{+}}^{1-\alpha ,\rho }\left({\tau }^{1-\rho }\frac{d}{d\tau }\phi \right)\left(t\right)=\frac{{\rho }^{\alpha }}{\mathsf{\Gamma }\left(1-\alpha \right)}{\int }_0^t\frac{{\phi }^{\prime }\left(\tau \right)}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{\alpha }}d\tau ,$$

(4)

where $\alpha \in \left(0,1\right),$ $\rho >0$ and

$${\mathcal{I}}_{0^{+}}^{\alpha ,\rho }\phi \left(t\right)=\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}\phi \left(\tau \right)d\tau ,\mathrm{with}\phi \in C\left(\left[0,T\right],\mathbb{R}\right).$$

(5)

At this point, it is worth mentioning that a fractional Cauchy-type problem was solved for an existence and uniqueness theorem in [20], a decomposition formula for the derivative of Caputo–Katugampola among others could, thus, be obtained as follows:

$${\mathcal{I}}_{0^{+}}^{\alpha ,\rho }{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\phi \left(t\right)=\phi \left(t\right)-\phi \left(0\right),\mathrm{for}\phi \in C\left(\left[0,T\right],\mathbb{R}\right).$$

(6)

It follows from (4) that if $\rho =1,$ Caputo–Katugampola derivative is found to be the well-known Caputo fractional derivative [9,10]. On the other hand, by applying the L’Hôspital rule, when $\rho \to 0^{+},$ we have

$$\begin{array}{cc}\hfill \underset{\rho \to 0^{+}}{lim}\frac{{\rho }^{\alpha }}{\mathsf{\Gamma }\left(1-\alpha \right)}{\int }_0^t\frac{{\phi }^{\prime }\left(\tau \right)}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{\alpha }}d\tau & =\frac{1}{\mathsf{\Gamma }\left(1-\alpha \right)}{\int }_0^t\underset{\rho \to 0^{+}}{lim}\frac{{\rho }^{\alpha }{\phi }^{\prime }\left(\tau \right)}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{\alpha }}d\tau \hfill \\ \hfill & =\frac{1}{\mathsf{\Gamma }\left(1-\alpha \right)}{\int }_0^t\frac{{\phi }^{\prime }\left(\tau \right)}{{\left(lnt-lns\right)}^{\alpha }}d\tau ,\hfill \end{array}$$

which is Caputo–Hadamard fractional derivative [19,31,32].

3. Analysis for the Modified SIRD Model of the Pandemic

Here, we present the solution’s feasibility region’s discussion and equilibrium points’ analysis.

Lemma 1.

The solution of the model under consideration is restricted to the feasible region given by

$$u=\left\{\left(\mathfrak{S},\mathfrak{I},\mathfrak{R},\mathfrak{D}\right)\in {\mathbb{R}}_{+}^4,0\le \mathcal{N}\left(t\right)\le {\mathcal{N}}_0\right\},$$

and the pandemic will occur if ${\mathfrak{S}}_0>\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0,$ where $\frac{\gamma +\kappa }{\beta }$ is referred to as a threshold phenomenon or a pandemic critical community size.

Proof. 

Let

$$\mathcal{N}\left(t\right)=\mathfrak{S}\left(t\right)+\mathfrak{I}\left(t\right)+\mathfrak{R}\left(t\right)+\mathfrak{D}\left(t\right),$$

(7)

then

$${}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathcal{N}\left(t\right)={}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)+{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)+{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R}\left(t\right)+{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\left(t\right).$$

Now, adding all the equations of (2), we obtain-4.6cm0cm

$$\begin{array}{cc}\hfill {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathcal{N}\left(t\right)& =-\upsilon \mathfrak{S}\left(t\right)-\beta \frac{\mathfrak{S}\left(t\right)\mathfrak{I}\left(t\right)}{{\mathcal{N}}_0}+\beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{{\mathcal{N}}_0}-\left(\gamma +\kappa \right)\mathfrak{I}\left(t\right)+\upsilon \mathfrak{S}\left(t\right)+\gamma \mathfrak{I}\left(t\right)+\kappa \mathfrak{I}\left(t\right)\hfill \\ \hfill & =0.\hfill \end{array}$$

(8)

Solving (8), for $\alpha \in \left(0,1\right)$ and $\rho >0,$ we obtain $\mathcal{N}\left(t\right)=Cte.$ As the initial population is represented with ${\mathcal{N}}_0,$ then we can symmetrically write:

$$\mathcal{N}\left(t\right)\le {\mathcal{N}}_0.$$

(9)

The dynamic model of the considered population is, thus, shown to be bounded.

Following that, according to the first equation of (2), we obtain ${}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\le 0,$ then $\frac{d}{dt}\mathfrak{S}\left(t\right)\le 0$ or

$$\mathfrak{S}\left(t\right)\le {\mathfrak{S}}_0.$$

(10)

The second equation of (2) gives us

$${}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)\le \frac{\beta {\mathfrak{S}}_0-\left(\gamma +\kappa \right){\mathcal{N}}_0}{{\mathcal{N}}_0}\mathfrak{I}\left(t\right).$$

If ${\mathfrak{S}}_0<\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0,$ then ${}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)<0.$ Therefore, there is no chance for a pandemic occurrence due to the symmetrically decreasing of the infected class $\mathfrak{I}.$

Additionally, if ${\mathfrak{S}}_0>\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0,$ we can find that ${}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)>0.$ Thus, the pandemic will occur due to the increasing of the infected class. The requisite result is demonstrated. □

Theorem 1.

The disease-free equilibrium point of (2) is

$$u^{\ast }=\left(\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0,0,{\mathfrak{R}}_0,0\right).$$

Proof. 

For this, we write (2) as

$$\left\{\begin{array}{ccc}{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\hfill & =\hfill & 0,\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)\hfill & =\hfill & 0,\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R}\left(t\right)\hfill & =\hfill & 0,\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\left(t\right)\hfill & =\hfill & 0,\hfill \end{array}\right.$$

(11)

where $u^{\ast }=\left({\mathfrak{S}}^{\ast },{\mathfrak{I}}^{\ast },{\mathfrak{R}}^{\ast },{\mathfrak{D}}^{\ast }\right)$ is its solution. Using (11), from the second equation, we have:

$$\frac{\beta \mathfrak{S}\left(t\right)-\left(\gamma +\kappa \right){\mathcal{N}}_0}{{\mathcal{N}}_0}\mathfrak{I}\left(t\right)=0,$$

then we can obtain

$$\mathfrak{S}\left(t\right)={\mathfrak{S}}^{\ast }=\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0.$$

We know that the equilibrium points for disease-free are the conditions in which COVID-19 does not spread, and that is when the death class in this pandemic decreases to its absence, with the absence of new infections.

Therefore, as all equations of (2) depend on $\mathfrak{I}\left(t\right)\ge 0$ and because ${\mathfrak{S}}^{\ast }=\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0,$ we find from (11) that $\upsilon =0$ and ${\mathfrak{I}}^{\ast }\le 0.$ Thus $\mathfrak{I}\equiv \mathfrak{D}\equiv 0,$ we also have from the third equation ${\mathfrak{R}}^{\ast }={\mathfrak{R}}_0,$ and the required disease-free equilibrium is

$$u^{\ast }=\left(\frac{\gamma +\kappa }{\beta }{\mathcal{N}}_0,0,{\mathfrak{R}}_0,0\right).$$

Hence the theorem is proved. □

Theorem 2.

The pandemic free equilibrium point of (2) is locally asymptotically stable If the susceptible class $\mathfrak{S}\left(t\right)<{\mathfrak{S}}^{\ast },$ but is unstable if $\mathfrak{S}\left(t\right)>{\mathfrak{S}}^{\ast }.$

Proof. 

Let $u=\left(\mathfrak{S},\mathfrak{I},\mathfrak{R},\mathfrak{D}\right)$ be the solution of

$$\left\{\begin{array}{ccc}{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\hfill & =\hfill & f_1\left(t,u\left(t\right)\right),\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)\hfill & =\hfill & f_2\left(t,u\left(t\right)\right),\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R}\left(t\right)\hfill & =\hfill & f_3\left(t,u\left(t\right)\right),\hfill \\ {}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\left(t\right)\hfill & =\hfill & f_4\left(t,u\left(t\right)\right),\hfill \end{array}\right.$$

(12)

where $f_{1\le i\le 4}\left(t,u\left(t\right)\right)$ represents the right hand side of (2). One can measure the Jacobian matrix for (12) as follows:

$$J=\left(\begin{array}{cccc}\frac{\partial f_1}{\partial \mathfrak{S}}& \frac{\partial f_1}{\partial \mathfrak{I}}& \frac{\partial f_1}{\partial \mathfrak{R}}& \frac{\partial f_1}{\partial \mathfrak{D}}\\ \frac{\partial f_2}{\partial \mathfrak{S}}& \frac{\partial f_2}{\partial \mathfrak{I}}& \frac{\partial f_2}{\partial \mathfrak{R}}& \frac{\partial f_2}{\partial \mathfrak{D}}\\ \frac{\partial f_3}{\partial \mathfrak{S}}& \frac{\partial f_3}{\partial \mathfrak{I}}& \frac{\partial f_3}{\partial \mathfrak{R}}& \frac{\partial f_3}{\partial \mathfrak{D}}\\ \frac{\partial f_4}{\partial \mathfrak{S}}& \frac{\partial f_4}{\partial \mathfrak{I}}& \frac{\partial f_4}{\partial \mathfrak{R}}& \frac{\partial f_4}{\partial \mathfrak{D}}\end{array}\right)=\left(\begin{array}{cccc}-\upsilon -\frac{\beta \mathfrak{I}}{{\mathcal{N}}_0}& -\frac{\beta \mathfrak{S}}{{\mathcal{N}}_0}& 0& 0\\ \frac{\beta \mathfrak{I}}{{\mathcal{N}}_0}& \frac{\beta \mathfrak{S}}{{\mathcal{N}}_0}-\gamma -\kappa & 0& 0\\ \upsilon & \gamma & 0& 0\\ 0& \kappa & 0& 0\end{array}\right).$$

(13)

Therefore, the characteristics equation of (13) can be given as

$$det\left(J-\lambda I\right)=\left|\begin{array}{cccc}-\upsilon -\frac{\beta \mathfrak{I}}{{\mathcal{N}}_0}-\lambda & -\frac{\beta \mathfrak{S}}{{\mathcal{N}}_0}& 0& 0\\ \frac{\beta \mathfrak{I}}{{\mathcal{N}}_0}& \frac{\beta \mathfrak{S}}{{\mathcal{N}}_0}-\gamma -\kappa -\lambda & 0& 0\\ \upsilon & \gamma & -\lambda & 0\\ 0& \kappa & 0& -\lambda \end{array}\right|=0,\mathrm{with}\lambda \ne 0,$$

then

$${\lambda }^2\left(\upsilon +\frac{\beta \mathfrak{I}}{{\mathcal{N}}_0}+\lambda \right)\left(\frac{\beta \mathfrak{S}}{{\mathcal{N}}_0}-\gamma -\kappa -\lambda \right)=0\mathrm{and}\lambda \ne 0.$$

Finally, as $\mathfrak{I}\equiv 0$ in $u^{\ast },$ we find the eigenvalue $\lambda =-\upsilon ,$ or is given by the expression

$$\lambda =\frac{\beta \mathfrak{S}}{{\mathcal{N}}_0}-\left(\gamma +\kappa \right),$$

which indicates that $\lambda$ is always had to be negative if $\mathfrak{S}\left(t\right)<{\mathfrak{S}}^{\ast },$ hence the required result is obtained. □

4. Main Results

In this section, we use the fixed point theory to substantiate that at least one solution of model (12) exists. Let $u=\left(\mathfrak{S},\mathfrak{I},\mathfrak{R},\mathfrak{D}\right)\in E,$ where $E={\left[C\left(\left[0,T\right],{\mathbb{R}}_{+}\right)\right]}^4$ is a Banach space equipped with the norm

$${∥u∥}_E={∥\mathfrak{S}∥}_{\infty }+{∥\mathfrak{I}∥}_{\infty }+{∥\mathfrak{R}∥}_{\infty }+{∥\mathfrak{D}∥}_{\infty }$$

and let $f=\left(f_1,f_2,f_3,f_4\right),$ be such that

$$\left\{\begin{array}{ccc}{f}_1\left(t,u\left(t\right)\right)\hfill & =\hfill & -\upsilon \mathfrak{S}\left(t\right)-\beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{{\mathcal{N}}_0},\hfill \\ f_2\left(t,u\left(t\right)\right)\hfill & =\hfill & \beta \frac{\mathfrak{I}\left(t\right)\mathfrak{S}\left(t\right)}{{\mathcal{N}}_0}-\left(\gamma +\kappa \right)\mathfrak{I}\left(t\right),\hfill \\ f_3\left(t,u\left(t\right)\right)\hfill & =\hfill & \upsilon \mathfrak{S}\left(t\right)+\gamma \mathfrak{I}\left(t\right),\hfill \\ f_4\left(t,u\left(t\right)\right)\hfill & =\hfill & \kappa \mathfrak{I}\left(t\right),\hfill \end{array}\right.$$

it is clear that the function $f\in {\left(\left[0,T\right]\times E\right)}^4$ is continuous.

By applying the fractional integral (5) to both sides of the system (12) and using (6), we obtain

$$\left\{\begin{array}{ccc}\mathfrak{S}\left(t\right)& =& {\mathfrak{S}}_0+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}{f}_1\left(\tau ,u\left(\tau \right)\right)d\tau ,\\ \mathfrak{I}\left(t\right)& =& {\mathfrak{I}}_0+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}{f}_2\left(\tau ,u\left(\tau \right)\right)d\tau ,\\ \mathfrak{R}\left(t\right)& =& {\mathfrak{R}}_0+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}{f}_3\left(\tau ,u\left(\tau \right)\right)d\tau ,\\ \mathfrak{D}\left(t\right)& =& {\mathfrak{D}}_0+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}{f}_4\left(\tau ,u\left(\tau \right)\right)d\tau ,\end{array}\right.$$

By choosing $u_0=\left(u_1,u_2,u_3,u_4\right)=\left({\mathfrak{S}}_0,{\mathfrak{I}}_0,{\mathfrak{R}}_0,{\mathfrak{D}}_0\right),$ we obtain

$$u\left(t\right)=u_0+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}f\left(\tau ,u\left(\tau \right)\right)d\tau .$$

(14)

In what follows, we present the principal theorems:

Theorem 3.

Let $\beta ,\upsilon ,\gamma ,\kappa ,\alpha ,\rho ,T\in {\mathbb{R}}_{+},$ be such that $\alpha \in \left(0,1\right)$ and

$$T<{\left(\frac{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}{4\left(\beta +\upsilon +\gamma +\kappa +3\right)}\right)}^{\frac{1}{\rho \alpha }},$$

(15)

then, there is at least one solution of the problem (2) and (3) on $\left[0,T\right].$

Proof. 

To begin the proof, we will transform the problem (2) and (3) into a fixed point problem $\mathcal{A}u\left(t\right)=u\left(t\right)$ (see [21,22,23,24,25,33]), with

$$\mathcal{A}u\left(t\right)=\left({\mathcal{A}}_{1}u\left(t\right),{\mathcal{A}}_{2}u\left(t\right),{\mathcal{A}}_{3}u\left(t\right),{\mathcal{A}}_{4}u\left(t\right)\right)$$

and

$$\mathcal{A}u\left(t\right)=u_0+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}f\left(\tau ,u\left(\tau \right)\right)d\tau .$$

(16)

We first notice that if $u\in E,$ then ${\left({\mathcal{A}}_{i}u\right)}_{1\le i\le 4},$ being an operator of a constant and a primitive of continuous functions is indeed continuous (see also the step 1 in this proof), and therefore $\mathcal{A}u$ is an element of E and is equipped with the norm

$${∥\mathcal{A}u∥}_E=\sum _{i=1}^4{∥{\mathcal{A}}_{i}u∥}_{\infty }$$

Because the problem (2) and (3) is equivalent to the fractional integral Equation (16), the fixed points of $\mathcal{A}$ are solutions to the problem (2) and (3).

Next, we prove that $\mathcal{A}$ satisfies the conditions of Schauder’s fixed point theorem (see [34]), through the following steps:

Step 1

$\mathcal{A}$ is a nonlinear continuous operator.

Let ${\left(u_n\right)}_{n\in \mathbb{N}}=\left({\mathfrak{S}}_n,{\mathfrak{I}}_n,{\mathfrak{R}}_n,{\mathfrak{D}}_n\right)$ be four positive sequences such that $\underset{n\to \infty }{lim}{u}_n=u$ in $E.$ Then for each $t\in \left[0,T\right],$ we have:

$$\left|{\mathcal{A}}_i{u}_n\left(t\right)-{\mathcal{A}}_{i}u\left(t\right)\right|\le \frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}\left|f_i\left(\tau ,u_n\left(\tau \right)\right)-f_i\left(\tau ,u\left(\tau \right)\right)\right|d\tau ,$$

(17)

where $f_i$ satisfies (12) for each $1\le i\le 4.$ Then, we can find easily that $f_i\left(t,u_n\right)\to f_i\left(t,u\right)$ in $\left[0,T\right]\times E.$ In fact, we have

$$\begin{array}{cc}\hfill \left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{S}}_n\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\right|& =\left|f_1\left(t,u_n\left(t\right)\right)-f_1\left(t,u\left(t\right)\right)\right|\hfill \\ \hfill & \le \upsilon \left|{\mathfrak{S}}_n\left(t\right)-\mathfrak{S}\left(t\right)\right|+\frac{\beta }{{\mathcal{N}}_0}\left|{\mathfrak{S}}_n\left(t\right){\mathfrak{I}}_n\left(t\right)-\mathfrak{S}\left(t\right)\mathfrak{I}\left(t\right)\right|\hfill \\ \hfill & \le \left(\upsilon +\frac{\beta }{{\mathcal{N}}_0}{\mathfrak{I}}_n\left(t\right)\right)\left|{\mathfrak{S}}_n\left(t\right)-\mathfrak{S}\left(t\right)\right|+\left|{\mathfrak{R}}_n\left(t\right)-\mathfrak{R}\left(t\right)\right|\hfill \\ \hfill & +\frac{\beta }{{\mathcal{N}}_0}\mathfrak{S}\left(t\right)\left|{\mathfrak{I}}_n\left(t\right)-\mathfrak{I}\left(t\right)\right|+\left|{\mathfrak{D}}_n\left(t\right)-\mathfrak{D}\left(t\right)\right|\hfill \\ \hfill & \le \left(\frac{\beta }{{\mathcal{N}}_0}\left(\underset{t\in \left[0,T\right]}{sup}\mathfrak{S}\left(t\right)+\underset{t\in \left[0,T\right]}{sup}{\mathfrak{I}}_n\left(t\right)\right)+\upsilon +2\right){∥u_n-u∥}_E.\hfill \end{array}$$

Using (7), (9) and (10), we obtain

$$\underset{t\in \left[0,T\right]}{sup}\mathfrak{S}\left(t\right)+\underset{t\in \left[0,T\right]}{sup}{\mathfrak{I}}_n\left(t\right)\le {\mathcal{N}}_0,$$

then

$$\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{S}}_n\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\right|\le \left(\beta +\upsilon +2\right){∥u_n-u∥}_E.$$

(18)

Similarly, we have

$$\begin{array}{ccc}\hfill \left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{I}}_n\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)\right|& \hfill \le & \hfill \left(\beta +\gamma +\kappa +2\right){∥u_n-u∥}_E,\\ \multicolumn{1}{c}{\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{R}}_n\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R}\left(t\right)\right|}& \multicolumn{1}{c}{\le }& \multicolumn{1}{c}{\left(\upsilon +\gamma +2\right){∥u_n-u∥}_E,}\\ \multicolumn{1}{c}{\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{D}}_n\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\left(t\right)\right|}& \multicolumn{1}{c}{\le }& \multicolumn{1}{c}{\left(\kappa +3\right){∥u_n-u∥}_E.}\end{array}$$

(19)

Since $u_n\to u$ in $E,$ we obtain

$$\left({}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{S}}_n,{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{I}}_n,{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{R}}_n,{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{D}}_n\right)\to \left({}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S},{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I},{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R},{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\right).$$

Then, for each $i=\overline{1,4},$ we obtain $f_i\left(t,u_n\left(t\right)\right)\to f_i\left(t,u\left(t\right)\right)$ as $n\to \infty$ for any $t\in \left[0,T\right].$

Now let $\mathcal{K}>0,$ be such that for each $t\in \left[0,T\right],$ we have:

$$\left|f_i\left(t,u_n\left(t\right)\right)\right|\le \mathcal{K},\left|f_i\left(t,u\left(t\right)\right)\right|\le \mathcal{K},\forall i=\overline{1,4}.$$

Then, we have:

$$\begin{array}{cc}\hfill \left|{\mathcal{A}}_i{u}_n\left(t\right)-{\mathcal{A}}_{i}u\left(t\right)\right|& \le \frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}\left|f_i\left(\tau ,u_n\left(\tau \right)\right)-f_i\left(\tau ,u\left(\tau \right)\right)\right|d\tau \hfill \\ \hfill & \le \frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}\left[\left|f_i\left(\tau ,u_n\left(\tau \right)\right)\right|+\left|f_i\left(\tau ,u\left(\tau \right)\right)\right|\right]d\tau \hfill \\ \hfill & \le \frac{2\mathcal{K}}{{\rho }^{\alpha -1}\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{\left(t^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}d\tau .\hfill \end{array}$$

For each $i=\overline{1,4},$ the function $\tau \to \frac{2\mathcal{K}}{{\rho }^{\alpha -1}\mathsf{\Gamma }\left(\alpha \right)}{\left(t^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}$ is integrable $\forall t\in \left[0,T\right].$ Therefore, there exists an implication based on Lebesgue’s dominated convergence theorem and (17), which gives us the following:

$$\left|{\mathcal{A}}_i{u}_n\left(t\right)-{\mathcal{A}}_{i}u\left(t\right)\right|\to 0\mathrm{as}n\to \infty ,$$

and hence:

$$\underset{n\to \infty }{lim}{∥\mathcal{A}{u}_n-\mathcal{A}u∥}_E=0.$$

Consequently, $\mathcal{A}$ is continuous.

Step 2

According to (15), we put the positive real

$$r\ge \frac{4{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)-4\left(\beta +\upsilon +\gamma +\kappa +3\right)T^{\rho \alpha }}{u}_i,\forall i=\overline{1,4}$$

and define the subset $E_r$ as follows:

$$E_r=\left\{u\in E:{∥u∥}_E\le r\right\}.$$

Clearly $E_r$ denotes a closed, bounded and convex subset of $E.$

Let $\mathcal{A}:E_r\to E$ be the integral operator given in (16), thus $\mathcal{A}\left(E_r\right)\subset E_r.$ In fact, using (18) and (19) we have for each $t\in \left[0,T\right]$:

$$\begin{array}{ccc}\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{S}\left(t\right)\right|\hfill & \le \hfill & \left(\beta +\upsilon +2\right){∥u∥}_E.\hfill \\ \multicolumn{1}{c}{\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{I}\left(t\right)\right|}& \multicolumn{1}{c}{\le }& \multicolumn{1}{c}{\left(\beta +\gamma +\kappa +2\right){∥u∥}_E,}\\ \left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{R}\left(t\right)\right|\hfill & \multicolumn{1}{c}{\le }& \left(\upsilon +\gamma +2\right){∥u∥}_E,\hfill \\ \left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }\mathfrak{D}\left(t\right)\right|\hfill & \multicolumn{1}{c}{\le }& \left(\kappa +3\right){∥u∥}_E.\hfill \end{array}$$

Then, in each case, we have

$$\left|f_i\left(t,u\left(t\right)\right)\right|\le \left(\beta +\upsilon +\gamma +\kappa +3\right)r,\forall i=\overline{1,4.}$$

Thus

$$\begin{array}{cc}\hfill \left|{\mathcal{A}}_{i}u\left(t\right)\right|& \le u_i+\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}\left|f_i\left(\tau ,u\left(\tau \right)\right)\right|d\tau \hfill \\ \hfill & \le u_i+\frac{\left(\beta +\upsilon +\gamma +\kappa +3\right)T^{\rho \alpha }}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}r\hfill \\ \hfill & \le \frac{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)-4\left(\beta +\upsilon +\gamma +\kappa +3\right)T^{\rho \alpha }}{4{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}r+\frac{\left(\beta +\upsilon +\gamma +\kappa +3\right)T^{\rho \alpha }}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}r\hfill \\ \hfill & \le \frac{1}{4}r,\forall i=\overline{1,4},\hfill \end{array}$$

or ${\left({∥{\mathcal{A}}_{i}u∥}_{\infty }\right)}_{1\le i\le 4}\le \frac{r}{4}.$ Then ${∥\mathcal{A}u∥}_E={\displaystyle \sum _{i=1}^4}{∥{\mathcal{A}}_{i}u∥}_{\infty }\le r.$ Consequently $\mathcal{A}\left(E_r\right)\subset E_r.$

Step 3

$\mathcal{A}\left(E_r\right)$ is relatively compact.

Let $t_1,t_2\in \left[0,T\right],$ $t_1<t_2$ and $u\in E_r.$ Then, for every $i=\overline{1,4},$ we obtain

$$\begin{array}{cc}\hfill \left|{\mathcal{A}}_{i}u\left(t_2\right)-{\mathcal{A}}_{i}u\left(t_1\right)\right|& =\left|\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{t_2}{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}{f}_i\left(\tau ,u\left(\tau \right)\right)d\tau \right.\hfill \\ \hfill -& \left.\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{t_1}{\left(t_1^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}{f}_i\left(\tau ,u\left(\tau \right)\right)d\tau \right|\hfill \\ \hfill & \le \frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{t_1}\left|\left({\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}-{\left(t_1^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}\right){\tau }^{\rho -1}{f}_i\left(\tau ,u\left(\tau \right)\right)\right|d\tau \hfill \\ \hfill & +\frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{t_1}^{t_2}{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}\left|f_i\left(\tau ,u\left(\tau \right)\right)\right|d\tau \hfill \\ \hfill & \le \frac{\left(\beta +\upsilon +\gamma +\kappa +3\right)r}{{\rho }^{\alpha -1}\mathsf{\Gamma }\left(\alpha \right)}\left({\int }_0^{t_1}\left|{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}-{\left(t_1^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}\right|{\tau }^{\rho -1}d\tau \right.\hfill \\ \hfill & +\left.{\int }_{t_1}^{t_2}{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}d\tau \right)\hfill \end{array}$$

(20)

We have:

$$\left({\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}-{\left(t_1^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}\right){\tau }^{\rho -1}=\frac{-1}{\alpha \rho }\frac{d}{d\tau }\left({\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha }-{\left(t_1^{\rho }-{\tau }^{\rho }\right)}^{\alpha }\right),$$

then

$${\int }_0^{t_1}\left|{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}-{\left(t_1^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}\right|{\tau }^{\rho -1}d\tau \le \frac{1}{\alpha \rho }\left[{\left(t_2^{\rho }-t_1^{\rho }\right)}^{\alpha }+\left(t_2^{\rho \alpha }-t_1^{\rho \alpha }\right)\right],$$

we have also

$$\begin{array}{cc}\hfill {\int }_{t_1}^{t_2}{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha -1}{\tau }^{\rho -1}d\tau & =\frac{-1}{\alpha \rho }{\left[{\left(t_2^{\rho }-{\tau }^{\rho }\right)}^{\alpha }\right]}_{t_1}^{t_2}\hfill \\ \hfill & \le \frac{1}{\alpha \rho }{\left(t_2^{\rho }-t_1^{\rho }\right)}^{\alpha }.\hfill \end{array}$$

Then (20) gives

$$\left|{\mathcal{A}}_{i}u\left(t_2\right)-{\mathcal{A}}_{i}u\left(t_1\right)\right|\le \frac{\left(\beta +\upsilon +\gamma +\kappa +3\right)r}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}\left[2{\left(t_2^{\rho }-t_1^{\rho }\right)}^{\alpha }+\left(t_2^{\rho \alpha }-t_1^{\rho \alpha }\right)\right].$$

It follows from $t_1\to t_2,$ that the right-hand side of the above-mentioned inequality tends to zero, $\forall i=\overline{1,4}.$

As a consequence of steps 1 to 3, and through Ascoli–Arzelà theorem, we infer the continuity of $\mathcal{A}:E_r\to E_r,$ its compact nature and its satisfaction of the assumption of Schauder’s fixed point theorem [34]. Therefore, $\mathcal{A}$ has a fixed point which solves the problem (2) and (3) on $\left[0,T\right].$ The proof is complete. □

Theorem 4.

Let $\alpha \in \left(0,1\right)$ and $\beta ,\gamma ,\kappa ,\rho ,\mu \in {\mathbb{R}}_{+},$ be such that

$$\mu =max\left\{\beta +\upsilon +2,\beta +\gamma +\kappa +2,\upsilon +\gamma +3,\kappa +3\right\}.$$

If

$$\frac{4\mu T^{\rho \alpha }}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}<1,$$

(21)

then the problem (2) and (3) admits a unique solution on $\left[0,T\right].$

Proof. 

In Theorem 3, we already achieved the transformation of the aforementioned problem (2) and (3) into a fixed point problem (16).

Let $u,v\in E$ satisfy the problem (2) and (3) respectively. This implies that:

$$\left|{\mathcal{A}}_{i}u\left(t\right)-{\mathcal{A}}_{i}v\left(t\right)\right|\le \frac{{\rho }^{1-\alpha }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t\frac{{\tau }^{\rho -1}}{{\left(t^{\rho }-{\tau }^{\rho }\right)}^{1-\alpha }}\left|f_i\left(\tau ,u\left(\tau \right)\right)-f_i\left(\tau ,v\left(\tau \right)\right)\right|d\tau$$

(22)

For all $t\in \left[0,T\right],$ we have:

$$\begin{array}{ccc}\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{S}}_u\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{S}}_v\left(t\right)\right|\hfill & \le \hfill & \left(\beta +\upsilon +2\right){∥u-v∥}_E.\hfill \\ \multicolumn{1}{c}{\left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{I}}_u\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{I}}_v\left(t\right)\right|}& \multicolumn{1}{c}{\le }& \multicolumn{1}{c}{\left(\beta +\gamma +\kappa +2\right){∥u-v∥}_E,}\\ \left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{R}}_u\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{R}}_v\left(t\right)\right|\hfill & \multicolumn{1}{c}{\le }& \left(\upsilon +\gamma +3\right){∥u-v∥}_E,\hfill \\ \left|{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{D}}_u\left(t\right)-{}^C{\mathcal{D}}_{0^{+}}^{\alpha ,\rho }{\mathfrak{D}}_v\left(t\right)\right|\hfill & \multicolumn{1}{c}{\le }& \left(\kappa +3\right){∥u-v∥}_E.\hfill \end{array}$$

Then

$$\left|f_i\left(t,u\left(t\right)\right)-f_i\left(t,v\left(t\right)\right)\right|\le \mu {∥u-v∥}_E,\forall i=\overline{1,4}.$$

From (22) we find:

$${∥{\mathcal{A}}_{i}u-{\mathcal{A}}_{i}v∥}_{\infty }\le \frac{\mu T^{\rho \alpha }}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}{∥u-v∥}_E,\forall i=\overline{1,4}.$$

Similarly, we can find that:

$${∥\mathcal{A}u-\mathcal{A}v∥}_E\le \frac{4\mu T^{\rho \alpha }}{{\rho }^{\alpha }\mathsf{\Gamma }\left(\alpha +1\right)}{∥u-v∥}_E.$$

According to (21), the above inequality indicates that $\mathcal{A}$ is a contraction operator.

As a consequence Banach’s contraction principle (see [34]), we conclude that $\mathcal{A}$ has only one fixed point which is the unique solution of the problem (2) and (3) on $\left[0,T\right].$ The proof is complete. □

5. Conclusions

In this paper, we discussed some analytical studies for a modified fractional-order SIRD mathematical model of the COVID-19 disease, with Caputo–Katugampola’s fractional derivative being used as the differential operator, which unifies the Hadamard and Caputo fractional derivatives into a single form. Using real data, the feasibility region of the proposed solution and the equilibrium points’ stability analysis were derived. The behavior of these solutions depends on some symmetrical parameters that satisfy some conditions which prevent the pandemic from occurring. The existence of one solution, at least, in addition to its uniqueness, requires some essential conditions derived from the Banach contraction principle and Schauder’s fixed point theorem.