Three Roads to the Geometric Constraint Formulation of Gravitational Theories with Boundaries
Abstract
1. Introduction and Preliminary Remarks
- (i)
- If boundary conditions have been introduced in the definition of , it is critical to take them into account when deriving the boundary Euler–Lagrange equations. This is so because the variations at the boundary will not be independent but will be constrained by the boundary conditions.
- (ii)
- Even when no boundary contribution is included in the action, there may still exist Euler–Lagrange equations at the boundary in addition to those at the bulk (usually coming from integrations by parts). As a consequence, the issue mentioned in the previous item will still be relevant [17].
- (iii)
- It is very important to understand that boundary conditions may appear as Euler–Lagrange equations at the boundary even if no such conditions are introduced in . Further, they do not need to be simple specifications of the values of some fields or their “spatial” derivatives but may be dynamical (this will happen in the models that we consider here).
2. Some Basic Facts about the Husain–Kuchař Model
3. The Generalized Husain–Kuchař–Pontryagin Action
- (i)
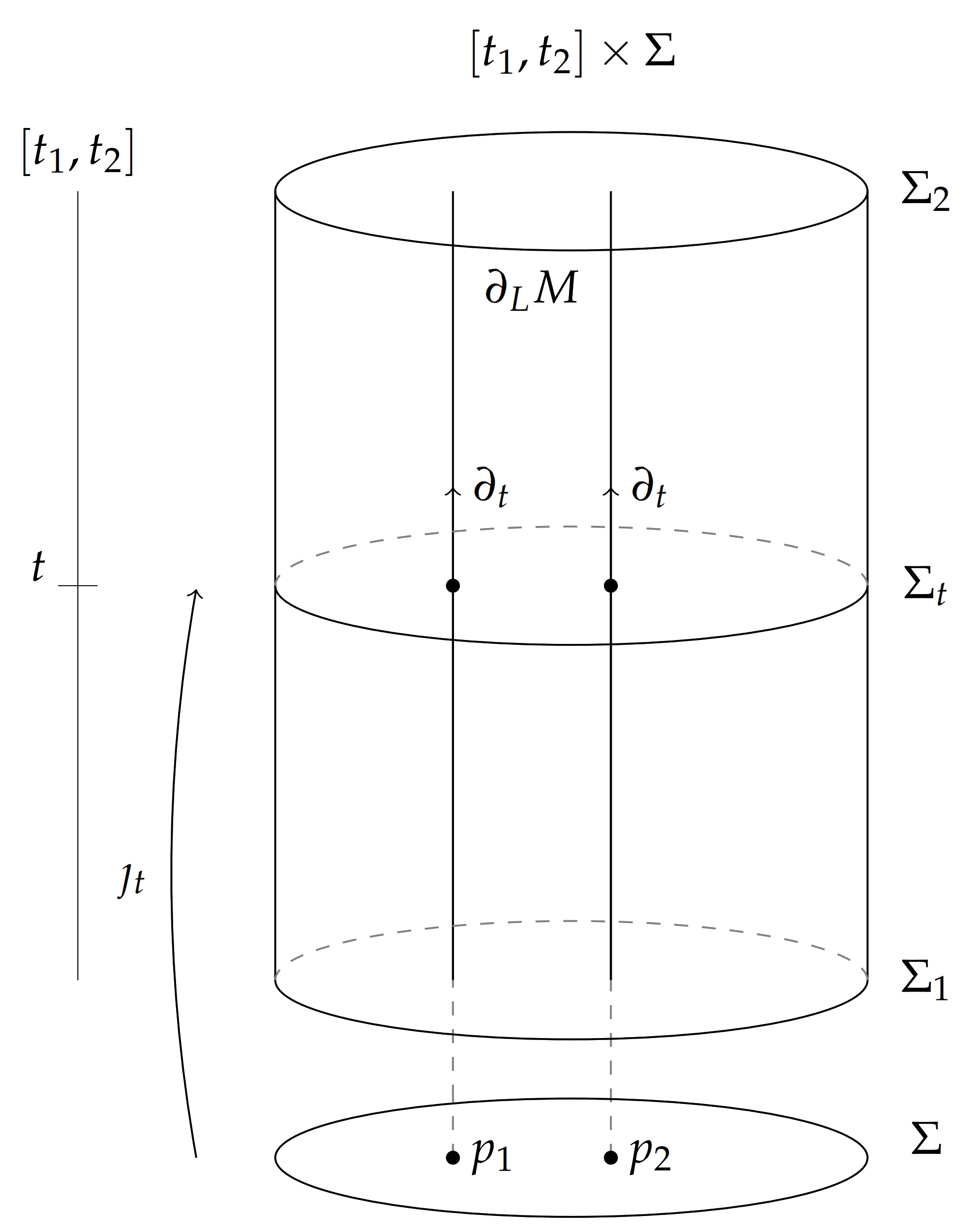
- Although we will not discuss in any detail functional analytic issues, something needs to be said about the smoothness conditions on the fields and how they are affected by the presence of a boundary. In the interior of M (the bulk), we will require the fields to be “smooth enough” so that the field equations make sense there. In order to make sense of the boundary equations it is also natural to add whatever smoothness requirements on the fields are necessary on . An additional smoothness requirement might also be considered: demanding that, when extended to an open smooth manifold containing M as a submersion, the bulk equations also hold at .This last point is relatively subtle. On one hand, it appears unnatural from the viewpoint of the action principle since it does not seem necessary to demand such condition for the stationarity of the action. For instance, if we require the function in the bulk to admit a sufficiently smooth extension to , and if the Euler–Lagrange equations have a sufficiently nice form, “their action on the bulk function” will be smooth and, by continuity, they will also hold at the boundary. On the other hand, it can be seen as a sensible requirement that can be imposed a posteriori to select a subfamily of solutions to the variational equations with good physical properties, or even, appear as consistency requirements for the dynamics. It is also conceivable that a particular choice of smoothness requirements, both in the bulk and at the boundary, suffices to guarantee extendibility in the above sense. For an ordinary variational problem, the treatment of the lateral boundary and the lids may have to be different. It may happen that the extendibility condition applies only to lateral boundaries and not to the lids.Some intuition about these questions can be gained by considering, for example, the Laplace equation on a bounded region of the plane and using the real or imaginary parts of complex analytic functions as examples. The last regularity requirement is, at least at face value, the strongest; we will proceed assuming it in the present work. As a last word of caution it should be mentioned that there may be consistency issues between the smoothness requirements in the bulk and at the boundary that we will also sidestep here.
- (ii)
- According to the regularity conditions that we are considering, the bulk equations must also hold when the fields are restricted to the boundary, so there are several sets of boundary equations. The content of these can be conveniently disentangled by either taking their pullback to the boundary and writing them in terms of pullbacks of the dynamical fields or first computing their interior product with the outer unit normal and then pulling them back. This procedure mimics one of the methods that we are going to follow in the paper to obtain the Hamiltonian formulation for the model given by the action (10).
- (iii)
- If there are only boundary equations. The dynamics in the bulk is arbitrary. This means that any field configuration with the correct “boundary dynamics” provides stationary points for the action. Otherwise the bulk dynamics is that of the Husain–Kuchař model. From the point of view of the action, this happens because a simple integration by parts of the terms involving can be used to cancel them, giving just boundary contributions to the action. Notice that the remaining terms can all be written as total derivatives, so that the action in this case is an integral over the boundary, which corresponds to an extension of three-dimensional (Euclidean) general relativity [10]. At this point it is worthwhile to advance that the Hamiltonian formulation for this theory will be obtained in the following in the same footing as the one corresponding to the bulk model.
- (iv)
- If the boundary equations tell us that and are proportional to and, hence, the pullbacks of the bulk Equations (11) and (12) automatically hold as can be seen by plugging the expressions for and in terms of into the pullbacks of (11) and (12) to the boundary. The physical meaning of the specific models obtained at the boundary for other parameter choices are discussed in [9].
3.1. GNH Analysis in the Cotangent Bundle
- The final Hamiltonian description lives in the primary constraint submanifold in phase space.
- Dynamical consistency is rephrased as a tangency condition. This has the advantage of altogether avoiding the use of Poisson brackets, which is useful in spacetime manifolds with boundary.
- Given a Lagrangian (which may come from a suitable 3 + 1 decomposition of an action) the main steps are: (i) the characterization of the primary constraint submanifold from the definition of momenta (fiber derivative), (ii) the definition of the Hamiltonian vector fields in terms of the simplectic form and the exterior derivative in field space of the Hamiltonian and (iii) checking consistency as a tangency requirement.
- (1)
- Conditions on the components of the vector field : There are two types of these associated with the bulk and the boundary, respectively. The bulk conditions are only present if in which case they areThe conditions at the boundary readThere are no conditions involving and neither at the bulk nor at the boundary.
- (2)
- Secondary constraints: Again we have constraints associated with the bulk and with the boundary. They come from the components of in that do not appear in and hence their coefficients must vanish. The bulk constraints are only present if . They areThe boundary constraints are
3.2. Geometric Constraint Algorithm in the Tangent Bundle
- Build a presimplectic form in the tangent bundle of the configuration space from the Lagrangian by using the so called Liouville vector field .
- Define the energy and find the vector fields that give the evolution of the system by solving Equation (33).
- Impose the second-order condition (necessary to guarantee the equivalence of the dynamics with that given by the Euler–Lagrange equations).
- (i)
- (ii)
- In , solutions are guaranteed to satisfy (33) but they need not satisfy (34). Since the solutions will have the form for , we have some freedom to choose in such a way that satisfies (34). This can be done in a submanifold of satisfying the condition , for all . This is called the non-dynamical constraint. Note that if is a solution to both (33) and (34), then for is also a solution.
- (iii)
- In , solutions to both (33) and (34) exist, however they are not tangent to in general. Since we still have the freedom to choose , we can take it in such a way that the resulting solution is tangent to in a (perhaps smaller) submanifold . Again, the chosen solution may not be tangent to , so we need to iterate this last step until no further constraints crop up.
3.3. The Field Equations Approach
- Pullback the field equations to by using to obtain constraints. To this end it will be useful to first define adapted fields by using the fact that .
- Compute the interior product of the field equations with the vector field canonically defined by the decomposition in terms of the objects introduced in the previous step. Then pull this back to .
- Write the previous result in terms of time derivatives of the fields and introduce in this way the vector fields that define the evolution of the system.
3.4. Final Consistency Analysis
4. Conclusions and Comments
Author Contributions
Funding
Conflicts of Interest
Appendix A. Some Useful Mathematical Results
References
- Wald, R.M. The thermodynamics of black holes. Living Rev. Relativ. 2001, 4, 1–44. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Krishnan, B. Isolated and dynamical horizons and their applications. Living Rev. Relativ. 2004, 7, 1–91. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. Asymptotic properties of fields and space-times. Phys. Rev. Lett. 1963, 10, 66. [Google Scholar] [CrossRef]
- Ashtekar, A.; Streubel, M. Symplectic geometry of radiative modes and conserved quantities at null infinity. Proc. R. Soc. Lond. A 1981, 376, 585–607. [Google Scholar] [CrossRef]
- Ashtekar, A.; Campiglia, M.; Laddha, A. Null infinity, the BMS group and infrared issues. Gen. Relativ. Gravit. 2018, 50, 140. [Google Scholar] [CrossRef]
- Ashtekar, A.; Engle, J.; Sloan, D. Asymptotics and Hamiltonians in a first order formalism. Class. Quantum Gravity 2008, 25, 095020. [Google Scholar] [CrossRef][Green Version]
- Hooft, G. On the quantum structure of a black hole. Nucl. Phys. B 1985, 256, 727–745. [Google Scholar] [CrossRef]
- Smolin, L. Holographic formulation of quantum general relativity. Phys. Rev. D 2000, 61, 084007. [Google Scholar] [CrossRef]
- Barbero, J.F.; Díaz, B.; Margalef-Bentabol, J.; Villaseñor, E.J.S. Generalizations of the Pontryagin and Husain-Kuchař-Pontryagin actions to manifolds with boundary. J. High Energy Phys. 2019, 10, 121. [Google Scholar] [CrossRef]
- Mielke, E.W.; Baekler, P. Topological gauge model of gravity with torsion. Phys. Lett. A 1991, 156, 399. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Lectures on Quantum Dynamics; Dover: Mineola, NY, USA, 2001. [Google Scholar]
- Gotay, M.; Nester, J.; Hinds, G. Presymplectic manifolds and the Dirac–Bergmann theory of constraints. J. Math. Phys. 1978, 19, 2388. [Google Scholar] [CrossRef]
- Gotay, M. Presymplectic Manifolds, Geometric Constraint Theory and the Dirac-Bergmann Theory of Constraints. Ph.D. Thesis, Center for Theoretical Physics of the University of Maryland, College Park, MD, USA, 1979. [Google Scholar]
- Gotay, M.; Nester, J.L. Generalized Constraint Algorithm and Special Presymplectic Manifolds; Lecture Notes in Mathematics 775, Geometric Methods in Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Barbero, J.F.; Díaz, B.; Margalef-Bentabol, J.; Villaseñor, E.J.S. Dirac’s algorithm in the presence of boundaries: A practical guide to a geometric approach. Class. Quantum Gravity 2019, 36, 205014. [Google Scholar] [CrossRef]
- Barbero, J.F.; Prieto, J.; Villaseñor, E.J.S. Hamiltonian treatment of linear field theories in the presence of boundaries: A geometric approach. Class. Quantum Gravity 2014, 31, 045021. [Google Scholar] [CrossRef]
- Regge, T.; Teitelboim, C. Role of surface integrals in the Hamiltonian formulation of general relativity. Ann. Phys. 1974, 88, 286. [Google Scholar] [CrossRef]
- Nester, J.M. Invariant derivation of the Euler-Lagrange equation. J. Phys. A Math. Gen. 1988, 21, L1013–L1017. [Google Scholar] [CrossRef]
- Cariñena, J.F.; López, C.; Rañada, M.F. Geometric Lagrangian approach to first-order systems and applications. Math. Phys. 1988, 29, 1134. [Google Scholar] [CrossRef]
- Muñoz-Lecanda, M.; Roman-Roy, N. Lagrangian theory for presymplectic systems. Annales de l’IHP Physique Théorique 1992, 57, 27–45. [Google Scholar]
- Barbero, J.F.; Díaz, B.; Margalef-Bentabol, J.; Villaseñor, E.J.S. Hamiltonian Gotay-Nester-Hinds analysis of the parametrized unimodular extension of the Holst action. Phys. Rev. D 2021, 103, 064062. [Google Scholar] [CrossRef]
- Husain, V.; Kuchar, K.V. General covariance, new variables, and dynamics without dynamics. Phys. Rev. D 1990, 42, 4070–4077. [Google Scholar] [CrossRef]
- Ashtekar, A. New variables for classical and quantum gravity. Phys. Rev. Lett. 1986, 57, 2244–2247. [Google Scholar] [CrossRef]
- Ashtekar, A. New Hamiltonian formulation of general relativity. Phys. Rev. D 1987, 36, 1587–1602. [Google Scholar] [CrossRef]
- Varadarajan, M.; Zapata, J.A. A Proposal for analyzing the classical limit of kinematic loop gravity. Class. Quantum Gravity 2000, 17, 4085–4110. [Google Scholar] [CrossRef]
- Barbero, J.F.; Tiemblo, A.; Treseguerres, R. The Husain-Kuchař model: Time variables and non-degenerate metrics. Phys. Rev. D 1998, 57, 6104. [Google Scholar] [CrossRef]
- Barbero, J.F. General relativity as a theory of two connections. Int. J. Mod. Phys. D 1994, 3, 379. [Google Scholar] [CrossRef]
- Barbero, J.F.; Villaseñor, E.J.S. BF actions for the Husain-Kuchař model. Phys. Rev. D 2001, 63, 084021. [Google Scholar] [CrossRef]
- Gotay, M.; Nester, J.M. Presymplectic Lagrangian systems. I: The constraint algorithm and the equivalence theorem. Annales de l’IHP Physique Théorique 1970, 30, 129–142. [Google Scholar]
- Gotay, M.; Nester, J.M. Presymplectic Lagrangian systems. II: The second-order equation problem. Ann. L’I.H.P. Phys. Théorique 1980, 32, 1–13. [Google Scholar]
- Crampin, M. Tangent bundle geometry Lagrangian dynamics. J. Phys. A Math. Gen. 1983, 16, 3755–3772. [Google Scholar] [CrossRef]
- Freidel, L.; Geiller, M.; Pranzetti, D. Edge modes of gravity. Part I. Corner potentials and charges. J. High Energy Phys. 2020, 11, 26. [Google Scholar] [CrossRef]
- Freidel, L.; Geiller, M.; Pranzetti, D. Edge modes of gravity. Part II. Corner metric and Lorentz charges. J. High Energy Phys. 2020, 11, 27. [Google Scholar] [CrossRef]
- Margalef-Bentabol, J.; Villaseñor, E.J.S. Geometric formulation of the covariant phase space methods with boundaries. Phys. Rev. D 2021, 103, 025011. [Google Scholar] [CrossRef]
- Barbero, J.F.; Margalef-Bentabol, J.; Varo, V.; Villaseñor, E.J.S. Covariant phase space for gravity with boundaries: Metric versus tetrad formulations. Phys. Rev. D 2021, in press. [Google Scholar]
- Barbero, J.F.; Margalef-Bentabol, J.; Varo, V.; Villaseñor, E.J.S. Palatini gravity with nonmetricity, torsion, and boundaries in metric and connection variables. Phys. Rev. D 2021, in press. [Google Scholar]
- Geiller, M. Edge modes and corner ambiguities in 3d Chern-Simons theory and gravity. Nucl. Phys. B 2017, 924, 312–365. [Google Scholar] [CrossRef]
- Geiller, M.; Goeller, C.; Merino, N. Most general theory of 3d gravity: Covariant phase space, dual diffeomorphisms, and more. J. High Energy Phys. 2021, 2, 120. [Google Scholar] [CrossRef]
- Barbero, J.F.; Díaz, B.; Margalef-Bentabol, J.; Villaseñor, E.J.S. Concise symplectic formulation for tetrad gravity. Phys. Rev. D 2021, 103, 024051. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbero, F.; Basquens, M.; Varo, V.; Villaseñor, E.J.S. Three Roads to the Geometric Constraint Formulation of Gravitational Theories with Boundaries. Symmetry 2021, 13, 1430. https://doi.org/10.3390/sym13081430
Barbero F, Basquens M, Varo V, Villaseñor EJS. Three Roads to the Geometric Constraint Formulation of Gravitational Theories with Boundaries. Symmetry. 2021; 13(8):1430. https://doi.org/10.3390/sym13081430
Chicago/Turabian StyleBarbero, Fernando, Marc Basquens, Valle Varo, and Eduardo J. S. Villaseñor. 2021. "Three Roads to the Geometric Constraint Formulation of Gravitational Theories with Boundaries" Symmetry 13, no. 8: 1430. https://doi.org/10.3390/sym13081430
APA StyleBarbero, F., Basquens, M., Varo, V., & Villaseñor, E. J. S. (2021). Three Roads to the Geometric Constraint Formulation of Gravitational Theories with Boundaries. Symmetry, 13(8), 1430. https://doi.org/10.3390/sym13081430





