The Uniform Poisson–Ailamujia Distribution: Actuarial Measures and Applications in Biological Science

Abstract

We propose a new asymmetric discrete model by combining the uniform and Poisson–Ailamujia distributions using the binomial decay transformation method. The distribution, named the uniform Poisson–Ailamujia, due to its flexibility is a good alternative to the well-known Poisson and geometric distributions for real data applications in public health, biology, sociology, medicine, and agriculture. Its main statistical properties are studied, including the cumulative and hazard rate functions, moments, and entropy. The new distribution is considered to be suitable for modeling purposes; its parameter is estimated by eight classical methods. Three applications to biological data are presented herein.

1. Introduction

Discrete distributions are quite useful for modeling discrete lifetime data in many situations. Recently, several continuous distributions have been discretized for modeling lifetime data, such as those summarized in Table 1.

Table 1. Some discretized continuous distributions.

Continuous Distribution	Discrete Distribution	Author
Weibull	Discrete Weibull	Nakagawa and Osaki [1]
Inverse Weibull	Discrete inverse Weibull	Stein and Dattero [2]
Normal and Rayleigh	Discrete normal and Rayleigh	Roy [3,4]
Burr XII and Pareto	Discrete Burr XII and Pareto	Krishna and Pundir [5]
Gamma	Discrete gamma	Chakraborty and Chakravarty [6]
Chen	Discrete Chen	Noughabi et al. [7]

On the other hand, a natural discrete analog of the continuous Lindley model, called natural discrete Lindley (NDL), was introduced by [8] as a mixture of the negative binomial and geometric distributions. Several reliability properties of the NDL were explored by [9].

Let N and X be two discrete random variables denoting the numbers of particles entering and leaving an attenuator, with their probability mass functions (pmfs) $p\left(n\right)$ and $P(X=x)$ that are connected by the binomial decay transformation introduced by Hu et al. [10]

$$P(X=x)=\sum _{n=x}^{\infty }\left(\genfrac{}{}{0pt}{}{n}{x}\right){(1-p)}^{n-x}{p}^{x}p\left(n\right),x=0,1,\dots ,$$

(1)

where $0\le p\le 1$ is the attenuating coefficient. Hu et al. [10] defined $p\left(n\right)$ as a pmf of a Poisson distribution with rate parameter $\lambda >0$ and illustrated that $P(X=x)$ is also a Poisson distribution with rate $\lambda p$. They investigated the quantitative relation between the input and output distributions after the attenuation. In recent studies, new discrete models have been constructed by compounding two discrete distributions. For example, Déniz [11] defined the uniform Poisson, Akdoğan et al. [12] proposed the uniform geometric, and Kuş et al. [13] introduced the binomial discrete Lindley.

In this paper, we introduce the asymmetric uniform Poisson–Ailamujia (UPA) distribution using the methodology of Hu et al. [10]. This distribution is a competitor to the Poisson–Ailamujia (PA) model, and it is suitable for fitting datasets with excesses of ones. We estimate the parameter $\alpha$ of the UPA distribution using eight classical methods and provide detailed simulations to explore the behavior of the estimators.

The rest of the paper is organized as follows. Section 2 defines the new one-parameter distribution and some of its properties. Two actuarial measures are calculated in Section 3. The estimation methods are discussed in Section 4. In Section 5, the efficiency of the estimators is studied via Monte Carlo simulations. Section 6 provides three real applications of the new distribution. Section 7 offers some conclusions.

2. The Discrete UPA Distribution

The PA distribution was derived from the Poisson compounding scheme based on the continuous Ailamujia distribution by Lv et al. [14]. It was pioneered by Hassan et al. [15] for modeling count data, offering a new alternative to the Poisson and the negative binomial, among other models. Its pmf has the form (for $\alpha >0$).

$$P\left(X=x\right)=\frac{4{\alpha }^2(1+x)}{{(1+2\alpha )}^{x+2}},x\in \mathbb{N}.$$

(2)

Equation (2) can be expressed as

$$P\left(X=x\right)=\sum _{n=x}^{\infty }P\left(N=n\right)P\left(X=x\mid N=n\right),$$

(3)

where $X|N=n$ has the binomial $B(n,p)$ model. Now, let $X|N=n$ have the discrete uniform U$\left(n\right)$ with parameter $n\ge 0$, and let N have a PA distribution with parameter $\alpha >0$. Then, the pmf of the UPA random variable ($rv$), say, $X\sim$UPA$\left(\alpha \right)$, is as follows (for $x=0,1,\dots$):

$$f\left(x\right)=P\left(X=x\right)=\sum _{n=x}^{\infty }\frac{1}{(n+1)}\frac{4{\alpha }^2(1+n)}{{(1+2\alpha )}^{n+2}}=\frac{2\alpha }{{(1+2\alpha )}^{x+1}}.$$

(4)

Figure 1 displays plots of the pmf of X, which is unimodal. The probabilities of $P(X=x)$ decrease when x increases.

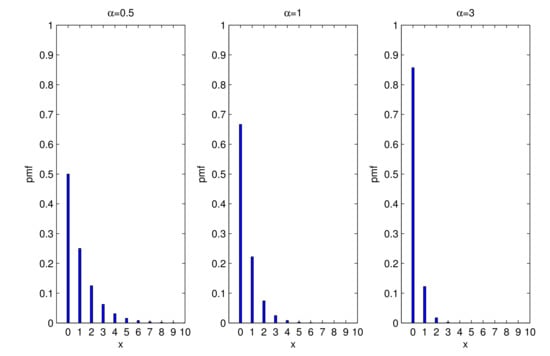
Figure 1. Pmf of the UPA$\left(\alpha \right)$ distribution for some values of $\alpha$.

2.1. Properties

The survival function (sf) of the UPA distribution is as follows (for $x=0,1,\dots$):

$$\begin{array}{c}\hfill S\left(x\right)=P\left(X\ge x\right)=1-P\left(X\le x-1\right)=1-\sum _{i=0}^{x-1}\frac{2\alpha }{{(1+2\alpha )}^{i+1}}=\frac{1}{{(1+2\alpha )}^x}.\end{array}$$

(5)

The cumulative distribution function (cdf) of X reduces to

$$\begin{array}{c}\hfill F\left(x\right)=P\left(X\le x\right)=\sum _{i=0}^x\frac{2\alpha }{{(1+2\alpha )}^{i+1}}=1-\frac{1}{{(1+2\alpha )}^{x+1}},x=0,1,\dots \end{array}$$

(6)

The hazard rate function (hrf) of X can be defined as $h\left(x\right)=P\left(X=x\mid X\ge x\right)=P\left(X=x\right)/P\left(X\ge x\right)$, where $P\left(X\ge x\right)>0$. Then, the hrf of the UPA distribution follows from Equations (4) and (5) as

$$h\left(x\right)=\frac{2\alpha }{(1+2\alpha )}.$$

(7)

The moment generating function of X is

$$\begin{array}{c}\hfill M_X\left(t\right)=E\left({\mathrm{e}}^{\mathrm{tX}}\right)=\sum _{x=0}^{\infty }{\mathrm{e}}^{\mathrm{tx}}\frac{2\alpha }{{(1+2\alpha )}^{x+1}}=\frac{2\alpha }{1+2\alpha -{\mathrm{e}}^{\mathrm{t}}}.\end{array}$$

(8)

The first fourth ordinary moments of X are

$$\begin{array}{c}\hfill E\left(X\right)=\frac{1}{2\alpha },E\left(X^2\right)=\frac{1+\alpha }{2{\alpha }^2},\end{array}$$

(9)

$$\begin{array}{c}\hfill E\left(X^3\right)=\frac{3+6\alpha +2{\alpha }^2}{4{\alpha }^3}\mathrm{and}E\left(X^4\right)=\frac{3+9\alpha +7{\alpha }^2+{\alpha }^3}{2{\alpha }^4}.\end{array}$$

(10)

The variance, skewness, and kurtosis of X are obtained from these expressions as

$$\begin{array}{c}\hfill Var\left(X\right)=\frac{2\alpha +1}{4{\alpha }^2},{\gamma }_1\left(X\right)=\frac{2(1+\alpha )}{\sqrt{1+2\alpha }}>0\mathrm{and}{\gamma }_2\left(X\right)=\frac{4{\alpha }^2+18\alpha +9}{1+2\alpha }>0.\end{array}$$

(11)

We note that the new distribution is over-dispersed since the index of dispersion (ID)

$$ID=\frac{Var\left(X\right)}{E\left(X\right)}=\frac{2\alpha \left(2\alpha +1\right)}{4{\alpha }^2}=\frac{2\alpha +1}{2\alpha }>1.$$

(12)

Hence, the UPA distribution can be used for modeling over-dispersed data. In addition, it is right-skewed and leptokurtic, since ${\gamma }_1\left(X\right) > 0$ and ${\gamma }_2\left(X\right) > 0$, respectively. The UPA distribution is a heavy-tailed distribution.

Table 2 gives some moments, variances, and IDs in terms of $\alpha$. Figure 2 displays the plots of the skewness and kurtosis versus $\alpha$. The ID decreases monotonically in $\alpha$, whereas the skewness and kurtosis monotonically increase for $\alpha \in \left(0,\infty \right)$.

Table 2. Moments and ID of the UPA$\left(\alpha \right)$ distribution.

$\mathit{\alpha }$	Mean	B	$\mathit{E}\left({\mathit{X}}^2\right)$	$\mathit{E}\left({\mathit{X}}^3\right)$	$\mathit{E}\left({\mathit{X}}^4\right)$	ID
0.25	2.0000	6.0000	10.0000	74.0000	730.0000	3.0000
0.75	0.6667	1.1111	1.5555	5.1111	22.2963	1.6667
1.00	0.5000	0.7500	1.0000	2.7500	10.0000	1.5000
1.25	0.4000	0.5600	0.7200	1.7440	5.5584	1.4000
1.50	0.3333	0.4444	0.5555	1.2222	3.5185	1.3333
1.75	0.2857	0.3673	0.4490	0.9154	2.4281	1.2857
2.00	0.2500	0.3125	0.3750	0.7187	1.7812	1.2500
2.25	0.2222	0.2716	0.3210	0.5844	1.3672	1.2222
2.50	0.2000	0.2400	0.2800	0.4880	1.0864	1.2000
2.75	0.1818	0.2149	0.2479	0.4162	0.8872	1.1818
3.25	0.1538	0.1775	0.2011	0.3177	0.6297	1.1538
3.75	0.1333	0.1511	0.1689	0.2542	0.4751	1.1333
4.50	0.1111	0.1234	0.1358	0.1934	0.3370	1.1111
5.50	0.0909	0.0992	0.1074	0.1450	0.2353	1.0909
7.50	0.0667	0.0711	0.0755	0.0951	0.1400	1.0667
9.50	0.0526	0.0554	0.0582	0.0701	0.0968	1.0526
10.00	0.0500	0.0525	0.0550	0.0657	0.0896	1.0500
50.00	0.0100	0.0101	0.0102	0.0106	0.0114	1.0100
75.00	0.0067	0.0067	0.0067	0.0069	0.0073	1.0067
100.00	0.0050	0.0050	0.0050	0.0051	0.0053	1.0050

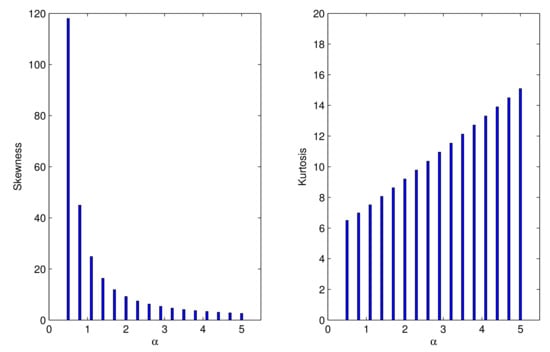
Figure 2. Skewness and kurtosis of the UPA$\left(\alpha \right)$ distribution.

2.2. Stochastic Orders of the Parameter $\alpha$

Shaked and Shanthikumar [16] showed that some stochastic orders exist and have several applications. Theorem 1 shows that the UPA distribution is ordered according to the strongest stochastic order, namely, the likelihood ratio ($lr$) order.

Definition 1.

Consider the two random variables X and Y with respective pmfs $f_X(·)$ and $f_Y(·)$. Then, X is said to be smaller than Y in the $lr$ order, denoted by $X{\le }_{lr}Y$, if  $f_X\left(x\right)/f_Y\left(x\right)$ is non-decreasing in x.

Theorem 1.

Let $X\sim$UPA$\left({\alpha }_1\right)$ and $Y\sim$UPA$\left({\alpha }_2\right)$. Then $X{\le }_{lr}Y$ for all ${\alpha }_1>{\alpha }_2$.

Proof. 

We have

$$\begin{array}{ccc}\hfill L_x& =& \frac{f_X\left(x\right)}{f_Y\left(x\right)}=\frac{{\alpha }_1}{{\alpha }_2}{\left(\frac{1+2{\alpha }_2}{1+2{\alpha }_1}\right)}^{x+1}\hfill \end{array}$$

(13)

and

$$\begin{array}{ccc}\hfill L_{x+1}& =& \frac{f_X(x+1)}{f_Y(x+1)}=\frac{{\alpha }_1}{{\alpha }_2}{\left(\frac{1+2{\alpha }_2}{1+2{\alpha }_1}\right)}^{x+2}.\hfill \end{array}$$

(14)

Clearly, one can note that

$$\begin{array}{ccc}\hfill \frac{L_{x+1}}{L_x}& =& \frac{1+2{\alpha }_2}{1+2{\alpha }_1}<1,\forall {\alpha }_1>{\alpha }_2.\hfill \end{array}$$

(15)

 □

2.3. Entropy

The Shannon entropy of X can be expressed as

$$\begin{array}{cc}H\left(X\right)\hfill & =-{\displaystyle \sum _{x=0}^{\infty }}P(X=x)log\left[P(X=x)\right]\hfill \\ \hfill & =-{\displaystyle \sum _{x=0}^{\infty }}\frac{2\alpha }{{(2\alpha +1)}^{x+1}}\left\{log\left(2\alpha \right)-\left(x+1\right)log(2\alpha +1)\right\}\hfill \\ \hfill & ={\left(2\alpha \right)}^{-1}log\left(2\alpha +1\right)+log\left(2\alpha +1\right)-log\left(2\alpha \right)\hfill \\ \hfill & =log\left(2\alpha +1\right)\left(\frac{1}{2\alpha }+1\right)-log\left(2\alpha \right).\hfill \end{array}$$

(16)

Table 3 gives some values of $H\left(X\right)$ in terms of the parameter $\alpha$. Figure 3 displays the plot of $H\left(X\right)$ versus $\alpha$. The entropy $H\left(X\right)$ is monotonically decreasing for $\alpha \in \left(0,\infty \right)$, and it proceeds to zero when $\alpha$ becomes larger.

Table 3. Entropy of the UPA$\left(\alpha \right)$ distribution.

$\mathit{\alpha }$	$\mathit{H}\left(\mathit{X}\right)$	$\mathit{\alpha }$	$\mathit{H}\left(\mathit{X}\right)$	$\mathit{\alpha }$	$\mathit{H}\left(\mathit{X}\right)$
		3.5	0.4306	7	0.2624
0.5	1.3863	4	0.3924	7.5	0.2494
1	0.9548	4.5	0.3612	8	0.2377
1.5	0.7498	5	0.3351	8.5	0.2272
2	0.6255	5.5	0.3129	9	0.2176
2.5	0.5407	6	0.2938	9.5	0.2090
3	0.4785	6.5	0.2771	10	0.2010

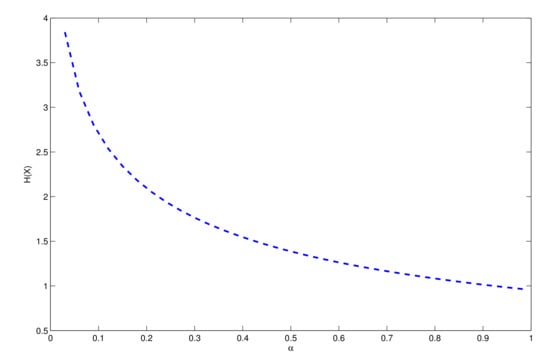
Figure 3. Entropy of the UPA$\left(\alpha \right)$ distribution.

2.4. Quantile Function

The quantile function (qf) of the UPA distribution is determined by inverting (6) as

$$Q\left(u\right)=-1-\frac{log\left(1-u\right)}{log\left(1+2\alpha \right)}.$$

(17)

The ath quantile $\left(x_a\right)$ of X can be expressed from Equation (17) as

$$x_a=\left\{\begin{array}{ccc}⌊-1-{\displaystyle \frac{log\left(1-u\right)}{log\left(1+2\alpha \right)}}⌋+1& ,& ⌊Q\left(a\right)⌋\ne Q\left(a\right)\\ \left\{⌊-1-\frac{log\left(1-u\right)}{log\left(1+2\alpha \right)}⌋,⌊-1-{\displaystyle \frac{log\left(1-u\right)}{log\left(1+2\alpha \right)}}⌋+1\right\}& ,& ⌊Q\left(a\right)⌋=Q\left(a\right)\end{array}\right.,$$

(18)

where $⌊x⌋$ denotes the integer part of x. The quantity $x_a$ satisfies $F\left(x_a^{-}\right)\le p\le F\left(x_a\right)$, where $F\left(x\right)$ is the cdf given in (6). The median of the UPA$\left(\alpha \right)$ distribution is $x_{0.5}$.

3. Actuarial Measures

In this section, we determine the value at risk (VaR) and tail value at risk (TVaR) of the UPA$\left(\alpha \right)$ distribution.

3.1. VaR Measure

Let X denote a loss $rv$. The VaR${}_p$ of X at the $100p\%$ level, say, ${\pi }_p$, is the $100p$ percentile of the distribution of X, namely,

$$\begin{array}{c}\hfill P\left(X>{\pi }_p\right)=1-p,\mathrm{and}\mathrm{then}{\pi }_p=F^{-1}\left(p\right),\end{array}$$

(19)

where $p\in \left(0,1\right)$, and $F\left(x\right)$ is the cdf of the UPA distribution given in (6). The quantity VaR${}_p$ of the UPA distribution comes from the qf (17) as follows:

$${\pi }_p=-1-\frac{log\left(1-p\right)}{log\left(1+2\alpha \right)}.$$

(20)

3.2. TVaR Measure

The TVaR of X at the $100p\%$ security level, say, TVAR${}_p$, has the form

$${\mathrm{TVAR}}_p=E\left(X\mid X>{\pi }_p\right)=\frac{{\displaystyle \sum _{x={\pi }_p}^{\infty }}xf\left(x\right)}{1-F\left({\pi }_p\right)}.$$

(21)

The TVaR${}_p$ measure for the UPA$\left(\alpha \right)$ model follows from Equations (4) and (6).

$$\begin{array}{c}\hfill {\mathrm{TVAR}}_p=\frac{{\left(1+2\alpha \right)}^{1+\frac{log\left(1-u\right)}{log\left(1+2\alpha \right)}}\left\{\left[1-2\alpha \right]log\left(1+2\alpha \right)-2\alpha log\left(1-p\right)\right\}}{2\alpha \left(1-p\right)log\left(1+2\alpha \right)}.\end{array}$$

(22)

Some VaR${}_p$ and TVaR${}_p$ values for the UPA distribution are listed in Table 4.

Table 4. The VaR and TVaR measures for the UPA$\left(\alpha \right)$ model.

$\mathit{\alpha }$	Security Level		VaR${}_{\mathit{p}}$			TVaR${}_{\mathit{p}}$
0.25	0.80		2.9694			7.4074
	0.85		3.6789			7.9012
	0.90		4.6789			9.2181
	0.95		6.3884			10.5350
	0.99		10.3577			15.0293
0.5	0.80		1.3219			4.6338
	0.85		1.7369			5.4739
	0.90		2.3219			6.6438
	0.95		3.3219			8.6438
	0.99		5.6438			13.2877
1.5	0.80		0.1610			1.9772
	0.85		0.3685			2.8073
	0.90		0.6610			3.9772
	0.95		1.1610			5.9772
	0.99		2.3219			10.6210

The figures in Table 4 and the plots in Figure 4 indicate that the VaR and TVaR measures are increasing functions of $\alpha$.

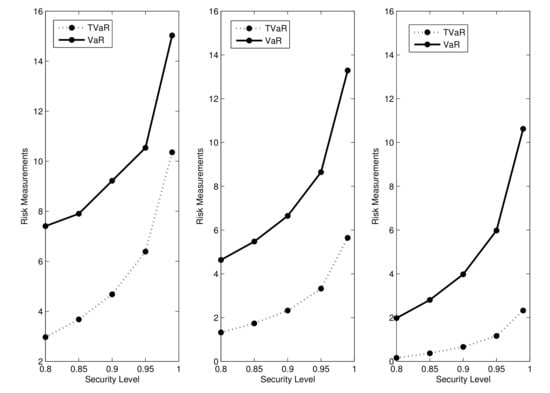
Figure 4. Plots of the VaR and TVaR measures for the UPA$\left(\alpha \right)$ distribution.

4. Estimation

In this section, the parameter $\alpha$ is estimated by eight methods, and their performances are investigated via Monte Carlo simulations. The proposed estimators are determined from the maximum likelihood, moments, proportions, ordinary and weighted least-squares, Cramér–von Mises, right-tail Anderson–Darling, and percentiles methods. For all methods, let $x_1,\dots ,x_n$ be n independent observations from the UPA distribution.

4.1. Maximum Likelihood

The log-likelihood function for $\alpha$ comes from (4) as follows:

$${\ell }_n\left(\alpha \right)=\sum _{i=0}^{n}log\left[f(x_i;\alpha )\right]=nlog\left(2\alpha \right)-\sum _{i=0}^n(x_i+1)log(1+2\alpha ).$$

(23)

Then, the maximum likelihood estimate (MLE) of $\alpha$, say, $\widehat{\alpha }$, is determined by maximizing ${\ell }_n\left(\alpha \right)$ with respect to this parameter as the solution of

$$\frac{d{\ell }_n\left(\alpha \right)}{d\alpha }=\frac{n}{\alpha }-\frac{2}{1+2\alpha }\sum _{i=0}^n(x_i+1)=0,$$

(24)

which gives $\widehat{\alpha }=1/\left(2\overline{x}\right)$ if $\overline{x}>0$, where $\overline{x}=n^{-1}{\sum }_{i=1}^n{x}_i$.

Under some regularity conditions, the distribution of $\widehat{\alpha }$ can be approximated by the $\mathcal{N}(\alpha ,1/I\left(\widehat{\alpha }\right))$ distribution, where $I\left(\alpha \right)$ is the observed Fisher information.

$$I\left(\alpha \right)=\left(-\frac{d^2{\ell }_n\left(\alpha \right)}{d{\alpha }^2}\right)=-\frac{n}{{\alpha }^2}-\frac{4}{{\left(1+2\alpha \right)}^2}\sum _{i=0}^n(x_i+1).$$

(25)

An asymptotic confidence interval for $\alpha$ at the level $(1-\gamma )100\%$ with $\gamma \in (0,1)$ has the form

$$\left[\widehat{\alpha }-z_{\gamma /2}\sqrt{1/I\left(\widehat{\alpha }\right)},\widehat{\alpha }+z_{\gamma /2}\sqrt{1/I\left(\widehat{\alpha }\right)}\right],$$

(26)

where $z_{\gamma /2}$ is the $(1-\gamma /2)$-quantile of the normal $\mathcal{N}(0,1)$ distribution.

4.2. Moments

The moment estimate (MOE) $\tilde{\alpha }$ of $\alpha$ follows from $E\left(X\right)$ given in Section 2.1 as

$$\tilde{\alpha }=\frac{1}{2\overline{x}},$$

(27)

if $\overline{x}>0$. From the central limit theorem,

$$\sqrt{n}\left(\overline{X}-\mu \right)\stackrel{d}{⟶}N\left(0,{\sigma }^2\right),$$

(28)

where

$$\mu =\frac{1}{2\alpha }\mathrm{and}{\sigma }^2=\frac{2\alpha +1}{4{\alpha }^2}.$$

(29)

Based on the delta method,

$$\sqrt{n}\left(\tilde{p}-p\right)\stackrel{d}{⟶}N\left(0,2\alpha +1\right).$$

(30)

For any $0<\gamma <1$, an approximate $100\left(1-\gamma \right)$ confidence interval for the parameter $\alpha$ comes from (30) as

$$P\left(\tilde{\alpha }-z_{\gamma /2}\frac{S}{\sqrt{n}}<\alpha <\tilde{\alpha }+z_{\gamma /2}\frac{S}{\sqrt{n}}\right)=1-\gamma ,$$

(31)

where $S=\sqrt{2\tilde{\alpha }+1}$.

4.3. Proportions

We define the indicator function $\nu (·)$ (for $i=1,\dots ,n$) as

$$\nu \left(x_i\right)=\left\{\begin{array}{c}1,x_i=0,\\ 0,x_i>0.\end{array}\right.$$

(32)

Clearly, the proportion $y=n^{-1}{\sum }_{i=1}^n\nu \left(x_i\right)$ refers to the proportion of zeros in the sample, and it is an unbiased and consistent estimate of the probability

$$f\left(0\right)=\frac{2\alpha }{1+2\alpha }.$$

(33)

Then, the proportions estimate (POE) of $\alpha$ [17] follows by solving

$$y=\frac{2\alpha }{1+2\alpha },$$

(34)

which leads to the estimate $\widehat{\alpha }=-y/\left[2(y-1)\right]$.

4.4. Ordinary and Weighted Least-Squares

Let $X_{j:n}$ be the jth-order statistic in a sample of size n. We adopt lower cases for sample values. It is well-known that $E\left[F\left(X_{j:n}\right)\right]=\frac{j}{1+n}$ and $V\left[F\left(X_{j:n}\right)\right]=\frac{j(n-j+1)}{{(n+1)}^2(n+2)}$.

The least-squares estimate (LSE) of $\alpha$, $\widehat{\alpha }$, follows by minimizing

$$\begin{array}{c}\hfill \sum _{j=1}^n{\left[1-\frac{1}{{(1+2\alpha )}^{x_{j:n}+1}}-\frac{j}{n+1}\right]}^2,\end{array}$$

(35)

in relation to $\alpha$.

The weighted least-squares estimate (WLSE) of $\alpha$, $\tilde{\alpha }$, is determined by minimizing

$$\begin{array}{c}\hfill \sum _{j=1}^n{\varphi }_j{\left[1-\frac{1}{{(1+2\alpha )}^{x_{j:n}+1}}-\frac{j}{n+1}\right]}^2,\end{array}$$

(36)

in relation to $\alpha$, where the weight function is ${\varphi }_j=\left[{(n+1)}^2(n+2)\right]/\left[j(n-j+1)\right]$.

4.5. Cramér-von Mises

The Cramér–von Mises estimate (CVME) (see [18,19]) is based on the difference between the estimate of the cdf and its empirical cdf [20]. The CVME of $\alpha$ follows by minimizing

$$C\left(\alpha \right)=\frac{1}{12n}+\sum _{j=1}^n{\left[1-\frac{1}{{(1+2\alpha )}^{x_{j:n}+1}}-\frac{2j-1}{2n}\right]}^2,$$

(37)

with respect to $\alpha$. Further, the CVME of $\alpha$ is also obtained by solving

$$\sum _{j=1}^n\left[1-\frac{1}{{(1+2\alpha )}^{x_{j:n}+1}}-\frac{2j-1}{2n}\right]\frac{2\left(x_{j:n}+1\right)}{{(1+2\alpha )}^{x_{j:n}+2}}=0.$$

(38)

4.6. Right-Tail Anderson–Darling

The right-tail Anderson–Darling estimate (RADE) of $\alpha$ follows by minimizing

$$R\left(\alpha \right)=\frac{n}{2}-2\sum _{j=1}^n\left[1-\frac{1}{{(1+2\alpha )}^{x_{j:n}+1}}\right]-\frac{1}{n}\sum _{j=1}^n\left(2j-1\right)log\left[1-\frac{1}{{(1+2\alpha )}^{x_{n+1-j:n}}}\right],$$

(39)

in relation to $\alpha$. The RADE of $\alpha$ is also found by solving the equation

$$-4\sum _{j=1}^n\frac{\left(x_{j:n}+1\right)}{{(1+2\alpha )}^{x_{j:n}+2}}+\frac{2}{n}\sum _{j=1}^n\left(2j-1\right)\frac{\left(x_{n+1-j:n}+1\right)}{{(1+2\alpha )}^2}=0.$$

(40)

4.7. Percentiles

The percentile estimate (PCE) is obtained by equating the sample percentile point to the population percentile. If $p_j$ denotes an estimate of $F(x_{j:n};\alpha )$, the PCE of $\alpha$, say ${\widehat{\alpha }}_{PCE}$, follows by minimizing

$$\begin{array}{c}\hfill P\left(\alpha \right)=\sum _{j=1}^n{\left[x_j-Q\left(p_j\right)\right]}^2,\end{array}$$

(41)

where $p_j=\frac{j}{1+n}$ is an unbiased estimator of $F(x_{j:n};\alpha )$ and

$$\begin{array}{c}\hfill Q\left(p_j\right)=-\frac{log\left[\left(1+2\alpha \right)\left(1-p_j\right)\right]}{log\left(1+2\alpha \right)}.\end{array}$$

(42)

5. Simulation Study

We conducted a simulation study to evaluate the accuracy of the eight estimators discussed before. We generated samples of sizes $n=30,75,100,150,200$, and 300 from the UPA distribution and then calculated the average values of the MLE, MOE, POE, LSE, WLSE, CVME, RADE, and PCE of $\alpha$ (AVEs), mean square errors (MSEs), average absolute biases (ABBs), and mean relative errors (MREs) when $\alpha =0.35,0.5,1.5$, and $3.0$. The ABBs, MSEs and MREs are given by

$$\widehat{ABB{s}_{\alpha }}=\frac{1}{N}{\sum }_{i=1}^N\left|\widehat{\alpha }-\alpha \right|,$$

(43)

$$\widehat{MS{E}_{\alpha }}=\frac{1}{N}{\sum }_{i=1}^N{\left(\widehat{\alpha }-\alpha \right)}^2$$

(44)

and

$$\widehat{MR{E}_{\alpha }}=\frac{1}{N}{\sum }_{i=1}^N\left|\widehat{\alpha }-\alpha \right|/\alpha .$$

(45)

We repeated the simulation 5000 times to calculate these measures for MLE, MOE, POE, LSE, WLSE, CVME, RADE, and PCE from the previous settings. The results reported in Table 5, Table 6, Table 7 and Table 8 were found using the optim-CG routine of R software.

Table 5. Simulation results of the UPA model for $\alpha =0.35$.

n		MLE	POE	MOE	LSE	WLSE	CVME	RADE	PCE
30	AVEs	0.3571	0.3333	0.3571	0.3633	0.3635	0.3754	0.3742	0.3724
	MSEs	0.3031	0.0076	0.0031	0.0039	0.0040	0.0205	0.0198	0.0764
	ABSs	0.0554	0.0875	0.0554	0.0626	0.0631	0.0863	0.0789	0.2624
	MREs	0.1583	0.2504	0.1583	0.1788	0.1804	0.2415	0.1428	0.8639
75	AVEs	0.3505	0.3523	0.3505	0.3555	0.3557	0.3495	0.3465	0.3639
	MSEs	0.0013	0.0027	0.0013	0.0017	0.0018	0.0101	0.0087	0.0458
	ABSs	0.0366	0.0521	0.0366	0.0415	0.0421	0.0774	0.0712	0.2139
	MREs	0.1046	0.1489	0.1046	0.1184	0.1204	0.2212	0.0712	0.6112
100	AVEs	0.3521	0.3474	0.3521	0.3525	0.3521	0.3394	0.3416	0.3480
	MSEs	0.0010	0.0019	0.0010	0.0013	0.0013	0.0057	0.0050	0.0065
	ABSs	0.0315	0.0435	0.0315	0.0355	0.0360	0.0602	0.0557	0.0634
	MREs	0.0901	0.1244	0.0908	0.1017	0.1029	0.1719	0.0557	0.1812
150	AVEs	0.3505	0.3523	0.3505	0.3524	0.3524	0.3397	0.3403	0.3478
	MSEs	0.0006	0.0018	0.0006	0.0008	0.0008	0.0045	0.0039	0.0049
	ABSs	0.0250	0.0428	0.0250	0.0291	0.0294	0.0537	0.0498	0.0556
	MREs	0.0714	0.1224	0.0714	0.0832	0.0841	0.1535	0.0498	0.1589
200	AVEs	0.3509	0.3474	0.3508	0.3525	0.3525	0.3354	0.3389	0.3418
	MSEs	0.0005	0.0012	0.0005	0.0006	0.0006	0.0023	0.0020	0.0024
	ABSs	0.0217	0.0349	0.0217	0.0247	0.0248	0.0392	0.0360	0.0393
	MREs	0.0621	0.0999	0.0621	0.0707	0.0710	0.1121	0.0360	0.1123
300	AVEs	0.3505	0.3522	0.3505	0.3519	0.3516	0.3463	0.3465	0.3488
	MSEs	0.0003	0.0007	0.0003	0.0004	0.0004	0.0010	0.0008	0.0009
	ABSs	0.0176	0.0272	0.0176	0.0203	0.0204	0.0261	0.0226	0.0236
	MREs	0.0504	0.0777	0.0504	0.0579	0.0583	0.0745	0.0226	0.0673

Table 6. Simulation results of the UPA model for $\alpha =0.5$.

n		MLE	POE	MOE	LSE	WLSE	CVME	RADE	PCE
30	AVEs	0.5172	0.5127	0.5172	0.5146	0.5155	0.4757	0.4785	0.4898
	MSEs	0.0069	0.0138	0.0069	0.0089	0.0089	0.0167	0.0147	0.0217
	ABBs	0.0833	0.1176	0.0833	0.0943	0.0944	0.1028	0.0967	0.1136
	MREs	0.1667	0.2353	0.1667	0.1886	0.1888	0.2050	0.1934	0.2273
75	AVEs	0.5145	0.4868	0.5145	0.5020	0.5016	0.4653	0.4713	0.4848
	MSEs	0.0029	0.0051	0.0029	0.0037	0.0038	0.0073	0.0060	0.0077
	ABBs	0.0536	0.0714	0.0536	0.0612	0.0615	0.0703	0.0634	0.0704
	MREs	0.1071	0.1429	0.1071	0.1224	0.1230	0.1407	0.1267	0.1408
100	AVEs	0.5126	0.4868	0.5127	0.5020	0.5016	0.4619	0.4588	0.4871
	MSEs	0.0024	0.0041	0.0024	0.0029	0.0029	0.0056	0.0045	0.0059
	ABBs	0.0495	0.0638	0.0495	0.0542	0.0542	0.0620	0.0562	0.0615
	MREs	0.0989	0.1277	0.0989	0.1085	0.1085	0.1241	0.1124	0.1230
150	AVEs	0.5098	0.5057	0.5097	0.5023	0.5019	0.4588	0.4678	0.4894
	MSEs	0.0016	0.0032	0.0016	0.0020	0.0019	0.0045	0.0036	0.0040
	ABBs	0.0396	0.0563	0.0396	0.0447	0.0441	0.0562	0.0497	0.0508
	MREs	0.0791	0.1127	0.0791	0.0894	0.883	0.1124	0.0993	0.1016
200	AVEs	0.5044	0.5005	0.5045	0.5011	0.5008	0.4600	0.4665	0.4906
	MSEs	0.0011	0.0023	0.0011	0.0014	0.0014	0.0037	0.0030	0.0030
	ABBs	0.0327	0.0476	0.0327	0.0379	0.0379	0.0510	0.0456	0.0442
	MREs	0.0654	0.0952	0.0654	0.0755	0.0758	0.1021	0.0911	0.0883
300	AVEs	0.5005	0.5004	0.5004	0.5003	0.5003	0.4573	0.4667	0.4914
	MSEs	0.0008	0.0015	0.0008	0.0010	0.0010	0.0031	0.0024	0.0019
	ABBs	0.0282	0.0385	0.0282	0.0312	0.0315	0.0480	0.0406	0.0354
	MREs	0.0563	0.0769	0.0563	0.0625	0.0630	0.0961	0.0813	0.0708

Table 7. Simulation results of the UPA model for $\alpha =1.5$.

n		MLE	POE	MOE	LSE	WLSE	CVME	RADE	PCE
30	AVEs	1.5421	1.6429	1.5521	1.6069	1.6044	1.1887	1.2015	1.5306
	MSEs	0.1406	0.2500	0.1406	0.2060	0.2029	0.2316	0.2203	1.0837
	ABBs	0.3750	0.5024	0.3750	0.4538	0.4504	0.4160	0.4045	0.4863
	MREs	0.2500	0.3333	0.2501	0.3025	0.3003	0.2773	0.2696	0.3241
75	AVEs	1.5215	1.4737	1.5257	1.4992	1.4941	1.1389	1.1612	1.4721
	MSEs	0.0428	0.0873	0.0428	0.0604	0.0617	0.1750	0.1594	0.1434
	ABBs	0.2069	0.2955	0.2069	0.2457	0.2483	0.3780	0.3598	0.2931
	MREs	0.1379	0.1970	0.1379	0.1638	0.1656	0.2520	0.2399	0.1954
100	AVEs	1.5152	1.5247	1.5152	1.5029	1.5028	1.1337	1.1641	1.4760
	MSEs	0.0475	0.0459	0.0475	0.0469	0.0470	0.1676	0.1450	0.1075
	ABBs	0.2179	0.2143	0.2179	0.2166	0.2169	0.3748	0.3471	0.2555
	MREs	0.1453	0.1429	0.1453	0.1444	0.1446	0.2499	0.2314	0.1703
150	AVEs	1.5158	1.5270	1.5247	1.5110	1.5120	1.1305	1.1600	1.4791
	MSEs	0.0278	0.0424	0.0278	0.0348	0.0347	0.1575	0.1364	0.0069
	ABBs	0.1667	0.2059	0.1667	0.1865	0.1862	0.3714	0.3431	0.2073
	MREs	0.1111	0.1373	0.1111	0.1243	0.1241	0.2476	0.2288	01382
200	AVEs	1.5152	1.5123	1.5152	1.5000	1.4995	1.1211	1.1522	1.4794
	MSEs	0.0221	0.0302	0.0220	0.0265	0.0265	0.1590	0.1306	0.0494
	ABBs	0.1486	0.1739	0.1486	0.1627	0.1629	0.3795	0.3479	0.1778
	MREs	0.0991	0.1159	0.0991	0.1084	0.1086	0.2530	0.2330	0.1186
300	AVEs	1.5045	1.5057	1.5098	1.5032	1.5028	1.1205	1.1522	1.4813
	MSEs	0.0127	0.0156	0.0127	0.0160	0.0159	0.1543	0.1306	0.0329
	ABBs	0.1129	0.1250	0.1129	0.1265	0.1260	0.3766	0.3479	0.1452
	MREs	0.0753	0.0833	0.0752	0.0844	0.0840	0.2531	0.2319	0.0968

Table 8. Simulation results of the UPA model for $\alpha =3.0$.

n		MLE	POE	MOE	LSE	WLSE	CVME	RADE	PCE
30	AVEs	3.4270	3.2500	3.2347	3.2366	3.2866	2.5001	2.5030	3.4441
	MSEs	0.7347	1.0124	0.7347	1.0417	1.0248	1.5788	1.5904	1.8639
	ABBs	0.8571	1.0147	0.8571	1.0206	1.0123	1.1359	1.1275	1.4804
	MREs	0.2857	0.3333	0.2857	0.3402	0.3374	0.3786	0.3758	0.4935
75	AVEs	3.1250	2.9091	3.1250	2.9339	2.9364	2.8859	2.9132	3.0907
	MSEs	0.4307	0.4444	0.4307	0.4302	0.4304	1.4055	1.3384	1.2770
	ABBs	0.6562	0.6667	0.6563	0.6560	0.6561	1.1236	1.0963	0.7931
	MREs	0.2188	0.2222	0.2188	0.2187	0.2187	0.3745	0.3654	0.2644
100	AVEs	3.1250	3.0714	3.1250	3.0711	3.0711	2.8642	2.8988	3.0839
	MSEs	0.3265	0.3122	0.3265	0.3318	0.3289	1.4062	1.3243	0.8779
	ABBs	0.5714	0.5588	0.5714	0.5760	0.5735	1.1388	1.1045	0.6850
	MREs	0.1905	0.1863	0.1905	0.1920	0.1912	0.3796	0.3681	0.2283
150	AVEs	3.0785	3.0714	3.0673	3.0650	3.0656	2.8513	2.8892	3.0408
	MSEs	0.1712	0.2001	0.1712	0.2026	0.2031	1.3906	1.3021	0.5301
	ABBs	0.4138	0.4474	0.4138	0.4502	0.4507	1.1487	1.1109	0.5437
	MREs	0.1379	0.1491	0.1379	0.1500	0.1502	0.3829	0.3703	0.1819
200	AVEs	3.0303	3.0714	3.0303	3.0578	3.0562	2.8470	2.8804	3.0547
	MSEs	0.1357	0.1406	0.1357	0.1439	0.1449	1.3820	1.3047	0.3779
	ABBs	0.3684	0.3750	0.3684	0.3794	0.3807	1.1530	1.1197	0.4726
	MREs	0.1228	0.1250	0.1228	0.1265	0.1269	0.3844	0.3732	0.1576
300	AVEs	3.0159	2.9884	3.0158	2.9923	2.9917	2.8412	2.8765	3.0507
	MSEs	0.1033	0.1198	0.1033	0.1178	0.1183	1.3785	1.2945	0.2502
	ABBs	0.3214	0.3462	0.3214	0.3432	0.3439	1.1588	1.1235	0.3854
	MREs	0.1071	0.1154	0.1071	0.1144	0.1146	0.3863	0.3745	0.1285

The numbers in Table 5, Table 6, Table 7 and Table 8 reveal that the AVEs became closer to the true values of $\alpha$ when the sample size n increased, as expected. Further, the ABBs, MREs, and MSEs for all estimators decreased when n increased. Moreover, the MLE and MOE were the best estimators under these criteria. The MLE and MOE were almost identical in terms of the ABBs, MSEs, and MREs, and both had better performances than the other estimators. Additionally, the biases and MSEs of all estimators decayed toward zero when n increased. In summary, the performance ordering of the proposed estimators, from best to worst, was MLE, MOE, WLSE, LSE, POE, PCE, RADE, and CVME. Hence, maximum likelihood was adopted for the work in the next section.

6. Modeling Biological Data

In this section, the UPA distribution is fitted to three real biological datasets and compared with the discrete Burr–Hatke (DBH) [21], discrete Poisson Lindley (DPL) [22], natural discrete Lindley (NDL) [8], discrete Pareto (DP) [5], PA and Poisson distributions according to the model’s ability. The first dataset (Catcheside et al. [23]) refers to numbers of chromatid aberrations, and it was adopted by Hassan et al. [15] for comparing the Poisson and PA distributions. We aimed to test whether the UPA model is a more reasonable choice for these data based on the chi-squared test. Under the null hypothesis, the estimated probabilities were

$$\widehat{{\alpha }_i}=\widehat{P}(X=i)=\frac{2\widehat{\alpha }}{{(1+2\widehat{\alpha })}^{i+1}},i=0,1.\dots$$

(46)

The estimated expected frequencies were $\widehat{e_i}=n\widehat{{\alpha }_i}$. The results of the chi-square test were reported in Table 9 considering five cells, where

$${\chi }^2=\sum _{i=1}^5\frac{{(o_i-\widehat{e_i})}^2}{\widehat{e_i}}=4.2507<{\chi }_{0.95}^2\left(4\right)=9.4877,$$

(47)

where $\widehat{e_i}$ and $o_i$ are, respectively, the expected and observed frequencies for $x=i$. Thus, we cannot reject $H_0$ at the 5% significance level, and then the UPA distribution is quite suitable for these data.

Table 9. Results of the ${\chi }^2$ test for the first dataset.

Count	Observed	Expected
		UPA	DBH	NDL	Poisson	Pareto	PA	DPL
0	268	264.03	282.33	258.76	238.99	292.41	252.96	262.44
1	87	89.75	71.52	95.87	123.09	57.68	103.60	91.61
2	26	30.51	25.79	31.57	31.70	20.97	31.82	30.92
3	9	10.37	10.78	9.75	5.44	9.98	8.69	10.19
4	10	3.53	4.89	2.89	0.70	5.54	2.22	3.30
Total	$n=$ 400
Parameters	$\widehat{\alpha }$	0.9709	0.5883	0.7530	0.5150	0.1504	1.9417	2.5012
	${\chi }^2$	5.33	6.49	7.54	29.41	15.17	11.37	5.94
	$-\widehat{\ell }$	388.44	389.76	390.99	408.63	405.12	392.55	388.74

We also report in Table 9 the results of the ${\chi }^2$ test for the UPA and other distributions based on the MLE of $\alpha$. The UPA distribution provided the best fit since it resulted in the smallest ${\chi }^2$ value. This conclusion can also be confirmed by the log-likelihood test. Figure 5 displays the empirical pmf and seven pmfs fitted to the first dataset, which confirm that the new distribution yielded the best fit to the current data.

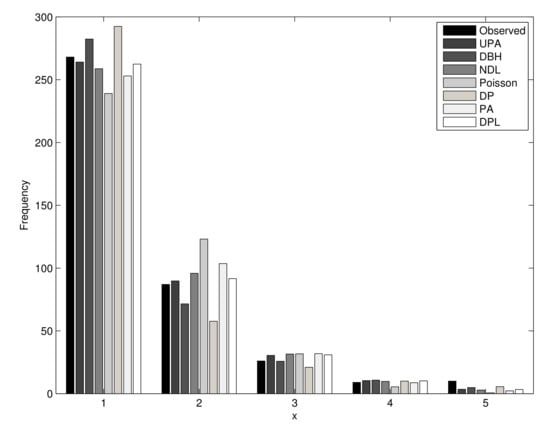
Figure 5. Fitted and empirical distributions for the first dataset.

The second dataset (Catcheside et al. [23]) represents the number of mammalian cytogenetic dosimetry lesions in rabbit lymphoblasts induced by streptonigrin (NSC-45383) exposure—70 3bc g/kg. We fitted the UPA and other distributions to these data.

Table 10 reports the results of the ${\chi }^2$ test for seven fitted distributions, and Figure 6 displays the empirical pmf and seven pmfs fitted to these data. We have

$${\chi }^2=\sum _{i=1}^5\frac{{(o_i-\widehat{e_i})}^2}{\widehat{e_i}}=4.9000<{\chi }_{0.95}^2\left(4\right)=9.4877.$$

(48)

Table 10. Results of the ${\chi }^2$ test for the second dataset.

Count	Observed	Expected
		UPA	DBH	NDL	Poisson	Pareto	PA	DPL
0	200	195.80	209.55	190.60	174.83	216.88	186.00	193.45
1	57	68.31	54.09	73.07	94.40	43.89	79.09	69.82
2	30	24.96	19.92	24.90	25.49	16.20	25.22	24.34
3	7	8.41	8.51	7.96	4.59	7.80	7.15	8.28
4≥	6	3.06	3.95	2.44	0.62	4.37	1.90	2.76
Total	$n=$ 300
Parameters	$\widehat{\alpha }$	0.9259	0.6030	0.7444	0.5400	0.1570	1.8518	2.4002
	${\chi }^2$	4.90	5.02	8.08	34.04	11.32	13.10	6.15
	$-\widehat{\ell }$	299.31	301.70	300.16	314.23	312.94	302.41	302.41

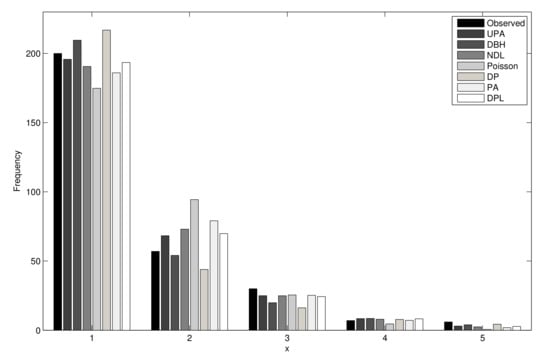
Figure 6. Fitted and empirical distributions for the second dataset.

Then, the hypothesis $H_0:X\sim$UPA$\left(\alpha \right)$ cannot be rejected at the 5% significance level. Thus, the UPA distribution is a reasonable model for these data.

Based on the ${\chi }^2$ tests, log-likelihood values, and Figure 6, we conclude that the UPA model provided a better fit for the second dataset than the other distributions.

The third dataset refers to counts of daily new COVID-19 deaths of Switzerland between 1 March to 30 June 2021 available at https://github.com/owid/COVID-19-data/tree/master/public/data/ (accessed on 6 July 2021). We adopt these data to show the flexibility of the UPA model comparing to other models based on three criteria: Akaike information criterion (AIC), Bayesian information criterion (BIC), and −maximized log-likelihood ($-\widehat{\ell }$). These daily new deaths are: 22, 17, 9, 8, 19, 5, 2, 8, 9, 17, 8, 14, 4, 4, 6, 29, 16, 20, 20, 0, 10, 26, 8, 29, 8, 14, 1, 1, 5, 17, 15, 13, 1, 0, 2, 24, 26, 29, 13, 5, 2, 1, 13, 6, 16, 10, 7, 0, 3, 13, 11, 14, 9, 11, 28, 13, 8, 26, 8, 7, 1, 1, 21, 12, 18, 10, 7, 2, 2, 9, 6, 4, 3, 2, 0, 1, 13, 8, 4, 4, 8, 7, 1, 3, 7, 3, 9, 3, 4, 1, 4, 16, 0, 2, 3, 1, 0, 9, 3, 7, 2, 6, 0, 0, 2, 5, 2, 0, 1, 0, 0, 7, 0, 0, 4, 2, 0, 0, 3, 2, 4. The Kolmogorov–Smirnov statistic for the UPA model is $0.1132$ with a p-value of $0.0920$.

Table 11 reports the estimates of $\alpha$, and the values of AIC, BIC and $-\widehat{\ell }$ for the UPA and other distributions. According to the figures in this table, the UPA distribution is more adequate for these data than the DPL, NDL, DPL, PA, DP, DBH, and Poisson distributions. This conclusion is also supported by Figure 7.

Table 11. Estimates, AIC, BIC, and $-\widehat{\ell }$ for the third dataset.

Model	$\widehat{\mathit{\alpha }}$	$\mathbf{AIC}$	$\mathbf{BIC}$	$-\mathit{\ell }$
UPA	0.0585	757.2386	757.3214	377.6193
DPL	0.2318	765.8140	765.8968	381.9070
NDL	0.1901	767.1740	767.2568	382.5870
PA	0.1275	778.3318	778.4146	388.1659
DP	0.5857	849.9678	850.0506	423.9839
DBH	0.9920	909.8294	910.0438	452.9147
Poisson	7.8430	1260.3650	1260.4478	629.1825

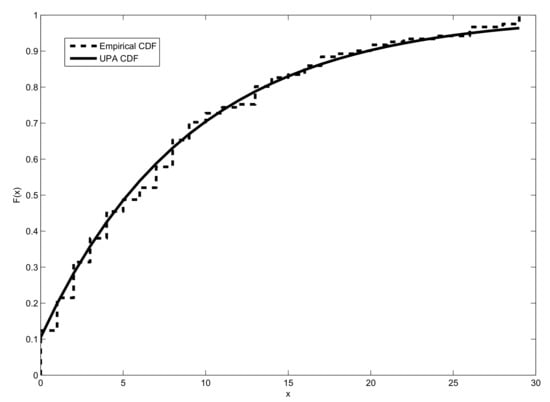
Figure 7. Empirical and estimated cdf of the UPA distribution for the third dataset.

Some useful probabilities can be easily calculated from the estimated cdf. For example, a researcher would like to know the risk that more than ten deaths occur in Switzerland in just one day during that coronavirus period.

7. Conclusions

New discrete distributions are very important for modeling real-life scenarios since the traditional ones have limited applications in failure times, reliability, counts, etc. We proposed and studied the uniform Poisson–Ailamujia (UPA) distribution, which can give better fits than other discrete distributions, especially when modeling over-dispersed count data. Seven methods were discussed to estimate its parameter, and Monte Carlo simulations showed that the maximum likelihood and moments are the best ones. The flexibility of the UPA model was proven empirically by means of three real biological datasets. Furthermore, the UPA distribution can be extended in some ways. For example, the transmuted UPA, exponentiated UPA, Beta UPA, Kumaraswamy UPA can be defined to provide more flexibility with two and three parameters and to increase the potential applicability of the UPA distribution. It is difficult, sometimes, to measure lifetimes or counts on a continuous scale. In practice, we come across situations, where lifetimes are discrete random variables. For example, the number of days that COVID-19 patients stay in hospital beds, the number of hospital beds occupied by coronavirus patients in a hospital, the number of comorbidities in these patients, etc. We point out examples of epidemiology, but it can be applied in several other areas.