Abstract
Control of supply chains with chaotic dynamics is an important, yet daunting challenge because of the limitations and constraints there are in the amplitude of control efforts. In real-world systems, applying control techniques that need a large amplitude signal is impractical. In the literature, there is no study that considers the control of supply chain systems subject to control input limitations. To this end, in the current study, a new control scheme is proposed to tackle this issue. In the designed control input, limitations in control inputs, as well as robustness against uncertainties, are taken into account. The proposed scheme is equipped with a fixed time disturbance observer to eliminate the destructive effects of uncertainties and disturbances. Additionally, the super-twisting sliding mode technique guarantees the fixed-time convergence of the closed-loop system. After that, a symmetric supply chain system is presented, and its chaotic attractors are demonstrated. Finally, the proposed controller is applied to the symmetric supply chain system. Numerical simulations exhibit the proposed scheme’s excellent performance even though the system is subjected to control input limitations and time-varying uncertainties.
1. Introduction
During recent decades, academics and decision makers have been striving for a reliable approach to handle advanced supply chain systems. In the past, decisions were often made based on intuition and experience [1,2]. However, over time, supply chains have become more and more complicated, resulting in the failure of traditional management techniques [3]. Business entities in the supply chain are tightly intertwined with uncertainties. Additionally, most supply chain systems possess nonlinear dynamics that sometimes provide chaotic responses. Hence, applying up-to-date techniques for their manganates is of crucial importance [4,5,6].
Nonlinear dynamical systems with an infinite number of different periodic responses that are susceptible to initial conditions are known as chaotic systems [7,8,9,10]. Although chaos can be useful in certain situations, it is often an unwelcome occurrence. The chaotic oscillations must be suppressed; thus, regulation mechanisms are needed [11,12]. Furthermore, due to minor faults, chaotic processes are prone to take entirely separate paths. As a result, control and stabilization are needed in chaotic systems [13,14]. The regulation of chaotic processes has been one of the most significant issues in the control engineering field after Ott, Grebogi, and Yorke (1990) successfully controlled a chaotic system [15]. To date, different approaches for dealing with chaotic processes have been suggested and tested [16,17,18].
Among all control schemes that have been used to control the actions of complex systems over the last few decades, sliding mode control (SMC), as the most common robust controller, has received a lot of attention because of its features, including ease of execution, guaranteed stability, and resistance to parameter variations [19,20,21]. In addition, numerous experiments have recently been conducted on the use of sliding mode control in the control of chaotic systems. However, SMC has some drawbacks [22,23,24,25]. For instance, SMC does not guarantee convergence in finite time. To this end, terminal sliding mode control (TSMC) was developed to overcome the issue of finite-time convergence [26,27].
As mentioned, a significant challenge in this field is designing control and management approaches that ensure the systems’ appropriate performance. Control theory has established a firm foundation for handling nonlinear dynamics [28,29,30,31,32,33,34]. Hence, the application of control theory can provide luminating results in managing supply chains with nonlinear dynamics [35]. Numerous methods developed in the control literature have been applied to supply chains over the last half-century [36]. Model predictive control (MPC) and neuro-dynamic programming are examples of increasingly advanced control methodologies applied to supply chain systems [37,38]. Despite a lot of efforts made by researchers, some issues still require more attention. For instance, no study in the literature considers finite-time convergence and limitations in control inputs in the control of supply chains.
Most financial processes possess nonlinear dynamics subjected to disturbances and control input limitations [39,40]. Hence, many studies have proposed robust techniques to control economic and financial systems [41]. Since the external disturbance cannot be directly evaluated in a nonlinear environment, nonlinear observers should be utilized to detect their dynamics [21,42]. On the other hand, input saturation, a nonsmooth nonlinearity, should be considered in real-world applications [43,44].
The abovementioned issues have motivated the current study. The present research proposes a new control scheme. The suggested scheme includes a fixed time disturbance observer to minimize the negative consequences of uncertainties and disruptions. Then, an uncertain, symmetric chaotic supply chain system has been considered with limited control inputs, and the performance of the designed control scheme has been assessed by presenting some numerical simulation results.
It is noteworthy that the proposed control technique improves some issues which occur in its counterparts. Compared to its state-of-the-art counterparts, the suggested controller has important advantages. For example, Chen et al. [45] have proposed a TSMC which is equipped with a finite time observer. Although their study was a breakthrough in this field of study, it suffers from several critical disadvantages. For instance, chattering was not investigated in their controller, and in some situations, that control scheme can result in severe vibration in systems. Huang has offered a fast TSMC with a novel fuzzy disturbance observer [46], in which the error of disturbance observation in that method converges asymptotically, and in real applications, it may take a long time to estimate unknown functions. In 2018, Liu et al. [47] proposed a disturbance observer-based fuzzy TSMC for a hypersonic vehicle. Although the finite-time convergence of the disturbance observer and the closed-loop system was proven in their study, the existence of control input saturation and chattering was ignored, which lowers the performance of that control scheme considerably. On the contrary, the super-twisting sliding surface we propose in the current research is chatter-free and takes the effects of control input saturation into account. More recently, an observer-based fuzzy TSMC has been offered by Vahidi-Moghaddam et al. [48] for MIMO systems. Convergence time is, however, a considerable drawback in their controller. They have only demonstrated the disturbance observer’s finite-time convergence; nonetheless, the closed-loop system is exponentially stable, and the convergence of the closed-loop system in fixed time is not guaranteed. As a result, convergence time may be extremely long in some circumstances. On the other hand, in the current study, we prove the fixed-time convergence of the disturbance observer and the closed-loop system simultaneously.
The rest of the current paper is organized as follows: In Section 2, the design procedure of the proposed scheme, including effects of uncertainties and limitation in control input, fixed-time disturbance observer, and super-twisting SMC, are delineated. Additionally, the stability of the closed-loop system is proven through the Lyapunov stability theorem. Then, in Section 3, the chaotic behavior symmetric supply chain system is described. In Section 4, the proposed control scheme is applied to control the chaotic behavior of the symmetric supply chain system, and various numerical simulations are presented. Finally, in Section 5, concluding remarks are given.
2. Controller Design
In this paper, we investigate the control of MIMO nonlinear supply chains. Let the state space of the MIMO system be as described below:
where is the state vector, f and g are nonlinear functions. The structural variation and uncertainty that there are in the dynamics of the system are represented by and . Additionally, stands for the external disturbance. In addition, denotes the control input.
2.1. Effects of Uncertainties and Limitation in Control Input
The whole unknown terms produced by structural variations, uncertainties, and disturbances, i.e., , and the external disturbance , are considered as a single disturbance term as follows:
Furthermore, control input limitations that may occur in many real systems act like nonsmooth nonlinearities. Since control input limitations are common to most systems, ignoring them in the design of control schemes for real-world applications could dramatically ruin the performance of the systems. To tackle this problem in the current study, we consider the effects of control limitations and saturation in the designed control. Under the control input constraints, the limited control input is given by
where is designed control command, and denotes the limited control input applied to the system. and are the bounds of the control input. Defining and substituting Equations (2) and (3) into Equation (1) result in
where is the compound disturbance imposed on the system.
2.2. Fixed-Time Disturbance Observer
Lemmas 1 and 2 are used in the design process of the fixed-time disturbance observer.
Lemma 1.
Letbe a continuous positive definite function satisfying the following inequality [49]
As a result, converges to its equilibrium point in the finite time which is given by
where , and .
Lemma 2.
Based on the triangle inequality, if and , then
The following auxiliary variables are defined for the disturbance observer
where z is given by
In which . Additionally, and both andare odd positive integers. Furthermore, k and ε are positive constants. The fixed-time disturbance observeris designed as [45,48]
Taking the derivative of (10) and considering (8), (9), and (4) give
Based on Equations (3), (10), and (11), the following equation is reached
Theorem 1.
Using the proposed fixed-time disturbance observer (8)–(10), the disturbance estimation error (12) converges to zero.
Proof.
Let a Lyapunov function be
By taking the time derivative of
, we reach
The last line of the equation above has been calculated through Lemma 3. □
Lemma 3.
Thus, we have
As is evident, =, consequently, we have
Therefore, following Lemmas 1, 2, and 3 as well as Equations (17) and (12), the auxiliary vector s and the disturbance approximation errorconverge to zero in the fixed time.
Remark 1.
Based on Lemma 1, the convergence time of disturbance approximation is as follows:
wheredenotes the initial time; hence, by choosing parameters of the disturbance and considering Equation (18), we could reach a fixed-time disturbance observer.
2.3. Super-Twisting SMC
The super-twisting algorithm is a well-known second-order sliding mode algorithm introduced in [50], and it has been widely used for control and observation. In the literature, the effectiveness of super-twisting sliding mode controllers in terms of the accuracy of the control scheme and reducing chattering has been proven. Using the disturbance observer developed in Section 2.1, the fixed-time super-twisting TSMC is designed for system (1). The tracking error of the system is given by
where is the required value for the state . We define the sliding surface as follows.
In which is the auxiliary variable, given in Equation (8), and is an appositive use defined constant. Finally, we propose the disturbance observer-based fixed-time super-twisting for system (1) as
where parameters and are positive.
Theorem 2.
Using the control law (21), the closed-loop system states (1) converge to the desired value in fixed time.
Proof.
The time-derivative of the sliding surface (Equation (20)) is given by
Based on Equation (12), , which results in
Hence, we have
Defining new variables as and and rewriting the above equation, we obtain
Equation (25) denotes a second-order super-twisting algorithm. Based on Theorem 2, in [51] and its proof, we consider the following Lyapunov function:
where is quadratic, robust, and strict and with symmetric and positive definite matrix P will fulfill
for symmetric and positive definite matrix . In addition, the trajectory originating at w(0) will reach the origin in a fixed time which is given by
The matrices and of the Lyapunov function can be selected in accordance with the procedure given in [51], which guarantees that the sliding variables and
go to zero in the fixed time. □
3. Symmetric Supply Chain System
Thus far, many researchers have tried to model supply chain systems. Among all models proposed for supply chain systems, the nonlinear model introduced by Anne et al. [52] has attracted a lot of attention. They introduced a nonlinear supply chain model that covers safety stock, information distortion, and retailer order satisfaction. That model is given by
where is the quantity demanded by the retailer in the current period, denotes the quantity distributors can supply in the current period, and indicates the quantity produced in the current period depending on the order. In addition, is the rate of customer demand satisfaction with the retailer. stands for the inventory level of distributors. is the safety stock coefficient of the manufacturer, and is the rate of information distortion of products demanded by the retailer.
This system is rotation symmetric around the -axis, since it is invariant under the change of coordinates The chaotic attractor of the supply chain system (29) when the system parameter values are selected as follows: as shown in Figure 1 and Figure 2. As illustrated in these figures, the nonlinear supply chain system shows chaotic behavior in this condition.
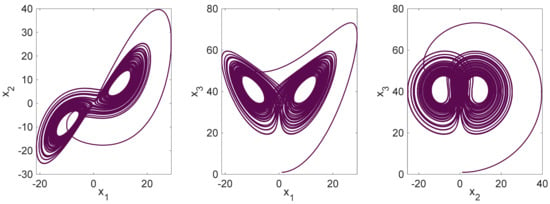
Figure 1.
The 2D phase portraits of the symmetric three-echelon supply chain system.
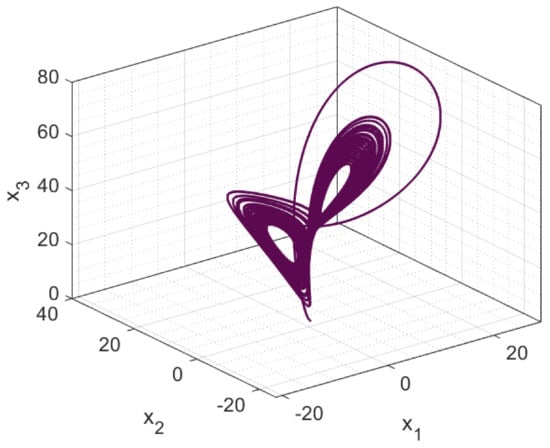
Figure 2.
The 3D phase portrait of the symmetric three-echelon supply chain system.
4. Simulation Study by Applying Control Input
In this section, the proposed scheme is applied to the symmetric chaotic supply chain system. In this section, it is assumed that all parameters of the system are varying by time through unknown functions. This way, in all simulations, the effects of uncertainties on the system are taken to account. The parameters of the system are considered as
where for the simulations, we consider the unknown functions as
Additionally, the user-defined parameters of the controller are designed as
4.1. Stabilization without Control Input Limitations
In this part, we aim to stabilize the symmetric supply chain system. At first, we consider no control limitation. Figure 3 shows the states of the system. As is shown in this figure, after a very short period of time (less than 0.1 time units), the system is completely stabilized. Additionally, the response of the systems is chatter-free. Figure 4 demonstrates the control input that is applied to the system. The control signals are chatter-free as well. However, now the most important issue regarding the control inputs is their large amplitudes. For instance, as is shown in Figure 4, the maximum value of is near 200, and it could be impossible to apply such a large control input in economic systems. This shows the importance of the proposed control input limitations. In the next subsection, we consider the control input limitations.
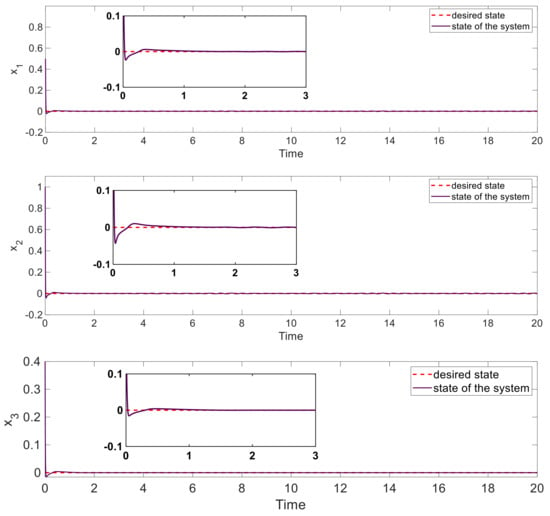
Figure 3.
The states of the symmetric supply chain system under the proposed fixed-time disturbance observer-based super-twisting sliding mode technique.
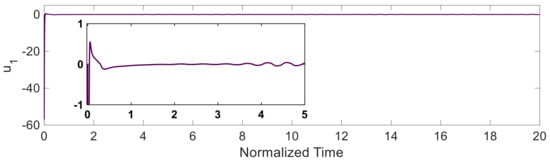
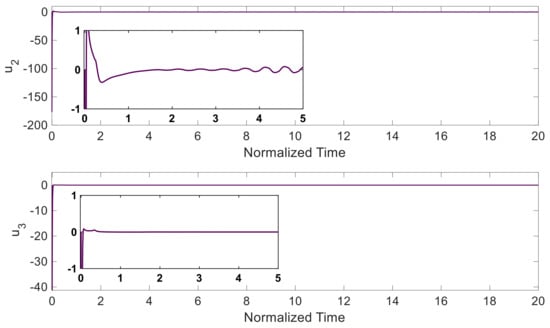
Figure 4.
The control input based on the proposed fixed-time disturbance observer-based super-twisting sliding mode technique.
4.2. Stabilization with Limited Control Input
The bounds of the control signals are considered as
The stabilized states of the system are illustrated in Figure 5. Although the control signals are limited, in the fixed time, the states of the system converge to zero. Figure 6 shows the limited control signals obtained through the proposed super-twisting sliding mode technique. It is noteworthy that when we limit the control input, the convergence time will be longer, but in this condition, the controller can be applied to practical systems.
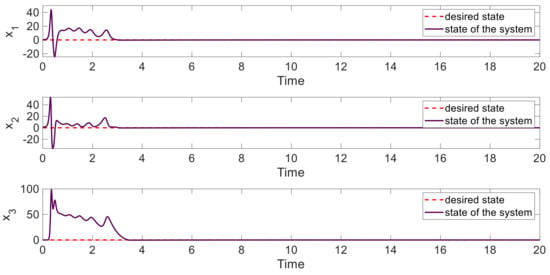
Figure 5.
The states of the symmetric supply chain system subject to control input limitations under the proposed fixed-time disturbance observer-based super-twisting sliding mode technique.
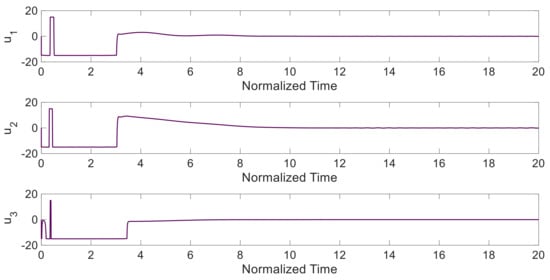
Figure 6.
The limited control input based on the proposed fixed-time disturbance observer-based super-twisting sliding mode technique.
4.3. Tracking Control with Limited Control Input
To investigate the performance of the proposed scheme, we consider the desired states as
Herein, the bounds of the control signals are considered as
The states of the system and the limited control input are displayed in Figure 7 and Figure 8. As shown in the tracking control results, the proposed control scheme satisfies the expected performance.
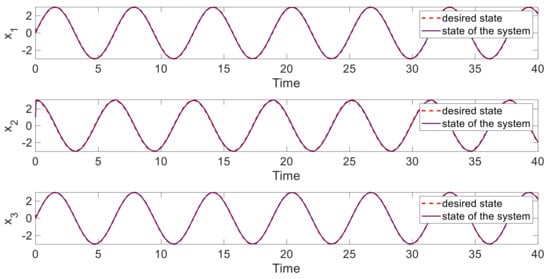
Figure 7.
The states of the symmetric supply chain system subject to control input limitations under the proposed technique in the tracking control.
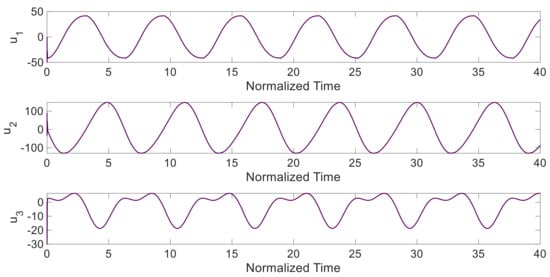
Figure 8.
The limited control input based on the proposed technique in the tracking control.
5. Conclusions
In this paper, we studied stabilization and tracking control of a symmetric chaotic supply chain system subject to control input limitations. To this end, we introduced a new control scheme which is an extension of sliding mode control that can provide chatter-free and fixed-time responses. In the proposed control scheme, the effects of the control input limitation, as well as uncertainties, are taken into account. The fixed-time convergence and stability of the system were proven through the Lyapunov stability theorem. Then, the chaotic response of the symmetric supply chain system was demonstrated. Lastly, through various numerical simulations, the proposed scheme’s effectiveness in different scenarios, including stabilization without input limitations, stabilization with input limitations, and tracking control with input limitations, was assessed. Numerical simulations clearly confirm all theoretical claims about the proposed control technique. The proposed scheme’s excellent performance even when the system is in the presence of control input limitation and time-varying uncertainties was displayed. As a feature suggestion, the proposed controller can be promoted through self-tuning algorithms. Additionally, the proposed method has a great potential to be customized or upgraded for various systems, including fractional-order ones.
Author Contributions
Conceptualization, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A.; Investigation, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A.; Methodology, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A.; Software, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A.; Supervision, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A.; Validation, B.W., H.J., C.V., S.B., A.Y., P.A., A.A.A.; Writing—original draft, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A.; Writing—review and editing, B.W., H.J., C.V., S.B., A.Y., P.A. and A.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Taif University Researchers Supporting Project number (TURSP-2020/77), Taif University, Taif, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sarimveis, H.; Patrinos, P.; Tarantilis, C.D.; Kiranoudis, C.T. Dynamic modeling and control of supply chain systems: A review. Comput. Oper. Res. 2008, 35, 3530–3561. [Google Scholar] [CrossRef]
- Perea-López, E.; Grossmann, I.E.; Ydstie, B.E.; Tahmassebi, T. Dynamic modeling and decentralized control of supply chains. Ind. Eng. Chem. Res. 2001, 40, 3369–3383. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B. Adaptive Supply Chain Management; Springer Science & Business Media: London, UK, 2009. [Google Scholar]
- Wilding, R.D. Chaos theory: Implications for supply chain management. Int. J. Logist. Manag. 1998, 9, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Wilson, M.M.J. Supply Chains Behaving Badly: A Dynamic Model of Inter-Organisational Supply Chain Exchange Behaviour under Rational, Relational and Chaotic Paradigms. Ph.D. Thesis, Lincoln University, Canterbury, New Zealand, 2006. [Google Scholar]
- Kocamaz, U.E.; Taşkın, H.; Uyaroğlu, Y.; Göksu, A. Control and synchronization of chaotic supply chains using intelligent approaches. Comput. Ind. Eng. 2016, 102, 476–487. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Brock, W.A.; Hsieh, D.A.; LeBaron, B.D.; Brock, W.E. Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Jahanshahi, H.; Orozco-López, O.; Munoz-Pacheco, J.M.; Alotaibi, N.D.; Volos, C.; Wang, Z.; Sevilla-Escoboza, R.; Chu, Y.-M. Simulation and experimental validation of a non-equilibrium chaotic system. Chaos Solitons Fractals 2021, 143, 110539. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Rajagopal, K.; Akgul, A.; Sari, N.N.; Namazi, H.; Jafari, S. Complete analysis and engineering applications of a megastable nonlinear oscillator. Int. J. Non-Linear Mech. 2018, 107, 126–136. [Google Scholar] [CrossRef]
- Agiza, H.N. On the analysis of stability, bifurcation, chaos and chaos control of Kopel map. Chaos Solitons Fractals 1999, 10, 1909–1916. [Google Scholar] [CrossRef]
- Chen, G.; Yu, X. Chaos Control: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 292. [Google Scholar]
- Yousefpour, A.; Haji Hosseinloo, A.; Reza Hairi Yazdi, M.; Bahrami, A. Disturbance observer–based terminal sliding mode control for effective performance of a nonlinear vibration energy harvester. J. Intell. Mater. Syst. Struct. 2020, 31, 1495–1510. [Google Scholar] [CrossRef]
- Wei, Z.; Yousefpour, A.; Jahanshahi, H.; Kocamaz, U.E.; Moroz, I. Hopf bifurcation and synchronization of a five-dimensional self-exciting homopolar disc dynamo using a new fuzzy disturbance-observer-based terminal sliding mode control. J. Frankl. Inst. 2021, 358, 814–833. [Google Scholar] [CrossRef]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196. [Google Scholar] [CrossRef]
- Wang, S.; Yousefpour, A.; Yusuf, A.; Jahanshahi, H.; Alcaraz, R.; He, S.; Munoz-Pacheco, J.M. Synchronization of a non-equilibrium four-dimensional chaotic system using a disturbance-observer-based adaptive terminal sliding mode control method. Entropy 2020, 22, 271. [Google Scholar] [CrossRef] [Green Version]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.-T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H. Fast disturbance-observer-based robust integral terminal sliding mode control of a hyperchaotic memristor oscillator. Eur. Phys. J. Spec. Top. 2019, 228, 2247–2268. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Peng, H.; Hu, Y.; Su, H. Fuzzy-torque approximation-enhanced sliding mode control for lateral stability of mobile robot. IEEE Trans. Syst. Man Cybern. Syst. 2021. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Wang, H.; Xu, F.; Wang, X.; Liang, B. Recursive sliding mode control with adaptive disturbance observer for a linear motor positioner. Mech. Syst. Signal Process. 2021, 146, 107014. [Google Scholar] [CrossRef]
- Jahanshahi, H. Smooth control of HIV/AIDS infection using a robust adaptive scheme with decoupled sliding mode supervision. Eur. Phys. J. Spec. Top. 2018, 227, 707–718. [Google Scholar] [CrossRef]
- Xiong, P.-Y.; Jahanshahi, H.; Alcaraz, R.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alsaadi, F.E. Spectral entropy analysis and synchronization of a multi-stable fractional-order chaotic system using a novel neural network-based chattering-free sliding mode technique. Chaos Solitons Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.-M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Yousefpour, A.; Vahidi-Moghaddam, A.; Rajaei, A.; Ayati, M. Stabilization of nonlinear vibrations of carbon nanotubes using observer-based terminal sliding mode control. Trans. Inst. Meas. Control 2020, 42, 1047–1058. [Google Scholar] [CrossRef]
- Chen, S.-B.; Beigi, A.; Yousefpour, A.; Rajaee, F.; Jahanshahi, H.; Bekiros, S.; Martínez, R.A.; Chu, Y. Recurrent Neural Network-Based Robust Nonsingular Sliding Mode Control With Input Saturation for a Non-Holonomic Spherical Robot. IEEE Access 2020, 8, 188441–188453. [Google Scholar] [CrossRef]
- Eskandari, B.; Yusefpour, A.; Ayati, M.; Kyyra, J.; Pouresmaeil, E. Finite-Time Disturbance-Observer-Based Integral Terminal Sliding Mode Controller for Three-Phase Synchronous Rectifier. IEEE Access 2020, 8, 152116–152130. [Google Scholar] [CrossRef]
- Chen, H.; He, S.; Azucena, A.D.P.; Yousefpour, A.; Jahanshahi, H.; López, M.A.; Alcaraz, R. A multistable chaotic jerk system with coexisting and hidden attractors: Dynamical and complexity analysis, FPGA-based realization, and chaos stabilization using a robust controller. Symmetry 2020, 12, 569. [Google Scholar] [CrossRef] [Green Version]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sajjadi, S.S.; Bekiros, S.; Aly, A.A. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller. Chaos Solitons Fractals 2021, 144, 110698. [Google Scholar] [CrossRef]
- Li, J.-F.; Jahanshahi, H.; Kacar, S.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alotaibi, N.D.; Alharbi, K.H. On the variable-order fractional memristor oscillator: Data security applications and synchronization using a type-2 fuzzy disturbance observer-based robust control. Chaos Solitons Fractals 2021, 145, 110681. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Bekiros, S.; Gritli, H.; Chu, Y.-M.; Gomez-Aguilar, J.F.; Aly, A.A. Tracking control and stabilization of a fractional financial risk system using novel active finite-time fault-tolerant controls. Fractals 2021. [Google Scholar] [CrossRef]
- Bekiros, S.; Jahanshahi, H.; Bezzina, F.; Aly, A.A. A novel fuzzy mixed H2/H∞ optimal controller for hyperchaotic financial systems. Chaos Solitons Fractals 2021, 146, 110878. [Google Scholar] [CrossRef]
- Wang, H.; Jahanshahi, H.; Wang, M.-K.; Bekiros, S.; Liu, J.; Aly, A.A. A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies. Entropy 2021, 23, 610. [Google Scholar] [CrossRef]
- Xu, X.; Lee, S.-D.; Kim, H.-S.; You, S.-S. Management and optimisation of chaotic supply chain system using adaptive sliding mode control algorithm. Int. J. Prod. Res. 2020, 59, 2571–2587. [Google Scholar] [CrossRef]
- Bertsimas, D.; Thiele, A. A robust optimization approach to supply chain management. In Integer Programming and Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2004; pp. 86–100. [Google Scholar]
- Dunbar, W.B.; Desa, S. Distributed MPC for dynamic supply chain management. In Assessment and Future Directions of Nonlinear Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2007; pp. 607–615. [Google Scholar]
- Van Roy, B.; Bertsekas, D.P.; Lee, Y.; Tsitsiklis, J.N. A neuro-dynamic programming approach to retailer inventory management. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997; pp. 4052–4057. [Google Scholar]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Chen, S.-B.; Jahanshahi, H.; Abba, O.A.; Solís-Pérez, J.E.; Bekiros, S.; Gómez-Aguilar, J.F.; Yousefpour, A.; Chu, Y.-M. The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization. Chaos Solitons Fractals 2020, 140, 110223. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, W.-h.; Lu, Y.; Wang, Z.-S. Optimal Control and Simulation for Enterprise Financial Risk in Industry Environment. Math. Probl. Eng. 2020, 2020, 6040597. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, T.; Sun, K.; Rudas, I.J.; Gao, H. Disturbance Observer-Based Adaptive Fuzzy Control for Strict-Feedback Nonlinear Systems with Finite-Time Prescribed Performance. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Wen, C.; Zhou, J.; Liu, Z.; Su, H. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Autom. Control 2011, 56, 1672–1678. [Google Scholar] [CrossRef]
- Boskovic, J.D.; Li, S.-M.; Mehra, R.K. Robust tracking control design for spacecraft under control input saturation. J. Guid. Control Dyn. 2004, 27, 627–633. [Google Scholar] [CrossRef]
- Chen, M.; Wu, Q.-X.; Cui, R.-X. Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems. ISA Trans. 2013, 52, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Huang, G. A fast terminal sliding mode control with novel fuzzy disturbance observer. In Proceedings of the 2010 International Conference on Web Information Systems and Mining, Sanya, China, 23–24 October 2010; pp. 95–99. [Google Scholar]
- Liu, H.; Bao, W.; Li, H.; Liao, Y. Multivariable Disturbance Observer–Based Fuzzy Fast Terminal Sliding Mode Attitude Control for a Hypersonic Vehicle. J. Aerosp. Eng. 2019, 32, 04018152. [Google Scholar] [CrossRef]
- Vahidi-Moghaddam, A.; Rajaei, A.; Ayati, M. Disturbance-observer-based fuzzy terminal sliding mode control for MIMO uncertain nonlinear systems. Appl. Math. Model. 2019, 70, 109–127. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Anne, K.R.; Chedjou, J.C.; Kyamakya, K. Bifurcation analysis and synchronisation issues in a three-echelon supply chain. Int. J. Logist. Res. Appl. 2009, 12, 347–362. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).