Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems
Abstract
1. Introduction
2. Some New Iterative Schemes with Memory
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ortega, J.M.; Rheinbolt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Torres-Hernandez, A.; Brambila-Paz, F.; Iturrará-Viveros, U.; Caballero-Cruz, R. Fractioaal Newton–Raphson method accelerated with Aitken’s method. Axioms 2021, 10, 47. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Newton’s method with fractional derivatives and various iteration processes via visual analysis. Numer. Algorithms 2021, 86, 953–1010. [Google Scholar] [CrossRef]
- Akgül, A.; Cordero, A.; Torregrosa, J.R. A fractional Newton method with 2αth-order of convergence and its sability. Appl. Math. Lett. 2019, 98, 344–351. [Google Scholar] [CrossRef]
- Cordero, A.; Girona, I.; Torregrosa, J.R. A variant of Chebyshev’s method with 3αth-order of convergence by using fractional derivatives. Symmetry 2019, 11, 1017. [Google Scholar] [CrossRef]
- Behl, R.; Bhalla, S.; Magreñán, Á.A.; Kumar, S. An efficient high order iterative scheme for large nonlinear systems with dynamics. J. Comp. Appl. Math. 2020, 113249. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Magreñán, Á.A. A biparametric extension of King’s fourth-order methods and their dynamics. Appl. Math. Comput. 2016, 282, 254–275. [Google Scholar] [CrossRef]
- Schwandt, H. A symmetric iterative interval method for systems of nonlinear equations. Computing 1984, 33, 153–164. [Google Scholar] [CrossRef]
- Barco, M.A.; Prince, G.E. New symmetry solution techniques for first-order non-linear PDEs. Appl. Math. Comput. 2001, 124, 169–196. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Hoboken, NJ, USA, 1964. [Google Scholar]
- Grau-Sánchez, M.; Grau, À.; Noguera, M. Ostrowski type methods for solving systems of nonlinear equations. Appl. Math. Comput. 2011, 218, 2377–2385. [Google Scholar] [CrossRef]
- Petković, M.S.; Sharma, J.R. On some efficient derivative-free iterative methods with memory for solving systems of nonlinear equations. Numer. Algorithms 2016, 71, 457–474. [Google Scholar] [CrossRef]
- Ahmad, F.; Soleymani, F.; Haghani, F.K.; Serra-Capizzano, S. Higher order derivative-free iterative methods with and without memory for systems of nonlinear equations. Appl. Math. Comput. 2017, 314, 199–211. [Google Scholar] [CrossRef]
- Kansal, M.; Cordero, A.; Bhalla, S.; Torregrosa, J.R. Memory in a new variant of king’s family for solving nonlinear sytstems. Mathematics 2020, 8, 1251. [Google Scholar] [CrossRef]
- Kurchatov, V.A. On a method of linear interpolation for the solution of functional equations. Dokl. Akad. Nauk SSSR 1971, 198, 524–526. [Google Scholar]
- Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. On the improvement of the order of convergence of iterative methods for solving nonlinear systems by means of memory. Appl. Math. Lett. 2020, 104, 106277. [Google Scholar] [CrossRef]
- Cordero, A.; Soleymani, F.; Torregrosa, J.R.; Khaksar Haghani, F. A family of Kurchatov-type methods and its stability. Appl. Math. Comput. 2017, 294, 264–279. [Google Scholar] [CrossRef][Green Version]
- Argyros, I.K.; Ren, H. On the Kurchatov method for solving equations under weak conditions. Appl. Math. Comput. 2016, 273, 98–113. [Google Scholar] [CrossRef]
- Candela, V.; Peris, R. A class of third order iterative Kurchatov-Steffensen(derivative free) methods for solving nonlinear equations. Appl. Math. Comput. 2019, 350, 93–104. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Ahmad, F.; Rehman, S.U.; Ullah, M.Z.; Aljahdali, H.M.; Ahmad, S.; Alshomrani, A.S.; Carrasco, J.A.; Ahmad, S.; Sivasankaran, S. Frozen Jocabian multistep iterative method for solving nonlinear IVPs and BVPs. Complexity 2017, 2017, 9407656. [Google Scholar] [CrossRef]
- Narang, M.; Bhatia, S.; Kanwar, V. New efficient derivative free family of seventh-order methods for solving systems of nonlinear equations. Numer. Algorithms 2017, 76, 283–307. [Google Scholar] [CrossRef]
- Petković, M.S.; Yun, B.I. Sigmoid-like functions and root finding methods. Appl. Math. Comput. 2008, 204, 784–793. [Google Scholar] [CrossRef]
- Yun, B.I. A non-iterative method for solving nonlinear equations. Appl. Math. Comput. 2008, 198, 691–699. [Google Scholar] [CrossRef]
- Yun, B.I. Iterative methods for solving nonliear equations with finitely any roots in an interval. J. Comput. Appl. Math. 2012, 236, 3308–3318. [Google Scholar] [CrossRef]
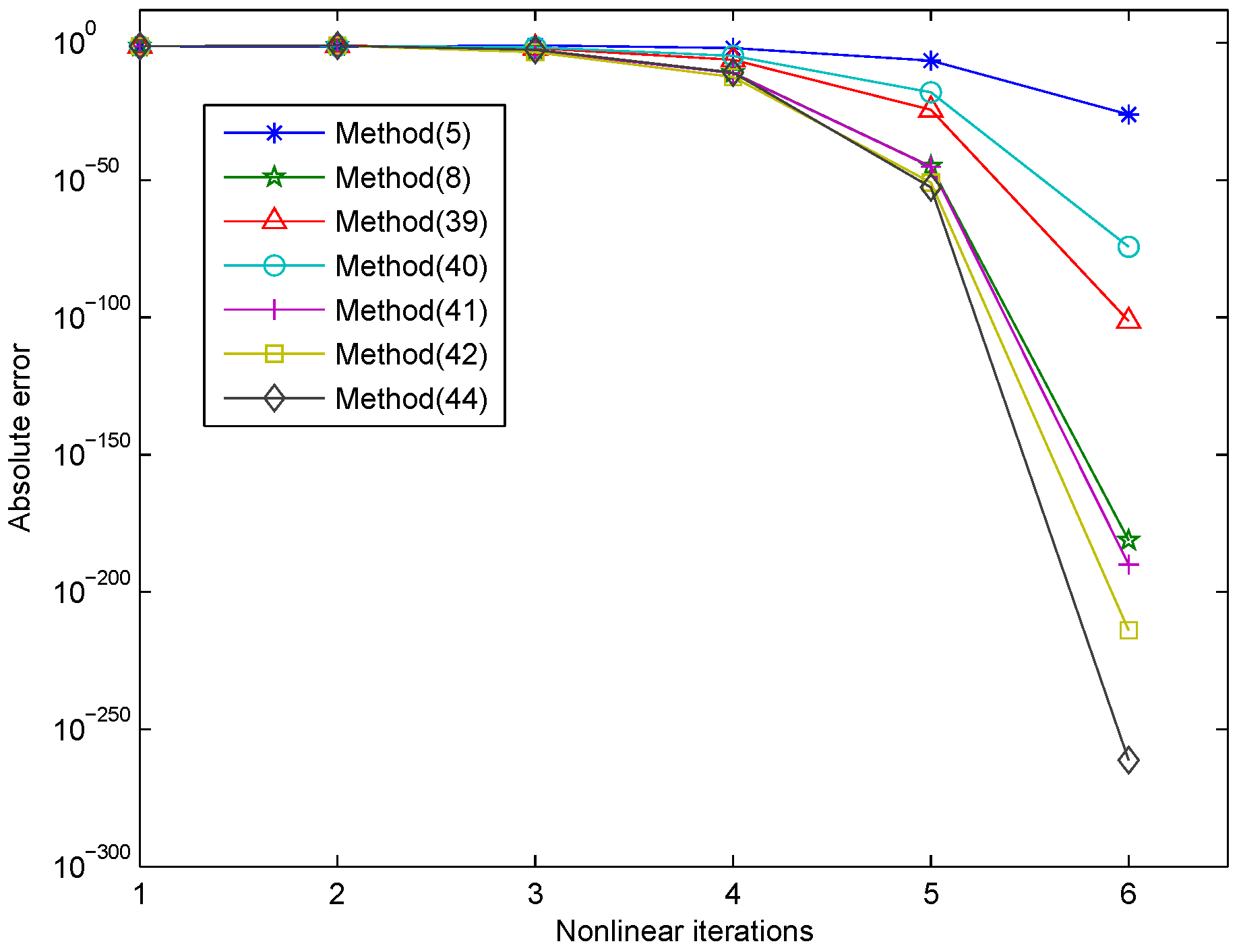
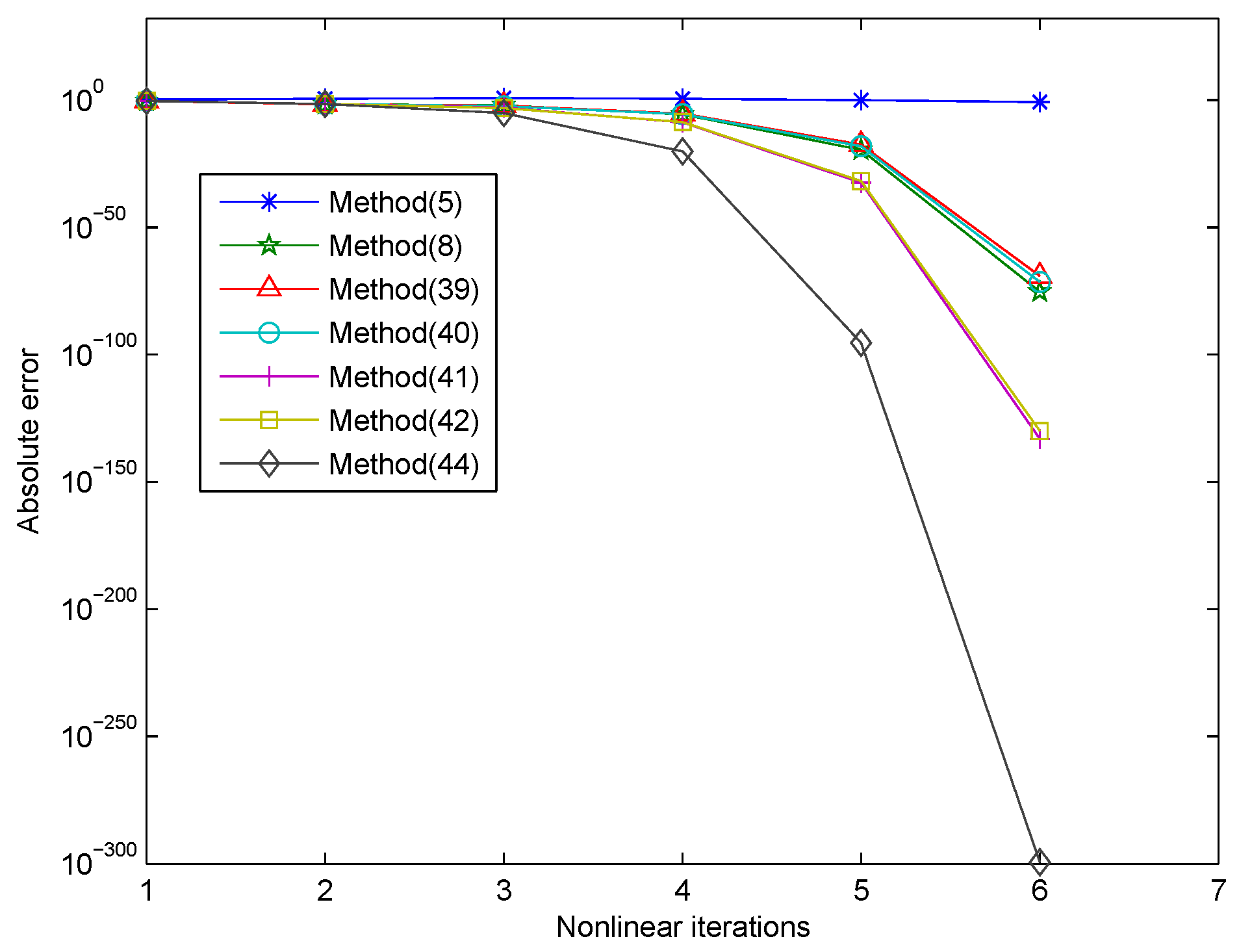
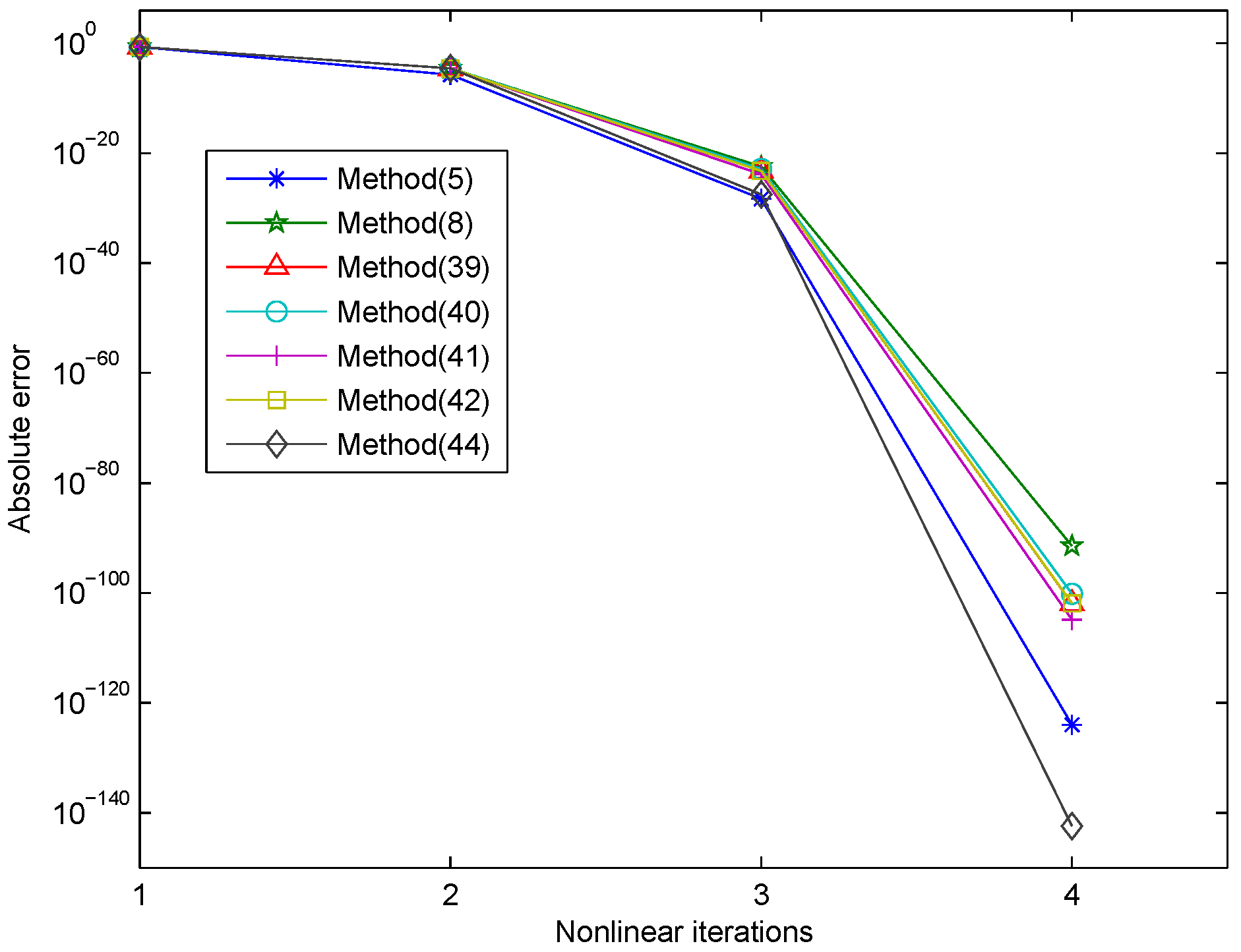

| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 7 | 4.577 × | 1.648 × | 4.22419 | 15.537 |
| (8) | 6 | 6.536 × | 5.328 × | 3.97864 | 15.428 |
| (39) | 6 | 5.041 × | 6.013 × | 4.23649 | 15.943 |
| (40) | 7 | 1.645 × | 1.562 × | 4.23601 | 18.111 |
| (41) | 6 | 9.817 × | 3.228 × | 4.23669 | 14.180 |
| (42) | 6 | 1.114 × | 3.614 × | 4.23381 | 15.319 |
| (43) | 6 | 5.202 × | 1.988 × | 5.00000 | 20.280 |
| (44) | 6 | 6.070 × | 4.302 × | 5.00000 | 20.623 |
| (45) | 6 | 5.833 × | 3.526 × | 5.00000 | 19.000 |
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 12 | 5.059 × | 3.088 × | 4.23598 | 39.998 |
| (8) | 7 | 3.408 × | 3.497 × | 3.99832 | 12.776 |
| (39) | 7 | 2.323 × | 9.941 × | 4.23562 | 14.242 |
| (40) | 7 | 2.484 × | 1.108 × | 4.23561 | 14.851 |
| (41) | 6 | 8.864 × | 2.159 × | 4.24093 | 10.966 |
| (42) | 6 | 1.014 × | 5.896 × | 4.23542 | 10.764 |
| (43) | 7 | 7.681 × | 2.609 × | 4.99965 | 25.256 |
| (44) | 6 | 3.898 × | 1.470 × | 5.00000 | 14.492 |
| (45) | 6 | 1.791 × | 1.796 × | 5.00000 | 13.135 |
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 4 | 9.478 × | 1.079 × | 4.23909 | 1.154 |
| (8) | 5 | 6.828 × | 1.072 × | 4.03695 | 1.669 |
| (39) | 4 | 1.172 × | 1.181 × | 4.20358 | 1.294 |
| (40) | 4 | 6.850 × | 7.002 × | 4.20758 | 1.372 |
| (41) | 4 | 1.353 × | 1.369 × | 4.19837 | 1.372 |
| (42) | 4 | 1.329 × | 2.014 × | 4.20446 | 1.357 |
| (43) | 4 | 3.818 × | 2.243 × | 5.00784 | 1.700 |
| (44) | 4 | 1.427 × | 1.637 × | 5.00409 | 1.794 |
| (45) | 4 | 1.841 × | 5.854 × | 5.00505 | 1.762 |
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 8 | 1.932 × | 3.291 × | 4.26779 | 9.750 |
| (8) | 6 | 6.690 × | 1.315 × | 3.54607 | 9.094 |
| (39) | 5 | 4.488 × | 4.446 × | 4.32150 | 7.410 |
| (40) | 5 | 4.697 × | 1.137 × | 4.23216 | 7.488 |
| (41) | 5 | 5.905 × | 4.505 × | 4.24952 | 7.534 |
| (42) | 5 | 5.803 × | 2.515 × | 4.27379 | 7.566 |
| (43) | 5 | 1.956 × | 6.081 × | 5.04097 | 9.687 |
| (44) | 5 | 3.845 × | 1.974 × | 5.05028 | 9.672 |
| (45) | 5 | 1.104 × | 7.583 × | 4.29476 | 9.703 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jin, Y.; Zhao, Y. Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems. Symmetry 2021, 13, 943. https://doi.org/10.3390/sym13060943
Wang X, Jin Y, Zhao Y. Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems. Symmetry. 2021; 13(6):943. https://doi.org/10.3390/sym13060943
Chicago/Turabian StyleWang, Xiaofeng, Yingfanghua Jin, and Yali Zhao. 2021. "Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems" Symmetry 13, no. 6: 943. https://doi.org/10.3390/sym13060943
APA StyleWang, X., Jin, Y., & Zhao, Y. (2021). Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems. Symmetry, 13(6), 943. https://doi.org/10.3390/sym13060943





