Abstract
Two principles govern the critical temperature for superconducting transitions: (1) intrinsic strength of the pair coupling and (2) the effect of the many-body environments on the efficiency of that coupling. Most discussions take into account only the former, but we argue that the properties of unconventional superconductors are governed more often by the latter, through dynamical symmetry relating to normal and superconducting states. Differentiating these effects is essential to charting a path to the highest-temperature superconductors.
Keywords:
superconductivity 1. Introduction
High-temperature superconductivity (HTSC) was discovered in 1986 for the copper oxides [1], but after 25 years there is no broad agreement on theoretical interpretation. In 2008, new high-temperature superconductivity was discovered in FeAs compounds [2], and in FeSe compounds in 2010 [3]. This new iron-based superconductivity also is not well understood, with many unanswered questions about the underlying mechanism and whether it is related to the mechanism for cuprate HTSC. Generally, superconductivity (SC) exhibiting many similarities with that of cuprate and iron superconductors has been found in diverse systems such as organics and heavy-fermion compounds [4,5]. With many experimental data and theoretical ideas tending to emphasize particular aspects of the problem at the expense of other aspects, it is important to sort out the important questions to be answered. Only when these questions are clearly and systematically addressed can one separate the essential from peripheral in understanding the HTSC mechanism, and be on solid ground to chart a path to the highest-temperature superconductors.
The properties of HTSC suggest a number of fundamental questions: (1) What physics determines the phase diagram? (2) What role do quantum phase transitions (QFT) and quantum critical behavior play, and what is their origin? (3) How does the Cooper instability generalize to a doped Mott insulator? (4) What causes the pseudogap (PG), and do “competing order” or “preformed pairs” explain its properties; how is the PG related to the antiferromagnetic (AF) and SC phases? (5) Why do underdoped cuprates exhibit complexity and disorder despite a highly universal overall phase diagram? (6) How are HTSC (and other unconventional superconductors) related to conventional SC? (7) Why is unusually high for unconventional superconductors? (8) What principles can guide searches for new high- superconductors? (9) How is HTSC related to the various forms of SC and superfluidity that occur in other fields of physics? These questions have been difficult to answer in a comprehensive way [6,7,8,9,10]. In our opinion, no standard approach can provide plausible answers to this entire list without ad hoc assumptions.
Conventional SC is described well by BCS theory [11] using spherical (s-wave) pairing [12] formfactors corresponding to phonon pair binding. Superconductors with formfactors that are not s-wave are termed unconventional; the most famous are cuprate high-temperature superconductors, which have d-wave pairing and high transition temperatures relative to conventional SC. Many other unconventional superconductors are known, often exhibiting larger than for conventional SC. Superconductors involve Cooper-pair condensates and stronger pairing favors survival of the condensate at higher T. Thus, enhancing phonon coupling by tuning atomic mass and lattice spacing can increase for conventional SC. For unconventional SC, the situation is more nuanced. The value of depends on intrinsic pairing strength (through electron correlations rather than phonons), but there is another factor, often more important and often overlooked in standard discussions, which is the effect of the many-body environment on the efficiency of that coupling.
In strongly correlated many-body systems, the Hilbert space is enormous and tractable theories must reduce this to a more manageable subspace. Two common philosophies may be followed in implementing such a truncation: microscopic properties truncation and emergent-symmetry truncation. Microscopic-properties truncation uses key microscopic physical features of the idealized weakly interacting system as a guide for truncating the full space. Hubbard or t-J models typically are of this form. In principle this implies no truncation of the configuration space but practical calculations require restriction to a small-enough subspace, often by assuming that only states below some energy cutoff in the non-interacting basis contribute. However, in high- superconductors the correlations may be so strong that dynamics can no longer be described in terms of individual fundamental particles of the weakly interacting system (see, for example, the discussion in Refs. [13,14,15]). This calls into question the validity of using properties of the weakly interacting system to determine a truncation scheme valid for strongly correlated states.
Truncation based on emergent symmetries is designed specifically to describe collective modes and long-range order. This approach identifies essential forms of the collective modes of interest and uses that as a guide to remove from the full space all states inconsistent with these forms, leaving a small collective subspace that describes economically the relevant collective modes. This could be called Michelangelo truncation, since the famous sculptor reported said that he created beautiful statues by looking at a block of stone, envisioning the statue trapped within it, and then chipped away everything that was not statue. The most powerful systematic method of determining the essential form of collective modes is to identify a symmetry associated with them. We therefore call this a symmetry of emergent modes, as opposed to symmetries of the weakly interacting system. It is essential to note that there is no fundamental reason to expect that the symmetries of the emergent modes are related to the symmetries of the weakly interacting system, since the weakly interacting and emergent modes are typically separated by phase transitions.
Motivated by cuprate phenomenology, our basic physical assumption in constructing emergent symmetries of high-temperature SC is that the configuration space for a minimal theory is built from coherent pairs representing superpositions of particles or holes centered on different lattice sites. The next step is to use phenomenology as a guide to identify a set of second-quantized operators that can be associated with the relevant physical degrees of freedom exhibited by this collective subspace. This is seen most clearly by viewing the SC transition from the perspective of fermion dynamical symmetry. The proposed solvable model with an adequate range of physics for the HTSC problem is possible by applying a set of mathematical tools originating in the theory of Lie algebras and generalized coherent states. Their validity is well established in strongly correlated fermion and boson systems for fields such as nuclear [16,17], elementary particle [18], molecular [19], and polymer physics [20]. The dynamical symmetry methods discussed here may be viewed as sophisticated generalizations of pseudospin models, which were introduced in application to the BCS model by Anderson [21]. Likewise, the method of generalized coherent states is a sophisticated extension of Glauber coherent states [22], which have often been employed often in condensed matter contexts.
Based on the dynamical symmetry considerations described above, we have constructed an SU(4) model of emergent high-temperature superconductivity, which is documented in a series of publications [23,24,25,26,27,28,29,30,31,32] and a comprehensive review [33]. Here we collect in one place a unified set of physical implications for this SU(4) dynamical symmetry, unobscured by technical detail. Hence, we shall write few equations, preferring to emphasize physical interpretation and referencing the literature where ample equations, derivations, and technical justification may be found.
2. Fermion Dynamical Symmetry and Superconductivity
The fermion dynamical symmetry method uses principles of dynamical symmetry to truncate a Hilbert space to a collective subspace, specified in terms of a Lie algebra having a relatively small number of fermionic generators, as illustrated in Figure 1a.
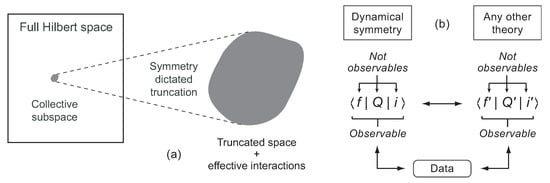
Figure 1.
(a) Emergent-symmetry truncation of Hilbert space to a collective subspace using principles of dynamical symmetry. (b) Comparison of matrix elements among different theories and data. Wavefunctions and operators are not observables. Only matrix elements are directly related to observables.
Within the subspace the most general Hamiltonian is a polynomial in the Casimir invariants for all the subgroup chains of the highest symmetry consistent with conservation laws, with coefficients of the terms determined by effective interactions representing the average effects of the space excluded by the truncation. Matrix elements can be determined exactly in specific limits and approximately using coherent state methods otherwise. As illustrated in Figure 1b, the theory is microscopic because the only valid comparison in quantum mechanics is for matrix elements.
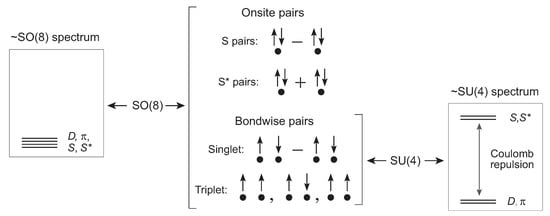
Figure 2.
Schematic difference between bondwise and onsite pair energies. If onsite repulsion is weak, the pairing states are nearly degenerated, yielding an SO(8) symmetry. If it is strong onsite pairs are pushed up in energy, reducing the symmetry to an effective SU(4) low-energy symmetry.
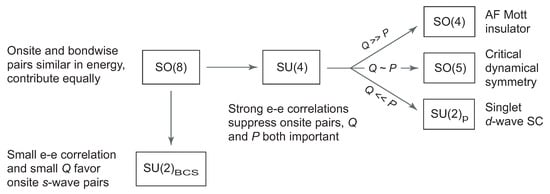
Figure 3.
The relationship between SO(4), SO(8), and BCS SU(2) symmetry for conventional and unconventional superconductors.
Restricting to the 28 generators describing onsite and nearest-neighbor pairing, antiferromagnetic, spin, and charge degrees of freedom, the minimal symmetry is SO(8). If Coulomb repulsion is weak and antiferromagnetic (AF) correlations are negligible, onsite pairs are favored over bondwise pairs (for simplicity we restrict to nearest-neighbor bondwise pairs here). This favors subgroup chains containing SU(2) pseudospin generators that give conventional SC described by SU(2)BCS symmetry. If Coulomb repulsion is strong and antiferromagnetism significant, onsite pairing is disfavored relative to bondwise pairing and antiferromagnetic operators become important in addition to pairing operators. This reduces SO(8) to a 15-generator subgroup SU(4), with generators representing AF, spin-singlet and spin-triplet bondwise pairs, spin, and charge operators; explicit forms for the operators and their commutation relations are given in Refs. [23,33]. Three dynamical symmetry chains have exact solutions and correspond (through their matrix elements) to physical states thought to be relevant for cuprate doped and undoped states:
- SU(4) ⊃ SO(4), which represents an antiferromagnetic (AF) Mott insulating state that is the low-temperature ground state for zero doping.
- SU(4) ⊃ SU(2), which represents a d-wave singlet superconducting (SC) state that can become the low-temperature ground state for non-zero doping.
- SU(4) ⊃ SO(5), which represents a critical dynamical symmetry interpolating between the SU(2) superconducting and SO(4) antiferromagnetic solutions.
3. SU(4) Dynamical Symmetry and Cuprate Phenomenology
Let us now apply the SU(4) model of HTSC to answering the questions posed in Section 1.
- Origin of the Phase Diagram: Universality of the cuprate phase diagram suggests a unifying principle independent of microscopic details. The SU(4) model implies that symmetry alone dictates many basic properties, and that these properties lead to a highly universal phase diagram, illustrated in Figure 4,that is described quantitatively by the SU(4) model. Only two significant parameters enter: the effective strength of singlet pairing and the effective strength of AF correlations (triplet pairing strength has minimal influence). The best fit is for the smooth dependence of and on the doping P shown in the inset of Figure 4, but the basic features survive if these parameters are held constant with doping (see Ref. [33]). Thus, the cuprate phase diagram is a consequence of SU(4) symmetry correlating emergent d-wave singlet pairing and antiferromagnetism; it depends only parametrically on microscopic details such as pairing formfactors.
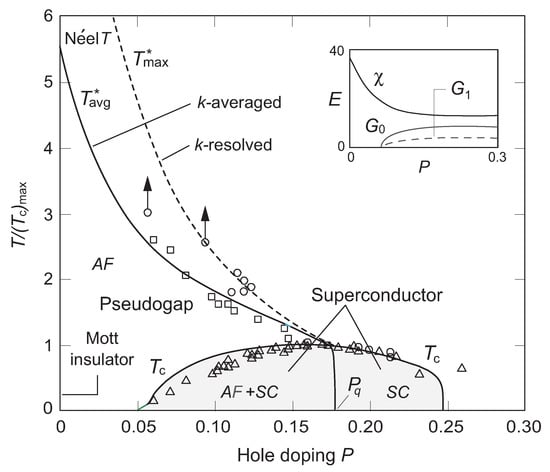 Figure 4. SU(4) cuprate temperature T and doping P phase diagram compared with data taken from Refs. [34,35]. Strengths of the AF and singlet pairing correlations were determined in Ref. [27] by global fits to cuprate data (inset plot). Pseudogap temperatures are indicated by . The two PG curves correspond to whether momentum is resolved or not in the experiment. The inset shows the variation of the AF and pairing coupling with doping P.
Figure 4. SU(4) cuprate temperature T and doping P phase diagram compared with data taken from Refs. [34,35]. Strengths of the AF and singlet pairing correlations were determined in Ref. [27] by global fits to cuprate data (inset plot). Pseudogap temperatures are indicated by . The two PG curves correspond to whether momentum is resolved or not in the experiment. The inset shows the variation of the AF and pairing coupling with doping P.
- AF Mott Insulator States at Half Filling: By counting, SU(4) symmetry requires no double occupancy of lattice sites by correlated fermions [25]. Hence, charge transport is suppressed at half band-filling and the undoped ground state is a Mott insulator. Moreover, this state has SU(4) ⊃ SO(4) dynamical symmetry and the matrix elements of an AF Néel state [23,24,33]. Thus, the undoped SU(4) ground state is an AF Mott insulator, just as observed for cuprates.
- Cooper Instability of the Doped Mott Insulator: The same SU(4) symmetry requiring the undoped ground state to be an AF Mott insulator implies that this state is fundamentally unstable against condensing Cooper pairs when doped [31,33]. This results in a quantum phase transition (QPT) to be discussed more extensively below, and implies a rapid transition to a superconducting state upon doping, as observed for data in Figure 4.
- Upper Doping Limit for Superconductivity: Direct counting implies that occupancy of more than of lattice sites by holes will break SU(4) and destroy SC [23,25]. This is in accordance with the data displayed in Figure 4, where only for doping less than ∼25% holes.
- Optimal Doping for Superconductivity: For doping larger than that near the peak of the superconducting dome (optimal doping) in Figure 4, SC properties were observed to become better defined. As discussed further below, this is a natural consequence of SU(4) symmetry, which implies a quantum phase transition near optimal doping exhibiting critical behavior [33]. At subcritical doping the superconducting wave function is perturbed by residual AF correlations. At the QFT the AF correlations vanish identically, leaving pure d-wave, BCS-like, singlet SC above critical doping. This is consistent with various cuprate experiments.
- Existence of a Pseudogap: A pseudogap is a partial gap at the Fermi surface above . From Figure 4, at lower doping it is the “normal state” from which SC can be produced by lowering the temperature through the doping-dependent critical temperature . As explained further below, a PG is expected from AF–SC competition in the SU(4) Hilbert subspace [33].
- Quantum Critical Behavior: A highest symmetry with multiple dynamical symmetry subchains leads naturally to quantum phase transitions as tuning parameters such as doping, magnetic field, or pressure shift the balance between competing dynamical symmetries. The SU(4) theory is microscopic so one can determine whether these transitions are associated with critical behavior and examine the corresponding physical consequences. Thus, SU(4) and its dynamical symmetry subchains are a laboratory for quantum critical behavior in HTSC. As we now discuss, the SU(4) model implies two fundamental instabilities, leading to quantum phase transitions that are central to understanding HTSC, and a critical dynamical symmetry that generalizes a quantum critical point to an entire quantum critical phase, which proves useful in understanding the underdoped region in general and the PG region in particular.
- The SU(4) Cooper Instability: The SU(4) solution at for the pairing order parameter given in Equation (24b) of Ref. [26] implies that [31]where x is doping and is a critical doping value predicted by the theory. (In Figure 4, the critical doping point is labeled with .) This implies a fundamental pairing instability at : the SU(4) AF Mott insulator ground state at half filling is intrinsically unstable against a QFT that condenses singlet hole pairs for infinitesimal hole doping in the presence of non-zero attractive pairing [31]. Figure 5a illustrates.
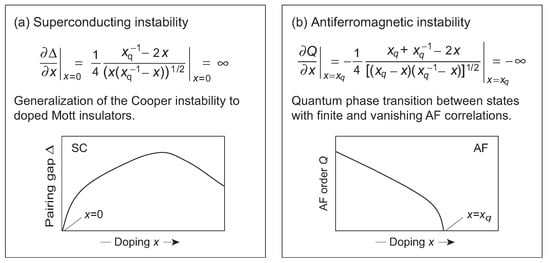 Figure 5. Two fundamental SU(4) instabilities that govern the behavior of high temperature superconductors. The plots illustrate (a) the generalized Cooper instability and (b) The AF instability in terms of the values of the order parameters calculated within coherent state approximation.
Figure 5. Two fundamental SU(4) instabilities that govern the behavior of high temperature superconductors. The plots illustrate (a) the generalized Cooper instability and (b) The AF instability in terms of the values of the order parameters calculated within coherent state approximation.
Hence, the rapid onset of SC with hole-doping in the cuprates results from a Cooper-like instability for d-wave pairs in an AF Mott insulator. The SU(4) solution reduces to ordinary d-wave BCS theory if the AF interaction vanishes and to an AF Mott insulator if the pairing interaction vanishes [26]. Thus, it generalizes the Cooper instability to doped Mott insulators and may be viewed as the traditional Cooper instability for a Fermi sea polarized by strong onsite Coulomb repulsion and AF correlations, or equivalently as a Fermi sea exhibiting SU(4) symmetry [33].
- The SU(4) AF Instability: SU(4) symmetry implies a second fundamental instability. From the SU(4) solution for the AF order parameter Q given by Equations (24b, 14) of Ref. [26],and a small change in doping causes a divergence in AF correlations near the critical doping in Figure 4 [32,33]. Figure 5b illustrates. This instability is associated with a QFT between a SC state still influenced by AF correlations and a pure SC state.
- Dynamical Symmetries and Critical Behavior: Quantum phase transitions and quantum critical points are a natural consequence of fermion dynamical symmetries, implying that quantum critical behavior is a corollary of unconventional superconductivity, not a cause. Furthermore, some dynamical symmetry solutions generalize quantum critical points to entire quantum critical phases exhibiting critical behavior [24,32,33]. The SU(4) ⊃ SO(5) dynamical symmetry is an example. This is seen most easily in generalized coherent state approximation [24], which represents symmetry-constrained Hartree–Fock–Bogoliubov solutions that permit SU(4) results to be expressed in terms of gap equations and quasiparticles, and that lead naturally to total energy surfaces connecting SU(4) solutions microscopically to Ginzburg–Landau theory. SU(4) coherent state energy surfaces are displayed in Figure 6a–c. The flat critical nature of the SO(5) surface is evident for low doping in Figure 6b.
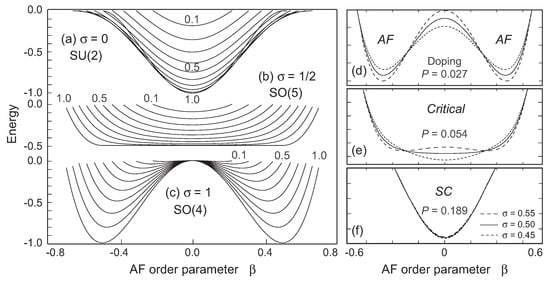 Figure 6. (a–c) Coherent-state energy surfaces for symmetry limits of the SU(4) Hamiltonian [24]. The horizontal axis measures AF order. Curves are labeled by lattice occupation fractions with the value 1 corresponding to half filling. The parameter is the ratio of AF coupling to the sum of AF and pairing coupling strengths. (d–f) Effect of altering the ratio for three values of doping in the cuprates. In (d,f) the system is in the stable minima associated with AF and SC, respectively, and changing by 10% hardly alters the location of the energy minima, but in (b) the energy surface is critical and the perturbation can flip the nature of the ground state between SC and AF minima.
Figure 6. (a–c) Coherent-state energy surfaces for symmetry limits of the SU(4) Hamiltonian [24]. The horizontal axis measures AF order. Curves are labeled by lattice occupation fractions with the value 1 corresponding to half filling. The parameter is the ratio of AF coupling to the sum of AF and pairing coupling strengths. (d–f) Effect of altering the ratio for three values of doping in the cuprates. In (d,f) the system is in the stable minima associated with AF and SC, respectively, and changing by 10% hardly alters the location of the energy minima, but in (b) the energy surface is critical and the perturbation can flip the nature of the ground state between SC and AF minima.
- Complexity in the Underdoped Region: As suggested in Figure 6d,f, the underdoped ∼SO(5) energy surface exhibits complexity because many potential ground states with very different order parameters have almost the same energy. Complexity implies susceptibility to fluctuations in AF and SC order induced by small perturbations and the phase defined by the SO(5) dynamical symmetry is a critical dynamical symmetry. Critical dynamical symmetries are a fundamental organizing principle for complexity in strongly correlated nuclear structure and condensed matter systems [32,33]. In Ref. [32] we have proposed that stripe and checkerboard patterns, amplification of proximity effects, and related phenomena common in underdoped compounds may be a consequence of complexity enabled by the critical nature of the energy surface there. This complexity can occur with or without associated spatial modulation of charge. Charge is not an SU(4) generator so it is not fundamental for HTSC, but it can play a secondary role by perturbing critical energy surfaces in underdoped compounds.
- Competing Order or Preformed Pairs: In the competing-order model the PG is an energy scale for order competing with SC. In the rival preformed pairs model pairs form at higher energy with phase fluctuations that suppress long-range order until at a lower energy the pairs condense into a SC with long-range order. In SU(4) the PG scale is an AF correlation competing with SC but the AF operators are generators of SU(4) and the collective subspace is a superposition of pairs. Thus, the PG results from a superposition of SU(4) pairs that can condense into a strong superconductor only after AF fluctuations are suppressed by doping. Hence the SU(4) pseudogap state results from competing AF and SC order in a basis of fermion pairs and SU(4) unifies the competing order and preformed pair pictures.
- Fermi Arcs and Anisotropy of Pseudogaps: The SU(4) cuprate model implies strong angular dependence in k-space, which leads to temperature and doping restrictions on regions of the Brillouin zone where ungapped Fermi surface can exist [30,33]. If this region is interpreted in terms of Fermi arcs, the SU(4) model gives a natural description of arc lengths as a function of temperature in quantitative accord with ARPES data [30,33]. If the Fermi surface is interpreted in terms of small pockets instead, SU(4) symmetry restricts their possible location and size.
- New Superconductors: In 2004 we argued that the essence of cuprate SC is non-abelian dynamical symmetry, and that compounds with similar symmetries but different microscopic structure should exist [25]. Discovery of Fe-based SC in 2008 validated this prediction [29,33].
- SU(4) and Conventional BCS Superconductivity: The relationship of SU(4) to BCS SC was given in Figure 3. Conventional SC is the limit of SO(8) ⊃ SU(4) SC when Coulomb repulsion is small and AF correlation is negligible. Thus, SO(8) ⊃ SU(4) dynamical symmetry provides a unified view of conventional and unconventional superconductivity [33].
- Dynamical Symmetry and Universality of Emergent States: Dynamical symmetries for a variety of emergent states suggest an even broader unification transcending fields and subfields Figure 7.
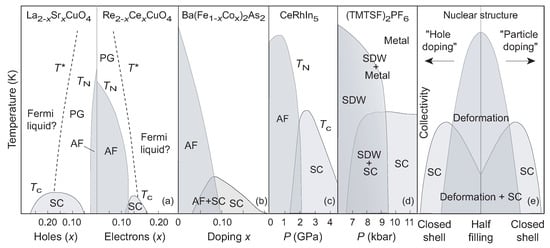 Figure 7. Universality of superconductivity and superfluidity. (a) Phase diagram for hole- and electron-doped cuprates [36]. Superconducting (SC), antiferromagnetic (AF), and pseudogap (PG) regions are labeled, as are Néel (), SC critical (), and PG () temperatures. (b) Phase diagram for Fe-based SC [37]. (c) Heavy-fermion phase diagram [38]. (d) Phase diagram for an organic superconductor (SDW denotes spin density waves) [39]. (e) Generic correlation-energy diagram for nuclear structure [40].
Figure 7. Universality of superconductivity and superfluidity. (a) Phase diagram for hole- and electron-doped cuprates [36]. Superconducting (SC), antiferromagnetic (AF), and pseudogap (PG) regions are labeled, as are Néel (), SC critical (), and PG () temperatures. (b) Phase diagram for Fe-based SC [37]. (c) Heavy-fermion phase diagram [38]. (d) Phase diagram for an organic superconductor (SDW denotes spin density waves) [39]. (e) Generic correlation-energy diagram for nuclear structure [40].
The discussion above shows that phase diagrams for unconventional SC emergent states in a broad range of condensed matter systems and in nuclear structure are remarkably similar, despite completely different microscopic physics (see Refs. [33,40] for further discussion). An even more remarkable universality of emergent states is shown in the coherent state energy surfaces displayed in Figure 8.
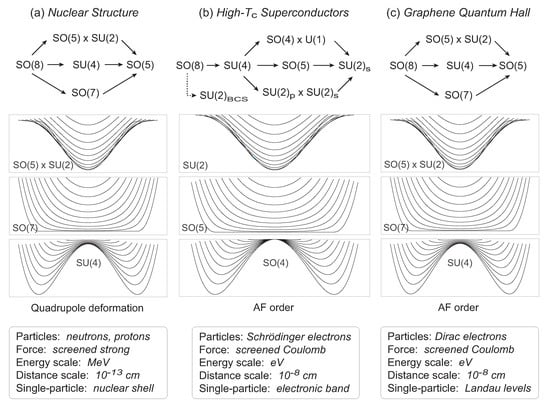
Figure 8.
Similarity in the dynamical symmetry chains and the ground coherent state energy surfaces for (a) dynamical symmetry in nuclear structure [16], (b) high-temperature SC [23,24], and (c) monolayer graphene in a strong magnetic field [41]. The plot contours show total energy as a function of an appropriate order parameter, with different curves corresponding to a particle number parameter.
Seemingly different emergent modes: collective states for atomic nuclei, for graphene in a magnetic field, and for cuprate high-temperature SC, give nearly identical energy surfaces under a suitable mapping of respective order parameters and rescaling of energy. Microscopically these modes differ fundamentally but they share a common Hilbert-space truncation to a collective subspace dictated by shared Lie algebras that care only about commutators of generators, not their microscopic structure [33].
4. Transition Temperatures for Unconventional Superconductors
The discussion above shows that SU(4) dynamical symmetry describes a broad range of cuprate SC properties using a minimum of adjustable parameters or adjustable assumptions. Having established that it should be taken seriously, let us ask what SU(4) symmetry has to say about . The generators of SO(4) antiferromagnetism and SU(2) superconductivity are also generators of SU(4). This implies that (1) AF and SC compete for the collective Hilbert subspace, and (2) AF states and SC states are related by a rotation within the SU(4) group space. As we now explain, this implies on fundamental grounds a higher than average for unconventional SC in general, and for cuprate and Fe-based HTSC in particular.
A generic reason for higher in unconventional SC is illustrated in Figure 9,where the x component of arrows may be viewed as the average competing-order matrix element squared and the y component as the average pairing matrix element squared. In the conventional BCS case of Figure 9a,b there is no net SC or AF in the initial state of Figure 9a and arrows are small and randomly oriented. To form the superconducting state from the parent state each arrow must be lengthened and ordered vertically in the SC phase transition, as in Figure 9b. This is a transition from a high-entropy initial state to a highly ordered final state, implying that it requires a corresponding low temperature to implement. In the competing order case the initial state of Figure 9c is already ordered such that a simple collective rotation can produce the SC state in Figure 9d. This is the general case when SC and the competing order are unified by symmetry. In essence, the collective vectors already exist as a highly ordered configuration in the parent state with a length proportional to the SU(4) Casimir expectation value, but they point in the AF direction. To produce a superconductor from a parent AF state, they need only be rotated uniformly to point in the SC direction; Figure 9e illustrates. Thus, if competing order and superconductivity are related by symmetry the parent state can “pre-condition” the phase transition, allowing it to occur at higher because the low-entropy competing-order state can be rotated collectively into the low-entropy superconducting state.
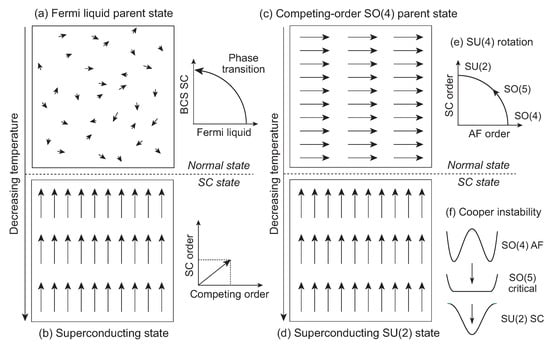
Figure 9.
(a,b) Formation of BCS superconductor by lowering the temperature of a Fermi liquid through . Direction of vectors indicates relative strength of competing order (x) and SC (y); length indicates total SU(4) strength. The SC transition converts a high-entropy state (a) into a highly ordered one (b), implying a low . (c,d) Formation of SC from a parent state having order that competes with SC but is related to SC by symmetry. This requires imposing SC order (d) on a state (c) already highly ordered, which can occur at a higher because it is a collective rotation in the group space between two low-entropy states. (e) Collective rotation in SU(4) group space. (f) SU(4) Cooper instability.
We have shown that the SU(4) model exhibits a generalized Cooper instability whereby the AF Mott insulator state reorganizes spontaneously into a superconductor when it is perturbed by adding holes [31]. The collective rotation in the SU(4) space indicated in Figure 9c–e is a schematic representation of this generalized Cooper instability, which can occur spontaneously if there is no barrier to the rotation. The SU(4) ⊃ SO(5) critical dynamical symmetry exhibits such a property, as illustrated in Figure 9f. At low doping the energy surface implies degenerate AF and SC ground states with no energy barrier between them [see Figure 6b for lattice occupation fraction of one]. This suggests that the AF and SC phases can be connected by a sequence of infinitesimal SU(4) rotations through intermediate states having different mixtures of AF and SC order that are degenerate in energy.
These entropy arguments are equivalently information arguments. Figure 9d is obtained from Figure 9c by collective rotation, which requires specification of a single angle. Conversely, there is no order in the parent state of Figure 9a and each arrow must be lengthened and oriented individually to give Figure 9b, which requires supplying much more information. Thus, the ordering necessary to condense the SC state is much larger in Figure 9a,b than in Figure 9c,d. The information argument also makes clear the essential difference between competing collective modes that are independent and those related by a symmetry. In the former case, a large amount of information is required to change the competing-order state into the SC state because they are unrelated: the symmetry of the parent state must be destroyed and the SC symmetry then constructed from the pieces. In the latter case, the symmetry already encodes the relationship between the two modes; hence only a small amount of information is required to produce the SC state from the competing-order state.
5. Conclusions
To conclude, we have presented a solvable microscopic theory based on SU(4) dynamical symmetry of unconventional superconductivity and antiferromagnetism on a lattice with double site occupancy suppressed by the symmetry. This permits an exact many-body solution for a minimal model having charge, spin, pairing, and antiferromagnetism degrees of freedom for special ratios of the coupling parameters, and an approximate coherent-state solution for arbitrary values of the coupling parameters. The formalism suggests that most cuprate phenomenology may be understood in terms of quantum phase transitions associated with two fundamental instabilities: the generalized Cooper instability, which accounts for the rapid appearance of superconductivity when the Mott insulator is doped with holes, and the antiferromagnetic instability, which accounts largely for the pseudogap and its properties.
We have applied the method of generalized SU(4) coherent states to relate the SU(4) many-body theory to its approximate (spontaneously) broken-symmetry solutions. This implements a standardized technology for constructing energy surfaces of many-body theories defined in terms of the algebra of their second-quantized operators, and provides a microscopic connection to Ginzburg-Landau methods. Equivalently, it implements the most general Hartree-Fock-Bogoliubov theory, subject to a symmetry constraint on the Hamiltonian. Thus, the coherent-state solution for SU(4) allows us to express results in language familiar in condensed matter: spontaneously broken symmetries, gap equations for quasiparticles, and variational energy surfaces.
Our discussion has emphasized cuprate SC examples but applies generally to unconventional SC. The crucial physics of unconventional superconductivity lies in the competition of other collective modes with pairing, and possible Coulomb repulsion effects. These polarize the pairing interaction and alter the geometry of the pairing formfactor, but that is symptomatic; the essential physics lies in the competing order, not the formfactor. Thus, the reason for high- proposed here should be operative in all unconventional SC, leading to the often abnormally high (on an appropriate scale) seen for cuprates, Fe-based SC, heavy-fermion SC, and other unconventional superconductors, by virtue of universal symmetry arguments depending only parametrically on microscopic details like pairing geometry.
Finally, we note the irony that this discussion may seem to be unconventional because of methodology, but it leads to the most conventional and conservative of physical conclusions. The high superconductors are described by a BCS formalism generalized to incorporate antiferromagnetism, pairing, and on-site Coulomb repulsion on an equivalent footing. Microscopic details like dimensionality, gap orbital symmetry, pair binding mechanism, nature of the magnetism, crystal structure, amount of disorder, and so on are important, but they influence the superconductor primarily by setting the value of coefficients in equations whose form has largely been determined by emergent dynamical symmetry, independent of those microscopic details. The emergent properties defining the essence of the superconducting state observed across many physical systems with fundamentally different microscopic structure require only that the microscopic conditions permit realization of emergent fermion dynamical symmetries of the Hamiltonian like the SU(4) symmetry described here, largely independent of further microscopic details.
Author Contributions
Conceptualization, M.G., Y.S., and L.-A.W.; methodology, M.G., Y.S., and L.-A.W.; writing M.G. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the National Natural Science Foundation of China, by the Basque Country Government, and by LightCone Interactive LLC..
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was partially supported by the National Key Program for S&T Research and Development (Grant No. 2016YFA0400501), and by LightCone Interactive LLC. L.-A.W. acknowledges grant support from the Basque Country Government (Grant No. IT986-16), and by PGC2018-101355-B-I00 (MCIU/AEI/FEDER, UE).
Conflicts of Interest
The authors declare no conflict of interest..
References
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. 1986, B64, 189–193. [Google Scholar] [CrossRef]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1-xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 1330, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Jin, S.; Wang, G.; Wang, S.; Zhu, K.; Zhou, T.; He, M.; Chen, X. Superconductivity in the iron selenide KxFe2Se2 (0 ≤ x ≤ 1.0). Phys. Rev. 2010, B82, 180520. [Google Scholar] [CrossRef]
- Norman, M.R. The Challenge of Unconventional Superconductivity. Science 2011, 332, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Jérome, D. Organic Superconductors: When correlations and magnetism walk in. arXiv 2012, arXiv:1201.5796. [Google Scholar] [CrossRef]
- Bonn, D.A. Are high-temperature superconductors exotic? Nat. Phys. 2006, 2, 159–168. [Google Scholar] [CrossRef]
- Norman, M.R.; Pépin, C. The electronic nature of high temperature cuprate superconductors. Rep. Prog. Phys. 2003, 66, 1547–1610. [Google Scholar] [CrossRef]
- Johnston, D.C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 2010, 59, 803–1061. [Google Scholar] [CrossRef]
- Paglione, J.; Greene, R.L. High-temperature superconductivity in iron-based materials. Nat. Phys. 2010, 6, 645–658. [Google Scholar] [CrossRef]
- Oh, H.; Moon, J.; Shin, D.; Moon, C.; Choi, H.J. Brief review on iron-based superconductors: Are there clues for unconventional superconductivity? Prog. Supercond. 2011, 13, 65–84. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Cooper, L.N. Bound Electron Pairs in a Degenerate Ferxai Gas. Phys. Rev. 1956, 104, 1189–1190. [Google Scholar] [CrossRef]
- Anderson, P.W. Spin-Charge Separation is the Key to the High Tc Cuprates. Physica 2000, C341–C348, 9–10. [Google Scholar] [CrossRef]
- Pines, D. Quantum Protectorates in the Cuprate Superconductors. Physica 2000, C341–C348, 59–62. [Google Scholar] [CrossRef]
- Laughlin, R.B.; Pines, D. The Theory of Everything. Proc. Natl. Acad. Sci. USA 2000, 97, 28–31. [Google Scholar] [CrossRef]
- Wu, C.L.; Feng, D.H.; Guidry, M.W. The fermion dynamical symmetry model. Adv. Nuc. Phys. 1994, 21, 227–443. [Google Scholar]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Bijker, R.; Iachello, F.; Leviatan, A. Algebraic Models of Hadron Structure. Ann. Phys. 1994, 236, 69–116. [Google Scholar] [CrossRef]
- Iachello, F.; Levine, R.D. Algebraic Theory of Molecules; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Iachello, F.; Truini, P. Algebraic Model of Anharmonic Polymer Chains. Ann. Phys. 1999, 276, 120–143. [Google Scholar] [CrossRef]
- Anderson, P.W. Random-Phase Approximation in the Theory of Superconductivity. Phys. Rev. 1958, 112, 1900–1916. [Google Scholar] [CrossRef]
- Glauber, R.J. Photon Correlations. Phys. Rev. Lett. 1963, 10, 84–86. [Google Scholar] [CrossRef]
- Guidry, M.W.; Wu, L.-A.; Sun, Y.; Wu, C.-L. SU(4) model of high-temperature superconductivity and antiferromagnetism. Phys. Rev. 2001, B63, 134516. [Google Scholar] [CrossRef]
- Wu, L.-A.; Guidry, M.W.; Sun, Y.; Wu, C.-L. SO(5) as a critical dynamical symmetry in the SU(4)model of high-temperature superconductivity. Phys. Rev. 2003, B67, 014515. [Google Scholar] [CrossRef]
- Guidry, M.W.; Sun, Y.; Wu, C.-L. Mott insulators, no double occupancy, and non-Abelian superconductivity. Phys. Rev. 2004, B70, 184501. [Google Scholar] [CrossRef]
- Sun, Y.; Guidry, M.W.; Wu, C.-L. Temperature-dependent gap equations and their solutions in the SU(4) model of high-temperature superconductivity. Phys. Rev. 2006, B73, 134519. [Google Scholar] [CrossRef]
- Sun, Y.; Guidry, M.W.; Wu, C.-L. Pairing gaps, pseudogaps, and phase diagrams for cuprate superconductors. Phys. Rev. 2007, B75, 134511. [Google Scholar] [CrossRef]
- Sun, Y.; Guidry, M.W.; Wu, C.-L. k-dependent SU(4) model of high-temperature superconductivity and its coherent-state solutions. Phys. Rev. 2008, B78, 174524. [Google Scholar] [CrossRef]
- Guidry, M.W.; Sun, Y.; Wu, C.-L. A unified description of cuprate and iron arsenide superconductors. Front. Phys. China 2009, 4, 433–446. [Google Scholar] [CrossRef][Green Version]
- Guidry, M.W.; Sun, Y.; Wu, C.-L. Strong anisotropy of cuprate pseudogap correlations: Implications for Fermi arcs and Fermi pockets. New J. Phys. 2009, 11, 123023. [Google Scholar] [CrossRef]
- Guidry, M.W.; Sun, Y.; Wu, C.-L. Generalizing the Cooper-pair instability to doped Mott insulators. Front. Phys. China 2010, 5, 171–175. [Google Scholar] [CrossRef]
- Guidry, M.W.; Sun, Y.; Wu, C.-L. Inhomogeneity, dynamical symmetry, and complexity in high-temperature superconductors: Reconciling a universal phase diagram with rich local disorder. Chin. Sci. Bull. 2011, 56, 367–371. [Google Scholar] [CrossRef][Green Version]
- Guidry, M.W.; Sun, Y.; Wu, L.-A.; Wu, C.-L. Fermion dynamical symmetry and strongly-correlated electrons: A comprehensive model of high-temperature superconductivity. Front. Phys. 2020, 15, 43301. [Google Scholar] [CrossRef]
- Dai, P.; Mook, H.A.; Hayden, S.M.; Aeppli, G.; Perring, T.G.; Hunt, R.D.; Doğan, F. The Magnetic Excitation Spectrum and Thermodynamics of High-Tc, Superconductors. Science 1999, 284, 1344–1347. [Google Scholar] [CrossRef] [PubMed]
- Campuzano, J.C.; Ding, H.; Norman, M.R.; Fretwell, H.M.; Randeria, M.; Kaminski, A.; Mesot, J.; Takeuchi, T.; Sato, T.; Yokoya, T.; et al. Electronic Spectra and Their Relation to the (π,π) Collective Mode in High-Tc Superconductors. Phys. Rev. Lett. 1999, 83, 3709–3712. [Google Scholar] [CrossRef]
- Armitage, N.P.; Fournier, P.; Greene, R.L. Progress and perspectives on electron-doped cuprates. Rev. Mod. Phys. 2010, 82, 2421–2487. [Google Scholar] [CrossRef]
- Fang, L.; Luo, H.-Q.; Cheng, P.; Wang, Z.-S.; Jia, Y.; Mu, G.; Shen, B.; Mazin, I.I.; Shan, L.; Ren, C. Roles of multiband effects and electron-hole asymmetry in the superconductivity and normal-state properties of Ba(Fe1-xCox)2As2. Phys. Rev. 2009, B80, 140508. [Google Scholar] [CrossRef]
- Knebel, G.; Aoki, D.; Floquet, J. Magnetism and Superconductivity in CeRhIn5. arXiv 2009, arXiv:0911.5223. [Google Scholar]
- Kang, N.; Salameh, B.; Auban-Senzier, P.; Jérome, D.; Pasquier, C.R.; Brazovskii, S. Domain walls at the spin-density-wave endpoint of the organic superconductor (TMTSF)2PF6 under pressure. Phys. Rev. 2010, B81, 100509. [Google Scholar] [CrossRef]
- Guidry, M.W.; Sun, Y. Superconductivity and superfluidity as universal emergent phenomena. Front. Phys. 2015, 10, 107404. [Google Scholar] [CrossRef]
- Wu, L.-A.; Guidry, M.W. The Ground State of Monolayer Graphene in a Strong Magnetic Field. Sci. Rep. 2016, 6, 22423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).