Survival and Reliability Analysis with an Epsilon-Positive Family of Distributions with Applications

Abstract

We introduce a new class of distributions called the epsilon–positive family, which can be viewed as generalization of the distributions with positive support. The construction of the epsilon–positive family is motivated by the ideas behind the generation of skew distributions using symmetric kernels. This new class of distributions has as special cases the exponential, Weibull, log–normal, log–logistic and gamma distributions, and it provides an alternative for analyzing reliability and survival data. An interesting feature of the epsilon–positive family is that it can viewed as a finite scale mixture of positive distributions, facilitating the derivation and implementation of EM–type algorithms to obtain maximum likelihood estimates (MLE) with (un)censored data. We illustrate the flexibility of this family to analyze censored and uncensored data using two real examples. One of them was previously discussed in the literature; the second one consists of a new application to model recidivism data of a group of inmates released from the Chilean prisons during 2007. The results show that this new family of distributions has a better performance fitting the data than some common alternatives such as the exponential distribution.

1. Introduction

The statistical analysis of reliability and survival data is an important topic in several areas, including medicine, epidemiology, biology, economics, engineering, and environmental sciences, to name a few. When using a parametric approach, one of the first steps for modeling the data is to choose a suitable distribution that can capture relevant features of the observations of interest. In this context, the gamma and Weibull distributions have become popular choices due to their flexibility that allows for a non-constant hazard rate function and to model skewed data. Although several alternatives were considered to accommodate different cases, researchers have continued to develop extensions and modifications of the standard distributions to increase the flexibility of the models see [1,2,3] for a few examples.

In this paper, we consider a generalization of the distributions with positive support and propose a new family of distributions, called the epsilon–positive family, whose construction is motivated by the ideas behind the generation of skew distributions using symmetric kernels. Specifically, we build upon the ideas from [4], where the authors start with a symmetric around zero distribution f, and define a family of distributions indexed by a parameter $\gamma >0$ as the set of densities of the form

$$h(x;\gamma )=\frac{2}{\gamma +{\gamma }^{-1}}\left(f(x/\gamma )1_{\{x\ge 0\}}+f\left(\gamma x\right)1_{\{x<0\}}\right),$$

(1)

where $1_A$ denotes the indicator function of the set A. Some extensions of this family include epsilon-skew-normal family introduced by [5] and the epsilon–skew–symmetric family introduced by [6], both discussed in some details in [7].

Here, starting with a probability density function g with positive support, we obtain a general class that extends the family of distributions with positive support, and that contains the Weibull, gamma and exponential distributions as special cases, depending on the choice of g. Furthermore, we discuss a stochastic representation and how to obtain maximum likelihood estimators for the members of this family. We also derive the corresponding survival and hazard functions and note that one interesting feature of this new class is that the hazard function is not necessarily constant.

The rest of the paper is organized as follows: in Section 2 we define the epsilon–positive family and obtain the hazard and survival functions, mean residual life and stress-strength parameters for this family. In addition, we discuss maximum likelihood estimation and how to obtain such estimates using an EM-type algorithm for the general case. In Section 3, we focus on one specific member of the family introduced in Section 2, namely epsilon–exponential distribution, and discuss its applicability in the analysis of survival data. In Section 4 we discuss two real data examples and we finish with a brief discussion in Section 5. We include Appendix A and Appendix B with some of the technical details.

2. The Epsilon–Positive Family

Let $g(·)=g_Y(·;\mathsf{\Psi })$ be a probability density function (pdf) with positive support and parameters $\mathsf{\Psi }\in {\Re }^p$. Then, for $0<\epsilon <1$, the corresponding epsilon–positive (EP) family of distributions is defined as

$$f_X(x;\mathsf{\Psi },\epsilon )=\frac{1}{2}\left[g\left(\frac{x}{1+\epsilon }\right)+g\left(\frac{x}{1-\epsilon }\right)\right],x>0.$$

(2)

If a random variable X has the density given in (2), we say that X has an epsilon–positive distribution and write $X\sim EP(\mathsf{\Psi },\epsilon )$.

Observe that as $\epsilon \downarrow 0$, $f_X\left(x;\mathsf{\Psi },\epsilon \right)\to g\left(x\right)1_{\{x>0\}}$ and therefore the distribution $g_Y(·;\mathsf{\Psi })$ can be seen as a particular member of the family.

The rth moment of $X\sim EP(\mathsf{\Psi },\epsilon )$, $r=1,2,\cdots ,$ is given by

$$E\left(X^r\right)=\left(\frac{{(1+\epsilon )}^{r+1}}{2}+\frac{{(1-\epsilon )}^{r+1}}{2}\right)E\left(Y^r\right),$$

(3)

where $E\left(Y^r\right)$ is the rth moment of $Y\sim g_Y(·;\mathsf{\Psi })$. From (3) we obtain that the mean, variance, skewness (CS) and kurtosis (CK) coefficients are (respectively)

$$E\left(X\right)=(1+{\epsilon }^2)E\left(Y\right)$$

$$Var\left(X\right)=(1+3{\epsilon }^2)E\left(Y^2\right)-{(1+{\epsilon }^2)}^2{E}^2\left(Y\right)$$

$$CS=\frac{(1+6{\epsilon }^2+{\epsilon }^4)E\left(Y^3\right)-3(1+4{\epsilon }^2+3{\epsilon }^4)E\left(Y\right)E\left(Y^2\right)+2{(1+{\epsilon }^2)}^3{E}^3\left(Y\right)}{{((1+3{\epsilon }^2)E\left(Y^2\right)-{(1+{\epsilon }^2)}^2{E}^2\left(Y\right))}^{3/2}}$$

and

$$CK=\frac{A}{{((1+3{\epsilon }^2)E\left(Y^2\right)-{(1+{\epsilon }^2)}^2{E}^2\left(Y\right))}^2},$$

$$\begin{array}{c}A=(1+10{\epsilon }^2+5{\epsilon }^4)E\left(Y^4\right)-4(1+7{\epsilon }^2+7{\epsilon }^4+{\epsilon }^6)E\left(Y\right)E\left(Y^3\right)\hfill \\ +6(1+5{\epsilon }^2+7{\epsilon }^4+3{\epsilon }^6)E^2\left(Y\right)E\left(Y^2\right)-3(1+4{\epsilon }^2+6{\epsilon }^4+4{\epsilon }^6+{\epsilon }^8)E^4\left(Y\right),\hfill \end{array}$$

where $E\left(Y^r\right)$, $r=1,2,3,4$, are the first four moments of the random variable $Y\sim g_Y(·;\mathsf{\Psi })$.

To draw observations from an epsilon–positive distribution, we first notice that for $0<\epsilon <1$, if $Y\sim g_Y(·;\mathsf{\Psi })$ and $U_{\epsilon }$ (independent from Y) satisfies $P\left(U_{\epsilon }=1+\epsilon \right)=1-P\left(U_{\epsilon }=1-\epsilon \right)=(1+\epsilon )/2$, then $X=U_{\epsilon }Y\sim EP(\mathsf{\Psi },\epsilon )$.

From this stochastic representation, it follows that we can generate EP random variables according to the Algorithm 1:

Algorithm 1 Algorithm to generate observations from an epsilon–positive distribution.

Require: Initialize the algorithm fixing $\mathsf{\Psi }$ and $\epsilon$

1: Generate Y from $g_Y(·)$ and U from $\mathcal{B}er\left(p=\frac{1+\epsilon }{2}\right)$

2: if $U=1$ then

3:  $U_{\epsilon }\leftarrow 1+\epsilon$

4: else

5:  $U_{\epsilon }\leftarrow 1-\epsilon$

6: end if

7: return $X=U_{\epsilon }Y.$

Finally, observe that the definition in (2) can be easily extended so we can represent the epsilon–positive family as a finite scale mixture of positive distributions. In fact, for any $0<\epsilon <1$ we can write

$$f_X(x;\mathsf{\Psi },\epsilon )=\sum _{\xi \in \mathcal{J}\left(\epsilon \right)}{\pi }_{\xi }\left(\epsilon \right)\frac{1}{\xi }g\left(\frac{x}{\xi }\right),$$

(4)

where $x>0$, ${\pi }_{\xi }\left(\epsilon \right)>0$ are mixing proportions satisfying ${\sum }_{\xi \in \mathcal{J}\left(\epsilon \right)}{\pi }_{\xi }\left(\epsilon \right)=1$, and $\mathcal{J}\left(\epsilon \right)$ is some finite subset of ℜ that will typically depend on $\epsilon$. For instance, taking $\mathcal{J}\left(\epsilon \right)=\{1-\epsilon ,1+\epsilon \}$ and ${\pi }_{\xi }\left(\epsilon \right)=(1\pm \epsilon )/2$ we recover the expression in (2). This representation will be particularly useful in order to obtain maximum likelihood estimates using EM–type algorithms, as we discuss in Section 2.5.

2.1. Reliability Properties

From the definition, we obtain that the survival function $S_X(x;\mathsf{\Psi },\epsilon )=P(X>x)$ for this family is given by

$$S_X(x;\mathsf{\Psi },\epsilon )=\left(\frac{1+\epsilon }{2}\right)S_Y\left(\frac{x}{1+\epsilon }\right)+\left(\frac{1-\epsilon }{2}\right)S_Y\left(\frac{x}{1-\epsilon }\right),$$

(5)

where $S_Y(·)$ is the survival function associated with the density $g_Y(·;\mathsf{\Psi })$. Similarly, the hazard function ${\lambda }_X(x;\mathsf{\Psi },ϵ)=f_X(x;\mathsf{\Psi },\epsilon )/S_X(x;\mathsf{\Psi },\epsilon )$ is given by

$${\lambda }_X(x;\mathsf{\Psi },ϵ)=\frac{1+r\left(x\right)}{(1+\epsilon )R\left(\frac{x}{1+\epsilon }\right)+(1-\epsilon )R\left(\frac{x}{1-\epsilon }\right)r\left(x\right)},$$

(6)

where $r\left(x\right)=g_Y\left(\frac{x}{1-\epsilon }\right)/g_Y\left(\frac{x}{1+\epsilon }\right)$, and $R(·)=S_Y(·)/g_Y(·)$ is the Mills ratio.

Table 1 shows some examples of the densities that can be extended using the definition of the epsilon–positive family, with the corresponding densities, survival and hazard functions. Figure 1 and Figure 2 show the pdf, survival and hazard functions of the epsilon-exponential, epsilon-Weibull, epsilon-log-logistic and epsilon-gamma distributions. We can see that in the case of the epsilon-Weibull, epsilon-log-logistic and epsilon-gamma distributions a bimodal shape is obtained when the value of the parameter $\epsilon$ is $0.9$.

Table 1. Hazard rate, $\lambda (·)$, Survival, $S(·)$, and density, $f(·)$, functions of some probability models that can be generalized using the definition in (2) In the table $I(a,\beta )={\int }_0^a\mathsf{\Gamma }{\left(\beta \right)}^{-1}{u}^{\beta -1}{e}^{-u}du$.

	$\mathit{\lambda }\left(\mathit{y}\right)$	$\mathit{S}\left(\mathit{y}\right)$	$\mathit{f}\left(\mathit{y}\right)$
Exponential	$\frac{1}{\sigma }(>0)$	$exp(-\frac{y}{\sigma })$	$\frac{1}{\sigma }exp(-\frac{y}{\sigma })$
Weibull	$\left(\frac{\beta }{{\sigma }^{\beta }}\right)y^{(\beta -1)}(\beta ,\sigma >0)$	$exp(-{\left[\frac{y}{\sigma }\right]}^{\beta })$	$\frac{\beta y^{(\beta -1)}}{{\sigma }^{\beta }}exp(-{\left[\frac{y}{\sigma }\right]}^{\beta })$
Log-logistic	$\frac{\left(\frac{\beta }{\sigma }\right){\left(\frac{y}{\sigma }\right)}^{\beta -1}}{1+{\left(\frac{y}{\sigma }\right)}^{\beta }}(\beta ,\sigma >0)$	${(1+{\left[\frac{y}{\sigma }\right]}^{\beta })}^{-1}$	$\frac{\left(\frac{\beta }{\sigma }\right){\left(\frac{y}{\sigma }\right)}^{\beta -1}}{{(1+{\left(\frac{y}{\sigma }\right)}^{\beta })}^2}$
Gamma	$\frac{f\left(y\right)}{S\left(y\right)}$	$1-I(y/\sigma ,\beta )$	$\frac{y^{(\beta -1)}exp(-\frac{y}{\sigma })}{{\sigma }^{\beta }\mathsf{\Gamma }\left(\beta \right)}$

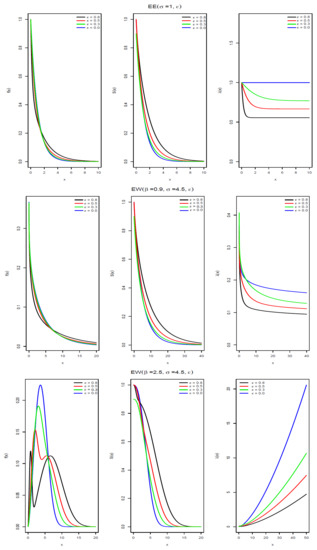
Figure 1. Examples of the probability density $f\left(x\right)$, survival $S\left(x\right)$ and hazard $\lambda \left(x\right)$ functions of epsilon-exponential distribution, $EE(\sigma ,\epsilon )$, and epsilon-Weibull distribution, $EW(\alpha ,\sigma ,\epsilon )$. Please note that the exponential and Weibull distributions correspond to the case $\epsilon =0$.

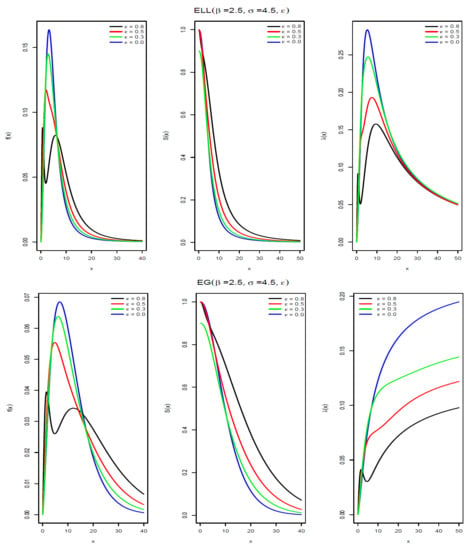
Figure 2. Examples of the probability density $f\left(x\right)$, survival $S\left(x\right)$ and hazard $\lambda \left(x\right)$ functions of epsilon-log-logistic distribution, $ELL(\sigma ,\epsilon )$, and epsilon-gamma distribution, $EG(\alpha ,\sigma ,\epsilon )$. Please note that the log-logistic and gamma distributions correspond to the case $\epsilon =0$.

2.2. Mean Residual Life

The mean residual life or life expectancy is an important characteristic of the model. It gives the expected additional lifetime given that a component has survived until time t. For a non-negative continuous random variable $X\sim EP(\mathsf{\Psi },\epsilon )$ the mean residual life ($mlr$) function is defined as

$$mrl\left(t\right)=E(X-t|X>t)=E(X|X>t)-t$$

(7)

where $t>0$. The above conditional expectation is given by

$$E\left(X\right|X>t)={\int }_t^{\infty }\frac{x{f}_X\left(x\right)}{P(X>t)}dx={\int }_t^{\infty }\frac{x{f}_X\left(x\right)}{1-F_X\left(t\right)}dx=\frac{1}{S_X\left(t\right)}{\int }_t^{\infty }x{f}_X\left(x\right)dx.$$

(8)

Calculation of the integral in (8) is done in the same way as the calculation of the mean. Thus,

$$I={\int }_t^{\infty }x{f}_X\left(x\right)dx={\int }_t^{\infty }x\frac{1}{2}\left[g_Y\left(\frac{x}{1+\epsilon }\right)+g_Y\left(\frac{x}{1-\epsilon }\right)\right]dx.$$

Making the changes of variables $z=\frac{x}{1+\epsilon }$ and $u=\frac{x}{1-\epsilon }$ we have

$$\begin{array}{cc}\hfill I& =\frac{{(1+\epsilon )}^2}{2}{\int }_{t/(1+\epsilon )}^{\infty }z{g}_Y\left(z\right)dz+\frac{{(1-\epsilon )}^2}{2}{\int }_{t/(1-\epsilon )}^{\infty }u{g}_Y\left(u\right)du\hfill \\ \hfill & =\frac{{(1+\epsilon )}^2}{2}{S}_Y\left(t_1\right){\int }_{t_1}^{\infty }\frac{z{g}_Y\left(z\right)}{S_Y\left(t_1\right)}dz+\frac{{(1-\epsilon )}^2}{2}{S}_Y\left(t_2\right){\int }_{t_2}^{\infty }\frac{u{g}_Y\left(u\right)}{S_Y\left(t_2\right)}du\hfill \\ \hfill & =\frac{{(1+\epsilon )}^2}{2}{S}_Y\left(t_1\right)E\left(Y\right|Y>t_1)+\frac{{(1-\epsilon )}^2}{2}{S}_Y\left(t_2\right)E\left(Y\right|Y>t_2)\hfill \\ \hfill & =\frac{{(1+\epsilon )}^2}{2}{S}_Y\left(t_1\right)\left(E(Y-t_1|Y>t_1)+t_1\right)+\frac{{(1-\epsilon )}^2}{2}{S}_Y\left(t_2\right)\left(E(Y-t_2|Y>t_2)+t_2\right)\hfill \\ \hfill & =\frac{{(1+\epsilon )}^2}{2}{S}_Y\left(t_1\right)\left(mr{l}_Y\left(t_1\right)+t_1\right)+\frac{{(1-\epsilon )}^2}{2}{S}_Y\left(t_2\right)\left(mr{l}_Y\left(t_2\right)+t_2\right),\hfill \end{array}$$

where $t_1=\frac{t}{1+\epsilon }$, $t_2=\frac{t}{1-\epsilon }$, and $mr{l}_Y\left(t_i\right)=E(Y-t_i|Y>t_i)$, $i=1,2$ corresponds to the mean residual life of the random variable $Y\sim g_Y(·)$. Finally, Equation (7) can be written as

$$mrl\left(t\right)=\frac{\frac{{(1+\epsilon )}^2}{2}{S}_Y\left(\frac{t}{1+\epsilon }\right)(ml{r}_Y\left(t_1\right)+t_1)+\frac{{(1-\epsilon )}^2}{2}{S}_Y\left(\frac{t}{1-\epsilon }\right)(mr{l}_Y\left(t_2\right)+t_2)}{\left(\frac{1+\epsilon }{2}\right)S_Y\left(\frac{t}{1+\epsilon }\right)+\left(\frac{1-\epsilon }{2}\right)S_Y\left(\frac{t}{1-\epsilon }\right)}-t.$$

(9)

2.3. Stress-Strength Parameter

An important concept in reliability theory is the stress-strength parameter. Let $X_1$ denote the strength of a system or component with a stress $X_2$. Then, the stress-strength parameter is defined as $R=P(X_2<X_1)$, which can be viewed as a measure of the system performance. In the next theorem, we look at this quantity when $X_1$ and $X_2$ are independent random variables with epsilon-positive distributions.

Theorem 1.

Suppose $X_1$ and $X_2$ are random variables independently distributed as $X_1\sim EP({\mathsf{\Psi }}_1,{\epsilon }_1)$ and $X_2\sim EP({\mathsf{\Psi }}_2,{\epsilon }_2)$, the reliability of the system with stress variable ($X_2$) and strength variable ($X_1$) is given by

$$\begin{array}{cc}\hfill R=P(X_2<X_1)& =\frac{{(1+{\epsilon }_2)}^2}{4}\left(aP(Y_2<a{Y}_1)+bP(Y_2<b{Y}_1)\right)\hfill \\ \hfill & +\frac{{(1-{\epsilon }_2)}^2}{4}\left(cP(Y_2<c{Y}_1)+dP(Y_2<d{Y}_1)\right),\hfill \end{array}$$

(10)

where $a=\frac{1+{\epsilon }_1}{1+{\epsilon }_2}$, $b=\frac{1-{\epsilon }_1}{1+{\epsilon }_2}$, $c=\frac{1+{\epsilon }_1}{1-{\epsilon }_2}$, $d=\frac{1-{\epsilon }_1}{1-{\epsilon }_2}$, and $Y_i\sim g_{Y_i}(·;{\mathsf{\Psi }}_i)$, $i=1,2$, with $Y_1$ independent of $Y_2$.

Proof of Theorem 1.

Making the changes of variables $z=\frac{x_1}{1+\epsilon }$ and $u=\frac{x_1}{1-\epsilon }$ we have

$$\begin{array}{cc}\hfill P(X_2<X_1)& ={\int }_0^{\infty }{F}_{X_2}\left(x_1\right)f_{X_1}\left(x_1\right)d{x}_1\hfill \\ \hfill & ={\int }_0^{\infty }\left[\left(\frac{1+{\epsilon }_2}{2}\right)G_{Y_2}\left(\frac{x_1}{1+{\epsilon }_2}\right)+\left(\frac{1-{\epsilon }_2}{2}\right)G_{Y_2}\left(\frac{x_1}{1-{\epsilon }_2}\right)\right]\hfill \\ \hfill & \times \left[\frac{1}{2}{g}_{Y_1}\left(\frac{x_1}{1+{\epsilon }_1}\right)+\frac{1}{2}{g}_{Y_1}\left(\frac{x_1}{1-{\epsilon }_1}\right)\right]d{x}_1\hfill \\ \hfill & =\frac{{(1+{\epsilon }_2)}^2}{4}a{\int }_o^{\infty }{G}_{Y_2}\left(az\right)g_{Y_1}\left(z\right)dz+\frac{{(1+{\epsilon }_2)}^2}{4}b{\int }_o^{\infty }{G}_{Y_2}\left(bu\right)g_{Y_1}\left(u\right)du\hfill \\ \hfill & \times \frac{{(1-{\epsilon }_2)}^2}{4}c{\int }_o^{\infty }{G}_{Y_2}\left(cz\right)g_{Y_1}\left(z\right)dz+\frac{{(1-{\epsilon }_2)}^2}{4}d{\int }_o^{\infty }{G}_{Y_2}\left(du\right)g_{Y_1}\left(u\right)du\hfill \\ \hfill & =\frac{{(1+{\epsilon }_2)}^2}{4}aP(Y_2<a{Y}_1)+\frac{{(1+{\epsilon }_2)}^2}{4}bP(Y_2<b{Y}_1)+\hfill \\ \hfill & \frac{{(1-{\epsilon }_2)}^2}{4}cP(Y_2<c{Y}_1)+\frac{{(1-{\epsilon }_2)}^2}{4}dP(Y_2<d{Y}_1).\hfill \end{array}$$

 □

Observe that the same concept can be used to make comparisons between two systems. For example, if $X_1$ and $X_2$ denote instead the lifetimes of systems $S_1$ and $S_2$ respectively, then, a probability $P(X_1<X_2)>0.5$ would indicate that the system $S_2$ is better than the system $S_1$ in a stochastic sense.

2.4. Maximum Likelihood Estimation

Let ${\tilde{X}}_n=(X_1,\cdots ,X_n)$ be a random sample from an $EP(\mathsf{\Psi },\epsilon )$ distribution. Then, the maximum likelihood estimator (MLE) of $\theta ={(\mathsf{\Psi },\epsilon )}^{\prime }$ is given by

$${\theta }_{MLE}={(\widehat{\mathsf{\Psi }},\widehat{\epsilon })}_{MLE}=arg\underset{\mathsf{\Psi },\epsilon }{max}\ell (\mathsf{\Psi },\epsilon ;{\tilde{X}}_n),$$

(11)

where $\ell (\mathsf{\Psi },\epsilon ;{\tilde{X}}_n)={\sum }_{i=1}^{n}log{f}_{X_i}(x_i;\mathsf{\Psi },\epsilon )$ is the log–likelihood.

Although the MLE for the $EP$ family is conceptually straightforward, typically closed form solutions are not available and the MLE need to be obtained numerically. One possibility is the Newton–Raphson algorithm, with iteration equation

$${\widehat{\theta }}^{(k+1)}={\widehat{\theta }}^{\left(k\right)}-{\left[H\left({\widehat{\theta }}^{\left(k\right)}\right)\right]}^{-1}u\left({\widehat{\theta }}^{\left(k\right)}\right),$$

(12)

where ${\theta }^{\left(k\right)}$ be the current estimate of $\theta$, $u\left(\theta \right)$ denote the vector of first derivatives of $\ell (\theta ;{\tilde{X}}_n)$, and $H\left(\theta \right)$.

A disadvantage of this approach is that it requires redthe calculation of the second derivatives of the likelihood function and repeated inversion of potentially large matrices, which can be computationally intensive. Instead, we can consider an expectation–maximization (EM) approach see [8] as a general iterative method for data sets with missing (or incomplete) data.

The mixture representation proposed in (4) is particularly useful in order to use an EM–type algorithm to estimate the model parameters, since it provides a hierarchical scheme for the $EP$ family. Next, we show how to implement maximum likelihood estimation using an EM–type algorithm for the $EP$ family.

2.5. MLE via the EM Algorithm

From (4), the log–likelihood takes the form,

$$\ell (\mathsf{\Psi },\epsilon ;{\tilde{X}}_n)=\sum _{i=1}^{n}log\left(\sum _{\xi \in \mathcal{J}\left(\epsilon \right)}{\pi }_{\xi }\left(\epsilon \right)\frac{1}{\xi }g\left(\frac{x_i}{\xi }\right)\right),$$

where the derivatives with respect to $\mathsf{\Psi }$ and $\epsilon$ typically lead to a system of equations with no closed form solution. To address this problem, we can “augment” the data ${\tilde{X}}_n$ using an unobservable matrix $W=\left(w_{ij}\right)$, $i=1,\cdots ,n;j=1,\dots ,m=\left|\mathcal{J}\right(\epsilon \left)\right|$, with elements $w_{ij}$ defined as

$$w_{ij}=\left\{\begin{array}{c}1, \mathrm{if} \mathrm{observation} x_i \mathrm{comes} \mathrm{from} \mathrm{the} \mathrm{distribution} \frac{1}{{\xi }_j}g\left(\frac{x}{{\xi }_j}\right)\hfill \\ 0, \mathrm{otherwise}\hfill \end{array}\right.,$$

where ${\xi }_1,\dots ,{\xi }_m$ denote the distinct elements of $\mathcal{J}\left(\epsilon \right)$. This way, each row of W contains only one 1 and zero 0, and the (complete) log-likelihood for the augmented data $Y=({\tilde{X}}_n,W)$ is given by

$${\ell }_c(\mathsf{\Psi },\epsilon ;Y)=\sum _{i=1}^n\sum _{j=1}^m{w}_{ij}\left(log\left(\frac{{\pi }_{{\xi }_j}\left(\epsilon \right)}{{\xi }_j}\right)+logg\left(\frac{x_i}{{\xi }_j}\right)\right).$$

Then, if we denote by ${\widehat{\theta }}^{\left(s\right)}=({\mathsf{\Psi }}^{\left(s\right)},{\epsilon }^{\left(s\right)})$ the estimate of $\theta =(\mathsf{\Psi },\epsilon )$ at iteration s, and by $\mathcal{Q}(\theta ,{\widehat{\theta }}^{\left(s\right)})$, the conditional expectation of ${\ell }_c(\theta ;Y)$ given ${\tilde{X}}_n$ and ${\widehat{\theta }}^{\left(s\right)}$, we obtain

$$\begin{array}{cc}\hfill \mathcal{Q}(\theta ,{\widehat{\theta }}^{\left(s\right)})& =E\left({\ell }_c(\theta ;Y)\right|{\tilde{X}}_n,{\widehat{\theta }}^{\left(s\right)})\hfill \\ \hfill & =\sum _{i=1}^n\sum _{j=1}^{m\left(s\right)}{w}_{ij}^{\left(s\right)}\left(log\left(\frac{{\pi }_{{\xi }_j}\left(\epsilon \right)}{{\xi }_j}\right)+logg\left(\frac{x_i}{{\xi }_j}\right)\right),\hfill \end{array}$$

where $m\left(s\right)=|\mathcal{J}\left({\epsilon }^{\left(s\right)}\right)|$, and

$${\displaystyle w_{ij}^{\left(s\right)}=\frac{\pi {\left({\epsilon }^{\left(s\right)}\right)}_j\frac{1}{{\xi }_j}g\left(\frac{x_i}{{\xi }_j}\right)}{{\sum }_{j=1}^{m\left(s\right)}{\pi }_{{\xi }_j}\left({\epsilon }^{\left(s\right)}\right)\frac{1}{{\xi }_j}g\left(\frac{x_i}{{\xi }_j}\right)}.}$$

From here, it follows that for $\mathcal{J}\left(\epsilon \right)=\{1-\epsilon ,1+\epsilon \}$, the iteration s of the EM algorithm takes the form:

• E–step: For $i=1,\cdots ,n$, compute

  $$w_{ij}^{\left(s\right)}=\frac{g\left(\frac{x_i}{1+{\epsilon }^{\left(s\right)}}\right)}{g\left(\frac{x_i}{1+{\epsilon }^{\left(s\right)}}\right)+g\left(\frac{x_i}{1-{\epsilon }^{\left(s\right)}}\right)},{\xi }_j=1+\epsilon .$$
• M–step: Given ${\epsilon }^{\left(s\right)}$ and ${\mathsf{\Psi }}^{\left(s\right)}$, compute

  $$\begin{array}{cc}\hfill {\epsilon }^{(s+1)}& =\frac{2}{n}\sum _{i=1}^n{w}_{ij}^{\left(s\right)}-1,j=1+\epsilon ,\hfill \\ \hfill {\mathsf{\Psi }}^{(s+1)}& =arg\underset{\mathsf{\Psi }}{max}\mathcal{Q}(\theta ,{\widehat{\theta }}^{\left(s\right)}).\hfill \end{array}$$

The E and M steps are alternated repeatedly until a convergence criteria is satisfied. For the variance estimation of the MLEs we consider the bootstrapping method suggested in [9].

3. The Epsilon–Exponential Distribution

If we take $g_Y(y;\mathsf{\Psi }=\sigma )=\frac{1}{\sigma }{e}^{-y/\sigma }{1}_{\{y>0\}}$, the pdf of an exponential distribution, the expression in (2) becomes

$$f_X(x;\sigma ,\epsilon )=\frac{1}{2\sigma }\left[e^{-x/(1+\epsilon )\sigma }+e^{-x/(1-\epsilon )\sigma }\right],x>0,$$

(13)

where $\sigma >0$ and $0<\epsilon <1$. We say that a random variable X has epsilon–exponential (EE) distribution with scale parameter $\sigma$ and shape parameter $\epsilon$ if its density has the form in (13), and we write $X\sim EE(\sigma ,\epsilon )$.

Recall that the rth moment, $r=1,2,\cdots ,$ of $Y\sim Exp\left(\sigma \right)$ is $E\left(Y^r\right)=r!{\sigma }^r$. From (3), when $X\sim EE(\sigma ,\epsilon )$, we obtain that the mean, variance, skewness (CS) and kurtosis (CK) coefficients are, respectively,

$$\begin{array}{cc}\hfill E\left(X\right)& =\left(1+{\epsilon }^2\right)\sigma \hfill \\ \hfill Var\left(X\right)& ={\sigma }^2\left(1+4{\epsilon }^2-{\epsilon }^4\right)\hfill \\ \hfill CS& =\frac{\left(2+18{\epsilon }^2-6{\epsilon }^4+2{\epsilon }^6\right)}{{\left(1+4{\epsilon }^2-{\epsilon }^4\right)}^{3/2}}\hfill \\ \hfill CK& =\frac{\left(9+120{\epsilon }^2+18{\epsilon }^4-3{\epsilon }^8\right)}{{\left(1+4{\epsilon }^2-{\epsilon }^4\right)}^2}.\hfill \end{array}$$

Please note that for any value of $\epsilon \in (0,1)$, $CS>0$ and $CK>0$. It can be seen that $2<CS<2.3$ and $9<CK<11.023$. Figure 3 depicts the behavior of the skewness (CS) and kurtosis (CK) coefficients as a function of $\epsilon$. In the figures we observe that the maximum skewness is attained ar $\epsilon =0.4$, while the maximum kurtosis coefficient is obtained when $\epsilon =0.37$.

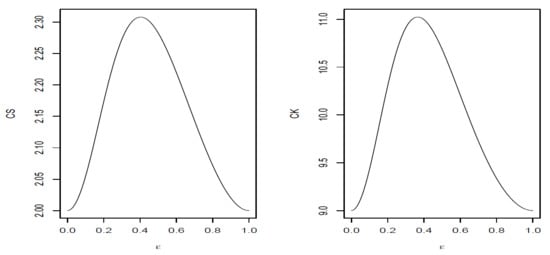
Figure 3. Skewness (CS) and kurtosis (CK) coefficientes for $X\sim EE(\sigma ,\epsilon )$.

Recall that the survival function of the exponential distribution is of the form $S_Y\left(y\right)=e^{-y/\sigma }{1}_{\{y>0\}}$ and the mean residual life is of the form $mr{l}_Y\left(t\right)=\sigma$. Then, it follows from (5), (6) and (9) that if $X\sim EE\left(\sigma ,\epsilon \right)$, then the survival and hazard functions and mean residual life are (respectively)

$$\begin{array}{cc}\hfill S(x;\sigma ,\epsilon )& =\frac{(1+\epsilon )}{2}{e}^{-x/(1+\epsilon )\sigma }+\frac{(1-\epsilon )}{2}{e}^{-x/(1-\epsilon )\sigma },\hfill \\ \hfill \lambda (x;\sigma ,\epsilon )& =\frac{1}{\sigma }\left[\frac{e^{-x/(1+\epsilon )\sigma }+e^{-x/(1-\epsilon )\sigma }}{(1+\epsilon )e^{-x/(1+\epsilon )\sigma }+(1-\epsilon )e^{-x/(1-\epsilon )\sigma }}\right] \mathrm{and}\hfill \\ \hfill mrl\left(t\right)& =\sigma \left[\frac{{(1+\epsilon )}^2{e}^{-t/(1+\epsilon )\sigma }+{(1-\epsilon )}^2{e}^{-t/(1-\epsilon )\sigma }}{(1+\epsilon )e^{-t/(1+\epsilon )\sigma }+(1-\epsilon )e^{-t/(1-\epsilon )\sigma }}\right].\hfill \end{array}$$

Interestingly, in contrast to the exponential distribution, it can be shown that the hazard function $\lambda (x;\sigma ,\epsilon )$ of the EE distribution is not constant, but decreasing in x. This feature can be easily observed in Figure 1 (top panel), where we show the pdf, survival and hazard functions of the EE distribution for different values of the parameter $\epsilon$ when $\sigma =1$. Please note that $\lambda (x;\sigma ,\epsilon )⟶{\lambda }_Y(x;\sigma )=1/\sigma$ as $\epsilon ⟶0$. Additionally, $mrl\left(t\right)⟶mr{l}_Y\left(t\right)=\sigma$ as $\epsilon ⟶0$.

Suppose $X_1$ and $X_2$ are random variables independently distributed as $X_1\sim EE({\sigma }_1,{\epsilon }_1)$ and $X_2\sim EE({\sigma }_2,{\epsilon }_2)$, using Theorem 1 the reliability of the system with stress variable ($X_2$) and strength variable ($X_1$) is given by

$$R=\frac{{(1+{\epsilon }_2)}^2}{4}\left(\frac{a^2{\sigma }_1}{a{\sigma }_1+{\sigma }_2}+\frac{b^2{\sigma }_1}{b{\sigma }_1+{\sigma }_2}\right)+\frac{{(1-{\epsilon }_2)}^2}{4}\left(\frac{c^2{\sigma }_1}{c{\sigma }_1+{\sigma }_2}+\frac{d^2{\sigma }_1}{d{\sigma }_1+{\sigma }_2}\right).$$

Please note that when $({\epsilon }_1,{\epsilon }_2)⟶(0,0)$, $R⟶\frac{{\sigma }_1}{{\sigma }_1+{\sigma }_2}$ which corresponds to the stress-strength reliability model of the exponential distributions with parameter ${\sigma }_1$ for $X_1$ (strength), and with parameter ${\sigma }_2$ for $X_2$ (stress), respectively.

Maximum likelihood estimations for the parameters $\sigma$ and $\epsilon$ of the epsilon-exponential distribution, can be obtained following the strategy described in Section 2.4 and Section 2.5 (see the Appendix B for details). Let $X_1,X_2,\dots ,X_n$ and $Y_1,Y_2,\dots ,Y_m$ be random samples from $EE({\sigma }_1,{\epsilon }_1)$ and $EE({\sigma }_2,{\epsilon }_2)$, respectively. Having estimates of $({\sigma }_1,{\epsilon }_1,{\sigma }_2,{\epsilon }_2)$, say $({\widehat{\sigma }}_1,{\widehat{\epsilon }}_1,{\widehat{\sigma }}_2,{\widehat{\epsilon }}_2)$, by the invariance property of the MLE, the MLE of R becomes

$$\widehat{R}=\frac{{(1+{\widehat{\epsilon }}_2)}^2}{4}\left(\frac{{\widehat{a}}^2{\widehat{\sigma }}_1}{\widehat{a}{\widehat{\sigma }}_1+{\widehat{\sigma }}_2}+\frac{{\widehat{b}}^2{\widehat{\sigma }}_1}{\widehat{b}{\widehat{\sigma }}_1+{\widehat{\sigma }}_2}\right)+\frac{{(1-{\widehat{\epsilon }}_2)}^2}{4}\left(\frac{{\widehat{c}}^2{\widehat{\sigma }}_1}{\widehat{c}{\widehat{\sigma }}_1+{\widehat{\sigma }}_2}+\frac{{\widehat{d}}^2{\widehat{\sigma }}_1}{\widehat{d}{\widehat{\sigma }}_1+{\widehat{\sigma }}_2}\right).$$

Numerical Experiments

To illustrate the properties of the estimators we performed a small simulation study considering 5000 simulated datasets for different pair of values of $\sigma$ and $\epsilon$ using Algorithm 1. The goal of the study is to observe the behavior of the MLEs for the model parameters using our proposed EM algorithm considering different sample sizes.

Table 2 summarizes the simulation results. In the table, the columns labeled as “estimate” show the average of the estimators obtained in the simulations, and the columns labeled “SD” show the sample standard deviation of the corresponding estimators. To obtain the standard errors we used the bootstrap method with $B=150$ samples. We observe that the estimates are quite stable and fairly accurate, reporting (on average) numbers close to the true values of the parameters in all cases. Please note that as expected, the precision of the estimates improves as the sample size increase.

Table 2. Summary of simulation results.

True Value		n	$\mathit{\sigma }$		$\mathit{\epsilon }$
$\mathit{\sigma }$	$\mathit{\epsilon }$		Estimate	SD	Estimate	SD
		n = 50	0.286	0.047	0.376	0.126
		n = 100	0.292	0.037	0.350	0.127
	0.3	n = 200	0.292	0.030	0.335	0.118
		n = 500	0.295	0.022	0.317	0.106
		n = 1000	0.299	0.017	0.302	0.089
		n = 50	0.287	0.054	0.558	0.133
		n = 100	0.290	0.043	0.542	0.129
0.3	0.5	n = 200	0.294	0.037	0.527	0.123
		n = 500	0.297	0.030	0.512	0.111
		n = 1000	0.298	0.023	0.506	0.091
		n = 50	0.299	0.059	0.818	0.126
		n = 100	0.299	0.047	0.809	0.122
	0.8	n = 200	0.301	0.038	0.801	0.108
		n = 500	0.303	0.029	0.794	0.088
		n = 1000	0.302	0.022	0.794	0.069
		n = 50	0.476	0.079	0.379	0.125
		n = 100	0.484	0.062	0.355	0.125
	0.3	n = 200	0.486	0.049	0.337	0.121
		n = 500	0.494	0.037	0.316	0.107
		n = 1000	0.497	0.029	0.303	0.088
		n = 50	0.477	0.088	0.558	0.133
		n = 100	0.484	0.074	0.542	0.131
0.5	0.5	n = 200	0.488	0.059	0.528	0.124
		n = 500	0.494	0.048	0.512	0.109
		n = 1000	0.498	0.039	0.502	0.091
		n = 50	0.484	0.104	0.838	0.129
		n = 100	0.499	0.076	0.809	0.119
	0.8	n = 200	0.503	0.064	0.799	0.110
		n = 500	0.505	0.049	0.793	0.089
		n = 1000	0.504	0.038	0.793	0.070
		n = 50	0.762	0.125	0.374	0.124
		n = 100	0.771	0.099	0.356	0.125
	0.3	n = 200	0.779	0.080	0.336	0.120
		n = 500	0.789	0.058	0.314	0.105
		n = 1000	0.796	0.046	0.301	0.089
		n = 50	0.765	0.139	0.555	0.134
		n = 100	0.771	0.116	0.543	0.134
0.8	0.5	n = 200	0.782	0.096	0.528	0.123
		n = 500	0.789	0.076	0.515	0.110
		n = 1000	0.797	0.062	0.503	0.091
		n = 50	0.791	0.153	0.815	0.130
		n = 100	0.800	0.126	0.804	0.122
	0.8	n = 200	0.798	0.103	0.798	0.106
		n = 500	0.806	0.079	0.794	0.089
		n = 1000	0.807	0.060	0.793	0.070

4. Survival and Reliability Analysis

Let $T\ge 0$ represent the survival time until the occurrence of a “death” event. In this context, suppose we have n subjects with lifetimes determined by a survival function $S\left(t\right)$, and that the ith subject is observed for a time $t_i$. If the individual dies at time $t_i$, its contribution to the likelihood function is given by ${\mathcal{L}}_i=f\left(t_i\right)$, where $f\left(t\right)=-S^{\prime }\left(t\right)$ is the event density associated with $S\left(t\right)$, or equivalently, ${\mathcal{L}}_i=S\left(t_i\right)\lambda \left(t_i\right)$, where $\lambda \left(t\right)$ is the corresponding hazard function. On the other hand, if the ith individual is still alive at time $t_i$ and therefore, under non–informative censoring, all we can say is that their lifetime exceeds $t_i$. It follows that the contribution of a censored observation to the likelihood is simply given by ${\mathcal{L}}_i=S\left(t_i\right)$. Notice that in either case we evaluate the survival function at time $t_i$, because in both cases the ith subject was alive until (at least) time $t_i$. A death will multiply this contribution by the hazard $\lambda \left(t_i\right)$, but a censored observation will not.

We can combine these contributions into a single expression using a death indicator $d_i$, taking the value one if individual i died and the value zero otherwise. The resulting likelihood function $\mathcal{L}$ is of the form

$$\mathcal{L}=\prod _{i=1}^n\lambda {\left(t_i\right)}^{d_i}S\left(t_i\right)=\prod _{i=1}^{n}f{\left(t\right)}^{d_i}S{\left(t\right)}^{1-d_i}.$$

In the next section we will assume that the random variable T follows an epsilon–positive family, and show how estimate the model parameters using the EM algorithm.

4.1. Estimation Using the EM Algorithm

Let $T_1,\cdots ,T_n$ denote the survival times, $T_i\sim EP(\mathsf{\Psi },\epsilon )$. Using the notation introduced in the previous section, the observed data are a collection of pairs ${\tilde{X}}_n=\{(T_1,d_1),\cdots ,(T_n,d_n)\}$, where the $d_i$, $i=1,\cdots ,n$, are the censoring indicators.

In order implement the EM algorithm, we augment the observed data ${\tilde{X}}_n$ with the unobservable matrix W defined in Section 2.5, and obtain the (complete) likelihood is given by

$$\begin{array}{cc}\hfill {\mathcal{L}}_c(\theta ;{\tilde{X}}_n,W)& =\prod _{i=1}^n\prod _{j=1}^m{\left\{{\pi }_{{\xi }_j}\left(\epsilon \right){\left[\frac{1}{{\xi }_j}g\left(\frac{t_i}{{\xi }_j}\right)\right]}^{d_i}{\left[S\left(\frac{t_i}{{\xi }_j}\right)\right]}^{1-d_i}\right\}}^{w_{ij}}\hfill \end{array}$$

with corresponding (complete) log–likelihood ${\ell }_c=log{\mathcal{L}}_c$.

Then, if ${\widehat{\theta }}^{\left(s\right)}={({\mathsf{\Psi }}^{\left(s\right)},{\epsilon }^{\left(s\right)})}^{\prime }$ be the estimate of $\theta ={(\mathsf{\Psi },\epsilon )}^{\prime }$ at iteration s, and we denote by $\mathcal{Q}(\theta ,{\widehat{\theta }}^{\left(s\right)})$ the conditional expectation of ${\ell }_c(\theta ;{\tilde{X}}_n,W)$ given the observed data ${\tilde{X}}_n$ and ${\widehat{\theta }}^{\left(s\right)}$, we obtain

$$\begin{array}{cc}\hfill \mathcal{Q}(\theta ,{\widehat{\theta }}^{\left(s\right)})& =E\left({\ell }_c(\theta ;{\tilde{X}}_n,W)\right|{\tilde{X}}_n,{\widehat{\theta }}^{\left(s\right)})\hfill \\ \hfill & =\sum _{i=1}^n\sum _{j=1}^{m\left(s\right)}{w}_{ij}^{\left(s\right)}\left\{log{\pi }_{{\xi }_j}\left(\epsilon \right)+d_{i}log\left[\frac{1}{{\xi }_j}g\left(\frac{t_i}{{\xi }_j}\right)\right]+(1-d_i)logS\left(\frac{t_i}{{\xi }_j}\right)\right\},\hfill \end{array}$$

where

$$w_{ij}^{\left(s\right)}=\frac{{\pi }_{{\xi }_j}\left(\epsilon \right){\left[\frac{1}{{\xi }_j}g\left(\frac{t_i}{{\xi }_j}\right)\right]}^{d_i}{\left[S\left(\frac{t_i}{{\xi }_j}\right)\right]}^{1-d_i}}{{\sum }_{j=1}^{m\left(s\right)}{\pi }_{{\xi }_j}\left(\epsilon \right){\left[\frac{1}{{\xi }_j}g\left(\frac{t_i}{{\xi }_j}\right)\right]}^{d_i}{\left[S\left(\frac{t_i}{{\xi }_j}\right)\right]}^{1-d_i}}.$$

Then, for $\mathcal{J}\left(\epsilon \right)=\{1-\epsilon ,1+\epsilon \}$, the iteration s of the algorithm takes the form:

• E–step: For $i=1,\cdots ,n$, compute

  $$w_{ij}^{\left(s\right)}=\frac{w_{i,+}}{w_{i,+}+w_{i,-}},for{\xi }_j=1+\epsilon ,$$

  where

  $$w_{i,+}={\left[g\left(\frac{t_i}{1+{\epsilon }^{\left(s\right)}}\right)\right]}^{d_i}{\left[(1+{\epsilon }^{\left(s\right)})S\left(\frac{t_i}{1+{\epsilon }^{\left(s\right)}}\right)\right]}^{1-d_i}$$

  and

  $$w_{i,-}={\left[g\left(\frac{t_i}{1-{\epsilon }^{\left(s\right)}}\right)\right]}^{d_i}{\left[(1-{\epsilon }^{\left(s\right)})S\left(\frac{t_i}{1-{\epsilon }^{\left(s\right)}}\right)\right]}^{1-d_i}.$$
• M–step: Given ${\epsilon }^{\left(s\right)}$ and ${\mathsf{\Psi }}^{\left(s\right)}$, compute

  $$\begin{array}{cc}\hfill {\epsilon }^{(s+1)}& =\frac{2}{n}\sum _{i=1}^n{w}_{ij}^{\left(s\right)}-1,{\xi }_j=1+\epsilon ,\hfill \\ \hfill {\mathsf{\Psi }}^{(s+1)}& =arg\underset{\mathsf{\Psi }}{max}\mathcal{Q}(\theta ,{\widehat{\theta }}^{\left(s\right)}).\hfill \end{array}$$

EM Algorithm for the Epsilon-Exponential Distribution

Suppose that the survival times $T_i\sim EE(\sigma ,\epsilon )$. Then the EM algorithm takes the form:

• E–step: For $i=1,\cdots ,n$, compute

  $$w_{ij}^{\left(s\right)}=\frac{w_{i,+}}{w_{i,+}+w_{i,-}},\mathrm{for}{\xi }_j=1+\epsilon ,$$

  where

  $$w_{i,+}={\left[\frac{1}{\sigma }{e}^{-t_i/(1+{\epsilon }^{\left(s\right)}){\sigma }^{\left(s\right)}}\right]}^{d_i}{\left[(1+{\epsilon }^{\left(s\right)})e^{-t_i/(1+{\epsilon }^{\left(s\right)}){\sigma }^{\left(s\right)}}\right]}^{1-d_i}$$

  and

  $$w_{i,-}={\left[\frac{1}{\sigma }{e}^{-t_i/(1-{\epsilon }^{\left(s\right)}){\sigma }^{\left(s\right)}}\right]}^{d_i}{\left[(1-{\epsilon }^{\left(s\right)})e^{-t_i/(1-{\epsilon }^{\left(s\right)}){\sigma }^{\left(s\right)}}\right]}^{1-d_i}.$$
• M–step: Given ${\epsilon }^{\left(s\right)}$ and ${\sigma }^{\left(s\right)}$, compute

  $$\begin{array}{cc}\hfill {\epsilon }^{(s+1)}& =\frac{2}{n}\sum _{i=1}^n{w}_{ij}^{\left(s\right)}-1,{\xi }_j=1+\epsilon ,\hfill \\ \hfill {\sigma }^{(s+1)}& =\sum _{i=1}^n\sum _{j\in \mathcal{J}\left({\epsilon }^{\left(s\right)}\right)}{w}_{ij}^{\left(s\right)}\left(\frac{t_i}{j}\right)/\sum _{i=1}^n\sum _{j\in \mathcal{J}\left({\epsilon }^{\left(s\right)}\right)}{w}_{ij}^{\left(s\right)}{d}_i.\hfill \end{array}$$

5. Real Data Examples

In this section, we use two examples to illustrate the proposed distributions using (un)censored data sets.

5.1. Example 1: Maintenance Data

First, we consider a real data set originally analyzed by [10]. The complete data set correspond active repair times (in hours) for an airborne communication transceiver, and can be found in Table 3.

Table 3. Repair times (in hours) of 46 transceivers.

0.2	0.3	0.5	0.5	0.5	0.5	0.6	0.6	0.7	0.7
0.7	0.8	0.8	1.0	1.0	1.0	1.0	1.1	1.3	1.5
1.5	1.5	1.5	2.0	2.0	2.2	2.5	2.7	3.0	3.0
3.3	3.3	4.0	4.0	4.5	4.7	5.0	5.4	5.4	7.0
7.5	8.8	9.0	10.3	22.0	24.5

Using the EM algorithm described in Section 4 we fit an epsilon–exponential (EE) distribution to the active repair times. We obtain that the maximized log–likelihood value $-103.806$. Alternatively, we also fit an exponential (Exp), exponentiated–exponential (EExp) and Weibull (Wei) distribution, obtaining the maximized log–likelihood values of $-105.006$, $-104.983$ and $-104.470$, respectively. For model comparison, we use the Akaike information criterion (AIC) introduced in [11], given by $AIC=-2\widehat{l}+2k$ where $\widehat{l}$ is the maximized log–likelihood and k is the number of parameters of the distribution under consideration.

The best model is deemed to be the one with the smallest AIC. For the data set in the example, we obtain $AI{C}_{EE}=211.611$, $AI{C}_{Exp}=212.012$, $AI{C}_{EExp}=213.966$, and $AI{C}_{Wei}=212.939$. It follows that in terms of the AIC criteria, the epsilon–exponential shows the best performance when fitting these data. Figure 4 shows the fit of the different models used in the example. Figure 5 displays the three estimated survival functions for this data set.

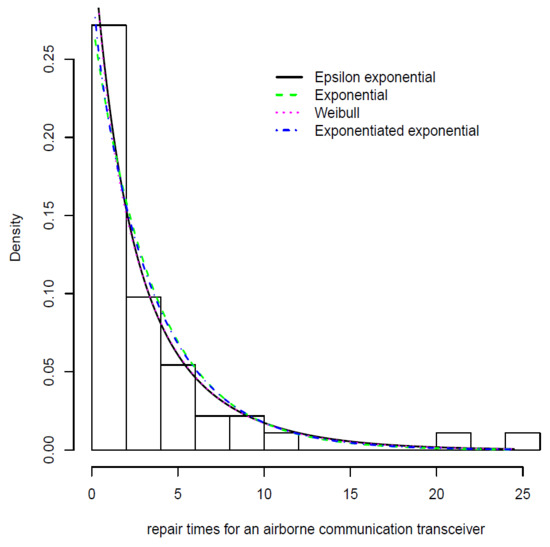
Figure 4. The density functions of the fitted epsilon exponential, exponential, Weibull and exponentiated exponential distributions.

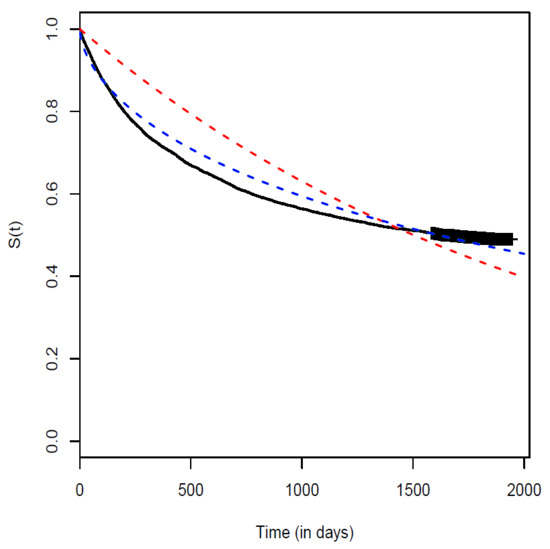
Figure 5. Fit of the survival functions: Kaplan–Meier estimator (solid line), exponential (dashed line red) and epsilon–exponential (dashed line blue) distributions.

5.2. Example 2: Recidivism Data

For the second example we use real data obtained from the official records of Gendarmerie of Chile on all inmates released from the Chilean prisons during 2007 after serving a sentence of imprisonment by robbery.

The data set contains records of 9477 inmates and the follow–up period from release until 30 April 2012. In this study, recidivism is defined to occur when a released prisoner goes back to prison for the original or any other offense.

Overall, 52.2% of the inmates in the cohort were convicted of one or more offenses and returned to prison within 64 months of release. About 11.8% of the cohort returned to prison within three months of release, and 30% returned within a year of release.

Table 4 shows the observed proportion of the cohort returning to prison within 1, 3, 6, 12, 18, 24, 36, 48 and 64 months of release. We observe that the cumulative proportion of recidivism grew quickly over the first 12 months after release, increasing by more than 7% every 3 months. After that, the percent increases were smaller and over longer periods.

Table 4. Observed recidivism by time after release.

Time after Release	% Observed Recidivists
1 month	4.7%
3 month	11.8%
6 month	19.9%
12 month	30.0%
18 month	35.9%
24 month	40.8%
36 month	46.6%
48 month	50.4%
64 month	52.2%

To analyze the time to recidivism, we determined the number of days between an inmate’s release and his return to prison. Because some inmates did not reoffend, we have censored data and we used the EM algorithm described in Section 4 to fit an epsilon–exponential distribution to the time to recidivism. The maximized log–likelihood value for an assumed epsilon–exponential distribution is easily calculated to be −42,067.84. In comparison, we also fit an exponential distribution yielding a maximized log–likelihood value of −42,632.81.

Looking at the AIC values, we obtain $AI{C}_{EE}$ = 84,139.68 and $AI{C}_{Exp}$ = 85,267.62 for the epsilon–exponential and exponential model respectively, and therefore we conclude, the epsilon–exponential is a better model for these data, based on this criteria.

Finally, we also analyzed the survival time using the Kaplan–Meier estimator. Figure 5 displays the three estimated survival functions for this data set. We observe a close agreement between the Kaplan–Meier survival curve and the epsilon–exponential distribution.

6. Discussion

We introduced a new class of distributions with positive support called epsilon–positive which are generated from any distributions with positive support. This new class of distributions includes the exponential, Weibull, log–normal, etc. ones as special cases. We discussed a stochastic representation for this family, as well as parameter estimation, using the maximum likelihood approach via the Newton–Raphson. In addition, we showed that the elements of this new family can be expressed as a finite scale mixture of positive distributions, which facilitates the implementation of EM-type of algorithms.

We then focused on particular member of this family, called epsilon–exponential distribution, and discuss its applicability in the analysis of survival and reliability data. In this context, we considered the censored data case, and we show how we can use this new family to analyze this type of data sets. For the new class of distributions and, in particular, for the epsilon–exponential distribution we estimate the model parameters using the EM algorithm. An interesting feature of the hazard function of the epsilon–exponential distribution is that is not constant at difference of the exponential one. This feature increases the flexibility of the models allowing its use in a broader range of scenarios.

This greater flexibility is corroborated in the two examples considered in this paper where the AIC criteria shows a better performance our proposed epsilon–exponential model when compared to commonly used alternatives such as the exponential one. The results suggests that the epsilon–exponential distribution should be considered to be a legitimate alternative for the analysis of survival and reliability data in both the censored and uncensored case.