Enhancing Ant-Based Algorithms for Medical Image Edge Detection by Admissible Perturbations of Demicontractive Mappings
Abstract
1. Introduction
2. Enriching Nonlinear Mappings by Admissible Perturbations
3. Admissible Perturbations of Demicontractive Mappings as Test Functions
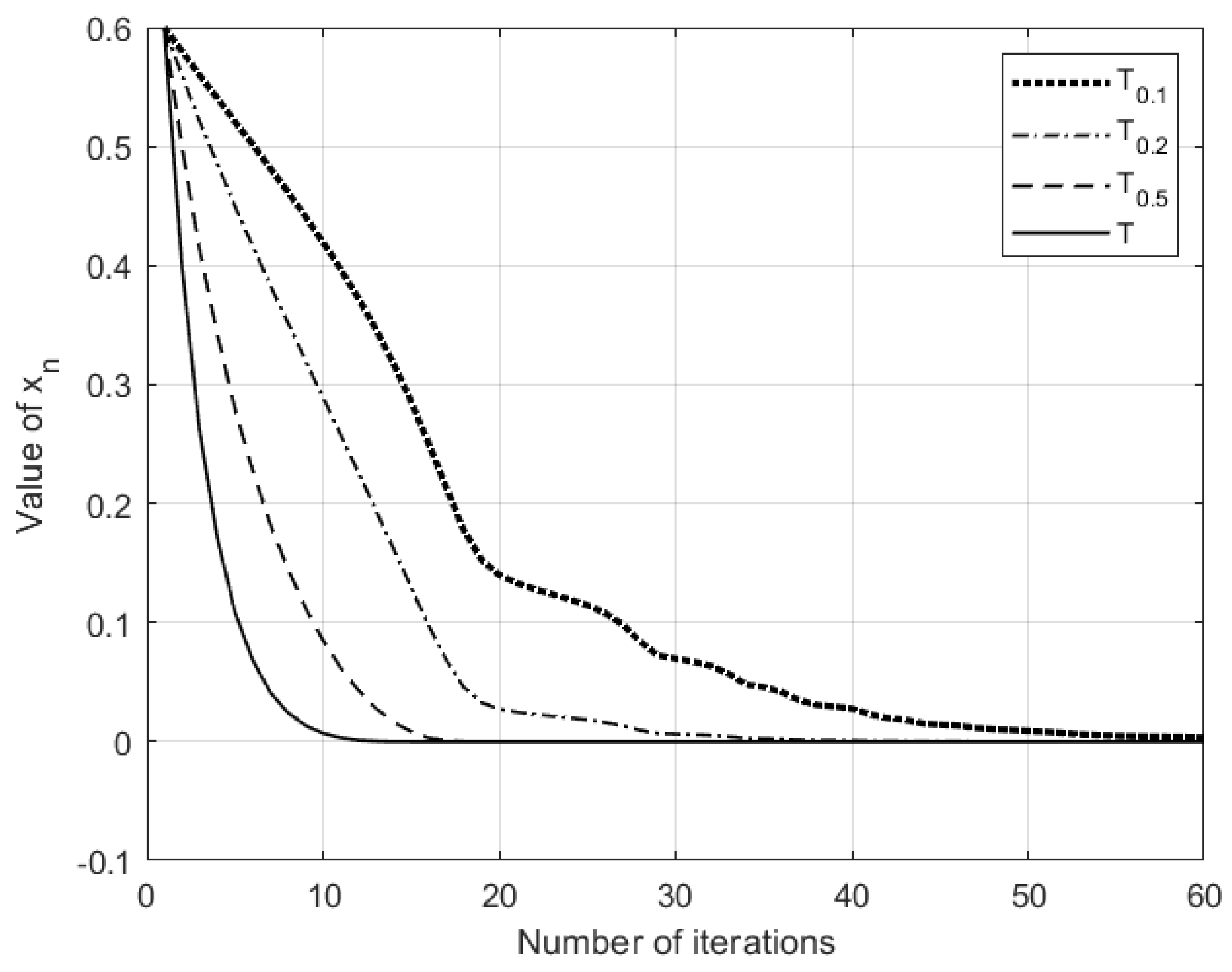
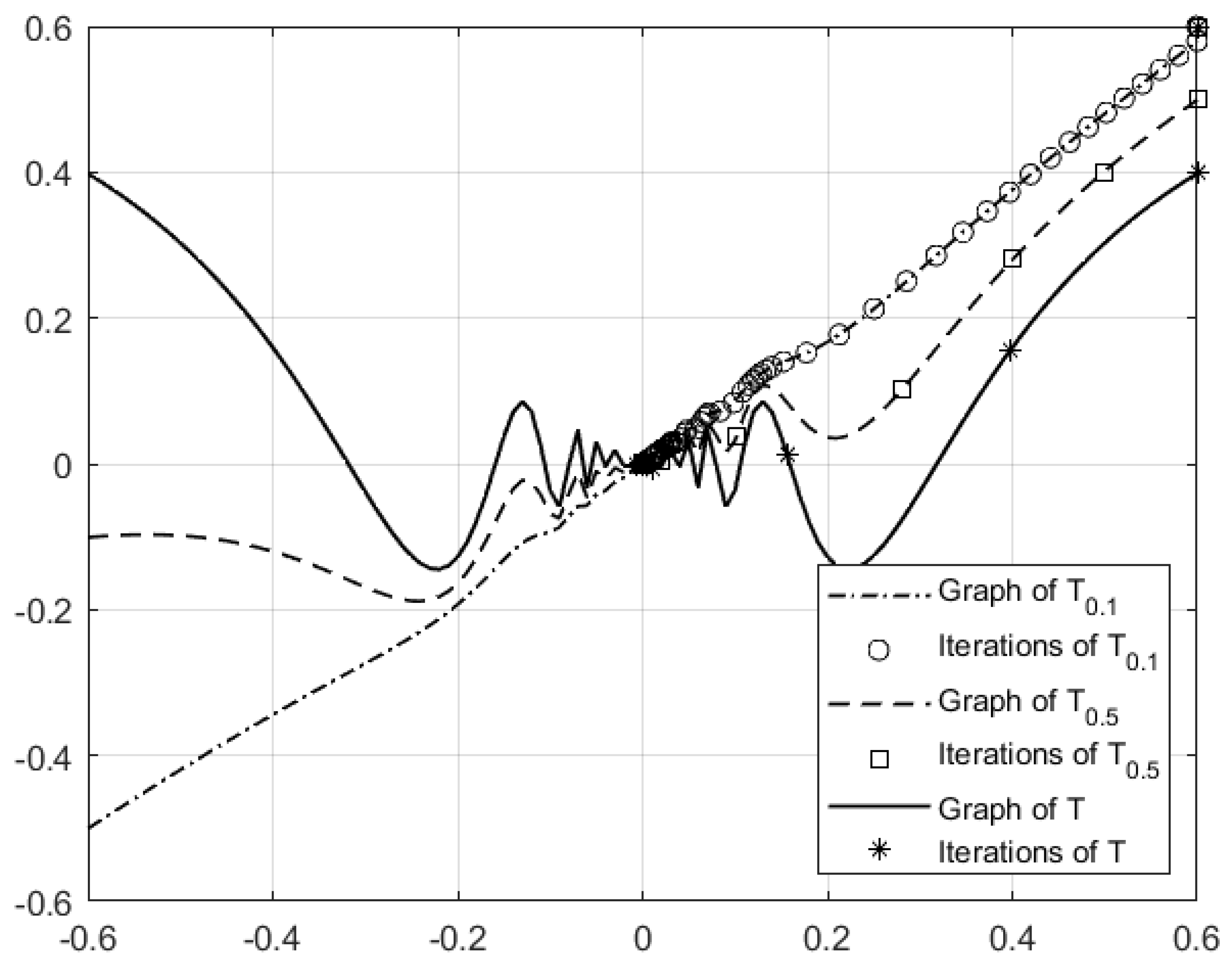
- , where T is defined in Example 1;
- , where;
- , where is a parameter which adjusts the shape of the operator, see Example 2 for the case ;
- , where adjusts the shape of the operator.
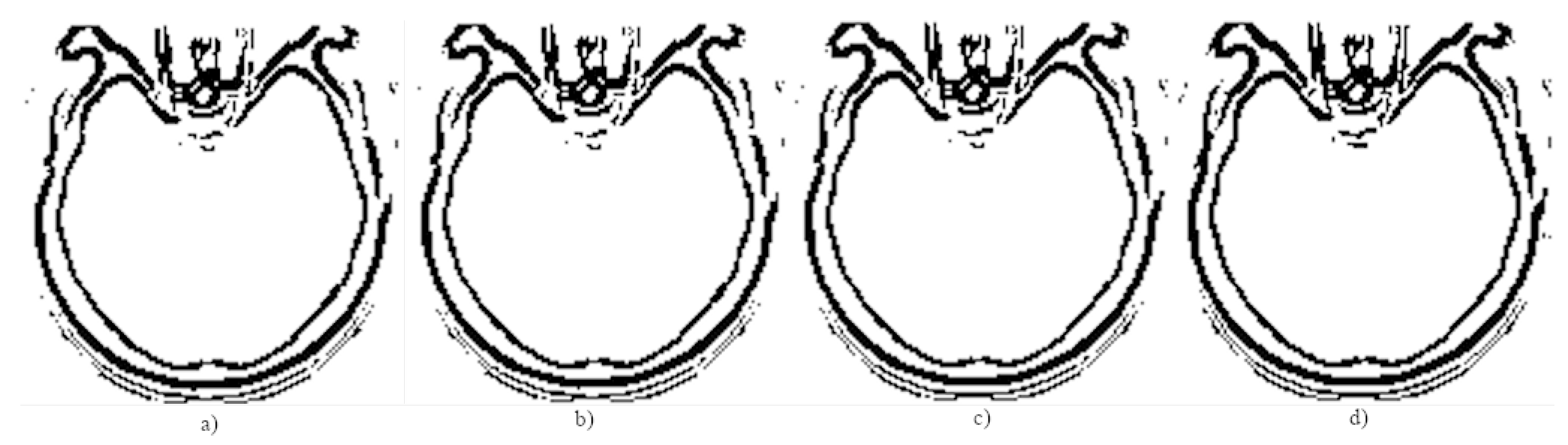
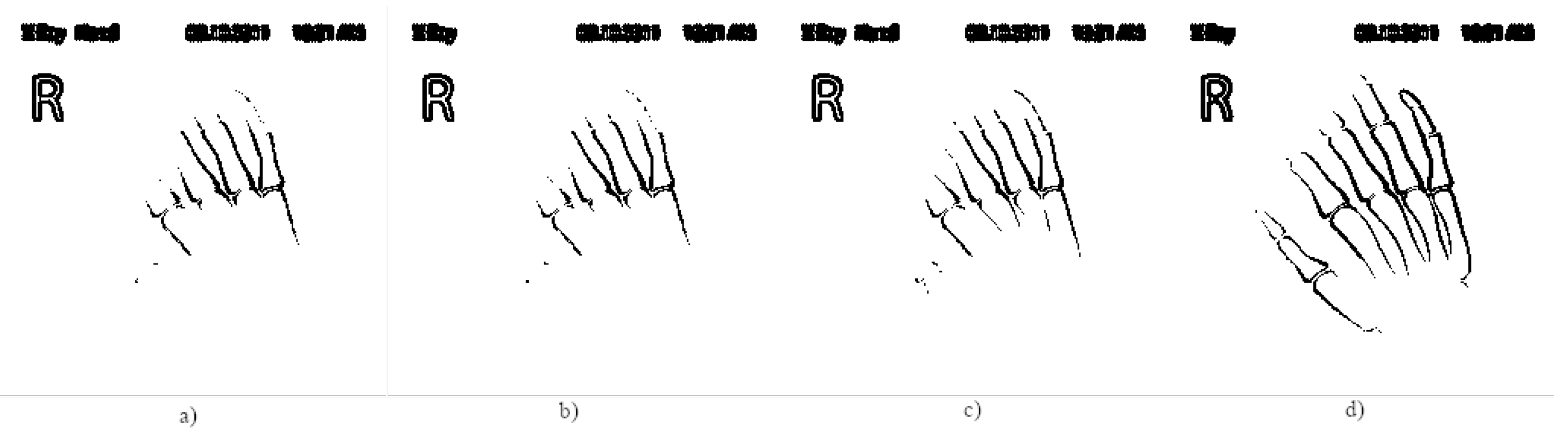
- applying filters to reduce the noise in the source image;
- segmenting the image before edge extraction, extracting the edge and reunite the obtained edges for more details;
- finding a method to eliminate the possible noise in the edge.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Byrne, C.L. Applied Iterative Methods; A K Peters, Ltd.: Wellesley, MA, USA, 2008. [Google Scholar]
- Ţicală, C.; Zelina, I.; Pintea, C.-M. Admissible perturbation of demicontractive operators within ant algorithms for medical images edge detection. Mathematics 2020, 8, 1040. [Google Scholar] [CrossRef]
- Măruşter, Ş. Sur le calcul des zéros d’un opérateur discontinu par itération. Can. Math. Bull. 1973, 16, 541–544. [Google Scholar] [CrossRef]
- Hicks, T.L.; Kubicek, J.D. On the Mann iteration process in a Hilbert space. J. Math. Anal. Appl. 1977, 59, 498–504. [Google Scholar] [CrossRef]
- Maingé, P.-E. A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J. Control Optim. 2008, 47, 1499–1515. [Google Scholar] [CrossRef]
- Măruşter, Ş. The solution by iteration of nonlinear equations in Hilbert spaces. Proc. Am. Math. Soc. 1977, 63, 69–73. [Google Scholar] [CrossRef]
- Qin, L.-J.; Wang, G. Multiple-set split feasibility problems for a finite family of demicontractive mappings in Hilbert spaces. Math. Inequal. Appl. 2013, 16, 1151–1157. [Google Scholar] [CrossRef]
- Suantai, S.; Phuengrattana, W. A hybrid shrinking projection method for common fixed points of a finite family of demicontractive mappings with variational inequality problems. Banach J. Math. Anal. 2017, 11, 661–675. [Google Scholar] [CrossRef]
- Thong, D.V.; Hieu, D.V. Modified subgradient extragradient algorithms for variational inequality problems and fixed point problems. Optimization 2018, 67, 83–102. [Google Scholar] [CrossRef]
- Vuong, P.T.; Strodiot, J.J.; Nguyen, V.H. On extragradient-viscosity methods for solving equilibrium and fixed point problems in a Hilbert space. Optimization 2015, 64, 429–451. [Google Scholar] [CrossRef]
- Browder, F.E.; Petryshyn, W.V. The solution by iteration of nonlinear functional equations in Banach spaces. Bull. Am. Math. Soc. 1966, 72, 571–575. [Google Scholar] [CrossRef]
- Krasnosel’skiǐ, M.A. Two remarks about the method of successive approximations. Uspehi Mat. Nauk 1955, 10, 123–127. [Google Scholar]
- Rus, I.A. An abstract point of view on iterative approximation of fixed points: Impact on the theory of fixed point equations. Fixed Point Theory 2012, 13, 179–192. [Google Scholar]
- Berinde, V. Convergence theorems for fixed point iterative methods defined as admissible perturbations of a nonlinear operator. Carpathian J. Math. 2013, 29, 9–18. [Google Scholar] [CrossRef]
- Berinde, V.; Khan, A.R.; Păcurar, M. Convergence theorems for admissible perturbations of ϕ-pseudocontractive operators. Miskolc Math. Notes 2014, 15, 27–37. [Google Scholar] [CrossRef]
- Berinde, V.; Măruşter, Ş.; Rus, I.A. An abstract point of view on iterative approximation of fixed points of nonself operators. J. Nonlinear Convex Anal. 2014, 15, 851–865. [Google Scholar]
- Toscano, E.; Vetro, C. Admissible perturbations of α-ψ-pseudocontractive operators: Convergence theorems. Math. Methods Appl. Sci. 2017, 40, 1438–1447. [Google Scholar] [CrossRef]
- Toscano, E.; Vetro, C. Fixed point iterative schemes for variational inequality problems. J. Convex Anal. 2018, 25, 701–715. [Google Scholar]
- Ţicală, C. Approximating fixed points of demicontractive mappings by iterative methods defined as admissible perturbations. Creat. Math. Inform. 2016, 25, 121–126. [Google Scholar]
- Ţicală, C. Approximating fixed points of asymptotically demicontractive mappings by iterative schemes defined as admissible perturbations. Carpathian J. Math. 2017, 33, 381–388. [Google Scholar] [CrossRef]
- Petruşel, A.; Rus, I.A. An abstract point of view on iterative approximation schemes of fixed points for multivalued operators. J. Nonlinear Sci. Appl. 2013, 6, 97–107. [Google Scholar] [CrossRef]
- Ţicală, C.; Zelina, I. New ant colony optimization algorithm in medical images edge detection. Creat. Math. Inform. 2020, 29, 101–108. [Google Scholar] [CrossRef]
- Head CT. Online Medical Free Image. Available online: http://www.libpng.org/pub/png/pngvrml/ct2.9-128x128.png (accessed on 1 May 2020).
- X-ray Hand. Vista Medical Pack. License: Free for Non Commercial Use. id, 236487. Available online: https://www.iconspedia.com/ (accessed on 1 May 2020).
- Tian, J.; Yu, W.; Xie, S. An ant colony optimization algorithm for image edge detection. In Proceedings of the IEEE Congress on Evolutionary Computation (IEEEWorld Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 751–756. [Google Scholar]
- Berinde, V. Weak and strong convergence theorems for the Krasnoselskij iterative algorithm in the class of enriched strictly pseudocontractive operators. An. Univ. Vest Timiş. Ser. Mat.-Inform. 2018, 56, 13–27. [Google Scholar] [CrossRef]
- Berinde, V. Approximating fixed points of enriched nonexpansive mappings by Krasnoselskij iteration in Hilbert spaces. Carpathian J. Math. 2019, 35, 293–304. [Google Scholar] [CrossRef]
- Berinde, V. Approximating fixed points of enriched nonexpansive mappings in Banach spaces by using a retraction-displacement condition. Carpathian J. Math. 2020, 36, 27–34. [Google Scholar] [CrossRef]
- Berinde, V.; Păcurar, M. Approximating fixed points of enriched contractions in Banach spaces. J. Fixed Point Theory Appl. 2020, 22, 1–10. [Google Scholar] [CrossRef]
- Berinde, V.; Păcurar, M. Kannan’s fixed point approximation for solving split feasibility and variational inequality problems. J. Comput. Appl. Math. 2021, 386, 113217. [Google Scholar] [CrossRef]
- Berinde, V.; Păcurar, M. Fixed point theorems for Chatterjea type mappings in Banach spaces. J. Fixed Point Theory Appl. 2021. under review. [Google Scholar]
- Berinde, V.; Păcurar, M. Krasnoselskij-type algorithms for variational inequality problems and fixed point problems in Banach spaces. arXiv 2021, arXiv:2103.10289. [Google Scholar]
- Berinde, V.; Păcurar, M. Existence and Approximation of Fixed Points of Enriched Contractions and Enriched φ-Contractions. Symmetry 2021, 13, 498. [Google Scholar] [CrossRef]
- Berinde, V.; Păcurar, M. Fixed Points Theorems for Unsaturated and Saturated Classes of Contractive Mappings in Banach Spaces. Symmetry 2021, 13, 713. [Google Scholar] [CrossRef]


| n | T | ||||
|---|---|---|---|---|---|
| 1 | |||||
| 10 | |||||
| 20 | |||||
| 30 | |||||
| 40 | |||||
| 50 | |||||
| 60 |
| Number of Pixels on the Edge | Head CT | Brain CT | Hand X-ray |
|---|---|---|---|
| D | 2233 | 2745 | 3060 |
| 1902 | 2737 | 2728 | |
| 2262 | 2780 | 3172 | |
| 2879 | 2886 | 3987 | |
| 3170 | 2940 | 4408 | |
| N | 1969 | 1593 | 1800 |
| Operator/Image | Head CT | Brain CT | Hand X-ray |
|---|---|---|---|
| 2854 | 1054 | 3437 | |
| 2710 | 966 | 4388 | |
| 2090 | 885 | ||
| 1127 | 671 | 982 | |
| 1117 | 413 | 4301 | |
| 1164 | 2987 | 4481 | |
| 534 | 471 | 4826 | |
| 1271 | 610 | 6803 | |
| 2799 | 921 | 3048 | |
| 1022 | 4872 | ||
| 3412 | 5274 | ||
| 1113 | 529 | 5533 | |
| 2641 | 805 | 4335 | |
| 3399 | 936 | 3429 | |
| 3250 | 3473 | 4936 | |
| 1951 | 715 | 6841 | |
| 2714 | 823 | 5438 | |
| 2538 | 3367 | 5299 | |
| 1261 | 615 | 4248 | |
| 1022 | 3086 | 4394 | |
| 898 | 2979 | 2324 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berinde, V.; Ţicală, C. Enhancing Ant-Based Algorithms for Medical Image Edge Detection by Admissible Perturbations of Demicontractive Mappings. Symmetry 2021, 13, 885. https://doi.org/10.3390/sym13050885
Berinde V, Ţicală C. Enhancing Ant-Based Algorithms for Medical Image Edge Detection by Admissible Perturbations of Demicontractive Mappings. Symmetry. 2021; 13(5):885. https://doi.org/10.3390/sym13050885
Chicago/Turabian StyleBerinde, Vasile, and Cristina Ţicală. 2021. "Enhancing Ant-Based Algorithms for Medical Image Edge Detection by Admissible Perturbations of Demicontractive Mappings" Symmetry 13, no. 5: 885. https://doi.org/10.3390/sym13050885
APA StyleBerinde, V., & Ţicală, C. (2021). Enhancing Ant-Based Algorithms for Medical Image Edge Detection by Admissible Perturbations of Demicontractive Mappings. Symmetry, 13(5), 885. https://doi.org/10.3390/sym13050885







