Abstract
The present research article is related to the analytical investigation of some fractional-order equal-width equations. The homotopy perturbation technique along with Elzaki transformation is implemented to discuss the fractional view analysis of equal-width equations. For better understanding of the proposed procedure some examples related to equal-width equations are presented. The identical behavior of the derived and actual solutions is observed. The proposed technique can be modified to study the fractional view analysis of other problems in various areas of applied sciences.
1. Introduction
In the past decade, fractional evaluation equations have been studied by many researchers due to their wide applicability in different areas of modern science and technology. It has been seen that fractional-order equations describe many physical systems and with their usage, various issues are solved. Along these lines, it is the overall goal to build up more fruitful outcomes for fractional calculus [1,2,3,4,5]. Simpson and Ford considered the Caputo fractional derivative [6] the most appropriate method for detecting fractional models, since it reliably includes the initial requirements that are not present in various individual models [7]. Oldham and Spanier found that fractional derivatives and integrals can be used to show far more valuable synthetic problems than conventional methods [8]. Moreover, later commitments on fractional theory and application, like fractal mathematics, are available in the literature. Interested readers are referred to [9,10,11,12,13,14,15,16,17,18,19].
For the last several years, partial evaluation equations have been concentrated upon by numerous researchers because of their wide applications in different areas of science and innovation. These fractional equations are fit for clarifying various significant marvels in fluid mechanics, electromagnetism, materials science, acoustics, electrochemistry, plasma physics, optical frameworks, viscoelasticity, etc. [20,21,22]. The non-linear time-fractional equal-width equations (FEWEs) are very significant partial differential equations that represent different complex non-linear phenomena in the area of applied sciences, especially in plasma waves, plasma physics, solid state physics, chemical physics, fluid mechanics, etc. The EW problems can define the behavior of non-linear waves in wide classes of non-linear schemes, such as hydromagnetic waves in ion-acoustic waves in plasma, cold plasma, surface waves in compressible fluids, acoustic waves in enharmonic crystal, shallow water waves, etc. [23,24,25,26].
Non-linear fractional differential equations have been solved by numerous researchers using different techniques. Many researchers have solved a lot of problems by utilizing different strategies. To achieve the target of significantly accurate results, several techniques are developed, for instance, the finite difference method, Adomian decomposition technique, finite element technique, generalized differential transform technique, fractional differential transform technique, perturbation methods, iterative strategies, homotopy analysis strategy, etc. [27,28,29,30,31,32,33,34,35]. The homotopy analysis technique (HAT) is a sublime scientific plan initially suggested and implemented by Liao [36,37,38]. Many researchers have promisingly utilized the HAT for examining various mathematical and physical models [39]. In addition, the homotopy analysis method can be converged with the combined Laplace transformation technique to improve a profoundly great approach known as the homotopy analysis transform technique. This creative converging of the HAM and the Laplace transform is utilized to investigate different physical issues [40,41]. These modifications encourage and improve the solving methodology contrasted with the standard techniques.
In contrast, the homotopy perturbation Elzaki transform method (HPETM) is liberated from a linear operator’s supposition and utilizes the Elzaki transform approach for the Caputo time-fractional derivative. Likewise, Tarig M. Elzaki and Sailh M. Elzaki in [42,43,44] developed an Elzaki method that was implemented to acquire the solutions in various circumstances. The Elzaki transform is an incredible asset for fathoming some differential equations that cannot be comprehended by some other techniques for handling linear and non-linear problems. Shakeri and Dehghan [45] and Sakar et al. [46] studied fractional partial differential equations using the homotopy perturbation method. Many researchers [47,48,49,50] have developed different techniques for solving fractional problems under various applied phenomena.
2. Preliminary Concepts
Definition 1.
The Caputo derivative of the arbitrary order of , , , , is expressed as
Definition 2.
The Elzaki transform of the Caputo fractional-order derivative is given as
Definition 3.
The Riemann–Liouville fractional-order integral , of a function , is defined as
Some properties of the operator:
For ,
Elzaki Transform Basic Concept
A new transform called the Elzaki transform is defined for functions of exponential order. We consider functions in the set A, defined by:
The constant M must be a finite number , and finite or infinite for a given function in the set. The Elzaki transform is described through the integral equation
We achieve the basic results
Theorem 1.
If is an Elzaki transform of , the Elzaki transform of the Riemann–Liouville derivative is defined as
Proof.
The Laplace transformation
when we put for , the Elzaki transformation of fractional-order of is as below:
□
3. Homotopy Perturbation Elzaki Transform Method
In this section, the homotopy perturbation Elzaki transform method for the general form of time-fractional partial differential equations is
with the initial condition
By taking the inverse Elzaki transform, we get
where
The perturbation procedure in terms of power series with parameter p is presented as
where the perturbation term is p and .
Nonlinear terms can be defined as
where are He’s polynomials of and can be determined as
Both sides having a comparison coefficient of p, we have
4. Implementation of the Technique
Example 1.
Consider the following non-linear time-fractional equal-width equation:
with the initial condition
Now using the inverse Elzaki transform we have
Now we implement HPM and we get
With the help of He’s polynomials , the nonlinear terms can be found
The He’s polynomials are defined as
Comparing p-like coefficients, we get
Provided the series form solution is
With Equation (18), putting , we achieve the result of the given problem as:
The exact result is:
Example 2.
Consider the following non-linear time-fractional modified equal-width equation:
with initial condition
Incorporating the Elzaki transform in Equation (21), we get
Using the initial condition in Equation (23), we have
By applying the inverse Elzaki transform, we have
Now we implement HPM and we get
With the help of He’s polynomials the nonlinear terms can be found
The He’s polynomials are defined as
Comparing p-like coefficients, we get
provided the series form solution is
Using Equation (28) putting , we achieve the result of the given problem as:
The exact result is:
Example 3.
Consider the following non-linear time-fractional modified equal-width equation:
with initial condition
Using the Elzaki transform in Equation (31), we get
Putting the initial condition in Equation (33), we have
By applying the inverse Elzaki transform, we have
Now we implement the HPM and we get
With the help of He’s polynomials we can find nonlinear terms
The He’s polynomials are defined as
Comparing p-like coefficients, we get
The series form solution is
Using Equation (38) and putting , we achieve the result of the given problem as:
The exact result is:
5. Results and Discussion
In Figure 1, the exact and HPETM solutions are plotted in (a) at and the close contact of the actual and HPETM solutions is analyzed. In Figure 1, the graph (b) represents the HPETM solutions at and of Example 1. The convergence of the fractional solutions can be analyzed to the integer-order solution of the problems. In Figure 2, the plot (a) expresses the HPETM and exact solution of each problem. The closed relation of the HPETM and exact results is established in Figure 2. In Figure 2, the sub-graph (b) is drawn to verify the results at different fractional orders at and . The convergence of fractional to integer-order solutions is investigated. In Figure 3, the subgraph (a) represents the exact and HPETM solutions at , and subgraph (b) represents different fractional orders of Example 3. A closed resemblance is found between the exact and HPETM results. It is found that fractional-order solutions are convergent towards integer-order solution of Example 3.
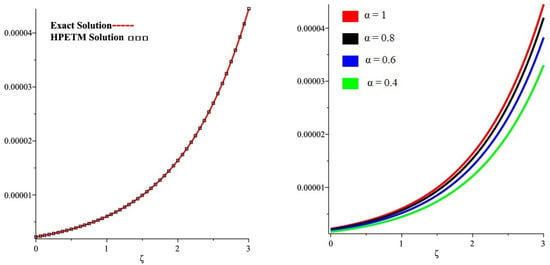
Figure 1.
(a) The exact and analytical solutions graph and (b) different fractional-order graph of Example 1.
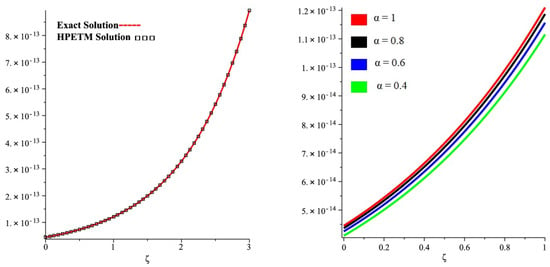
Figure 2.
(a) Exact and analytical solutions graph and (b) different fractional-order graph of Example 2.
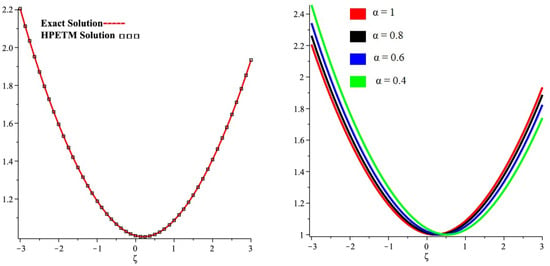
Figure 3.
(a) Exact and analytical solutions graph and (b) different fractional-order graph of Example 3.
6. Conclusions
In this article, we evaluated fractional-order equal-width equations, using a homotopy perturbation Elzaki transformation technique. The solutions for certain examples were explained and implemented for the suggested method. The HPETM result was close to the actual result for the given examples. The current methods were used to calculate the results of fractional-order problems. The graphical analysis of the fractional-order solutions obtained verified the convergence towards solutions of integer order.
In future, the proposed techniques can be extended for solutions of higher nonlinear fractional-order partial differential equations and their systems. The fractional difference and difference differential equations can be handled by using the suggested techniques.
Author Contributions
Conceptualization, N.A.S. and J.D.C.; methodology, N.A.S.; software, I.D. and J.D.C.; validation, J.D.C.; formal analysis, N.A.S. and I.D.; data curation, N.A.S.; writing—original draft preparation N.A.S.; writing—review and editing, I.D.; supervision, J.D.C.; project administration, N.A.S.; funding acquisition, J.D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by a Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korean government (MOTIE) (No. 20192010107020, Development of hybrid adsorption chiller using unutilized heat source of low temperature).
Conflicts of Interest
The authors have no conflicts of interest.
References
- Baleanu, D.; Guvenc, Z.B.; Machado, J.T. (Eds.) New Trends in Nanotechnology and Fractional Calculus Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Shah, N.; Dassios, I.; Chung, J. A Decomposition Method for a Fractional-Order Multi-Dimensional Telegraph Equation via the Elzaki Transform. Symmetry 2020, 13, 8. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, Y.; Kurths, J. Active vibration suppression of a novel airfoil model with fractional order viscoelastic constitutive relationship. J. Sound Vib. 2018, 432, 50–64. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Liu, D. A method to stochastic dynamical systems with strong nonlinearity and fractional damping. Nonlinear Dyn. 2016, 83, 2311–2321. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Liu, D.; Jia, W.; Huang, H. Responses of Duffing oscillator with fractional damping and random phase. Nonlinear Dyn. 2013, 74, 745–753. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Ford, N.J.; Simpson, A.C. The numerical solution of fractional differential equations: Speed versus accuracy. Numer. Algorithms 2001, 26, 333–346. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Acadamic Press: New York, NY, USA, 1974. [Google Scholar]
- Ahmed, N.; Shah, N.; Vieru, D. Two-Dimensional Advection–Diffusion Process with Memory and Concentrated Source. Symmetry 2019, 11, 879. [Google Scholar] [CrossRef]
- Ryzhkov, S.V.; Kuzenov, V.V. New realization method for calculating convective heat transfer near the hypersonic aircraft surface. Z. Fur Angew. Math. Und Phys. 2019, 70, 1–9. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A New Integral Transform: ARA Transform and Its Properties and Applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 2, 731–785. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of the new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 2, 87–92. [Google Scholar]
- Shah, N.; Agarwal, P.; Chung, J.; El-Zahar, E.; Hamed, Y. Analysis of Optical Solitons for Nonlinear Schrödinger Equation with Detuning Term by Iterative Transform Method. Symmetry 2020, 12, 1850. [Google Scholar] [CrossRef]
- Baleanu, D.; Mustafa, O.G. On the global existence of solutions to a class of fractional differential equations. Comput. Math. Appl. 2010, 59, 1835–1841. [Google Scholar] [CrossRef]
- Yousef, F.; Alquran, M.; Jaradat, I.; Momani, S.; Baleanu, D. Ternary-fractional differential transform schema: Theory and application. Adv. Differ. Eqs. 2019, 2019, 197. [Google Scholar] [CrossRef]
- Bokhari, A.; Baleanu, D.; Belgacem, R. Application of Shehu transform to Atangana-Baleanu derivatives. J. Math. Comput. Sci. 2019, 20, 101–107. [Google Scholar] [CrossRef]
- He, J.H.; Ji, F.Y. Two-scale mathematics and fractional calculus for thermodynamics. Therm. Sci. 2019, 21, 2131–2133. [Google Scholar] [CrossRef]
- Wang, K.L.; Yao, S.W.; Yang, H.W. A fractal derivative model for snow’s thermal insulation property. Therm. Sci. 2019, 23, 2351–2354. [Google Scholar] [CrossRef]
- Kakutani, T.; Ono, H. Weak non-linear hydromagnetic waves in a cold collision-free plasma. J. Phys. Soc. Jpn. 1969, 26, 1305–1318. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.M.; Machado, J.A. A new fractional derivative without singular kernel: Application to the modelling of the steady heat flow. Therm. Sci. 2016, 20, 753–756. [Google Scholar] [CrossRef]
- Yang, X.J. Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. Therm. Sci. 2017, 21, 1161–1171. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kumar, S. A new fractional model of nonlinear shock wave equation arising in flow of gases. Nonlinear Eng. 2014, 3, 43–50. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T. A new fractional operator of variable order: Application in the description of anomalous diffusion. Phys. A Stat. Mech. Appl. 2017, 481, 276–283. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic field in terms of geometric curvature in membrane MEMS devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar]
- Lei, Y.; Wang, H.; Chen, X.; Yang, X.; You, Z.; Dong, S.; Gao, J. Shear property, high-temperature rheological performance and low-temperature flexibility of asphalt mastics modified with bio-oil. Constr. Build. Mater. 2018, 174, 30–37. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R.K. Analytical solution of the Bagley Torvik equation by Adomian decomposition method. Appl. Math. Comput. 2005, 168, 398–410. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, J. High-order finite element methods for time-fractional partial differential equations. J. Comput. Appl. Math. 2011, 235, 3285–3290. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S.; Erturk, V.S. Generalized differential transform method: Application to differential equations of fractional order. Appl. Math. Comput. 2008, 197, 467–477. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Liu, J.; Tang, B. Homotopy perturbation method for two dimensional time-fractional wave equation. Appl. Math. Model. 2014, 38, 5545–5552. [Google Scholar] [CrossRef]
- Prakash, A. Analytical method for space-fractional telegraph equation by homotopy perturbation transform method. Nonlinear Eng. 2016, 5, 123–128. [Google Scholar] [CrossRef]
- Dhaigude, C.; Nikam, V. Solution of fractional partial differential equations using iterative method. Fract. Calc. Appl. Anal. 2012, 15, 684–699. [Google Scholar] [CrossRef]
- Safari, M.; Ganji, D.D.; Moslemi, M. Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV-Burgers-Kuramoto equation. Comput. Math. Appl. 2009, 58, 2091–2097. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S. Homotopy analysis method: A new analytical technique for nonlinear problems. Commun. Nonlinear Sci. Numer. Simulation 1997, 2, 95–100. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hashemi, M.S.; Hashim, I. On convergence of homotopy analysis method and its application to fractional integro-differential equations. Quaest. Math. 2013, 36, 93–105. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A fractional model of convective radial fins with temperature-dependent thermal conductivity. Rom. Rep. Phys. 2017, 69, 103. [Google Scholar]
- Kumar, D.; Agarwal, R.P.; Singh, J. A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math. 2018, 339, 405–413. [Google Scholar] [CrossRef]
- Elzaki, T.M. The new integral transform ‘Elzaki transform’. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Elzaki, T.M. Applications of new transform “Elzaki transform” to partial differential equations. Glob. J. Pure Appl. Math. 2011, 7, 65–70. [Google Scholar]
- Elzaki, T.M.; Hilal, E.M.; Arabia, J.S.; Arabia, J.S. Homotopy perturbation and Elzaki transform for solving nonlinear partial differential equations. Math. Theory Model. 2012, 2, 33–42. [Google Scholar]
- Shakeri, F.; Dehghan, M. Solution of delay differential equations via a homotopy perturbation method. Math. Comput. Model. 2008, 48, 486–498. [Google Scholar] [CrossRef]
- Sakar, M.G.; Uludag, F.; Erdogan, F. Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 2016, 40, 6639–6649. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys. A Stat. Mech. Appl. 2019, 524, 563–575. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Purohit, S.D.; Swroop, R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math. Model. Nat. Phenomena 2019, 14, 304. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Baleanu, D.; Abo-Dahab, S.M.; Bouslimi, J.; Omri, M. Oblique explicit wave solutions of the fractional biological population (BP) and equal width (EW) models. Adv. Differ. Eqs. 2020, 2020, 1–17. [Google Scholar]
- Li, X.; Haq, A.U.; Zhang, X. Numerical solution of the linear time fractional Klein-Gordon equation using transform based localized RBF method and quadrature. AIMS Math. 2020, 5, 5287. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).