R²-Cosmology and New Windows for Superheavy Dark Matter

Abstract

Evolution and heating of the universe in $R^2$-modified gravity are considered. It is shown that the universe’s history can be separated into four different epochs: (1) inflation, (2) heating due to curvature oscillations (scalaron decay), (3) transition to matter dominated period, and (4) conventional cosmology governed by General Relativity. Cosmological density of dark matter (DM) particles for different decay channels of the scalaron is calculated. The bounds on the masses of DM particles are derived for the following dominant decay modes: to minimally coupled scalars, to massive fermions, and to gauge bosons.

1. Introduction

The mystery of dark matter (DM) is one of the central problem of modern cosmology. There is a large set of independent pieces of observations which unambiguously point to the existence of a new invisible form of matter disclosing itself through its gravitational action. For a review and list of references see [1,2,3].

According to multiple observations, summarized in Ref. [4], the fractional mass density of dark matter is:

$$\begin{array}{c}\hfill {\Omega }_{DM}=\frac{{\rho }_{DM}}{{\rho }_{crit}}\approx 0.265.\end{array}$$

(1)

Here ${\rho }_{crit}$ is the critical energy density of the universe:

$$\begin{array}{c}\hfill {\rho }_{crit}=\frac{3H_0^2{M}_{Pl}^2}{8\pi }\approx 5{\mathrm{keV}/\mathrm{cm}}^3,\end{array}$$

(2)

where $M_{Pl}=1.22\times {10}^{19}$ GeV $=2.18\times {10}^{-5}$ g is the Planck mass related to the Newton gravitational constant as $G_N=1/M_{Pl}^2$ (We use the natural system of units with $c=k=\hslash =1$) and $H_0$ is the present day value of the Hubble parameter, for which we took

$$\begin{array}{c}\hfill H_0=100{\mathrm{h}\mathrm{km}\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}\approx 70{\mathrm{km}\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}.\end{array}$$

(3)

Thus, the observed mass density of dark matter in contemporary universe is:

$$\begin{array}{c}\hfill {\rho }_{DM}=1{\mathrm{keV}/\mathrm{cm}}^3.\end{array}$$

(4)

The existence of DM and the magnitude of its contribution into the total mass density of the universe follow from the analysis of the data on:

• flat rotational curves around galaxies;
• equilibrium of hot gas in rich galactic clusters;
• the spectrum of the angular fluctuations of Cosmic Microwave Background (CMB) Radiation;
• onset of Large Scale Structure (LSS) formation at the redshift $z_{LSS}={10}^4$ prior to hydrogen recombination at $z_{rec}=1100$.

Presently, possible carriers of dark matter are supposed to belong to two distinct groups: microscopically small (elementary particles) and macroscopically large. The latter may include primordial black holes (PBH) with masses starting from ${10}^{20}$ g up to tens solar masses, topological or non-topological solitons, and possible macroscopic objects consisting e.g., from the so-called mirror matter. A popular form of elementary particle dark matter is called WIMPs (Weakly Interacting Massive Particles), while quite a few other particles types are also discussed in the literature. Macroscopic dark matter of stellar size is abbreviated as MACHO(Massive Astrophysical Compact Halo Object).

The Zoo of the dark matter particles includes, in particular, axions with masses ${10}^{-5}$ eV or even smaller, heavy neutral leptons with the mass of a few GeV, particles of mirror matter, the so-called superheavy Wimpzillas, and many others. Until recently, one of the most popular candidates was the Lightest Supersymmetric Particle (LSP) which, according to the low energy minimal supersymmetric (SUSY) model, should have a mass of several hundred GeV. With the interaction strength typical for this model the cosmological mass density of these particles was predicted to be close to the observed density of DM. However, the absence of signal from supersymmetric partners at Large Hadron Collider (LHC), if not excluded, but considerably restrict the parameter space of the minimal supersymmetric model.

In the present review, we consider cosmological evolution in the theory where the linear in curvature term is supplemented by the quadratic one. In other words, the Lagrangian density of General Relativity (GR) is modified as follows:

$$\begin{array}{c}\hfill -\frac{M_{Pl}^2}{16\pi }R⟶-\frac{M_{Pl}^2}{16\pi }\left(R-\frac{R^2}{6M_R^2}\right),\end{array}$$

(5)

where R is a curvature scalar and $M_R$ is a constant parameter with dimension of mass.

We show that in such a theory, cosmological evolution can be separated into four distinct epochs.

• Quasi-exponential (inflationary) expansion, which was realised if the initial value of R was sufficiently large. During this period, R slowly decreased to zero.
• Curvature (scalaron) dominated regime, when R oscillated around zero with the amplitude inversely proportional to time. At this stage oscillations of R led to particle production and to universe heating.
• Transition period when R dominance was changing to the dominance of (relativistic) matter.
• Onset of the conventional cosmology governed by General Relativity.

In the course of this review, we assume that the cosmological background is described by the spatially flat Friedmann-Lemaître-Robertson-Walker (FLRW) metric:

$$\begin{array}{c}\hfill d{s}^2=d{t}^2-a^2\left(t\right){\delta }_{ij}d{x}^{i}d{x}^j,\end{array}$$

(6)

where $a\left(t\right)$ is the cosmological scale factor and $H=\dot{a}/a$ is the Hubble parameter at an arbitrary time moment.

2. Freezing of LSP in Conventional Cosmology

The number density of stable dark matter particles in contemporary universe is determined by the relation of their annihilation rate to the rate of the cosmological expansion. At a certain moment, the annihilation efficiently stops and the number density of the particles tends to a constant value in the comoving volume. This process is called the freezing of species and was first studied in Refs. [5,6].

Calculations of the frozen number density of stable relic particles, X, are based on the kinetic equation, derived by Zeldovich in 1965 [5]:

$$\begin{array}{c}\hfill {\dot{n}}_X+3H{n}_X=-\langle {\sigma }_{ann}v\rangle \left(n_X^2-n_{eq}^2\right),\end{array}$$

(7)

where $n_X$ is a number density of particles X, ${\sigma }_{ann}$ is $X\overline{X}$-annihilation cross-section into light particles, v is the center-of-mass velocity. The angle brackets mean thermal averaging over the medium. We have made the standard assumption of absence of the charge asymmetry between X and $\overline{X}$-particles, i.e., assumed equality of their number densities: $n_X=n_{\overline{X}}$.

For annihilation of non-relativistic particles in S-wave the thermal averaging is trivially reduced to the product ${\sigma }_{ann}v$ in the limit of the vanishing velocity of colliding X-particles. As a guiding example for the cross-section estimate we take the well known cross-section of non-relativisitc $e^{+}{e}^{-}$-annihilation into photons (see e.g., [7]):

$$\begin{array}{c}\hfill \sigma (e^{+}{e}^{-}\to 2\gamma )=\frac{\pi {\alpha }_{em}^2}{2m_e^{2}v},\end{array}$$

(8)

where ${\alpha }_{em}=1/137$ is the fine structure constant at low energies and v is the electron (or positron) center-of-mass velocity. Using this result we estimate the annihilation cross-section of heavy X-particles into all light relativistic species as

$$\begin{array}{c}\hfill {\sigma }_{ann}v=\frac{\pi {\alpha }^2{\beta }_{ann}}{2M_X^2},\end{array}$$

(9)

where $M_X$ is the X-particle mass, $\alpha$ is a coupling constant, in supersymmetric theories $\alpha \sim {10}^{-2}$, and ${\beta }_{ann}$ is a numerical parameter proportional to the number of open annihilation channels, which can be of order of ten or even larger. The contribution to ${\beta }_{ann}$ from bosons and fermions may be somewhat different but we ignore this complication.

In the case that X-particles are the Majorana fermions, hence they should be in antisymmetric state, the annihilation proceeds in P-wave. So we take for the annihilation cross-section the expression

$$\begin{array}{c}\hfill \langle {\sigma }_{ann}v\rangle =\frac{3\pi {\alpha }^2{\beta }_{ann}}{2M_X^2}\frac{T}{M_X},\end{array}$$

(10)

where the last factor came from thermal averaging of the squared velocity of X-particles, equal to $\langle v^2\rangle =3T/M_X$.

The equilibrium number density of X-particles, $n_{eq}$, in non-relativistic limit is given by the expression

$$\begin{array}{c}\hfill n_{eq}=g_s{\left(\frac{M_{X}T}{2\pi }\right)}^{3/2}{e}^{-M_X/T},\end{array}$$

(11)

where $g_s$ is the number of the spin states of X-particles.

The Zeldovich Equation (7) was first applied to calculations of cosmological number density of heavy neutral leptons, which could be viable dark matter particles, in Refs. [8,9]. After publication [8] Equation (7) took the name “Lee-Weinberg equation”, but the proper name, in our opinion, is the Zeldovich equation.

Equation (7) can be solved analytically with quite high accuracy. The standard procedure of the solution is the following. At high temperatures, the number density of X-particles should be close to the equilibrium one, since the annihilation rate ${\Gamma }_{ann}=\langle {\sigma }_{ann}v\rangle n_{eq}$ is typically much larger than the Hubble expansion rate. According to the Friedmann equation, the Hubble parameter in a spatially flat universe is related to the energy density of the cosmological matter as $\rho =3H^2{M}_{Pl}^2/\left(8\pi \right)$. If the cosmic plasma is in the state of thermal equilibrium, then $\rho ={\pi }^2{T}^4{g}_{\ast }/30$. Hence in the conventional Friedmann cosmology the Hubble parameter is given by the expression:

$$\begin{array}{c}\hfill H={\left(\frac{8{\pi }^3{g}_{\ast }}{90}\right)}^{1/2}\frac{T^2}{M_{Pl}},\end{array}$$

(12)

where T is the temperature of the equilibrium cosmological plasma and $g_{\ast }$ is the total effective number of particle species, to which bosons and fermions contribute respectively 1 and $7/8$ for each spin state. Since the number of particle species decreases with dropping temperature $g_{\ast }$ is a function of temperature and drops down from 100 down to 10 at $T\sim 1$ MeV.

Initially, the reaction rate is supposed to be much higher than the Hubble rate and at this stage the particle number density is close to the equilibrium one, $n_X=n_{eq}\left(1+\delta \right)$ with $\delta \ll 1$. So Equation (7) can be approximately linearized in first order in $\delta$. It is convenient to consider the dimensionless number density, $f\left(t\right)$, in the comoving volume:

$$\begin{array}{c}\hfill n_X=n_{in}{\left(\frac{a_{in}}{a}\right)}^{3}f,\end{array}$$

(13)

where $n_{in}$ is the value of X-particle density at $a=a_{in}$ and $T=T_{in}\gg M_X$, where a is the cosmological scale factor defined below Equation (6), so the X-particles can be considered to be relativistic and thus

$$\begin{array}{c}\hfill n_{in}\approx 0.1g_s{T}_{in}^3,\end{array}$$

(14)

because the number density of massless particles in thermal equilibrium is $0.12g_s{T}^3$ for bosons and $0.09T^3$ for fermions, we have taken the approximate value for the numerical coefficient equal 0.1 valid for both cases. As we see in what follows, the final result does not depend upon initial conditions.

During the radiation dominated stage the Hubble parameter and the scale factor behave as:

$$\begin{array}{c}\hfill H=1/\left(2t\right),a\left(t\right)\sim t^{1/2}.\end{array}$$

(15)

Using Equation (12) we find the connection between temperature and time in cosmology based on General Relativity:

$$\begin{array}{c}\hfill t{T}^2={\left(\frac{90}{32{\pi }^3{g}_{\ast }}\right)}^{1/2}{M}_{Pl}=const.\end{array}$$

(16)

Correspondingly,

$$\begin{array}{c}\hfill \frac{\dot{T}}{T}=-\frac{1}{2t}.\end{array}$$

(17)

In terms of new function f Equation (13) and dimensionless variable $x=M_X/T$ Equation (7) takes the form:

$$\begin{array}{c}\hfill \frac{df}{dx}=-Q{\left(\frac{a_{in}}{a}\right)}^3\frac{n_{in}}{T^3}\frac{f^2-f_{eq}^2}{x^2},\end{array}$$

(18)

where

$$\begin{array}{c}\hfill Q=M_{Pl}{M}_X{\left(\frac{45}{4{\pi }^3{g}_{\ast }\left(T_{in}\right)}\right)}^{1/2}\langle {\sigma }_{ann}v\rangle \end{array}$$

(19)

and $f_{eq}$ is defined as

$$\begin{array}{c}\hfill f_{eq}=\frac{n_{eq}}{n_{in}}{\left(\frac{a}{a_{in}}\right)}^3,\end{array}$$

(20)

where $n_{eq}$ and $n_{in}$ are given by Equations (11) and (14) respectively.

The product $a^3{T}^3$ in Equation (18) is approximately constant up to the corrections induced by the heating of the plasma by the massive particle annihilation when the temperature drops below these particle masses. That is why the number density of X-particles calculated in GR cosmology are normalised to the entropy density which is conserved in the comoving volume. Up to this effect the temperature drops down as the inverse scale factor, $a/a_{in}=T_{in}/T$. According to Equation (14) the coefficient $\left(a_{in}^3{n}_{in}\right)/\left(a^3{T}^3\right)$ in the GR regime is equal to $0.1g_s$ and Equation (18) turns into:

$$\begin{array}{c}\hfill \frac{df}{dx}=-0.1g_{s}Q\frac{f^2-f_{eq}^2}{x^2},\end{array}$$

(21)

where $f_{eq}$ is given by Equation (20) with $n_{eq}$ and $n_{in}$ defined in Equations (11) and (14) respectively, so:

$$\begin{array}{c}\hfill f_{eq}=10{\left(\frac{x}{2\pi }\right)}^{3/2}{e}^{-x}.\end{array}$$

(22)

Due to a very large value of Q, the solution, $f\left(x\right)$, is initially close to equilibrium:

$$\begin{array}{c}\hfill f=f_{eq}(1+\delta )\end{array}$$

(23)

with $\delta \ll 1$. In this quasi-equilibrium regime Equation (21) can be algebraically solved as

$$\begin{array}{c}\hfill \delta =-\frac{x^2}{0.2g_{s}Q{f}_{eq}^2}\frac{d{f}_{eq}}{dx}\approx \frac{x^2}{0.2g_{s}Q{f}_{eq}}=\frac{{\left(2\pi \right)}^{3/2}{x}^{1/2}{e}^x}{2g_{s}Q},\end{array}$$

(24)

because $d{f}_{eq}/dx\approx -f_{eq}$ for large x, see Equation (22).

This solution is approximately valid till $\delta$ remains smaller than unity. The condition $\delta \left(x_{fr}\right)=1$ defines the so-called freezing temperature $T_{fr}=M_X/x_{fr}$, where $x_{fr}$ is equal to:

$$\begin{array}{c}\hfill x_{fr}\approx ln\frac{2g_{s}Q}{{\left(2\pi \right)}^{3/2}}-\frac{1}{2}ln{x}_{fr}\approx ln\frac{2g_{s}Q}{{\left(2\pi \right)}^{3/2}}-\frac{1}{2}lnln\frac{2g_{s}Q}{{\left(2\pi \right)}^{3/2}}.\end{array}$$

(25)

Dimensionless number density f at the moment of freezing is given by the expression:

$$\begin{array}{c}\hfill f_{fr}=f\left(x_{fr}\right)=2f_{eq}\left(x_{fr}\right)=\frac{10x_{fr}^2}{g_{s}Q}=\frac{10}{g_{s}Q}{ln}^2\left(\frac{2g_{s}Q}{{\left(2\pi \right)}^{3/2}}\right).\end{array}$$

(26)

When x becomes larger than $x_{fr}$, one can neglect $f_{eq}^2$ in r.h.s. of Equation (21) and this equation takes the form

$$\begin{array}{c}\hfill \frac{df}{dx}=-0.1g_{s}Q\frac{f^2}{x^2}.\end{array}$$

(27)

We need to integrate Equation (27) with the initial condition $f_{in}=f_{fr}$ at $x_{in}=x_{fr}$, where $f_{fr}$ is defined by Equation (26).

For S-wave annihilation Q does not depend upon x and using Equations (19) and (9) we find:

$$\begin{array}{c}\hfill Q=\frac{{\alpha }^2{\beta }_{ann}}{4}{\left(\frac{45}{\pi g_{\ast }\left(T_{in}\right)}\right)}^{1/2}\frac{M_{Pl}}{M_X}.\end{array}$$

(28)

and Equation (27) is integrated as:

$$\begin{array}{c}\hfill f\left(x\right)=\frac{f_{fr}}{1-0.1g_{s}Q{f}_{fr}\left(\frac{1}{x}-\frac{1}{x_{fr}}\right)}\underset{x\to \infty }{⟶}\frac{f_{fr}}{1+0.1g_{s}Q\frac{f_{fr}}{x_{fr}}}⟶\frac{10x_{fr}}{g_{s}Q}\equiv f_{as}.\end{array}$$

(29)

The last limit transition is true if $\left(0.1g_{s}Q{f}_{fr}\right)/x_{fr}\gg 1$. Remind that the asymptotically constant value, $f_{as}=const$, is the dimensionless concentration of X-particles in the present day universe, defined according to Equation (13). It means that asymptotically the number density of X-particles drops down as $1/a^3$, or, in other words, it is conserved in the comoving volume. Let us denote as $T_{as}$ the temperature below which the asymptotically constant value $f_{as}$ is reached.

For P-wave annihilation we have to substitute into Equations (24) and (27) the factor $Q_P=3Q/x$ instead of Q and take into account that Equations (25) and (26) are changed as:

$$\begin{array}{c}\hfill x_{fr}^P\approx ln\frac{6g_{s}Q}{{\left(2\pi \right)}^{3/2}}-\frac{3}{2}ln{x}_{fr}^P\approx ln\frac{6g_{s}Q}{{\left(2\pi \right)}^{3/2}}-\frac{3}{2}lnln\frac{6g_{s}Q}{{\left(2\pi \right)}^{3/2}}.\end{array}$$

(30)

$$\begin{array}{c}\hfill f_{fr}^P=f\left(x_{fr}^P\right)=2f_{eq}\left(x_{fr}^P\right)=\frac{10{\left(x_{fr}^P\right)}^3}{3g_{s}Q}=\frac{10}{3g_{s}Q}{ln}^3\left(\frac{6g_{s}Q}{{\left(2\pi \right)}^{3/2}}\right).\end{array}$$

(31)

In this case, Equation (27) is transformed into:

$$\begin{array}{c}\hfill \frac{d{f}^P}{dx}=-0.3g_{s}Q\frac{{\left(f^P\right)}^2}{x^3},\end{array}$$

(32)

with initial conditions (30) and (31). The solution has the form

$$\begin{array}{ccc}\hfill f^P\left(x\right)=f_{fr}^P{\left(1-\frac{0.3g_{s}Q{f}_{fr}^P}{2}\left(\frac{1}{x^2}-\frac{1}{{\left(x_{fr}^P\right)}^2}\right)\right)}^{-1}& \underset{x\to \infty }{⟶}& \frac{f_{fr}^P}{1+0.3g_{s}Q{f}_{fr}^P/(2{\left(x_{fr}^P\right)}^2)}\hfill \\ & ⟶& \frac{20{\left(x_{fr}^P\right)}^2}{3g_{s}Q}\equiv f_{as}^P.\hfill \end{array}$$

(33)

We apply the obtained above results for calculations of the present day number and energy densities of relic X-particles. To this end we will use the law of entropy conservation in the comoving volume, see e.g., [10]:

$$\begin{array}{c}\hfill s=\frac{\rho +P}{T}\sim {\left(\frac{a_{as}}{a}\right)}^3,\end{array}$$

(34)

where T, $\rho$, and P are respectively the temperature, energy density and pressure of the cosmological matter, which is predominantly relativistic. We normalised entropy at the value of the scale factor, $a_{as}$, at the temperature $T_{as}$, when f reaches its asymptotic value $f_{as}$. For relativistic matter

$$\begin{array}{c}\hfill \rho =\frac{{\pi }^2{g}_{\ast }}{30}{T}^4,P=\frac{\rho }{3},\end{array}$$

(35)

where $g_{\ast }\sim 100$ at $T\sim M_X$.

Since the asymptotic number density of X-particles conserves in the comoving volume, its ratio to the entropy stays constant:

$$\begin{array}{c}\hfill \frac{n_X(a>a_{as})}{s(a>a_{as})}=const.\end{array}$$

(36)

According to Equations (13) and (14):

$$\begin{array}{c}\hfill n_X\left(a\right)=0.1g_s{T}_{as}^3{\left(\frac{a_{as}}{a}\right)}^3{f}_{as}.\end{array}$$

(37)

Entropy density is equal to:

$$\begin{array}{c}\hfill s\left(T\right)=\frac{4{\pi }^2{g}_{\ast }\left(T\right)}{90}{T}^3.\end{array}$$

(38)

Hence the ratio (36) is:

$$\begin{array}{c}\hfill \frac{n_X}{s}=\frac{9g_s{f}_{as}}{4{\pi }^2{g}_{\ast }\left(T\right)}{\left(\frac{a_{as}}{a}\right)}^3{\left(\frac{T_{as}}{T}\right)}^3,\end{array}$$

(39)

where $g_{\ast }\left(T_{as}\right)\approx 100$ is the number of effective degrees of freedom at $T=T_{as}$. Due to entropy conservation the quantity $g_{\ast }\left(T\right)T^3$ remains constant in comoving volume for the primeval plasma in thermal equilibrium. So we can rely on this conservation down to temperatures $T_1\approx 1$ MeV, when $g_{\ast }\left(T_1\right)=10.75$. Below this temperature neutrinos decouple from the primeval plasma, while photons and $e^{+}{e}^{-}$-pairs remain in equilibrium with the effective number of degrees of freedom $g_{\ast }^{em}\left(T_1\right)=5.5$. After $e^{+}{e}^{-}$-annihilation the effective number of degrees of freedom in electromagnetic component of the plasma becomes $g_{\ast }^{em}(T\ll m_e)=2$, where $m_e=0.511$ MeV is the electron mass. The issues of neutrino decoupling and the effective number of degrees of freedom are described in detail in Ref. [11].

The number density of X-particles at $T=T_1$, as follows from the conservation law (36), is:

$$\begin{array}{c}\hfill n_X\left(T_1\right)=s\left(T_1\right)\frac{n_{as}}{s_{as}},\end{array}$$

(40)

where according to Equation (37)

$$\begin{array}{c}\hfill n_{as}=n_X\left(a_{as}\right)=0.1g_s{T}_{as}^3{f}_{as}\end{array}$$

(41)

and $s_{as}$ is given by Equation (38) at $T=T_{as}$.

Below $T=T_1$ entropy is conserved only in the electromagnetic part of the plasma, so

$$\begin{array}{c}\hfill \frac{n_X\left(T_1\right)}{s_{em}\left(T_1\right)}=\frac{n_{X0}}{s_{em0}},\end{array}$$

(42)

where $s_{em}$ is the entropy of electromagnetic component of the plasma consisting of photons and $e^{+}{e}^{-}$-pairs and sub-zero indicates that the corresponding quantities are taken in the present day universe.

The entropy of photons in the contemporary universe is expressed through the photon number density, $n_{\gamma 0}=0.24T_0^3$, as

$$\begin{array}{c}\hfill s_{em0}=\frac{4{\pi }^2}{90}{g}_{\ast }^{em}{T}_0^3=\frac{4{\pi }^2}{0.24·90}{g}_{\ast }^{em}{n}_{\gamma 0},\end{array}$$

(43)

where $n_{\gamma 0}=412$ cm${}^{-3}$, see e.g., astrophysics summery table in [4].

So the present day number density of X-particles is:

$$\begin{array}{ccc}\hfill n_{X0}& =& \frac{n_X\left(T_1\right)}{s_{em}\left(T_1\right)}{s}_{em0}=\frac{s\left(T_1\right)}{s_{em}\left(T_1\right)}\frac{n_{as}{f}_{as}}{s_{as}}{s}_{em0}=\frac{g_{\ast }\left(T_1\right)}{g_{\ast }^{em}\left(T_1\right)}\frac{0.1g_s{f}_{as}}{g_{\ast }\left(T_{as}\right)}\frac{g_{\ast }^{em}{n}_{\gamma 0}}{0.24}\hfill \\ & =& 13.4f_{as}{\mathrm{cm}}^{-3}.\hfill \end{array}$$

(44)

Let us apply the obtained above results for determination of cosmological energy density, ${\rho }_{X0}=M_X{n}_{X0}$, of LSP in the low energy supersymmetric model. Substituting in (28) $\alpha ={10}^{-2}$, ${\beta }_{ann}=10$, and $g_{\ast }\left(T_{in}\right)=100$, we achieve by an order of magnitude the estimate:

$$\begin{array}{c}\hfill Q=\frac{1.15·{10}^{12}}{M_{TeV}},\end{array}$$

(45)

where $M_{TeV}=M_X/TeV$. With the chosen values of parameters the cosmological energy density of X-particles at the present time would be:

$$\begin{array}{c}\hfill \rho \approx 0.33M_{TeV}^2{\mathrm{keV}/\mathrm{cm}}^3,\end{array}$$

(46)

which is quite close to the observed value of the dark matter energy density (4).

Typical lower bounds on masses of supersymmetric partners, according to LHC data, are in TeV region, see e.g., [4,12]. LSPs with the masses of order of a few TeV or higher would overclose the universe and so they should be excluded from the pool of possible dark matter candidates, provided the conventional Friedmann cosmology is valid. In what follows we consider modified cosmological scenario which allows lifting this constraint and to reopen the chance for superheavy particles with interaction strength typical for SUSY to be DM carriers.

3. Cosmological Evolution in $R^2$-Gravity Prior to the Universe Heating

3.1. Action Modification

The canonical action of General Relativity, the Einstein-Hilbert action [13,14,15], has the form:

$$\begin{array}{c}\hfill S_{EH}=-\frac{M_{Pl}^2}{16\pi }\int d^{4}x\sqrt{-g}R,\end{array}$$

(47)

where R is the curvature scalar and g is the determinant of the metric tensor $g_{\mu \nu }$ with the signature convention $(+,-,-,-)$. The Riemann tensor describing the curvature of space-time is determined according to $R_{\mu \beta \nu }^{\alpha }={\partial }_{\beta }{\Gamma }_{\mu \nu }^{\alpha }+\cdots$, $R_{\mu \nu }=R_{\mu \alpha \nu }^{\alpha }$, and $R=g^{\mu \nu }{R}_{\mu \nu }$.

This action is supplemented by the action of matter, $S_m$, which provides the source of gravitational field, the energy-momentum tensor of matter, $T_{\mu \nu }$:

$$\begin{array}{c}\hfill T_{\mu \nu }=\frac{2}{\sqrt{-g}}\frac{\delta S_m}{\delta g^{\mu \nu }}.\end{array}$$

(48)

Taking variation of the total action, $S_{EH}+S_m$, over $\delta g^{\mu \nu }$ we arrive to the classical Einstein equations:

$$\begin{array}{c}\hfill R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R=\frac{8\pi }{M_{Pl}^2}{T}_{\mu \nu }.\end{array}$$

(49)

In Refs. [16,17,18] corrections to vacuum Einstein action have been calculated by performing quantum averaging of $T_{\mu \nu }$ in external curved space-time. In particular the addition to the action contains the following terms:

$$\begin{array}{c}\hfill \delta S\sim B{R}^2+C{R}^{2}lnR,\end{array}$$

(50)

where the coefficient $C=1/\left(144\pi M_{Pl}^2\right)$, while B depends upon the renormalisation and is unknown. According to Ref. [18] sufficiently large coefficient B leads to exponential expansion of the universe (inflation) at the early stage. The corresponding effective action is taken as:

$$\begin{array}{c}\hfill S_{tot}=-\frac{M_{Pl}^2}{16\pi }\int d^{4}x\sqrt{-g}\left(R-\frac{R^2}{6M_R^2}\right)+S_m,\end{array}$$

(51)

where $M_R$ is a parameter with the dimension of mass and, according to assumption, $M_R\ll M_{Pl}$.

The modified Einstein equations for theory (51) are the following:

$$\begin{array}{c}\hfill R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R-\frac{1}{3M_R^2}\left(R_{\mu \nu }-\frac{1}{4}R{g}_{\mu \nu }+g_{\mu \nu }{D}^2-D_{\mu }{D}_{\nu }\right)R=\frac{8\pi }{M_{Pl}^2}{T}_{\mu \nu },\end{array}$$

(52)

where $D^2\equiv g^{\mu \nu }{D}_{\mu }{D}_{\nu }$ is the covariant D’Alembert operator.

Taking the trace of Equation (52) yields

$$\begin{array}{c}\hfill D^{2}R+M_R^{2}R=-\frac{8\pi M_R^2}{M_{Pl}^2}{T}_{\mu }^{\mu }.\end{array}$$

(53)

The General Relativity limit can be recovered when $M_R\to \infty$. In this case, we expect to obtain the usual algebraic relation between the curvature scalar and the trace of the energy-momentum tensor of matter:

$$\begin{array}{c}\hfill M_{Pl}^2{R}_{GR}=-8\pi T_{\mu }^{\mu }.\end{array}$$

(54)

3.2. Modified Evolution Equations

Let us start from an empty universe, where $T_{\mu }^{\mu }=0$ and the curvature R does not depend on space coordinates, $R=R\left(t\right)$. In FLRW-metric (6), Equation (53) takes the form:

$$\begin{array}{c}\hfill \ddot{R}+3H\dot{R}+M_R^{2}R=0.\end{array}$$

(55)

This is exactly the same equation as the Klein-Gordon equation for a homogeneous massive scalar field in curved space-time background. That is why R has the name “scalaron” with $M_R$ being the scalaron mass.

In metric (6) the curvature scalar is expressed through the Hubble parameter as:

$$\begin{array}{c}\hfill R=-6\dot{H}-12H^2.\end{array}$$

(56)

Equations (55) and (56) completely define the cosmological evolution in the absence of matter.

We assume that the cosmological matter distribution is homogeneous and isotropic with the equation of state

$$\begin{array}{c}\hfill P=w\rho ,\end{array}$$

(57)

where $\rho$ is the energy density, P is the pressure of matter, and w is a constant parameter during a certain sufficiently long-lasting cosmological epoch e.g., for non-relativistic matter $w=0$, for relativistic matter $w=1/3$, and for the vacuum-like state $w=-1$.

Correspondingly, the energy-momentum tensor of matter $T_{\nu }^{\mu }$ has the following diagonal form:

$$\begin{array}{c}\hfill T_{\nu }^{\mu }=diag(\rho ,-P,-P,-P).\end{array}$$

(58)

The energy-momentum tensor satisfies the covariant conservation condition $D_{\mu }{T}_{\nu }^{\mu }=0$, which in FLRW-metric (6) has the form:

$$\begin{array}{c}\hfill \dot{\rho }=-3H(\rho +P)=-3H(1+w)\rho .\end{array}$$

(59)

In the presence of matter Equation (55) turns into:

$$\begin{array}{c}\hfill \ddot{R}+3H\dot{R}+M_R^{2}R=-\frac{8\pi M_R^2}{M_{Pl}^2}(1-3w)\rho .\end{array}$$

(60)

It is convenient to introduce dimensionless time variable and dimensionless functions:

$$\begin{array}{c}\hfill \tau =M_{R}t,H=M_{R}h,R=M_R^{2}r,\rho =M_R^{4}y.\end{array}$$

(61)

Equations (56), (59) and (60) now become:

$$\begin{array}{ccc}& & h^{\prime }+2h^2=-r/6,\hfill \end{array}$$

(62)

$$\begin{array}{ccc}& & r^{\prime \prime }+3h{r}^{\prime }+r=-8\pi {\mu }^2(1-3w)y,\hfill \end{array}$$

(63)

$$\begin{array}{ccc}& & y^{\prime }+3(1+w)hy=0,\hfill \end{array}$$

(64)

where prime means derivative over $\tau$ and $\mu =M_R/M_{Pl}$.

3.3. Inflationary Stage

Here we show that with sufficiently large initial value of R, the devoid of matter universe would expand quasi exponentially [18] long enough to provide solution of flatness, horizon and homogeneity problems existing in Friedmann cosmology, for the review see e.g., textbook [19].

We perform a numerical and analytical solution of the system of Equations (55) and (56), which in terms of dimensionless quantities (61) take the form:

$$\begin{array}{ccc}& & r^{\prime \prime }+3h{r}^{\prime }+r=0,\hfill \\ & & h^{\prime }+2h^2=-r/6.\hfill \end{array}$$

(65)

The initial conditions should be chosen in such a way that at least 70 e-foldings during inflation are ensured:

$$\begin{array}{c}\hfill N_e={\int }_0^{{\tau }_{inf}}hd\tau \ge 70,\end{array}$$

(66)

where ${\tau }_{inf}$ is the moment when inflation terminated, to be determined in what follows. This can be achieved if the initial value of r is sufficiently large, practically independent on the initial value of h.

Following Refs. [18,20] (see also the subsequent work [21]), we can roughly estimate the duration of inflation neglecting higher derivatives in Equations (65), so we arrive to the simplified set of equations:

$$\begin{array}{ccc}\hfill h^2& =& -r/12,\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill 3h{r}^{\prime }& =& -r.\hfill \end{array}$$

(68)

These equations are solved as:

$$\begin{array}{c}\hfill \sqrt{-r\left(\tau \right)}=\sqrt{-r_0}-\tau /\sqrt{3},\end{array}$$

(69)

where $r_0$ is the initial value of r at $\tau =0$. According to Equation (67), the Hubble parameter behaves as $h\left(\tau \right)=(\sqrt{-3r_0}-\tau )/6$. The duration of inflation is roughly determined by the condition $h=0$:

$$\begin{array}{c}\hfill {\tau }_{inf}=\sqrt{-3r_0}.\end{array}$$

(70)

After $h\left(t\right)$ reaches zero it started to oscillate with the amplitude decreasing as $2/\left(3t\right)$ and the exponential (inflationary) rise of the scale factor turns into a power law one.

The number of e-folding is equal to the area of the triangle below the line $h\left(\tau \right)$, thus $N_e\approx |r_0/4|$. It is in excellent agreement with numerical solutions of Equation (65) depicted in Figure 1.

The evolution of the dimensionless curvature scalar, r, during inflation is presented in the left panel of Figure 2. Inflation terminates when both h and r reach zero. After that, curvature starts to oscillate, as is presented in the right panel of Figure 2, efficiently producing elementary particles.

3.4. Post-Inflationary Stage Prior to the Universe Heating

In this subsection we consider the evolution of r and h solving numerically Equation (65) for the values of $\tau$ exceeding duration of inflation, $\tau >{\tau }_{inf}$ (70). We assume that the density of matter is negligibly small and take $y=0$. Numerical solution for $r\left(\tau \right)$ immediately after the end of inflation is presented in the right panel of Figure 2. For larger $\tau$ the solutions, $r\left(\tau \right)\tau$ and $h\left(\tau \right)\tau$, take very simple forms depicted in Figure 3. Both $r\left(\tau \right)\tau$ and $h\left(\tau \right)\tau$ oscillate with constant amplitudes, so that the curvature, $\tau r\left(\tau \right)$, oscillates around zero, while the Hubble parameter, $\tau h\left(\tau \right)$, oscillates around $2/3$ almost touching zero at the minima.

Simulated by the numerical solution and following Refs. [22,23] we search for the asymptotic expansion of h and r at $\tau \gg 1$ in the form:

$$\begin{array}{ccc}\hfill r& =& \frac{r_{1}cos(\tau +{\theta }_r)}{\tau }+\frac{r_2}{{\tau }^2},\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill h& =& \frac{h_0+h_{1}sin(\tau +{\theta }_h)}{\tau }.\hfill \end{array}$$

(72)

Here $r_j$ and $h_j$, $j=1,2$, are some constant coefficients to be calculated from Equation (65), while the constant phases ${\theta }_{r,h}$ are determined from the initial conditions and will be adjusted by the best fit of the asymptotic solution to the numerical one.

Substituting expressions (71) and (72) into the r.h.s. of second equation of system (65) we obtain:

$$\begin{array}{ccc}\hfill h^{\prime }& =& -\frac{2{[h_0+h_{1}sin(\tau +{\theta }_h)]}^2}{{\tau }^2}-\frac{1}{6}\left(\frac{r_{1}cos(\tau +{\theta }_r)}{\tau }+\frac{r_2}{{\tau }^2}\right),\hfill \end{array}$$

(73)

where $h^{\prime }$ is found by the differentiation of (72):

$$\begin{array}{ccc}\hfill h^{\prime }& =& \frac{h_{1}cos(\tau +{\theta }_h)}{\tau }-\left[\frac{h_0+h_{1}sin(\tau +{\theta }_h)}{{\tau }^2}\right].\hfill \end{array}$$

(74)

Comparison of the $1/\tau$ and $1/{\tau }^2$ leads respectively to the equations:

$$\begin{array}{ccc}& & h_1=-r_1/6,{\theta }_h={\theta }_r\equiv \theta ,\hfill \end{array}$$

(75)

$$\begin{array}{ccc}& & h_0+h_{1}sin(\tau +{\theta }_h)=2{\left[h_0+h_{1}sin(\tau +{\theta }_h)\right]}^2+r_2/6.\hfill \end{array}$$

(76)

Neglecting the oscillating $sine$-terms, which vanish on the average, and taking the average of ${sin}^2(\tau +\theta )=1/2$, we find:

$$\begin{array}{c}\hfill h_0=2h_0^2+h_1^2+r_2/6.\end{array}$$

(77)

Similarly, we explore the first equation of system (65) for r and to this end we need to find expressions for $r^{\prime }$, and $r^{\prime \prime }$ from Equation (71):

$$\begin{array}{ccc}\hfill r^{\prime }& =& -\frac{r_{1}sin(\tau +{\theta }_r)}{\tau }-\frac{r_{1}cos(\tau +{\theta }_r)}{{\tau }^2}-\frac{2r_2}{{\tau }^3},\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill r^{\prime \prime }& =& -\frac{r_{1}cos(\tau +{\theta }_r)}{\tau }+\frac{2r_{1}sin(\tau +{\theta }_r)}{{\tau }^2}+\frac{2r_{1}cos(\tau +{\theta }_r)}{{\tau }^3}+\frac{6r_2}{{\tau }^4}.\hfill \end{array}$$

(79)

Now, substituting the expressions for r, $r^{\prime }$, $r^{\prime \prime }$, and h into Equation (65) we arrive at:

$$\begin{array}{ccc}& & -\frac{r_{1}cos(\tau +\theta )}{\tau }+\frac{2r_{1}sin(\tau +\theta )}{{\tau }^2}+\frac{2r_{1}cos(\tau +\theta )}{{\tau }^3}+\frac{6r_2}{{\tau }^4}\hfill \\ & & -3\left[\frac{r_{1}sin(\tau +\theta )}{\tau }+\frac{r_{1}cos(\tau +\theta )}{{\tau }^2}+\frac{2r_2}{{\tau }^3}\right]\left(\frac{h_0+h_{1}sin(\tau +\theta )}{\tau }\right)\hfill \\ & & +\frac{r_{1}cos(\tau +\theta )}{\tau }+\frac{r_2}{{\tau }^2}=0\hfill \end{array}$$

(80)

The leading terms proportional to ${\tau }^{-1}$ neatly cancel out. The terms of the order of ${\tau }^{-2}$ leads to:

$$\begin{array}{c}\hfill h_0=2/3,\mathrm{and}{r}_2=3h_1{r}_1/2.\end{array}$$

(81)

Here, as usually, we have taken ${sin}^2(\tau +\theta )=1/2$. Now using Equations (75) and (77), we find:

$$\begin{array}{c}\hfill h_1=2/3\mathrm{and}{r}_1=r_2=-4,\end{array}$$

(82)

so finally:

$$\begin{array}{ccc}& & h=\frac{2}{3\tau }\left[1+sin(\tau +\theta )\right],\hfill \end{array}$$

(83)

$$\begin{array}{ccc}& & r=-\frac{4cos(\tau +\theta )}{\tau }-\frac{4}{{\tau }^2}.\hfill \end{array}$$

(84)

These asymptotic solutions perfectly well agree with numerical ones presented in Figure 3.

The law of the scale factor evolution corresponding to the Hubble parameter (83) was obtained in Ref. [18].

The effect of particle production on the evolution of curvature, $R\left(t\right)$, is usually described by an addition of $\Gamma \dot{R}$-term into the l.h.s. of Equation (55) with a constant $\Gamma$:

$$\begin{array}{c}\hfill \ddot{R}+(3H+\Gamma )\dot{R}+M_R^{2}R=0.\end{array}$$

(85)

This is exactly the same as the Klein-Gordon equation for unstable scalar particle with the decay width $\Gamma$. For $\Gamma \ll M_R$ and negligible H the solution of Equation (85) looks as

$$\begin{array}{c}\hfill R\left(t\right)\sim cos(M_{R}t+\theta )exp(-\Gamma t/2).\end{array}$$

(86)

The value of $\Gamma$ depends on the decay channel of the scalaron and is calculated in the following section for different types of the decay.

Note in conclusion that this simple description of the decay by $\Gamma \dot{R}$-term in Equation (85) is valid only for harmonic oscillations of $R\left(t\right)$. For arbitrary temporary evolution of R the equation becomes integro-differential, non-local in time one [22,24].

4. Calculation of the Scalaron Decay Widths

4.1. Decay into Minimally Coupled Scalars

The scalaron decay width into two massless (or very low mass) scalar bosons was calculated in refs. [18,22,25]. Here we follow our paper [22], where more rigorous approach was used based on the paper [24], which allows deriving closed equation for an arbitrary time evolution of the source field (in our case the scalaron, $R\left(t\right)$), while the traditional methods are valid only for the harmonic oscillations of the source.

The action of a real scalar field $\varphi$ with an arbitrary non-minimal coupling to curvature has the form:

$$S_{\varphi }^{\left(0\right)}=\frac{1}{2}\int d^{4}x\sqrt{-g}\left(g^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -\xi R{\varphi }^2\right).$$

(87)

Minimal coupling to gravity means that $\xi =0$, this is the case which is considered in the present subsection.

In spatially flat FLRW background (6) action (87) with $\xi =0$, leads to the following equation of motion:

$$\ddot{\varphi }+3H\dot{\varphi }-\frac{1}{a^2}\Delta \varphi =0.$$

(88)

In turn field $\varphi$ enters the equation of motion for R (53) via the trace of its energy-momentum tensor:

$$T_{\mu }^{\mu }\left(\varphi \right)=-g^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi \equiv -{(\partial \varphi )}^2.$$

It is convenient to study particle production in terms of the conformally rescaled field and the conformal time defined according to the equations:

$$\begin{array}{ccc}& & \chi =a\left(t\right)\varphi ,\hfill \end{array}$$

(89)

$$\begin{array}{ccc}& & d\eta =dt/a\left(t\right).\hfill \end{array}$$

(90)

Using these quantities we can rewrite the equations of motion as:

$$\begin{array}{ccc}\hfill & & {\partial }_{\eta }^{2}R+2\frac{{\partial }_{\eta }a}{a}{\partial }_{\eta }R+a^2{M}_R^{2}R=\hfill \\ & & \frac{8\pi }{a^2}\frac{M_R^2}{M_{Pl}^2}\left[{\left({\partial }_{\eta }\chi \right)}^2-{\left(\overrightarrow{\nabla }\chi \right)}^2+\frac{{\left({\partial }_{\eta }a\right)}^2}{a^2}{\chi }^2-\frac{{\partial }_{\eta }a}{a}[\chi {\partial }_{\eta }\chi +\left({\partial }_{\eta }\chi \right)\chi ]\right],\hfill \end{array}$$

(91)

$$\begin{array}{c}\hfill R=-6\frac{{\partial }_{\eta }^{2}a}{a^3},\end{array}$$

(92)

$$\begin{array}{c}\hfill {\partial }_{\eta }^2\chi -\Delta \chi +\frac{1}{6}{a}^{2}R\chi =0,\end{array}$$

(93)

while action (87) turns into:

$$S_{\chi }=\frac{1}{2}\int d\eta d^{3}x\left({\left({\partial }_{\eta }\chi \right)}^2-{(\overrightarrow{\nabla }\chi )}^2-\frac{a^{2}R}{6}{\chi }^2\right).$$

(94)

Above and below ${\partial }_{\eta }$ denotes derivative with respect to conformal time.

Our aim is to derive a closed equation for R taking the average value of the $\chi$-dependent quantum operators in the r.h.s. of Equation (91) over vacuum, in the presence of an external classical gravitational field R. Our arguments essentially repeat those of Ref. [24], where the equation was derived in one-loop approximation.

The free field ${\chi }^{\left(0\right)}$ is quantized in the usual way:

$${\chi }^{\left(0\right)}\left(x\right)=\int \frac{d^{3}k}{{\left(2\pi \right)}^{3}2E_k}\left[{\widehat{a}}_k{e}^{-ik·x}+{\widehat{a}}_k^{†}{e}^{ik·x}\right],$$

(95)

where $x^{\mu }=(\eta ,\mathbf{x})$, $k^{\mu }=(E_k,\mathbf{k})$, and $k_{\mu }{k}^{\mu }=0$. The creation-annihilation operators satisfy the commutation relations:

$$\begin{array}{c}\hfill \left[{\widehat{a}}_k,{\widehat{a}}_k^{†}\right]={\left(2\pi \right)}^{3}2E_k{\delta }^{\left(3\right)}(\mathbf{k}-{\mathbf{k}}^{\prime }).\end{array}$$

(96)

Equation (93) can be transformed into the following integro-differential equation convenient for perturbative solution:

$$\begin{array}{c}\hfill \chi \left(x\right)={\chi }^{\left(0\right)}\left(x\right)-\frac{1}{6}\int d^{4}yG(x,y)a^2\left(y\right)R\left(y\right)\chi \left(y\right)\equiv {\chi }^{\left(0\right)}\left(x\right)+\delta \chi \left(x\right),\end{array}$$

(97)

where the massless Green’s function is

$$G(x,y)=\frac{1}{4\pi |\mathbf{x}-\mathbf{y}|}\delta \left((x_0-y_0)-|\mathbf{x}-\mathbf{y}|\right)\equiv \frac{1}{4\pi r}\delta (\Delta \eta -r).$$

(98)

The particle production effects are assumed to weakly perturb the free solution, so Equation (97) can be solved as

$$\chi \left(x\right)\simeq {\chi }^{\left(0\right)}\left(x\right)-\frac{1}{6}\int d^{4}yG(x,y)a^2\left(y\right)R\left(y\right){\chi }^{\left(0\right)}\left(y\right)\equiv {\chi }^{\left(0\right)}\left(x\right)+{\chi }^{\left(1\right)}\left(x\right).$$

(99)

Now we calculate the vacuum expectation values of the various terms in the r.h.s. of Equation (91), keeping only the contribution from the terms linear in ${\chi }^{\left(1\right)}$. The terms of zero order which contain only ${\chi }^{\left(0\right)}$ and its derivatives have nothing to do with particle production and can only change the parameters of the theory through the renormalization procedure.

The terms relevant to the particle production are calculated on the basis of the equations:

$$\begin{array}{ccc}& & {\partial }_x\int d^{4}yG(x,y)a^2\left(y\right)R\left(y\right)\chi \left(y\right)=\int d^{4}yG(x,y)\left[a^{2}R{\partial }_y\chi +{\partial }_y\left(a^{2}R\right)\chi \right],\hfill \end{array}$$

(100)

$$\begin{array}{ccc}& & {\int }_0^{\infty }dk{e}^{i\alpha k}=\pi \delta \left(\alpha \right)+i\mathcal{P}\left(\frac{1}{\alpha }\right).\hfill \end{array}$$

(101)

Thus we obtain:

$$\begin{array}{c}\hfill \langle {\chi }^2\rangle \simeq -\frac{1}{48{\pi }^2}{\int }_{{\eta }_0}^{\eta }d{\eta }_1\frac{a^2\left({\eta }_1\right)R\left({\eta }_1\right)}{\eta -{\eta }_1},\end{array}$$

(102)

$$\begin{array}{c}\hfill \langle {\left({\partial }_{\eta }\chi \right)}^2-{(\overrightarrow{\nabla }\chi )}^2\rangle \simeq -\frac{1}{96{\pi }^2}{\int }_{{\eta }_0}^{\eta }d{\eta }_1\frac{{\partial }_{{\eta }_1}^2\left(a^2\left({\eta }_1\right)R\left({\eta }_1\right)\right)}{\eta -{\eta }_1},\end{array}$$

(103)

$$\begin{array}{c}\hfill \langle \chi {\partial }_{\eta }\chi +\left({\partial }_{\eta }\chi \right)\chi \rangle \simeq -\frac{1}{48{\pi }^2}{\int }_{{\eta }_0}^{\eta }d{\eta }_1\frac{{\partial }_{{\eta }_1}\left(a^2\left({\eta }_1\right)R\left({\eta }_1\right)\right)}{\eta -{\eta }_1}.\end{array}$$

(104)

Inserting these expressions into (91), we obtain a closed integro-differential equation for R, which will be transformed into ordinary differential equation for harmonic oscillations of R neglecting the slow power law decrease of their amplitude at the scale of very fast oscillation time.

By the same reason the scale factor a varies very little during many oscillation times ${\omega }^{-1}=M_R^{-1}$. Thus, we expect that $d\eta /\eta \sim dt/t$ and that the dominant part in the integrals in Equations (102)–(104) is given by derivatives of R, since $R^{\prime }\sim \omega R+t^{-1}R\simeq \omega R$. So the dominant contribution of particle production is given by Equation (103), and is reduced to:

$$\begin{array}{c}\hfill \ddot{R}+3H\dot{R}+M_R^{2}R\simeq -\frac{1}{12\pi }\frac{M_R^2}{M_{Pl}^2}\frac{1}{a^4}{\int }_{{\eta }_0}^{\eta }d{\eta }_1\frac{{\partial }_{{\eta }_1}^2\left(a^2\left({\eta }_1\right)R\left({\eta }_1\right)\right)}{\eta -{\eta }_1}\\ \hfill \simeq -\frac{1}{12\pi }\frac{M_R^2}{M_{Pl}^2}{\int }_{t_0}^{t}d{t}_1\frac{\ddot{R}\left(t_1\right)}{t-t_1}.\end{array}$$

(105)

The equation is naturally non-local in time since the effect of particle production depends upon all the history of the system evolution.

The rigorous determination of the decay width of the scalaron is described in Ref. [22]. Here we present it in a simpler and intuitively clear way. We will look for the solution of Equation (105) in the form:

$$\begin{array}{c}\hfill R=R_{amp}cos(\omega t+\theta )exp(-\Gamma t/2),\end{array}$$

(106)

where $R_{amp}$ is the slowly varying amplitude of R-oscillations, $\theta$ is a constant phase depending upon initial conditions, and $\omega$ and $\Gamma$ is to be determined from Equation (105). The term $3H\dot{R}$ is not essential in the calculations presented below and will be neglected.

Assuming that $\Gamma$ is small, so the terms of order of ${\Gamma }^2$ are neglected and treating the r.h.s. of Equation (105) as perturbation we obtain:

$$\begin{array}{c}\hfill \left[\left(-{\omega }^2+M_R^2\right)cos(\omega t+\theta )+\Gamma \omega sin(\omega t+\theta )\right]e^{-\Gamma t/2}=\\ \hfill \frac{{\omega }^2{M}_R^2}{12\pi M_{Pl}^2}{e}^{-\Gamma t/2}{\int }_0^{t-t_0}\frac{d{t}_1}{t_1}\left[cos(\omega t+\theta )cos\omega t_1+sin(\omega t+\theta )sin\omega t_1\right]\end{array}$$

(107)

The first, logarithmically divergent, term in the integrand leads to mass renormalization and can be included into physical $M_R$, while the second term is finite and can be analytically calculated at large upper limit of integration, $\omega t\gg 1$, according to:

$$\begin{array}{c}\hfill {\int }_0^{t-t_0}\frac{d{t}_1}{t_1}sin\omega t_1={\int }_0^{\omega (t-t_0)}\frac{d\tau }{\tau }sin\tau ={\int }_{-\infty }^{\infty }\frac{d\tau }{\tau }\frac{e^{i\tau }-e^{-i\tau }}{4i}=\frac{\pi }{2},\end{array}$$

(108)

by closing the integration contour in the upper complex half-plane.

Comparing the l.h.s. and r.h.s. of Equation (107) we can conclude that $\omega =M_R$ and

$$\begin{array}{c}\hfill {\Gamma }_{\varphi ,0}=\frac{M_R^3}{24M_{Pl}^2},\end{array}$$

(109)

where sub-indices $(\varphi ,0)$ indicate that we consider the decay width of scalaron into a pair of scalar bosons $\varphi$ minimally coupled to curvature, i.e., $\xi =0$.

Our result coincides with the width of the scalaron decay into two massless minimally coupled scalars calculated in paper [25] and presented also in Ref. [26]. However, the width of the same process obtained in Ref. [27] is twice smaller, seemingly because of a numerical error.

4.2. Decay into Minimally Coupled Scalars, another Method

Now we calculate the rate of the scalaron decay into the same channel in a different way dealing with the energy loss of the scalaron into the produced particles. To this end we will use the equation of motion of the decay products and calculate the energy density of particles, $\varphi$, created by the oscillating gravitational field of the scalaron per unit time, ${\dot{\rho }}_{\varphi }$. Then we compare it to the energy density of the canonically normalized scalaron field [23]:

$$\begin{array}{c}\hfill \Phi =\frac{M_{Pl}}{\sqrt{48\pi }{M}_R^2}R.\end{array}$$

(110)

In what follows we use for R the dominant part of solution (84), which in physical time has the form:

$$\begin{array}{c}\hfill R=\frac{4M_{R}cos(M_{R}t+\theta )}{t},\end{array}$$

(111)

where $\theta$ is a constant phase determined by the initial conditions.

For this R the energy density of the scalaron is equal to:

$$\begin{array}{c}\hfill {\rho }_R=\frac{{\dot{\Phi }}^2+M_R^2{\Phi }^2}{2}=\frac{M_{Pl}^2({\dot{R}}^2+M_R^2{R}^2)}{96\pi M_R^4}\approx \frac{M_{Pl}^2}{6\pi t^2}.\end{array}$$

(112)

Please note that this is formally equal to the critical energy density of matter dominated universe.

Due to the energy conservation ${\dot{\rho }}_{\varphi }=-{\dot{\rho }}_R$. So for the rate of the energy dissipation of the scalaron we find:

$$\begin{array}{c}\hfill \Gamma ={\dot{\rho }}_{\varphi }/{\rho }_R,\end{array}$$

(113)

where ${\dot{\rho }}_{\varphi }$ is calculated along the standard lines of particle production theory in external time-dependent fields [28].

According to the Parker theorem [29,30] massless particles conformally coupled to gravity are not created by the gravitational field induced by the conformally flat FLRW metric. This is fulfilled for massless spin 1/2-fermions, massless gauge boson (up to conformal anomaly [31,32]), but is not always true for scalar bosons, as in the following lines.

The action of a real massive scalar field $\varphi$ with non-minimal coupling to gravity, $\xi {\varphi }^{2}R$, has the form:

$$S_{\varphi }^{\left(m\right)}=\frac{1}{2}\int d^{4}x\sqrt{-g}\left(g^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -\xi R{\varphi }^2-m_{\varphi }^2{\varphi }^2\right),$$

(114)

leading to the equation of motion:

$$\ddot{\varphi }+3H\dot{\varphi }-\frac{1}{a^2}\Delta \varphi +\left(\xi R+m_{\varphi }^2\right)\varphi =0.$$

(115)

It is convenient to study particle production in terms of the conformally rescaled field, and the conformal time according to Equation (90). In terms of these variables, Equation (115) transforms into

$$\begin{array}{c}\hfill {\partial }_{\eta }^2\chi -\Delta \chi +\left(\xi -\frac{1}{6}\right)a^{2}R\chi +m_{\varphi }^2{a}^2\chi =0,\end{array}$$

(116)

where $R=-6{\partial }_{\eta }^{2}a/a^3$.

The particle production by external time-dependent field $V\left(t\right)$ was studied in many works dedicated to the universe heating, see e.g., [33,34]. In particular, the production rate was calculated perturbatively (but not only) in textbook [10] for the (inflaton) field with the harmonic dependence on time:

$$\begin{array}{c}\hfill V\left(\eta \right)=V_{0}cos({\Omega }_c\eta +\theta ),\end{array}$$

(117)

where $V_0$ as well as ${\Omega }_c$ may slowly depend on time. The field $\chi$ satisfies the equation:

$$\begin{array}{c}\hfill {\partial }_{\eta }^2\chi -\Delta \chi +V\left(\eta \right)\chi =0.\end{array}$$

(118)

Since $dt=ad\eta$, and $\Omega dt={\Omega }_{c}d\eta$, the conformal frequency is ${\Omega }_c=a\Omega =a{M}_R$.

It was shown in Ref. [33] that the number density of particles created per unit of conformal time is:

$$\begin{array}{c}\hfill {\partial }_{\eta }{N}_{\chi }=\frac{V_0^2}{32\pi },\end{array}$$

(119)

where the number density is expressed in canonical way through the transformed field $\chi =\varphi /a$, namely

$$\begin{array}{c}\hfill N_{\chi }\sim \chi {\partial }_{\eta }\chi \sim a^3{N}_{\varphi }.\end{array}$$

(120)

Hence in physical time

$$\begin{array}{c}\hfill {\dot{N}}_{\varphi }=\frac{V_0^2}{32\pi a^4}.\end{array}$$

(121)

Now we apply this result for $\chi$ satisfying Equation (116) with $\xi =0$, $m_{\varphi }=0$, R determined by Equation (84), and the potential:

$$\begin{array}{c}\hfill V\left(t\right)=-\frac{1}{6}{a}^{2}R=-\frac{4a^2{M}_{R}cos(M_{R}t+\theta )}{6t}.\end{array}$$

(122)

Keeping in mind that each particle $\chi$ carries energy $M_R/2$ we find for the energy production rate per unit of physical time:

$$\begin{array}{c}\hfill {\dot{\rho }}_{\varphi }=\frac{1}{2}{M}_R{\dot{N}}_{\varphi }=\frac{M_R^3}{144\pi t^2}.\end{array}$$

(123)

And finally

$$\begin{array}{c}\hfill \Gamma (\xi =0,m_{\varphi }=0)=\frac{{\dot{\rho }}_{\varphi }}{{\rho }_R}=\frac{M_R^3}{24M_{Pl}^2},\end{array}$$

(124)

which coincides with the result obtained in the previous subsection.

4.3. Decay into Fermions

Here we calculate the probability of fermion-antifermion pair production by scalar field $\Phi$:

$$\begin{array}{c}\hfill \Phi ={\Phi }_{0}cos{M}_{R}t={\Phi }_0\frac{e^{i{M}_{R}t}+e^{-i{M}_{R}t}}{2}.\end{array}$$

(125)

We start from the calculation of the decay width of the $\Phi$-meson with mass $M_R$ into a pair of light fermions, assuming that the interaction Lagrangian has the form:

$$\begin{array}{c}\hfill L_{\psi }=g\Phi \overline{\psi }\psi ,\end{array}$$

(126)

where g is a dimensionless coupling constant and $\psi$ and $\overline{\psi }$ are the quantum field operators of the Dirac fermions. Making standard calculations we need to take matrix element of operators of the above Lagrangian between one-particle initial $\Phi$-state with zero momentum and fermion-antifermion final state, using the plane wave decomposition of the wave-function operators. In particular the positive energy projection of state (125) $\Phi \to a_{\Phi }exp(-i{M}_{R}t)$, where $a_{\Phi }$ is the annihilation operator of one-particle $\Phi$ state, hopefully it is not confused with the cosmological scale factor a. Taking matrix element squared and integrating over the phase space we find for the decay width the known expression

$$\begin{array}{c}\hfill {\Gamma }_{decay}=\frac{1}{2M_R}\int d{\tau }_2{\left|A_{\psi }\right|}^2=\frac{g^2{M}_R}{8\pi }.\end{array}$$

(127)

Here $d{\tau }_2$ is the invariant phase space of the fermion-antifermion pair and the factor $1/\left(2M_R\right)$ is related to standard relativistic normalisation of the plane wave function of $\Phi$ (see any introductory book on elementary particle physics, e.g., [35]). The chosen normalisation corresponds to a single particle over all space.

Now let us turn to the number density of fermions produced by the oscillating field (125). In the case of the decay the initial scalar particle is described by the plane wave $exp(-i{M}_{R}t)$ with positive energy. The number density of the initial particles is equal to:

$$\begin{array}{c}\hfill N_{\Phi }=i{\Phi }^{\ast }\overleftrightarrow{\partial }\Phi =i({\Phi }^{\ast }\dot{\Phi }-{\dot{\Phi }}^{\ast }\Phi )=\frac{1}{2}{M}_R{\Phi }_0^2.\end{array}$$

(128)

So the densities of fermions and antifermions produced per unit time can be obtained from Equation (127) by multiplication with $M_R{\Phi }_0^2/2$:

$$\begin{array}{c}\hfill {\dot{N}}_{\psi }={\dot{N}}_{\overline{\psi }}=\frac{1}{2}{\Gamma }_{decay}{M}_R{\Phi }_0^2=\frac{g^2}{16\pi }{M}_R^2{\Phi }_0^2.\end{array}$$

(129)

Now we have to go to conformal time and conformally transformed field, $\psi ={\psi }_c/a^{3/2}$, $\Phi ={\Phi }_c/a$. The equation of motion for ${\psi }_c$ becomes as is well know the free Dirac equation with mass scaled as $m_{\psi }\to m_{\psi }a$. The relation between the conformally transformed quantities and the physical ones on the l.h.s of Equation (129) has the form:

$$\begin{array}{c}\hfill {\partial }_{\eta }{N}_{{\psi }_c}=a^4{\dot{N}}_{\psi }.\end{array}$$

(130)

Analogously the factor $a^4$ arises in the r.h.s. of Equation (129).

The time dependence $a\left(t\right)$ is determined by the Hubble parameter (83):

$$\begin{array}{c}\hfill H=\frac{\dot{a}}{a}=\frac{2}{3t}[1+sin(M_{R}t+\theta )].\end{array}$$

(131)

Integrating this equation we obtain up to unessential constant factor:

$$\begin{array}{c}\hfill a\left(t\right)\sim t^{2/3}\left(1-\frac{2}{3t{M}_R}cos(M_{R}t+\theta )\right)\sim a_c\left(t\right)\left(1-\frac{2}{3t{M}_R}cos(M_{R}t+\theta )\right),\end{array}$$

(132)

where $a_c\left(t\right)\sim t^{2/3}$ and transition to conformal time is achieved with the relation $d\eta =dt/a_c\left(t\right)$.

In the considered case the particle production is induced by the oscillating part of the scale factor and we have to substitute in Equation (129) instead of $g\Phi$ the product of the fermion mass, $m_{\psi }$, by the amplitude of the oscillating part of the scale factor:

$$\begin{array}{c}\hfill g{\Phi }_0\to \frac{2m_{\psi }}{3t{M}_R}.\end{array}$$

(133)

Therefore, we obtain:

$$\begin{array}{c}\hfill {\dot{N}}_{\psi }=\frac{m_{\psi }^2}{36\pi t^2}.\end{array}$$

(134)

The decay width of scalaron by definition is $\Gamma =-{\dot{\rho }}_R/{\rho }_R$. Due to energy conservation ${\dot{\rho }}_R=-2{\dot{\rho }}_{\psi }$. Produced by the oscillating curvature, fermions have the energy $M_R/2$ each, so ${\dot{\rho }}_{\psi }=M_R{\dot{N}}_{\psi }/2$. Consequently, the width of the scalaron decay into a pair of massive fermions is:

$$\begin{array}{c}\hfill {\Gamma }_{\psi }=\frac{M_R{\dot{N}}_{\psi }}{{\rho }_R},\end{array}$$

(135)

where ${\dot{N}}_{\psi }$ and ${\rho }_R$ are given by Equations (134) and (112) respectively. Finally we obtain:

$$\begin{array}{c}\hfill {\Gamma }_{\psi }=\frac{m_{\psi }^2{M}_R}{36\pi t^2}·\frac{6\pi t^2}{M_{Pl}^2}=\frac{m_{\psi }^2{M}_R}{6M_{Pl}^2}.\end{array}$$

(136)

This result coincides with that presented in Refs. [18,26].

5. Heating of the Universe in $R^2$-Gravity

5.1. Generalities

In this section we consider the impact of particle production on the damping of the curvature oscillations and the effect of the created matter on the cosmological evolution. Consequently, Equations (55) and (60) acquire respectively the damping term, $\Gamma \dot{R}$. The equation for the curvature evolution in the presence of matter with the equation of state $P=w\rho$ takes the form:

$$\begin{array}{c}\hfill \ddot{R}+(3H+\Gamma )\dot{R}+M_R^{2}R=-\frac{8\pi M_R^2}{M_{Pl}^2}(1-3w)\rho .\end{array}$$

(137)

Due to particle production the covariant conservation (59) of the energy density of the primeval plasma is no longer valid:

$$\begin{array}{c}\hfill \dot{\rho }+3H(\rho +P)=\dot{\rho }+3H(1+w)\rho =\overline{S}\left[R\right]\ne 0.\end{array}$$

(138)

For the description of the energy influx we introduced in the right hand side of this equation non-zero source term, $\overline{S}\left[R\right]$, to be identified in what follows, see Equations (143) and (144). Equation (56) for the Hubble parameter remains the same.

For dimensionless functions and time (61) we obtain the following system of equations:

$$\begin{array}{ccc}& & h^{\prime }+2h^2=-r/6,\hfill \end{array}$$

(139)

$$\begin{array}{ccc}& & r^{\prime \prime }+(3h+\gamma )r^{\prime }+r=-8\pi {\mu }^2(1-3w)y,\hfill \end{array}$$

(140)

$$\begin{array}{ccc}& & y^{\prime }+3(1+w)hy=S\left[r\right],\hfill \end{array}$$

(141)

where $\mu =M_R/M_{Pl}$ and $\gamma =\Gamma /M_R$.

In what follows we solve these equations for different decay modes of the scalaron.

5.2. Minimally Coupled Scalar Mode

According to the calculations of Section 4.1 and Section 4.2, the width of the scalaron decay into two minimally coupled scalars is equal to:

$$\begin{array}{c}\hfill \Gamma =\frac{M_R^3}{24M_{Pl}^2}.\end{array}$$

(142)

Hence the source which is the contribution to ${\dot{\rho }}_{\varphi }=\Gamma {\rho }_R$ according to Equations (123) and (112) is:

$$\begin{array}{c}\hfill \overline{S}\left[R\right]={\dot{\rho }}_{\varphi }=\frac{M_R^3}{144\pi t^2}=\frac{M_R{R}_{ampl}^2}{2304\pi },\end{array}$$

(143)

where $R_{ampl}=4M_R/t$ is the amplitude of $R\left(t\right)$-oscillations. In terms of the dimensionless quantities the source term can be written as:

$$\begin{array}{c}\hfill S\left[r\right]=\frac{\langle r^2\rangle }{2304\pi }.\end{array}$$

(144)

Here $\langle r^2\rangle$ means amplitude squared of harmonic oscillations, $r_{ampl}^2$, of the dimensionless curvature $r\left(\tau \right)$. However, $r\left(\tau \right)$ not always oscillates harmonically. In this case we approximate $\langle r^2\rangle$ as $2{\left(r^{\prime }\right)}^2$ or $(-2r^{\prime \prime }r)$. For harmonic oscillations these expressions averaged over oscillation period coincide with $r_{ampl}^2$. The function $\langle r^2\rangle$ slowly changes with time.

5.2.1. Asymptotic Solution at $t\gg 1$, but $\Gamma t\le 1$.

Let us find asymptotic behaviour of the solutions of Equations (139)–(141), assuming that the matter is relativistic ($w=1/3$) and considering $\tau \gg 1$, but $\gamma \tau \le 1$. In such case we can neglect $\gamma$ in comparison with h in Equation (140) and the system (139)–(141) takes the following simple form:

$$\begin{array}{ccc}& & h^{\prime }+2h^2=-r/6,\hfill \end{array}$$

(145)

$$\begin{array}{ccc}& & r^{\prime \prime }+3h{r}^{\prime }+r=0,\hfill \end{array}$$

(146)

$$\begin{array}{ccc}& & y^{\prime }+4hy=\frac{<r^2>}{2304\pi }.\hfill \end{array}$$

(147)

The first two equations of this system coincide with Equation (65), so we can use asymptotic solutions (83) and (84) for the dimensionless Hubble parameter and the curvature scalar to find the energy density, $y\left(\tau \right)$, from Equation (147). In the r.h.s. of Equation (147) $\langle r^2\rangle$ can be understood as the square of the amplitude of the harmonic oscillations of r, i.e., $\langle r^2\rangle =16/{\tau }^2$. Equation (147) can be analytically integrated as:

$$\begin{array}{c}\hfill y\left(\tau \right)=\frac{1}{144\pi }{\int }_{{\tau }_0}^{\tau }\frac{d{\tau }_2}{{\tau }_2^2}exp\left[-4{\int }_{{\tau }_2}^{\tau }d{\tau }_{1}h\left({\tau }_1\right)\right],\end{array}$$

(148)

where ${\tau }_0\ll \tau$ is some initial value of the dimensionless time. The asymptotic result weakly depends upon ${\tau }_0$.

Taking $h\left(\tau \right)$ from Equation (83) we can partly perform integration over $d{\tau }_1$ as

$$\begin{array}{c}\hfill {\int }_{{\tau }_2}^{\tau }d{\tau }_{1}h\left({\tau }_1\right)=\frac{2}{3}ln\frac{\tau }{{\tau }_2}+{\int }_{{\tau }_2}^{\tau }\frac{d{\tau }_1}{{\tau }_1}sin({\tau }_1+\theta ).\end{array}$$

(149)

It is convenient to introduce new integration variables:

$$\begin{array}{c}\hfill {\eta }_1={\tau }_1/\tau ,{\eta }_2={\tau }_2/\tau .\end{array}$$

(150)

In terms of these variables we lastly obtain:

$$\begin{array}{c}\hfill y\left(\tau \right)=\frac{1}{144\pi \tau }{\int }_{{\eta }_0}^{1}d{\eta }_2{\eta }_2^{2/3}exp\left[-\frac{8}{3}{\int }_{{\eta }_2}^1\frac{d{\eta }_1}{{\eta }_1}sin\left(\tau {\eta }_1+\theta \right)\right].\end{array}$$

(151)

As we see below, the integral in the exponent is small, so the exponential factor in expression (151) is close to unity and thus the dominant asymptotic term is $y\left(\tau \right)\sim 1/\left(240\pi \tau \right)$. Higher order oscillating corrections we estimate as follows. To calculate the asymptotic behavior of the integral

$$\begin{array}{c}\hfill I={\int }_{{\eta }_2}^1\frac{d{\eta }_1}{{\eta }_1}sin\left(\tau {\eta }_1+\theta \right)\end{array}$$

(152)

at large $\tau$ we present the oscillating factor as

$$\begin{array}{c}\hfill sin\left(\tau {\eta }_1+\theta \right)=\frac{1}{2i}\left[e^{i(\tau {\eta }_1+\theta )}-e^{-i(\tau {\eta }_1+\theta )}\right].\end{array}$$

(153)

The integral over ${\eta }_1$ along the real axis from ${\eta }_2$ to 1 can be reduced to two integrals over $\zeta$ from 0 to ∞ along ${\eta }_1={\eta }_2\pm i\zeta$ and ${\eta }_1=1\pm i\zeta$. The signs in front of $i\zeta$ are chosen so that the corresponding exponent in Equation (153) vanishes at infinity. Finally we obtain:

$$\begin{array}{c}\hfill I={\int }_0^{\infty }d\zeta e^{-\tau \zeta }\left[\frac{{\eta }_{2}cos\left(\tau {\eta }_2+\theta \right)+\zeta sin\left(\tau {\eta }_2+\theta \right)}{{\eta }_2^2+{\zeta }^2}-\frac{cos\left(\tau +\theta \right)+\zeta sin\left(\tau +\theta \right)}{1+{\zeta }^2}\right].\end{array}$$

(154)

The effective value of $\zeta$ in this integral is evidently $\sim 1/\tau$, thus I is inversely proportional to $\tau$ in the leading order. At large $\tau$ it is much smaller than unity, so we can expand the exponential function $exp(-8I/3)$, see Equation (151), up to the first order and obtain:

$$\begin{array}{c}\hfill y_{1/3}=\frac{1}{240\pi \tau }+\frac{1}{90\pi }\frac{cos\left(\tau +\theta \right)}{{\tau }^2}-\frac{1}{54\pi {\tau }^2}{\int }_{ϵ}^1\frac{d{\eta }_2}{{\eta }_2^{1/3}}cos\left(\tau {\eta }_2+\theta \right),\end{array}$$

(155)

where the subindex (1/3) indicates that $w=1/3$ and $ϵ={\tau }_0/\tau \ll 1$. The last integral is proportional to $1/{\tau }^{2/3}$ and is subdominant. We neglect it in what follows.

In Figure 4 the dimensionless energy density $240\pi y\left(\tau \right)$ is presented as a result of numerical calculation of the integral (148) or equivalently (151) (solid), which is the exact solution of the differential Equation (147). It is compared with the analytic asymptotic expansion (155) of the same integral (148) (dotted). The calculations are done for mildly and very large $\tau$. One can see that the agreement is very good.

Now let us consider the asymptotic solution at $\tau \gg 1$, $\gamma \tau \le 1$ for non-relativistic matter with $w=0$.

In this case Equations (62)–(64) take the form

$$\begin{array}{ccc}& & h^{\prime }+2h^2=-r/6,\hfill \end{array}$$

(156)

$$\begin{array}{ccc}& & r^{\prime \prime }+3h{r}^{\prime }+r=-8\pi {\mu }^{2}y,\hfill \end{array}$$

(157)

$$\begin{array}{ccc}& & y^{\prime }+3hy=S\left[r\right],\hfill \end{array}$$

(158)

Since $\mu \ll 1$ the impact of the r.h.s. in Equation (157) is not essential and we can use the expressions (83) and (84) for h and r from the previous subsection. Moreover, the numerical solutions presented in Figure 3 strongly support this presumption. The only essential difference with the $w=1/3$ case arises in Equation (158) governing the evolution of the energy density. So to calculate $y\left(\tau \right)$ we can use slightly modified obtained above results. We need to solve Equation (158). Correspondingly, there appears a coefficient (−3) in the exponent, instead of (−4), as in Equation (148):

$$\begin{array}{c}\hfill y\left(\tau \right)=\frac{1}{144\pi }{\int }_{{\tau }_0}^{\tau }\frac{d{\tau }_2}{{\tau }_2^2}exp\left[-3{\int }_{{\tau }_2}^{\tau }d{\tau }_{1}h\left({\tau }_1\right)\right].\end{array}$$

(159)

Repeating the same calculations as above we obtain instead of Equation (155):

$$\begin{array}{c}\hfill y_0=\frac{1}{144\pi \tau }+\frac{cos\left(\tau +\theta \right)}{72\pi {\tau }^2}.\end{array}$$

(160)

5.2.2. LSP Density for the Scalaron Decay into Minimally Coupled Scalars

In this section, we find the frozen number density of X-particles assuming that the scalaron decays into two minimally coupled scalars with the decay width (142). According to the solution (155) the energy density of relativistic massless scalars, ${\rho }_s$, created by the oscillating curvature, $R\left(t\right)$, drops down with time as:

$$\begin{array}{c}\hfill {\rho }_s=\frac{M_R^3}{240\pi t}.\end{array}$$

(161)

This expression can be compared with the energy density of matter in the standard GR cosmology:

$$\begin{array}{c}\hfill {\rho }_{GR}=\frac{3H^2{M}_{Pl}^2}{8\pi }\approx \frac{3M_{Pl}^2}{32\pi t^2}.\end{array}$$

(162)

Because of the difference between the cosmological evolution in the $R^2$-theory and General Relativity, the conditions for thermal equilibrium in the primeval plasma also differs very much. Assuming that the equilibrium with temperature T is established, we estimate the particle reaction rate as

$$\begin{array}{c}\hfill {\Gamma }_{scat}\sim {\alpha }^2{\beta }_{scat}T,\end{array}$$

(163)

where $\alpha$ is the coupling constant of the particle interactions, typically $\alpha \sim {10}^{-2}$, and ${\beta }_{scat}$ is the number of scattering channels, ${\beta }_{scat}\sim 100$, see discussion below Equation (9). Equilibrium is enforced if ${\Gamma }_{scat}>H\sim 1/t$ or ${\alpha }^2{\beta }_{scat}Tt>1$. The energy density of relativistic matter in thermal equilibrium is expressed through the temperature as:

$$\begin{array}{c}\hfill {\rho }_{therm}=\frac{{\pi }^2{g}_{\ast }}{30}{T}^4,\end{array}$$

(164)

where $g_{\ast }$ is the number of relativistic species in the plasma. We take $g_{\ast }\sim 100$. This number is generally accepted and includes 3 families of coloured quarks and antiquarks (36), gluons (16), intermediate bosons and photons (6), three families of leptons (12), Higgs bosons (4) and possibly supersymmetric partners. All together this is the number about 100.

Using Equations (161) and (164), we find the equilibrium condition for the case of scalaron decay into a pair of massless scalars:

$$\begin{array}{c}\hfill {\left({\alpha }^2{\beta }_{scat}Tt\right)}_s=\frac{{\alpha }^2{\beta }_{scat}}{8{\pi }^3{g}_{\ast }}{\left(\frac{M_R}{T}\right)}^3\approx 4·{10}^{-7}{\left(\frac{M_R}{T}\right)}^3>1.\end{array}$$

(165)

On the other hand, for the GR-cosmology, it follows from Equations (162) and (164) that the equilibrium is established when:

$$\begin{array}{c}\hfill {\left({\alpha }^2{\beta }_{scat}Tt\right)}_{GR}={\alpha }^2{\beta }_{scat}{\left(\frac{90}{32{\pi }^3{g}_{\ast }}\right)}^{1/2}\frac{M_{Pl}}{T}\approx 3·{10}^{-4}\frac{M_{Pl}}{T}>1.\end{array}$$

(166)

Let us estimate now the so-called heating temperature, i.e., the temperature of the cosmological plasma after complete decay of the scalaron. It can be estimated from the expression for the energy density of matter at the time moment equal to the inverse decay width $t_d=1/\Gamma$. For the decay into scalars, $\Gamma$ is given by Equation (142) and

$$\begin{array}{c}\hfill {\rho }_s(t_d=1/{\Gamma }_s)=\frac{M_R^3}{240\pi t_d}=\frac{M_R^6}{5760\pi M_{Pl}^2}=\frac{{\pi }^2}{30}{g}_{\ast }{T}_{hs}^4.\end{array}$$

(167)

Hence the heating temperature for the dominant decay of the scalaron into scalar particles is equal to:

$$\begin{array}{c}\hfill T_{hs}\approx \frac{M_R}{{\left(192{\pi }^3{g}_{\ast }\right)}^{1/4}}{\left(\frac{M_R}{M_{Pl}}\right)}^{1/2}.\end{array}$$

(168)

For $M_R=3\times {10}^{13}$ GeV and $g_{\ast }=100$ the heating temperature is $T_{hs}\approx {10}^9$ GeV.

We see that the heating temperature is considerably lower than the temperature at which thermal equilibrium is established, see Equation (165).

Equating the energy density (161) to the energy density of relativistic plasma with temperature T given by Equation (164)

$$\begin{array}{c}\hfill {\rho }_s=\frac{M_R^3}{240\pi t}=\frac{{\pi }^2{g}_{\ast }{T}^4}{30},\end{array}$$

(169)

we obtain:

$$\begin{array}{c}\hfill t{T}^4=\frac{M_R^3}{8{\pi }^3{g}_{\ast }}=const\end{array}$$

(170)

and

$$\begin{array}{c}\hfill \frac{\dot{T}}{T}=-\frac{1}{4t}.\end{array}$$

(171)

Comparing Equations (170) and (171) with analogous Equations (16) and (17), we see that the connection between temperature and time in $R^2$-theory very much differs from that in the conventional cosmology governed by GR.

Considering relations (170) and (171) we find that the Zeldovich Equation (7) for the dimensionless function f (13) with the annihilation cross-section (9) takes the form:

$$\begin{array}{c}\hfill \frac{df}{dx}=-\frac{{\alpha }^2{\beta }_{ann}}{4{\pi }^2{g}_{\ast }}{\left(\frac{M_R}{M_X}\right)}^3{\left(\frac{a_{in}}{a}\right)}^3\frac{n_{in}}{T^3}\left(f^2-f_{eq}^2\right).\end{array}$$

(172)

In $R^2$ theory $T\sim t^{-1/4}$, $a\sim t^{2/3}$, and $a^3{T}^3\sim 1/T^5$, so the ratio ${(a_{in}/a\left(t\right))}^3$ can be estimated as

$$\begin{array}{c}\hfill {\left(\frac{a_{in}}{a\left(t\right)}\right)}^3={\left(\frac{t_{in}}{t}\right)}^2={\left(\frac{T_{in}}{T}\right)}^{-8}=\frac{1}{x^8},\end{array}$$

(173)

where $x=M_X/T$. The initial number density of X-particles can be taken as $n_{in}=0.12g_s{T}_{in}^3=0.12g_s{M}_X^3$ (the final asymptotic result does not depend upon the intial value), and so

$$\begin{array}{c}\hfill \frac{n_{in}}{T^3}=0.12g_s{\left(\frac{M_X}{T}\right)}^3=0.12g_s{x}^3.\end{array}$$

(174)

Since the density of X-particles is given by Equation (13), its ratio to the number density of photons, $n_{\gamma }=0.24T^3$, is equal to:

$$\begin{array}{c}\hfill \frac{n_X}{n_{\gamma }}=\frac{g_s}{2}\frac{f}{x^5}.\end{array}$$

(175)

Equation (172) governing the evolution of X-particles in the scalaron dominated regime is transformed to

$$\begin{array}{c}\hfill \frac{df}{dx}=-\frac{0.03g_s{\alpha }^2{\beta }_{ann}}{{\pi }^2{g}_{\ast }}{\left(\frac{M_R}{M_X}\right)}^3\frac{f^2-f_{eq}^2}{x^5}\equiv -Q_{sc}\frac{f^2-f_{eq}^2}{x^5},\end{array}$$

(176)

where

$$\begin{array}{c}\hfill Q_{sc}=\frac{0.03g_s{\alpha }^2{\beta }_{ann}}{{\pi }^2{g}_{\ast }}{\left(\frac{M_R}{M_X}\right)}^3.\end{array}$$

(177)

Since the coefficient $Q_{sc}$ in front of $(f^2-f_{eq}^2)$ in Equation (176) is normally huge, then initially the solution is close to the equilibrium one, $f=f_{eq}(1+\delta )$, with $\delta$ equal to

$$\begin{array}{c}\hfill \delta =-\frac{x^5}{2Q_{sc}{f}_{eq}^2}\frac{d{f}_{eq}}{dx}\approx \frac{x^5}{2Q_{sc}{f}_{eq}}.\end{array}$$

(178)

Please note that $d{f}_{eq}/dx\approx -f_{eq}$ for large x. This solution is valid till $\delta$ remains small, $\delta \le 1$. According to Equations (11), (13), and (173)

$$\begin{array}{c}\hfill f_{eq}=\frac{1}{0.12}{\left(\frac{x}{2\pi }\right)}^{3/2}{e}^{-x}{x}^5.\end{array}$$

(179)

and according to Equations (178) and (173) we have:

$$\begin{array}{c}\hfill \delta =\frac{x^5}{2Q_{sc}{f}_{eq}}=\frac{0.06}{Q_{sc}}{\left(\frac{x}{2\pi }\right)}^{-3/2}{e}^x,\end{array}$$

(180)

where $Q_{sc}$ is given by Equation (177).

The freezing temperature $T_{fr}=M_X/x_{fr}$ at which deviation from equilibrium becomes of order of unity in this case is approximately:

$$\begin{array}{c}\hfill x_{fr}\approx ln{Q}_{sc}+\frac{3}{2}ln(ln{Q}_{sc})-\frac{3}{2}ln\left(2\pi \right)+ln0.06\approx ln{Q}_{sc}+\frac{3}{2}ln(ln{Q}_{sc})-5.7.\end{array}$$

(181)

Since $Q_{sc}\gg 1$, then $x_{fr}$ is also large, typically $x_{fr}\sim (10-100)$ depending upon the interaction strength.

After x becomes larger than $x_{fr}$, $f_{eq}^2$ can be neglected in comparison to $f^2$ and Equation (176) with the initial condition $f=f_{fr}$ at $x=x_{fr}$ is simply integrated giving the asymptotic result at $x\to \infty$:

$$\begin{array}{c}\hfill f\left(x\right)=\frac{f_{fr}}{1+\frac{Q_{sc}{f}_{fr}}{4}\left(\frac{1}{x_{fr}^4}-\frac{1}{x^4}\right)}\underset{x\to \infty }{⟶}\frac{4x_{fr}^4}{Q_{sc}}\equiv f_{as}.\end{array}$$

(182)

The last asymptotic limit is valid when $x\gg x_{fr}$ and $Q_{sc}{f}_{fr}/\left(4x_{fr}^4\right)>1$. It is fulfilled because $x_{fr}\sim ln{Q}_{sc}$ is sufficiently large and according to Equations (180) and (179)

$$\begin{array}{c}\hfill \frac{Q_{sc}{f}_{fr}}{4x_{fr}^4}\sim x_{fr}^{5/2}\gg 1.\end{array}$$

(183)

Thus, $f\left(x\right)$ tends to a constant value, $f_{as}$ (182), but, according to Equation (175), the ratio of the number densities of X-particles with respect to photons drops down strongly, as $1/x^5$, in contrast to the analogous ratio in GR regime. This decrease is induced by the rise of the density of relativistic species created by the scalaron decay. This drop continues till $\Gamma t\sim 1$, when scalaron field disappears and the cosmology returns to the usual GR one. It happens at the temperature given by Equation (168). This temperature should be compared with the temperature of the establishment of thermal equilibrium $T_{eq}\approx 2\times {10}^{-3}{M}_R$, as follows from Equation (165).

Our results are valid if $T_{eq}>M_X>T_{hs}$. However, if the condition $T_{eq}>M_X$ is not fulfilled, the cosmological number density of heavy massive particles with masses larger than $T_{hs}$ would still be suppressed and even stronger than in the case of $T_{eq}>M_X$.

After the complete scalaron decay, the ratio of the number densities of X-particles to that of photons remains essentially constant, as it normally happens in GR cosmology. Therefore, the present day ratio $n_X/n_{\gamma }$ can be estimated as the value of this ratio at $T=T_{hs}$ (168), i.e., at x equal to:

$$\begin{array}{c}\hfill x_{hs}={\left(192{\pi }^3{g}_{\ast }\right)}^{1/4}\left(\frac{M_X}{M_R}\right){\left(\frac{M_{Pl}}{M_R}\right)}^{1/2}.\end{array}$$

(184)

Using Equations (175), (177) and (182) we estimate the number density of the X-particles at the present time as

$$\begin{array}{c}\hfill {\left(\frac{n_X}{n_{\gamma }}\right)}_{now}=\frac{2g_s{x}_{fr}^4}{Q_{sc}{x}_{hs}^5}=\frac{2{\pi }^2{g}_{\ast }{x}_{fr}^4}{0.03{\left(192{\pi }^3{g}_{\ast }\right)}^{5/4}{\alpha }^2{\beta }_{ann}}{\left(\frac{M_R}{M_X}\right)}^2{\left(\frac{M_R}{M_{Pl}}\right)}^{5/2},\end{array}$$

(185)

where $x_{fr}$ is determined by Equation (181).

To calculate the present day energy density of X-particles one needs to multiply the r.h.s. of Equation (185) by $M_X$ and by the present day number density of photons $n_{\gamma ,0}=412$/cm${}^3$. Taking $g_{\ast }\approx 100$, $\alpha \approx 0.01$, ${\beta }_{ann}\approx 10$, and $M_R=3\times {10}^{13}$ GeV we obtain the estimate:

$$\begin{array}{c}\hfill {\rho }_X\approx {10}^8\left(\frac{{10}^{10}\mathrm{GeV}}{M_X}\right)\mathrm{GeV}/{\mathrm{cm}}^3.\end{array}$$

(186)

This is to be compared with the observed energy density of dark matter ${\rho }_{DM}\approx 1$ keV/cm${}^3$. We see that X-particles must have huge mass, much higher than $M_R$ to make reasonable dark matter density. However, if $M_X>M_R$, the decay of the scalaron into $X\overline{X}$-channel would be strongly suppressed and such LSP with the mass slightly larger than $M_R$ could successfully make the cosmological dark matter. We will not further pursue this possibility here but turn in the next section to LSP being a fermion.

5.3. Fermion Decay Mode

Let us assume now that the scalaron decays only to fermions. According to the calculations in Section 4.3 the width of the scalaron decay into a pair of massive fermions with mass $m_f$, as given by Equation (136) is equal to:

$$\begin{array}{c}\hfill {\Gamma }_f=\frac{M_R{m}_f^2}{6M_{Pl}^2},\end{array}$$

(187)

which agrees with Refs. [18,26].

Decay probability is dominated by the heaviest fermion. The largest contribution into the cosmological energy density at scalaron dominated regime is presented by the decay into heaviest fermion species.

According to Equation (134):

$$\begin{array}{c}\hfill {\dot{\rho }}_f=\frac{M_R{\dot{N}}_{\psi }}{2}=\frac{M_R{m}_f^2}{72\pi t^2}.\end{array}$$

(188)

This expression can be rewritten in terms of the amplitude of the curvature oscillations, $R_{ampl}=4M_R/t$ as:

$$\begin{array}{c}\hfill {\dot{\rho }}_f=\frac{m_f^2{R}_{ampl}^2}{1152\pi M_R}.\end{array}$$

(189)

Integrating Equation (147) and making transformation to physical quantities, we achieve that the energy density of the produced relativistic fermions is equal to:

$$\begin{array}{c}\hfill {\rho }_f=\frac{M_R{m}_f^2}{120\pi t}.\end{array}$$

(190)

From (164) and (190) follows that thermal equilibrium in the case of the decay into a pair of fermions is established, when

$$\begin{array}{c}\hfill {\left({\alpha }^2{\beta }_{scat}Tt\right)}_f=\frac{{\alpha }^2{\beta }_{scat}}{4{\pi }^3{g}_{\ast }}\frac{M_R{m}_f^2}{T^3}\approx 8·{10}^{-7}\frac{M_R{m}_f^2}{T^3}>1.\end{array}$$

(191)

Using Equations (187) and (190), we find the temperature of the universe heating for the case of scalaron decay into fermions is:

$$\begin{array}{c}\hfill T_{hf}=\frac{1}{{\left(24{\pi }^3{g}_{\ast }\right)}^{1/4}}{\left(\frac{M_R}{M_{Pl}}\right)}^{1/2}{m}_f\approx {10}^{-4}{m}_f.\end{array}$$

(192)

We assume that the mass of the lightest supersymmetric particle is considerably smaller than the masses of the other decay products, $m_X<<m_f$, at least as $m_X\le 0.1m_f$. Then the direct production of X-particles by $R\left(t\right)$ can be neglected. In such a case LSP are dominantly produced by the secondary reactions in the plasma, which was created by the scalaron production of heavier particles.

Using expression (192) for the temperature of the universe heating after the scalaron decay, we find

$$\begin{array}{c}\hfill x_{hf}\equiv \frac{m_X}{T_{hf}}\approx {10}^4\frac{m_X}{m_f}.\end{array}$$

(193)

According to Equation (191) cosmic plasma thermalised at temperatures below

$$\begin{array}{c}\hfill T_{eqf}\approx {10}^{-2}{m}_f{\left(\frac{M_R}{m_f}\right)}^{1/3}.\end{array}$$

(194)

The time-temperature dependence, as follows from Equations (190) and (164), is:

$$\begin{array}{c}\hfill t{T}^4=\frac{M_R{m}_f^2}{4{\pi }^3{g}_{\ast }}.\end{array}$$

(195)

Kinetic equation for freezing of fermionic species can be solved in complete analogy with what was done in the previous section. The relative number density, f, is defined by the same relation (13) and the kinetic equation for f has the same form:

$$\begin{array}{c}\hfill \frac{df}{dx}=-Q_f\frac{f^2-f_{eq}^2}{x^5},\end{array}$$

(196)

where

$$\begin{array}{c}\hfill Q_f=\frac{{\alpha }^2{\beta }_{ann}}{2{\pi }^2{g}_{\ast }}\frac{M_R{m}_f^2}{m_X^6}{n}_{in},\end{array}$$

(197)

and $n_{in}=0.09g_s{m}_X^3$ is the initial number density of X-particles at the temperatures $T\sim m_X$.

We take as in Section 5.2.2

$$\begin{array}{c}\hfill f\approx f_{eq}(1+\delta ),\end{array}$$

(198)

where

$$\begin{array}{c}\hfill \delta \approx \frac{x^5}{2Q_f{f}_{eq}}.\end{array}$$

(199)

The equilibrium relative number density, $f_{eq}$, is slightly different from the similar quantity for bosons (179) and is equal to:

$$\begin{array}{c}\hfill f_{eq}=\frac{1}{0.09}{\left(\frac{x}{2\pi }\right)}^{3/2}{e}^{-x}{x}^5.\end{array}$$

(200)

The freezing temperature is defined by

$$\begin{array}{c}\hfill x_{fr}\approx ln{Q}_f+\frac{3}{2}ln(ln{Q}_f)-\frac{3}{2}ln\left(2\pi \right)+ln0.045\approx ln{Q}_f+\frac{3}{2}ln(ln{Q}_f)-5.86,\end{array}$$

(201)

and the so-called frozen value of f is equal to

$$\begin{array}{c}\hfill f_{fr}=\frac{x_{fr}^5}{Q_f}.\end{array}$$

(202)

Using expression (197) for $Q_f$ we find that the frozen number density of X-particles, i.e., taken at $T=T_{fr}=m_X/x_{fr}$ is

$$\begin{array}{c}\hfill n_{Xfr}=\frac{{\pi }^2{g}_{\ast }}{2{\alpha }^2{\beta }_{ann}{ln}^3{Q}_f}\frac{m_X^6}{M_R{m}_f^2}.\end{array}$$

(203)

Some additional burning of X-particles takes place during the period, when $f>f_{eq}$ and Equation (196) is simplified to:

$$\begin{array}{c}\hfill \frac{df}{dx}=-Q_f\frac{f^2}{x^5}.\end{array}$$

(204)

The solution of this equation with the initial condition $f\left(x_{fr}\right)=f_{fr}$ for the asymptotic value at large $x\gg x_{fr}$ is trivially found:

$$\begin{array}{c}\hfill f\left(x\right)=\frac{f_{fr}}{1+\frac{Q_f{f}_{fr}}{4}\left(\frac{1}{x_{fr}^4}-\frac{1}{x^4}\right)}x\to \infty ⟶\frac{4x_{fr}^4}{Q_f}\equiv f_{as}.\end{array}$$

(205)

This would be the asymptotic value of the relative number density of the heavy stable relics in the standard approach. However, $n_X$ does not drop down as $1/a^3$, but much faster due to the extra heating of plasma by the scalaron decay, which does not create X-particles if their coupling to the scalaron is sufficiently weak, as is assumed above. One should, however, remember that there exists a continuous production of heavier fermions, which as is mentioned in the second paragraph of this Section, is much stronger than the direct production of LSP, i.e., of the X-particles. However, the heavy fermions f are produced with huge energy $E_f\sim M_R/2$. This energy is thermalized and is transformed into the energy of relativistic species producing $M_R/T$ relativistic particles per one X particles created by the f decays. Moreover, some heavy fermions could annihilate without creation of X particles, but this effect is rather weak, even with an account of relativistic delay of the decay.

Let us calculate now the ratio of the number densities of X-particles, to the density of the relativistic species. The latter is taken as $m_X^3$ at the initial temperature, $T_{in}=m_X$, but in realistic case it can be higher by a factor of a few. E.g. the number density of photons is $0.24T^3$ and the same is true for other relativistic species: leptons, quarks, gluons, and even for the electroweak bosons, so our assumption leads to some overestimate of X density. The precise value depends upon the concrete model.

After freezing, the number density of X-particles remains constant in the comoving volume, i.e.,

$$\begin{array}{c}\hfill n_X=n_{fr}{\left(\frac{a_{fr}}{a}\right)}^3=n_{fr}{\left(\frac{t_{fr}}{t}\right)}^2=n_{fr}{\left(\frac{x_{fr}}{x}\right)}^8,\end{array}$$

(206)

where $n_{fr}$ is frozen number density of X-particles, $a_{fr}$ is the value of the cosmological scale factor at the moment of freezing, and we used the expansion law $a\sim t^{2/3}$ and the relation between time and temperature $t{T}^4=const$.

The energy density of the relativistic particles drops in the course of expansion from the moment of X-freezing as:

$$\begin{array}{c}\hfill {\rho }^{rel}={\rho }_{fr}^{rel}\left(\frac{t_{fr}}{t}\right)={\rho }_{fr}^{rel}{\left(\frac{x_{fr}}{x}\right)}^4,\end{array}$$

(207)

where

$$\begin{array}{c}\hfill {\rho }_{fr}^{rel}=\frac{{\pi }^2{g}_{\ast }}{30}{T}_{fr}^4,\end{array}$$

(208)

is the energy density of relativistic matter at the moment of X-freezing.

The number density of relativistic particles is related to their energy density according to

$$\begin{array}{c}\hfill n^{rel}\approx \frac{{\rho }^{rel}}{3T}=n_{fr}^{rel}{\left(\frac{x_{fr}}{x}\right)}^3,\end{array}$$

(209)

where $n^{relf}\approx {\pi }^2{g}_{\ast }{T}_{fr}^3/90$. We neglected here the difference between the effective number of relativistic species, $g_{\ast }$, in the expression for the energy density and the similar coefficient in the expression for the number density.

Correspondingly:

$$\begin{array}{c}\hfill \frac{n_X}{n^{rel}}=\frac{n_{Xfr}}{n_{fr}^{rel}}{\left(\frac{x_{fr}}{x}\right)}^5=\frac{n_X^{\left(in\right)}}{n_{fr}^{rel}}{\left(\frac{x_{fr}}{x}\right)}^5{\left(\frac{x_{in}}{x_{fr}}\right)}^8\frac{x_{fr}^5}{Q_f}.\end{array}$$

(210)

Substituting $Q_f$ from Equation (197) we find:

$$\begin{array}{c}\hfill \frac{n_X}{n^{rel}}=\frac{180}{{\alpha }^2{\beta }_{ann}}\frac{m_X^3}{M_R{m}_f^2}{\left(\frac{x_{fr}}{x}\right)}^5.\end{array}$$

(211)

This ratio would evolve in this way as a function of x till the complete decay of the scalaron at $T=T_{hf}$ (192). Using (193) and (201) we ultimately find:

$$\begin{array}{c}\hfill {\left(\frac{n_X}{n^{rel}}\right)}_h=\frac{180{(ln\left(Q_f\right))}^5}{{\alpha }^2{\beta }_{ann}{x}_{hf}^5}\frac{m_X^3}{M_R{m}_f^2}=\frac{180{(ln\left(Q_f\right))}^5}{{\alpha }^2{\beta }_{ann}{\left(24{\pi }^3{g}_{\ast }\right)}^{5/4}}{\left(\frac{M_R}{M_{Pl}}\right)}^{5/2}\frac{m_f^3}{M_R{m}_X^2}.\end{array}$$

(212)

Later on at GR stage this ratio does not change much, decreasing only due to the heating of the plasma by the massive particle annihilation.

As is discussed above, after Equation (205), there could be an additional production of X-particles by the decays of heavier fermions f. However, the contribution of such decays into the ratio $n_X/n^{rel}$ (211) at the freezing temperature $T_{fr}$ is $T_{fr}/M_R$ and decreases with dropping temperature. The freezing temperature is determined by Equation (201). Hence the extra contribution to the number density of X-particles can be safely neglected, if

$$\begin{array}{c}\hfill \frac{180\pi }{{\alpha }^2{\beta }_{ann}}{\left(\frac{m_X}{m_f}\right)}^{2}ln{Q}_f>1.\end{array}$$

(213)

In fact, the effect of the additional X-production is somewhat weaker due to $f\overline{f}$-annihilation, which eliminates the creation of X-particles. An account of several types of bosonic and fermionic superpartners does not change our estimates if they are heavier than X roughly by factor ten.

The contemporary energy density of X-particle can be approximately estimated as

$$\begin{array}{c}\hfill {\rho }_X=m_X{n}_{\gamma }{\left(\frac{n_X}{n_{rel}}\right)}_h=7·{10}^{-9}\frac{m_f^3}{m_X{M}_R}{\mathrm{cm}}^{-3},\end{array}$$

(214)

where $n_{\gamma }\approx 412$/cm${}^3$ and we take $\alpha =0.01$, ${\beta }_{ann}=10$, $g_{\ast }=100$, $m_f={10}^5$ GeV, and $m_X={10}^4$ GeV. For the chosen values of the parameters $Q_f\approx 2.7\times {10}^4$, and $ln{Q}_f\approx 10$.

This energy density should be close to the energy density of the cosmological dark matter, ${\rho }_{DM}\approx 1$ keV/cm${}^3$. It can be easily achieved with $m_X\sim {10}^6$ GeV and $m_f\sim {10}^7$ GeV:

$$\begin{array}{c}\hfill {\rho }_X=0.23{\left(\frac{m_f}{{10}^7\mathrm{GeV}}\right)}^3\left(\frac{{10}^6\mathrm{GeV}}{m_X}\right)\frac{\mathrm{keV}}{{\mathrm{cm}}^3}.\end{array}$$

(215)

5.4. Gauge Bosons Mode

In this section we consider the scalaron decay induced by the conformal anomaly. Production of massless gauge bosons by conformally flat gravitational field was first studied in Refs. [31,32] and applied to the problem of heating in $R^2$-inflation in Ref. [36]. The scalaron decay width for this channel is equal to:

$$\begin{array}{c}\hfill {\Gamma }_{anom}=\frac{{\beta }_1^2{\alpha }^{2}N}{96{\pi }^2}\frac{M_R^3}{M_{Pl}^2},\end{array}$$

(216)

where ${\beta }_1$ is the first coefficient of the beta-function, N is the rank of the gauge group, and $\alpha$ is the gauge coupling constant. We take ${\beta }_1^2=49$, $N=8$. The coefficient ${\beta }_1^{2}N$ includes also the contribution from fermionic loops into charge renormalisation. However, the fermion corrections are relatively unimportant and are not included.

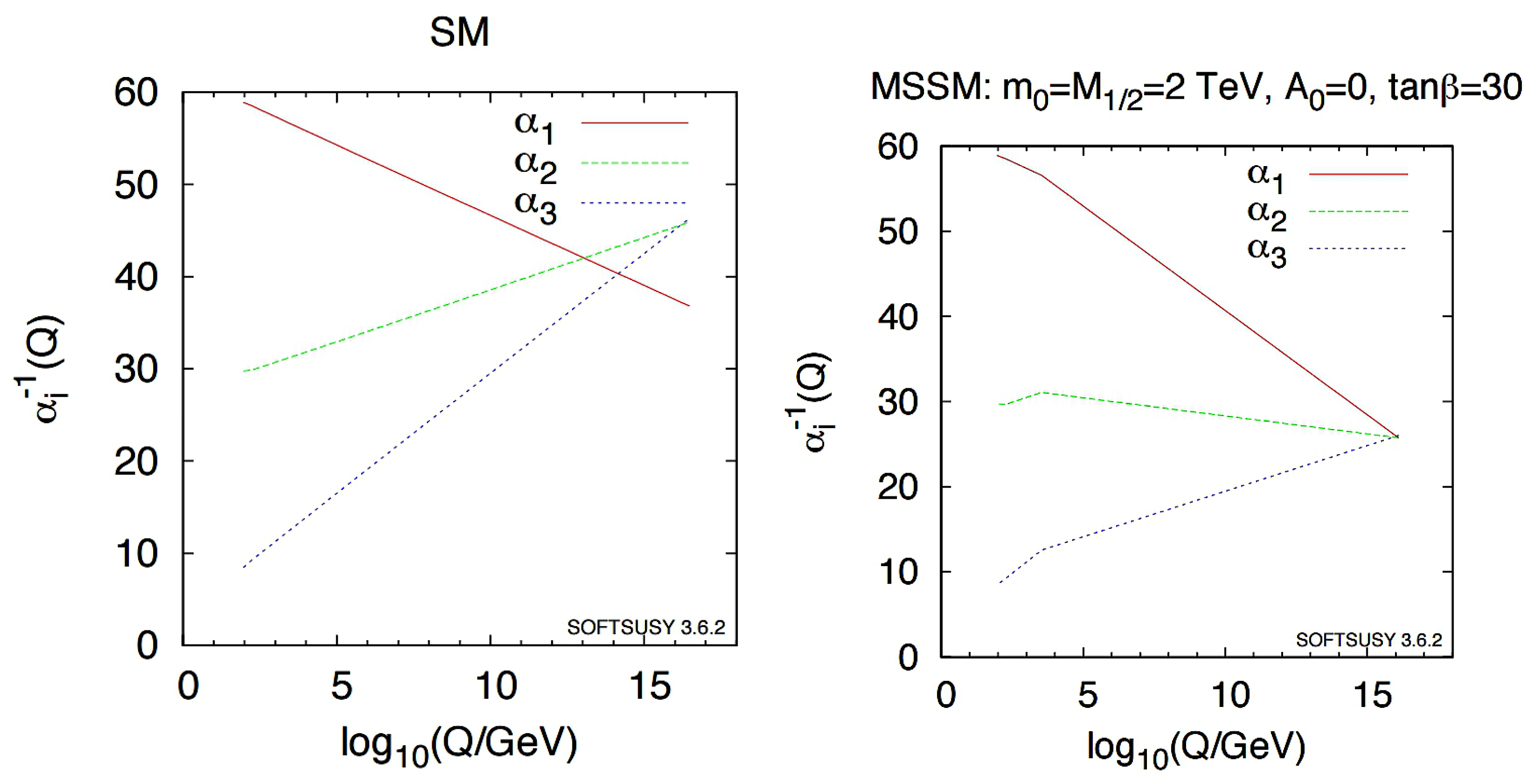
The coupling constant $\alpha$ at very high energies depends upon the theory and is, strictly speaking, unknown. The evolution of $\alpha$ in the minimal standard model (MSM) is presented in Figure 5, left panel, and the same in the minimal standard supersymmetric model (MSSM) with supersymmetry at TeV scale is presented in the right panel. We can conclude that at the scalaron mass scale, $Q=3\times {10}^{13}$ GeV, ${\alpha }_3\approx 0.025$ in MSM, while in MSSM it is ${\alpha }_3\approx 0.04$. At $Q={10}^{10}$ GeV they are ${\alpha }_3\approx 0.033$ for MSM and ${\alpha }_3\approx 0.05$ for MSSM.

The values of the running coupling constants are known to depend upon the set of contributing particles. In the case of MSM we take into account all known particles, while in MSSM there is some freedom depending on the explicit form of the SUSY model. However, the variation of the couplings related to this uncertainty does not lead to strong variation of our estimates of the allowed range of massess of dark matter particles.

Here we have taken into account the evolution of the coupling constants only, because their values are known at low energies and the values at high energies can be calculated knowing the underlying theory. The variation of the couplings is quite significant. On the other hand, the mass of the scalaron is fixed at high energies by the magnitude of the density perturbations generated at inflation. As for the masses of the decay products they are fixed on their mass shell and the quantum renormalization corrections are relatively weak. They can acquire some temperature corrections, which could lead to a difference of mass values over vacuum and high temperature plasma. However, we do not claim to know the exact values of masses of the possible DM particles with the interaction strength typical for supersymmetry. We have only presented an order of magnitude estimates of their masses.

Since, according to our results presented below, supersymmetry may possibly be realized at energies about ${10}^{12}$–${10}^{13}$ GeV, the running of couplings according to MSM without inclusion of SUSY particles is probably correct below the SUSY scale. Recall that for particles produced at the scalaron decay $Q=3\times {10}^{13}$ GeV, while at the universe heating temperature after the complete decay of the scalaron it is near ${10}^{10}$ GeV.

So numerically the decay width is:

$$\begin{array}{c}\hfill {\Gamma }_{anom}=2.6\times {10}^{-4}{\left(\frac{\alpha }{0.025}\right)}^2\frac{M_R^3}{M_{Pl}^2}.\end{array}$$

(217)

The calculations of the energy density of created gauge bosons can be done in complete analogy with calculations of the energy density of massless scalars bosons performed in Section 5.2. Of course we need to take into account the difference of the corresponding decay width (142) and (216). Correspondingly, the energy density of matter created by the scalaron decay into a pair of massless gauge bosons would be:

$${\rho }_{anom}=\frac{{\beta }_1^2{\alpha }^{2}N}{4{\pi }^2}\frac{M_R^3}{240\pi t}\approx 0.8\times {10}^{-5}{\left(\frac{\alpha }{0.025}\right)}^2\frac{M_R^3}{t}.$$

(218)

Following our paper [38] we present alternative, more rigorous arguments leading to introduction of canonically normalised field $\Phi$ (110). To this end we rewrite the first term of action (51) in the Jordan frame in the high frequency limit in terms of the cosmological scale factor $a\left(t\right)$ in the way analogous to the derivation of the Friedmann equations performed in Ref. [39]. For high frequency oscillations and large value of $M_{R}t$ we have found the solutions (83) and (84), which in physical quantities have the form:

$$H=\frac{2}{3t}\left[1+sin(M_{R}t+\theta )\right],R=-\frac{4M_{R}cos(M_{R}t+\theta )}{t}.$$

(219)

Curvature scalar is related to the Hubble parameter according to:

$$\begin{array}{c}\hfill R=-6\dot{H}-12H^2\to -6\dot{H}.\end{array}$$

(220)

The last relation is valid in high frequency limit and for the oscillating parts of H and R which presumably give dominant contribution to the energy density.

Keeping this in mind we can rewrite action (51) as:

$$\begin{array}{ccc}\hfill S\left(a\right)& =& \frac{6M_{Pl}^2}{16\pi M_R^2}\int d^{4}x{a}^3\left[M_R^2(\dot{H}+2H^2)+{\dot{H}}^2\right]\hfill \\ & =& \frac{3M_{Pl}^2}{4\pi M_R^2}\int d^{4}x{a}^3\left[-\frac{M_R^2{H}^2}{2}+\frac{{\dot{H}}^2}{2}\right].\hfill \end{array}$$

(221)

The last equality is obtained through integration by parts.

Varying action (221) over the scalar field H we obtain the equation of motion:

$$\begin{array}{c}\hfill \ddot{H}+M_R^{2}H=-\frac{4\pi M_R}{3M_{Pl}^2}(1-3w)\rho ,\end{array}$$

(222)

compare to Equation (137). This equation has the oscillating solution multiplied by a slow function of time, such as the presented above solution $H\sim sin(M_{R}t+\theta )/t$.

Now we need to introduce canonically normalized scalar field $\Phi$ linearly connected with H for which the kinetic term in the Lagrangian is equal to ${(\partial \Phi )}^2/2$:

$$\begin{array}{c}\hfill \Phi =\sqrt{\frac{3}{4\pi }}\frac{M_{Pl}}{M_R}H.\end{array}$$

(223)

In high frequency limit it is essentially the same field as defined above in Equation (110).

According to the standard theory the energy density of the scalar field $\Phi$ is

$$\begin{array}{c}\hfill {\rho }_{\Phi }=\frac{{\dot{\Phi }}^2+M_R^2{\Phi }^2}{2}.\end{array}$$

(224)

In high frequency limit Equation (220) leads to identification $R=-6\dot{H}\sim M_{R}cos\left(M_{R}t\right)$ and Equation (224) can be rewritten in terms of R as

$$\begin{array}{c}\hfill {\rho }_R=\frac{M_{Pl}^2({\dot{R}}^2+M_R^2{R}^2)}{96\pi M_R^4}=\frac{M_{Pl}^2}{6\pi t^2},\end{array}$$

(225)

where expression (219) has been used. This result coincides with the expression (112) for the total cosmological energy density in spatially flat matter dominated universe. This agreement confirms the validity of our approach.

The presented equations are valid if the energy density of matter remains smaller than the energy density of the scalaron until it decays.

It is instructive to compare the rate of the energy transferred to matter produced in three different cases of the scalaron decay into minimally coupled scalars, fermions, and gauge bosons due to conformal anomaly with the energy density of the scalaron. Comparing Equations (161), (190), and (218) with (225) we find that in all the cases $t_{cr}\Gamma =5/3$, where $t_{cr}$ is the time when the matter energy density, formally taken, is equal to the scalaron energy density. So the used above equations are not unreasonable. Let us note that the energy density of matter in the case of scalaron decay into fermion-antifermion pair is equal to doubled energy density of fermions (190).

The scalaron completely decays at $t\sim 1/\Gamma$ (up to log-correction) and the cosmology turns into the usual Friedmann one governed by the equations of General Relativity. Before that moment the universe expansion was dominated by the scalaron.

If the primeval plasma is thermalized, the following relation between the cosmological time and the temperature is valid:

$$\begin{array}{c}\hfill {\rho }_{anom}=1.3\times {10}^{-2}{\alpha }_R^2\frac{M_R^3}{t}=\frac{{\pi }^2{g}_{\ast }}{30}{T}^4,\end{array}$$

(226)

where subindex R at ${\alpha }_R$ means that the coupling is taken at the energies equal to the scalaron mass, since the energy influx to the plasma is supplied by the scalaron decay, and $g_{\ast }\approx 100$ is the number of relativistic species. Consequently,

$$\begin{array}{c}\hfill t{T}^4\approx \frac{0.4}{{\pi }^2{g}_{\ast }}{\alpha }_R^2{M}_R^3\equiv C\equiv C_0{M}_R^3,\end{array}$$

(227)

with $C_0=2.5\times {10}^{-7}{({\alpha }_R/0.025)}^2$.

Thermal equilibrium is established if the reaction rate is larger than the Hubble expansion rate $H=2/\left(3t\right)$. The reaction rate is determined by the cross-section of two-body reactions between relativistic particles. The typical value of this cross-section at high energies, $E\gg m$, is [40]:

$$\begin{array}{c}\hfill {\sigma }_{rel}=\frac{4\pi \beta {\alpha }^2}{s}\left(ln\frac{s}{4m^2}+1\right),\end{array}$$

(228)

where $\beta \sim 10$ is the number of the open reaction channels and $s={(p_1+p_2)}^2=4E^2$ is the total energy of the scattering particles in their center-of-mass frame, where E is the energy of an individual particle.

Hence the reaction rate is

$$\begin{array}{c}\hfill {\Gamma }_{rel}\equiv \frac{\dot{n}}{n}=\langle {\sigma }_{rel}v{n}_{rel}\rangle ,\end{array}$$

(229)

where angular brackets mean averaging over thermal bath with temperature T, $n_{rel}\approx 0.1g_{\ast }{T}^3$ (we do not distinguish between bosons and fermions in the expression), $v=1$ is the particle velocity in the center-of-mass system. We perform thermal averaging naively taking $E=T$ in all expressions so $s\to 4T^2$, instead of $m^2$ we substitute the particle thermal mass in plasma, i.e., $m^2\to 4\pi \alpha T^2/3$ [41,42,43]. Since thermal equilibrium is established when the reaction rate $\Gamma$ exceeds the Hubble parameter $H=(2/3t)$ we obtain the following equilibrium thermal condition:

$$\begin{array}{c}\hfill \frac{3}{2}t{\Gamma }_{rel}=0.15\pi {\alpha }^2\beta g_{\ast }\left(ln\frac{3}{4\pi \alpha }+1\right)Tt>1.\end{array}$$

(230)

Using Equation (227), we find that equilibrium is established at the temperatures below

$$T_{eq}={\left(0.15\pi {\alpha }^2\beta g_{\ast }{C}_0\right)}^{1/3}{M}_R=7.3\times {10}^{-3}{M}_R.$$

(231)

Here we took ${\alpha }_R=0.025$ and $\alpha =0.033$, where ${\alpha }_R$ is defined below Equation (226) and we took the value of coupling constant from Figure 5. Constant $\alpha$ determines the scattering of relativistic particles (228), which for the energies of the order of temperature is equal to 0.033.

The time corresponding to this temperature is equal to

$$\begin{array}{c}\hfill t_{eq}=C/T_{eq}^4\approx 90M_R^{-1},\end{array}$$

(232)

where C is defined in Equation (227). Hence $M_R{t}_{eq}\gg 1$, which is sufficiently long time for efficient particle production.

Another essential temperature for our consideration, is the temperature of the universe heating, when scalaron essentially decayed and the expansion regime turned to the conventional GR one. This temperature is determined by the scalaron energy density at the moment $t=1/{\Gamma }_{anom}$:

$$\begin{array}{c}\hfill {\rho }_R=\frac{M_{Pl}^2{\Gamma }_{anom}^2}{6\pi }=\frac{{\pi }^2{g}_{\ast }}{30}{T}_h^4,\end{array}$$

(233)

so

$$T_h=3.2\times {10}^{-3}\sqrt{M_R/M_{Pl}}{M}_R=5.1\times {10}^{-6}{M}_R.$$

(234)

5.4.1. Direct X-Particle Production through the Scalaron Decay

There are two possible channels to produce massive stable X-particles: first, directly through the scalaron decay into a pair of $X\overline{X}$ and another by inverse annihilation of relativistic particles in plasma.

First, let us consider the scalaron decay. The probability of the scalaron decay into a pair of fermions is determined by decay width (187) with the substitution $M_X$ instead of $m_f$:

$$\begin{array}{c}\hfill {\Gamma }_X=\frac{M_R{M}_X^2}{6M_{Pl}^2}.\end{array}$$

(235)

The branching ratio of this decay is equal to:

$$\begin{array}{c}\hfill BR(R\to X\overline{X})=\frac{{\Gamma }_X}{{\Gamma }_{anom}}\approx 6.4\times {10}^2{\left(\frac{M_X}{M_R}\right)}^2.\end{array}$$

(236)

The number density of X-particles created by the scalaron decay only, but not by inverse annihilation of relativistic particles in plasma, is governed by the equation:

$$\begin{array}{c}\hfill {\dot{n}}_X+3H{n}_X={\Gamma }_X{n}_R,\end{array}$$

(237)

where ${\Gamma }_X$ is given by Equation (235), $n_R={\rho }_R/M_R$, and ${\rho }_R$ is defined in Equation (225). So Equation (237) turns into

$$\begin{array}{c}\hfill {\dot{n}}_X+3H{n}_X=\frac{M_X^2}{36\pi t^2}.\end{array}$$

(238)

In the scalaron dominated regime non-oscillating part of the Hubble parameter is $H=2/\left(3t\right)$ and the equation is solved as

$$\begin{array}{c}\hfill n_X=\frac{M_X^2}{36\pi t}.\end{array}$$

(239)

The equations presented above are valid if the inverse decay of the scalaron can be neglected. This approximation is true if the produced particles are quickly thermalized down to the temperatures much smaller than the scalaron mass.

We are interested in the ratio of $n_X$ to the number density of relativistic species at the moment of the complete scalaron decay when the temperature dropped down to $T_h$ (234) after which the universe came to the conventional Friedmann cosmology and the ratio $n_X/n_{rel}$ remained constant to the present time. This ratio is equal to:

$$\begin{array}{c}\hfill F\equiv \frac{n_X}{n_{rel}}|T=T_h=\left[\frac{0.04M_X^2}{6\pi t_h}\right]\times {\left[\frac{{\pi }^2{g}_{\ast }{T}_h^4}{90T_h}\right]}^{-1}\\ \hfill =2.3\times {10}^{-3}{\left(\frac{0.025}{{\alpha }_R}\right)}^2{\left(\frac{M_X}{M_R}\right)}^2.\end{array}$$

(240)

If dark matter totally consists of X-particles, their energy density in the present day universe should be equal to the observed energy density of dark matter:

$$\begin{array}{c}\hfill {\rho }_X^{\left(0\right)}=412{\mathrm{cm}}^{-3}{M}_{X}F={\rho }_{DM}\approx 1{\mathrm{keV}/\mathrm{cm}}^3.\end{array}$$

(241)

From this condition it follows that $M_X\approx {10}^7$ GeV. For larger masses ${\rho }_X^{\left(0\right)}$ would be unacceptably larger than ${\rho }_{DM}$. On the other hand, for such a small, or smaller $M_X$, the probability of X-particle production through the inverse annihilation would be too strong and would again lead to very large energy density of X-particles, see the following section.

A possible way out of this “catch-22” is to find a mechanism to suppress the scalaron decay into a pair of X-particles. In addition, it does exist. If X-particles are the Majorana fermions, then in this case particles and antiparticles are identical and so they must be in antisymmetric state. Thus, the decay of a scalar field, scalaron, into a pair of identical fermions is forbidden, since the scalaron can produce a pair of identical particles in symmetric state only.

5.4.2. Production of X-Particles in Thermal Plasma

Here we turn to the X-production through the inverse annihilation of relativistic particles in the thermal plasma. The number density $n_X$ is governed by the Zeldovich Equation (7):

$$\begin{array}{c}\hfill {\dot{n}}_X+3H{n}_X=\langle {\sigma }_{ann}v\rangle \left(n_{eq}^2-n_X^2\right),\end{array}$$

(242)

where $\langle {\sigma }_{ann}v\rangle$ is the thermally averaged annihilation cross-section of X-particles and $n_{eq}$ is their equilibrium number density.

The thermally averaged annihilation cross-section of non-relativistic X-particles, which enters Equation (7), for our case can be taken as (see Equation (10)):

$$\begin{array}{c}\hfill \langle {\sigma }_{ann}v\rangle =\frac{3\pi {\alpha }^2{\beta }_{ann}}{2M_X^2}\frac{T}{M_X},\end{array}$$

(243)

where the last factor came from thermal averaging of the velocity squared of X-particles, equal to $\langle v^2\rangle =T/M_X$, which appears because the annihilation of Majorana fermions proceeds in P-wave. We take the coupling constant at the energy scale around $M_X$ equal to $\alpha =0.033$ and the number of the annihilation channels ${\beta }_{ann}=10$. This expression is only an order of magnitude estimate. The exact form depends upon particle spins, the form of the interaction, and may contain the statistical factor $1/n!$, if there participate n identical particles. In what follows we neglect these subtleties.

The equilibrium distribution of non-relativistic X-particles has the form:

$$\begin{array}{c}\hfill n_{eq}=g_s{\left(\frac{M_{X}T}{2\pi }\right)}^{3/2}exp\left(-\frac{M_X}{T}\right)=g_s{M}_X^3{\left(2\pi y\right)}^{-3/2}exp(-y),\end{array}$$

(244)

where $y=M_X/T$ and $g_s$ is the number of spin states of X-particles. The non-relativistic approximation is justified if $M_X>T_{eq}\approx M_R/100=3\times {10}^{11}$ GeV, see Equation (231).

Equation (242) will be solved with the initial condition $n_X\left(t_{in}\right)=0$. This condition is essentially different from the solution of this equation in the canonical case, when it is assumed that initially $n_X=n_{eq}$ and in the course of the evolution $n_X$ becomes much larger than $n_{eq}$, reaching the so-called frozen density. As we see in what follows, for certain values of the parameters the similar situation can be realized, when $n_X$ approaches the equilibrium value and freezes at much larger value. The other limit when $n_X$ always remains smaller than $n_{eq}$ is also possible.

For better insight into the problem we first make simple analytic estimates of the solution when $n_X\ll n_{eq}$ and after that solve exact Equation (242) numerically.

In the limit $n_X\ll n_{eq}$ Equation (242) is trivially integrated:

$$\begin{array}{c}\hfill n_{X0}\left(y\right)=\frac{6\pi {\alpha }^2{\beta }_{ann}{g}_s^2}{{\left(2\pi \right)}^3}\frac{C_0{M}_R^3}{y^8}{\int }_{y_{in}}^{y}d{y}_1{y}_1^7{e}^{-2y_1}\\ \hfill =2\times {10}^{-7}\frac{{\alpha }^2{\beta }_{ann}{g}_s^2}{{\pi }^2}{\left(\frac{{\alpha }_R}{0.025}\right)}^2{M}_R^3{\int }_{y_{in}/y}^{1}dz{z}^7{e}^{-2zy},\end{array}$$

(245)

where the new integration variable is defined as $z=y_1/y$, the subindex “0” means that the solution is valid for $n_X\ll n_{eq}$, $y=M_X/T$ and we have used Equation (227) and the expression for $C_0$ below this equation.

For the initial temperature we take $T_{in}=T_{eq}\approx 7\times {10}^{-3}{M}_R$, according to Equation (231), and $T_{fin}=T_h=5.1\times {10}^{-6}{M}_R$ (234). Correspondingly $y_{in}=1.4\times {10}^2{M}_X/M_R$, and $y_{fin}=2\times {10}^5{M}_X/M_R$ and so $y_{fin}/y_{in}\approx {10}^3$.

To check validity of this solution we have to compare $n_{X0}\left(y\right)$ to $n_{eq}$ (244):

$$\begin{array}{c}\hfill F_2\left(y\right)\equiv \frac{n_{X0}\left(y\right)}{n_{eq}}=4\sqrt{2}\times {10}^{-7}\frac{{\alpha }^2{\beta }_{ann}{g}_s}{\sqrt{\pi }}{\left(\frac{{\alpha }_R}{0.025}\right)}^2{e}^y{y}^{3/2}{\int }_{y_{in}/y}^{1}dz{z}^7{e}^{-2zy}\\ \hfill \approx 7\times {10}^{-9}{\left(\frac{M_R}{M_X}\right)}^3{e}^y{y}^{3/2}{\int }_{y_{in}/y}^{1}dz{z}^7{e}^{-2zy},\end{array}$$

(246)

where we have taken $g_s=2$, ${\beta }_{ann}=10$ and lastly, according to the line below Equation (231), $\alpha =0.033$ and ${\alpha }_R=0.025$.

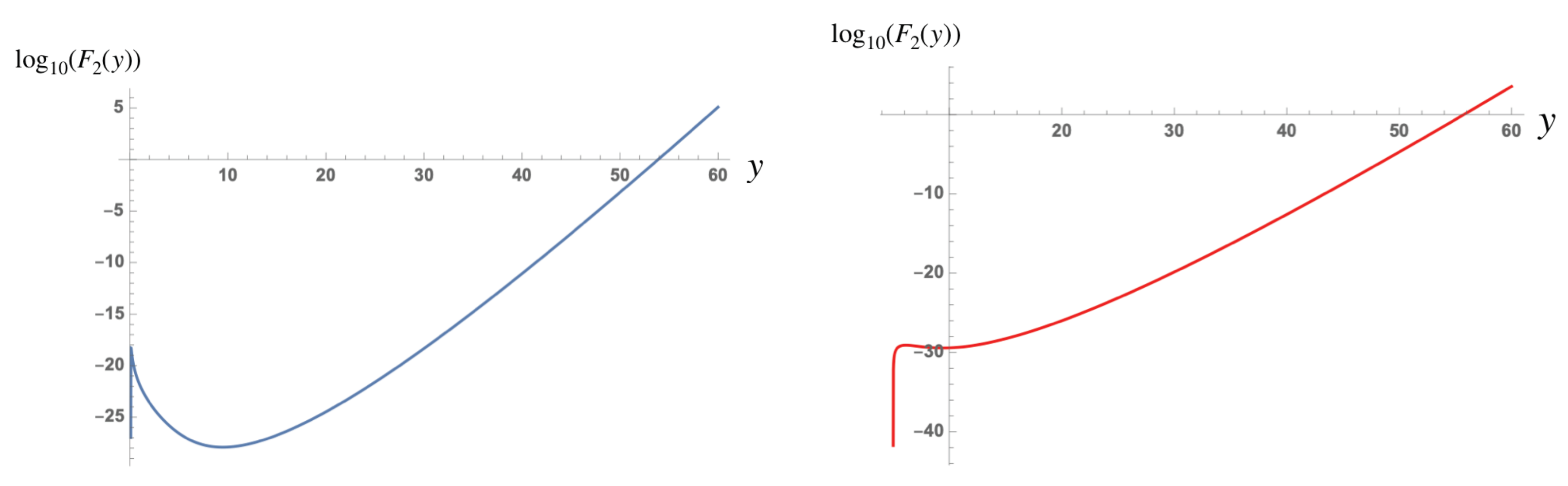
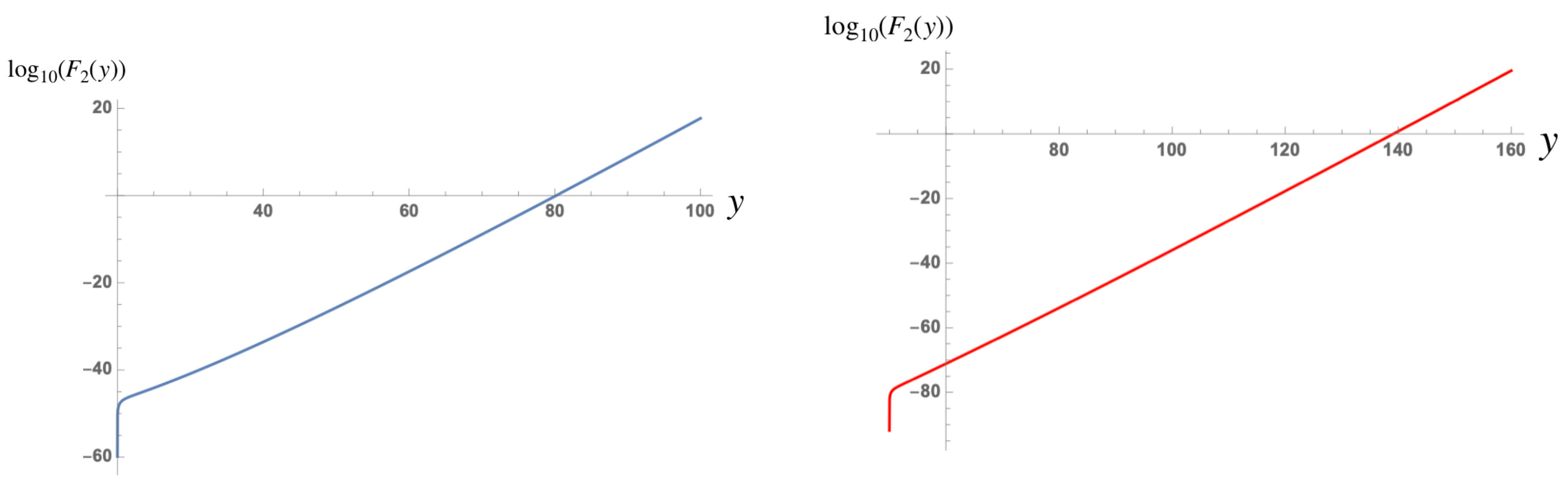
The ratio $F_2\left(y\right)$ is depicted in Figure 6 and Figure 7 as function of y for different values of $y_{in}$. The ratio remains smaller than unity for sufficiently small $y<y_{max}=50-150$ depending upon $y_{in}$. If $y_{fin}<y_{max}$, the assumption $n_X\ll n_{eq}$ is justified and the solution (245) is a good approximation to the exact solution. In the opposite case, when $y_{fin}>y_{max}$, we have to solve Equation (242) numerically.

To solve Equation (242) it is convenient to introduce the new function according to:

$$\begin{array}{c}\hfill n_X=g_s{\left(\frac{a_{in}}{a\left(t\right)}\right)}^3{M}_X^{3}z\left(t\right)=g_s{M}_X^3{\left(\frac{T_{in}}{T}\right)}^{-8}z,\end{array}$$

(247)

where $a\left(t\right)$ is the cosmological scale factor and $a_{in}$ is its initial value at some time $t=t_{in}$, when X-particles became non-relativistic. In terms of z, Equation (242) is reduced to:

$$\begin{array}{c}\hfill \dot{z}=\langle {\sigma }_{ann}v\rangle M_X^3{\left(\frac{a_{in}}{a}\right)}^3\left(z_{eq}^2-z^2\right),\end{array}$$

(248)

Next, let us change the variables from t to $y=M_X/T$. Evidently $\dot{y}=-y(\dot{T}/T)$. Using time-temperature relation (227), we find

$$\begin{array}{c}\hfill \frac{dz}{dt}=\frac{M_X^4}{4C_0{M}_R^3{y}^3}\frac{dz}{dy}.\end{array}$$

(249)

Keeping in mind that

$$\begin{array}{c}\hfill {\left(\frac{a_{in}}{a}\right)}^3={\left(\frac{t_{in}}{t}\right)}^2={\left(\frac{y_{in}}{y}\right)}^8,\end{array}$$

(250)

we find finally:

$$\frac{dz}{dy}=6\pi g_s{C}_0{\alpha }^2{\beta }_{ann}{\mu }^3\frac{y_{in}^8}{y^6}\left(\frac{y^{13}}{8{\pi }^3{y}_{in}^{16}{e}^{2y}}-z^2\right),$$

(251)

where $\mu =M_R/M_X$.

With the chosen above values of ${\alpha }_R$ and $\alpha$, see the discussion after Equations (227) and (243), we find that the value of the coefficient in the r.h.s. of Equation (251) is $6\pi g_s{C}_0{\alpha }^2{\beta }_{ann}\approx {10}^{-7}$.

Numerical solution of this equation indicates that $z\left(y\right)$ tends asymptotically at large y to a constant value $z_{asym}$. The energy density of X-particles is expressed through $z_{asym}$ as follows. We assume that below $T=T_h$ the ratio of number density of X-particles to the number density of relativistic particles remains constant and hence is equal to the ratio $n_X/n_{CMB}$ at the preset time, where $n_{CMB}=412/{\mathrm{cm}}^3$ is the contemporary number density of photons in cosmic microwave background radiation. The number density of X-particles is expressed through z according to Equation (247). Thus, the asymptotic ratio of the number densities of X to the number density of relativistic particles is

$$F_{asym}=\frac{n_X\left(T_h\right)}{n_{rel}\left(T_h\right)}=\left[M_X^3{\left(y_{in}/y_h\right)}^8{z}_{asym}\right]·{\left[{\pi }^2{g}_{\ast }{T}_h^3/90\right]}^{-1}.$$

(252)

We assume that $y_{in}\approx {10}^2/\mu$, $y_{fin}=y_h=2\times {10}^5/\mu$, according to the discussion after Equation (245), and so $y_{fin}/y_{in}\approx 2\times {10}^3$. Hence the energy density of X-particles today would be equal to:

$${\rho }_X^{\left(0\right)}=(412/{\mathrm{cm}}^3)M_X{F}_{asym}=3\times {10}^9{\mu }^{-4}{z}_{asym}\frac{\mathrm{keV}}{{\mathrm{cm}}^3},$$

(253)

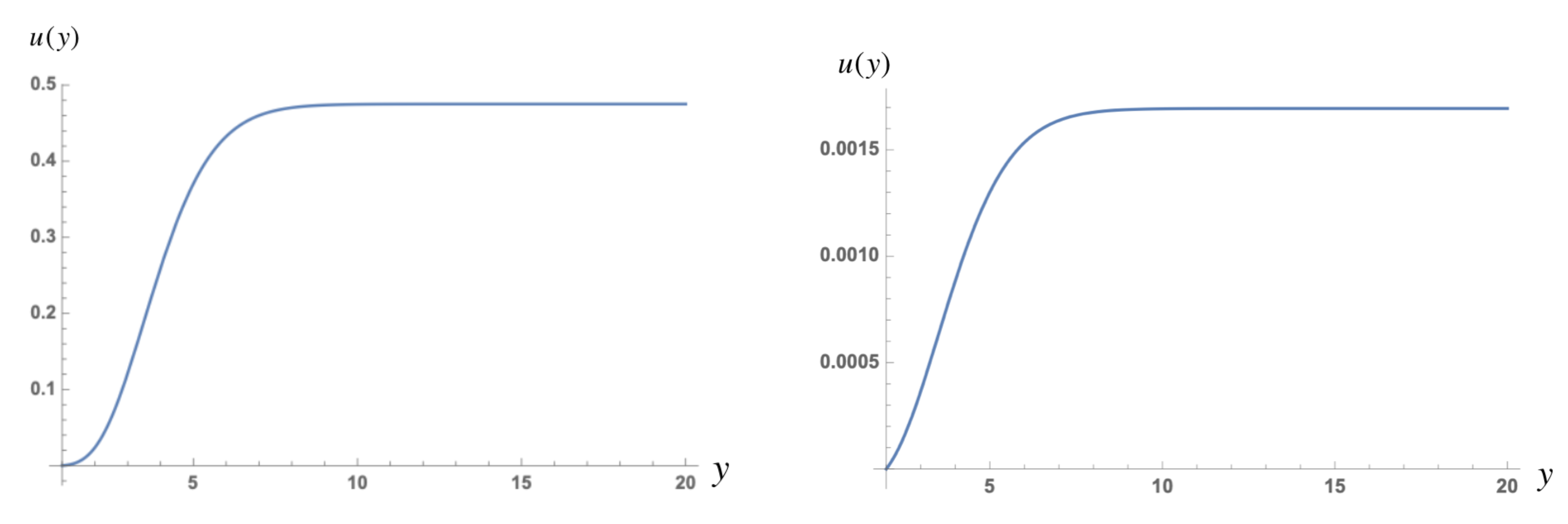
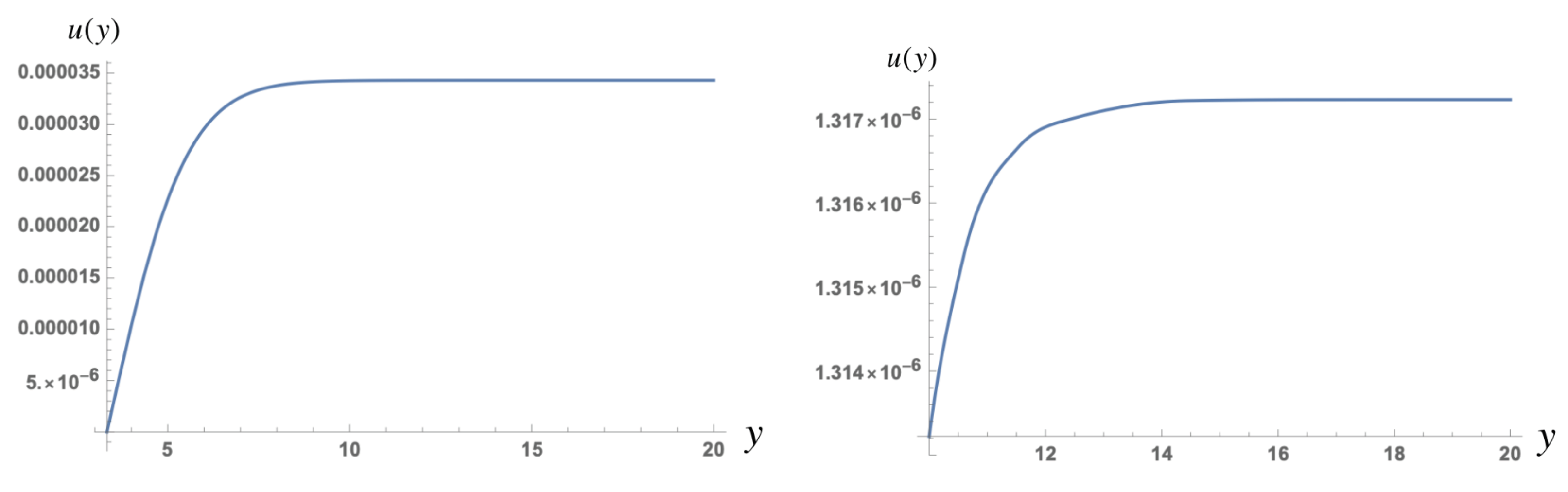
where $z_{asym}$ is the asymptotic value of $z\left(y\right)$ at large y but still smaller than $y_h$. The value of $z_{asym}$ can be found from the numerical solution of Equation (251). However, the solution demonstrates surprising feature: its derivative changes sign at $y\le 10$, when $n_X\ll n_{eq}$, as is seen from the value of $F_2$ presented in Figure 6 and Figure 7. Probably this evidently incorrect result for $z\left(y\right)$ originated from a very small coefficient in front of the brackets in Equation (251).

The problem can be avoided if we introduce the new function $u\left(y\right)$ according to:

$$\begin{array}{c}\hfill z\left(y\right)=\frac{u\left(y\right)}{{\left(2\pi \right)}^{3/2}{y}_{in}^{3/2}exp\left(y_{in}\right)}.\end{array}$$

(254)

In terms of $u\left(y\right)$, kinetic equation (251) takes the form:

$$\frac{du}{dy}=\frac{{10}^{-7}{\mu }^3{y}_{in}^{13/2}}{{\left(2\pi \right)}^{3/2}{y}^{6}exp\left(y_{in}\right)}\left[{\left(\frac{y}{y_{in}}\right)}^{13}{e}^{2(y_{in}-y)}-u^2\right].$$

(255)

The numerical solution of this equation does not show any pathological features and may be trusted, so we express the contemporary energy of dark matter made of stable X-particles through the asymptotic value of $u\left(y\right)$ as

$$\begin{array}{c}\hfill {\rho }_X^{\left(0\right)}=\frac{3\times {10}^9{\mu }^{-4}{u}_{asym}}{{\left(2\pi \right)}^{3/2}{y}_{in}^{3/2}exp\left(y_{in}\right)}\frac{\mathrm{keV}}{{\mathrm{cm}}^3}.\end{array}$$

(256)

Remind that $y_{in}\approx 100/\mu$ and presumably $\mu >1$.

The asymptotic value $u_{asym}$ is found from the numerical solution of Equation (255) and is depicted in Figure 8 and Figure 9 for different values of $\mu$.

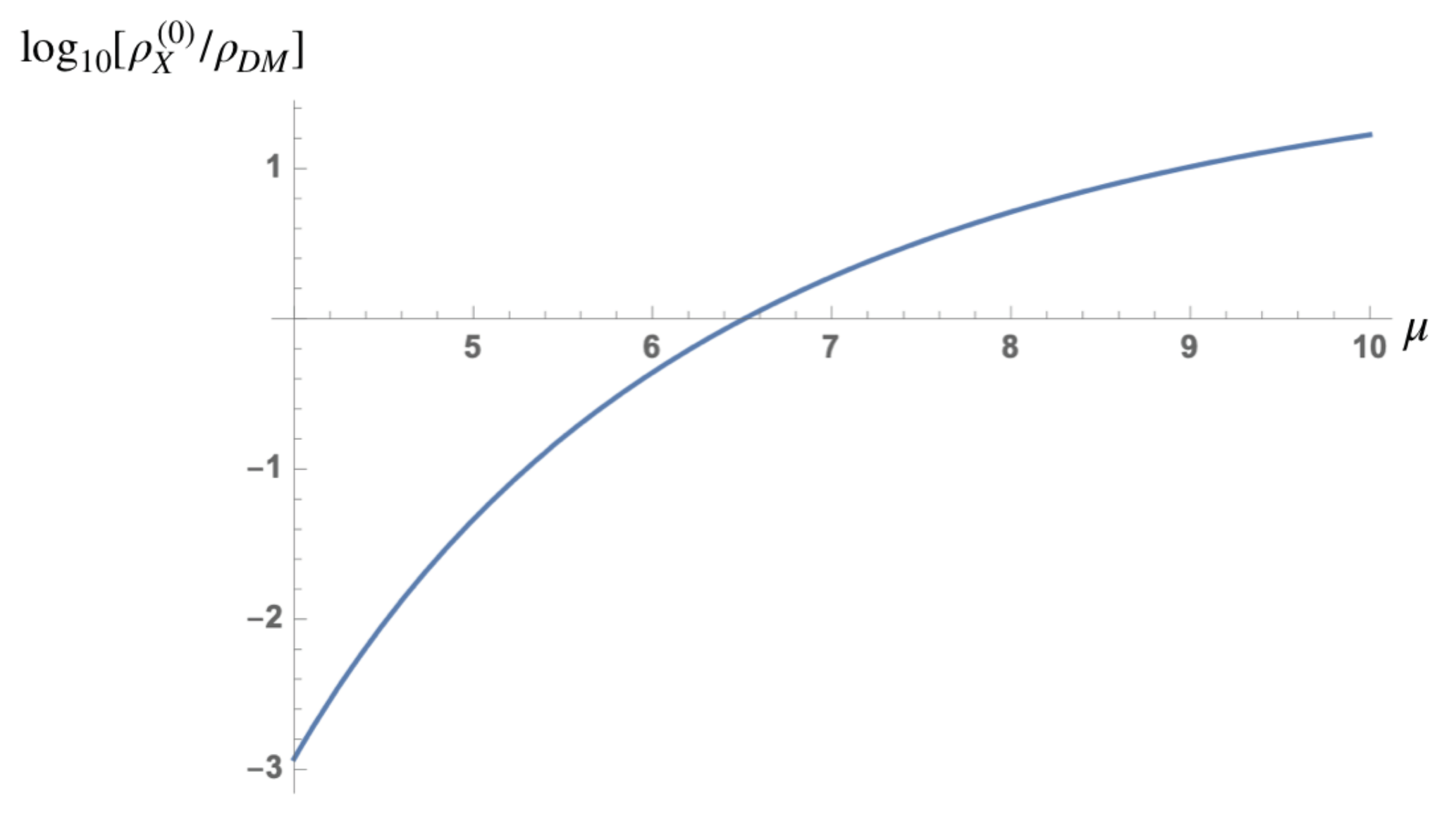
The logarithm of the energy density of X-particles (256) with respect to the observed energy density of dark matter as a function of $M_X$ is presented in Figure 10. If $M_X\approx 5\times {10}^{12}$ GeV, X-particles may be viable candidates for the carriers of the cosmological dark matter.

5.5. Possible Observations

This section contains a discussion of some possibilities of observation of the products of X-particle slow decay or enhanced annihilation in ultra high energy cosmic rays. More detailed study of the phenomena considered below demands more work.

There are two possibilities to make X-particles visible: first, due to possible high density of $X\overline{X}$-systems and, secondly, because of hypothetical instability of X-particles.

According to results of our papers [23,38,44] the mass of dark matter particles, with the interaction strength typical for supersymmetric ones, can be in the range from ${10}^6$ to the value exceeding the scalaron mass, $M_R={10}^{13}$ GeV. It is tempting to find if and how they could be observed, except for their gravitational effects on galactic and cosmological scales.

The average cosmological energy/mass density of dark matter particles in the universe is approximately 1 keV/cm${}^3$, while in galaxies it is about 1 GeV/cm${}^3$. So their number densities should respectively be:

$$\begin{array}{c}\hfill n_{cosm}={10}^{-12}{M}_6^{-1}/{\mathrm{cm}}^3,n_{gal}={10}^{-6}{M}_6^{-1}/{\mathrm{cm}}^3,\end{array}$$

(257)

where $M_6=M_X/\left({10}^6\mathrm{GeV}\right)$.

The characteristic annihilation time in a galaxy is:

$$\begin{array}{c}\hfill {\tau }_{gal}^{ann}=1/\left[{\sigma }_{ann}v{n}_{gal}\right]\approx {10}^{37}{M}_6^3\mathrm{s},\end{array}$$

(258)

where we have taken ${\sigma }_{ann}v\approx {10}^{-2}/M_X^2$.

The total energy flux from all annihilations in the Galaxy of the size $R_{gal}\approx 10\mathrm{kpc}={10}^{22}\mathrm{cm}$ would be

$$\begin{array}{c}\hfill L_{gal}=n_{gal}E{R}_{gal}/{\tau }_{gal}^{ann}\approx {10}^{-15}{M}_6^{-3}\mathrm{GeV}/{\mathrm{cm}}^2/\mathrm{s}\\ \hfill =3\times {10}^2{M}_6^{-3}\mathrm{GeV}/{\mathrm{km}}^2/\mathrm{year},\end{array}$$

(259)

with characteristic energy of the order of $E\sim M_X$.

The annihilation would be strongly enhanced in clusters (clumps) of dark matter [45], especially in neutralino stars [46]. Based on the latter reference, for the annihilation cross-section ${\sigma }_{ann}v=4\times {10}^{-42}{M}_6^{-2}{\mathrm{cm}}^2\approx {10}^{-31}$$M_6^{-2}{\mathrm{cm}}^3/\mathrm{s}$, we can conclude that the observation of $X\overline{X}$-annihilation from neutralino stars is not unrealistic.

Due to their huge mass, relic X-particles might form gravitationally bound states and then annihilate such as positronium. Instead of fine structure constant $\alpha =1/137$ we must use the gravitational coupling constant ${\alpha }_G={(M_X/M_{Pl})}^2$. In complete analogy with para-positronium decay the lifetime of such bound state with respect to annihilation would be

$$\begin{array}{c}\hfill {\tau }_G\sim {\left({\alpha }_G^5{M}_X\right)}^{-1}\approx 5\times {10}^{23}{M}_{13}^{-11}\mathrm{s},\end{array}$$

(260)

where $M_{13}=M_X/\left({10}^{13}\mathrm{GeV}\right)$.

The flux of ultra-high energy cosmic rays (UHECR) with energies ${10}^{21}$–${10}^{22}$ eV produced by the population of the bound states of $X\overline{X}$, say, from the sphere of the radius of $R=1$ Gpc would be:

$$\begin{array}{c}\hfill F=n_{gal}Rf/{\tau }_G=2\times {10}^{5}f{M}_{13}^{10}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1},\end{array}$$

(261)

where f is the fraction of the gravitationally bound states of $X\overline{X}$ with respect to the total number of X-particles.

Comparing this result with the data presented in ref. [47] we can conclude that the flux of the UHECR produced in the decay of $X\overline{X}$ bound states would agree with the data if $f\sim {10}^{-11}$.

Calculation of f is subject to many uncertainties and demand an extensive work. It will be done elsewhere.

Another chance for observation of X-particles appears if they are unstable. Heavy X-particles would decay though formation of virtual black holes, according to the Zeldovich mechanism [48,49]. If X-particles are composite states of three fundamental constituents, as proton made of three quarks, their life-time with respect to virtual BH simulated decay would be

$$\begin{array}{c}\hfill {\tau }_{X,BH}\sim \frac{M_{Pl}^4}{M_X^5}\sim {10}^{-13}\mathrm{s}{\left(\frac{{10}^{13}\mathrm{GeV}}{M_X}\right)}^5.\end{array}$$

(262)

To make the time ${\tau }_{X,BH}$ larger than the universe age $t_U\approx 4\times {10}^{17}$ s, we need $M_X<{10}^7$ GeV. In this case the products of the decays of X-particles with such masses could be observable in the flux of the cosmic rays with energy somewhat below ${10}^7$ GeV.

The life-time may be further diminished if we apply the conjecture of Ref. [50] which leads to a strong suppression of the decay through virtual black holes for spinning or electrically charged X-particles. However, this suppression does not operate for spinless neutral particles. Moreover it would not be efficient enough to sufficiently suppress the decay probability of the superheavy particles of dark matter with masses of the order of ${10}^{13}$ GeV. The decay rate may be strongly diminished if X-particles consist of more than three fundamental constituents. For example, if X-particles consist of six fundamental constituents, then the decay life-time would be

$$\begin{array}{c}\hfill {\tau }_{X,BH}^{\prime }\sim \frac{M_{Pl}^{10}}{M_X^{11}}\sim {10}^{23}\mathrm{s}{\left(\frac{{10}^{13}\mathrm{GeV}}{M_X}\right)}^5.\end{array}$$

(263)

This life-time is safely above the universe age $t_U\approx 4\times {10}^{17}$ s.

6. Conclusions and Discussion

There is general agreement that the conventional Friedmann cosmology is in tension with the existence of stable particles with interaction strength typical for supersymmetry and heavier than several TeV. A possible way to save the life of such particles, we call them here X-particles, may be a modification of the standard cosmological expansion law in such a way that the density of such heavy relics would be significantly reduced. A natural way to realize such a reduction is the now popular Starobinsky inflationary model [18]. If the epoch of the domination of the curvature oscillations (the scalaron domination) lasted after freezing of massive species, their density with respect to the plasma entropy could be noticeably suppressed by the production of the relativistic species created by the scalaron decay.

The concrete range of the allowed mass values of X-particles, if they constitute the cosmological dark matter, depends upon the dominant decay mode of the scalaron. If the scalaron is minimally coupled to scalar particles $X_S$, the decay amplitude does not depend upon the scalar particle mass and leads to too high energy density of X-particles, if $M_{X_S}\ll M_R$. An acceptably low density of $X_S$ can be achieved if $M_{X_S}\ge M_R\approx 3\times {10}^{13}$ GeV, since in this case X-particles should be produced in multi-scalaron processes.

If scalaron decays into fermion-antifermion pair, its decay width is proportional to $m_f^2$ and the decay probability is dominated by the heaviest fermion. In this case X-particles could be produced in secondary reactions in plasma. For sufficiently small $m_f$ the energy density of the produced fermions would be small enough and respectively the energy density of X-particles produced either through the fermion decays or annihilation could be close to the observed density of dark matter for $M_X\sim {10}^6$ GeV [23].

The scalaron could also decay into a pair of gauge bosons due to existence of conformal anomaly. In this case, the cosmological plasma initially would dominantly consist from the gauge bosons. In the process of thermalisation of this primeval plasma the X-particles of would-be dark matter could be created. There are two possible processes through which X-particles could be produced: direct decay of the scalaron into a pair of $\overline{X}X$ and the thermal production of X’s in plasma. If scalaron decays into a pair of $X\overline{X}$-fermions, the energy density of X-particles would be close to the observed energy density of dark matter for the X-particle mass below ${10}^7$ GeV. However, in this case the thermal production of X’s would be too strong. We can resolve this inconsistency if the direct decay of the scalaron into X-particles is suppressed and due to the fact that a larger $M_X$ is allowed, so the thermal production would not be dangerous. The direct decay can be very strongly suppressed if X-particles are Majorana fermions, which cannot be created by a scalar field in the lowest order of perturbation theory. This opens the possibility for X-particles to make proper amount of dark matter, if their mass is about $5\times {10}^{12}$ GeV [38].

However, conformal anomaly is not necessarily present in supersymmetry inspired theories. There are some versions of SUSY theories where conformal anomaly is absent, for example $N=4$ supersymmetry for which beta-function vanishes, see e.g., review ([51], Section 13.2), and references therein.

On the other hand, $N=4$ super Yang-Mills theories are believed to be unrealistic because they do not allow introducing chiral fermions, even if the symmetry is broken spontaneously. Though spontaneous symmetry breaking is considered to be the most appealing way to deal with the theories with broken symmetries, it is not obligatory and the symmetry can be broken explicitly. It is possible to break the symmetry “by hand” introducing different masses to particles in the same multiplet. This would allow to construct a phenomenologically acceptable model. Since the symmetry is broken by mass, the theory would remain renormalizable. At higher energies, much larger than the particle masses, it would behave as $N=4$ super Yang-Mills theory and at this energy scale the trace anomaly would vanish.

Apart from that there are phenomenologically acceptable $N=1$ and $N=2$ supersymmetric theories which possess the so-called conformal window, i.e., in this theories with a certain set of the multiplets trace anomaly vanishes. For a review and the list of references see [52].

Thus, a supersymmetric type of dark matter particles seems to be possible if their mass is quite high from ${10}^6$ up to $5\times {10}^{12}$ GeV, or even higher than the scalaron mass, $M_R=3\times {10}^{13}$ GeV. There is not a chance to discover these particles in accelerator experiments in foreseeable future, but they may be observable through cosmic rays from their annihilations in high density clumps of dark matter, or from annihilation in their gravitationally bound two-body states, or through the products of their decays, since they naturally should be unstable.

It is worth mentioning that with the standard inflation is impossible to relax the conventional bounds on the masses of dark matter particles. The reason for the difference between the scalaron and inflaton cosmologies, implicitly mentioned in the review, is that the scalaron decays much slower than the inflaton and due to that there is a constant and slow influx of energy to the plasma from the scalaron, which diluted the fraction of very massive DM particles. As is mentioned in the review the essential processes of the scalaron decay took place during long time with $\Gamma t\le 1$, while for the inflaton decay the thermalization took place almost instantly. The difference between inflaton and scalaron is related to a huge difference between their couplings to matter. The typical value of the coupling constant of the inflaton decay into a pair of fermions through the interaction $g\Phi \overline{\psi }\psi$ is $g\sim {10}^{-3}$, while in the case of the scalaron it is inversely proportional to the Planck mass squared. The equivalent of g for the scalaron is $m_{\psi }^2/M_{Pl}^2$. Even for the case of the minimally coupled scalars $g^2\sim {(M_R/M_{Pl})}^2\approx {10}^{-11}$.

Let us note that according to Equations (168), (192), and (234) the temperature of the primordial plasma after the complete scalaron decay is higher than the temperature of BBN by several orders of magnitude. So the temperature when the universe turned to the usual FLWR cosmology is much higher than the BBN temperature equal to 1 MeV and thus BBN remained undisturbed. The energy density of stable would-be particles of dark matter is negligibly small at BBN.

Let us summarise. In the conventional cosmology masses of the stable supersymmetric relics (candidates for the DM particles) should be typically below 1 TeV. This is in conflict with the LHC bounds on the low energy SUSY. On the other hand, in $R^2$-gravity the masses of the stable particles with the interaction strength typical for SUSY could be much higher depending upon the dominant decay mode of the scalaron. As we showed, for the decay into minimally coupled scalars the mass of the stable relics could be as large as the scalaron mass, $M_R=3\times {10}^{13}$ GeV. If the scalaron predominantly decays into a pair of massive fermions the mass of DM particles could be about ${10}^6$ GeV. If the scalaron predominantly decays into gauge bosons due to trace anomaly, the allowed value of mass of DM particles could be about $5\times {10}^{12}$ GeV.