Behavior of the Free Surface of Two-Phase Fluid Flow Near the Taphole in a Tank
Abstract
1. Introduction
2. Governing Equations and Mathematical Formulation
2.1. Governing Equations of Fluid Flow
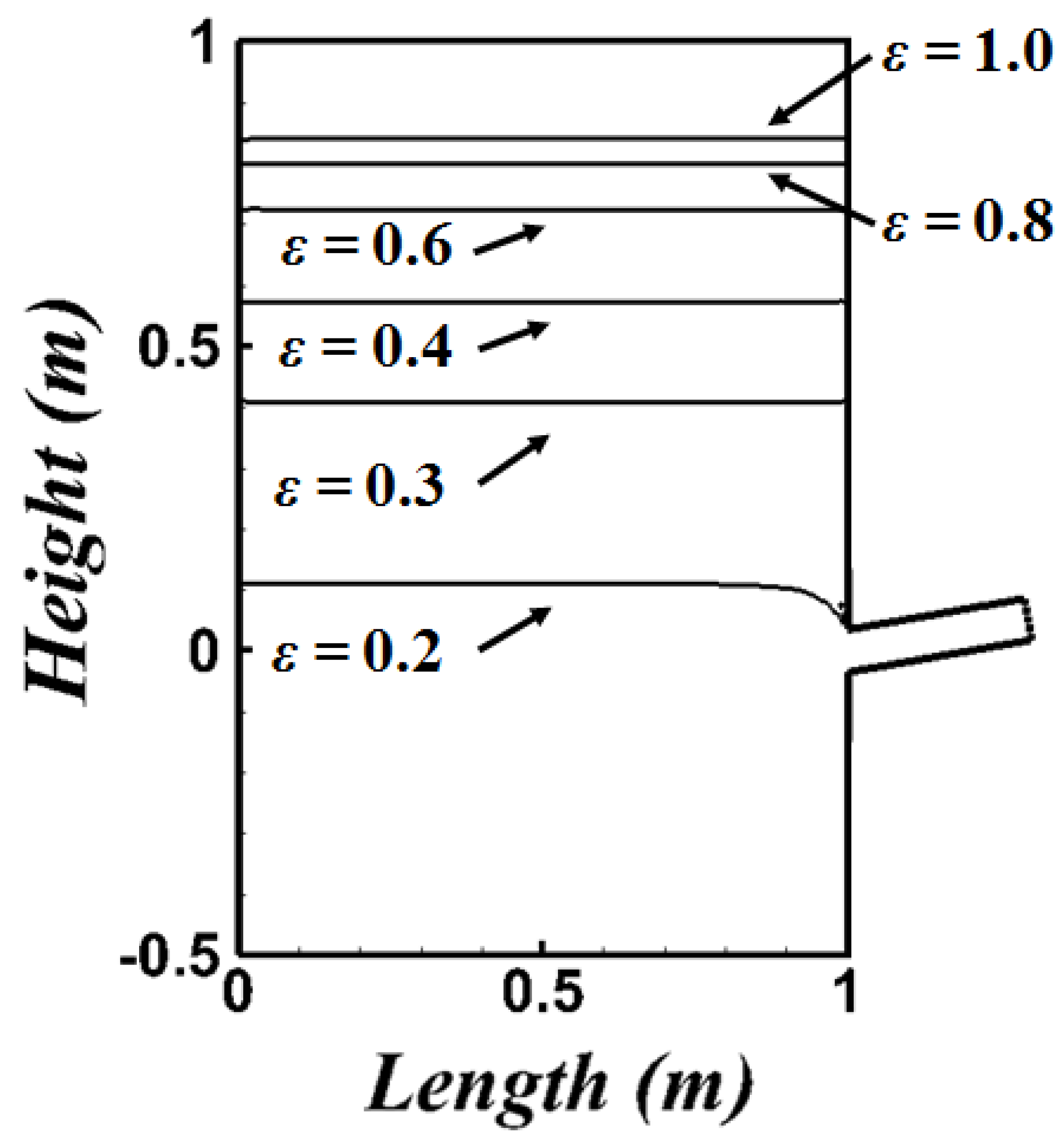
2.2. Computational Domain and Boundary Conditions
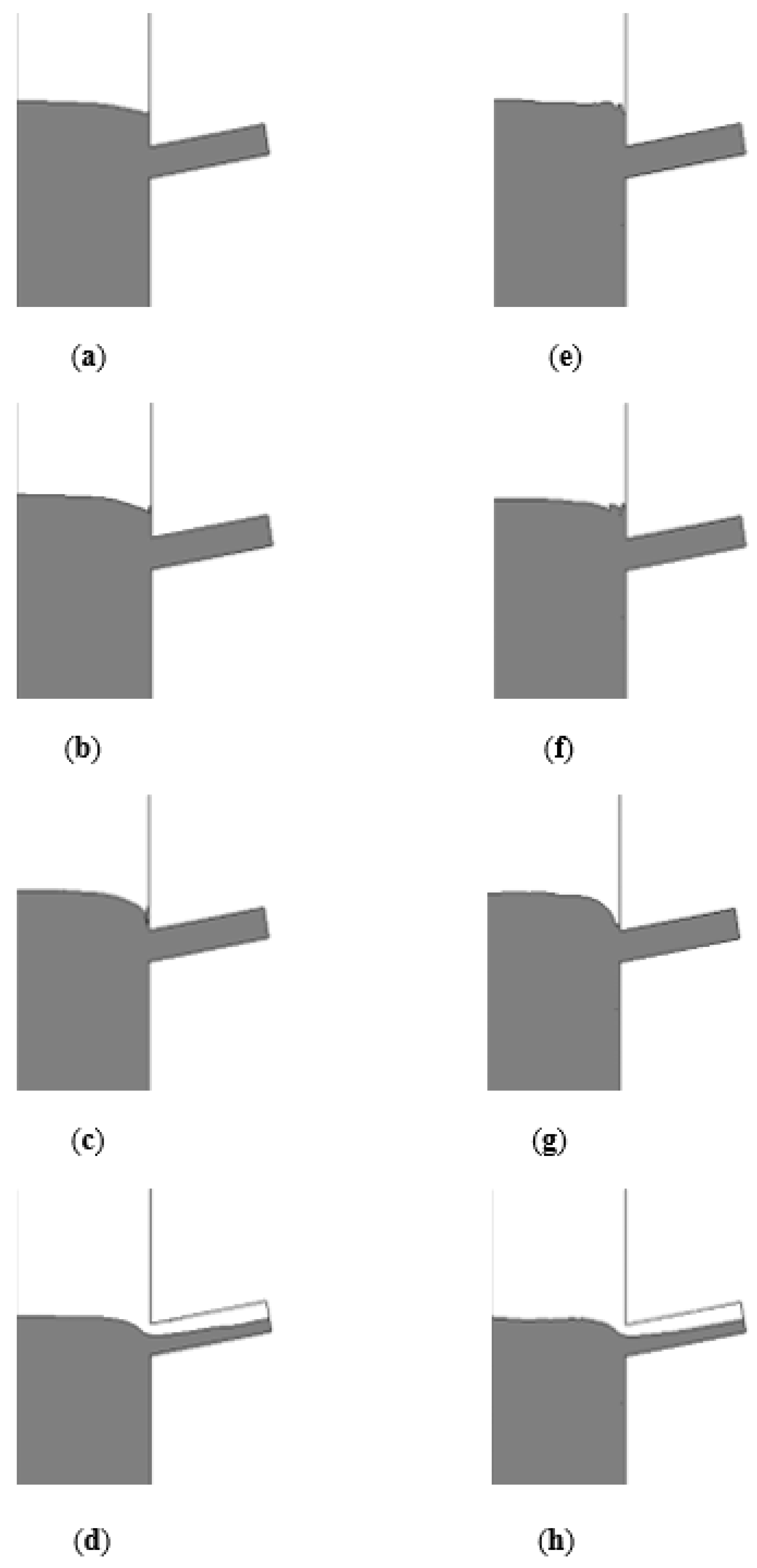
2.3. Validation
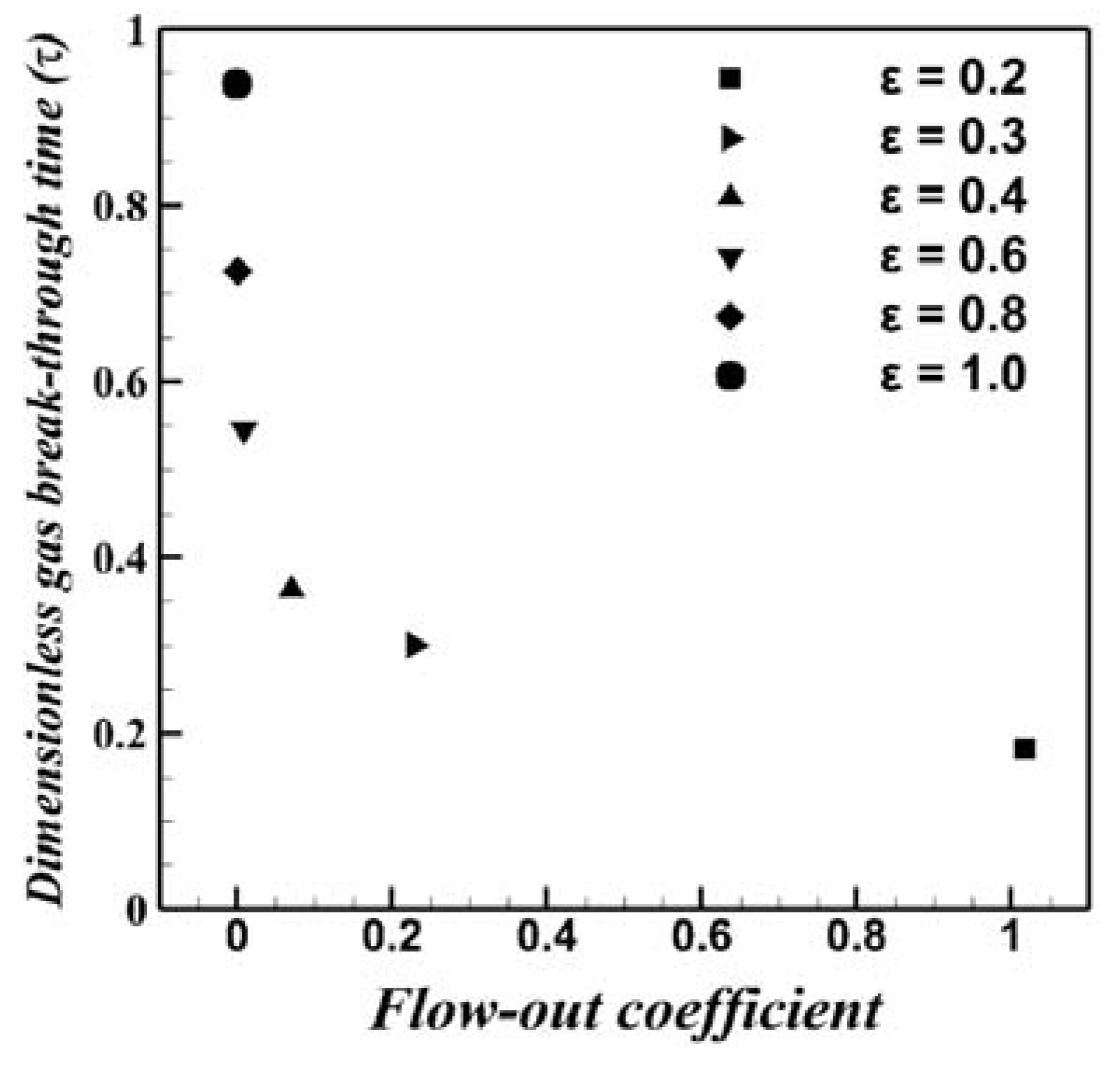
3. Results and Discussion
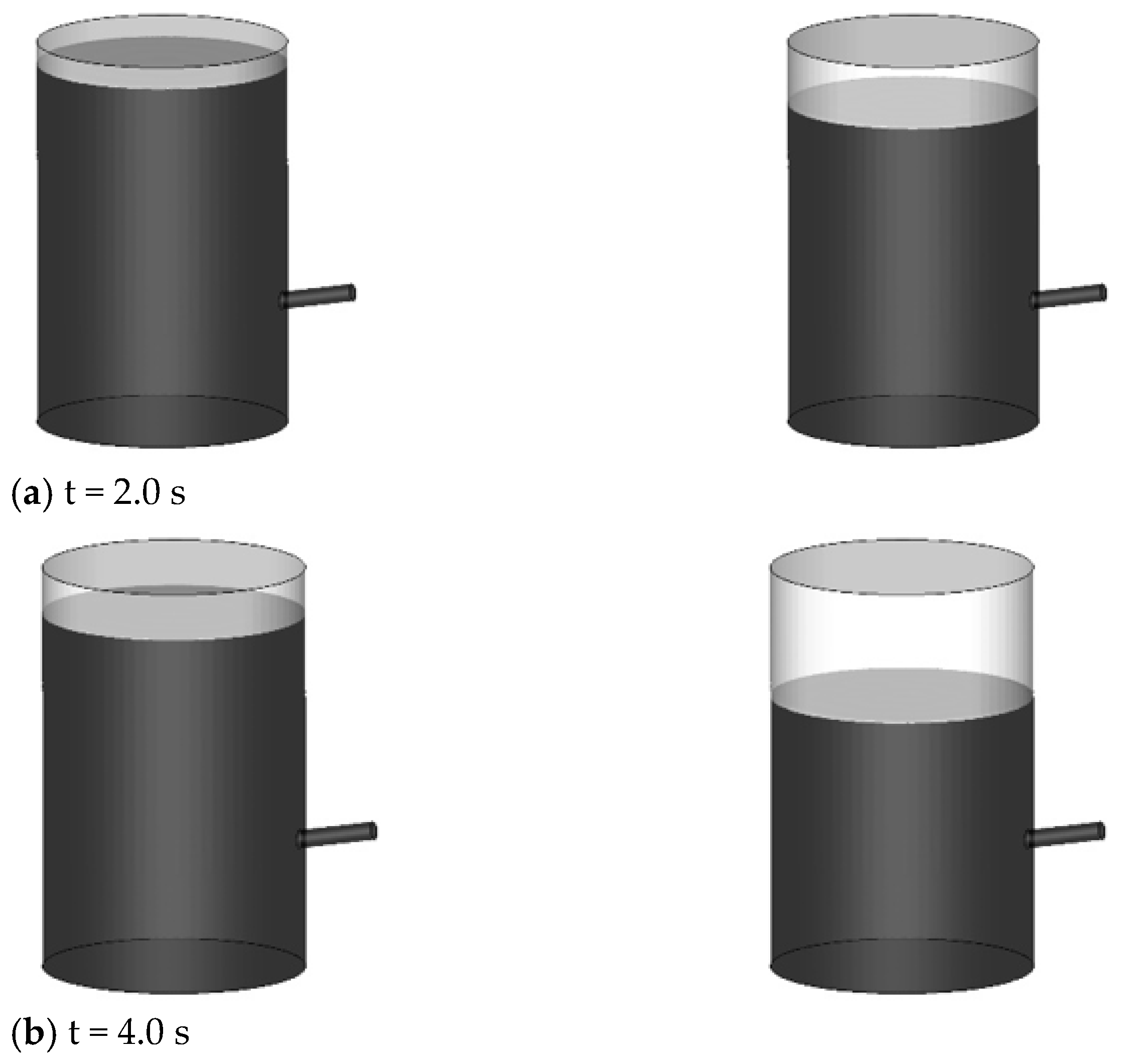
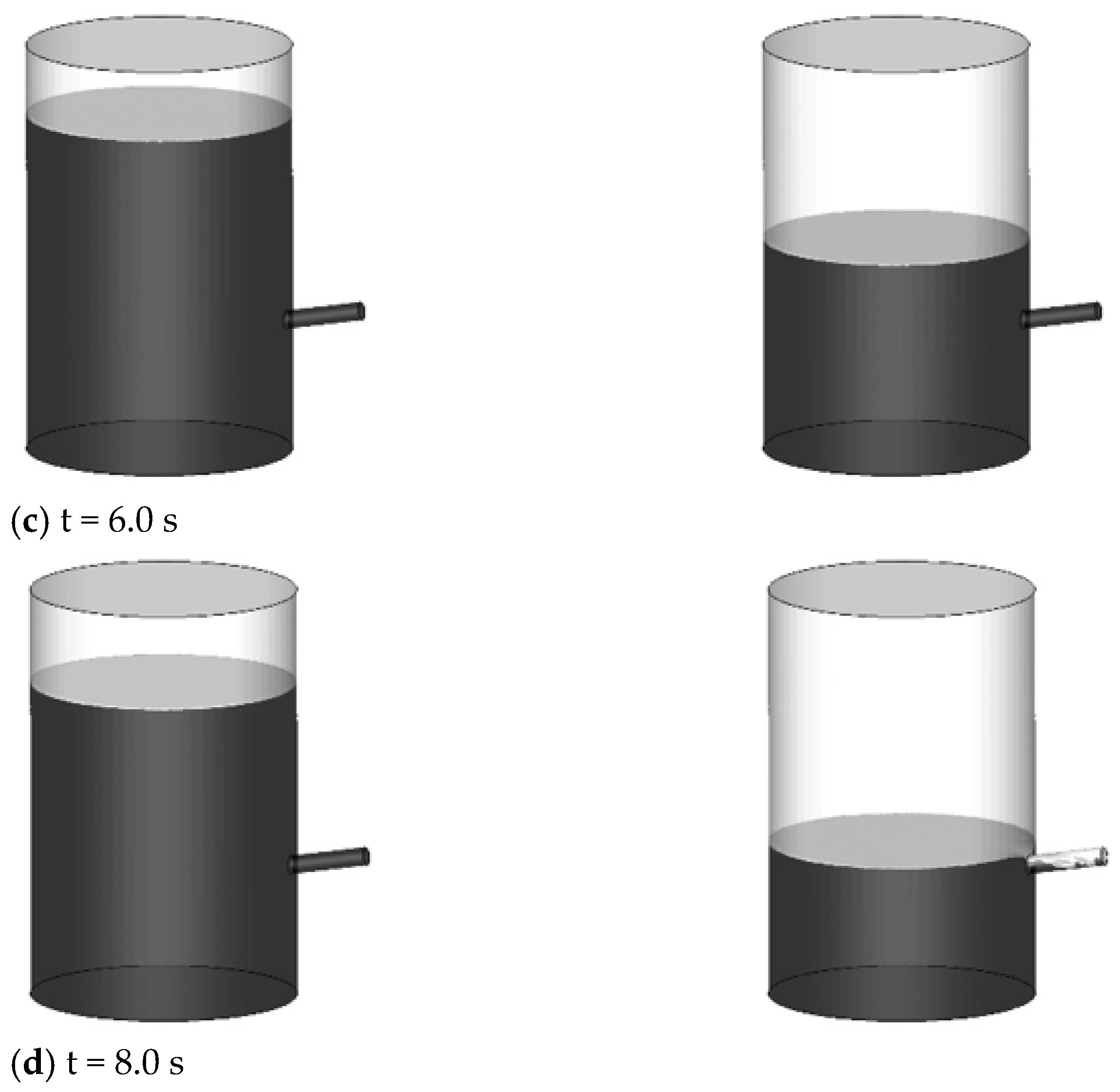
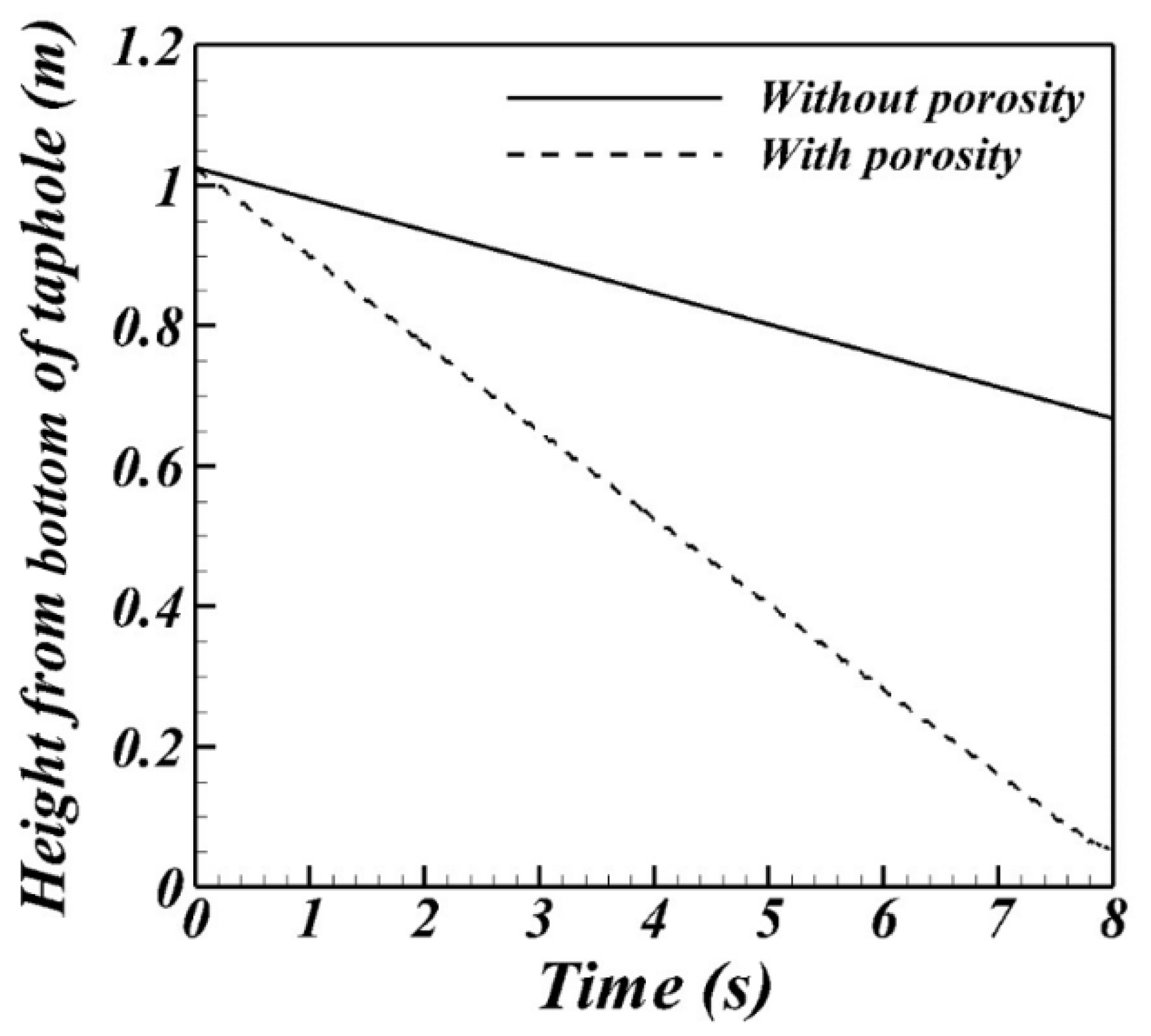
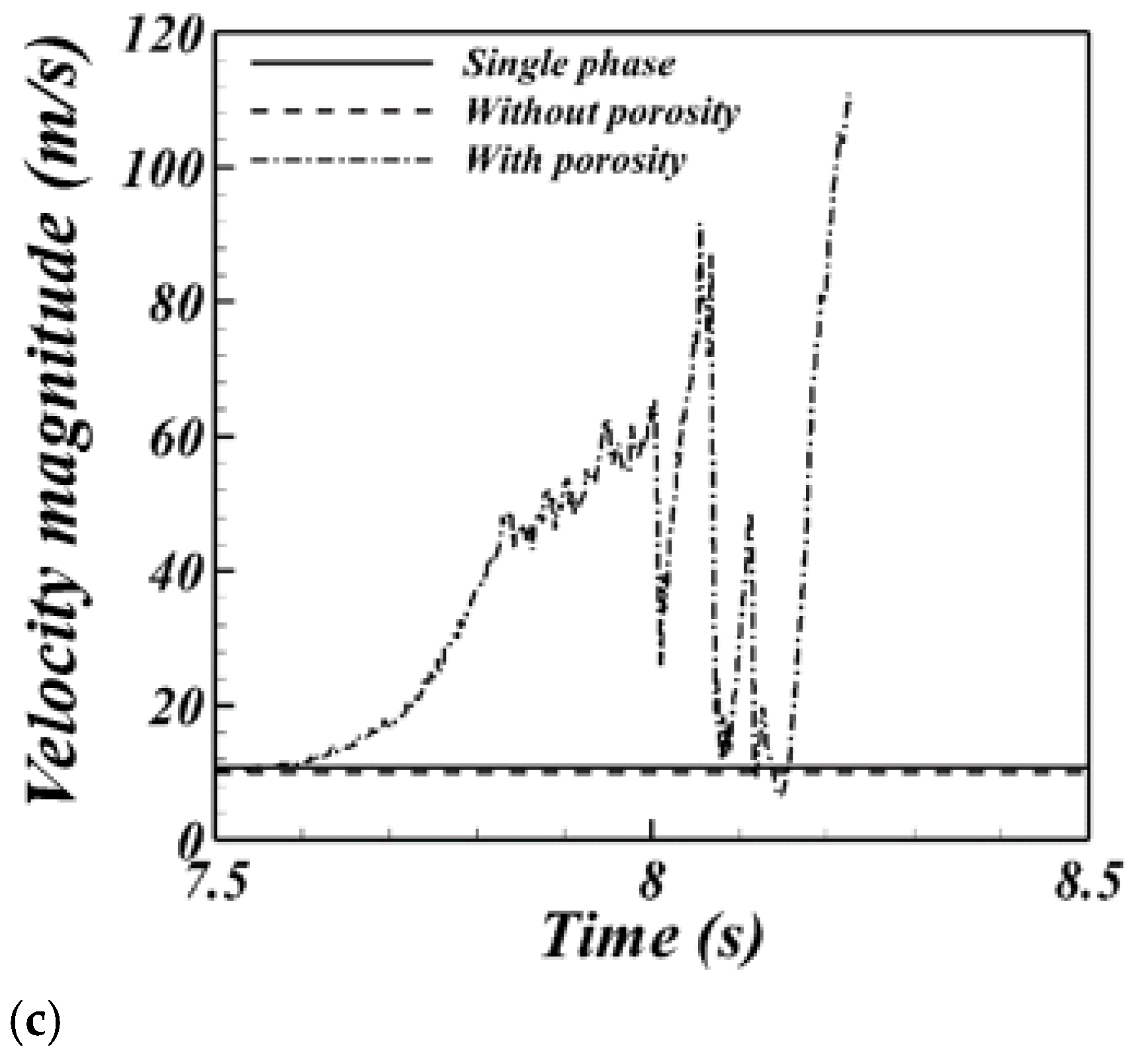
3.1. Interface Behavior with and without Porosity
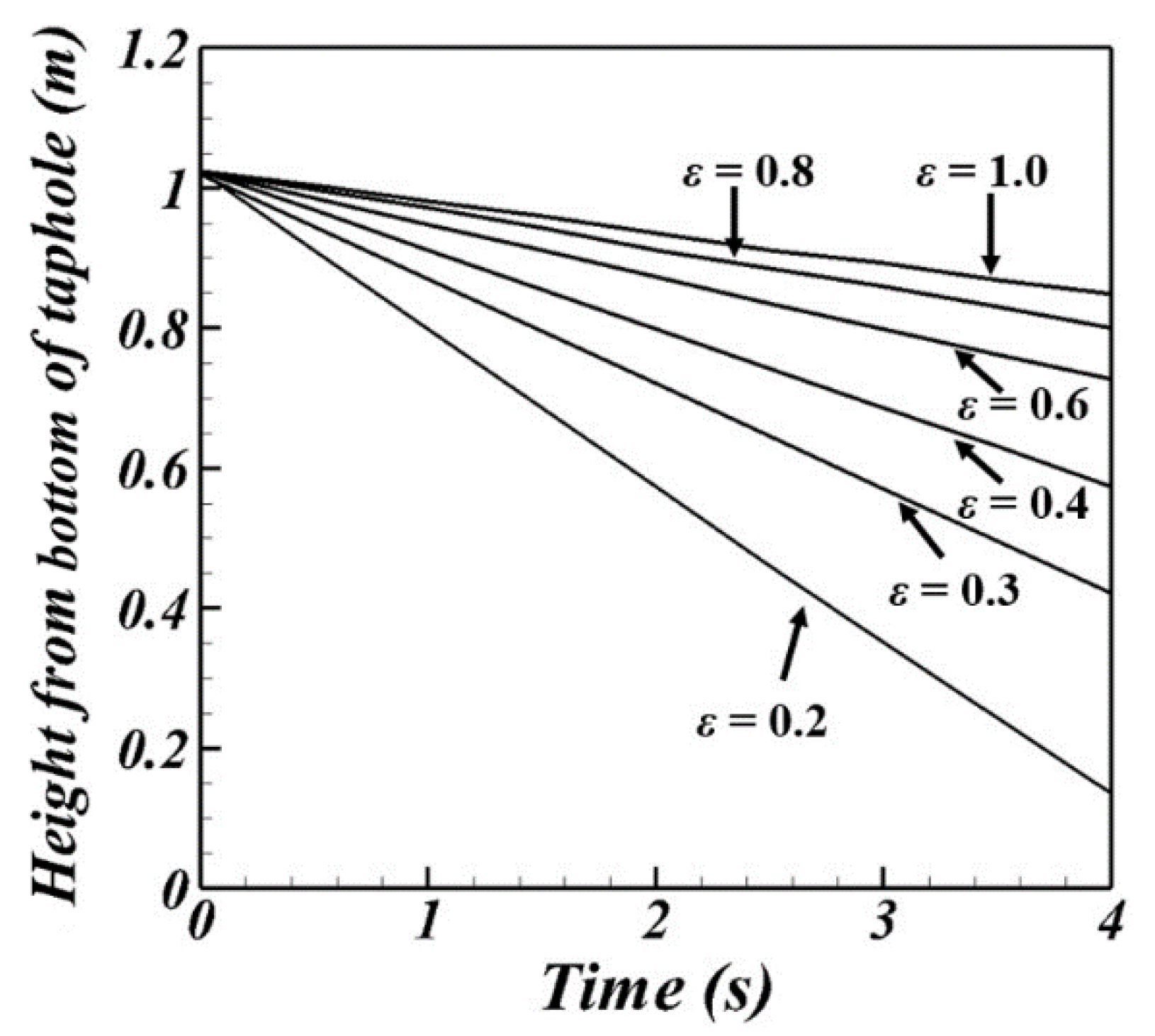
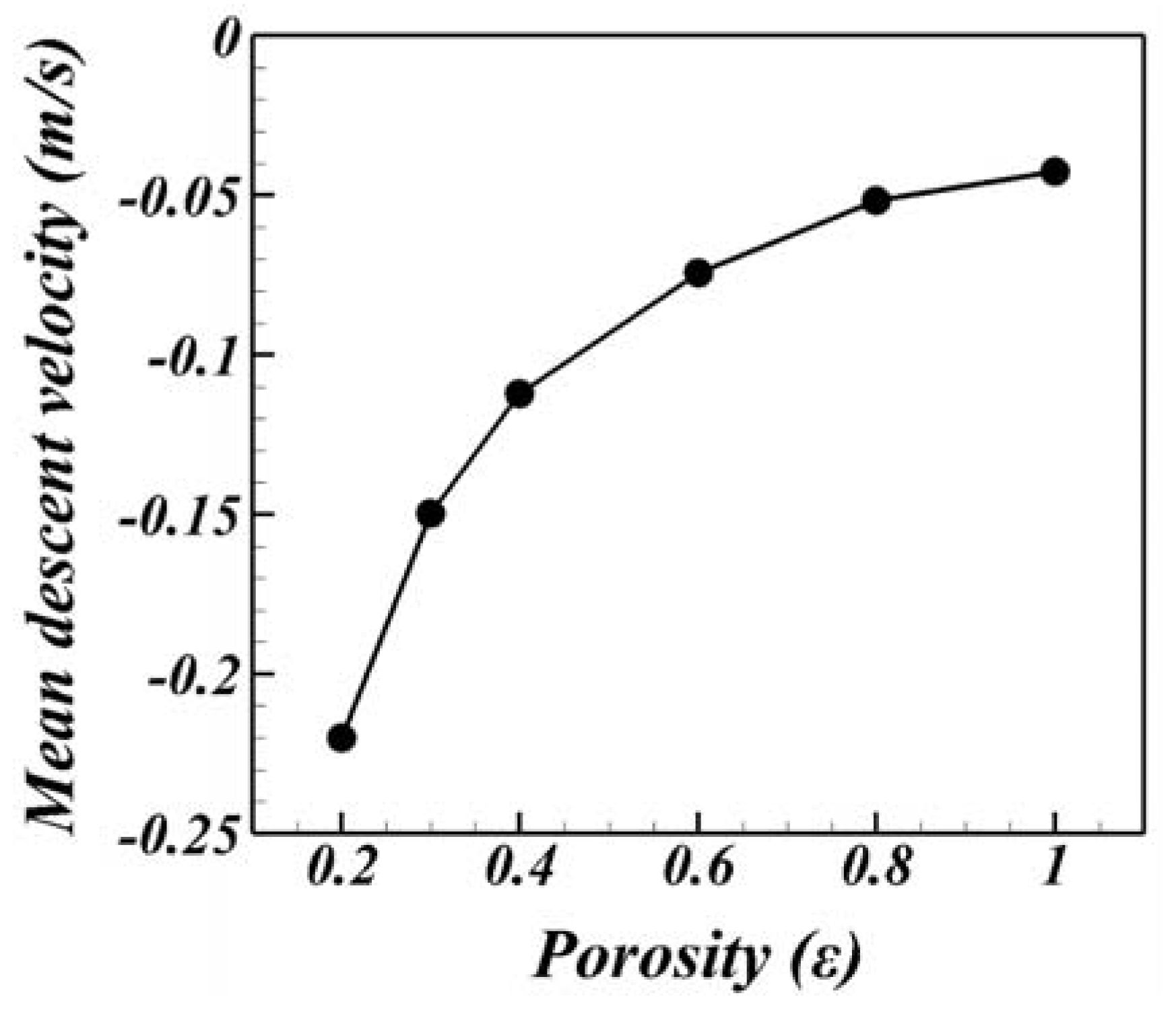
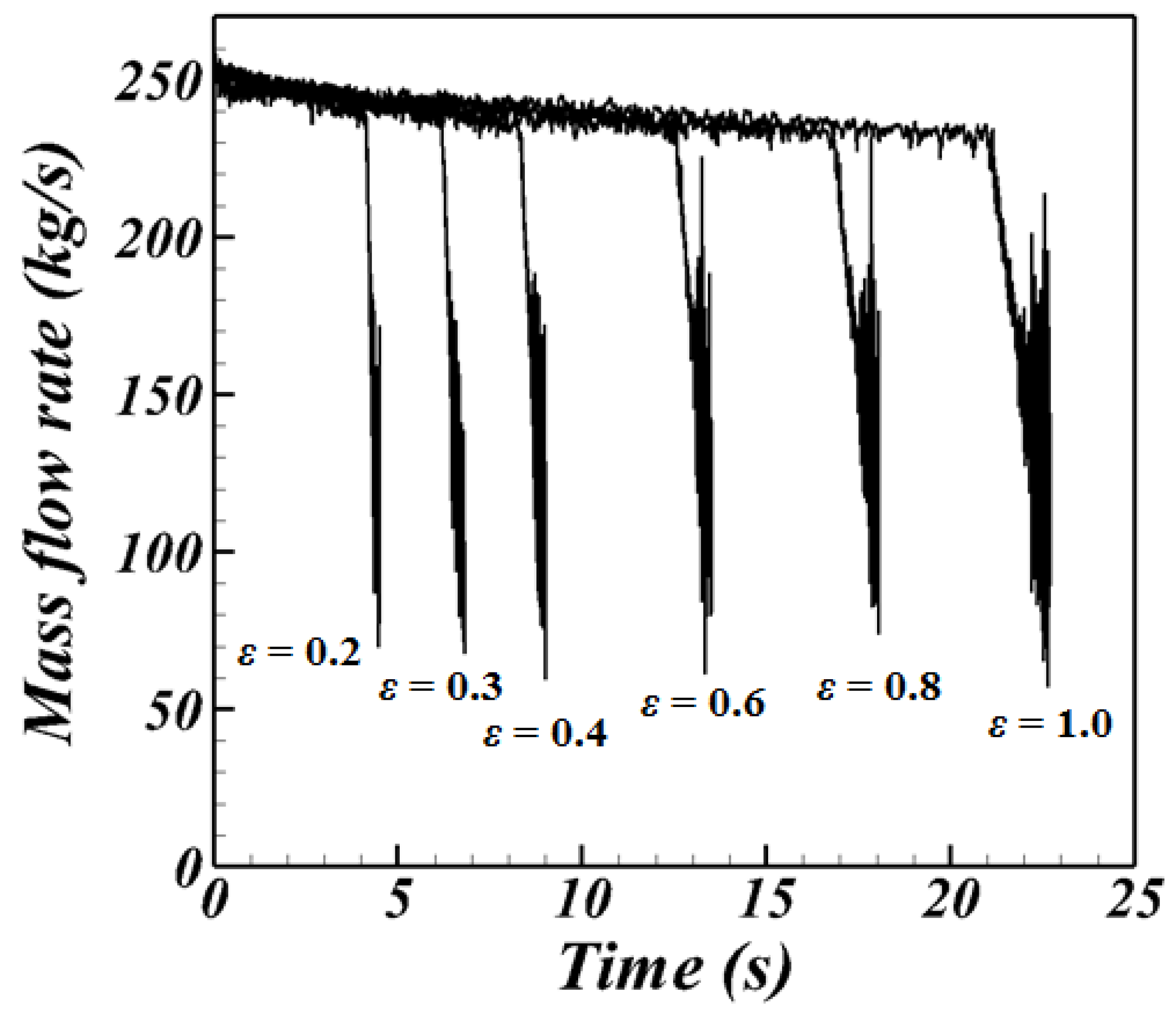
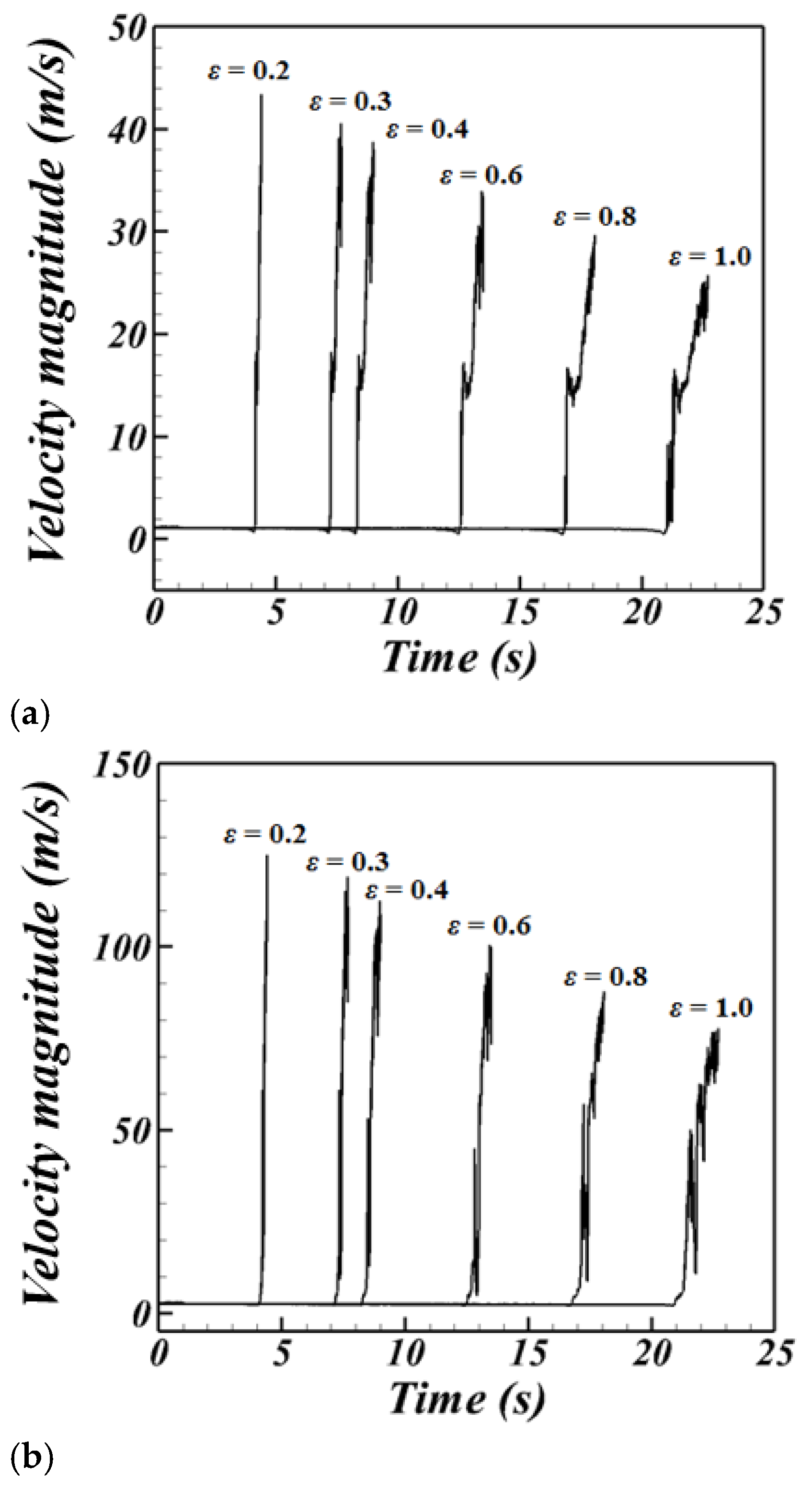
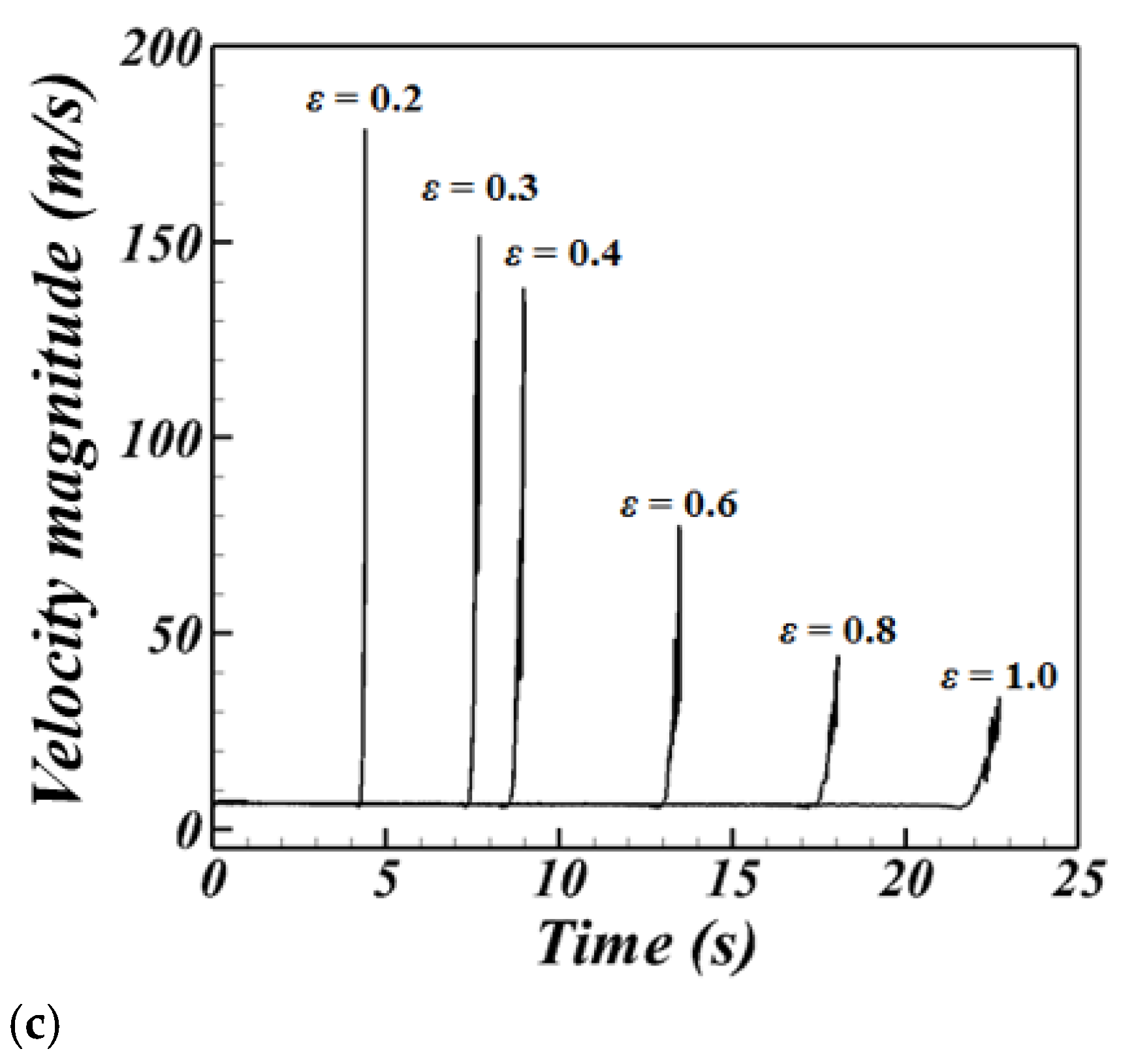
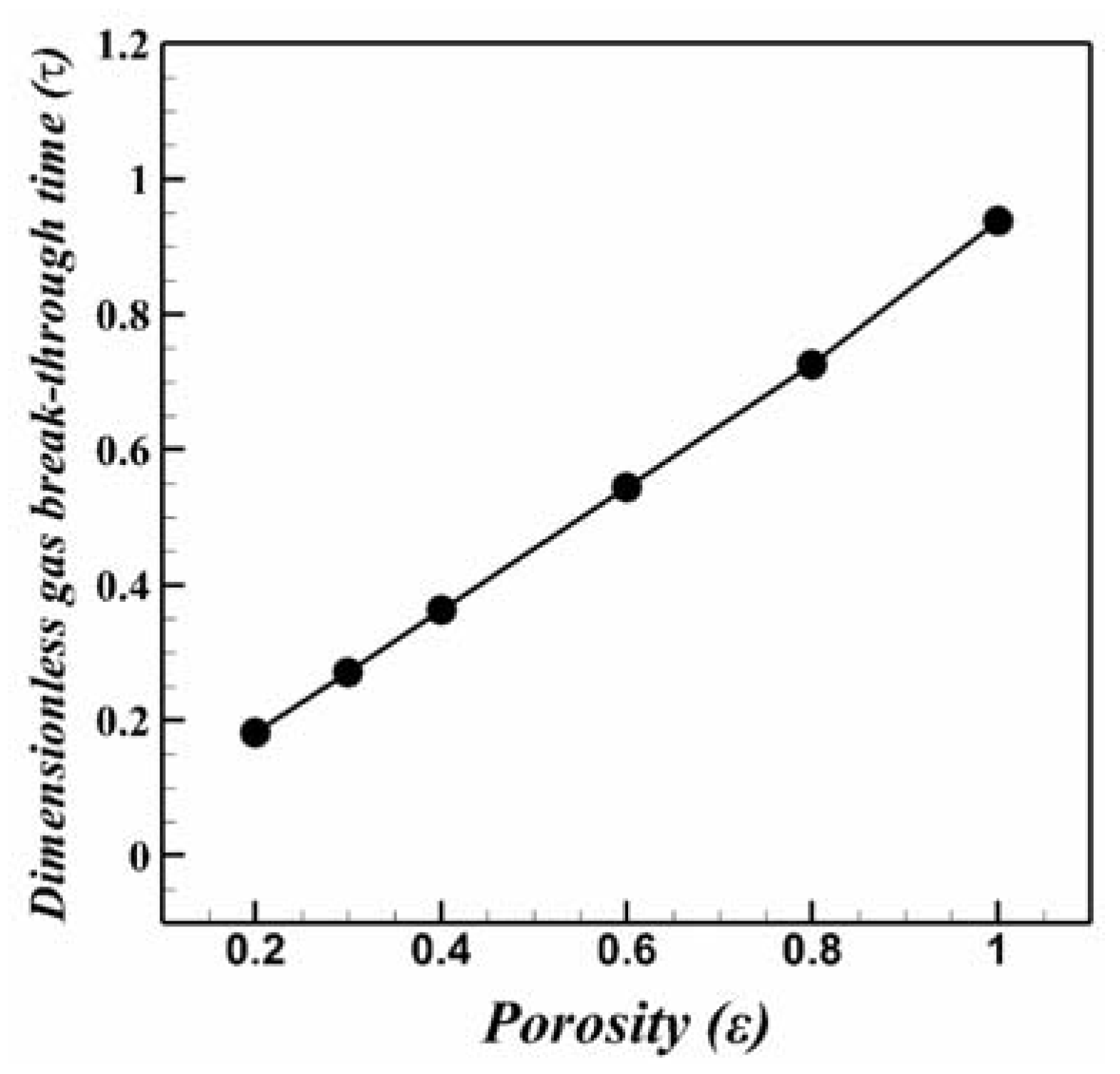
3.2. Effect of the Porosity Magnitude
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kashiwaya, Y.; Kanbe, M.; Ishii, K. Reaction behavior of facing pair between hematite and graphite: A coupling phenomenon of reduction and gasification. ISIJ Int. 2001, 41, 818–826. [Google Scholar] [CrossRef]
- Yang, J.; Mori, T.; Kuwabara, M. Mechanism of carbothermic reduction of hematite in hematite-carbon composite pellets. ISIJ Int. 2007, 47, 1394–1400. [Google Scholar] [CrossRef]
- Iwai, Y.; Ishiwata, N.; Murai, R.; Matsuno, H. Control technique of coke rate in shaft furnace by controlling coke reactivity. ISIJ Int. 2016, 56, 1723–1727. [Google Scholar] [CrossRef]
- Nemoda, S.; Mladenović, M.; Belošević, S.; Mladenović, R.; Dakić, D. Numerical model of gaseous fuel jet injection into a fluidized furnace. Int. J. Heat Mass Transf. 2009, 52, 3427–3438. [Google Scholar] [CrossRef]
- Fu, D.; Tang, G.; Zhao, Y.; D’Alessio, J.; Zhou, C.Q. Modeling of iron ore reactions in blast furnace. Int. J. Heat Mass Transf. 2016, 103, 77–86. [Google Scholar] [CrossRef]
- Natsui, S.; Takai, H.; Nashimoto, R.; Kikuchi, T.; Suzuki, R.O. Model study of the effect of particles structure on the heat and mass transfer through the packed bed in ironmaking blast furnace. Int. J. Heat Mass Transf. 2015, 91, 1176–1186. [Google Scholar] [CrossRef]
- Reddy, B.V.; Basu, P. A model for heat transfer in a pressurized circulating fluidized bed furnace. Int. J. Heat Mass Transf. 2001, 44, 2877–2887. [Google Scholar] [CrossRef]
- Kontogeorgos, D.A.; Keramida, E.P.; Founti, M.A. Assessment of simplified thermal radiation models for engineering calculations in natural gas-fired furnace. Int. J. Heat Mass Transf. 2007, 50, 5260–5268. [Google Scholar] [CrossRef]
- Wu, L.; Xu, X.; Zhou, W.; Su, Y.; Li, X. Heat transfer analysis of blast furnace stave. Int. J. Heat Mass Transf. 2008, 51, 2824–2833. [Google Scholar] [CrossRef]
- Zhang, Y.; Deshpande, R.; Huang, D.F.; Chaubal, P.; Zhou, C.Q. Numerical analysis of blast furnace hearth inner profile by using CFD and heat transfer model for different time periods. Int. J. Heat Mass Transf. 2008, 51, 186–197. [Google Scholar] [CrossRef]
- Steinboeck, A.; Wild, D.; Kiefer, T.; Kugi, A. A mathematical model of a slab reheating furnace with radiative heat transfer and non-participating gaseous media. Int. J. Heat Mass Transf. 2010, 53, 5933–5946. [Google Scholar] [CrossRef]
- Jang, J.H.; Lee, D.E.; Kim, M.Y.; Kim, H.G. Investigation of the slab heating characteristics in a reheating furnace with the formation and growth of scale on the slab surface. Int. J. Heat Mass Transf. 2010, 53, 4326–4332. [Google Scholar] [CrossRef]
- Johansson, R.; Leckner, B.; Andersson, K.; Johnsson, F. Influence of particle and gas radiation in oxy-fuel combustion. Int. J. Heat Mass Transf. 2013, 65, 143–152. [Google Scholar] [CrossRef]
- Courtessole, C.; Etay, J. Flows and mass transfers in two superimposed liquid layers in an induction furnace. Int. J. Heat Mass Transf. 2013, 65, 893–906. [Google Scholar] [CrossRef]
- Gu, M.; Chen, G.; Liu, X.; Wu, C.; Chu, H. Numerical simulation of slab heating process in a regenerative walking beam reheating furnace. Int. J. Heat Mass Transf. 2014, 76, 405–410. [Google Scholar] [CrossRef]
- Blaszczuk, A.; Nowak, W. Heat transfer behavior inside a furnace chamber of large-scale supercritical CFB reactor. Int. J. Heat Mass Transf. 2015, 87, 464–480. [Google Scholar] [CrossRef]
- Han, Y.; Yu, E.; Han, Z. Study on temperature distribution non-uniformity of inner grooved copper tubes during pit furnace annealing. Int. J. Heat Mass Transf. 2017, 104, 749–758. [Google Scholar] [CrossRef]
- Su, C.R.; Liu, W.L.; Lai, H.Y. Estimation for inner surface geometry of furnace wall using inverse process combined with grey prediction model. Int. J. Heat Mass Transf. 2009, 52, 3595–3605. [Google Scholar] [CrossRef]
- Han, S.H.; Chang, D. Optimum residence time analysis for a walking beam type reheating furnace. Int. J. Heat Mass Transf. 2012, 55, 4079–4087. [Google Scholar] [CrossRef]
- Yagi, J. Mathematical modeling of the flow of four fluids in a packed bed. ISIJ Int. 1993, 33, 619–639. [Google Scholar] [CrossRef]
- Dong, X.; Yu, A.; Yagi, J.; Zulli, P. Modelling of multiphase flow in a blast furnace: Recent developments and future work. ISIJ Int. 2007, 47, 1553–1570. [Google Scholar] [CrossRef]
- Dong, X.F.; Yu, A.B.; Burgess, J.M.; Pinson, D.; Chew, S.; Zulli, P. Modelling of multiphase flow in ironmaking blast furnace. Ind. Eng. Chem. Res. 2009, 48, 214–226. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, A.; Yu, A.; Zulli, P. Numerical investigation of the transient multiphase flow in an ironmaking blast furnace. ISIJ Int. 2010, 50, 515–523. [Google Scholar] [CrossRef]
- Ueda, S.; Natsui, S.; Nogami, H.; Yagi, J.; Ariyama, T. Recent progress and future perspective on mathematical modeling of blast furnace. ISIJ Int. 2010, 50, 914–923. [Google Scholar] [CrossRef]
- Ren, W.; Zhao, A.; Jin, N. Void fraction measurement of Oil–Gas–Water three-phase flow using mutually perpendicular Ultrasonic sensor. Sensors 2020, 20, 481. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, W.; Fatayerji, A.; Elsaftawy, A.; Hassan, M.; Weaver, D.; Riznic, J. A new capacitance sensor for measuring the void fraction of two-phase flow through tube bundles. Sensors 2020, 20, 2088. [Google Scholar] [CrossRef] [PubMed]
- Roshani, M.; Phan, G.; Roshani, G.H.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Measurement 2021, 168, 108427. [Google Scholar] [CrossRef]
- Roshani, M.; Pahn, G.T.T.; Ali, P.J.M.; Roshani, G.H.; Hanus, R.; Duong, T.; Corniani, E.; Nazemi, E.; Kalmoun, E.M. Evaluation of flow pattern recognition and void fraction measurement in two phase flow independent of oil pipeline’s scale layer thickness. Alex. Eng. J. 2021, 60, 1955–1966. [Google Scholar] [CrossRef]
- Stevenson, P.; He, Q. Slug flow in a blast furnace taphole. Chem. Eng. Proc. 2005, 44, 1094–1097. [Google Scholar] [CrossRef]
- He, Q.; Evans, P.; Zulli, P.; Tanzil, F. Cold model study of blast gas discharge from the taphole during the blast furnace hearth drainage. ISIJ Int. 2012, 52, 774–778. [Google Scholar] [CrossRef]
- He, Q.; Zulli, P.; Lee, B.; Dunning, J.; Evans, G. Flow characteristics of a blast furnace taphole stream and its effects on trough refractory wear. ISIJ Int. 2002, 42, 235–242. [Google Scholar] [CrossRef]
- He, Q.; Zulli, P.; Evans, G.; Tanzil, F. Free surface instability and gas entrainment during blast furnace drainage. Dev. Chem. Eng. Miner. Proc. 2006, 14, 429. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A Mat. 1958, 245, 312–329. [Google Scholar]
- Hill, S. Channelling in packed columns. Chem. Eng. Sci. 1952, 1, 247–253. [Google Scholar] [CrossRef]
- Tabeling, P.; Zocchi, G.; Libchaber, A. An experimental study of the Saffman-Tayloer instability. J. Fluid Mech. 1987, 177, 67–82. [Google Scholar] [CrossRef]
- Siemens. STAR-CCM+ User Guide Version 9.04; Siemens: New York, NY, USA, 2011. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: New York, NY, USA, 1972; pp. 157–162. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1959, 48, 89–94. [Google Scholar]
- Huang, H.; Ayoub, J.A. Applicability of the Forchheimer Equation for Non-Darcy Flow in Porous Media. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; p. SPE-102715-MS. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Shao, L.; Saxen, H. A simulation study of two-liquid flow in the taphole of the blast furnace. ISIJ Int. 2013, 53, 988–994. [Google Scholar] [CrossRef][Green Version]
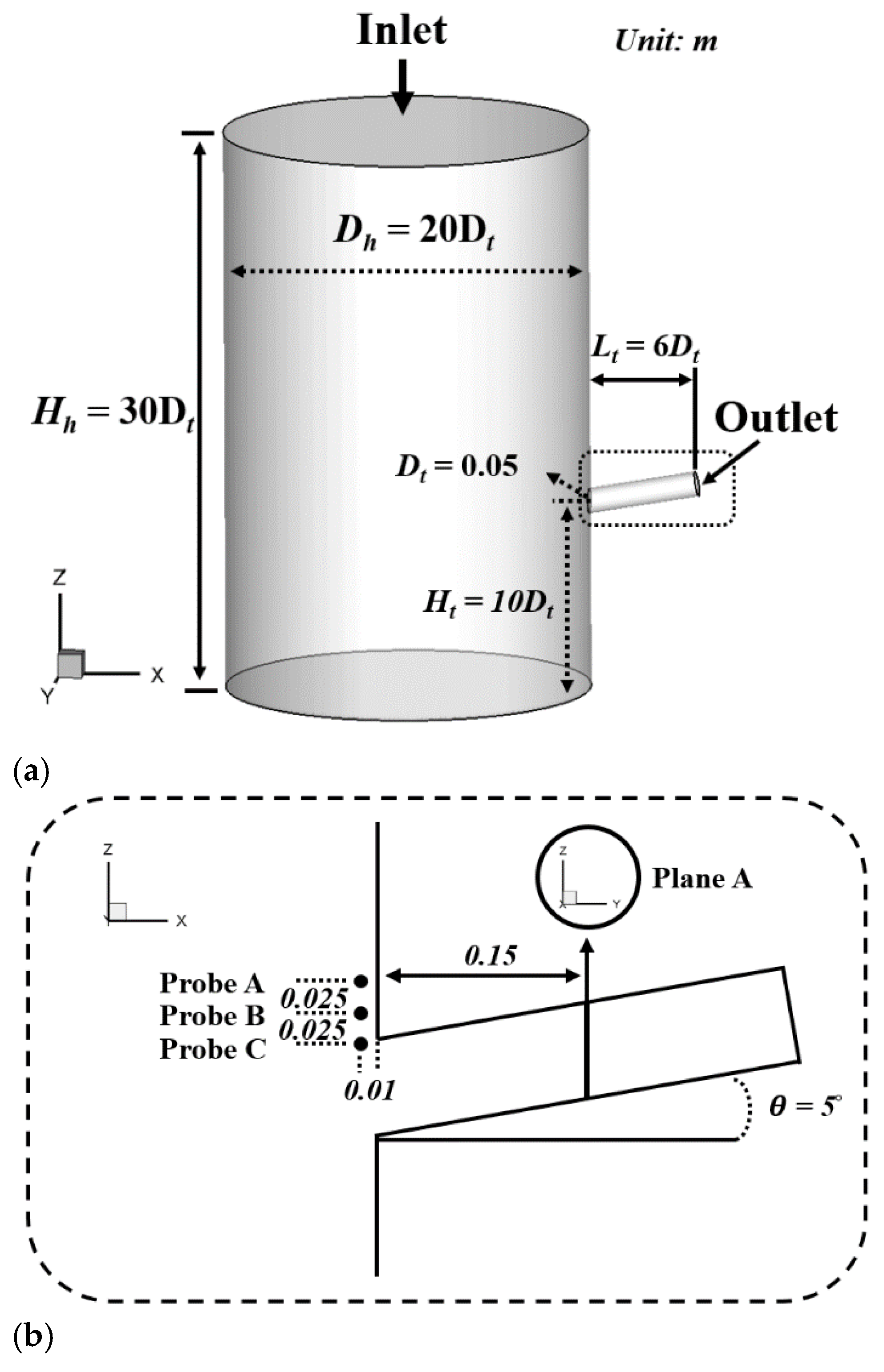
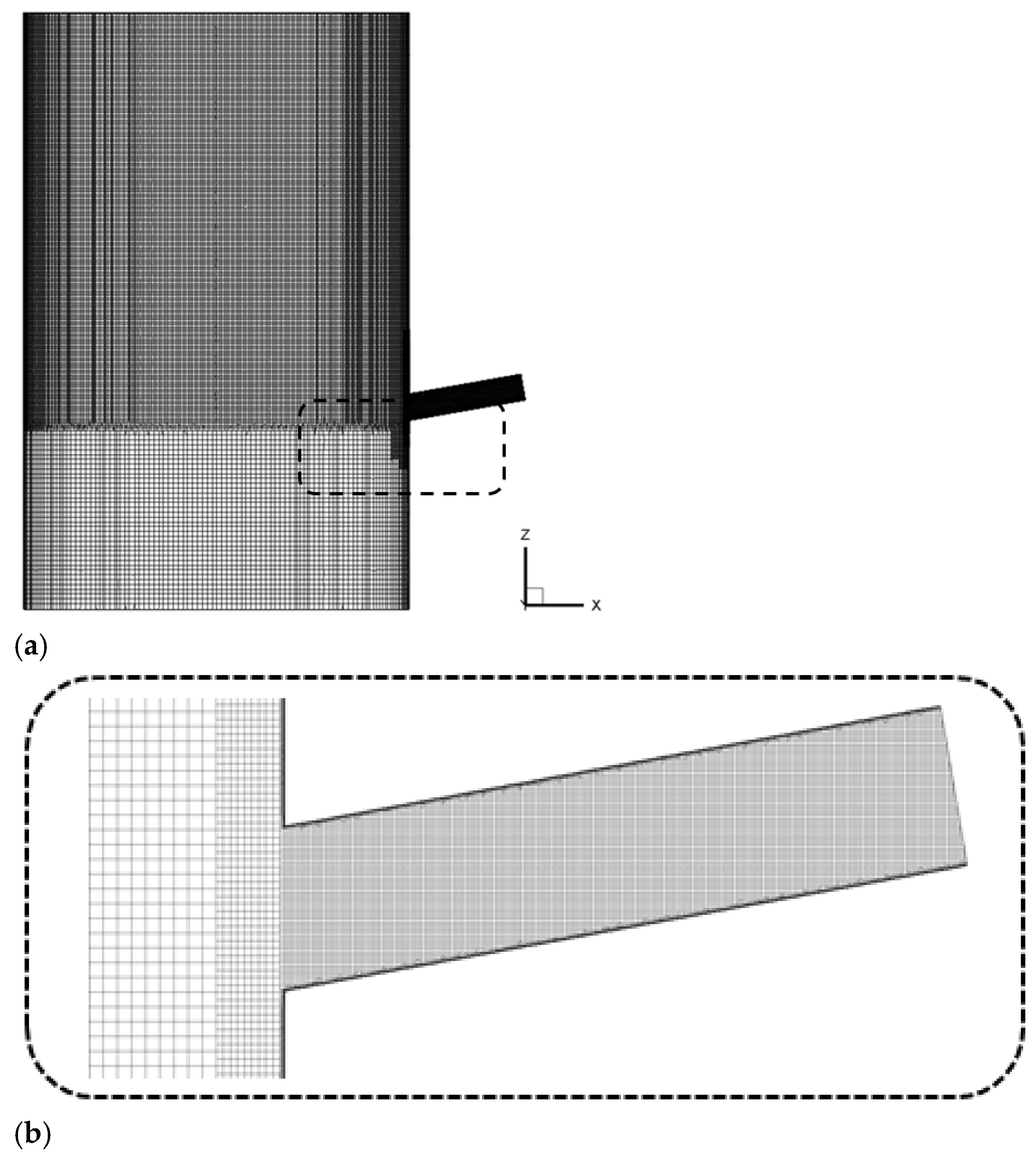
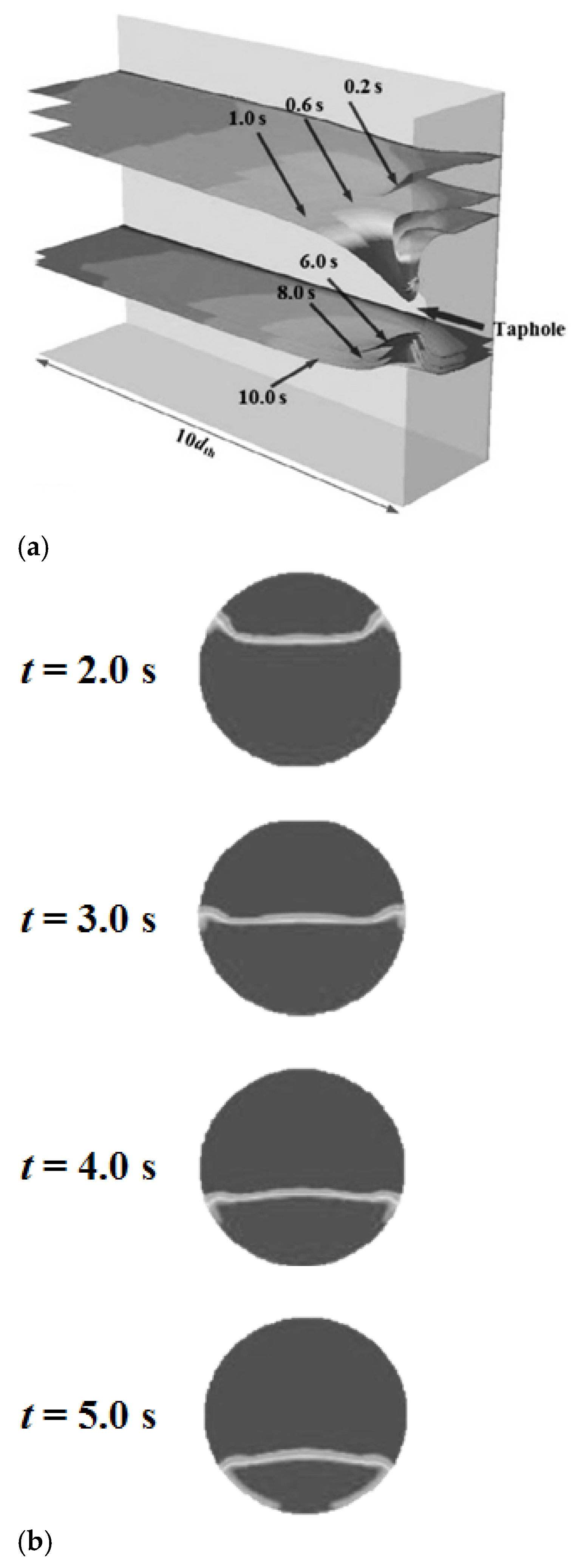
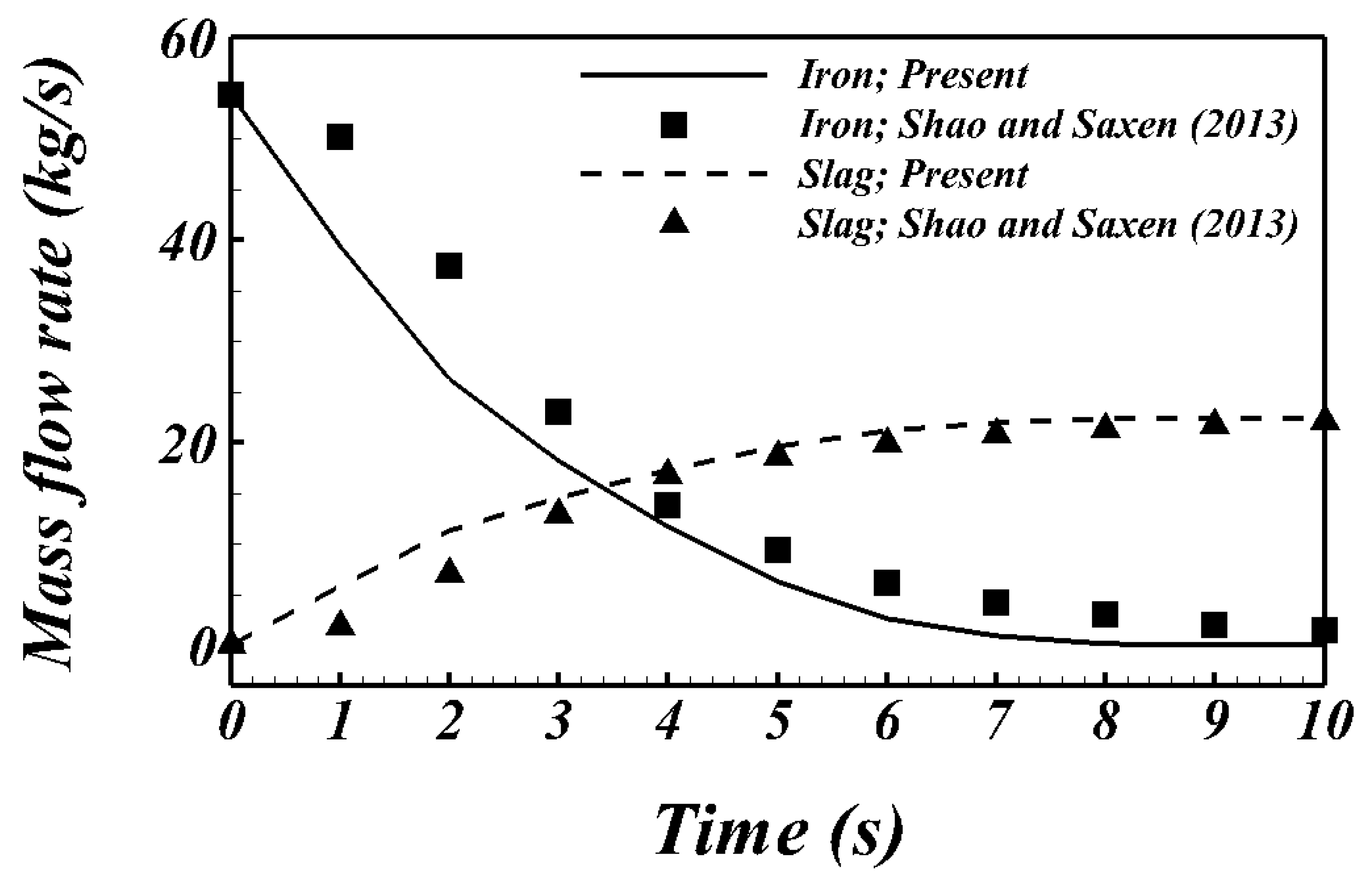


| Variable | Value |
|---|---|
| Hearth diameter, Dh (m) | 1 |
| Hearth height, Hh (m) | 1.5 |
| Taphole diameter, Dt (m) | 0.05 |
| Taphole height, Ht (m) | 0.5 |
| Taphole length, Lt (m) | 0.3 |
| Tilting angle of taphole, () | 5 |
| Molten iron density, (kg/m3) | 7000 |
| Molten iron viscosity, (Pa·s) | 7.15 × 10−3 |
| Air density, (kg/m3) | 1.18 |
| Air viscosity, (Pa·s) | 1.85 × 10−5 |
| Pressure drop, Pinlet−Poutlet (kPa) | 450 |
| Porosity, | 0.2, 0.3, 0.4, 0.6, 0.8, 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, H.-S.; Park, K.-M. Behavior of the Free Surface of Two-Phase Fluid Flow Near the Taphole in a Tank. Symmetry 2021, 13, 875. https://doi.org/10.3390/sym13050875
Yoon H-S, Park K-M. Behavior of the Free Surface of Two-Phase Fluid Flow Near the Taphole in a Tank. Symmetry. 2021; 13(5):875. https://doi.org/10.3390/sym13050875
Chicago/Turabian StyleYoon, Hyun-Sik, and Kyung-Min Park. 2021. "Behavior of the Free Surface of Two-Phase Fluid Flow Near the Taphole in a Tank" Symmetry 13, no. 5: 875. https://doi.org/10.3390/sym13050875
APA StyleYoon, H.-S., & Park, K.-M. (2021). Behavior of the Free Surface of Two-Phase Fluid Flow Near the Taphole in a Tank. Symmetry, 13(5), 875. https://doi.org/10.3390/sym13050875





