Abstract
We present an overview of multisoliton chains arising in various non-integrable field theories and discuss different mechanisms which may lead to the occurrence of such axially-symmetric classical solutions. We explain the pattern of interactions between different solitons, in particular Q-balls, Skyrmions, and monopoles, and show how chains of interacting non-BPS solitons may form in a dynamic equilibrium between repulsive and attractive forces.
1. Introduction
There has been astonishing progress over the past sixty years in our understanding of nonlinear phenomena. Up until the 1960s nonlinear systems were given little attention mainly because of their complexity; in most cases the corresponding dynamical equations do not possess analytical solutions. The situation changed drastically with the dawning of computational physics, which made it possible to find reasonably accurate solutions for nearly any properly formulated physical problem. This development yields many surprising results and discoveries.
One of the most interesting properties of various non-linear systems is that they may support solitons, stable, non-dissipative, localized configurations, behaving in many ways like particles (for review, see, e.g., in [1,2,3,4]). Solitons emerge in diverse contexts in various situations in nonlinear optics, condensed matter, nuclear physics, cosmology, and supersymmetric theories. In some situations, their existence is related to topological properties of the model; in other cases, they appear due to balance between the effects of nonlinearity and dispersion. However, unlike the usual particles, solitons are extended objects; they possess a core in which most energy is localized and an asymptotic tale, which is responsible for the long-range interaction between the well-separated solitons. Further, there is a tower of linearized excitations around a soliton, which belong to the perturbative spectrum. As a result, the pattern of interaction between the solitons becomes very complicated, in some situations there are both repulsive and attractive forces with different asymptotic behavior and the process of the collision between the solitons is very different from the simple picture of elastic scattering of point-like particles.
The study of the interactions between solitons, the processes of their scattering, radiation, and annihilation has attracted a lot of attention in many different contexts. First, almost immediately after discovery of the solitons in pioneering works [5,6], the mathematical concept of integrability was developed. It turns out that some models, which may support solitons, are completely solvable, in other words, all solutions can be presented analytically in closed form. Moreover, in integrable theories the collision between the solitons is always completely elastic. Further, there is a very special class of so-called self-dual solitons, whose exactly saturate the topological energy bound. In such a case, the energy of interaction between the solitons is always zero, then various multisoliton configurations can be constructed via implication of diverse beautiful differential-geometrical mathods, see, e.g., in [1,2].
The situation is completely different in non-integrable theories. Perhaps one of the simplest examples of such theory is a family of (1 + 1)-dimensional models with a polynomial potential possessing two or more degenerated minima, for example, modes with a double-well potential [3]. Another example is the Skyrme model [7], it is very well known as a prototype of a relativistic field theory which supports non-BPS topological solitons, see, for example, in [1,8]. Historically, the 3 + 1 dimensional Skyrme model was proposed as a model of atomic nuclei, in such a framework baryons are considered as solitons with identification of the baryon number and the topological charge of the field configuration. A new development is related to the lower dimensional version of the Skyrme model in 2 + 1 dimensions as solitons of that type were experimentally observed in planar magnetic structures and liquid crystals (for a review, see, e.g., in [9]). Notably, a simplest Skyrmion of topological degree one is rotationally invariant, however, solutions of higher degrees may possess very interesting geometric shapes [1,10]. This is because the interaction between the Skyrmions is mediated by the long-range dipole forces, and therefore there are both repulsive and attractive channels. Thus, the pattern of interaction between the solitons become rather involved. Further, a particular choice of the potential of the model defines the structure of multisoliton configurations, in some cases pairs of solitons in equilibrium may appear.
Static solutions of the theory and the Skyrme model represent a class of topological solitons. There are also non-topological solitons, for example, stationary field configurations, commonly named Q-balls, that may exist in some models with a suitable self-interaction potential [11,12,13]. When Q-balls are coupled to gravity so-called boson stars emerge, they represent compact stationary configurations with a harmonic time dependence of the scalar field and unbroken global symmetry [14,15]. Notably, the character of the interaction between Q-balls depends on their relative phase [16,17]. In general, a pair of Q-balls is not stable in Minkowski spacetime; however, the gravitational attraction may stabilize it. Further, extended linear chains of rotating boson stars can be formed via this mechanism [18].
Another famous example of topological solitons are monopoles; they appear as classical solutions of the non-abelian Yang-Mills-Higgs theory in 3 + 1 dimensions [19,20], for a review see, e.g., in [21]. The magnetic charge of the non-abelian monopole is proportional to the topological charge. However, the pattern of interaction between the monopoles is far from naive picture of Coulomb interaction of two point-like magnetic charges. The ’t Hooft–Polyakov solution is a coupled topologically stable configuration of gauge and Higgs fields which may have different asymptotic behavior. In particular, in the so-called Bogomol’nyi–Prasad–Sommerfield (BPS) limit of vanishing Higgs potential, both the gauge and the scalar fields become massless, then there is an exact balance of two long-range interactions between the BPS monopoles, which are mediated by the massless photon and the massless scalar particle, respectively. By contrast, attractive scalar interaction between two non-BPS monopoles becomes stronger than magnetic repulsion, the corresponding charge two configuration with double zero of the Higgs field at the origin possess axial symmetry [22]. On the other hand, it it possible to construct monopole–anti-monopole pair solution in a static equilibrium [23,24]. This configuration represent a sphaleron, a saddle point solution of the classical field equations. Similar solutions also exist in the Skyrme model [25,26].
Pairs of non-selfdual solitons in a static equilibrium can be considered as basic building blocks of chains of non-selfdual solitons. The main purpose of the present short review is to discuss such solution in a few different models. First, we briefly consider the mechanism of interaction between the kinks in one spatial dimension and describe how static multisoliton bound states can be formed due to exchange interaction mediated by the localized fermion states (Section 2). Then, we review the interactions between the Skyrmions and their dependency on the structure of the potential. This yields some insight on the existence of chains of Skyrmions in two and three spatial dimensions (Section 3 and Section 4, respectively). In Section 5, we discuss interactions between the Q-balls and possible mechanism of formation of pairs of Q-balls in equilibrium. Here, we also include the gravitational interaction and consider chains of boson stars. Finally, in Section 6, we revisit construction of monopole–anti-monopole pairs and chains. Conclusions and remarks are formulated in the last Section.
2. Chains of Kinks
The simplest example of solitons are the kinks; they are classical solutions of the relativistic, nonlinear scalar field theory in dimensions with Lagrangian density
with a smooth non-negative potential possessing some set of minima . The static kink solution of this model interpolates between different vacua as space coordinate x runs from to ∞. For example, in the model the quartic potential
possesses two vacua, . Then, the field equation of the model (1)
yields the well-known non-trivial kink solution interpolating between and . By contrast, the anti-kink solution connects the vacua and .
There are other examples of kinks in one spatial dimension, in particular the sine-Gordon model with infinitely degenerated periodic potential supports static kink solution which connects two neighboring vacua . Similarly, the model with triple degenerated vacuum , , supports two different kinks
Further examples of kinks are discussed in [27,28,29] and other papers.
A few comments are in order here. First, for any model in one spatial dimension, the second order field Equation (3) can always be reduced to the first order equation
where a superpotential is defined as
The Equation (5), often referred to as BPS equation, is a simple realization of the self-duality of the model (1). In other words, kinks always saturate the topological energy bound, their mass is proportional to the topological charge of the soliton.
As our discussion focuses on chains of solitons, we are now looking for a possibility to construct such static multisoltion solutions in one spatial dimensions. However, the energy of interaction between the kinks is not zero, there is always a force acting between the solitons. This force can be evaluated when we consider an initial configuration of two widely separated kinks, for example, in the sine-Gordon model
where is the kink solution mentioned above, and d is the separation parameter. Then, we can expand the corresponding energy of the configuration in powers of and subtract the mass of two infinitely separated kinks. This yields the interaction energy
Evidently, it is the Yukawa-type interaction, it is repulsive for the kinks and it is attractive in the case of the kink–anti-kink pair. Further, there is no multisoliton solution in the model with double degenerated vacuum, the only possible structure of chains of solitons in such a case could be static linear configuration consisting of kinks and anti-kinks in alternating order. However, the energy of interaction between the solitons is not zero again, by analogy with (7) one can find that in the model , so there is an attractive force in the kink–anti-kink pair, again. In other words, there is no static multisoliton solutions in the model (1).
However, the situation can be different if we extend the model (1), for example, we can consider coupled two-component system with one of the scalar components having the kink structure and the second component being a non-topological soliton [30,31], or modify the model (1), in such a way, that it still supports the kinks but possess a biharmonic spatial derivative term [32]. In the latter case, it is possible to construct a static kink–anti-kink pair. Similarly, such configuration exist as a static solution of the (1 + 1) dimensional scalar field theory coupled to an impurity [33] which anchors the kinks.
Another way to construct a bounded kink–anti-kink pair is to include interaction between the kinks and fermions [34,35,36,37,38]. Such an extended model is defined by the following Lagrangian,
where the self-interacting real scalar field is coupled with a two-component Dirac spinor and are the bare mass of the fermions and the Yukawa coupling constant, respectively. The matrices are , where are the Pauli matrices, and .
Let us show that the coupling with fermions may provide an additional force stabilizing the kink–anti-kink pair. We make use of the usual parametrization for a two-component spinor
it results in the following coupled system of dynamical equations,
This system is supplemented by the normalization condition which we impose as a constraint on the system (9). Clearly, in the decoupled limit , the model (8) is reduced to the scalar model (1) which supports the kinks.
We can easily see that for all such solutions, the system (9) possesses a fermionic zero mode which is exponentially localized on the kink. This mode exists for any value of the Yukawa coupling g, there is no level crossing spectral flow in one spatial dimension [34]. Notably, for large values of the Yukawa coupling, other localized fermionic states with non-zero energy eigenvalues may appear in the spectrum [34,35,37,39].
Consideration of the fermion modes bounded to a kink usually is related with an assumption that the back-reaction of the localized fermions is negligible [34,35]. However, coupling to the higher localized modes may significantly distort the kink [37]. Further, as such exponentially localized fermion modes may occur in multisoliton systems, localized fermions could mediate the exchange interaction between the solitons.
Indeed, numerical solution of the full system of dynamical Equation (9) shows that, as the Yukawa coupling increases slightly above zero, a non-topological soliton emerge in the scalar sector, this lump is linked to a localized fermionic mode extracted from the positive continuum [38]. As g increases further, the lump becomes larger, it represents tightly bounded kink–anti-kink pair, as seen in Figure 1.
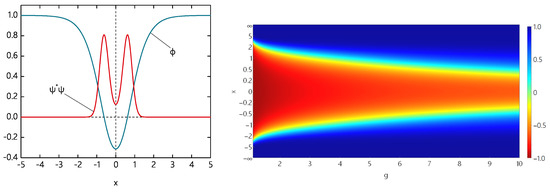
Figure 1.
kink–antikink pair bounded by fermions. Profiles of the scalar field and fermion density distribution of the collective mode at (left plot) and scalar field of the configuration bounded to this mode vs. Yukawa coupling g (right plot). Reprinted (without modification) from [38], with permission of APS.
Further, we found collective fermions localized on various multi-kink configurations. For example, a tower of localized fermion modes exist on a coupled pair of sG kinks in the sector of topological degree two [38], similarly, there are bounded pairs of kinks and anti-kinks, see Figure 2.
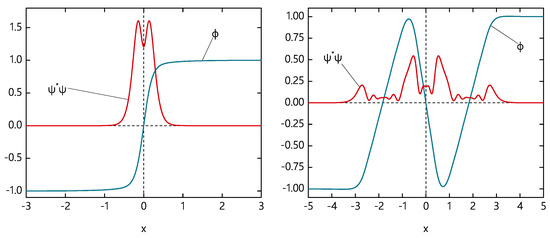
Figure 2.
multi-kink configurations bounded by fermions. Profiles of the scalar field and fermion density distribution of the collective fermionic mode(left plot) and the chain of the kinks bounded to the higher fermionic mode (right plot). Reprinted (without modification) from the work in [38], with permission of APS.
Further, even more complicated bounded multisoliton configuration, which represent multicomponent kink–anti-kink chains with localized fermion modes may exist in the extended model (8). As a particular example, in the right plot of Figure 2, we represent the chain of the kinks bounded by the higher fermion mode. Note that similar phenomena are observed in other related models, the mechanism of the fermionic exchange interaction in multisoliton congurations is universal [38].
3. Chains of Baby Skyrmions
Clearly, in one spatial dimension any bounded multisoliton configuration represents a chain of solitons. However, chains of solitons exist in many other higher dimensional models. In all cases, their existence is warranted due to a balance of repulsive and attractive interactions between the solitons. In this section, as a simple example of such configuration we will consider 2 + 1 dimensional planar Skyrme model [40,41,42]. The model is defined by the Lagrangian
Here, the triplet of real scalar fields , is constrained to the surface of unit sphere, . In other words, this is a topological map which is classified by the homotopy group . The planar Skyrme model supports soliton solutions, which are classified in terms of the topological invariant:
The explicit choice of the potential term of the model (10) is important because it defines the asymptotic form of the field of the localized soliton. The most common choice is the symmetry breaking potential
where is the rescaled mass parameter. Indeed, the soliton of topological degree one can be constructed using the rotationally invariant ansatz
where is some monotonically decreasing profile function. As the field must approach the vacuum on the spacial asymptotic, it satisfies the boundary condition as , i.e., . The system of field equations of the baby Skyrme model (10) then is reduced to a single ordinary differential equation on the function :
Linearizing this equation on the spatial infinity yields the asymptotic tail of the profile function . Evidently, this corresponds to the Yukawa-type decay with the mass of scalar excitation . On the other hand, the parameter defines the characteristic size of a Skyrmion, for the potential (12) the usual choice [43] corresponds to the localization of the energy within a region of diameter . More precisely, the asymptotic equation on the scalar field of the baby Skyrmion has the form
Therefore, the asymptotic field may be thought of as generated by a doublet of orthogonal dipoles, with the strength p, one for each of the massive components and . The component remains massless [43,44].
Let us now consider two widely separated unit charge Skyrmions. The leading term in the energy of interaction of the solitons, evaluated by analogy with (7), is
where the separation d between the solitons is supposed to be much larger than the size of the core of the Skyrmion, , and is the relative angle of orientation of two pairs of orthogonal dipoles of equal strength p.
Thus, we conclude that the interaction of two separated Skyrmions is most attractive when the two solitons are exactly out of phase, , and it is most repulsive when the relative phase . However, nonlinear effects may seriously affect this result even at intermediate separation of the solitons, one can expect some deformations of the core of the solitons may induce a repulsive quasi-elastic force which may balance the long-range attraction.
Indeed, numerical simulations confirm, the model with the standard potential (12) supports existence of multisoliton configurations [43,44,45,46]. First, as , the attractive force between two Skyrmions of unit charge is stronger than repulsive quasi-elastic force, which is induced by deformations of the overlapping cores of the solitons. Thus, the global minimum of the sector of degree two is also rotationally invariant, further, the dipole moment of the baby Skyrmion is zero.
The situation changes for baby Skyrmions of higher topological charges [43,44,45,46,47]. As , the multisoliton solutions represent a stable chain of aligned, charge two baby skyrmions, see Figure 3. Another linear configuration of baby Skyrmions was constructed by Foster [47], it represents a chain on charge one Skyrmion with both ends capped by two solitons, see Figure 4. In such a chain each soliton is rotated by with respect to its neighbor around the axis of symmetry. The physical picture here is somewhat similar to the mechanism of formation of chain of dipoles in classical electrodynamics, the energy of the chain is minimal with respect to all other possible configurations. Notably, the linear configuration is formed dynamically. The energy of such a chain, which yields a global minimum of energy in a given topological sector is slightly lower than the energy of the chain of aligned Skyrmions, for example, the chain of five aligned Skyrmions of degree two displayed in Figure 3 has energy about higher than the Foster’s cupped chain [47].
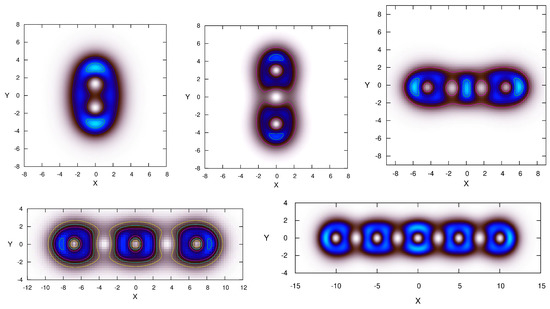
Figure 3.
Contour plots of the energy density distributions of the solutions of the planar Skyrme model with the potential (12) in the sectors of degrees and .
Another way to construct linear chains of baby Skyrmions is to consider the model (10) on a cylinder imposing anti-periodic boundary conditions [47,48]
where is the period of the chain. This parametrization fixes a relative phase between the neighboring Skyrmions. Then, the energy of an infinitely charged chain becomes a function of the periodicity , it can be minimized to find lowest energy configuration. Numerical evaluations suggest that for it corresponds to the period [48].
Some comments are in order here. First, linear periodic chains of planar Skyrmions exist because of the balance of a short-range repulsion and a long-range attraction between two single solitons. The long-range attraction is mediated by the dipole forces; however, the asymptotic form of the scalar field of the baby skyrmion and the character of interaction between them, strongly depends on the particular choice of the potential term . For example, the model (10) with the double-vacuum potential [46] always supports rotationally invariant multi-soliton solutions. By contrast, the choice of the holomorphic potential [42] invariably yields repulsive interaction, whatever the separation and relative orientation of the Skyrmions [49], and there are no multisoliton solutions in such a model. More complicated form of the potential may induce weak attraction, it allows for existence of various multi-soliton configuration, including Skyrmions chains [50].
Second, the existence of chains of baby Skyrmions is an intrinsic property of the model (10), it is not necessarily to modify it by analogy with 1 + 1 dimensional scalar model (1). On the other hand, coupling to other fields may significantly affect the character of interaction between the solitons, in particular, presence of fermionic modes localized by the baby Skyrmion yields two additional pairs of asymptotic dipoles [51], then the pattern of interaction between the solitons becomes more involved. Similarly, the asymptotic forces in the gauged baby Skyrme model include contribution from the magnetic flux associated with the soliton [52]. Even more complicated the pattern of interactions between planar Skyrmions becomes in the gauged baby Skyrme model with Chern–Simons term [53]. However, for some set of parameters of the model, there are solutions, which represent linear chains of electrically charged solitions with associated magnetic fluxes [53].
Note that Skyrmion configurations in 2 + 1 dimensions have recently been subject of considerable interest as solitons of that type were experimentally observed in magnetic structures [9]. A magnetic Skyrmion is a stable vortex-like configuration that exist in a thin film of chiral magnets, or in nematic crystals. However, the usual Skyrme term in the model (10) is replaced by the Dzyaloshinskii–Moriya chiral interaction term [54,55]. Similarly, such solutions exist in various condensed matter systems, in particular, in chiral nematic liquid crystals [56]. Further, these topological excitations minimize the Oseen–Frank free energy functional, which also includes surface terms, see, e.g., in [57].
Notably, there in no multisoliton solutions in the baby Skyrme model with Dzyaloshinskii–Moriya term supplemented by the Zeeman interaction term. The situation here is similar to the case of the usual baby Skyrme model with holomorphic potential [42], the interaction between chiral Skyrmions can be only repulsive. However, modification of the boundary conditions, or extension of the free energy functional, allows for existence of bounded multisoliton solutions [58,59,60,61]. In particular, a strong boundary electric field may generate chains of dynamical planar Skyrmions in a chiral nematic crystal [59], see Figure 5.
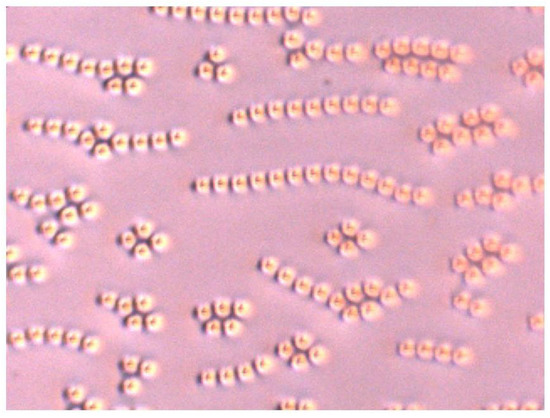
Figure 5.
Chains of planar Skyrmions in a nematic crystal. (Courtesy of Ivan Smalyukh.)
4. Chains of Skyrmions
The above-mentioned scheme of construction of baby Skyrmions can be extended to the original Skyrme model in 3 + 1 dimensions. The field of the model is the unitary, unimodular matrix , , which can be written as an expansion in quartet of scalar fields restricted to the surface of the sphere :
Here, are the three usual Pauli matrices. Introducing the quartet of scalar fields , restricted as , we can write the Lagrangian of the model in the form
where . The vacuum boundary condition means that the scalar field component remains massless, while the triplet of pion fields has a mass . The topological charge of the Skyrmion is the winding number
Skyrmion solution of degree is spherically symmetric, it can be constructed on the hedgehog ansatz
where is a real monotonically decreasing function of the radial variable with the boundary conditions and . Setting the boundary conditions and yields the winding number , this is the anti-Skyrmion solution. The profile function satisfies the ordinary differential equation of second order
The solution of this equation can be found numerically.
As it was outlined above, the character of long-range interaction between two separated solitons depends on the asymptotic form of the field . As , and . Then, the asymptotic form of the solution of the Equation (22) is
where d is some constant. Therefore, the corresponding asymptotic triplet of massive pion fields, , represents the field of three mutually orthogonal scalar dipoles of equal dipole strength d:
Consequently, the pattern of the long-distance interactions of two separated Skyrmions depends on their relative orientation [62]. If the solitons are aligned, they repel each other, by analogy with above consideration of planar Skyrmions. The strongest repulsive force occurs as one of the Skyrmions is rotated by about the axis joining the Skyrmions. The attractive channel in interaction of the solitons corresponds to the case when one of the Skyrmions is rotated by about an axis perpendicular to axis R. However, for the usual choice of the potential function in (19), the attractive interaction in that channel is stronger than quasi-elastic forces of deformation of the core, the resulting charge two configuration is axially-symmetric [63,64,65,66,67]. Note that, asymptotically, the field of the axially symmetric Skyrmion has only one non-vanishing dipole component, associated with the axis of symmetry of the configuration. Indeed, composing two Skyrmions into the axially symmetric configuration, we cancel the dipole fields which are orthogonal to the axis of symmetry while the components directed along this axis will add. Thus, the dipole strength of the Skyrmion is approximately two times larger than asymptotic dipole field.
In order to construct pair of bounded Skyrmions, one has to consider a nonstandard choice of potential term, which combines both repulsive and attractive interactions [68,69]. However, the dipoles forces of the lightly bounded pair, which are orthogonal to the axis of symmetry, do not support existence of a linear chain of Skyrmions of unit charge.
On the other hand, a Skyrme chain can be constructed in a way analogous to the construction of arrays of baby Skyrmions outlined above [70]. The field of the chain is supposed to be periodic in z-direction, i.e., where matrix of iso-rotations . Therefore, each Skyrmion in the chain is iso-rotated by R with respect to its neighbors. Effectively, it corresponds to compactification of z-axis onto a circle . This construction can be thought of as a one-dimensional reduction of Skyrme crystals [71,72,73].
Another possibility is to consider Skyrmion–anti-Skyrmion (SAS) pair in a static equilibrium, such configuration represents a saddle point solution, a sphaleron [25]. The SAS pair solution corresponds to a middle of a non-contractible loop on the functional space of the Skyrme model. Physically, as said above, the charge 2 axially-symmetric Skyrmion possesses only one asymptotic dipole field, the dipole interaction may stabilize the SAS pair.
The SAS saddle point solution can be constructed numerically using the axially symmetric parametrization of the field
where the triplet of pion fields is
and . In this parametrization, the integer counts the winding of the field in the plane.
For the SAS pair, the boundary conditions imposed on the functions are
This yields a configuration with zero net topological charge, as one can see directly from (20). Further generalization of this construction is possible, if we impose , where m is an integer number, which counts the number of constituents in the resulting SAS chain configuration [26]. Together with the winding number n of each individual Skyrmion appearing in (26), it yields the net topological charge of the axially symmetric chain:
Clearly, the case corresponds to the (multi)-Skyrmions of topological charge , while gives a pair with zero net topological charge consisting of a charge Skyrmion and a charge anti-Skyrmion. More generally, for odd values of m the winding number, n coincides with the topological charge of the Skyrmion Q, whereas even values of m correspond to the deformations of the topologically trivial sector. Thus, we can construct a chain of charge n Skyrmions and charge anti-Skyrmions placed along the axis of symmetry in alternating order. Note that the solitons are dynamically arranged in such a linear configuration, in a contrary, the periodic Skyrmions constructed on the ansatz , where R is a rotation matrix, by definition represent a one-dimensional cluster of equally spaced Skyrmions. Such a chain, may only contract or extend itself as the period varies [70].
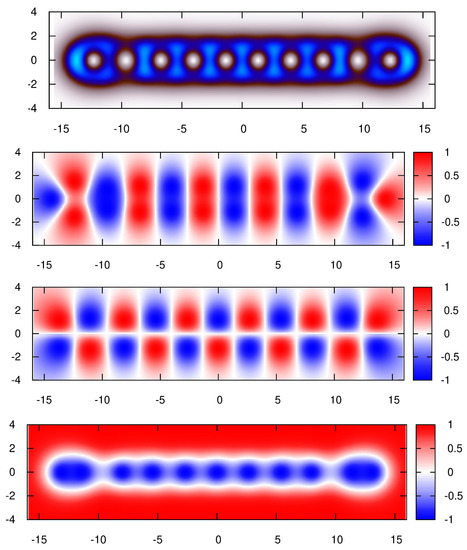
In Figure 6, we represent the energy density isosurfaces of the SAS chains for zero pion mass. Notably, there is no such a saddle point solution for a single Skyrmion–anti-Skyrmion pair [25,26]. However, coupling to gravity [74,75] may provide an additional attractive force, it stabilizes the SAS pair in curved spacetime [76,77].
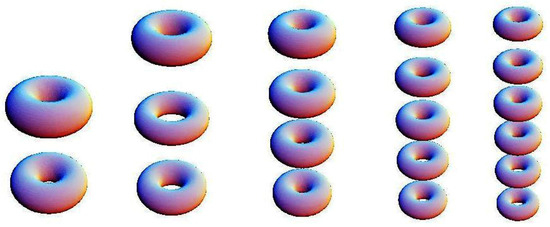
Figure 6.
Skyrmion–anti-Skyrmion chains. Reprinted (without modification) from the work in [26], with STM Permission.
5. Chains of Q-Balls and Boson Stars
In the previous sections, we considered linear chains of topological solitons in various spatial dimensions. Another type of chain can be constructed in models which support non-topological solitons. One of the simplest examples in flat space is given by Q-balls, stationary spinning configurations of a complex scalar field with a suitable self-interaction potential [11,12,13]. When Q-balls are coupled to gravity so-called boson stars emerge, which represent compact stationary configurations with a harmonic time dependence of the scalar field [14,15].
Both Q-balls and boson stars carry a Noether charge associated with an unbroken continuous global symmetry. This charge is proportional to the angular frequency of the complex boson field and represents the boson particle number of the configurations [12,13].
Localized Q-ball solutions appear in a simple 3 + 1 dimensional complex scalar model with the Lagrangian [13]
and appropriate choice of the nonlinear potential . The fundamental spherically symmetric solution in this case represents a stationary spinning configuration where is the real function of radial variable. This function satisfied the equation of motion
with the boundary conditions and . Then the solution of the Equation (30) must decay asymptotically as
where is the mass of the scalar excitation. In other words, the configuration is exponentially localized at the origin.
Evidently, the properties of the Q-balls depend on the particular choice of the potential and its parameters. It is convenient to make use of the nonlinear sextic potential [78,79,80,81]
where the positive parameters are taken as , , and . Setting reduces the model to the usual Klein–Gordon system in the flat space, which does not support any localized solutions.
As the angular frequency tends to its upper critical value, , the Q-balls become linked to the perturbative excitations of the Klein–Gordon model,
where is the Bessel function of the first kind of order l and
are the usual spherical harmonics with . Here, are the associated Legendre functions. The spherically symmetric fundamental Q-ball corresponds to the spherical harmonic while the simplest non-spherical excitation corresponds to the harmonic , and induces a pair of oscillating perturbations with opposite phases. Such excitations can be considered as droplets of bosonic condensate, they may exist in various models, in particular in a Bose–Einstein condensate with dipole–dipole interaction [82,83].
It was pointed out that, similarly to the case of dipole–dipole interactions between the Skyrmions, the character of the interaction between Q-balls in Minkowski spacetime depends on their relative phase [16,17]. If the Q-balls are in phase, the interaction is attractive, if they are out of phase, there is a repulsive force between them. Thus, an axially symmetric excitation of the complex scalar field of the form is in general not stable in Minkowski spacetime, however the gravitational interaction may stabilize it. Consequently, a decrease of the angular frequency increases the size of the configuration producing a binary system of boson stars spinning in opposite phases. Such a pair represents a building block of linear chains of Q-balls in curved space-time [18,84].
Let us now consider a self-interacting complex scalar field , which is minimally coupled to Einstein gravity. The corresponding action of the system is
where R is the Ricci scalar curvature with respect to the metric , g denotes the determinant of the metric, is the gravitational coupling constant, G is Newton’s constant, and L is the matter field Lagrangian (29). Below we consider axially-symmetric configurations, which can be parameterized by the ansatz and make use of the Lewis–Papapetrou metric
where the metric functions , and l are functions of r and only.
Below we will consider axially symmetric configurations, composed of several constituents, whose centers are localized on the symmetry axis. Such solutions can be obtained numerically [18,84], the results show that, indeed, there are multisoliton linear solutions with k nodes on the symmetry axis. For relatively small values of gravitational coupling and angular frequencies a bit lower than the mass threshold, all solitons assembled into a chain possess similar sizes, shapes, and distance from their next neighbors. However, this very democratic picture changes as we move along the set of branches that form as the angular frequency is varied (for a given coupling ). In Figure 7, we displayed a few examples of such chains of boson stars at and .
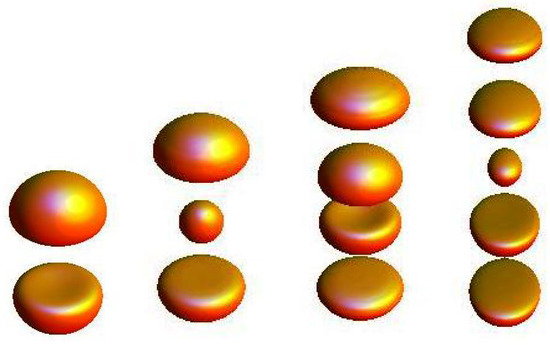
Figure 7.
Chains of boson stars: Energy density isosurfaces on the fundamental branch for at (in different scales).
As said above, pairs and chains of boson stars do not possess flat space limit, repulsive interaction between constituents of the chain should be balanced by some attractive force. Such a force can appear if we consider spinning gauged Q-balls with non-zero angular momentum [85].
Notably, there are two families of the spinning Q-balls with positive and negative parity, the corresponding solutions are symmetric or anti-symmetric with respect to reflections in the equatorial plane [81]. Apart the the above-mentioned fundamental spherically symmetric Q-balls, there are both radially and angularly excited Q-balls [79,80,81,86]. The radially excited solutions are still spherically symmetric, however the scalar field possesses some set of radial nodes. Such radially excited gauged Q-balls also exist in the gauged model [87]. The angularly excited solutions with some set of nodes in -direction, can be parity-even, or parity-odd.
The angularly excited axially symmetric Q-balls with non-zero angular momentum possess an additional azimuthal phase factor of the spinning field [78,79,81]. In the gauged theory, such configurations induce a toroidal magnetic field [88,89], these solutions can be viewed as vortons, the finite energy localized spinning loops with non-zero angular momentum and magnetic flux [78,90,91,92].
We consider the two-component gauged Friedberg–Lee–Sirlin–Maxwell model [85,89], which describes a coupled system of a real self-interacting scalar field and a complex scalar field , minimally interacting with the Abelian gauge field . The corresponding Lagrangian density is
where denotes the covariant derivative. Here, is the electromagnetic field strength tensor, g is the gauge coupling constant and m is the scalar coupling constant. The symmetry breaking quartic potential of the real scalar field is Notably, the model (35) can be considered as a generalization of the Abelian Higgs model, in other words gauged Q-ball behaves like a superconductor [93] with the field component playing a role of the order parameter.
The Lagrangian (35) is invariant under the local gauge transformations of the fields, the corresponding conserved Noether current is
This current is a source in the Maxwell equation
Two other dynamical equations correspond to the variations of the Lagrangian (35) with respect to the fields and , respectively:
Below, we consider stationary spinning axially-symmetric solutions of the model (35). The corresponding parametrization of the scalar fields is
where is the angular frequency of the spinning complex field , and is the azimuthal winding number. Further, in the static gauge the electromagnetic potential is
therefore, the spinning gauged Q-ball with non-zero angular momentum possess both electric charge and magnetic flux. Clearly, both electric and magnetic field of the Q-ball contribute to the energy of interaction between two solitons, together with Yukawa interactions mediated by the scalar fields.
In order to construct saddle point solution, which represent a pair of Q-balls in a static equilibrium, we have to balance the attractive and repulsive forces. Note that the real scalar component may induce only attractive interaction, while the spinning complex field of two Q-balls in opposite phases generates repulsive force. Further, electric charge of the components of the pair always yields a repulsive Coulomb interaction, this piece can be compensated by the solenoidal magnetic field of the pair. Indeed, this pattern is confirmed with numerical simulations [85], we found linear chains of spinning gauged Q-balls, located symmetrically with respect to the origin along the symmetry axis. These solutions are classified by the winding number n and the number of constituents k. In Figure 8, we displayed an example of such a chain with six components. Note that the neighboring complex components of the system are in opposite phases, as expected. Interestingly, there are two branches of solutions of the system (35), the chains exist only in a frequency range, which is restricted from below by some critical value of angular frequency. The electric repulsion provides a leading contribution to the interaction energy on the lower in energy branch, in a contrary, the magnetic energy rapidly grows along the upper, magnetic branch, it extends forward as the frequency increases. Peculiar feature if this branch is that the strong magnetic field of the vortex destroys the superconductive phase in some region inside the spinning Q-ball [85,89].
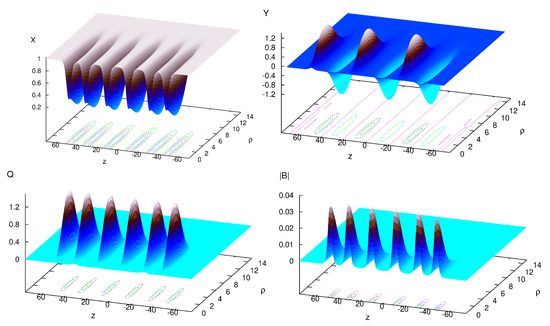
Figure 8.
Axially-symmetric chain of gauged Q-balls: The field components X (upper left) and Y (upper right), the electric charge density distribution (bottom left), and the magnitude of the magnetic field distribution (bottom right) of the chain [85].
6. Monopole–Anti-Monopole Chains
As we have seen in previous section, some localized configurations may possess a few different types of asymptotic fields. In such situations, all of the corresponding interactions in a pair of separated solitons have to be balanced to provide a zero net force. An interesting example of such a system with different types of asymptotic fields is the monopole–anti-monopole chains in the non-Abelian Yang–Mills–Higgs theory [23,24,94,95,96,97,98].
The Yang–Mills–Higgs theory has the Lagrangian density
with gauge potential , field strength tensor , and covariant derivative of the Higgs field . Here e is the gauge coupling and is the strength of the scalar self-coupling.
The static solutions of the corresponding field equations can be constructed numerically by employing of the axially-symmetric ansatz [94,95,96]
where the matrices , , and are defined as a product of these vectors with the usual Pauli matrices :
where and . Note that the ansatz (42) is axially symmetric, a spatial rotation around the z-axis can be compensated by an Abelian gauge transformation . Variation of the Lagrangian (41) yields a system of six second-order nonlinear partial differential equations in the coordinates r and , these equations can be solved numerically, see in [94,95,96]. The well-known spherically symmetric ‘t Hooft–Polyakov ansatz is recovered as we impose the constraints .
The generalized monopoles (42) are characterized by two integers, the winding number m in polar angle and the winding number n in azimuthal angle . Making use of the usual definition of the topological charge of the configuration and taking into account the boundary conditions of the profile functions, we obtain [96]
where is the normalized Higgs field. Therefore, the configurations with even values of the winding number m are axially-symmetric deformations of the topologically trivial sector, while the configurations with odd values of m are deformations of the fundamental ‘t Hooft–Polyakov solution [96]. Note that here we discuss solutions of the second order equations, they do not satisfy the first-order BPS monopole equations.
Simplest non-trivial solution represent a monopole–anti-monopole pair in a static equilibrium. The reason of existence of such a solution, a magnetic dipole, is related to an exact balance of short-range Yukawa interactions mediated be the vector and scalar fields.
Indeed, the pattern of interaction between non-abelian monopoles does not correspond to a naive picture of electromagnetic Coulomb interaction between two point-like magnetic charges. First, there is an attractive force between well separated monopoles, it is mediated by the component of the Yang–Mills field. However, this field is massless only on the spatial infinity, such interaction is short-ranged. On the other hand, there is a scalar attraction mediated by a massive Higgs boson, so the monopoles attract each other with double force.
The situation is different in the BPS limit, then both the gauge and the scalar field possess long-range Coulomb asymptotic. Further, in such a case repulsive gauge interaction between the monopoles is always balanced by the scalar interaction for any separation, any system of BPS monopoles can be static.
It was pointed out by Taubes [99] that, for non-BPS monopoles, the massive vector bosons also mediate the short-range Yukawa interactions between the monopoles and contribute to the interaction energy. Furthermore, the sign of this contribution to the net interaction potential depends on the relative orientation of the monopoles. The monopole–anti-monopole pair is a saddle point configuration where the attractive short-range forces, mediated both by the vector boson and the Higgs boson, are balanced by the repulsive interaction due to massive vector bosons with opposite orientation in the group space [98]. The effective net potential of the interaction between a monopole and an anti-monopole is attractive for large separation and it is repulsive on a short distance, it resembles as that of well known Van der Waals molecular potential. The pair is a sphaleron solution in the topologically trivial sector, it corresponds to the middle of non-contractible loop on the configuration space of the system. This loop corresponds to the creation of a monopole–anti-monopole pair with relative orientation in the internal space from the vacuum, separation of the pair, rotation of the monopole by , and annihilation of the pair back into vacuum [99].
Furthermore, each topological sector of the Yang–Mills–Higgs model (41) contains besides the (multi)monopole solutions further regular, finite mass solutions, which do not satisfy the first order Bogomolnyi equations, but only the set of second order field equations, even for vanishing Higgs potential [99]. Such solutions form saddlepoints of the energy functional, and possess a mass above the BPS bound.
The simplest solution of that type, , monopole–anti-monopole pair, posses two zeros of the Higgs field located symmetrically on the positive and negative z axis, the peaks of the energy density distribution are associated with these zeros. Further generalizations of this solution correspond to the chains of monopoles and anti-monopoles, each carrying charge in alternating order. In Figure 9, we displayed two examples of these chains with and at . The chains with even number of constituents m are deformations of the topologically trivial sector, while the chains with odd values of m represent deformations of the charge n monopole. Positions of the partons in a chain depend on these integers, for and relatively small values of the scalar coupling the solitons are located on the symmetry axis. Note that the asymptotic field of the monopole–anti-monopole pair represents a magnetic dipole [94]
where d is the dipole moment. The emergency of the chains can be explained as formation of the system of aligned dipoles, just in the same way as Skyrmion chains are formed.
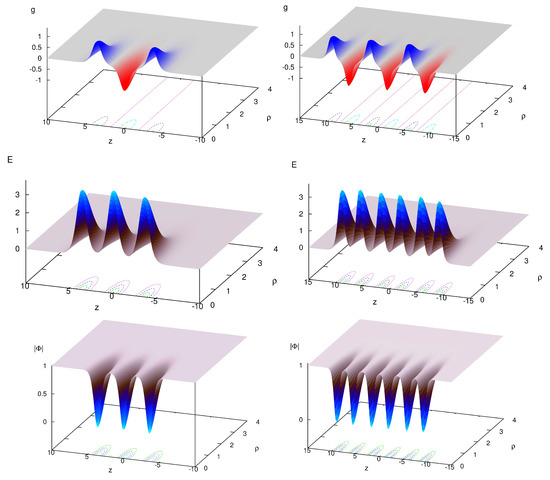
Figure 9.
Monopole–anti-monopole chains: The magnetic charge density distributions (upper plots), the energy density distributions (middle plots)) and the magnitude of the Higgs field (bottom plots), of the and chains.
Note that, as the charge n of the monopole and anti-monopole in the chain increases beyond , it becomes favorable for the monopole–anti-monopole system to form a system of vortex rings, in which the Higgs field vanishes on a ring centered around the symmetry axis [95,96,97]. For larger values of the scalar mass also more complicated configurations can appear, which consist of monopole–anti-monopole pairs or chains as well as vortex rings, the situation becomes much more complex as gravity is included into consideration [100], and/or an electric charge is added to the monopoles in the chain [101].
Remarkably, that there is certain similarity with the Skyrmion–anti-Skyrmion chains we discussed previously in the Section 4. In both cases the soliton–anti-soliton chains represent axially symmetric saddle-point sphaleron-type solutions which are characterized by two integers, one of which yields the number of constituents in the chain, and another corresponds to the absolute value of the topological charge of a component. Further, the component of the Skyrme field shows a clear relation to the corresponding behavior of the magnitude of the Higgs field in the Yang–Mills–Higgs system [25]. However, the dipole–dipole interaction between the components of the SAS pair is weaker than the short-range Yukawa interactions in the monopole–anti-monopole pair, in the flat space the SAS pair may exist only if the topological charge of the components is higher than two [25]. However, the effect of the pion mass term [26] or coupling to gravity [76,77], open a possibility for existence of the Skyrmion–anti-Skyrmion chains with constituents carrying unit topological charge.
Our final remark is related with a possibility to construct Euclidean counterparts of the MAP solutions in four dimensional Yang–Mills theory [102]. These non-self-dual instanton–anti-instanton saddle point configurations are obtained numerically by analogy with the construction of the above-mentioned axially-symmetric MAP solution. As the holonomy of Yang–Mills instantons provides a very good approximations to Skyrmions [103], it is of no surprise that the holonomy of the chains of interpolating calorons–anti-calorons gives a nice approximation to the corresponding Skyrmion–anti-Skyrmion chains [104].
7. Conclusions
The main purpose of this short review was to provide a comparative analysis of different types of linear chains of non-self dual solitons in various models. Such solutions exist because of balancing of repulsive and attractive interactions, the solitons forms a bounded pair which becomes a building block of the chain. The pair may represents a sphaleron-like configurations, a deformation of topologically trivial sector, examples include Skyrmion–anti-Skyrmion pair [25,26] of monopole–anti-monopole solution [94]. Other examples, like pairs of planar Skyrmions, or boson stars, correspond to bounded systems of two solitons, which may also possess a dipole moment.
Apparently, any multisoliton solution in one spatial dimension represents a chain; however, such static configuration may exist only if there is a dynamic equilibrium between the repulsive and attractive forces. A particular example is a real scalar theory coupled to the Dirac fermions, here scalar repulsion between the kinks is evened out by fermionic exchange interaction. Other higher-dimensional examples include self-gravitating chains of boson stars, where the scalar repulsion is compensated by the gravitational attraction of the solitons and Skyrmion–anti-Skyrmion chains, which are stabilized by the dipole–dipole interactions. The pattern of interactions between the constituents of linear chains of spinning gauged Q-balls in two-component Friedberg–Lee–Sirlin model is more complicated, it includes both scalar and electromagnetic forces. Similarly, the monopole–anti-monopole chains exist because of precise balance of the scalar and gauge short-range Yukawa interactions mediated by the Higgs boson and by the massive vector bosons , respectively. Notably, there is a certain similarity between the monopole–anti-monopole chains in the non-abelian Yang–Mills–Higgs model, and Skyrmion–anti-Skyrmion chains, related with the Atiyah–Manton construction [103].
Funding
This research was funded by Ministry of Education of Russian Federation, project FEWF-2020-0003.
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to non-applicability for studies in theoretical physics.
Informed Consent Statement
Patient con-sent was waived due to non-applicability for studies in theoretical physics.
Data Availability Statement
Data supporting reported results can be obtained from the author by request.
Acknowledgments
I am grateful to Carlos Herdeiro, Burhard Kleihaus, Jutta Kunz, Viktor Loiko, Ilya Perapechka, Eugen Radu, Albert Samoilenka, Tigran Tchrakian, and Gleb Zilin for valuable collaboration, many results of our joint work are reviewed in this brief survey. I would like to acknowledge discussions with Yuki Amari, David Foster, Muneto Nitta, Derek Harland, Nick Manton, Tomasz Romańczukiewicz, Ivan Smalyukh, Paul Sutcliffe, Nobuyuki Sawado, and Wojtek Zakrzewski. Computations were performed on the cluster HybriLIT (Dubna).
Conflicts of Interest
The author declares no conflict of interest.
References
- Manton, N.S.; Sutcliffe, P. Topological Solitons; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Babelon, O.; Bernard, D.; Talon, M. Introduction to Classical Integrable Systems; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kevrekidis, P.; Cuevas-Maraver, J. (Eds.) A Dynamical Perspective on the ϕ4 Model; Nonlinear Systems and Complexity Series; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2019; Volume 26. [Google Scholar]
- Shnir, M.Y. ‘Topological and Non-Topological Solitons in Scalar Field Theories’; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Fermi, E.; Pasta, J.; Ulam, S. Studies of Nonlinear Problems, I; Los Alamos Report LA-1940; Los Alamos, USA, 1955. Available online: https://www.physics.utah.edu/~detar/phys6720/handouts/fpu/FermiCollectedPapers1965.pdf (accessed on 30 January 2021).
- Zabusky, N.; Kruskal, M. Interactions of solitons in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A nonlinear field theory. Proc. R. Soc. Lond. A 1961, 260, 127–138. [Google Scholar]
- Brown, E.G.; Rho, M. (Eds.) The Multifaceted Skyrmion; World Scientific: Singapore, 2010. [Google Scholar]
- Liu, J.P.; Zhang, Z.; Zhao, G. (Eds.) Skyrmions: Topological Structures, Properties, and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Houghton, J.C.; Manton, S.N.; Sutcliffe, M.P. Rational maps, monopoles and Skyrmions. Nucl. Phys. 1998, B 510, 507–537. [Google Scholar] [CrossRef]
- Rosen, G. Particlelike Solutions to Nonlinear Complex Scalar Field Theories with Positive-Definite Energy Densities. J. Math. Phys. 1968, 9, 996–999. [Google Scholar] [CrossRef]
- Friedberg, R.; Lee, T.D.; Sirlin, A. A Class of Scalar-Field Soliton Solutions in Three Space Dimensions. Phys. Rev. 1976, 13, 2739–2761. [Google Scholar] [CrossRef]
- Coleman, S.R. Q-Balls. Nucl. Phys. 1985, 262, 263. [Google Scholar] [CrossRef]
- Kaup, D.J. Klein-Gordon Geon. Phys. Rev. 1968, 172, 1331–1342. [Google Scholar] [CrossRef]
- Ruffini, R.; Bonazzola, S. Systems of selfgravitating particles in general relativity and the concept of an equation of state. Phys. Rev. 1969, 187, 1767–1783. [Google Scholar] [CrossRef]
- Battye, R.; Sutcliffe, P. Dynamics of Q-Balls. Nucl. Phys. 2000, 590, 329–363. [Google Scholar] [CrossRef]
- Bowcock, P.; Foster, D.; Sutcliffe, P. Q-balls, integrability and duality. J. Phys. 2009, 42, 085403. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Kunz, J.; Perapechka, I.; Radu, E.; Shnir, Y. Multipolar boson stars: Macroscopic Bose-Einstein condensates akin to hydrogen orbitals. Phys. Lett. 2021, 812, 136027. [Google Scholar] [CrossRef]
- Hooft, G. Magnetic Monopoles in Unified Gauge Theories. Nucl. Phys. 1974, 79, 276–284. [Google Scholar] [CrossRef]
- Polyakov, M.A. Particle spectrum in quantum field theory. Pis’ma JETP 1974, 20, 430–433. [Google Scholar]
- Shnir, M.Y. Magnetic Monopoles; Texts and Monographs in Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Ward, R.S.; Yang-Mills, A. Higgs Monopole of Charge 2. Commun. Math. Phys. 1981, 79, 317–325. [Google Scholar] [CrossRef]
- Nahm, W. Bernhard Ruëber. Diploma Thesis, University of Bonn, Bonn, Germany, 1985, unpublished. [Google Scholar]
- Kleihaus, B.; Kunz, J. Monopole-antimonopole solution of the SU(2) Yang-Mills-Higgs model. Phys. Rev. 1999, 61, 025003. [Google Scholar] [CrossRef]
- Krusch, S.; Sutcliffe, P. Sphalerons in the Skyrme model. J. Phys. 2004, 37, 9037. [Google Scholar] [CrossRef]
- Shnir, Y.; Tchrakian, D.H. Skyrmion-Anti-Skyrmion Chains. J. Phys. 2010, 43, 025401. [Google Scholar] [CrossRef]
- Manton, N.S. Forces between Kinks and Antikinks with Long-range Tails. J. Phys. 2019, 52, 065401. [Google Scholar] [CrossRef]
- Christov, I.C.; Decker, R.J.; Demirkaya, A.; Gani, V.A.; Kevrekidis, P.G.; Khare, A.; Saxena, A. Kink-kink and kink-antikink interactions with long-range tails. Phys. Rev. Lett. 2019, 122, 171601. [Google Scholar] [CrossRef]
- Khare, A.; Saxena, A. Family of Potentials with Power-Law Kink Tails. J. Phys. 2019, 52, 365401. [Google Scholar] [CrossRef]
- Rajaraman, R. Solitons of Coupled Scalar Field Theories in Two-dimensions. Phys. Rev. Lett. 1979, 42, 200. [Google Scholar] [CrossRef]
- Halavanau, A.; Romanczukiewicz, T.; Shnir, Y. Resonance structures in coupled two-component ϕ4 model. Phys. Rev. 2012, 86, 085027. [Google Scholar]
- Decker, R.J.; Demirkaya, A.; Manton, N.S.; Kevrekidis, P.G. Kink–antikink interaction forces and bound states in a biharmonic ϕ4 model. J. Phys. 2020, 53, 375702. [Google Scholar]
- Adam, C.; Oles, K.; Queiruga, J.M.; Romanczukiewicz, T.; Wereszczynski, A. Solvable self-dual impurity models. JHEP 2019, 7, 150. [Google Scholar] [CrossRef]
- Jackiw, R.; Rebbi, C. Solitons with Fermion Number 1/2. Phys. Rev. 1976, 13, 3398–3409. [Google Scholar]
- Chu, Y.Z.; Vachaspati, T. Fermions on one or fewer kinks. Phys. Rev. 2008, 77, 025006. [Google Scholar] [CrossRef]
- Gani, V.A.; Ksenzov, V.G.; Kudryavtsev, A.E. Example of a self-consistent solution for a fermion on domain wall. Phys. At. Nucl. 2010, 73, 1889–1892. [Google Scholar] [CrossRef]
- Klimashonok, V.; Perapechka, I.; Shnir, Y. Fermions on kinks revisited. Phys. Rev. 2019, 100, 105003. [Google Scholar] [CrossRef]
- Perapechka, I.; Shnir, Y. Kinks bounded by fermions. Phys. Rev. 2020, 101, 021701. [Google Scholar] [CrossRef]
- Liu, Y.X.; Zhang, L.D.; Zhang, L.J.; Duan, Y.S. Fermions on Thick Branes in Background of Sine-Gordon Kinks. Phys. Rev. 2008, 78, 065025. [Google Scholar] [CrossRef]
- Bogolubskaya, A.A.; Bogolubsky, I.L. Stationary Topological Solitons in the Two-dimensional Anisotropic Heisenberg Model With a Skyrme Term. Phys. Lett. 1989, 136, 485–488. [Google Scholar] [CrossRef]
- Bogolyubskaya, A.A.; Bogolyubsky, L.I. On Stationary Topological Solitons In Two-dimensional Anisotropic Heisenberg Model. Lett. Math. Phys. 1990, 19, 171–177. [Google Scholar] [CrossRef]
- Leese, A.R.; Peyrard, M.; Zakrzewski, W.J. Soliton Stability in the O(3) σ Model in (2 + 1)-dimensions. Nonlinearity 1990, 3, 387–412. [Google Scholar] [CrossRef]
- Piette, B.M.A.G.; Schroers, B.J.; Zakrzewski, W.J. Dynamics of baby skyrmions. Nucl. Phys. 1995, 439, 205–235. [Google Scholar] [CrossRef]
- Piette, A.B.M.; Zakrzewski, J.W.; Mueller-Kirsten, H.J.W.; Tchrakian, H.D. Chern-Simons solitons in a CP(1) model. Phys. Lett. 1994, 320, 294–298. [Google Scholar] [CrossRef]
- Piette, A.B.M.; Schroers, J.B.; Zakrzewski, J.W. Multisolitons in a two-dimensional Skyrme model. Z. Phys. 1995, 65, 165–174. [Google Scholar]
- Weidig, T. The Baby skyrme models and their multiskyrmions. Nonlinearity 1999, 12, 1489. [Google Scholar] [CrossRef]
- Foster, D. Baby Skyrmion chains. Nonlinearity 2010, 23, 465. [Google Scholar] [CrossRef][Green Version]
- Harland, D.; Ward, R.S. Walls and chains of planar skyrmions. Phys. Rev. 2008, D 77, 045009. [Google Scholar] [CrossRef]
- Sutcliffe, P.M. The interaction of Skyrme-like lumps in (2 + 1) dimensions. Nonlinearity 1991, 4, 1109–1121. [Google Scholar] [CrossRef]
- Salmi, P.; Sutcliffe, P. Aloof Baby Skyrmions. J. Phys. 2015, 48, 035401. [Google Scholar] [CrossRef]
- Perapechka, I.; Sawado, N.; Shnir, Y. Soliton solutions of the fermion-Skyrmion system in (2 + 1) dimensions. JHEP 2018, 10, 081. [Google Scholar] [CrossRef]
- Samoilenka, A.; Shnir, Y. Gauged multisoliton baby Skyrme model. Phys. Rev. 2016, 93, 065018. [Google Scholar] [CrossRef]
- Samoilenka, A.; Shnir, Y. Gauged baby Skyrme model with a Chern-Simons term. Phys. Rev. 2017, 95, 045002. [Google Scholar] [CrossRef]
- Dzyaloshinskii, E.I. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Chaikin, M.P.; Lubensky, C.T. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Foster, D.; Kind, C.; Ackerman, J.P.; Tai, B.J.S.; Dennis, R.M.; Smalyukh, I.I. Two-dimensional skyrmion bags in liquid crystals and ferromagnets. Nat. Phys. 2019, 15, 655–659. [Google Scholar] [CrossRef]
- Ackerman, J.P.; Boyle, T.; Smalyukh, I.I. Squirming motion of baby skyrmions in nematic fluids. Nat. Commun. 2017, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rybakov, N.F.; Kiselev, S.N. Chiral magnetic skyrmions with arbitrary topological charg. Phys. Rev. 2019, 99, 064437. [Google Scholar] [CrossRef]
- Schroers, B.J. Gauged Sigma Models and Magnetic Skyrmions. SciPost Phys. 2019, 7, 030. [Google Scholar] [CrossRef]
- Schroers, B.J. Dynamics of moving and spinning Skyrmions. Z. Phys. 1994, 61, 479–494. [Google Scholar] [CrossRef][Green Version]
- Braaten, E.; Townsend, S.; Carson, L. Novel Structure of Static Multi - Soliton Solutions in the Skyrme Model. Phys. Lett. 1990, 235, 147–152. [Google Scholar] [CrossRef]
- Braaten, E.; Carson, L. The Deuteron as a Toroidal Skyrmion. Phys. Rev. 1988, 38, 3525. [Google Scholar] [CrossRef]
- Kopeliovich, B.V.; Stern, E.B. Exotic Skyrmions. JETP Lett. 1987, 45, 203–207. [Google Scholar]
- Manton, N.S. Is the B = 2 Skyrmion Axially Symmetric? Phys. Lett. 1987, 192, 177. [Google Scholar] [CrossRef]
- Verbaarschot, M.J.J. Axial Symmetry of Bound Baryon Number Two Solution of the Skyrme Model. Phys. Lett. 1987, 195, 235–239. [Google Scholar] [CrossRef]
- Gillard, M.; Harland, D.; Speight, M. Skyrmions with low binding energies. Nucl. Phys. 2015, 895, 272–287. [Google Scholar] [CrossRef]
- Gillard, M.; Harland, D.; Kirk, E.; Maybee, B.; Speight, M. A point particle model of lightly bound skyrmions. Nucl. Phys. 2017, 917, 286–316. [Google Scholar] [CrossRef]
- Harland, D.; Ward, R.S. Chains of Skyrmions. JHEP 2008, 12, 093. [Google Scholar] [CrossRef]
- Klebanov, R.I. Nuclear Matter in the Skyrme Model. Nucl. Phys. 1985, 262, 133–143. [Google Scholar] [CrossRef]
- Kugler, M.; Shtrikman, S. A New Skyrmion Crystal. Phys. Lett. 1988, 208, 491–494. [Google Scholar] [CrossRef]
- Castillejo, L.; Jones, P.S.J.; Jackson, A.D.; Verbaarschot, J.J.M.; Jackson, A. Dense Skyrmion Systems. Nucl. Phys. 1989, 501, 801–812. [Google Scholar] [CrossRef]
- Bizon, P.; Chmaj, T. Gravitating skyrmions. Phys. Lett. 1992, 297, 55–62. [Google Scholar] [CrossRef]
- Nelmes, S.G.; Piette, B.M.A.G. Phase Transition and Anisotropic Deformations of Neutron Star Matter. Phys. Rev. 2012, 85, 123004. [Google Scholar] [CrossRef]
- Shnir, Y. Gravitating sphalerons in the Skyrme model. Phys. Rev. 2015, 92, 085039. [Google Scholar] [CrossRef]
- Shnir, Y. Black holes with Skyrmion-anti-Skyrmion hairs. Phys. Lett. 2020, 810, 135847. [Google Scholar] [CrossRef]
- Radu, E.; Volkov, S.M. Existence of stationary, non-radiating ring solitons in field theory: Knots and vortons. Phys. Rep. 2008, 468, 101–151. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; List, M. Rotating boson stars and Q-balls. Phys. Rev. 2005, 72, 064002. [Google Scholar]
- Kleihaus, B.; Kunz, J.; List, M.; Schaffer, I. Rotating Boson Stars and Q-Balls. II. Negative Parity and Ergoregions. Phys. Rev. 2008, 77, 064025. [Google Scholar] [CrossRef]
- Volkov, S.M.; Wohnert, E. Spinning Q balls. Phys. Rev. 2002, 66, 085003. [Google Scholar]
- Xi, T.K.; Saito, H. Droplet formation in a Bose-Einstein condensate with strong dipole-dipole interaction. Phys. Rev. 2016, 93, 011604. [Google Scholar] [CrossRef]
- Luo, H.L.; Pang, W.; Liu, B.; Li, Y.Y.; Malomed, A.B. A new form of liquid matter: Quantum droplets. Front. Phys. 2021, 16, 1. [Google Scholar] [CrossRef]
- Herdeiro, R.C.A.; Kunz, J.; Perapechka, I.; Radu, E.; Shnir, Y. Chains of Boson Stars. arXiv 2021, arXiv:2101.06442. [Google Scholar]
- Loiko, V.; Perapechka, I.; Shnir, Y. Q-chains in the U(1) gauged Friedberg-Lee-Sirlin model. arXiv 2020, arXiv:2012.01052. [Google Scholar]
- Brihaye, Y.; Hartmann, B. Angularly excited and interacting boson stars and Q-balls. Phys. Rev. 2009, 79, 064013. [Google Scholar]
- Loginov, A.Y.; Gauzshtein, V.V. Radially and azimuthally excited states of a soliton system of vortex and Q-ball. Eur. Phys. J. 2020, 80, 1123. [Google Scholar] [CrossRef]
- Shiromizu, T. Generation of magnetic field due to excited Q balls. Phys. Rev. 1998, 58, 107301. [Google Scholar]
- Loiko, V.; Shnir, Y. Q-balls in the U(1) gauged Friedberg-Lee-Sirlin model. Phys. Lett. 2019, 797, 134810. [Google Scholar] [CrossRef]
- Witten, E. Superconducting Strings. Nucl. Phys. 1985, 249, 557–592. [Google Scholar] [CrossRef]
- Davis, R.L.; Shellard, E.P.S. Cosmic Vortons. Nucl. Phys. 1989, 323, 209–224. [Google Scholar] [CrossRef]
- Garaud, J.; Radu, E.; Volkov, M.S. Stable Cosmic Vortons. Phys. Rev. Lett. 2013, 111, 171602. [Google Scholar] [CrossRef]
- Lee, K.; Stein-Schabes, J.A.; Watkins, R.; Widrow, L.M. Gauged q Balls. Phys. Rev. 1989, 39, 1665. [Google Scholar]
- Kleihaus, B.; Kunz, J.; Shnir, Y. Monopole anti-monopole chains. Phys. Lett. 2003, 570, 237–243. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Shnir, Y. Monopoles, antimonopoles and vortex rings. Phys. Rev. 2003, 68, 101701. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Shnir, Y. Monopole-antimonopole chains and vortex rings. Phys. Rev. 2004, 70, 065010. [Google Scholar] [CrossRef]
- Kunz, J.; Neemann, U.; Shnir, Y. Transitions between vortex rings and monopole-antimonopole chains. Phys. Lett. 2006, 640, 57. [Google Scholar] [CrossRef]
- Shnir, Y. Electromagnetic interaction in the system of multimonopoles and vortex rings. Phys. Rev. 2005, 72, 055016. [Google Scholar] [CrossRef]
- Taubes, H.C. Min-max theory for the Yang-Mills-Higgs equations. Commun. Math. Phys. 1985, 97, 473–540. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Shnir, Y. Gravitating monopole-antimonopole chains and vortex rings. Phys. Rev. 2005, 71, 024013. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Neemann, U. Gravitating stationary dyons and rotating vortex rings. Phys. Lett. 2005, 623, 171–178. [Google Scholar] [CrossRef]
- Radu, E.; Tchrakian, D.H. Self-dual instanton and nonself-dual instanton-antiinstanton solutions in d = 4 Yang-Mills theory. Phys. Lett. 2006, 636, 201–206. [Google Scholar] [CrossRef]
- Atiyah, M.F.; Manton, N.S. Skyrmions From Instantons. Phys. Lett. 1989, 222, 438–442. [Google Scholar] [CrossRef]
- Shnir, Y.; Zhilin, G. Sphaleron solutions of the Skyrme model from Yang-Mills holonomy. Phys. Lett. 2013, 723, 236–240. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).