System of Time Fractional Models for COVID-19: Modeling, Analysis and Solutions
Abstract
1. Introduction
2. Preliminaries
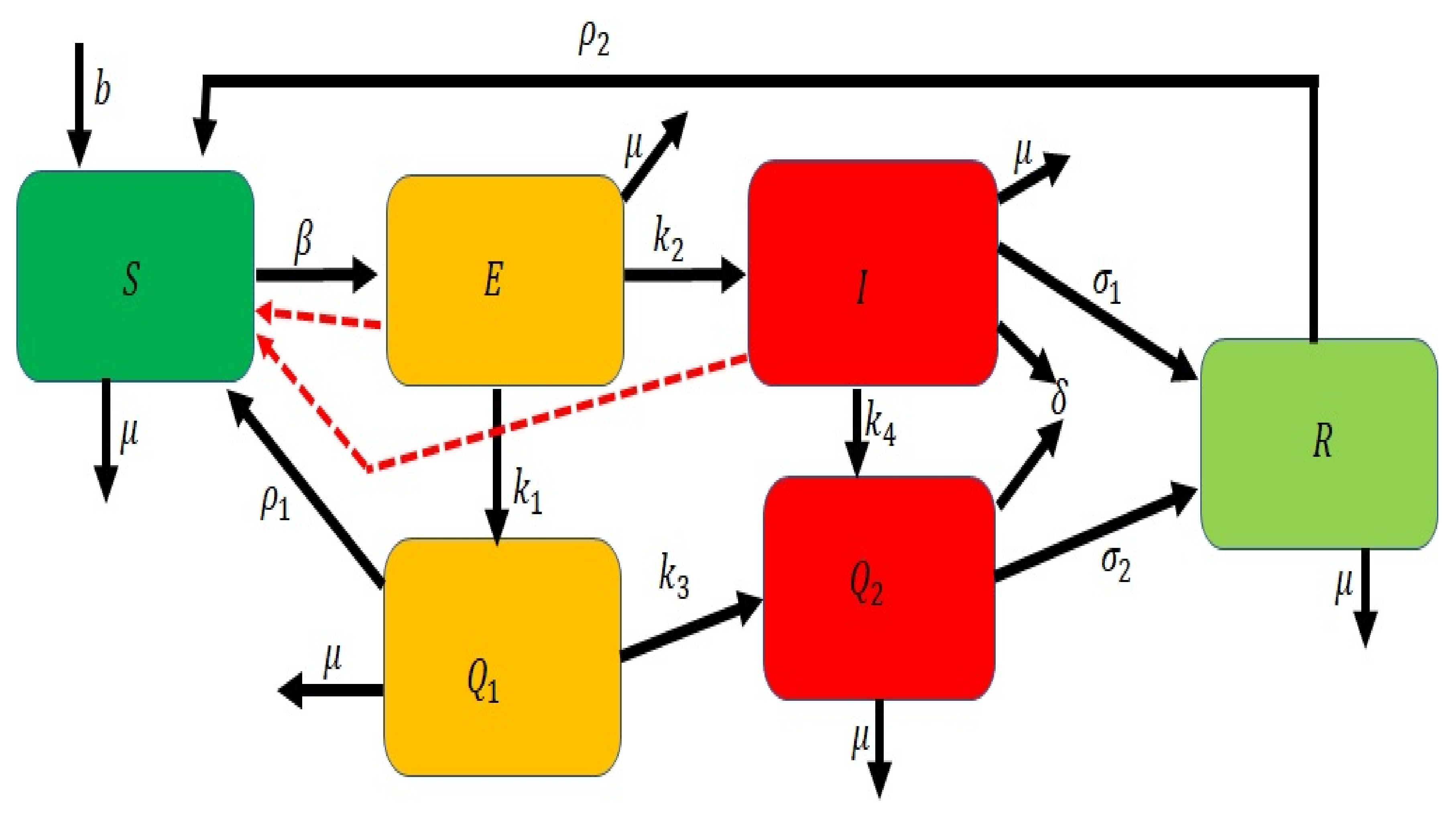
3. Model Formulation
4. Analysis of the Time-Fractional COVID-19 Model
4.1. Results on the Existence and Uniqueness Of Solutions
- (a)
- the function u is non-decreasing if , .
- (b)
- the function u is non-increasing if , .
4.2. Existence, Stability, and Equilibrium Results for COVID-19 Model of Fractional Type
4.2.1. Computation of
4.2.2. Stability Results
4.2.3. Computation of an Endemic Equilibrium
4.2.4. Sensitivity Analysis
- Quarantining infected people may be an essential prevention measure to reduce the spread of COVID-19 infection.
- Reducing the transmission parameter is essential in reducing the transmission of the infection. To reduce the transmission parameter, compliance with protocols such as social distancing, wearing a face mask, and washing hands are necessary.
5. Numerical Analysis and Simulation
5.1. Adams–Bashforth–Moulton Method for Fractional-Order
5.2. Numerical Simulation and Analysis
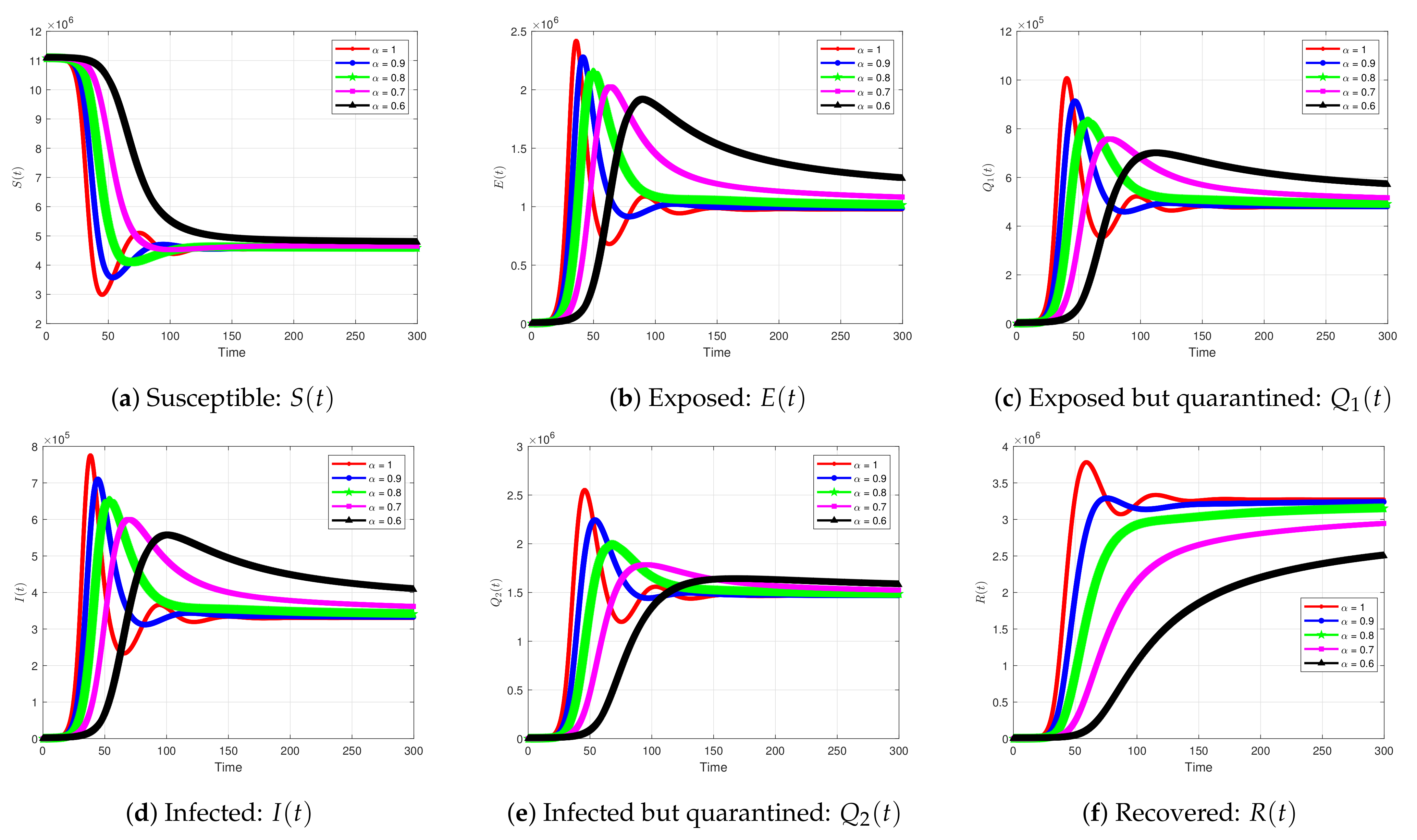
5.2.1. Impact of Time-Fractional-Order on the Solution Profiles for the COVID-19 Model
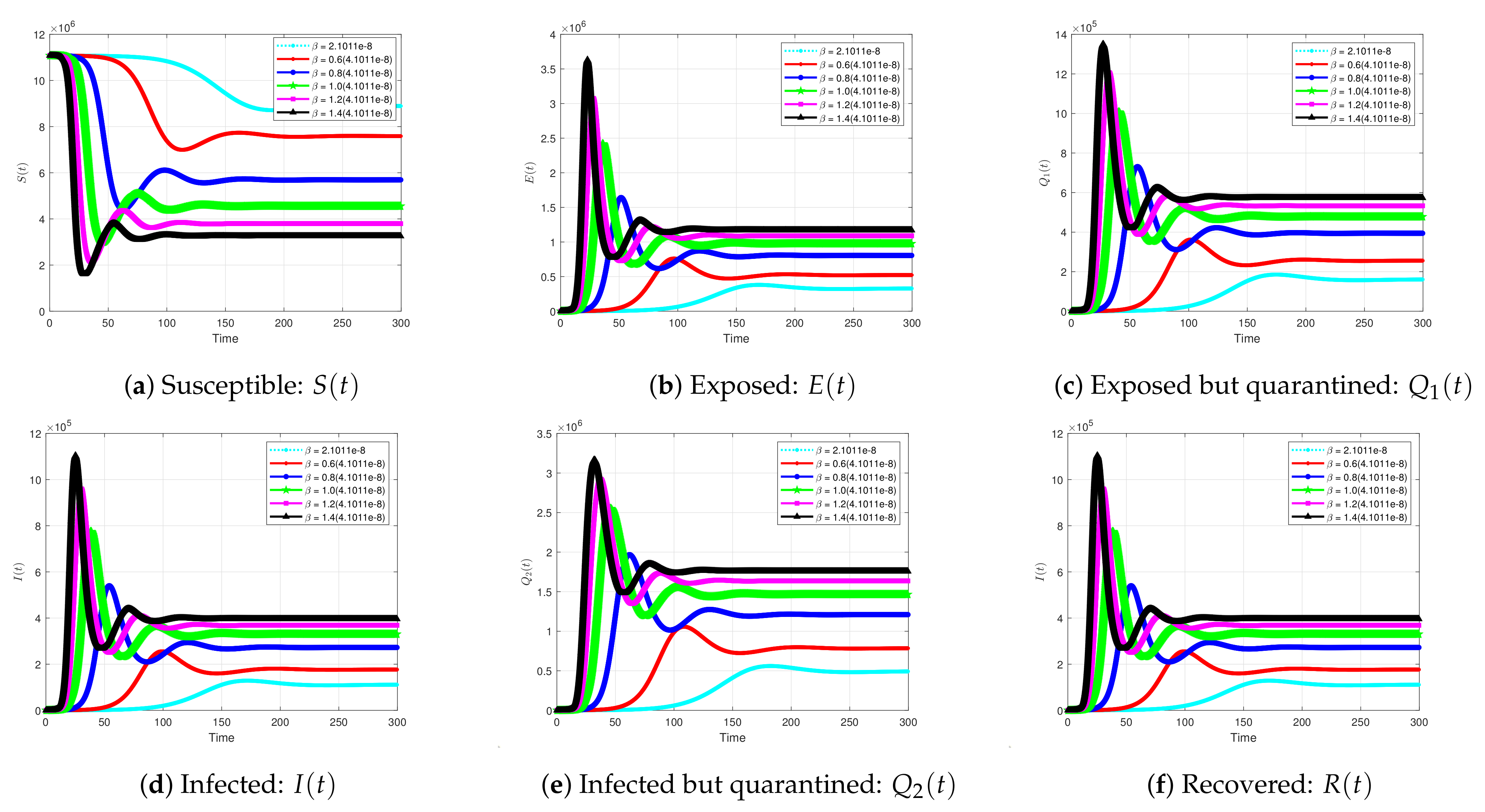
5.2.2. Impact of the Effective Contact Rate on the Solution Profiles for the Coivd-19 Model
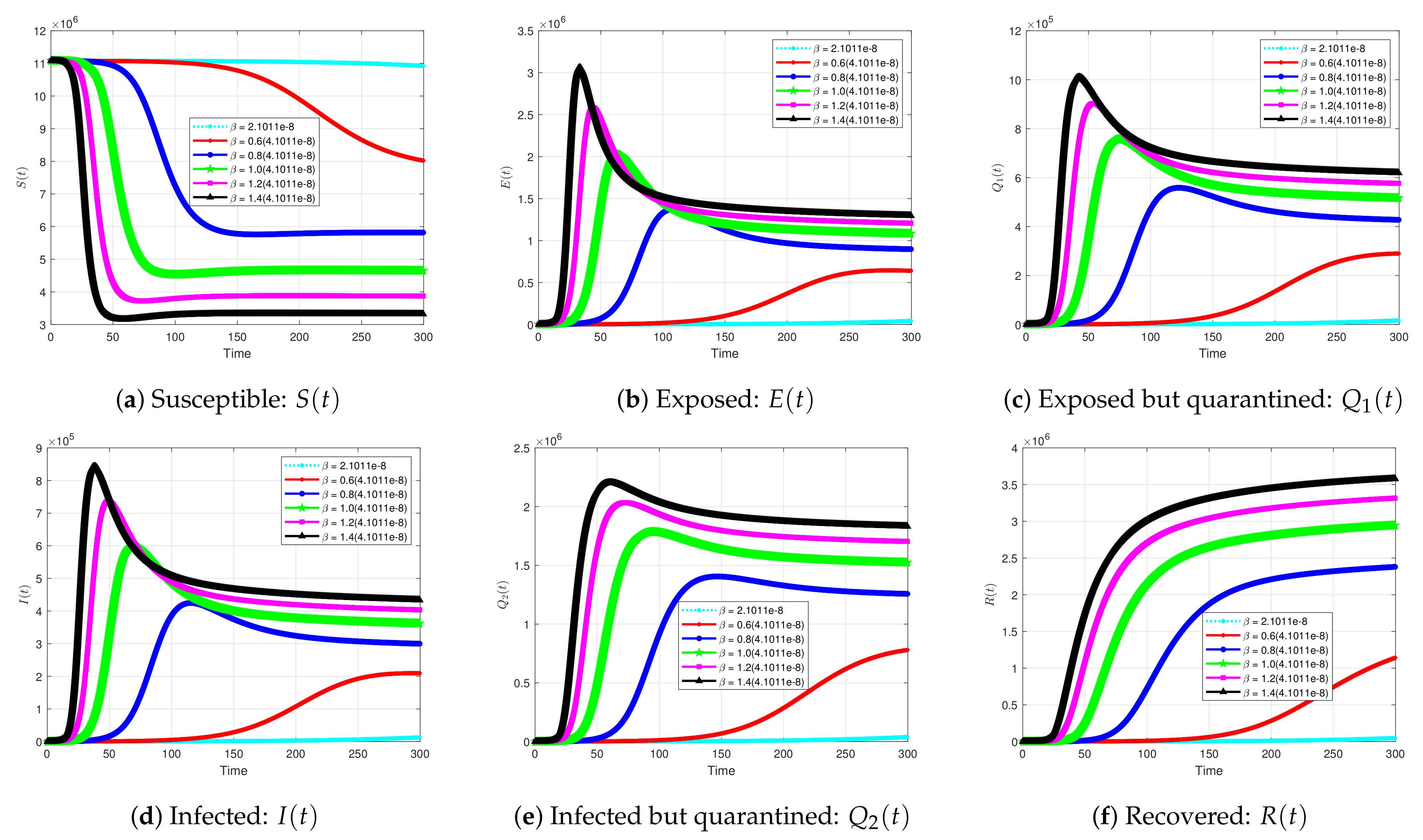
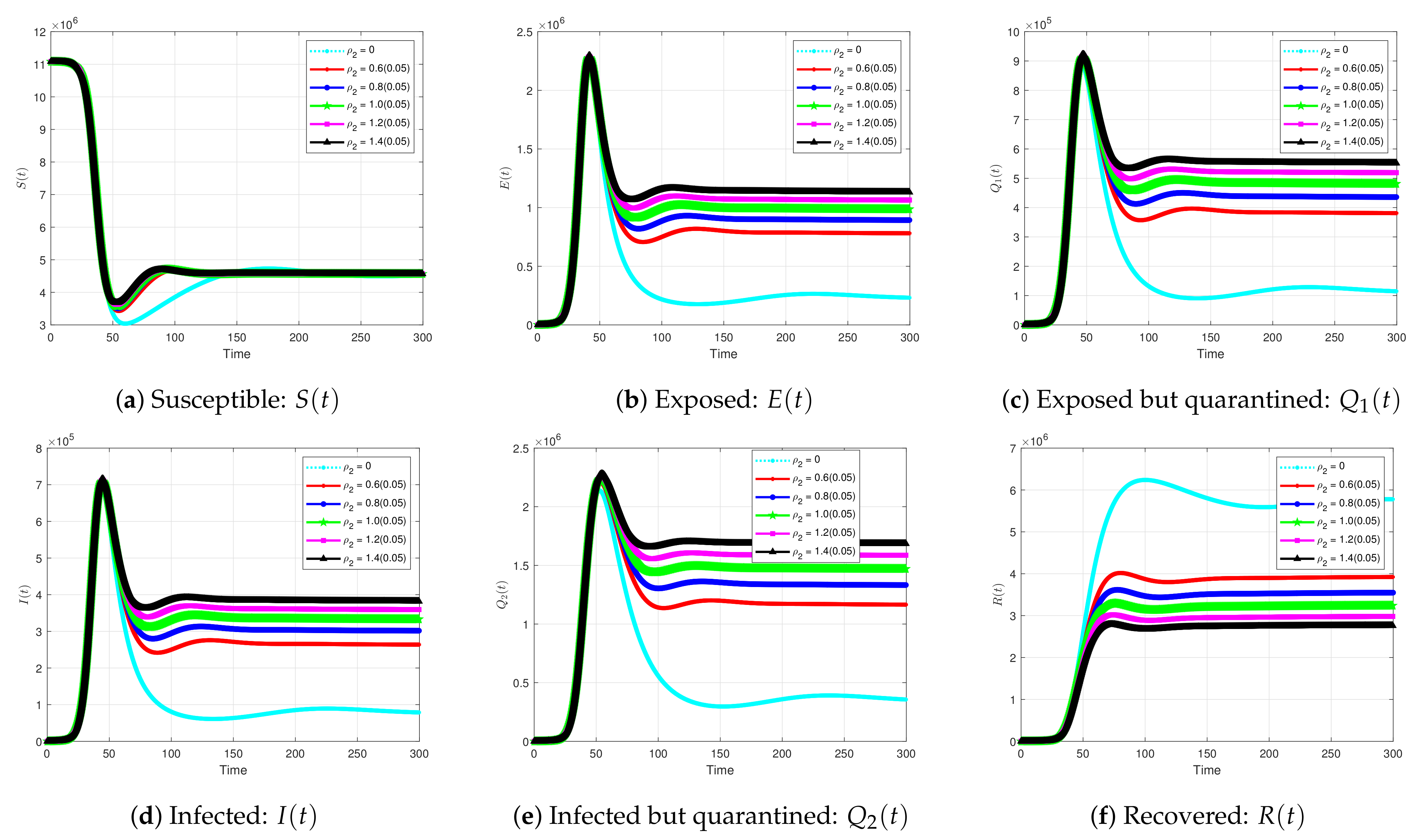
5.2.3. Impact of Quarantining Exposed Individuals on the Solution Profiles for the Coivd-19 Model
5.2.4. The Impact of the Loss of Immunity
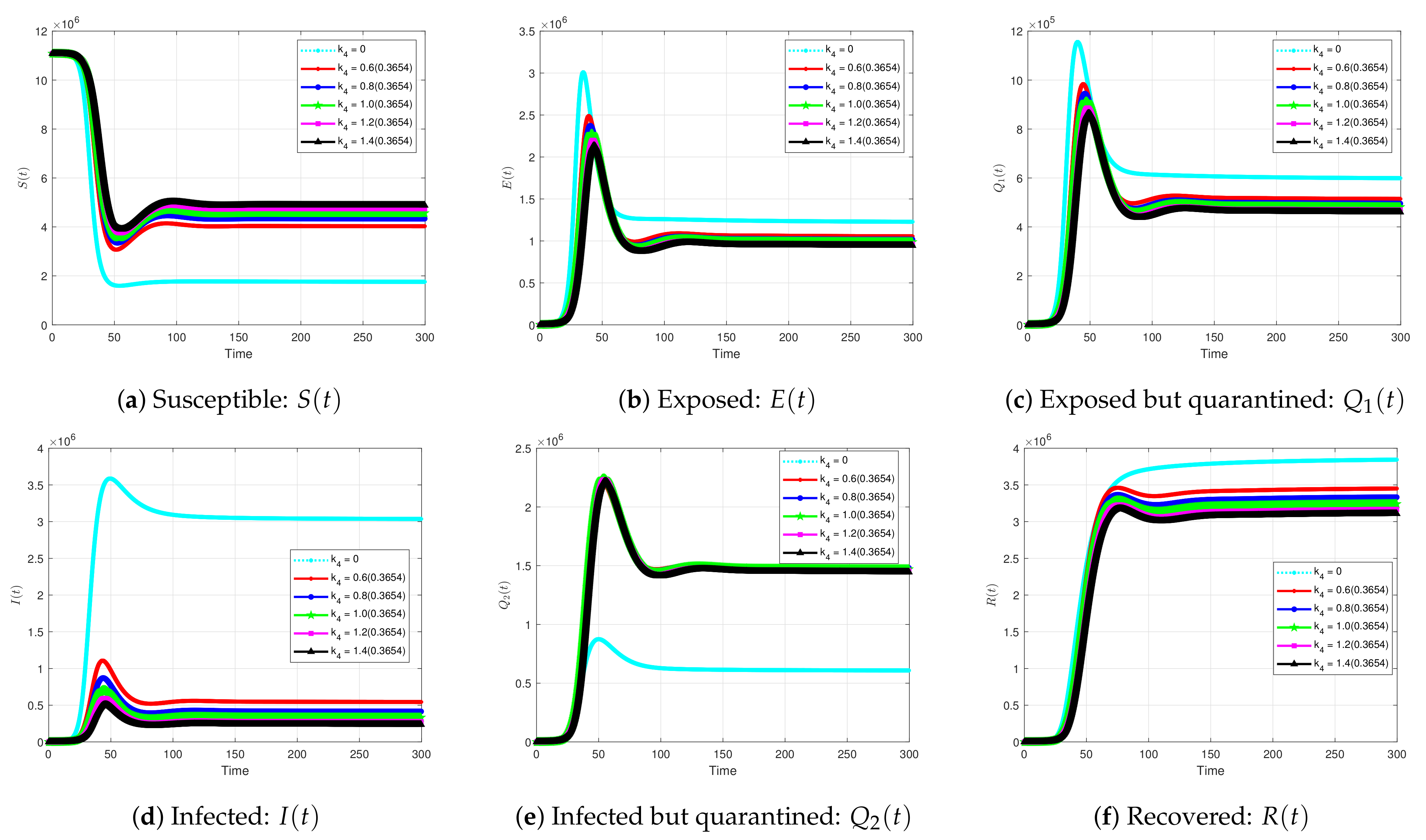
5.2.5. The Impact of Quarantine Infected Individuals on the Solution Profiles for the Coivd-19 Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization (WHO). Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/media-resources/news (accessed on 19 June 2020).
- Iyiola, O.S.; Oduro, B.; Akinyemi, L. Analysis and solutions of generalized Chagas vectors re-infestation model of fractional order type. Chaos Solitons Fractals 2021, 145, 110797. [Google Scholar] [CrossRef]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Owusu-Mensah, I.; Akinyemi, L.; Oduro, B.; Iyiola, O.S. A fractional order approach to modeling and simulations of the novel COVID-19. Adv. Differ. Equ. 2020, 1, 1–21. [Google Scholar]
- Rong, X.; Yang, L.; Chu, H.; Fan, M. Effect of delay in diagnosis on transmission of COVID-19. MBE 2020, 17, 2725–2740. [Google Scholar] [CrossRef]
- Fang, Y.; Nie, Y.; Penny, M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: A data-driven analysis. J. Med. Virol. 2020, 92, 645–659. [Google Scholar] [CrossRef]
- Adeniyi, M.O.; Matthew, I.E.; Iluno, C.; Ogunsanya, A.S.; Akinyemi, J.A.; Oke, S.I.; Matadi, M.B. Dynamic model of COVID-19 disease with exploratory data analysis. Sci. Afr. 2020, 9, e00477. [Google Scholar] [CrossRef]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS ONE 2020, 15, e0230405. [Google Scholar] [CrossRef]
- Oke, S.I.; Ojo, M.M.; Adeniyi, M.O.; Matadi, M.B. Mathematical modeling of malaria disease with control strategy. Commun. Math. Biol. Neurosci. 2020, 43. [Google Scholar] [CrossRef]
- Okedoye, A.M.; Salawu, S.O.; Oke, S.I.; Oladejo, N.K. Mathematical analysis of affinity hemodialysis on T-Cell depletion. Sci. Afr. 2020, 8, e00427. [Google Scholar] [CrossRef]
- Gbadamosi, B.; Ojo, M.M.; Oke, S.I.; Matadi, M.B. Qualitative analysis of a Dengue fever model. Math. Comput. Appl. 2018, 23, 33. [Google Scholar] [CrossRef]
- Gatta, V.L.; Moscato, V.; Postiglione, M.; Sperli, G. An epidemiological neural network exploiting dynamic graph structured data applied to the COVID-19 outbreak. IEEE Trans. Big Data 2021, 7, 45–55. [Google Scholar] [CrossRef]
- Ardabili, S.F.; Mosavi, A.; Ghamisi, P.; Ferdinand, F.; Varkonyi-Koczy, A.R.; Reuter, U.; Rabczuk, T.; Atkinson, P.M. COVID-19 outbreak prediction with machine learning. Algorithms 2020, 13, 249. [Google Scholar] [CrossRef]
- Pinter, G.; Felde, I.; Mosavi, A.; Ghamisi, P.; Gloaguen, R. COVID-19 pandemic prediction for Hungary; a hybrid machine learning approach. Mathematics 2020, 8, 890. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Band, S.S.; Varkonyi-Koczy, A.R. Coronavirus disease (COVID-19) global prediction using hybrid artificial intelligence method of ANN trained with Grey Wolf optimizer. medRxiv 2020. [Google Scholar] [CrossRef]
- Mahmoudi, M.R.; Heydari, M.H.; Qasem, S.N.; Mosavi, A.; Band, S.S.; Varkonyi-Koczy, A.R. Principal component analysis to study the relations between the spread rates of COVID-19 in high risks countries. Alex. Eng. J. 2021, 60, 457–464. [Google Scholar] [CrossRef]
- Tabrizchi, H.; Mosavi, A.; Szabo-Gali, A.; Felde, I.; Nadai, L. Rapid COVID-19 diagnosis using deep learning of the computerized tomography Scans. In Proceedings of the 2020 IEEE 3rd International Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 18–19 November 2020. [Google Scholar]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumor. Am. Inst. Phys. Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.C.; Zeng, S.D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Nasrolahpour, H. A note on fractional electrodynamics. Commun. Nonlinear. Sci. Numer. Simul. 2013, 18, 2589–2593. [Google Scholar] [CrossRef]
- Hilfer, R.; Anton, L. Fractional master equations and fractal time random walks. Phys. Rev. 1995, 51, R848–R851. [Google Scholar] [CrossRef]
- Zhang, Y.; Pu, Y.F.; Hu, J.R.; Zhou, J.L. A class of fractional-order variational image in-painting models. Appl. Math. Inf. Sci. 2012, 6, 299–306. [Google Scholar]
- Pu, Y.F. Fractional differential analysis for texture of digital image. J. Alg. Comput. Technol. 2007, 1, 357–380. [Google Scholar]
- Baleanu, D.; Guvenc, Z.B.; Machado, J.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Tarasov, V.E.; Tarasova, V.V. Time-dependent fractional dynamics with memory in quantum and economic physics. Ann. Phys. 2017, 383, 579–599. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear. Sci. Numer. Simulat. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Senol, M. Analytical and approximate solutions of (2+1)-dimensional time-fractional Burgers-Kadomtsev-Petviashvili equation. Commun. Theor. Phys. 2020, 72, 1–11. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S. Exact and approximate solutions of time-fractional models arising from physics via Shehu transform. Math. Methods Appl. Sci. 2020, 1–23. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S. A reliable technique to study nonlinear time-fractional coupled Korteweg-de Vries equations. Adv. Differ. Equ. 2020, 169, 1–27. [Google Scholar] [CrossRef]
- Akinyemi, L. q-Homotopy analysis method for solving the seventh-order time-fractional Lax’s Korteweg–de Vries and Sawada–Kotera equations. Comp. Appl. Math. 2019, 38, 1–22. [Google Scholar] [CrossRef]
- Şenol, M.; Iyiola, O.S.; Daei Kasmaei, H.; Akinyemi, L. Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent-Miodek system with energy-dependent Schrödinger potential. Adv. Differ. Equ. 2019, 2019, 1–21. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S.; Akpan, U. Iterative methods for solving fourth- and sixth order time-fractional Cahn-Hillard equation. Math. Methods Appl. Sci. 2020, 43, 4050–4074. [Google Scholar] [CrossRef]
- Iyiola, O.S. Exact and Approximate Solutions of Fractional Diffusion Equations with Fractional Reaction Terms. Progr. Fract. Differ. Appl. 2016, 2, 21–30. [Google Scholar] [CrossRef]
- Iyiola, O.S. On the solutions of nonlinear time-fractional gas dynamic equations: An analytical approach. Int. J. Pure Appl. Math. 2015, 98, 491–502. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. In Vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Prabhakar, T.R. A singular integral equation with a generalized mittag-leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Iyiola, O.S.; Asante-Asamani, E.O.; Wade, B.A. A real distinct poles rational approximation of generalized Mittag–Leffler functions and their inverses: Applications to fractional calculus. J. Comput. Appl. Math. 2018, 330, 307–317. [Google Scholar] [CrossRef]
- Furati, K.M.; Iyiola, O.S.; Mustapha, K. An inverse source problem for a two-parameter anomalous diffusion with local time datum. Comput. Math. Appl. 2017, 73, 1008–1015. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- World Health Organization. WHO COVID-19 Dashboard. Available online: https://who.sprinklr.com (accessed on 7 April 2020).
- Tang, B.; Bragazzi, N.L.; Li, Q.; Tang, S.; Xiao, Y.; Wu, J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect. Dis. Model. 2020, 5, 248–255. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Haman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef]
- Liu, T.; Hu, J.; Kang, M.; Lin, L.; Zhong, H.; Xiao, J.; He, G.; Song, T.; Huang, Q.; Rong, Z.; et al. Transmission dynamics of 2019 novel coronavirus (2019-nCoV). bioRxiv 2020. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Guan, L. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics. Kindle Edition; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Heesterbeek, J.A.P. A brief history of R0 and a recipe for its calculation. Acta Biotheor. 2002, 50, 189–204. [Google Scholar] [CrossRef]
- Gumel, A.B.; Lubuma, J.M.; Sharomi, O.; Terefe, Y.A. Mathematics of a sex-structured model for syphilis transmission dynamics. Math. Methods Appl. Sci. 2017, 1–26. [Google Scholar] [CrossRef]
- Suryanto, A.; Darti, I.; Panigoro, H.S.; Kilicman, A. A fractional-order predator-prey model with ratio-dependent functional response and linear harvesting. Mathematics 2019, 7, 1100. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Okosun, K.O.; Rachid, O.; Marcus, N. Optimal control strategies and cost-effectiveness analysis of a malaria model. BioSystems 2013, 111, 83–101. [Google Scholar] [CrossRef]
- Oduro, B.; Apenteng, O.O.; Nkansah, H. Assessing the effect of fungicide treatment on Cocoa black pod disease in Ghana: Insight from mathematical modeling. Stat. Optim. Inf. Comput. 2020, 8, 374–385. [Google Scholar] [CrossRef]
- Ndairou, F.; Area, I.; Nieto, J.J.; Torres, D.F.M. Mathematical Modeling of COVID-19 Transmission Dynamics with a Case Study of Wuhan. Chaos Solitons Fractals 2020, 109846. [Google Scholar] [CrossRef] [PubMed]
- Diethelm, K.; Freed, A.D. The FracPECE subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen 1998; Heinzel, S., Plesser, T., Eds.; Gessellschaft fur Wissenschaftliche Datenverarbeitung: Gottingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Garrappa, R. On linear stability of predictor-corrector algorithms for fractional differential equations. Internat. J. Comput. Math. 2010, 87, 2281–2290. [Google Scholar] [CrossRef]
- Garrappa, R. Predictor-Corrector PECE Method for Fractional Differential Equations. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/32918-predictor-corrector-pece-method-for-fractional-differential-equations (accessed on 14 May 2020).


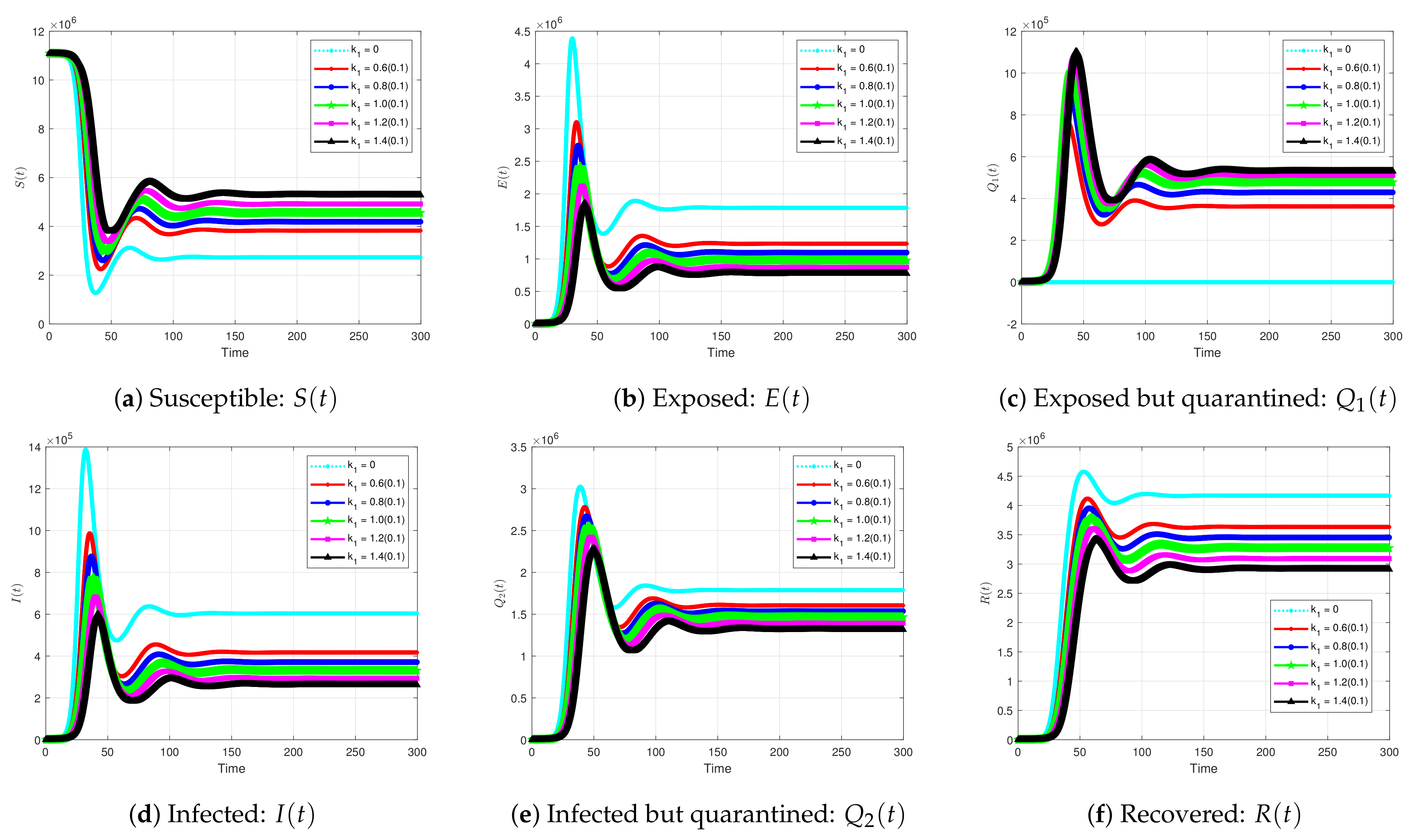
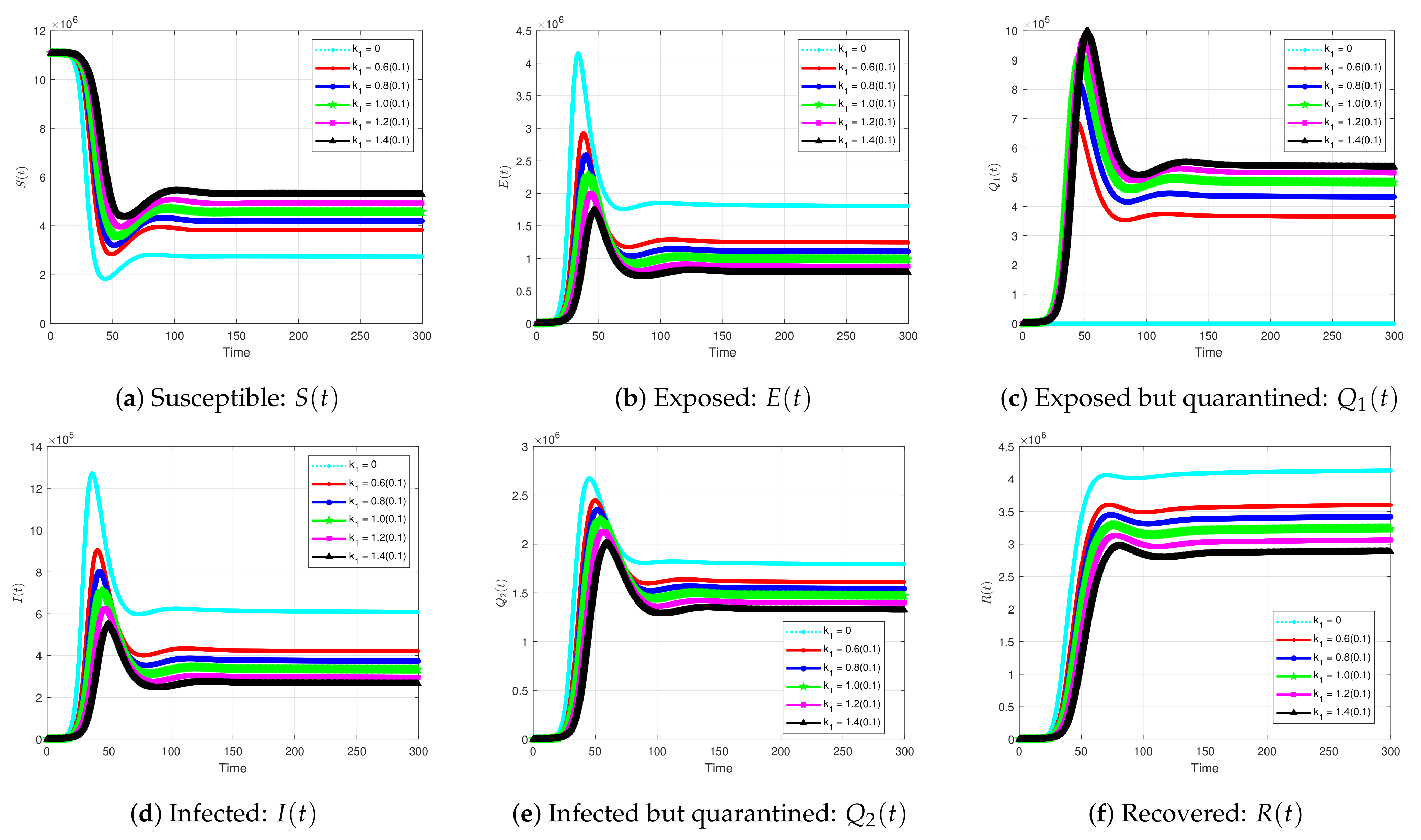
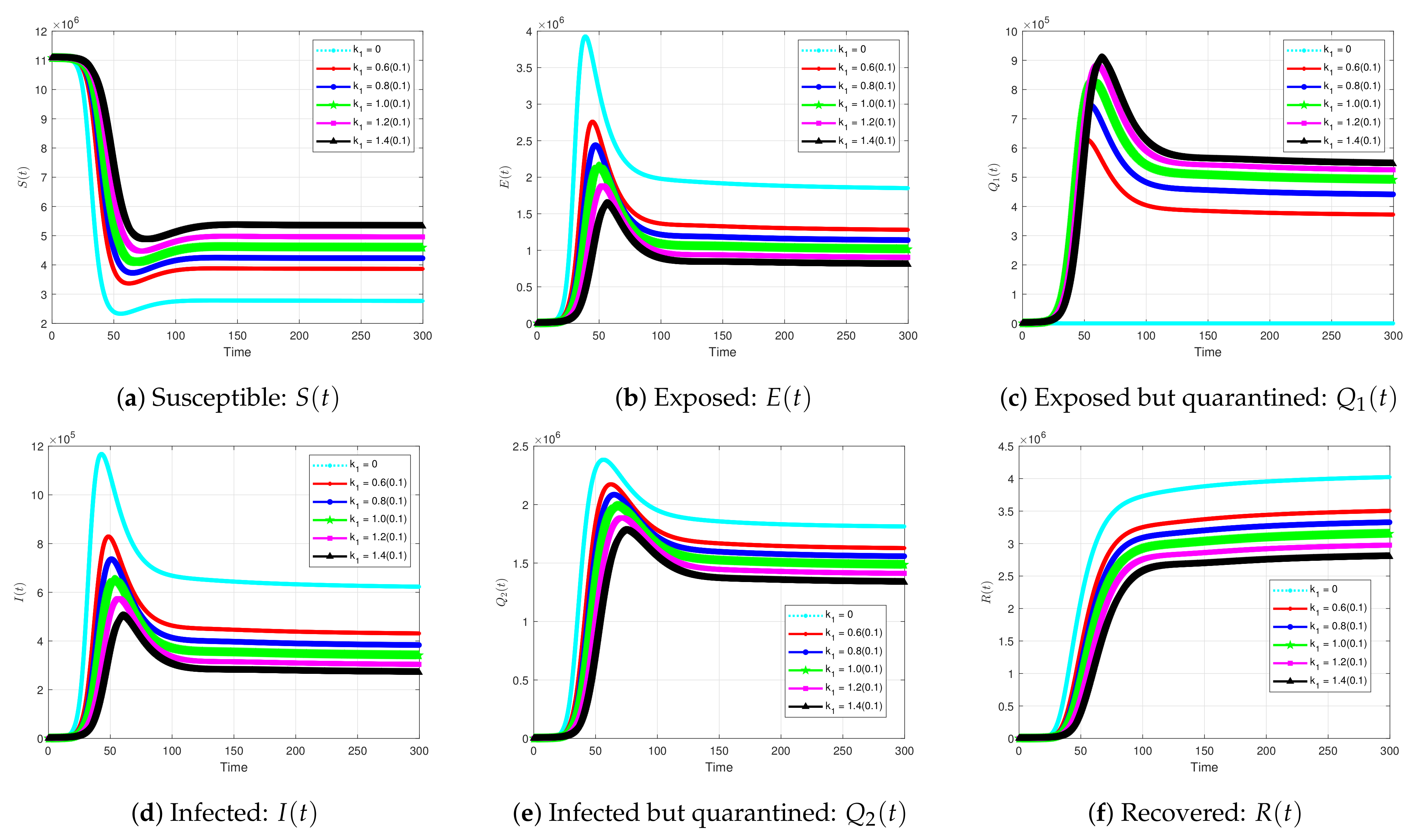
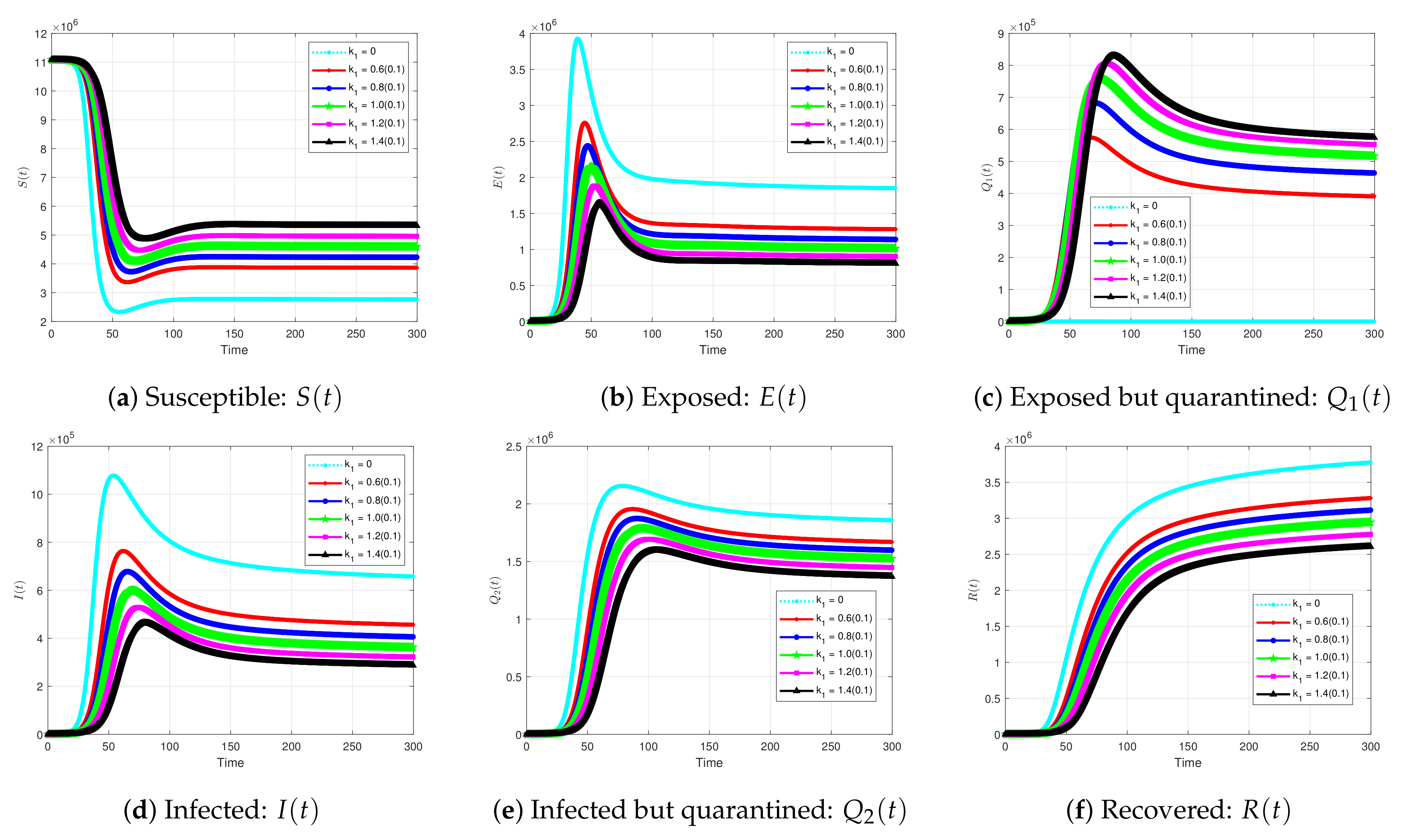






| Parameter | Likely Range (Sources) | Default Value |
|---|---|---|
| b (Recruitment rate of the population) | 78,680 | |
| (Effective contact rate) | [5,43] | day |
| (Transition rate from exposed quarantined to susceptible individuals) | 1/14 [43] | 1/14 |
| (Transition rate from recovered to susceptible individuals) | Assumed | 5/100 |
| (Quarantine rate of exposed individuals) | 1/10 [5] | 1/10 day |
| (Transition rate from exposed to infected class ) | 1/14–1/3 [43,44,45] | 1/7 day |
| (Transition from exposed quarantined to infected quarantined) | 0.1259 [43] | 0.1259 |
| (Quarantining rate of individuals in the class) | 0.2– 1 [43,46] | 0.3654 day |
| (Disease-induced death rate) | [5,43] | |
| (Natural death rate) | 7.1/1000 | 7.1/1000 |
| (Natural recovery rate) | 1/30–1/3 day [43,47] | 1/20 day |
| (Recovery rate of quarantine infected) | 0.11624 [43,48] | 0.11624 day |
| (Initial value of the susceptible) | [5] | 11,081,000 |
| (Initial value of the expose) | [5] | 399 |
| (Initial value of the expose, quarantined) | [5] | 159 |
| (Initial value of the infected) | [5] | 54 |
| (Initial value of the infected, quarantined) | [5] | 28 |
| (Initial value of the recovered) | [5] | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iyiola, O.; Oduro, B.; Zabilowicz, T.; Iyiola, B.; Kenes, D. System of Time Fractional Models for COVID-19: Modeling, Analysis and Solutions. Symmetry 2021, 13, 787. https://doi.org/10.3390/sym13050787
Iyiola O, Oduro B, Zabilowicz T, Iyiola B, Kenes D. System of Time Fractional Models for COVID-19: Modeling, Analysis and Solutions. Symmetry. 2021; 13(5):787. https://doi.org/10.3390/sym13050787
Chicago/Turabian StyleIyiola, Olaniyi, Bismark Oduro, Trevor Zabilowicz, Bose Iyiola, and Daniel Kenes. 2021. "System of Time Fractional Models for COVID-19: Modeling, Analysis and Solutions" Symmetry 13, no. 5: 787. https://doi.org/10.3390/sym13050787
APA StyleIyiola, O., Oduro, B., Zabilowicz, T., Iyiola, B., & Kenes, D. (2021). System of Time Fractional Models for COVID-19: Modeling, Analysis and Solutions. Symmetry, 13(5), 787. https://doi.org/10.3390/sym13050787







