Efficacious Analytical Technique Applied to Fractional Fornberg–Whitham Model and Two-Dimensional Fractional Population Model
Abstract
1. Introduction
2. Preliminaries
- (a)
- (b)
- (c)
- .
3. The -HATM Technique
4. Application to the Fractional Fornberg–Whitham Equation
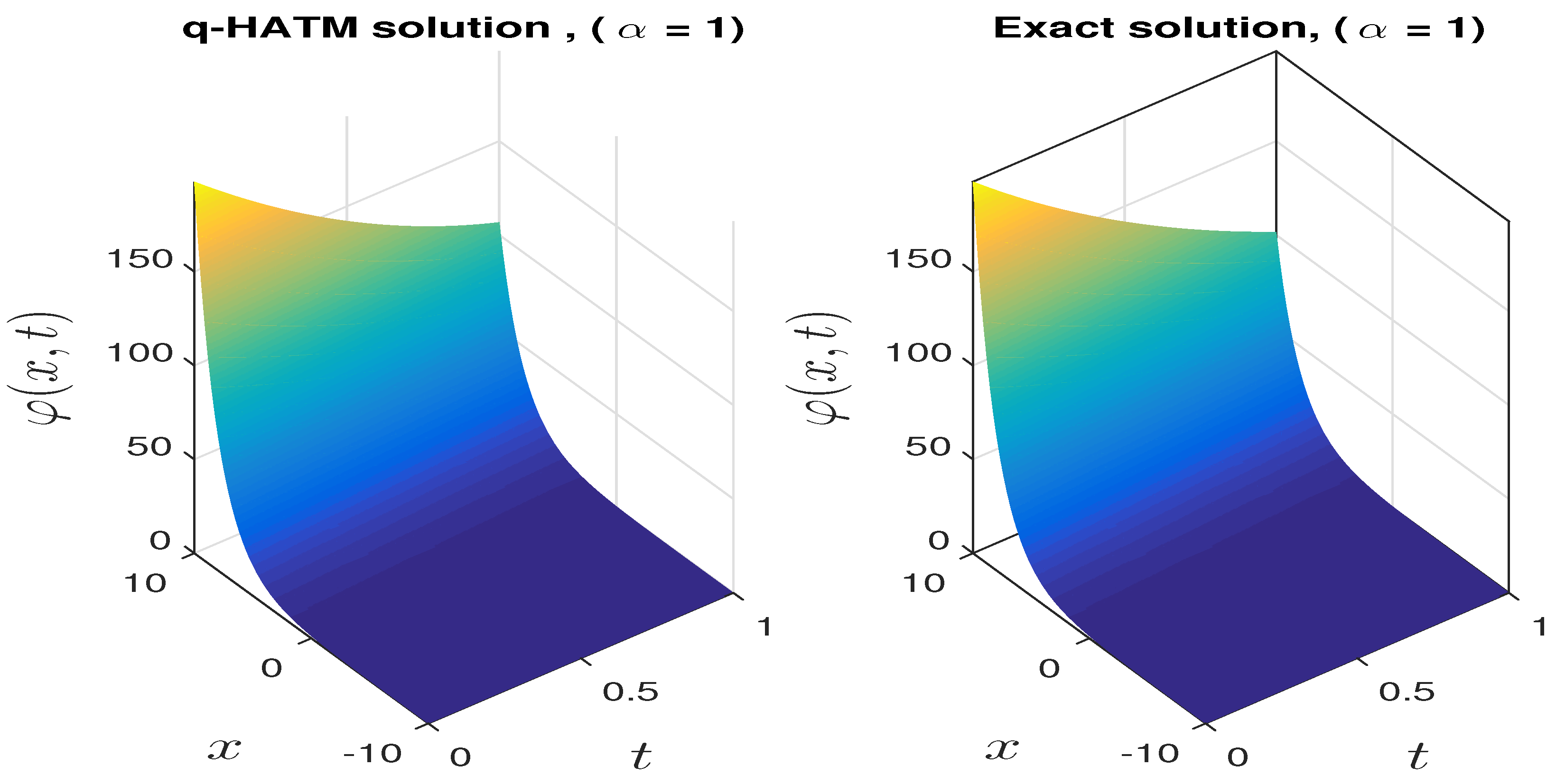
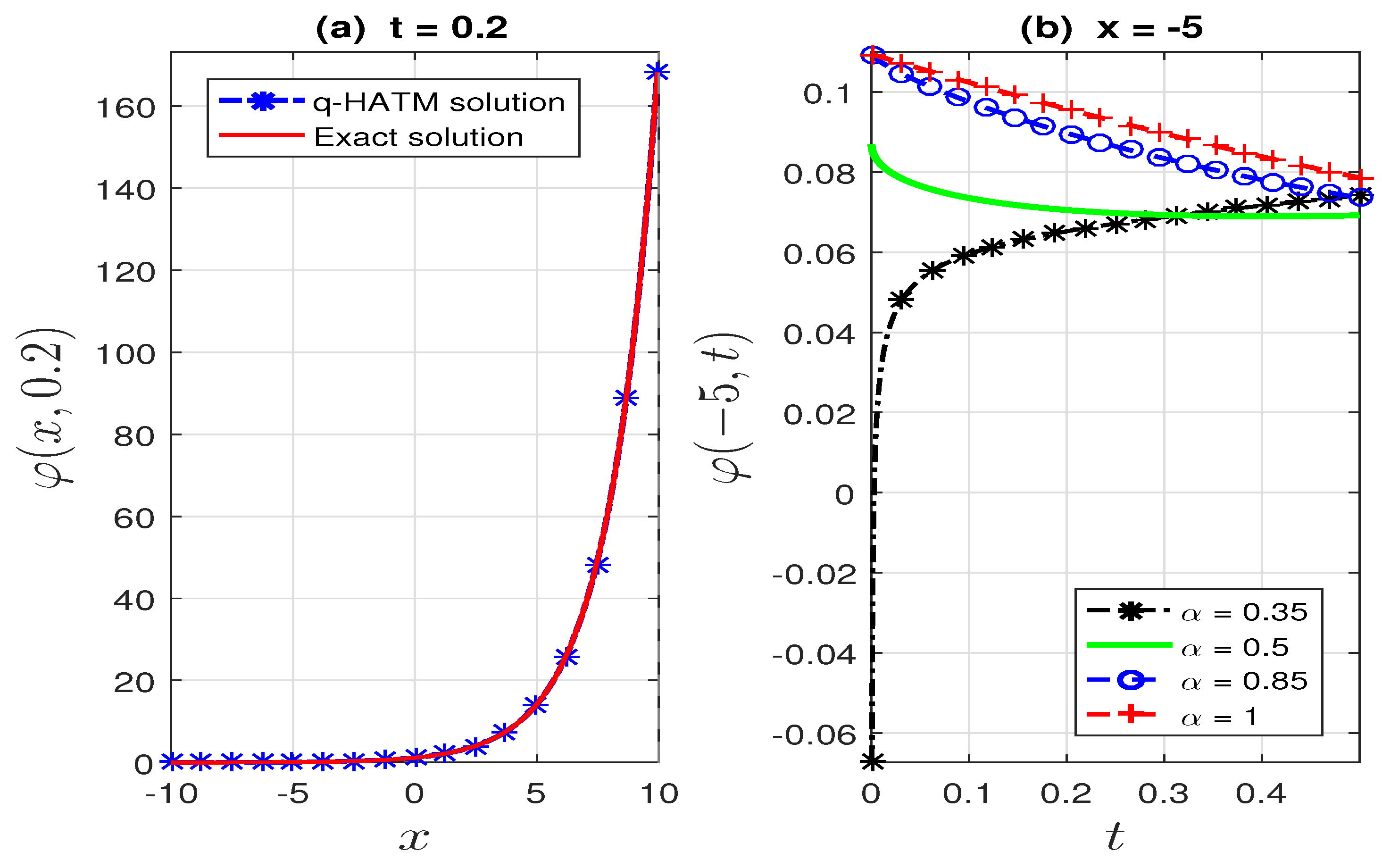
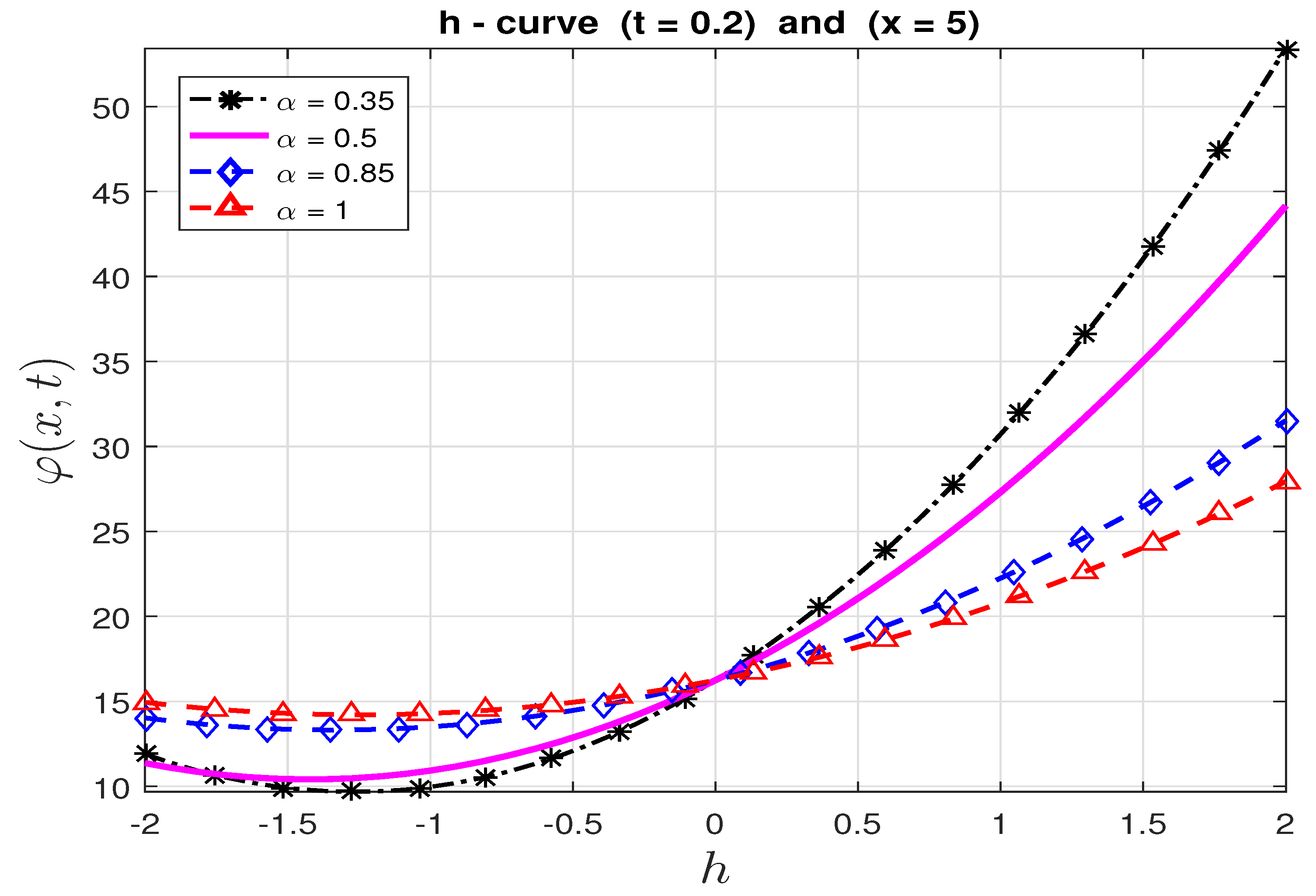
Numerical Comparison
- (ii)
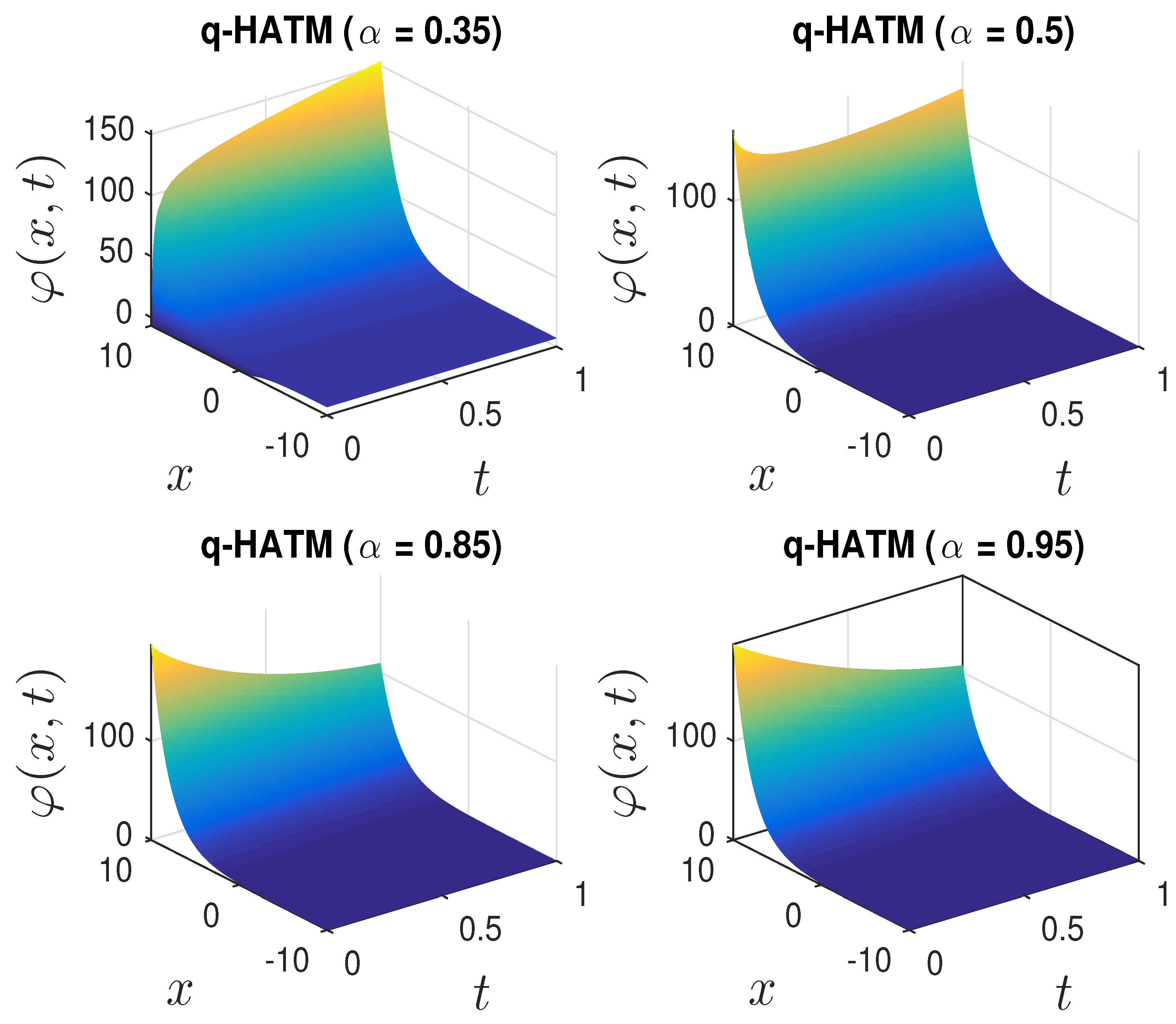
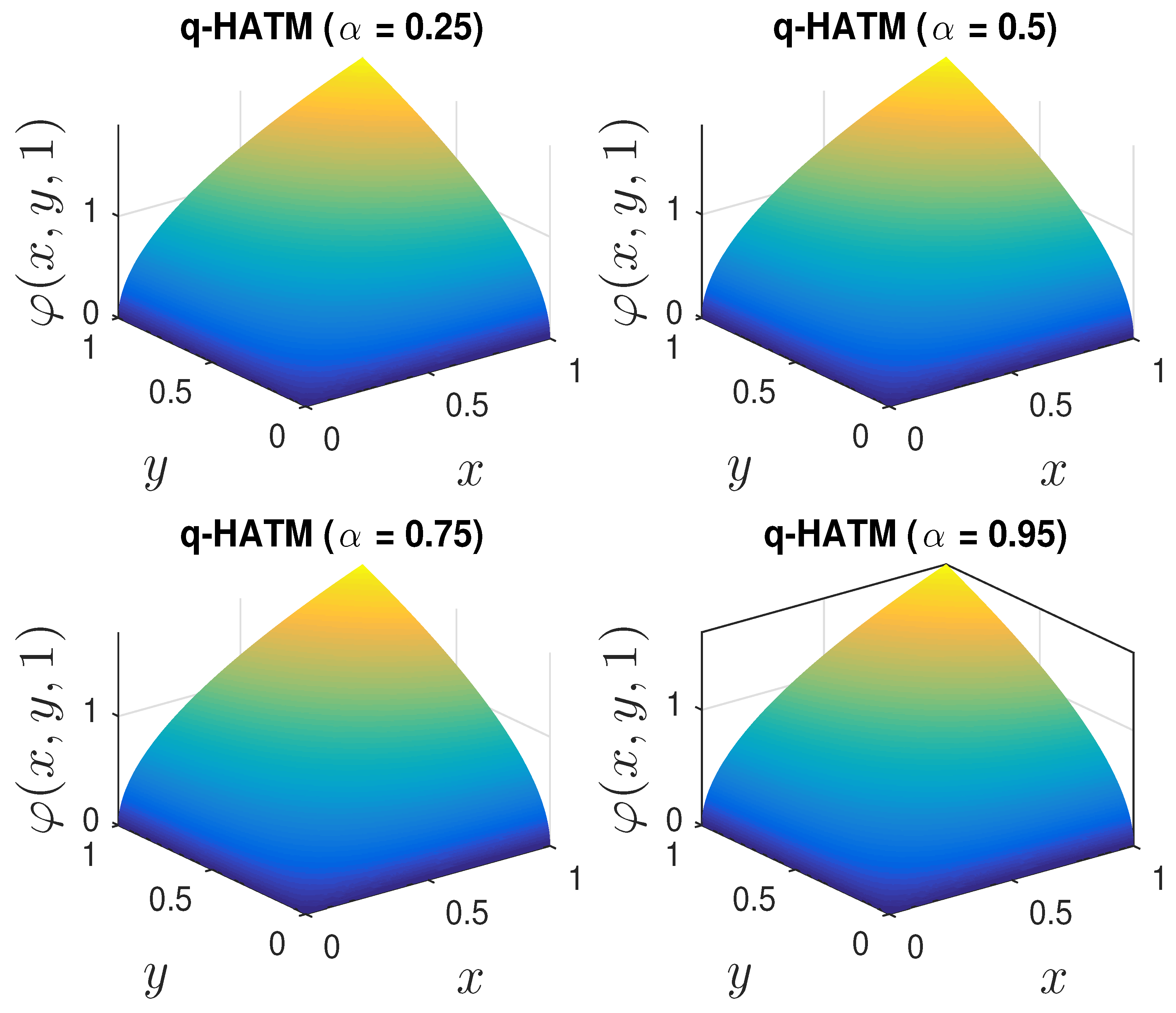
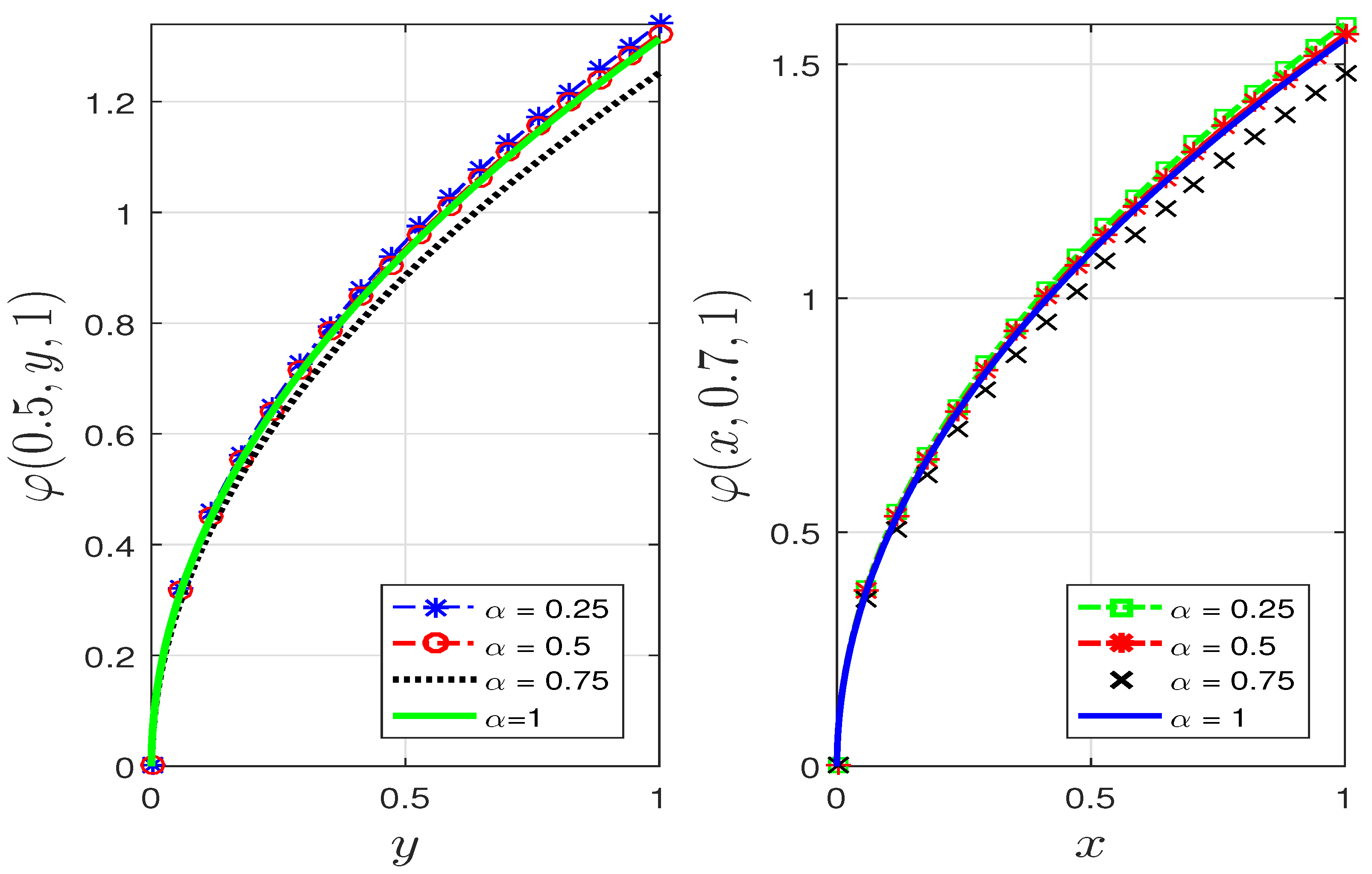
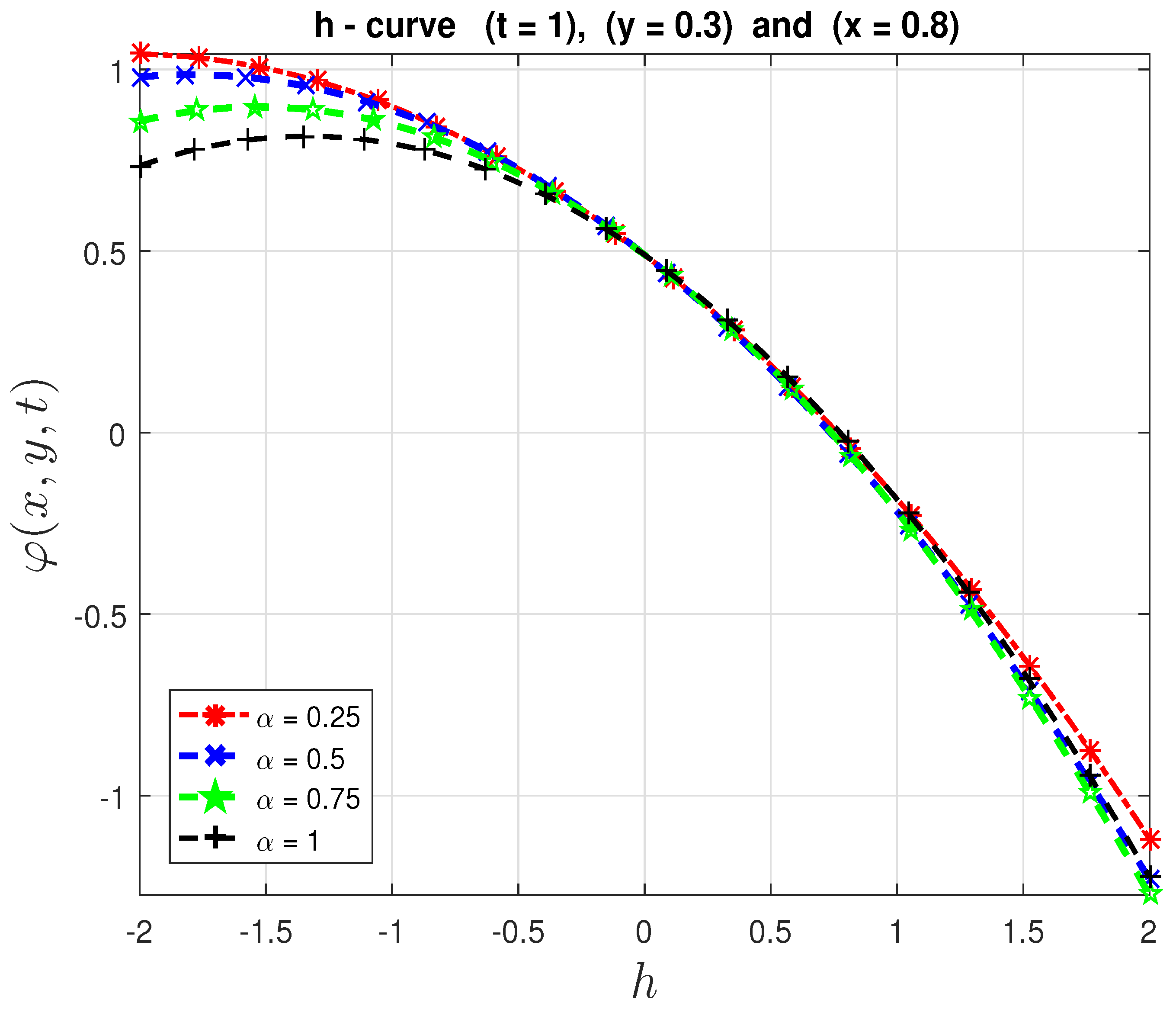
- Figure 3 and Figure 4b show the changes in the dynamics of the Fornberg–Whitham equation as the value of α changes. This, in essence, depicts why it is imperative to consider studying the fractional Fornberg–Whitham equation, as this will give additional information about the dynamics of the equation in real life situations.
- (iii)
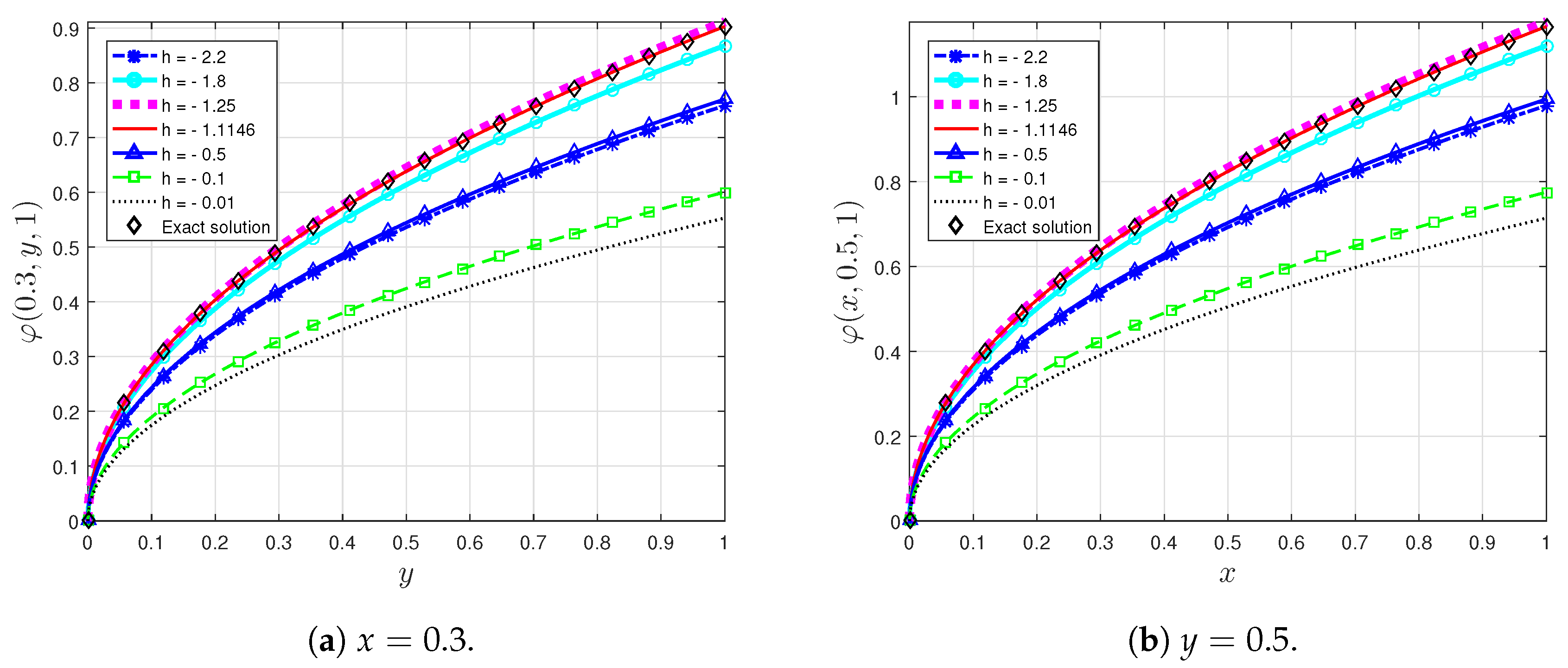
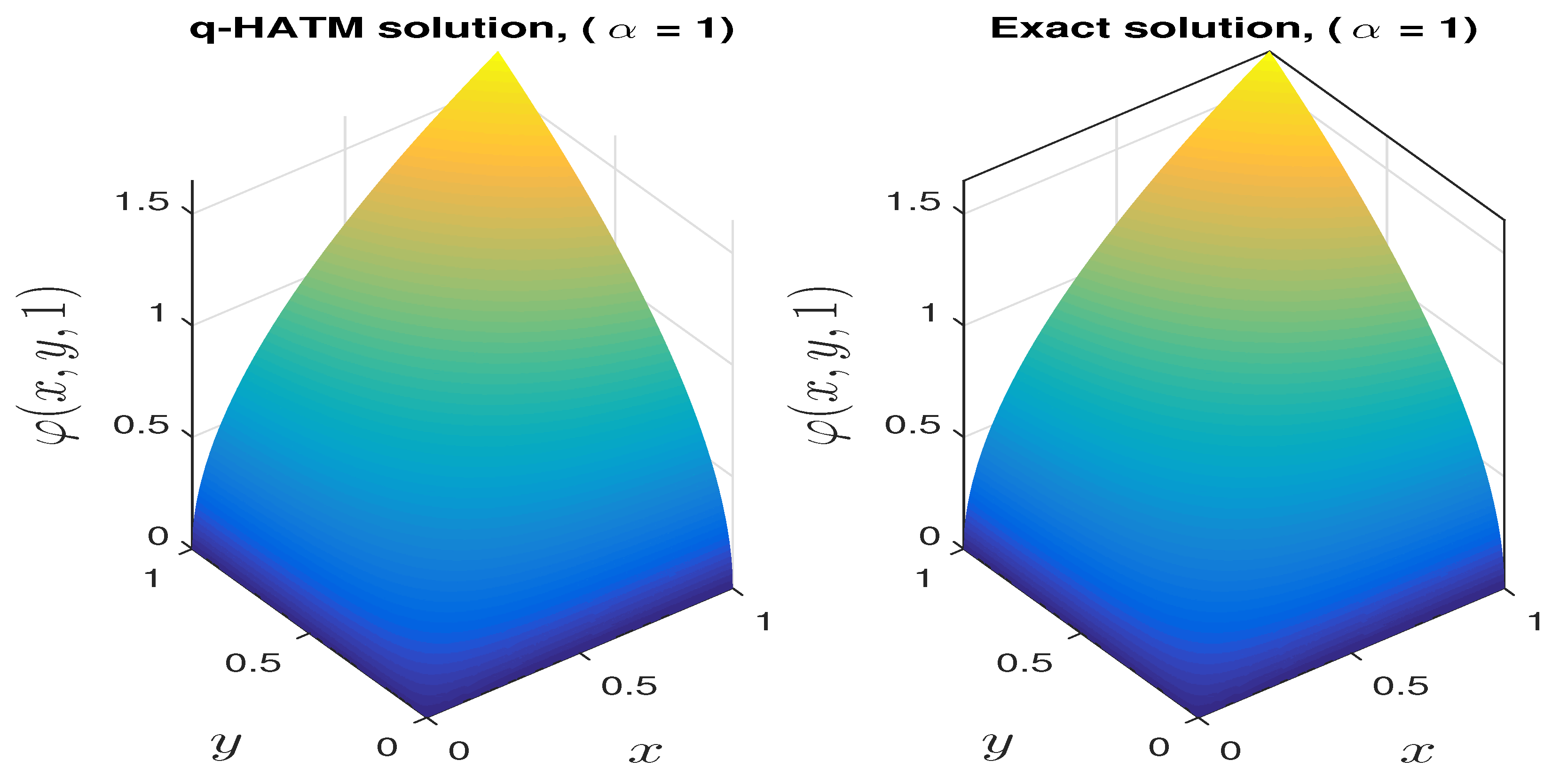
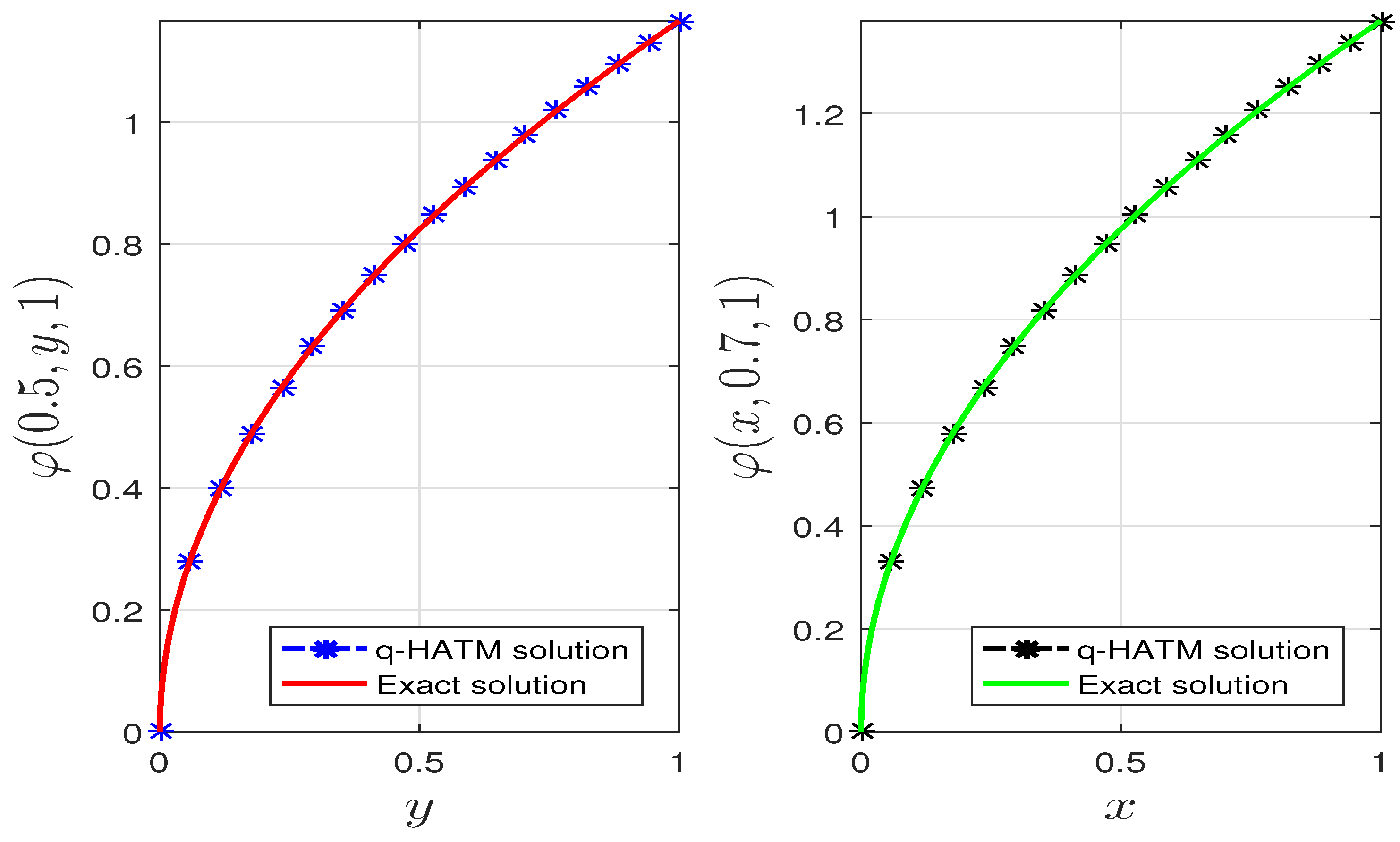
5. Application to a Fractional Biological Population Model
Numerical Comparison
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Debnath, L. A brief historical introduction to fractional calculus. Int. J. Math. Educ. Sci. Technol. 2004, 35, 487–501. [Google Scholar] [CrossRef]
- Pu, Y.F. Fractional differential analysis for texture of digital image. J. Algorithms Comput. Technol. 2007, 3, 357–380. [Google Scholar]
- Zhang, Y.; Pu, Y.F.; Hu, J.R.; Zhou, J.L. A class of fractional-order variational image in-painting models. Appl. Math. Inf. Sci. 2012, 6, 299–306. [Google Scholar]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.B.; Machado, J.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Agarwal, P.; Dragomir, S.S.; Jleli, M.; Samet, B. Advances in Mathematical Inequalities and Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Baleanu, D.; Jajarmi, A.; Sajjadi, S.S.; Mozyrska, D. A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083127. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Agarwal, P. Numerical solution of multiterm variable order fractional differential equations via shifted Legendre polynomials. Math. Methods Appl. Sci. 2019, 42, 3978–3991. [Google Scholar] [CrossRef]
- El-Tawil, M.A.; Huseen, S.N. The Q-homotopy analysis method (QHAM). Int. J. Appl. Math. Mech. 2012, 8, 51–75. [Google Scholar]
- Fornberg, B.; Whitham, G.B. A numerical and theoretical study of certain nonlinear wave phenomena. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1978, 298, 373–404. [Google Scholar]
- Iyiola, O.S. A numerical study of Ito equation and Sawada–Kotera equation both of time-fractional type. Adv. Math. Sci. J. 2013, 2, 71–79. [Google Scholar]
- Iyiola, O.S. On the solutions of non-linear time-fractional gas dynamic equations: An analytical approach. Int. J. Pure Appl. Math. 2015, 98, 491–502. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Soh, M.E.; Enyi, C.D. Generalised homotopy analysis method (q-HAM) for solving foam drainage equation of time fractional type. Math. Eng. Sci. Aerosp. 2013, 4, 105. [Google Scholar]
- Jain, S.; Agarwal, P.; Kilicman, A. Pathway fractional integral operator associated with 3m-parametric Mittag-Leffler functions. Int. J. Appl. Comput. Math. 2018, 4, 115. [Google Scholar] [CrossRef]
- Jain, S.; Mehrez, K.; Baleanu, D.; Agarwal, P. Certain Hermite–Hadamard inequalities for logarithmically convex functions with applications. Mathematics 2019, 7, 163. [Google Scholar] [CrossRef]
- Jajarmi, A.; Arshad, S.; Baleanu, D. A new fractional modelling and control strategy for the outbreak of dengue fever. Phys. A Stat. Mech. Appl. 2019, 535, 122524. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Sajjadi, S.S.; Asad, J.H. A new feature of the fractional Euler–Lagrange equations for a coupled oscillator using a nonsingular operator approach. Front. Phys. 2019, 7, 196. [Google Scholar] [CrossRef]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modelling and optimal control of diabetes and tuberculosis co-existence. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 093111. [Google Scholar] [CrossRef] [PubMed]
- Jajarmi, A.; Yusuf, A.; Baleanu, D.; Inc, M. A new fractional HRSV model and its optimal control: A non-singular operator approach. Phys. A Stat. Mech. Appl. 2020, 547, 123860. [Google Scholar] [CrossRef]
- Nigmatullina, R.R.; Agarwal, P. Direct evaluation of the desired correlations: Verification on real data. Phys. A Stat. Mech. Appl. 2019, 534, 121558. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Fractional derivatives applied to MSEIR problems: Comparative study with real world data. Eur. Phys. J. Plus 2019, 134, 171. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Mathematical modeling for the impacts of deforestation on wildlife species using Caputo differential operator. Chaos Solitons Fractals 2019, 126, 32–40. [Google Scholar] [CrossRef]
- Rekhviashvili, S.; Pskhu, A.; Agarwal, P.; Jain, S. Application of the fractional oscillator model to describe damped vibrations. Turk. J. Phys. 2019, 43, 236–242. [Google Scholar] [CrossRef]
- Ruzhansky, M.V.; Cho, Y.J.; Agarwal, P.; Area, I. Advances in Real and Complex Analysis with Applications; Springer: Singapore, 2017. [Google Scholar]
- Sakar, M.G.; Erdogan, F.; Yildirim, A. Variational iteration method for the time-fractional Fornberg-Whitham equation. Compt. Math. Appl. 2012, 63, 1382–1388. [Google Scholar] [CrossRef]
- Saoudi, K.; Agarwal, P.; Kumam, P.; Ghanmi, A.; Thounthong, P. The Nehari manifold for a boundary value problem involving Riemann–Liouville fractional derivative. Adv. Differ. Equ. 2018, 2018, 263. [Google Scholar] [CrossRef]
- Senol, M.; Iyiola, O.S.; Kasmaei, H.D.; Akinyemi, L. Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent–Miodek system with energy-dependent Schrödinger potential. Adv. Differ. Equ. 2019, 2019, 462. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kumar, S. New treatment of fractional Fornberg-Whitham equation via Laplace transform. Ain Shams Eng. J. 2013, 4, 557–562. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Swroop, R. Numerical solution of time and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D.; Rathore, S. An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl. Math. Comput. 2018, 335, 12–24. [Google Scholar] [CrossRef]
- Soh, M.E.; Enyi, C.D.; Iyiola, O.S.; Audu, J.D. Approximate analytical solutions of strongly nonlinear fractional BBM-Burger’s equations with dissipative term. Appl. Math. Sci. 2014, 8, 7715–7726. [Google Scholar] [CrossRef][Green Version]
- Srivastava, H.M.; Kumar, D.; Singh, J. An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 2017, 45, 192–204. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Qurashi, M.A.; Baleanu, D. A reliable technique for fractional modified Boussinesq and approximate long wave equations. Adv. Differ. Equ. 2019, 2019, 253. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, C. A one-step optimal homotopy analysis method for nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2026–2036. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 299, 6–25. [Google Scholar]
- Yabushita, K.; Yamashita, M.; Tsuboi, K. An analytic solution of projectile motion with the quadratic resistance law using the homotopy analysis method. J. Phys. A Math. Theor. 2007, 40, 8403–8416. [Google Scholar] [CrossRef]
- Yıldız, T.A.; Jajarmi, A.; Yıldız, B.; Baleanu, D. New aspects of time fractional optimal control problems within operators with nonsingular kernel. Discrete Contin. Dyn. Syst. 2020, 13, 407–428. [Google Scholar] [CrossRef]
- Yu, J.X.; Yuan, G.; Yua, L.S. Approximate homotopy symmetry method: Homotopy series solutions to the sixth-order Boussinesq equation. Sci. China Ser. G-Phys. Mech. Astron. 2009, 52, 1169–1178. [Google Scholar]
- Yusuf, A.; Qureshi, S.; Shah, S.F. Mathematical analysis for an autonomous financial dynamical system via classical and modern fractional operators. Chaos Solitons Fractals 2020, 132, 109552. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy analysis method and its applications in mathematics. J. Basic Sci. Eng. 1997, 5, 111–125. [Google Scholar]
- Liao, S.J. Homotopy analysis method: A new analytic method for nonlinear problems. Appl. Math. Mech. 1998, 19, 957–962. [Google Scholar]
- Akinyemi, L. q-homotopy analysis method for solving the seventh-order time-fractional Lax’s Korteweg–de Vries and Sawada–Kotera equations. Comput. Appl. Math. 2019, 38, 191. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S.; Akpan, U. Iterative methods for solving fourth- and sixth-order time-fractional Cahn–Hillard equation. Math. Methods Appl. Sci. 2020, 43, 4050–4074. [Google Scholar] [CrossRef]
- Kumar, D.; Agarwal, R.P.; Singh, J. A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math. 2018, 399, 405–413. [Google Scholar] [CrossRef]
- Kumar, D.; Singha, J.; Baleanu, D. A new analysis for fractional model of regularized long-wave equation arising in ion acoustic plasma waves. Math. Methods Appl. Sci. 2017, 40, 5642–5653. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur. Phys. J. Plus 2019, 134, 19. [Google Scholar] [CrossRef]
- Abidi, F.; Omrani, K. The homotopy analysis method for solving the Fornberg-Whitham equation and comparison with the Adomian’s decomposition method. Comp. Maths. Appl. 2010, 59, 2743–2750. [Google Scholar] [CrossRef]
- Lu, J. An analytical approach to the Fornberg-Whitham type equations by using variational iteration method. Comp. Maths. Appl. 2011, 61, 2010–2013. [Google Scholar] [CrossRef][Green Version]
- Alderremy, A.A.; Khan, H.; Shah, R.; Aly, S.; Baleanu, D. The analytical analysis of time-fractional Fornberg—Whitham equations. Mathematics 2020, 8, 987. [Google Scholar] [CrossRef]
- Al-luhaibi, M.S. An analytical treatment to fractional Fornberg—Whitham equation. Math Sci. 2017, 11, 1–6. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis of the Fornberg-Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur. Phys. J. Plus 2018, 133, 70. [Google Scholar] [CrossRef]
- Merdan, M.; Gökdoğan, A.; Yıldırım, A.; Mohyud-Din, S.T. Numerical simulation of fractional Fornberg-Whitham equation by differential transformation method. Abstract Appl. Anal. 2012, 2012, 965367. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S.; Akpan, U. A reliable technique to study nonlinear time-fractional coupled Korteweg—de Vries equations. Adv. Difference Equ. 2020, 2020, 169. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Luchko, Y.F.; Srivastava, H.M. The exact solution of certain differential equations of fractional order by using operational calculus. Comput. Math. Appl. 1995, 29, 73–85. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer: New York, NY, USA, 2008. [Google Scholar]
- Abbasbandy, S.; Jalili, M. Determination of optimal convergence-control parameter value in homotopy analysis method. Numer. Algor. 2013, 64, 593–605. [Google Scholar] [CrossRef]
- Liao, S.J. The Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, J.; Wei, Z.; Li, L.; Zhou, C. Least-squares residual power series method for the time fractional differential equations. Complexity 2019, 2019, 6159024. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Zhang, Y. Homotopy perturbation method to fractional biological population equation. Diff. Calculus. 2011, 1, 117–127. [Google Scholar] [CrossRef]

| Abs Error | Abs Error | Abs Error | Abs Error | ||||
|---|---|---|---|---|---|---|---|
| x | t | Exact | q-HATM | q-HATM | LSRPSM [63] | RPSM [63] | VIM [26] |
| itr = 2 | itr = 2 | itr = 2 | itr = 5 | itr = 2 | |||
| 0.1 | 0.00840453 | 0.00840436 | 1.70560 | 1.21387 | 1.41249 | 1.75478 | |
| 0.2 | 0.00786250 | 0.00786159 | 9.10243 | 1.58400 | 1.58400 | 1.71128 | |
| 0.3 | 0.00735542 | 0.00735561 | 1.90881 | 1.35139 | 3.77120 | 1.66654 | |
| 0.4 | 0.00688105 | 0.00688643 | 5.38732 | 7.41498 | 4.74372 | 1.62077 | |
| 0.5 | 0.00643727 | 0.00645405 | 1.67882 | 3.47756 | 5.59422 | 1.57418 | |
| 0.1 | 0.10238812 | 0.10238604 | 2.07785 | 1.47879 | 1.72077 | 2.13776 | |
| 0.2 | 0.09578480 | 0.09577371 | 1.10890 | 1.92971 | 3.24664 | 2.08477 | |
| 0.3 | 0.08960735 | 0.08960968 | 2.32540 | 1.64633 | 4.59427 | 2.03026 | |
| 0.4 | 0.08382830 | 0.08389393 | 6.56310 | 9.03330 | 5.77904 | 1.97450 | |
| 0.5 | 0.07842196 | 0.07862648 | 2.04522 | 4.23654 | 6.81515 | 1.91774 | |
| 0.1 | 2.05652035 | 2.05647862 | 4.17347 | 2.97023 | 3.45626 | 4.29380 | |
| 1 | 0.2 | 1.92388916 | 1.92366643 | 2.22729 | 3.87592 | 6.52104 | 4.18737 |
| 0.3 | 1.79981174 | 1.79985845 | 4.67070 | 3.30675 | 9.22783 | 4.07788 | |
| 0.4 | 1.68373646 | 1.68505469 | 1.31823 | 1.81439 | 1.16075 | 3.96588 | |
| 0.5 | 1.57514722 | 1.57925515 | 4.10793 | 8.50920 | 1.36886 | 3.85189 |
| x | t | |||
|---|---|---|---|---|
| 0.1 | 0.05416316 | 0.07351917 | 0.09275676 | |
| 0.2 | 0.06658185 | 0.07054802 | 0.08474062 | |
| −5 | 0.3 | 0.07288553 | 0.06931123 | 0.07889088 |
| 0.4 | 0.07719428 | 0.06897222 | 0.07438139 | |
| 0.5 | 0.08054278 | 0.06920693 | 0.07085670 | |
| 0.1 | 8.03852633 | 10.91121208 | 13.76632402 | |
| 0.2 | 9.88162297 | 10.47025429 | 12.57662352 | |
| 5 | 0.3 | 10.81717115 | 10.28669902 | 11.70844537 |
| 0.4 | 11.45664676 | 10.23638510 | 11.03917664 | |
| 0.5 | 11.95360852 | 10.27121975 | 10.51606638 |
| Abs Error | Abs Error | Abs Error | Abs Error | ||||
|---|---|---|---|---|---|---|---|
| x | t | Exact | q-HATM | q-HATM | HAM [48] | NIM [51] | NDM [50] |
| itr = 2 | itr = 2 | itr = 5 | itr = 3 | itr = 3 | |||
| 0.1 | 0.00630340 | 0.00630348 | 8.43252 | 1.25020 | 9.90107 | 4.86602 | |
| 0.2 | 0.00589687 | 0.00589576 | 1.11391 | 5.33187 | 1.84777 | 6.13163 | |
| 0.3 | 0.00551656 | 0.00551478 | 1.78726 | 1.22446 | 2.56333 | 4.76202 | |
| 0.4 | 0.00516078 | 0.00516054 | 2.44846 | 2.19875 | 3.12832 | 1.60584 | |
| 0.5 | 0.00482795 | 0.00483305 | 5.09516 | 3.45598 | 3.53532 | 2.59733 | |
| 0.1 | 0.07679109 | 0.07679212 | 1.02729 | 1.52306 | 1.20620 | 5.92803 | |
| 0.2 | 0.07183860 | 0.07182503 | 1.35702 | 6.49555 | 2.25104 | 7.46985 | |
| 0.3 | 0.06720551 | 0.06718374 | 2.17733 | 1.49169 | 3.12278 | 5.80133 | |
| 0.4 | 0.06287123 | 0.06286824 | 2.98283 | 2.67863 | 3.81107 | 1.95632 | |
| 0.5 | 0.05881647 | 0.05887854 | 6.20718 | 4.21025 | 4.30690 | 3.16419 | |
| 0.1 | 1.54239027 | 1.54241090 | 2.06337 | 3.05915 | 2.42271 | 1.19068 | |
| 0.2 | 1.44291687 | 1.44264430 | 2.72565 | 1.30467 | 4.52134 | 1.50036 | |
| 1 | 0.3 | 1.34985881 | 1.34942148 | 4.37328 | 2.99615 | 6.27227 | 1.16523 |
| 0.4 | 1.26280234 | 1.26274243 | 5.99118 | 5.38018 | 7.65474 | 3.92937 | |
| 0.5 | 1.18136041 | 1.18260716 | 1.24675 | 8.45651 | 8.65064 | 6.35545 |
| Abs Error | Abs Error | Abs Error | Abs Error | ||||
|---|---|---|---|---|---|---|---|
| x | y | Exact | q-HATM | q-HATM | LSRPSM [63] | RPSM [63] | HPM [64] |
| itr = 2 | itr = 2 | itr = 2 | itr = 2 | itr = 2 | |||
| 0.1 | 0.16487213 | 0.16487251 | 3.7943 | 9.62 | 2.37 | 2.3721 | |
| 0.2 | 0.23316440 | 0.23316493 | 5.3660 | 1.36 | 3.35 | 3.3547 | |
| 0.1 | 0.3 | 0.28556690 | 0.28556756 | 6.5719 | 1.67 | 4.11 | 4.1086 |
| 0.4 | 0.32974425 | 0.32974501 | 7.5886 | 1.92 | 4.74 | 4.7443 | |
| 0.5 | 0.36866528 | 0.36866613 | 8.4843 | 2.15 | 5.30 | 5.3042 | |
| 0.1 | 0.28556690 | 0.28556756 | 6.5719 | 1.67 | 4.11 | 4.1086 | |
| 0.2 | 0.40385258 | 0.40385351 | 9.2941 | 2.36 | 5.81 | 5.8105 | |
| 0.3 | 0.3 | 0.49461638 | 0.49461752 | 1.1383 | 2.89 | 7.12 | 7.1164 |
| 0.4 | 0.57113380 | 0.57113512 | 1.3144 | 3.33 | 8.22 | 8.2173 | |
| 0.5 | 0.63854700 | 0.63854847 | 1.4695 | 3.73 | 9.19 | 9.1872 | |
| 0.1 | 0.36866528 | 0.36866613 | 8.4843 | 2.15 | 5.30 | 5.3042 | |
| 0.2 | 0.52137144 | 0.52137264 | 1.1999 | 3.04 | 7.50 | 7.5013 | |
| 0.5 | 0.3 | 0.63854700 | 0.63854847 | 1.4695 | 3.73 | 9.19 | 9.1872 |
| 0.4 | 0.73733057 | 0.73733226 | 1.6969 | 4.30 | 1.06 | 1.0608 | |
| 0.5 | 0.82436064 | 0.82436253 | 1.8971 | 4.81 | 1.19 | 1.1861 | |
| 0.1 | 0.52137144 | 0.52137264 | 1.1999 | 3.04 | 7.50 | 7.5013 | |
| 0.2 | 0.73733057 | 0.73733226 | 1.6969 | 4.30 | 1.06 | 1.0608 | |
| 1.0 | 0.3 | 0.90304183 | 0.90304391 | 2.0782 | 5.27 | 1.30 | 1.2993 |
| 0.4 | 1.04274289 | 1.04274529 | 2.3997 | 6.09 | 1.50 | 1.5003 | |
| 0.5 | 1.16582199 | 1.16582467 | 2.6830 | 6.80 | 1.68 | 1.6773 |
| x | y | |||
|---|---|---|---|---|
| 0.1 | 0.32691706 | 0.31767975 | 0.29415547 | |
| 0.2 | 0.46233054 | 0.44926700 | 0.41599866 | |
| 0.3 | 0.3 | 0.56623696 | 0.55023746 | 0.50949222 |
| 0.4 | 0.65383413 | 0.63535949 | 0.58831095 | |
| 0.5 | 0.73100878 | 0.71035351 | 0.65775163 | |
| 0.1 | 0.59686617 | 0.41012279 | 0.53705196 | |
| 0.2 | 0.84409623 | 0.58000121 | 0.75950617 | |
| 1 | 0.3 | 1.03380253 | 0.71035351 | 0.93020128 |
| 0.4 | 1.19373233 | 0.82024557 | 1.07410392 | |
| 0.5 | 1.33463332 | 0.91706243 | 1.20088469 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enyi, C.D. Efficacious Analytical Technique Applied to Fractional Fornberg–Whitham Model and Two-Dimensional Fractional Population Model. Symmetry 2020, 12, 1976. https://doi.org/10.3390/sym12121976
Enyi CD. Efficacious Analytical Technique Applied to Fractional Fornberg–Whitham Model and Two-Dimensional Fractional Population Model. Symmetry. 2020; 12(12):1976. https://doi.org/10.3390/sym12121976
Chicago/Turabian StyleEnyi, Cyril D. 2020. "Efficacious Analytical Technique Applied to Fractional Fornberg–Whitham Model and Two-Dimensional Fractional Population Model" Symmetry 12, no. 12: 1976. https://doi.org/10.3390/sym12121976
APA StyleEnyi, C. D. (2020). Efficacious Analytical Technique Applied to Fractional Fornberg–Whitham Model and Two-Dimensional Fractional Population Model. Symmetry, 12(12), 1976. https://doi.org/10.3390/sym12121976





