Abstract
This paper deals with uncertainty, asymmetric information, and risk modelling in a complex power system. The uncertainty is managed by using probability and decision theory methods. More specifically, influence diagrams—as extended Bayesian network functions with interval probabilities represented through credal sets—were chosen for the predictive modelling scenario of replacing the most critical circuit breakers in optimal time. Namely, based on the available data on circuit breakers and other variables that affect the considered model of a complex power system, a group of experts was able to assess the situation using interval probabilities instead of crisp probabilities. Furthermore, the paper examines how the confidence interval width affects decision-making in this context and eliminates the information asymmetry of different experts. Based on the obtained results for each considered interval width separately on the action to be taken over the considered model in order to minimize the risk of the power system failure, it can be concluded that the proposed approach clearly indicates the advantages of using interval probability when making decisions in systems such as the one considered in this paper.
1. Introduction
The main goal of every enterprise is to preserve and optimize the quality of its operations and services. Nowadays, the complex power grid is becoming more responsive, safe, and efficient due to large amounts of data that are being collected, stored, and analyzed using new technologies. This analysis provides stakeholders with new insights that are not possible to gain with conventional information technology (IT) and based on which well-informed decisions can be made. Contemporary power systems are coping with serious challenges, such as integration of renewables and active demand and the uncertainty and asymmetric information it brings into the whole system of power operation, planning, and control.
New technologies in the energy sector include risk-based and predictive maintenance to replace aging infrastructure by minimizing its costs, fault detection, fault diagnosis, etc. The technologies can also be applied to monitoring and to routine daily operations, making them more accurate, efficient, and resilient [1].
Maintaining reliability, minimizing operation costs, and making a profit are hard to achieve without proper risk analysis and uncertainty management [2].
Having in mind that a complex power system consists of many interdependent subsystems, analyzing the system’s state, keeping reliability at a desired level, and mitigating losses becomes harder than ever [3,4]. That is why new risk assessment methodologies that deal with uncertainty are introduced. The main challenge for this research was to develop a risk assessment methodology when the accurate failure equipment database and the probability distribution of equipment states are missing. For instance, when a group of experts evaluate risk, their evaluation of event probability can be expressed only as an interval value.
Circuit breakers are a vital element of the energy system, which is why there is a need for their continuous improvement through the analysis of increasing reliability and the determination of their remaining life. This is achieved by constant monitoring of work, regular maintenance, and analysis of data from its exploitation.
Another important reason for analyzing them lies in the ability to reduce costs. It is important to know the data of a circuit breaker approaching the end of its life, because it significantly affects the business economy. Therefore, such data make it possible to plan the replacement of the circuit breaker in a timely manner, which is a better scenario in relation to its unplanned failure [5,6].
Regular monitoring of the operation of a circuit breaker, as well as indicators of its condition, provides knowledge of its reliability, i.e., its remaining service life. Based on such data, the cost-effectiveness of the replacement and its scope, as well as the timeframe can be planned [5,6].
Replacing the most risky circuit breakers is a good basis for increasing the reliability of the energy system, reducing the amount of undelivered electricity, and thus eliminating the additional involvement of labor if a circuit breaker is replaced before its unplanned failure. Today, low-oil circuit breakers are replaced with circuit breakers based on modern technologies, such as vacuum and SF6 circuit breakers.
However, despite this, most substations still have a large number of low-oil circuit breakers in operation. With low-oil circuit breakers, there is a need for frequent maintenance, such as changing or refilling oil and lubricating the mechanism, as well as frequent visual inspection.
For these reasons, there is a need to replace old technology circuit breakers, which is why it is necessary to determine the criteria and the pace of their replacement. Analysis of the condition of circuit breakers and determination of risk would provide insight into the number of the most risky circuit breakers. Additionally, from the aspect of energy system stability and business economy, circuit breakers whose failures may produce the greatest consequences would be defined. In this way, the circuit breakers with the highest risk should be proposed for urgent replacement [5,6].
Literature shows different techniques that examine circuit breaker condition analyses. Data mining techniques that include classification techniques and expert opinion, such as fuzzy set theory, are used to examine circuit breakers’ lifetime and operation mode [7,8]. Unlike these data-driven prognostics, there is a model-based prognostic that includes engineering knowledge within the considered model [9,10]. Furthermore, literature shows evidence of hybrid prognostic techniques that combine discrete and continuous events within a system. Hybrid approaches comprehensively consider the parameters that affect the operation of a system.
Frequently used hybrid prognostic techniques for circuit breaker analyses are piecewise deterministic Markov processes [11]. In [12,13], it is shown that the use of these models is very suitable for the creation of hybrid prognostic applications. The so-called shock model is a model based on which behavior of a system is modeled during a failure. In [13], a component of the random evolution of the system was added to the shock model, which is described using continuous-time Markov chains.
Additionally, dynamic reliability problems are solved using piecewise deterministic Markov processes [14,15]. In these systems, depending on the operating conditions, it is possible to separately observe and model each component of interest for the reliable operation of the system. In addition to this technique, dynamic Bayesian networks (BNs) [16] are very often used for the problem of dynamic reliability. A new method developed for hybrid prognostics approaches based on a combination of deterministic and stochastic properties called hybrid particle Petri nets is described in [17]. Hybrid bond graphs that form the basis of the model described in [18] represent another tool for hybrid prognostics, which with the help of Monte Carlo simulations enable the determination of variables with constraints in the predictive model.
The necessary conditions for the usage of all previously explained methodologies is an accurate failure equipment database and the already known probability distribution of equipment states. Very few research studies have addressed the uncertainties, accuracy, and confidence of the inspection results, although the simulations and decision models are directly dependent on these results. Probabilistic uncertainties require appropriate mathematical modeling and quantification when predicting a future state of the nature or the value of certain parameters.
The notion of probability is very closely related to the notion of symmetry. Based on symmetry, we can talk about equal conditions for random events. We can extend the notion of probability to interval probabilities, especially when determining the aggregate probability value estimated by several experts and a situation where there is imperfect knowledge (when one party has different information to another).
An integrated framework consisting of intuitionistic fuzzy-failure mode effect analysis (IF-FMEA) and IF-technique for order preference by similarity to ideal solution (IF-TOPSIS) techniques, taking into account the vague concept and the hesitation of experts, was presented in [19]. Similarly, to assess the uncertain and imprecise nature of e-service evaluation in [20], a combination of fuzzy analytical hierarchy process (F-AHP) and fuzzy measurement alternatives and ranking according to compromise solution (F-MARCOS) was used. For the most accurate determination of weights under fuzziness, the fuzzy full consistency method (FUCOM-F) has been proposed in [21]. Additionally, criteria weights have been determined by the fuzzy SWARA (step-wise weight assessment ratio analysis) method, as described in [22]. In [22], for such criteria weights, a combination of fuzzy TOPSIS, fuzzy WASPAS, and fuzzy ARAS methods was used to perform evaluation and selection of suppliers for the considered example. Fuzzy set theory and interval analysis [23] represent one highly performing method for determining parametric uncertainties.
In situations where an estimate needs to be made under uncertain information where attribute values can describe the interval gray numbers, in [24] it is proposed to use a multi-criteria decision-making model that combines the interval gray numbers and normalized weighted geometric Dombi–Bonferroni mean operator.
The origin of the uncertainty in engineering systems come from both aleatoric and epistemic reasons. The review of hybrid uncertainty problems when both of these types are present, including uncertainty modeling, propagation analysis, structural reliability analysis, and reliability-based design optimization, is given in [25].
Probability-boxes (p-boxes) are often used in engineering analysis when the exact probability of a random variable probability distribution is unknown [26]. They offer a mathematically straightforward description of imprecise probabilities, defined via lower and upper bounds on the cumulative distribution function. P-boxes are used in acoustic analysis [27], structural reliability [28], risk analysis [29], and many other engineering fields.
The p-box framework that explains imprecision in stochastic processes by considering additional epistemic uncertainty in the process’ autocorrelation structure is described in [30,31]. Surrogate models for propagating probability-boxes include Kriging models [32] and polynomial response surface models [33]. Adaptive schemes based on Gaussian process models that can be applied to parametric and distribution-free p-boxes are given in [34]. Most often, the propagation of p-boxes is analyzed using the Monte Carlo simulation, but the comprehensive review of computational methods for p-boxes propagation in input models is given in [26]. A study of Monte Carlo methods for the general case of propagating imprecise probabilities is described in [35].
Previous methodologies offer a complete solution for the analysis of possible bounds of a certain random variable. However, the practical implementation of these bounds in risk-based decision-making has not been explored so far.
In this paper, authors use a new technique based on influence diagrams (IDs) with interval probabilities for failure prognostics. Based on the derived conclusions on the influence of interval width on the decision-making for the considered scenario, a group of experts evaluated all considered variables with interval probabilities, where the interval width was set in accordance with the previously derived conclusions. We sought to predict the best scenario of replacing the most critical circuit breakers in optimal time.
The novelty of this method is the usage of interval probabilities in standard influence diagrams. Furthermore, the paper examines how the confidence interval width affects decision-making in this context. The method can be easily implemented to any other kind of decision process presented by the influence diagram.
The paper is organized as follows—the second section discusses circuit breaker risk assessment, followed by a section that deals with uncertainty, definition, and properties of BNs and IDs; a case study with results and discussion is given in section four, which is followed by a conclusion.
2. Circuit Breaker Risk Assessment
2.1. Risk Assessment Model
The practice of equipment maintenance in power systems is a combination of corrective maintenance, maintenance at fixed intervals, and maintenance based on monitoring the condition of the equipment. Maintenance at fixed time intervals is defined by statutory deadlines for inspection, testing and inspection of equipment, or manufacturer’s instructions regarding when it is necessary to take certain actions on the equipment. Maintenance based on monitoring the condition of the equipment includes visual inspections and audits that are performed on a regular basis, and any repairs or other preventive actions are performed on the basis of audit reports [5,6].
The downside of this approach is that maintenance is performed on the basis of mandatory periodic tests within the deadlines provided by regulations and recommendations, regardless of the condition of the equipment and importance. Existing maintenance practices, however, do not provide an optimal level of maintenance.
All the above facts lead to the conclusion that existing maintenance practice and funds (tangible and intangible) invested in maintenance are not optimal and that a mechanism that would enable the optimization of these funds should be sought [5,6].
Risk-based maintenance is the next generation of reliability centered maintenance (RCM). Like RCM, RBI (risk-based inspection) is a systematic process for optimizing maintenance in technical systems. RBI is very similar to the RCM approach in that its goals are actually the answer to the same questions about system functionality.
For qualitative risk analysis for each component, each part of the system, or the whole system, assessments of the status and correctness of the component or system are formed, or a risk matrix is formed on the basis of which facility and which maintenance actions should be performed, and the actions that should be performed are prioritized. The quantitative approach establishes an analytical link between risk and actions that reduces that risk. Higher risk means less reliability and vice versa [5,6].
Replacing low-oil circuit breakers is not an easy task. First of all, the investment of replacing the circuit breaker in one substation is a big capital endeavor. Next, the time to replace one circuit breaker can take up to 8 h, which in some situations can be a problem if customers cannot be supplied with electricity from another outlet. Replacing circuit breakers in some situations may require replacing or reconstructing other equipment in the cell, such as busbars and circuit breaker stands, then bringing power to the circuit breaker (if the motor power supply differs), which increases investment costs and time [5,6].
Replacing old circuit breakers would reduce the need for frequent maintenance and thus reduce labor engagement, and in addition, the reliability of the system would be increased because even overhauling an old circuit breaker increases its reliability only in a short period because the remaining parts can wear out, fail, and become the cause of a new malfunction, which was previously unpredictable.
2.2. Risk Assessment Using Influence Diagram
Bayesian networks (BNs) and influence diagrams (IDs), as probabilistic methods for uncertain reasoning, are vastly used in complex engineering systems to aid making the best decisions possible in uncertain environments/industries—nuclear, chemical, environmental, maritime, etc. A clear graphical representation sets these methods apart from the others because they show in a very clear and precise way complex causal relationships using simple structures, whereas the main disadvantage is that not every belief can be represented as an exact number or single probability measure. Decision makers are also allowed to represent their imprecise beliefs or knowledge through probability sets, called credal sets [36,37,38,39].
A credal network based on credal sets actually represents a graphical probabilistic method by which a belief is displayed using sets of interval probabilities. The use of sets of interval probabilities enables a clearer assessment of epistemic uncertainty, while with the increase of available information, the uncertainty decreases.
The next subsections examine in a more detailed way both BNs and IDs in an environment of uncertainty.
2.3. Definition and Properties of Bayesian Networks
The parents of , according to an acyclic directed graph G, are the joint variable , for , where represents set of variables that are in one-to-one correspondence with the nodes of G. Set of variables takes its values on the finite set , where in , for . Cartesian set product is marked with symbol. As described in [40], any variable is conditionally independent of its non-descendant non-parents given its parents. This means the graph G represents stochastic independence relations if the Markov condition is fulfilled.
The specification of a conditional probability mass function for each and induces through the graph for each the factorization [41]:
where the values of and are those consistent with . Equation (1) and expression that represent specification of the conditional probability mass functions form BN.
The local models of , , actually represent the mass functions for written in the form . From Equation (1), using the joint probability mass function we establish inference in BN. For example, by summing out other variables from the joint probability, mass function marginal are determined, as described in Equation (2) [41]:
where , whereas instead of , is used. Additionally, the value from Equation (2) can be calculated in another way using the procedure linear combination of the local probabilities associated with an arbitrary :
In this case, from the BN specification the probabilities are determined, from Equation (2) the unconditional probabilities are obtained, and for the conditional ones , assuming the condition is valid. From Equation (3), assuming that follows:
For , the previous equation becomes:
From the previous expressions it can be noticed that, for example, in the case of determining the marginal, local models do not affect the probability, which means that the local models of have no effect on values of and , where and . Determining is not affected by the values of , with the condition where for all the variables in , child is [41].
In case we want to determine a conditional probability, local model can also be irrelevant for a certain part of the calculation; that is, the local models of can be excluded when determining .
ID, as extensions of BN, were proposed in [42] as a tool to simplify modelling and analysis of decision trees. They are a graphical aid to decision-making under uncertainty, representing the causal relationships of possible causes and effects. Unlike a decision tree, an ID shows dependencies among variables more clearly. Thanks to clear links between variables, IDs allow for maximum reduction of a decision maker’s confusion during decision-making [43]. Both the BN and the ID are probabilistic networks. The difference is that the BN is used for belief update, while the ID is used for reasoning about decision-making under uncertainty [44].
In addition to the traditional BN, IDs have, besides an external influence (an exogenous variable—a variable whose values are not affected by the decision being made), a decision node; that is, a decision made by the decision maker.
An intermediate variable depicts an endogenous variable whose values are computed as functions of decision, exogenous, and other endogenous variables. A value node (objective variable) is a quantitative criterion that is the subject of optimization. A chance node represents a random variable whose value is dictated by some probability distribution. An arrow shows the influence between variables.
The methods for evaluating and solving IDs are based on probabilities, and efficient algorithms have been developed to analyze them [45,46,47,48,49]. Like in BNs, the input and output values of a node are based on the Bayesian theorem. The use of probability tables with many elements is, however, very difficult because of the combinatorial explosion arising from the requirement that the solution must be extracted by the cross product of all probability tables.
Because it is very difficult to determine the precise probabilities of the remaining lifetime of circuit breakers and the risk they pose to the entire power system, in this paper we introduce a new concept of interval probability in order to find the best strategy for a given circuit breaker set. Namely, based on the collected and available data on circuit breakers, a group of experts evaluated the situation with interval probabilities instead of crisp probabilities.
As described in [50,51], the product of event probability p(E) and its consequence Cons(E) for the considered event E determines the risk associated with that event.
In the case where empirical scaling parameters x, y, and w are observed, the previous equation becomes [52]:
In general, for the calculated probabilities described by Equations (1)–(7), the risk can be calculated as follows:
The risk can also be presented in a table, such as the example given in the Figure 1.
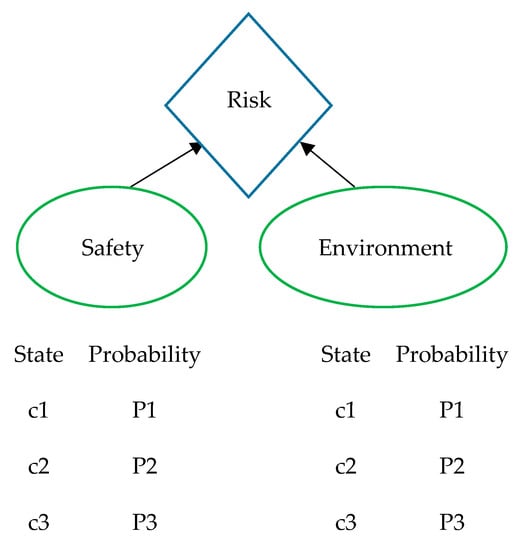
Figure 1.
Risk assessment based on two criteria.
Based on the level of these two criteria, the risk can take values in the range from 1 (no risk) to 10 (highest risk). Risk assessment using crisp probabilities for the example given in Figure 1 is shown in Table 1

Table 1.
Risk assessment using crisp probabilities for the example given in Figure 1.
A complete model of the risk assessment of the circuit breaker maintenance strategy considered in this paper is represented in Figure 2. The graphical symbols in Figure 2 indicate the following: an orange ellipse shows an external influence, i.e., an exogenous variable, the value of which is not conditioned by previous decisions; red and green ellipses denote chance nodes described by random variables defined by discrete probability distributions. The decision is represented by a purple rectangle. Endogenous variables determined as functions of decision and other variables are represented by intermediate variables. The blue diamond represents the subject of optimization and is classified as a quantitative criterion. Influence between variables is described by an arrow.
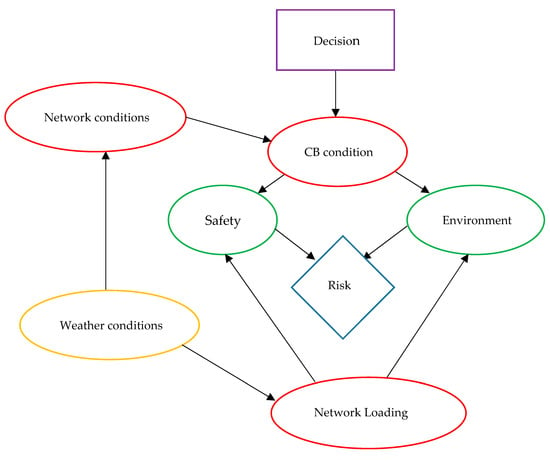
Figure 2.
Circuit breaker risk assessment model.
The example shown in Figure 2 was created to assess the risk of a substation with low-oil circuit breakers. The three alternatives that are considered and used for decision-making are do nothing, perform minor interventions, or perform major interventions. Safety and environment are two risk assessment criteria based on which alternatives are assessed. Both criteria are aggregated in the one influence diagram value node, after being assessed according to their risk.
The breaker is in operating conditions (OK), failure to close (FC), and failure to open (FO)—the three modes of operation of the switches that are important in the assessment. Bad weather conditions cause the circuit breakers to be exposed to more difficult operating conditions because the number of failures increases, which leads to a deterioration of the network condition and an increase in the network load. This is further expressed in the case when the distribution network is mostly overhead and when there are frequent power outages. The type of distribution network significantly affects the state of the attachment. The condition of the circuit breaker affects the environment in such a way that oil leaks can have a detrimental effect on the environment. In terms of safety, the condition of the circuit breaker can cause a dangerous effect of electric current on a person, and it can also lead to mechanical injuries, the impact of electromagnetic radiation, and excessive noise.
Due to the uncertainty about the weather forecast—and consequently network technical condition, network maximal demand power (loading) and possible failure modes—probabilities elicited by experts are also uncertain.
According to the diagram presented in Figure 2, the total risk by circuit breakers is calculated as a combination of two individual risks, which are:
- Safety risk, primarily associated to the health and safety of the operators of the substation;
- Environmental risk in terms of spillage of transformer oil into soil or watercourses and ignition of transformer oil and its evaporation.
The components shown in Figure 2 that affect risk and decision-making are described below.
CB condition: the assessment of the condition of this component is based on data from several categories, such as the age of the circuit breaker, i.e., how long the circuit breaker has been in operation, ambient and operational conditions, regularity of maintenance, and test results.
The following scale is used to describe the CB condition:
- grade 1: Poor—switch long in operation, under poor ambient and operating conditions, irregular maintenance and testing, poor test results;
- grade 2: Medium poor—switch long in operation, under poor ambient and operational conditions, some test results are poor;
- grade 3: Medium—switch long in operation, under poor ambient and operational conditions, but regularly maintained and tested, satisfactory results;
- grade 4: Very good—newer generation circuit breakers, works under good operating conditions, satisfactory results;
- grade 5: Excellent—newer circuit breakers, short in operation, satisfactory test results, regular maintenance and testing.
These ratings for CB condition are actually formed based on the collected data on aging, CB type, and maintenance.
Ageing: A rating in the range of 1 to 5 can be used to estimate the age of the circuit breaker, with lower values indicating better equipment condition (“less is more”). The grade is awarded depending on the range to which the circuit breaker belongs according to its age (<10 years, 10–20 years, 21–30 years, 31–40 years, >40 years).
CB type: The three most commonly used types of circuit breakers in substations are observed: low-oil, vacuum, and SF6 circuit breakers. Depending on the applied technology, each circuit breaker is characterized by a certain intensity of failure, which can be called characteristic and which is a feature of the technology itself. However, the actual intensity of failures depends on many additional factors, of which the two most important are the conditions (operational and ambient) in which the circuit breaker operates and the condition of the circuit breaker itself. Operating conditions refer to load level, protection condition, network condition supplied by this substation. Ambient conditions refer primarily to the temperature in the station itself, which significantly affects the condition of the equipment. As each of these effects is very difficult to quantify, the principle of a correction factor is often adopted, which determines a more realistic value of the failure rate.
Maintenance: Regularity and quality of maintenance are important factors that affect the condition of the equipment itself. The quality of maintenance involves several factors:
- Periodicity and scope of testing;
- Training of maintenance personnel;
- Availability of spare parts;
- Circuit breaker condition monitoring.
The following scale with five rating levels can be used to assess the level of maintenance:
- grade 1—Maintenance is performed at regular intervals, all spare parts are easily accessible, there is online monitoring of the condition of the circuit breaker. The staff is well trained. Existing control parameters almost certainly detect a fault;
- grade 2—Maintenance is performed at regular intervals, staff is well trained. High probability that the monitored parameters will signal a fault;
- grade 3—Moderate probability that the monitored parameters will signal a failure;
- grade 4—Low probability that the monitored parameters will signal a failure;
- grade 5—No existing monitored parameters can detect a fault. Maintenance is not performed at regular intervals, spare parts are not easily accessible, and there is no online monitoring of the condition of the circuit breaker. The staff is not well trained.
Network conditions and Network loading: The type and load of the network also significantly affect the condition of the circuit breaker. A scale with five levels of assessment can be used for the assessment, where after the assessment of the conditions the value of the correction factor is determined, which is used for further calculations. The description of the grades is as follows:
- grade 1—Extremely low load. The distribution network is mostly underground, with short cables and the possibility of reservations;
- grade 2—Medium load, average percentage of overhead distribution network, rare power outages;
- grade 3—Medium load, higher percentage of overhead distribution network, frequent power outages;
- grade 4—High load, especially in winter conditions. High percentage of overhead distribution network representation, frequent power outages;
- grade 5—Load extremely high. The distribution network is mostly overhead, with long lines and without the possibility of reservations. The fault occurs without warning.
Weather conditions: Network conditions and loading directly depend on weather conditions. Bad weather conditions correlate with an increased number of failures, which means that circuit breakers will be exposed to more difficult operating conditions because the condition of the network will deteriorate, and the network load will increase. Good weather conditions improve the condition of the network, reduce the load on the network, and provide stable operating conditions for circuit breakers.
Safety and environment criteria evaluations are also expressed in numerical grades (from 1 to 5).
Safety:
- grade 1—Very dangerous effect of electric current on humans; toxic and carcinogenic effects of polychlorinated biphenyls (pyralene transformer oil); the danger of mechanical injuries during work on substations is very high if the exposure to danger is very frequent (exposure to danger during one shift of 61–80% of working time); very large impact of electromagnetic radiation on humans; very great influence of noise on the organs of hearing;
- grade 2—Dangerous effects of electric current on humans; the risk of mechanical injuries during work on substations is high if the exposure to danger is frequent (exposure to danger during one shift of 41–60% of working time); great influence of electromagnetic radiation on humans; great influence of noise on the organs of hearing;
- grade 3—Medium dangerous effect of electric current on humans; the risk of mechanical injuries during work on substations is medium if the exposure to danger is occasional (exposure to danger during one shift of 21–40% of working time); average effect of electromagnetic radiation on humans; moderate impact of noise on the senses of hearing;
- grade 4—Low dangerous effect of electric current on humans; the danger of mechanical injuries during work on substations is small if the exposure to danger is very rare (exposure to danger during one shift is less than 20% of working time); small impact of electromagnetic radiation on humans; small noise effect on the senses of hearing;
- grade 5—Negligible effect of electric current on humans; the danger of mechanical injuries during work on substations is negligible if the exposure to danger is very rare (exposure to danger during one shift is less than 20% of working time); negligible impact of electromagnetic radiation on humans; negligible effect of noise on the senses of hearing;
Environment:
- grade 1—The substation is located in a city center or in a densely populated place, the proximity of watercourses or water supply facilities is less than 10 m, or there are immovable cultural heritage properties, no communal infrastructure, or the road to the substation is not paved;
- grade 2—The substation is located on the outskirts of a city (near the substation are mostly small households), distance to watercourses or water supply facilities is 50 m, there are immovable cultural heritage properties, communal infrastructure is partially built, the substation is reached by unpaved road that separates from the local paved road;
- grade 3—The substation is located on the outskirts of a city, the populated area is at a distance of 50 m, no endangered plant and animal species, no immovable cultural heritage properties, the proximity to watercourses or water sources is 200 m, an asphalt road that separates from the regional or main road leads to the substation, there is a built communal infrastructure;
- grade 4—The substation is outside the settlement, there are individual residential buildings at a distance of 150 m, there are no watercourses or water supply facilities at a distance of 300 m, no endangered plant and animal species, no immovable cultural heritage properties, there is communal infrastructure, an asphalt road (regional or highway) leads to the substation;
- grade 5—The substation is outside the settlement, the nearest residential buildings are at a distance of 300 m, there are no watercourses or water supply facilities at a distance of 500 m, no endangered plant and animal species, no immovable cultural heritage properties, there is communal infrastructure, an asphalt road (regional or highway) leads to the substation.
3. Extended Risk Model Based on Interval Probabilities
3.1. Definition and Properties of Interval Probability
The intervals represent the interval probability if and only if for any there exists , so the following applies:
where X—random variable and finite set [53,54].
In order for L to satisfy the condition described in Equation (9), it must satisfy the following two expressions [53,55,56,57]:
where .
The elicited interval probabilities may or may not satisfy the two previous equations. However, it is not difficult to check whether they satisfy the following inequalities:
Condition (12) is a necessary but insufficient condition of (10) and (11). The intervals marked with represent semi-interval probabilities if the condition (12) is fulfilled. Solving the linear programming problem as described with the following function [53]:
enables the selection of interval probabilities from semi-interval probabilities .
3.2. Determining Risk with Interval Probabilities
Rough set theory is one of the important tools with which it is possible, without additional assumptions or some adjustments, to manage uncertain and subjective information [58,59,60]. To manage uncertain information, determining the lower and upper approximations is a basic task. The lower and upper approximations of X with respect to I, marked with and , are defined with the following expressions:
where , U is the universe consisting of a non-empty finite set of objects and I is the indiscernibility relation. Ordered pair (U, I) represents the approximation space.
For the lower and upper approximations defined in this way, the boundary region equals:
The degree of vagueness is determined by the range of boundary region. Depending on whether the boundary region of X is empty or not, X will be a crisp set or a rough set.
Extended lower and upper approximation and the rough boundary interval described with the previous expressions enables expert evaluation and manipulations in conditions of uncertainty [61].
Definition 1.
Letbe the set containing n classes of human opinions. The classes are ordered in the manner of, and Y is the arbitrary object of U,and.
Then, the lower and the upper approximations and the boundary region of Xi can be expressed as
The lower and the upper limit, marked with and , where rough number (RN) can be a replacement for the class , equals:
The number of objects in these approximations are marked with NL and NU.
In line with the definition of these limits, expert opinion can be expressed by a rough interval. The degree of preciseness is described with the interval of boundary region (IBR). A rough number and an interval of boundary region are equal to:
For the two rough numbers RN1 and RN2, the following applies (λ is a nonzero constant) [62]
In interval mathematics, all the possible relations of different interval numbers are defined, which significantly helps in making decisions based on expert assessment in conditions of uncertainty [63,64,65].
Definition 2.
Assuming thatandare two interval numbers. Meanwhile, the interval numbersandare assumed as the random variables with uniform distributions in their intervals. The probability for the random variablelarger or smaller than the random variableis expressed asor.
The relationship between and is described with the following equation.
From the previous Equation (27), we can determine the relationship between and with the degree , where . For the case where means that is larger than , and implies that is smaller than , while represents that and are equal.
In Figure 3, a risk assessment framework based on expert assessment using interval probability is presented.
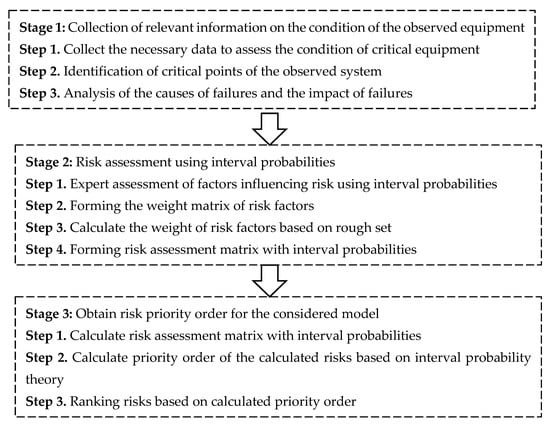
Figure 3.
The framework of the proposed model risk assessment using interval probabilities.
The proposed method consists of three main steps. First, data of interest are collected, followed by an assessment of the critical points of the observed system and an analysis of the causes and effects of failures. Then, an expert assessment of the factors influencing the risk by interval probabilities is performed, as well as the formation and calculation of appropriate matrices based on the experts’ assessment. Finally, the total risk is calculated and the obtained risks are ranked based on interval probability theory; that is, the minimum risk for the observed case is determined.
4. Case Study
In this case study, two risk calculations were performed based on Figure 4. In the first calculation, crisp probabilities were used for the risk calculation, while in the second calculation the interval probabilities were used.
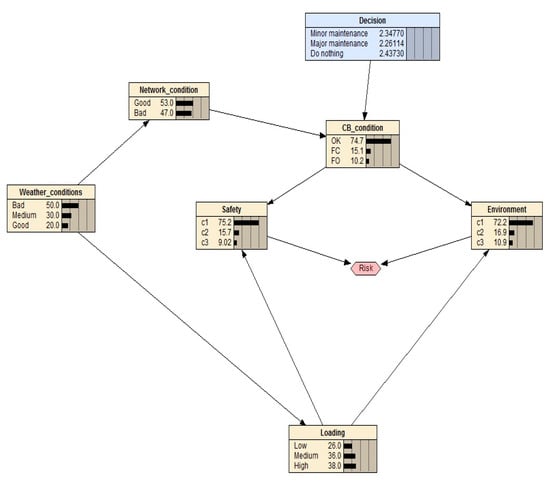
Figure 4.
Influence diagram with crisp probabilities.
The decision about the possible replacement of the circuit breaker depends on the calculated risk for keeping the existing breakers in service. The risk consists of safety and environmental risk, characterized with three possible states (denoted with c1, c2, and c3 in Figure 4). Both the safety and environmental impact of the equipment depend on the breaker condition, influenced by the maintenance level (decision node), weather, network condition, and network loading (chance nodes).
As can be seen in Figure 4, regular operating condition (OK), failure to close (FC), and failure to open (FO) represent the three possible states of the considered circuit breakers. The final decision on whether minor maintenance, major maintenance, or do nothing will be applied is made based on two criteria, safety and environment. Based on the level of these two criteria, the risk can take values in the range from 1 (no risk) to 10 (highest risk).
In this paper, for the problem defined in Figure 4, a group of 5 experts was formed who met the following conditions—they were highly qualified for the considered domain, had sufficient experience in assessing the state of a system similar to the observed system, were familiar with probability thinking, and were able to model the system in relation to the available data. We selected 5 experts due to the complexity of the system we were observing and in order to achieve greater overall accuracy during evaluation.
Based on the experts’ opinion and based on previously collected data, the probabilities of the occurrence of each of the conditions were determined: weather conditions, loading and network condition. Additionally, experts determined the conditional probabilities on the basis of which values of the condition in the nodes CB condition, safety, and environment were calculated. The probability values correspond to the mean probability values obtained from the experts. For the probability values shown in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, using Equations (1)–(5), we obtained the results shown in Figure 4.

Table 2.
Probability of weather states.

Table 3.
Conditional probabilities of network conditions.

Table 4.
Conditional probabilities of network loading levels.

Table 5.
Conditional probabilities of CB condition.

Table 6.
Conditional probabilities of consequences.

Table 7.
Safety and Environment criteria grades.
Safety and environment criteria evaluations are expressed in numerical grades (from 1 to 10) and represented in Table 7.
Based on Table 7 and Equation (8), the final decision to be taken based on the example given in Figure 4 is shown in Table 8. As can be seen from Table 8, for the crisp values of the variables shown in Figure 4 “Major maintenance” is taken as the final strategy because of the lowest value of risk.

Table 8.
Decision values for crisp probability.
In the second case, we worked with interval probabilities. Instead of crisp probability values for the assessment of possible states of the chance nodes, the allowable interval width by which experts assessed the condition was determined by first examining how the interval width affected the final estimate.
The crisp numbers , used to determine risk in case 1, could be transformed into interval numbers form based on Equations (17)–(22):
In Equation (28), the lower and upper limits of the interval number are marked with and , whereas represent kth expert for the sth failure mode with respect to the jth risk factor.
In our case, the interval number matrix is:
The average interval number , , based on Equations (24)–(26) is:
The lower and upper limits of the average interval number are marked with and .
In order to enable the experts to have as wide an interval as possible during the evaluation, an analysis was first made of how much the width of the interval influenced the decision for the example given in Figure 4.
The analysis was done so that, in relation to the values of crisp probabilities shown in Figure 4, an interval probability was formed in accordance with Equations (28)–(32), where the values of crisp probabilities represent the center of the newly formed interval.
The analysis was performed for an interval width of 1% to 10%. The obtained results are shown in Table 9.

Table 9.
Decision values influenced by interval width.
Based on the obtained results, it can be concluded that experts can be allowed to form an interval width from 5% to 10%. This means that experts gave interval probabilities instead of crisp probabilities when evaluating, with the restriction that crisp probabilities were within that interval or represented the lower or upper limit of the interval.
The expert opinion about the circuit breaker condition was obtained from the measurement data covering 42 power stations 35/10 kV and 427 circuit breakers, mounted on 10 kV and 35 kV feeders. Measurement of static resistance of contacts by measuring voltage drop was collected over the past 10 years, with voltage drop measured during every second year.
Other data related to circuit breakers collected for the purposes of analysis were: circuit breaker voltage level, type of terminal, year of production, number of faults, number of short circuit current disconnections, number of consumers at the terminal, and average energy consumption.
The average lifespan of a circuit breaker depends on many factors, such as the intensity of operation, operating conditions, and level of maintenance. The main cause of the deterioration of the circuit breaker is its age, then the number of operations performed at normal load and failure, and operating conditions, such as temperature and environmental pollution.
The resistance of the contacts is an indicator of the general condition of the circuit breaker. It does not depend on environmental conditions until foreign materials penetrate the contact surface. For this reason, any increase in resistance is an indication of the existence of foreign material on the contact surface. This can lead to a local temperature increase and thus to a worsening of the circuit breaker condition.
Measuring voltage drops is equivalent to measuring resistance. Due to the ease of measurement, voltage drop is more often used as a criterion in practice. As for the allowed values of voltage drops, they are more influenced by the height of the rated current of the circuit breaker than the values of its rated voltage.
The permissible values of voltage drops prescribed by the manufacturer are given in the manufacturer’s instructions. Permitted overdraft value is + 25%. In the case of a circuit breaker that is already in operation, the permissible voltage drop is 20% higher in than a circuit breaker that is first operated.
The circuit breakers analyzed in this paper were low-oil medium voltage circuit breakers, manufactured by Minel and tested according to the manufacturer’s instructions. The test was performed every other year, as defined [66]. This type of maintenance is called time-based maintenance, which is performed according to a predefined schedule at precisely defined time intervals.
In the first step, the state of each circuit breaker was determined depending on whether its voltage drop exceeded the allowable value or not. The year in which they reached this state was determined for the failed circuit breakers. These data were further divided into the following categories:
- circuit breakers mounted on 35 kV terminals
- circuit breakers mounted on 10 kV terminals
- circuit breakers mounted on overhead terminals
- circuit breakers mounted on cable terminals
- all circuit breakers.
From the manufacturer’s instructions, the allowable voltage drop depends on the rated current and rated voltage of the circuit breaker, and the manufacturer allows these values to be exceeded by 25%. For this reason, the circuit breakers were also analyzed through the following two criteria: the maximum value of the voltage drop was as in the manufacturer’s table and the maximum value of the voltage drop was 25% higher than the value from the table.
In this way, the influence of both criteria on circuit breaker failure was considered. The manufacturer’s instructions [66] state that a circuit breaker must be completely repaired after 10–12 years of operation, or 5000 manipulations, or 6 interrupted short-circuit currents, whichever occurs first. Based on these data, the experts assigned interval probabilities first of 5% width, then 6%, and continued up to 10%.
Additionally, values for nodes, such as weather conditions, network condition, loading, safety, and environment, experts assigned on the basis of collected and available data.
It is important to note that experts were not given predefined values of the center of the interval for any node, but they made their assessments of the interval values solely on the basis of the available data and their expertise. As for the risk, the rule used was 1—the lowest risk, 10—the highest risk (as shown in Table 10).

Table 10.
Risk assessment using interval probabilities for the example given in Figure 4.
Using the previously described methodology for the case of an ID with interval probabilities, based on expert assessments, in combination with Monte Carlo simulation respecting the following condition:
Table 11 includes the obtained results.

Table 11.
Risk values obtained by experts’ assessment for different interval width.
In this paper, it is proposed that the final decision on which action will be implemented is made by forming an interval based on Equations (30)–(32).
Based on these equations, the final decision on which action will be implemented for each interval range separately is shown in Table 12.

Table 12.
Final risk values for each interval range separately.
Based on the data presented in Table 12, it can be concluded that the proposed model of determining risk using interval probabilities greatly facilitates the work of experts and gives a very realistic picture of the actions to be taken.
Using Equation (27), we performed a comparison of the interval of different potential decisions to obtain the comparison probability so that we could rank the risk priorities of the considered decisions. The obtained results are given in Table 13. Taking Minor Maintenance and Do Nothing for 5% interval width as an example, the interval Minor Maintenance is [1.94, 3.00], while FM6 is [2.05, 3.03] based on Equation (27):

Table 13.
The comparison results for interval decision.
Because , the risk priority of Do Nothing is higher than Minor Maintenance. Similarly, other comparison probabilities are given in Table 13.
Based on the results obtained from the previous table, the following table shows the ranking results of different decisions for each width interval individually.
On the values of the intervals shown in Table 14, it is easy to conclude that the best choice for the observed system is “Major Maintenance” because the risk priority is the highest and it is obtained for this decision for each interval width shown (except for the 9% interval width, where it is second by priority). With this in mind, as well as the result obtained for the crisp values, it can be seen how much better a solution is the decision model applied in this paper. Namely, unlike crisp values, which are very difficult to determine in conditions of uncertainty, allowing experts to assess the state of a system in a wide range of values significantly facilitates proper decision-making. It has been shown that allowing experts to use interval values instead of crisp values, which are very difficult in conditions of uncertainty, can significantly influence the final decision.

Table 14.
The ranking results of different decision.
5. Conclusions
Risk prediction using IDs with interval probabilities is a very popular methodology for determining causal relationships of events in conditions of uncertainty. The knowledge and experience of experts is one of the main links in the formation of the IDs model and the determination of the state of the considered elements for increasing the reliability of power systems. In order to increase the accuracy of the assessment of the state of the considered elements, in this case circuit breakers, in this paper it is proposed to allow experts to use interval probabilities instead of crisp probabilities. An analysis was performed that shows how the width of the interval affects the final decision, and accordingly, the experts were allowed to base their estimates on interval probabilities. The obtained results for the case presented in the paper are also in the form of interval probabilities. Based on the obtained results, it can be concluded that the proposed model of risk prediction using IDs with interval probabilities is an excellent solution for deciding which action should be taken to increase the reliability of circuit breakers. The proposed model of determining risk using interval probabilities greatly facilitates the work of experts and gives a very realistic picture of the actions to be taken. Unlike crisp values, which are very difficult to determine in conditions of uncertainty, allowing experts to assess the state of the system in a wide range of values significantly facilitates proper decision-making.
Although the proposed method shows significant advantages when making decisions in conditions of uncertainty, it can also have certain disadvantages. First, an increase in the number of observed alternatives that affect decision-making can lead to an increase in the required computer power and the required real time to perform computational operations, which can increase the costs and time of decision-making.
The methodology should be tested on high dimension models with a great number of nodes, and this will be the focus of our future research.
Author Contributions
Conceptualization, J.D.V. and A.J.; methodology, J.D.V.; validation, J.D.V. and A.J.; formal analysis, J.D.V.; investigation, J.D.V.; data curation, J.D.V.; writing—original draft preparation, J.D.V.; writing—review and editing, A.J.; supervision, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research receive no extra funding.
Institutional Review Board Statement
Not applicable.
Acknowledgments
This work was supported by the Serbian Ministry of Education, Science and Technological Development through the Mathematical Institute of the Serbian Academy of Sciences and Arts.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gao, D.W.; Wang, Q.; Zhang, F.; Yang, X.; Huang, Z.; Ma, S.; Li, Q.; Gong, X.; Wang, F.-Y. Application of AI techniques in Monitoring and Operation of Power Systems. Front. Energy 2018, 13, 71–85. [Google Scholar] [CrossRef]
- Peng, C.; Lei, S.; Hou, Y.; Wu, F. Uncertainty Management in Power System Operation. CSEE J. Power Energy Syst. 2015, 1, 28–35. [Google Scholar] [CrossRef]
- Jordehi, A.R. How to Deal with Uncertainties in Electric Power Systems? A Review. Renew. Sustain. Energy Rev. 2018, 96, 145–155. [Google Scholar] [CrossRef]
- Reinders, J.; Morren, J.; Slootweg, J.G. Uncertainty in Power System Planning and Operation: An Integrated Approach. In Proceedings of the IEEE Young Researchers Symposium in Electrical Power Engineering (YRS 2018), Bruxelles, Belgium, 24–25 May 2018. [Google Scholar]
- Vachtsevanos, G.; Lewis, F.; Roemer, M.; Hess, A.; Wu, B. Intelligent Fault Diagnosis and Prognosis for Engineering Systems; Wiley: Hoboken, NJ, USA, 2006; Volume 456. [Google Scholar]
- Daigle, M.J.; Goebel, K. Model-Based Prognostics with Concurrent Damage Progression Processes. IEEE Trans. Syst. Man. Cybern. Syst. 2013, 43, 535–546. [Google Scholar] [CrossRef]
- Strachan, S.M.; McArthur, S.D.J.; Stephen, B.; McDonald, J.R.; Campbell, A. Providing Decision Support for the Condition-Based Maintenance of Circuit Breakers Through Data Mining of Trip Coil Current Signatures. IEEE Trans. Power Deliv. 2007, 22, 178–186. [Google Scholar] [CrossRef]
- Lin, P.; Gu, J.; Yang, M. Intelligent Maintenance Model for Condition Assessment of Circuit Breakers using Fuzzy Set Theory and Evidential Reasoning. IET Gener. Trans. Distrib. 2014, 8, 1244–1253. [Google Scholar] [CrossRef]
- Razi-Kazemi, A.A.; Vakilian, M.; Niayesh, K.; Lehtonen, M. Data Mining of Online Diagnosed Waveforms for Probabilistic Condition Assessment of SF $_ {6} $ Circuit Breakers. IEEE Trans. Power Deliv. 2015, 30, 1354–1362. [Google Scholar] [CrossRef]
- Westerlund, P.; Hilber, P.; Lindquist, T.; Kraftnat, S. A Review of Methods for Condition Monitoring, Surveys and Statistical Analyses of Disconnectors and Circuit Breakers. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014; pp. 1–6. [Google Scholar]
- Davis, M.H. Markov Models & Optimization; CRC Press: Florida, FL, USA, 1993; Volume 49. [Google Scholar]
- Lorton, A.; Fouladirad, M.; Grall, A. A Methodology for Probabilistic Model-Based Prognosis. Eur. J. Oper. Res. 2013, 225, 443–454. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Dieulle, L.; Grall, A. Remaining Useful Lifetime Prognosis of Controlled Systems: A Case of Stochastically Deteri-orating Actuator. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Chiquet, J.; Limnios, N. A Method to Compute the Transition Function of a Piecewise Deterministic Markov Process with Ap-plication to Reliability. Stat. Probab. Lett. 2008, 78, 1397–1403. [Google Scholar] [CrossRef]
- Chiacchio, F.; D’Urso, D.; Compagno, L.; Pennisi, M.; Pappalardo, F.; Manno, G. SHyFTA, a Stochastic Hybrid Fault Tree Automaton for the Modelling and Simulation of Dynamic Reliability Problems. Expert Syst. Appl. 2016, 47, 42–57. [Google Scholar] [CrossRef]
- Codetta-Raiteri, D.; Portinale, L. Approaching Dynamic Reliability with Predictive and Diagnostic Purposes by Exploiting Dy-namic Bayesian Networks. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 488–503. [Google Scholar]
- Gaudel, Q.; Chanthery, E.; Ribot, P. Hybrid Particle Petri Nets for Systems Health Monitoring under Uncertainty. Int. J. Progn. Health Manag. 2015, 6. [Google Scholar] [CrossRef]
- Daigle, M.; Roychoudhury, I.; Bregon, A. Model-Based Prognostics of Hybrid Systems. Annu. Conf. Progn. Health Manag. Soc. 2015, 18–24. [Google Scholar] [CrossRef]
- Kushwaha, D.K.; Panchal, D.; Sachdeva, A. Risk Analysis of Cutting System under Intuitionistic Fuzzy Environment. Rep. Mech. Eng. 2020, 1, 162–173. [Google Scholar] [CrossRef]
- Bakır, M.; Atalık, Ö. Application of Fuzzy AHP and Fuzzy Marcos Approach for the Evaluation of E-Service Quality in the Airline Industry. Decis. Mak. Appl. Manag. Eng. 2021, 4, 127–152. [Google Scholar] [CrossRef]
- Pamucar, D.; Ecer, F. Prioritizing the Weights of the Evaluation Criteria under Fuzziness: The Fuzzy Full Consistency Method-Fucom-F. Facta Univ. Ser. Mech. Eng. 2020, 18, 419–437. [Google Scholar] [CrossRef]
- Petrović, G.; Mihajlović, J.; Ćojbašić, Žarko; Madić, M.; Marinković, D. Comparison of Three Fuzzy Mcdm Methods for Solving the Supplier Selection Problem. Facta Univ. Ser. Mech. Eng. 2019, 17, 455–469. [Google Scholar] [CrossRef]
- Faes, M.; Moens, D. Recent Trends in the Modeling and Quantification of Non-probabilistic Uncertainty. Arch. Comput. Methods Eng. 2020, 27, 633–671. [Google Scholar] [CrossRef]
- Pamucar, D. Normalized Weighted Geometric Dombi Bonferoni Mean Operator with Interval Grey Numbers: Application in Multicriteria Decision Making. Rep. Mech. Eng. 2020, 1, 44–52. [Google Scholar] [CrossRef]
- Jiang, C.; Zheng, J.; Han, X. Probability-Interval Hybrid Uncertainty Analysis for Structures with both Aleatory and Epistemic Uncertainties: A Review. Struct. Multidiscip. Optim. 2017, 57, 2485–2502. [Google Scholar] [CrossRef]
- Faes, M.G.R.; Daub, M.; Marelli, S.; Patelli, E.; Beer, M. Engineering Analysis with Probability Boxes: A Review on Computational Methods; ETH Zurich: Zürich, Switzerland, 2021. [Google Scholar]
- Chen, N.; Yu, D.; Xia, B.; Beer, M. Uncertainty Analysis of a Structural–Acoustic Problem using Imprecise Probabilities based on P-Box Representations. Mech. Syst. Signal Process. 2016, 80, 45–57. [Google Scholar] [CrossRef]
- Crespo, L.G.; Kenny, S.P.; Giesy, D.P. Reliability Analysis of Polynomial Systems Subject to P-Box Uncertainties. Mech. Syst. Signal Process. 2013, 37, 121–136. [Google Scholar] [CrossRef]
- Montgomery, V.J.; Coolen, F.P.A.; Hart, A.D.M. Bayesian Probability Boxes in Risk Assessment. J. Stat. Theory Pr. 2009, 3, 69–83. [Google Scholar] [CrossRef]
- Dannert, M.M.; Fau, A.; Fleury, R.M.; Broggi, M.; Nackenhorst, U.; Beer, M. A Probability-Box Approach on Uncertain Correlation Lengths by Stochastic Finite Element Method. PAMM 2018, 18, e201800114. [Google Scholar] [CrossRef]
- Faes, M.; Moens, D. Imprecise Random Field Analysis with Parametrized Kernel Functions. Mech. Syst. Signal Process. 2019, 134, 106334. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L. An Active Learning Reliability Method Combining Kriging Constructed with Exploration and Exploitation of Failure Region and Subset Simulation. Reliab. Eng. Syst. Saf. 2019, 188, 90–102. [Google Scholar] [CrossRef]
- Sofi, A.; Muscolino, G.; Giunta, F. Propagation of Uncertain Structural Properties Described by Imprecise Probability Density Functions via Response Surface Method. Probab. Eng. Mech. 2020, 60, 103020. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B. Structural Reliability Analysis for P-Boxes using Multi-Level Meta-Models. Probab. Eng. Mech. 2017, 48, 27–38. [Google Scholar] [CrossRef]
- Troffaes, M.C. Imprecise Monte Carlo Simulation and Iterative Importance Sampling for the Estimation of Lower Previsions. Int. J. Approx. Reason. 2018, 101, 31–48. [Google Scholar] [CrossRef]
- Mancuso, A.; Compare, M.; Salo, A.; Zio, E. Portfolio Optimization of Safety Measures for Reducing Risks in Nuclear Systems. Reliab. Eng. Syst. Saf. 2017, 167, 20–29. [Google Scholar] [CrossRef]
- Yuan, Z.; Khakzad, N.; Khan, F.; Amyotte, P. Risk Analysis of Dust Explosion Scenarios Using Bayesian Networks. Risk Anal. 2014, 35, 278–291. [Google Scholar] [CrossRef] [PubMed]
- Carriger, J.F.; Barron, M.G.; Newman, M.C. Bayesian Networks Improve Causal Environmental Assessments for Evidence-Based Policy. Environ. Sci. Technol. 2016, 50, 13195–13205. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Thai, V.V.; Yuen, K.F.; Loh, H.S.; Zhou, Q. Addressing the Epistemic Uncertainty in Maritime Accidents Modelling using Bayesian Network with Interval Probabilities. Saf. Sci. 2018, 102, 211–225. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Antonucci, A.; de Campos, C.P.; Huber, D.; Zaffalon, M. Approximate Credal Network Updating by Linear Programming with Applications to Decision Making. Int. J. Approx. Reason. 2015, 58, 25–38. [Google Scholar] [CrossRef]
- Howard, R.A. Influence Diagrams, The principles and Applications of Decision Analysis, RA Howard and JE Matheson; Strategic Decisions Group: Menlo Park, CA, USA, 1984; Volume 2. [Google Scholar]
- Shachter, R.D.; Peot, M.A. Decision Making Using Probabilistic Inference Methods. In Computational Morphology—A Computational Geometric Approach to the Analysis of Form; Elsevier BV: Amsterdam, The Netherlands, 1992; pp. 276–283. [Google Scholar]
- Kjaerulff, U.B.; Madsen, A.L. Bayesian Networks and Influence Diagrams. Springer Sci. Bus. Media. 2008, 200, 114. [Google Scholar]
- Shachter, R.D. Evaluating Influence Diagrams. Oper. Res. 1986, 34, 871–882. [Google Scholar] [CrossRef]
- Shenoy, P.P. Valuation-Based Systems for Bayesian Decision Analysis. Oper. Res. 1992, 40, 463–484. [Google Scholar] [CrossRef]
- Jensen, F.; Jensen, F.V.; Dittmer, S.L. From Influence Diagrams to Junction Trees. In Uncertainty Proceedings 1994; Morgan Kaufmann: Burlington, MA, USA, 1994; pp. 367–373. [Google Scholar]
- Yang, C.C.; Cheung, K.M. Fuzzy Bayesian Analysis with Continuous-Valued Evidence. In Proceedings of the 1995 IEEE International Conference on Systems, Man and Cybernetics, Intelligent Systems for the 21st Century, Vancouver, BC, Canada, 22–25 October 1995; Volume 1, pp. 441–446. [Google Scholar]
- Zhang, N.L. Probabilistic Inference in Influence Diagrams. Comput. Intell. 1998, 14, 475–497. [Google Scholar] [CrossRef]
- Janjić, A.; Stanković, M.; Velimirović, L. Multi-Criteria Influence Diagrams—A Tool for the Sequential Group Risk Assessment. In Granular Computing and Decision-Making; Springer: Cham, Switzerland, 2015; pp. 165–193. [Google Scholar]
- Janjic, A.; Stajic, Z.; Radovic, I. A Practical Inference Engine for Risk Assessment of Power Systems based on Hybrid Fuzzy In-fluence Diagrams. Latest Adv. Inf. Sci. Circuits Syst. 2011, 2011, 29–34. [Google Scholar]
- Zhang, Z.; Jiang, Y.; McCalley, J. Condition based Failure Rate Estimation for Power Transformers. In Proceedings of the 35th North American Power Symposium, Rolla, MO, USA, 19–21 October 2003. [Google Scholar]
- Guo, P.; Tanaka, H. Decision Making with Interval Probabilities. Eur. J. Oper. Res. 2010, 203, 444–454. [Google Scholar] [CrossRef]
- Hu, X.; Luo, H.; Fu, C. Probability Elicitation in Influence Diagram Modeling by Using Interval Probability. Int. J. Intell. Sci. 2012, 2, 89–95. [Google Scholar] [CrossRef]
- Tessem, B. Interval Probability Propagation. Int. J. Approx. Reason. 1992, 7, 95–120. [Google Scholar] [CrossRef][Green Version]
- De Campos, L.M.; Huete, J.F.; Moral, S. Uncertainty Management using Probability Intervals. In Advances in Intelligent Computing, Proceedings of the International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Paris, France, 4–8 July 1994; Springer: Berlin/Heidelberg, Germany, 1994; pp. 190–199. [Google Scholar]
- Weichselberger, K. The Theory of Interval-Probability as a Unifying Concept for Uncertainty. Int. J. Approx. Reason. 2000, 24, 149–170. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets. Int. J. Parallel Program. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Qian, Y.; Liang, J.; Pedrycz, W.; Dang, C. Positive Approximation: An Accelerator for Attribute Reduction in Rough Set Theory. Artif. Intell. 2010, 174, 597–618. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.; Miao, D.; Gao, C. Bayesian Rough Set Model: A Further Investigation. Int. J. Approx. Reason. 2012, 53, 541–557. [Google Scholar] [CrossRef]
- Zhai, L.-Y.; Khoo, L.-P.; Zhong, Z.-W. A Rough Set Enhanced Fuzzy Approach to Quality Function Deployment. Int. J. Adv. Manuf. Technol. 2008, 37, 613–624. [Google Scholar] [CrossRef]
- Wagman, D.; Schneider, M.; Shnaider, E. On the Use of Interval Mathematics in Fuzzy Expert Systems. Int. J. Intell. Syst. 1994, 9, 241–259. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Tanaka, H. Multiobjective Programming in Optimization of the Interval Objective Function. Eur. J. Oper. Res. 1990, 48, 219–225. [Google Scholar] [CrossRef]
- Jiang, C.; Han, X.; Liu, G.R.; Liu, P.G. A Nonlinear Interval Number Programming Method for Uncertain Optimization Problems. Eur. J. Op. Res. 2008, 188, 1–13. [Google Scholar] [CrossRef]
- Ouyang, L.; Zhou, D.; Park, C.; Chen, J.; Tu, Y. Ensemble Modelling Technique for a Micro-Drilling Process based on a Two-Stage Bootstrap. Eng. Optim. 2018, 51, 503–519. [Google Scholar] [CrossRef]
- Operating Manual for Medium Voltage Medium Oil Circuit Breakers for Internal Assembly; Minel: Zrenjanin, Serbia, 1984.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).