1. Introduction
There are different opinions in the literature concerning the possible existence and physical interpretation of quantum systems for which the electric charge is not locally conserved, that is, the continuity condition is not valid everywhere.
Wang et al. [
1,
2] point out explicitly that in first-principles calculations of the current in molecular devices, based on single-particle non-equilibrium Green’s function (NEGF) and density-functional theory (DFT), the usual quantum-mechanical current
does not satisfy the continuity condition and must be complemented by a non-local term. The recourse to the NEGF-DFT formalism is necessary in order to take into account the contribution of the inner atomic shells. In principle a full quantum field theory of the system, if it can be formulated in a standard way including all the internal electrons, would yield a conserved
bare current; in practice, such a formulation does not exist for realistic systems [
3], and even if it could be achieved, it cannot be excluded that it needs to be renormalized, giving rise to quantum anomalies (effective breaking of symmetries and local conservation properties of the bare theory, like for the ABJ anomaly in condensed matter [
4,
5]).
An appealing feature of the approach by Wang et al., is that the additional current they propose is exactly the same as that originating from the extended Maxwell equations of Aharonov-Bohm without any consideration of the microscopic/quantum aspects. These equations represent essentially the only possible covariant extension of Maxwell’s theory which is compatible with the established standard phenomenology of classical electromagnetism and QED and is also applicable to currents that are not locally conserved [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17].
In a series of papers, starting in 2018 [
18,
19,
20,
21], Jensen, Garner and collaborators have analysed in depth the concept of density current in quantum transport, applying it to specific molecules and obtaining results compatible with the approach by Wang et al.
Reference [
18] sets the general theoretical framework and notes that besides legitimate physical reasons for the non-conserving character of local currents, there are technical problems related to the choice of the basis in the first-principles calculations. The authors describe simulations of elastic and inelastic local currents in a benzenedithiol junction, showing that the local flux does not always follow molecular bonds. A part of the flux appears instead to go “through space”.
In [
19], the current density is investigated in saturated chains of alkanes, silanes and germanes. The current density is defined in this context as
where
are the matrix elements of the lesser Green function in a standard non-orthogonal basis
. The authors show that an enlargement of the eigenbasis for the
ab initio calculations does not substantially improve the conservation of current density in this case (while it does lead to an improvement in other cases, notably for graphene ribbons [
22]). They then apply the recipe by Wang et al., computing the secondary currents via a Poisson equation.
In [
20,
21], linear carbon wires are considered. Detailed plots of the integrated local current density are given, as compared to the (constant) total current.
For general reviews on molecular devices we refer the reader to References [
23,
24]. It was first proposed in the 1970s that single molecules could be embedded between electrodes, performing the basic functions of digital circuits. By 2000, the concept had been realized for individual components. As further explained in Reference [
25], investigating the relationship between current density and molecular structure is important because it may help in the design and optimization of the devices, showing the occurrence of possible weak points. Moreover, the analysis of current density can give information on the structure/function relation, for example in biological systems.
There are also wave equations in quantum mechanics which do not derive from a microscopic theory but are proposed as effective models with several important applications, in which the current is not locally conserved [
26,
27,
28,
29,
30,
31,
32,
33,
34]. It is important in our opinion to develop a formalism that allows us to compute the electromagnetic field generated by local currents also in those cases.
In this work, after recalling recent progress in the theory and numerical solutions of the extended Maxwell-Aharonov-Bohm equations, we derive in
Section 2 the corresponding wave equations for the electric and magnetic field. These equations allow to compute
and
directly from the physical sources
and
, without any reference to the scalar field
S which in the traditional formulation has the role to restore local conservation through an additional (or “secondary“) charge density proportional to
and an additional current density proportional to
. The general solution for localized sources is written in the form of retarded integrals. In
Section 2.1, we compute for the first time the electric and magnetic dipole radiation in far-field approximation. We point out that in general a longitudinal electric radiation field
can be present; this is one of the main predictions of the extended theory for the case of an oscillating current that is not locally conserved. On the other hand we note that the magnetic field
is simply proportional to the curl
, like in Maxwell’s theory. Therefore in the limit of stationary currents, in the anomalous case in which
is not zero everywhere (presence of charge sinks/sources),
is insensitive to the secondary current
, but can reveal the discontinuities in the current simply because to the “missing links“ of current correspond missing contributions to
in the Biot-Savart formula. Such effects are expected to be small, but detectable with accurate experiments, as briefly discussed in
Section 3. Finally, in
Section 4, we present some numerical solutions for the case of stationary currents, obtained not through the direct wave equations derived in this work, but through the double-retarded integrals written in [
14,
35]. In this way it is possible to display explicitly the contributions of the auxiliary field
S, confirming that such contributions cancel out and the only consequence for
is the missing field effect. In the
Appendix we give the solution of the wave equations in SI units. The presentation with both units is useful to different practitioners either from field theory, or from technological applications. An alternative proof of the independence of the e.m. fields on the scalar source is also given.
Our final message can be summarized as follows—microscopic models for the computation of the current density in molecular devices can and should continue to improve their performance and their precision without worrying about local conservation of , because the extended Maxwell equations allow, in any case, a reliable and efficient computation of the resulting fields. This investigation may lead to interesting discoveries in those cases where the e.m. fields generated by molecular currents are strong enough to play a significant role.
2. General Equations for and and Their Radiative Solution
In this section we write the general wave equations for the electric and magnetic field in extended electrodynamics, in a form in which the auxiliary field S is completely eliminated, and we find their radiative solution.
The extended Maxwell equations in the Aharonov-Bohm theory are [
13,
14]
where CGS units have been employed and
S is an auxiliary field whose source is the extra-current
, namely
The field S is clearly zero in the pure Maxwell theory, which requires strict local conservation of the current.
It is possible to interpret the extended Equations (
2), (
5) and (
6) as involving some additional or “secondary” sources, namely a secondary charge density proportional to
and a secondary current density proportional to
. Including these additional charge and current densities gives total densities which satisfy the continuity equation. Note that the solution of (
6) for a localized extra-source yields
S as a retarded integral:
with
. Therefore,
S is not localized in the region where the physical sources are present. For this reason we have called the secondary charge and current in our previous work “cloud charge” and “cloud current” and we have evaluated them in some specific cases (see also the numerical simulations in
Section 4 of this work).
The secondary current, in particular, coincides with the additional current predicted by the Landauer-Büttiker theory for systems with quantum transport in which local conservation of the current fails [
1,
2].
It is possible, however, to write wave equations for
and
in which the field
S and the secondary charge and current are completely absent. This is in some sense reassuring, because it implies that the physical fields only depend on the localized, physical sources, and that there is no reason to regard the secondary currents as real and to care, for instance, about their dissipation properties. (See also an alternative proof of the independence of the electric and magnetic fields on the scalar source in
Appendix B).
Although the extended Aharonov-Bohm theory has only a limited gauge invariance, it is possible to define potentials
and
with the usual relations to
and
, namely
and to write their wave equations as
where once again the role of the secondary charge and current is evident. The solutions of (
7) and (
8) are
By taking the gradient of (
7) and adding the time derivative of (
8) one obtains an equation for
without
S, while taking the curl of (
8) one obtains an equation for
without
S:
These equations have also been derived in [
16], starting from the extended field Equations (
2), (
5) and (
6) and using some vector calculus identities.
For localized sources the corresponding solutions are
We recall that the current density
can be in general written as the sum of an “irrotational” part, which is the gradient of a scalar field and has zero curl, plus a “solenoidal” part, which is the curl of a vector field and has zero divergence:
According to Equation (
12), the irrotational part has no influence on the magnetic field. It follows in particular that interruptions in the current inevitably cause a “missing field” effect, as discussed in
Section 3 and
Section 4. (Because the secondary current
, which restores current conservation in the extended equations is purely irrotational.) On the other hand, any change in the solenoidal part (like e.g., in Reference [
36]) does not affect current conservation but is reflected in a change in the field.
One can further operate on the expressions (
11) and (
12) considering that
and that
where the surface integral is zero because there is no charge on the external surface of the volume of the source, and the change from
to
in the integral in the second line was done because the function on which it operates is of argument
.
We have in a similar manner
The expressions of the fields thus reduce to
These expressions show that the EM fields are obtained from the potentials evaluated without considering their source terms depending on S.
2.1. Radiative Solution in the Dipole Approximation
For a pure temporal Fourier mode:
,
, the general solution for the corresponding scalar potential, without the source, depending on
S, is of the form
, with
where
. For a distant observation point and wavelength large as compared with the source dimension, the expression is approximated by
with
, and
.
Even if the charge is not conserved locally, it is conserved globally, so that
and thus
where
is the Fourier amplitude of the usual charge dipole.
The solution to the corresponding Fourier amplitude of the vector potential is, with the same approximations,
Using the identity
where in the second line it was used that there is no current leaving or entering the volume of the source, and also allowing for charge non-conservation, so that
we have
where the dipolar moment of the Fourier amplitude of the extra source
I was defined.
The Fourier amplitude of the radiative electric field is thus
Transforming back to the time domain the EM fields are given by
and
The first term of
vanishes when it is multiplied by
and therefore represents the transverse component. The longitudinal component is just
, that is,
To fix the ideas, suppose that the moment of the extra-current is directed along the z-axis. Then the component at a fixed distance r is seen to be maximum on the z-axis and zero in the x-y plane. The opposite happens with the transverse component.
A simple formal example of oscillating extra-current has been introduced in [
37]. Consider a point-like charge
q which oscillates between the positions
and
, without a corresponding current:
The moment in this case has the only non-zero component . If we assign the physical parameters q, a and it is straightforward to compute the longitudinal far field and we have along the z-axis (in SI units: ). The transverse far field is vanishing.
More realistically we can suppose that if a local violation of charge conservation occurs, this will only concern a small fraction of the oscillating charge, while the rest of the charge will have a corresponding current and consequently will not generate any longitudinal radiation field. In that case, the ratio between and will approximately be equal to .
In Reference [
37], we performed a numerical simulation of a source of this kind with
cm,
·
Hz,
(
is the 3D polar coordinate), and we obtained that for a totally anomalous source (i.e.,
, the entire charge oscillates without a current) the longitudinal field is much larger that the transverse field that would be generated by a corresponding regular source at the same position. The field was computed at a relatively small distance (
r varied between
and
), therefore the result cannot be directly compared with Equation (
23), which holds for larger distances; still it confirms the presence of a longitudinal field, because even in the near-field range it is impossible to obtain such big longitudinal components if the source satisfies local conservation.
In conclusion, if oscillating currents exist that violate even partially the continuity condition, a sizable longitudinal electric radiation should be generated which is obviously incompatible with the standard Maxwell equations.
3. Possible Experimental Signatures of a Missing and a Radiative
Let us first consider a possible experimental observation of the missing field effect for stationary currents. As discussed in Reference [
35] and confirmed in
Section 2 and
Section 3 of this work, if in a linear conductor there are regions in which a violation of continuity occurs and a fraction
of the current does not flow as “physical current
” but as “secondary current
”, then the magnetic field generated by the secondary current is zero, as a consequence of Equation (
10). To detect the missing field, we proposed in Reference [
35] to measure at a fixed distance
r the field of a normal conductor carrying a current
i, and then the field of the anomalous conductor carrying the same current. A differential measurement with three wires was devised, in order to minimize errors. The scheme was especially suited for brief current pulses and for the case when the supposed anomalous conductor is a superconductor, which can be driven in/out a normal state by changing its temperature.
Another possible technique, which employs stationary currents and one single wire, is based on the measurement of the ratio at a fixed distance in dependence on i (supposing that a variable external bias allows to change i). This would work if the ratio depends on i, in which case is expected to change, in open violation of the Maxwell equations. In fact, the current patterns and local discontinuities observed in simulations of molecular devices depend in general on the total current.
Possible errors could originate from slight changes in the spatial distribution of the current at different i, if the conductor has a radius that cannot be disregarded compared to the distance r. This radius depends on how “elementary” the conductor is (for example, a single carbon nanowire vs. a bundle of nanowires); in turn, that depends on how much current is needed for the measurement, and thus indirectly on r (because of the size and sensitivity of the detector).
For example, suppose that a single carbon nanowire can carry a current of A and the detector can be placed at a distance of m, very large compared to the radius of the wire. The field would then be of the order of T, that is, accessible to a sensitive SQUID. If the ratio is of the order of and the error on the current is negligible, the SQUID is required to detect a variation in the field of T.
Turning now to electric fields, the possible generation and detection of a longitudinal e.m. radiation has rarely been explored in the past decades [
38,
39,
40,
41,
42,
43]. A recent preliminary experiment and its relation to the extended electromagnetic theory has been described in [
16], including a discussion of error sources. A distinctive feature of longitudinal electric radiation would be its ability to penetrate thin layers of good conductors much easier than a transverse radiation. Even in favourable cases; however, a predominant transverse component would be present, causing interference and noise. If future developments can lead to a clean selective detection of the longitudinal component, the possible technological applications would be manifold.
There is also much to do, of course, concerning the design of efficient antennas. First, one would need to identify materials with local non-conservation that can support a sufficiently large current at high frequency. Then the most appropriate antenna geometry should be studied. For this purpose, the general equations developed in this paper constitute a firm starting point.
4. Numerical Solutions of the Extended Equations with the Potentials
Consider again the equations for the potentials, written in the form
where
is an assigned extra-current. By solving Equations (
25) and (
26) we obtain for
and
expressions which contain “double-retarded integrals” of the extra-current
I. In [
35] we gave some numerical computations of these integrals for a slowly varying source, as recalled below. In this section we consider the stationary case and the resulting expressions are much simpler. For the numerical integration we employ a 6D Monte Carlo, which can be quite time consuming but is straightforward and does not require any analytical approximations.
The idea is to take, instead of a source with a slow temporal variation, a truly stationary source. Then the retarded integrals become simple space integrals. We recall that the typical time scale of the source in the work [
35] was
s, chosen because (1) it corresponds to the proposed experimental conditions, being the characteristic discharge time of the circuit; (2) it allows to disregard certain phenomena occurring only at high frequency, like the intervention of stray capacitance and temporary charge accumulation.
In [
35] we considered a case of local non-conservation involving a point-like sink, where current partially disappears, and a point-like source where the current reappears. More precisely, the sizes of sink and source were given by a regulator
of the order of
cm. The regulator was applied after the first 3D integration (analytical) in
. Then the second numerical integration was made (in
, over the extended secondary cloud current decreasing like
), using the command
NIntegrate of
Mathematica and checking the results by comparison with a Monte Carlo integration in 3D.
The disadvantage of that procedure is the complication at the formal-algebraic level. The expressions obtained after the first integration are quite bulky. At the same time, the assumption of point-like sources is limiting, because when the failure of local conservation occurs in a quantum wavefunction, the regions where are not pointlike but extended, with a shape more similar to that of a couple of disks.
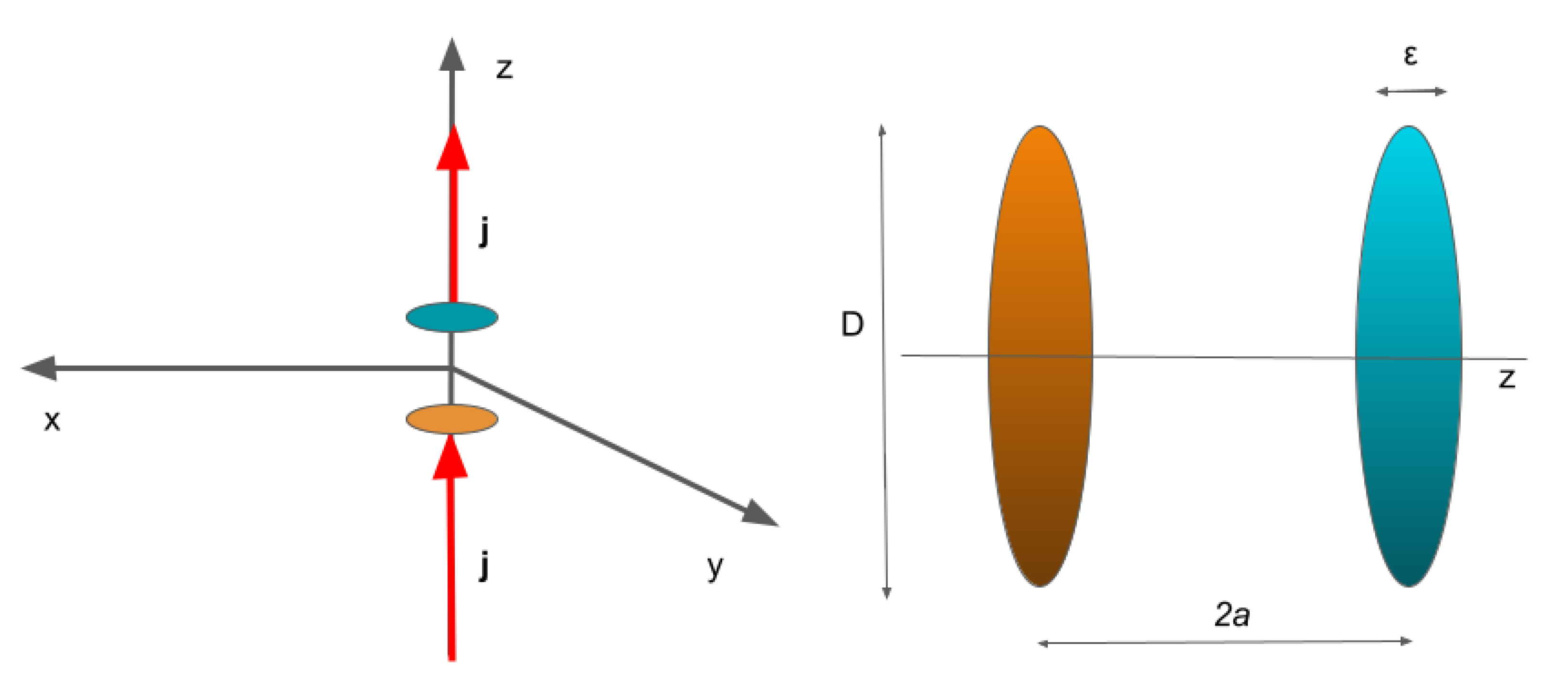
Therefore we model here the extra-current source with a double Gaussian (
Figure 1), and the method actually applies to any geometrical shape:
The auxiliary anomalous vector potential written as double integral of the extra-current is
When we compute the magnetic field at the position
, its only non-zero component is
:
The derivative of the first term is
The other derivatives are similar, and in total we obtain, also considering that
in this particular configuration:
This expression is simpler and more direct than those obtained in Reference [
35] and suitable for a 6D Monte Carlo algorithm which first generates random values of
in a quite narrow range, corresponding to the support of the Gaussian (
28), that is, inside the primary source. The main computational difficulty is (as before, actually) that for
it is necessary to sample a much wider region. Typically for each value of
we need to generate tens of values of
in the sampling.
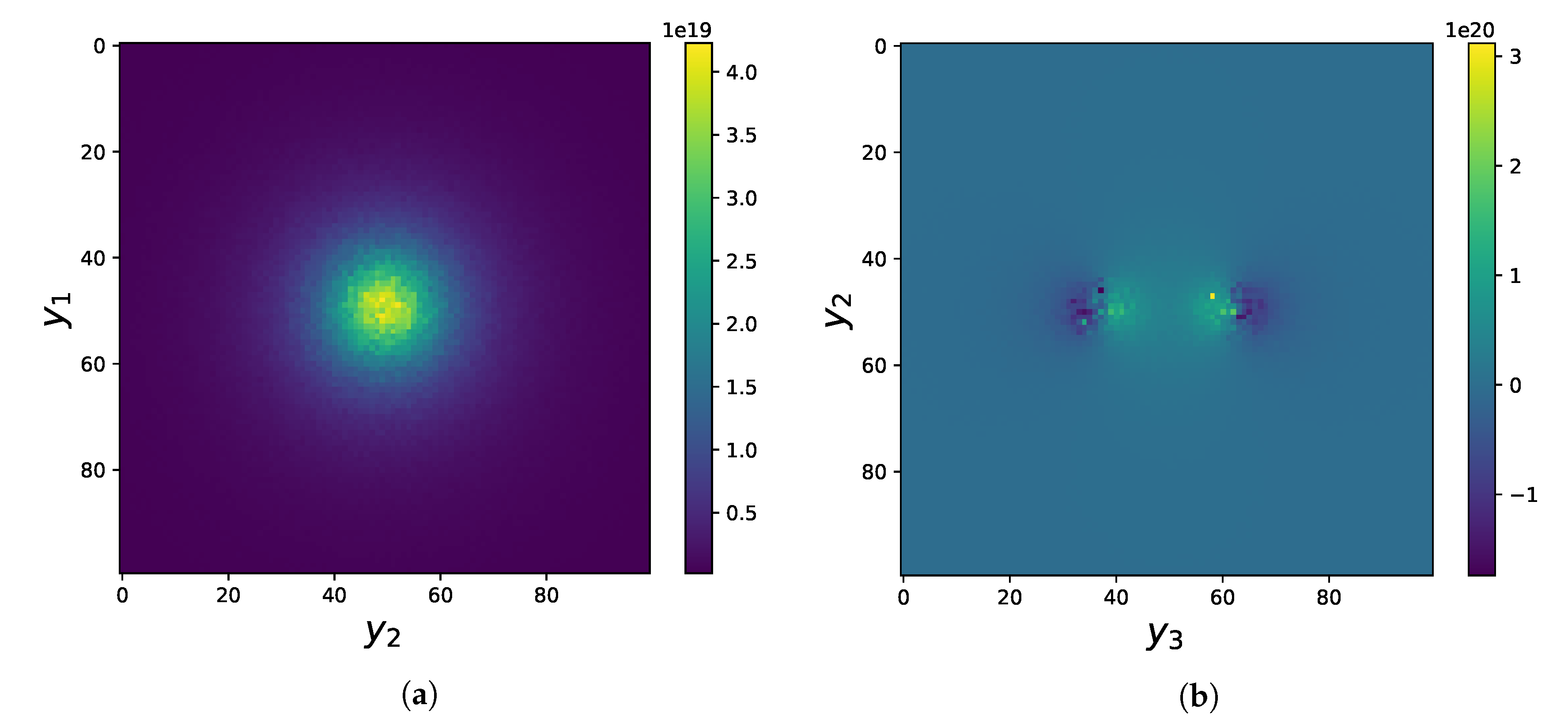
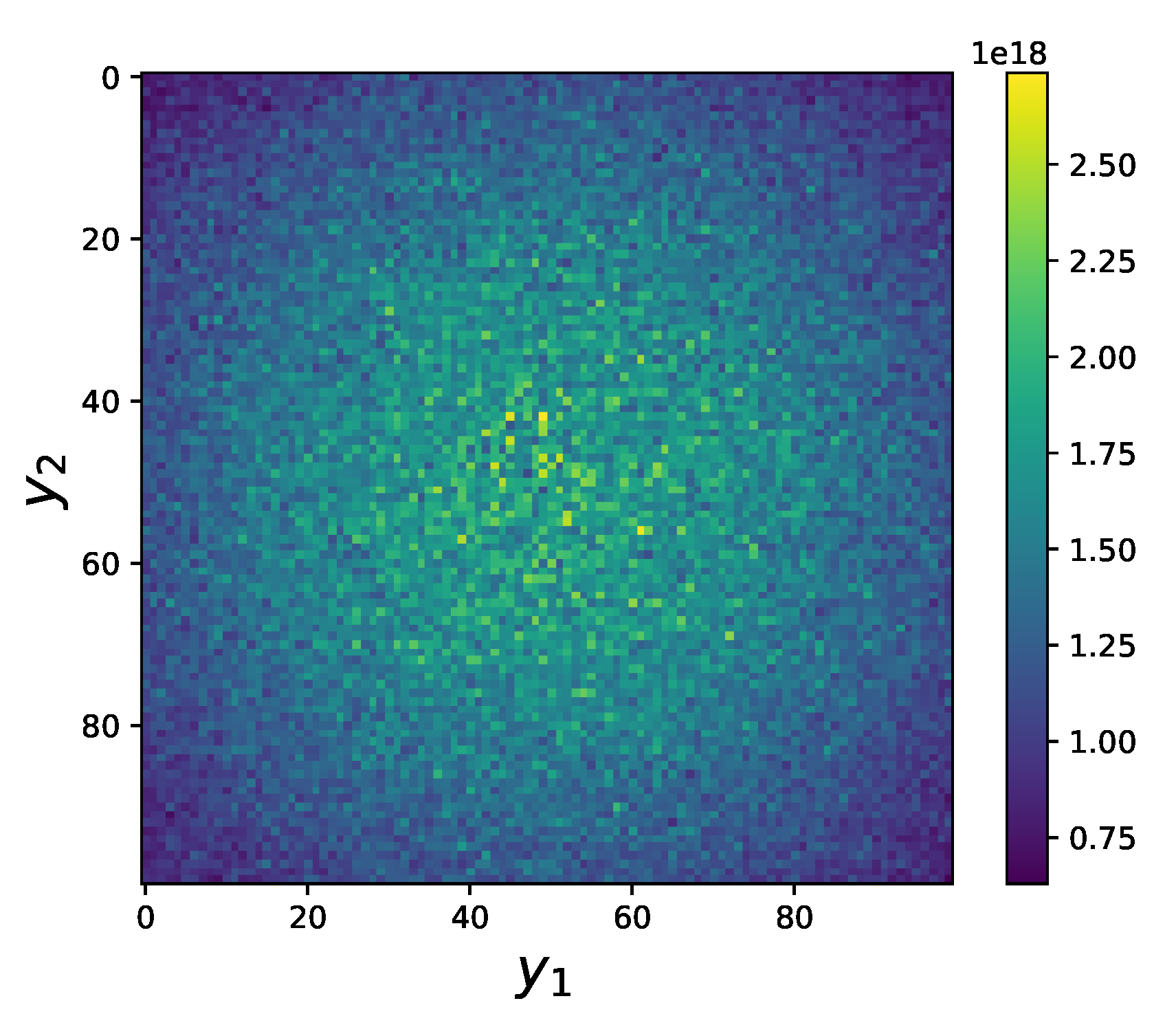
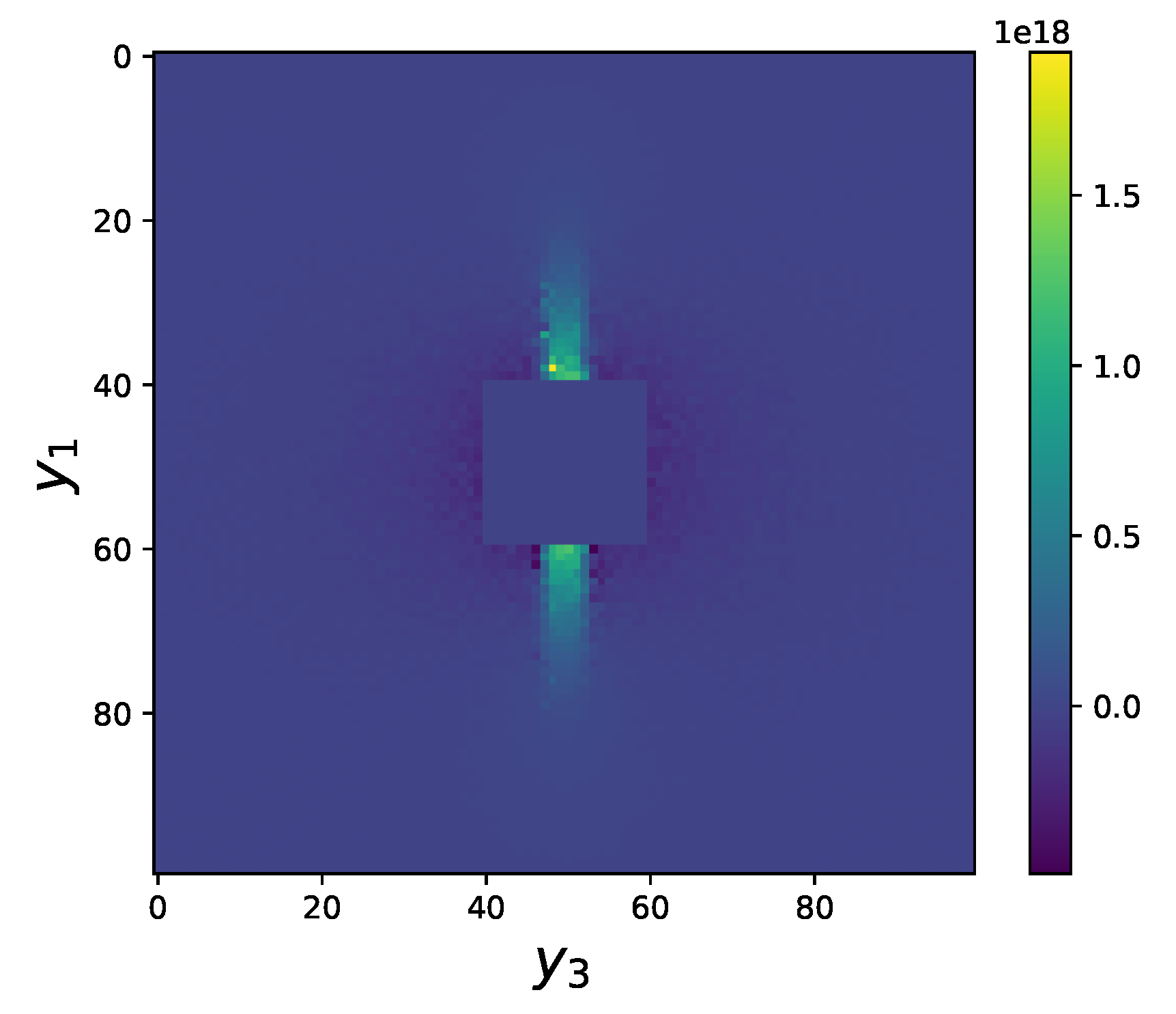
While we sample the integrand in order to evaluate the total integral, we also make a map of the function resulting from the partial integration in
. For this purpose we divide the 3D cube of integration in
(with variable side
) into 100 cells along each direction. The contribution to the magnetic field from each cell can be interpreted as being generated by a secondary current, or “cloud” current, proportional to the gradient of the field
S. As seen from
Table 1 and
Table 2 and from
Figure 2,
Figure 3,
Figure 4 and
Figure 5, the regions with the largest secondary current density are those between the current source and sink and close to them, but the large cloud that extends around them and whose density decreases slowly with distance also gives a relevant contribution to the total integral; in the end, the latter contribution exactly cancels that of the localized sources. In order to evaluate the far contributions we sample the integrand over cubes of
of increasing size, excluding each time a cubic core equal to the previous cube. This is necessary because the number of sampling points cannot be increased beyond a practical limit of the order or
, and if we would sample the cores together with the periphery, the cores would produce too much noise. All the physical parameters have been chosen of the same magnitude order as in Reference [
35].
5. Conclusions
In summary, we have shown on general grounds that, for any charge density
and current density
given by a microscopic model, the generated e.m. field is given by Equations (
9) and (
10), no matter if the continuity equation is satisfied or not.
In the case of oscillating charges and currents, the radiated longitudinal electric field is given by Equation (
17) or (
22). For example, if a fraction
of a charge
q oscillating along the
z-axis over a distance
lacks a corresponding current, the predicted maximum longitudinal field (along
z) is
. It is tempting to speculate that this kind of oscillations could happen in graphene-based nanojunctions or carbon nano-wires [
21,
22,
44,
45,
46].
The equation for the magnetic field (
10) indicates that it is possible in principle to observe experimentally whether a fraction
of a stationary current flows in a conductor with microscopic spatial “interruptions” affecting a volume that is a fraction
of the total volume—in that case, the average Biot-Savart magnetic field generated will be
, where
is the field generated by the same total current flowing in a conductor where
everywhere. The microscopic models cited in this work allow in principle to estimate the fractions
and
. On the experimental side, a possible strategy to prove some anomalies (though not to disprove them) consists of looking for changes in the ratio
in dependence on
i. We have briefly discussed the possible uncertainties associated with this measurement.
Finally, we note that the control of magnetic field patterns in molecular devices may be interesting for applications to high-density memory storage consisting of single molecular magnets (see [
25] and refs.). It has been further suggested that NMR-type experiments can be performed in order to observe the spatial fluctuations of magnetic fields generated by DC current flow [
47].