Figure 1.
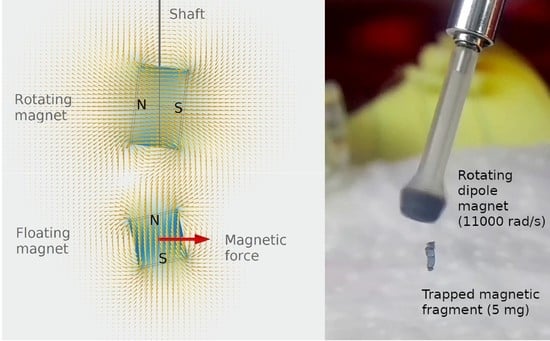
A scaled-down MBS realization where a tiny fragment of a NdFeB magnet weighing about 5 mg is levitated at the tip of rotator assembly consisting of an irregular magnet fragment of ~3 mm in size coupled to a micro motor having dimensions ⌀4 × 10 mm running at 105,000 RPM (11,000 rad/s).
Figure 1.
A scaled-down MBS realization where a tiny fragment of a NdFeB magnet weighing about 5 mg is levitated at the tip of rotator assembly consisting of an irregular magnet fragment of ~3 mm in size coupled to a micro motor having dimensions ⌀4 × 10 mm running at 105,000 RPM (11,000 rad/s).
Figure 2.
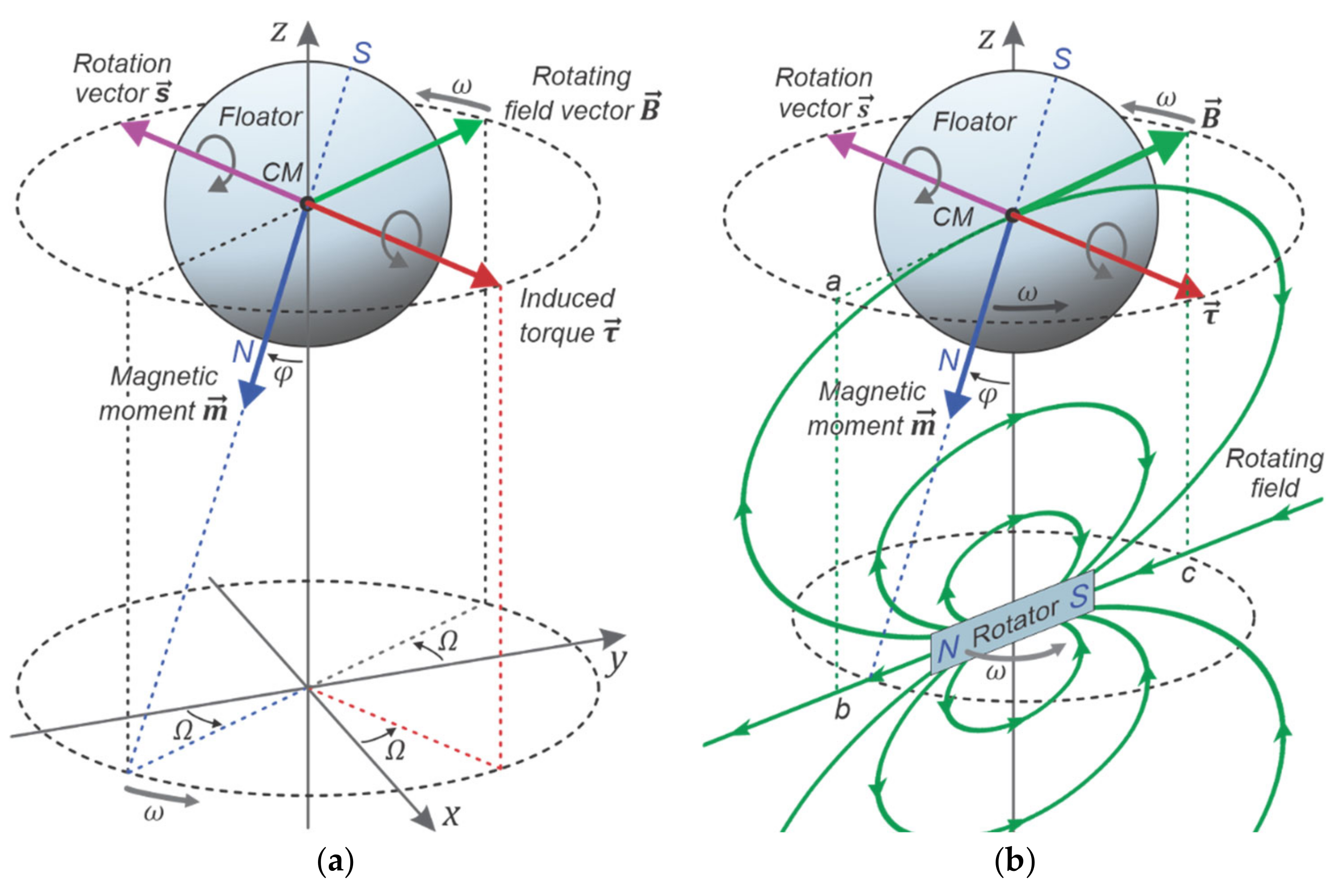
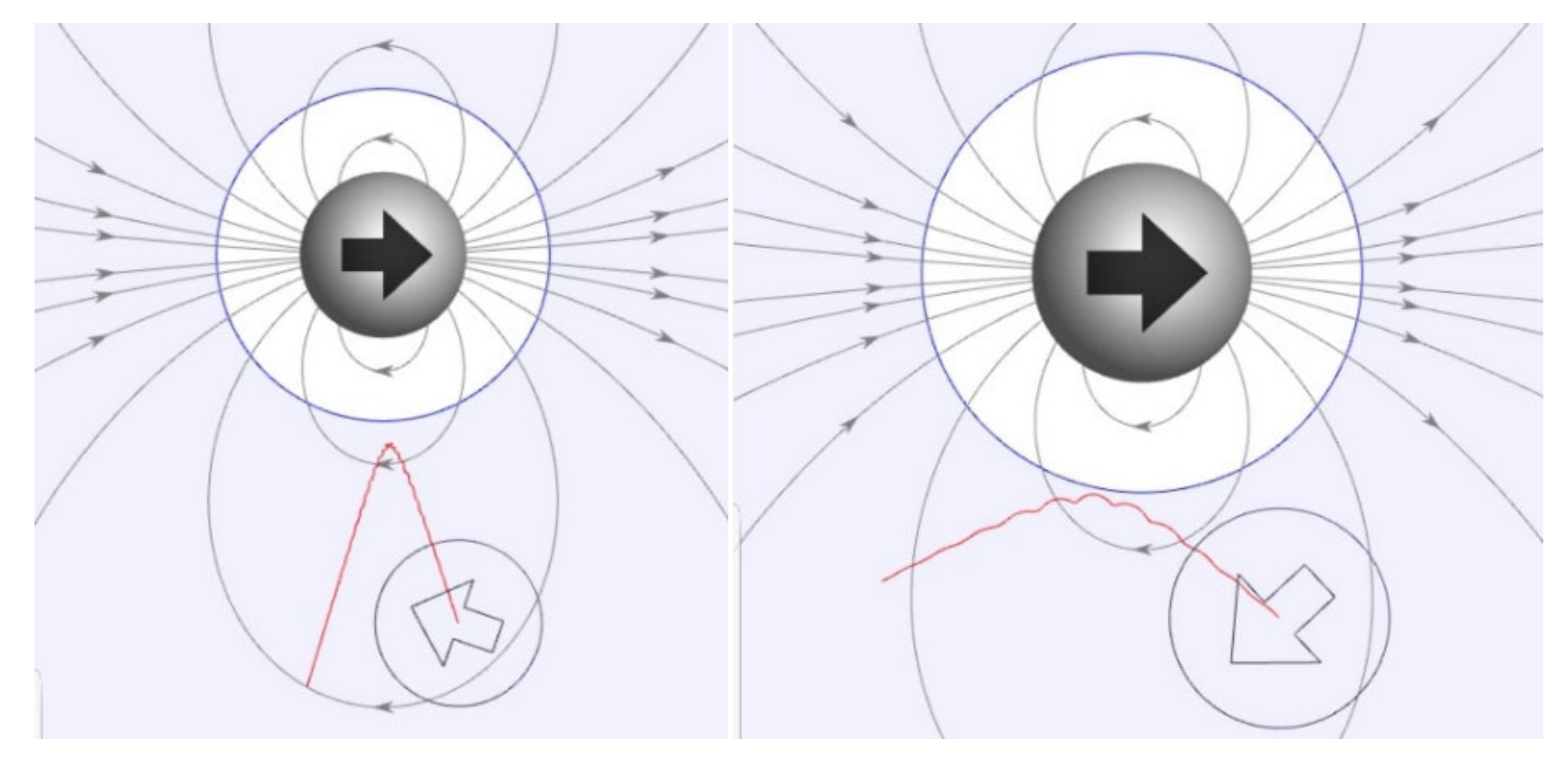
(a) Motion of a free body (floator) endowed with a magnetic dipole moment subject to uniform rotating magnetic field around axis-z with angular velocity ω. Within suitable configuration parameters and initial conditions, it is expected that the floator draws a conical angular motion around the axis-z, synchronized with the rotating field. The torque experiences the floator can be calculated as . According to the model of the motion, the rotation vector of the body becomes antiparallel to torque vector which share the same unit vector with angular acceleration vector . The angle φ is the result of the dynamics and can have a constant value with suitable initial conditions. This value can be calculated according to the model (Equation (29)) and initial angular velocities using Equation (17), (t = 0). Under this conical motion, azimuthal angles of vectors can be expressed as ωT + A where . Symbol Ω denotes ωT. It is remarkable that this relation is forced by the DHM even these angles at initial condition are different. In this diagram, the torque vector is shown on the xy plane; that is, it has no z component. This is valid when azimuthal angle between B and m is zero or π. Otherwise, this component get a value proportional to sine of this angle. (b) Similar configuration but floator is exposed to inhomogeneous field of a rotating dipole (rotator) centered on axis-z. This ensures the vector B at the CM point rotates on xy plane. Here it can be seen the floator pole N deviates from the axis-z toward rotator pole N and can cause a repulsion between dipoles. It should be noted that under the inhomogeneous field of the rotator, the rotation center is not at CM since the body also involves in a translational motion on the xy plane where the CM follows a small circle around axis-z. This shifts the RC away from rotator on axis-z. Rotator’s force lines are shown on the plane defined by its dipole orientation (cb) and the axis-z. The characteristics of the motion and obtained torque do not depend on rotation direction of the rotating field.
Figure 2.
(a) Motion of a free body (floator) endowed with a magnetic dipole moment subject to uniform rotating magnetic field around axis-z with angular velocity ω. Within suitable configuration parameters and initial conditions, it is expected that the floator draws a conical angular motion around the axis-z, synchronized with the rotating field. The torque experiences the floator can be calculated as . According to the model of the motion, the rotation vector of the body becomes antiparallel to torque vector which share the same unit vector with angular acceleration vector . The angle φ is the result of the dynamics and can have a constant value with suitable initial conditions. This value can be calculated according to the model (Equation (29)) and initial angular velocities using Equation (17), (t = 0). Under this conical motion, azimuthal angles of vectors can be expressed as ωT + A where . Symbol Ω denotes ωT. It is remarkable that this relation is forced by the DHM even these angles at initial condition are different. In this diagram, the torque vector is shown on the xy plane; that is, it has no z component. This is valid when azimuthal angle between B and m is zero or π. Otherwise, this component get a value proportional to sine of this angle. (b) Similar configuration but floator is exposed to inhomogeneous field of a rotating dipole (rotator) centered on axis-z. This ensures the vector B at the CM point rotates on xy plane. Here it can be seen the floator pole N deviates from the axis-z toward rotator pole N and can cause a repulsion between dipoles. It should be noted that under the inhomogeneous field of the rotator, the rotation center is not at CM since the body also involves in a translational motion on the xy plane where the CM follows a small circle around axis-z. This shifts the RC away from rotator on axis-z. Rotator’s force lines are shown on the plane defined by its dipole orientation (cb) and the axis-z. The characteristics of the motion and obtained torque do not depend on rotation direction of the rotating field.
![Symmetry 13 00442 g002 Symmetry 13 00442 g002]()
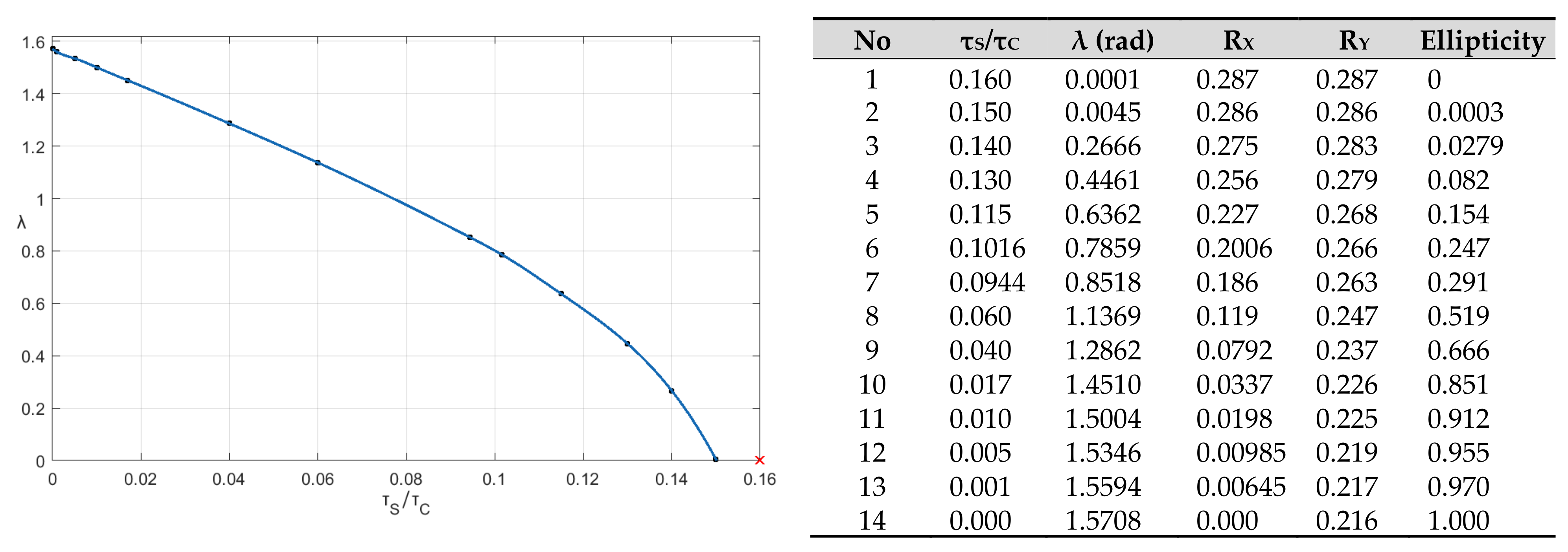
Figure 3.
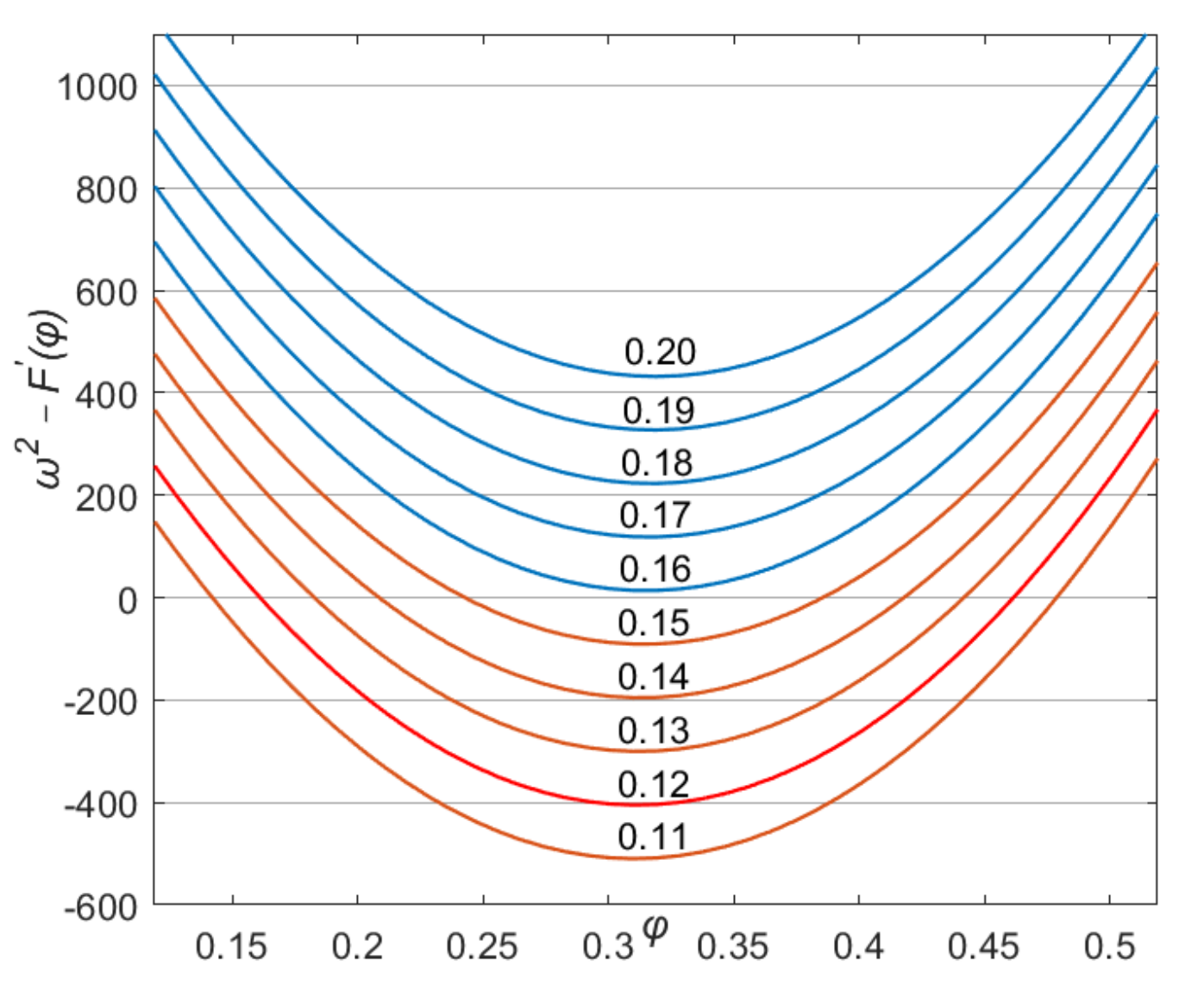
Plot of stability criterion term
covering configurations based cases 13 to 19 in
Table 1 where ω is 60
π rAd/S,
JC = 11000. Identifiers 0.20 to 0.11 correspond to τ
S/τ
C ratios. Ratios 0.16 to 0.20 correspond to stable configurations as the criterion term is always above zero. These configurations can perform stable conical motion around axis-
z with fixed angle
φ =
φE. Below this ratio, the axis of the conical motion drifts and the angle
φ cannot settle to
φE, but the body motion may still have stability depending on initial conditions.
Figure 3.
Plot of stability criterion term
covering configurations based cases 13 to 19 in
Table 1 where ω is 60
π rAd/S,
JC = 11000. Identifiers 0.20 to 0.11 correspond to τ
S/τ
C ratios. Ratios 0.16 to 0.20 correspond to stable configurations as the criterion term is always above zero. These configurations can perform stable conical motion around axis-
z with fixed angle
φ =
φE. Below this ratio, the axis of the conical motion drifts and the angle
φ cannot settle to
φE, but the body motion may still have stability depending on initial conditions.
Figure 4.
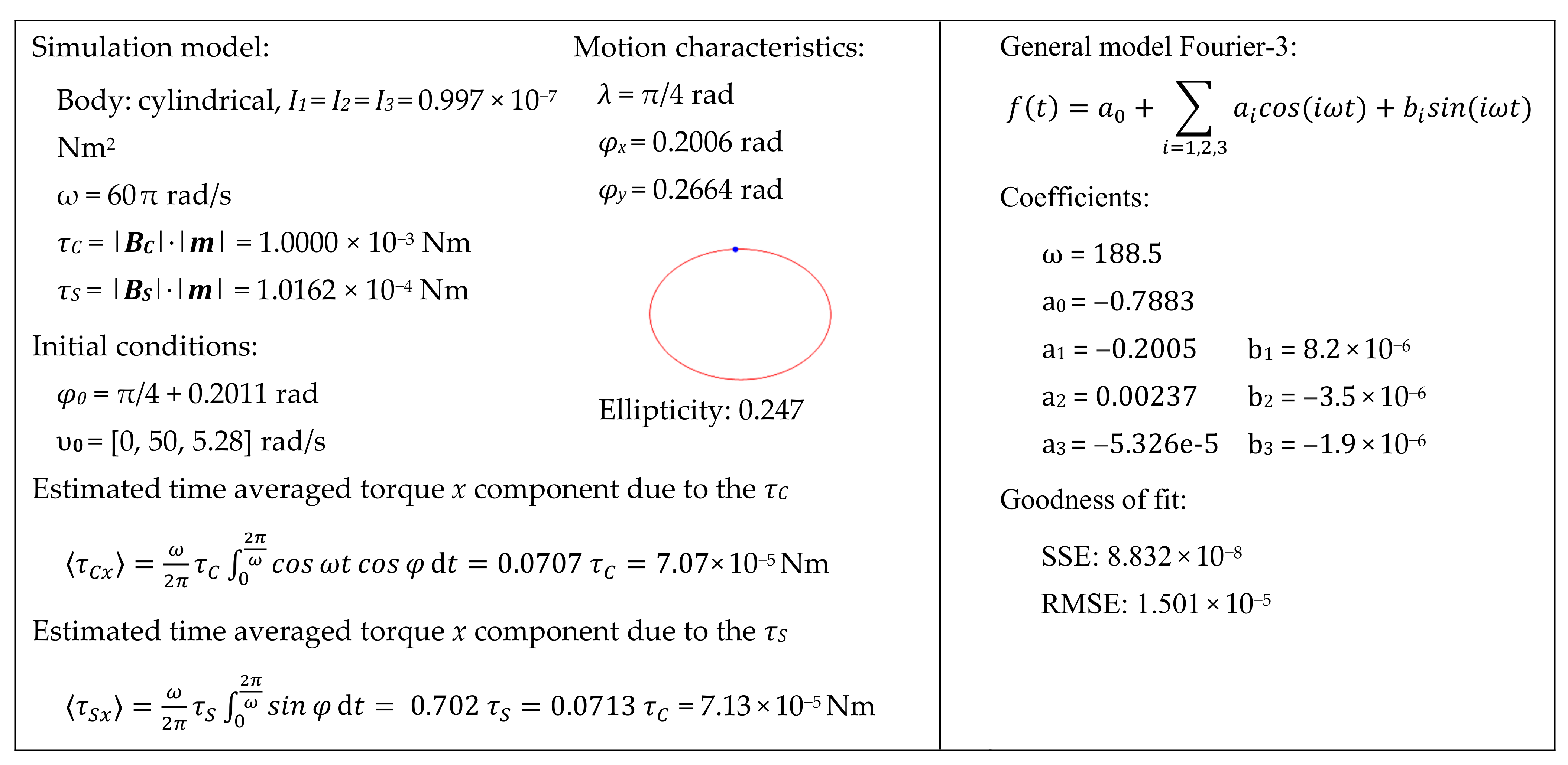
Estimation of x component of the net torque ⟨τCx⟩ due to the cyclic torque τC. In this simulation, the strength of the static torque τS is not sufficient to keep the body’s conical motion axis on z (λ = 0), but allows to find a stable equilibrium at λ = π/4. At this angle, it is expected that ⟨τCx⟩ is compensated by the average static torque ⟨τSx⟩. Calculation results support this model by providing these torque figures with a close match with an error less than 1%. The elliptical figure here shows the trajectory of the top center point of the body is seen from the direction of the axis of the conical motion. Figures on the right are Fourier analysis of the zenith angle φ obtained from the simulation (top left) of the motion which consist of harmonics with cosine terms where coefficient a0 is the angle λ and with negligible sine terms. It should be noted that only axisymmetric bodies are found to have stable motion when angle λ is not zero. In this simulation, principal moments of inertia are equal.
Figure 4.
Estimation of x component of the net torque ⟨τCx⟩ due to the cyclic torque τC. In this simulation, the strength of the static torque τS is not sufficient to keep the body’s conical motion axis on z (λ = 0), but allows to find a stable equilibrium at λ = π/4. At this angle, it is expected that ⟨τCx⟩ is compensated by the average static torque ⟨τSx⟩. Calculation results support this model by providing these torque figures with a close match with an error less than 1%. The elliptical figure here shows the trajectory of the top center point of the body is seen from the direction of the axis of the conical motion. Figures on the right are Fourier analysis of the zenith angle φ obtained from the simulation (top left) of the motion which consist of harmonics with cosine terms where coefficient a0 is the angle λ and with negligible sine terms. It should be noted that only axisymmetric bodies are found to have stable motion when angle λ is not zero. In this simulation, principal moments of inertia are equal.
![Symmetry 13 00442 g004 Symmetry 13 00442 g004]()
Figure 5.
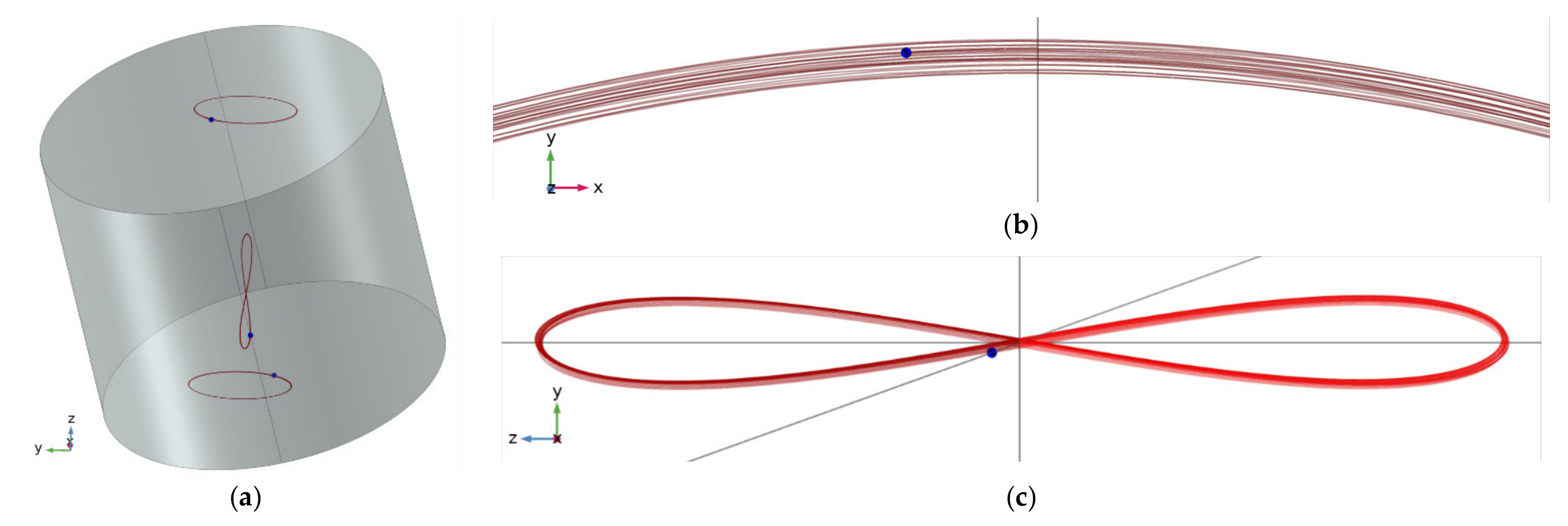
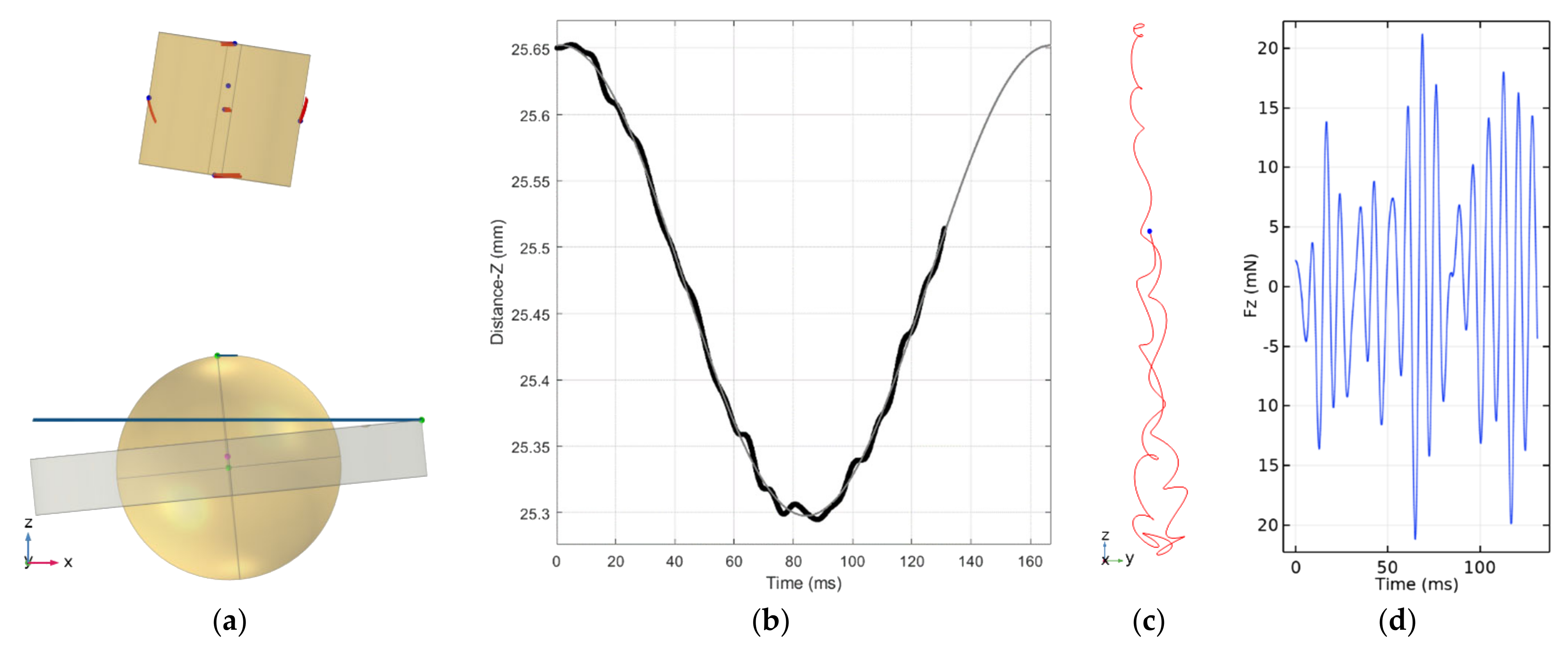
Simulations of motion a cylindrical body having a dipole moment in its axial direction subject a rotating field BC around axis-z and orthogonal to it with constant velocity equal to 60 π rAd/S And wITh constant magnitude. A static field BS in z direction having strength of 0.18 BC IS AlSo preSenT. Torque figures Are τC = ||BC||·||m|| = 1.2 × 10−3 Nm, τS = 0.18 τC. This ratio is slightly above the required ratio 0.174 to obtain conical motion with fixed zenith angle according to Equation (51). Initial condition are given in order to obtain a smooth conical motion, but not finely tuned. Angle φ set initially to 0.3455 rad and kept almost constant. As a result, body’s main axis draws conical circular motions around axis-z with zenith angle φ = 0.345. Body dimensions are chosen in order to obtain principal moments are inertia are equal to 1 × 10−7 Nm2 (0.999 × 10−7 Nm2 used by simulation) has MoI equal to 1 × 10−7 kg m2 on all its principal axes. Its mass is 6.68 g, radius is 5.4711 mm, height is 9.4763 mm and has uniform density of 7.5 g/cm3. Angular velocity of the applied torque is 60 π = 188.5 rad/s. Left figure shows an instance of the body with traces of top and bottom center points (1, 2) and middle side point (3) of the body. Trace 3 have ‘eight’ shape because presence of angular motion second harmonic in z direction in accordance of Equation (65). Right figures show zoomed view of traces where the top figure corresponds to the arc from the circular trace of top point projected on xy plane at instance T = 0.767 ms where the motion completes its 23rd cycle. Bottom figure similarly shows the rotated ‘eight’ figure on zy plane. Vertical and horizontal hairlines in this figure are z and y axes and the diagonal is the main axis of the cylinder.
Figure 5.
Simulations of motion a cylindrical body having a dipole moment in its axial direction subject a rotating field BC around axis-z and orthogonal to it with constant velocity equal to 60 π rAd/S And wITh constant magnitude. A static field BS in z direction having strength of 0.18 BC IS AlSo preSenT. Torque figures Are τC = ||BC||·||m|| = 1.2 × 10−3 Nm, τS = 0.18 τC. This ratio is slightly above the required ratio 0.174 to obtain conical motion with fixed zenith angle according to Equation (51). Initial condition are given in order to obtain a smooth conical motion, but not finely tuned. Angle φ set initially to 0.3455 rad and kept almost constant. As a result, body’s main axis draws conical circular motions around axis-z with zenith angle φ = 0.345. Body dimensions are chosen in order to obtain principal moments are inertia are equal to 1 × 10−7 Nm2 (0.999 × 10−7 Nm2 used by simulation) has MoI equal to 1 × 10−7 kg m2 on all its principal axes. Its mass is 6.68 g, radius is 5.4711 mm, height is 9.4763 mm and has uniform density of 7.5 g/cm3. Angular velocity of the applied torque is 60 π = 188.5 rad/s. Left figure shows an instance of the body with traces of top and bottom center points (1, 2) and middle side point (3) of the body. Trace 3 have ‘eight’ shape because presence of angular motion second harmonic in z direction in accordance of Equation (65). Right figures show zoomed view of traces where the top figure corresponds to the arc from the circular trace of top point projected on xy plane at instance T = 0.767 ms where the motion completes its 23rd cycle. Bottom figure similarly shows the rotated ‘eight’ figure on zy plane. Vertical and horizontal hairlines in this figure are z and y axes and the diagonal is the main axis of the cylinder.
![Symmetry 13 00442 g005 Symmetry 13 00442 g005]()
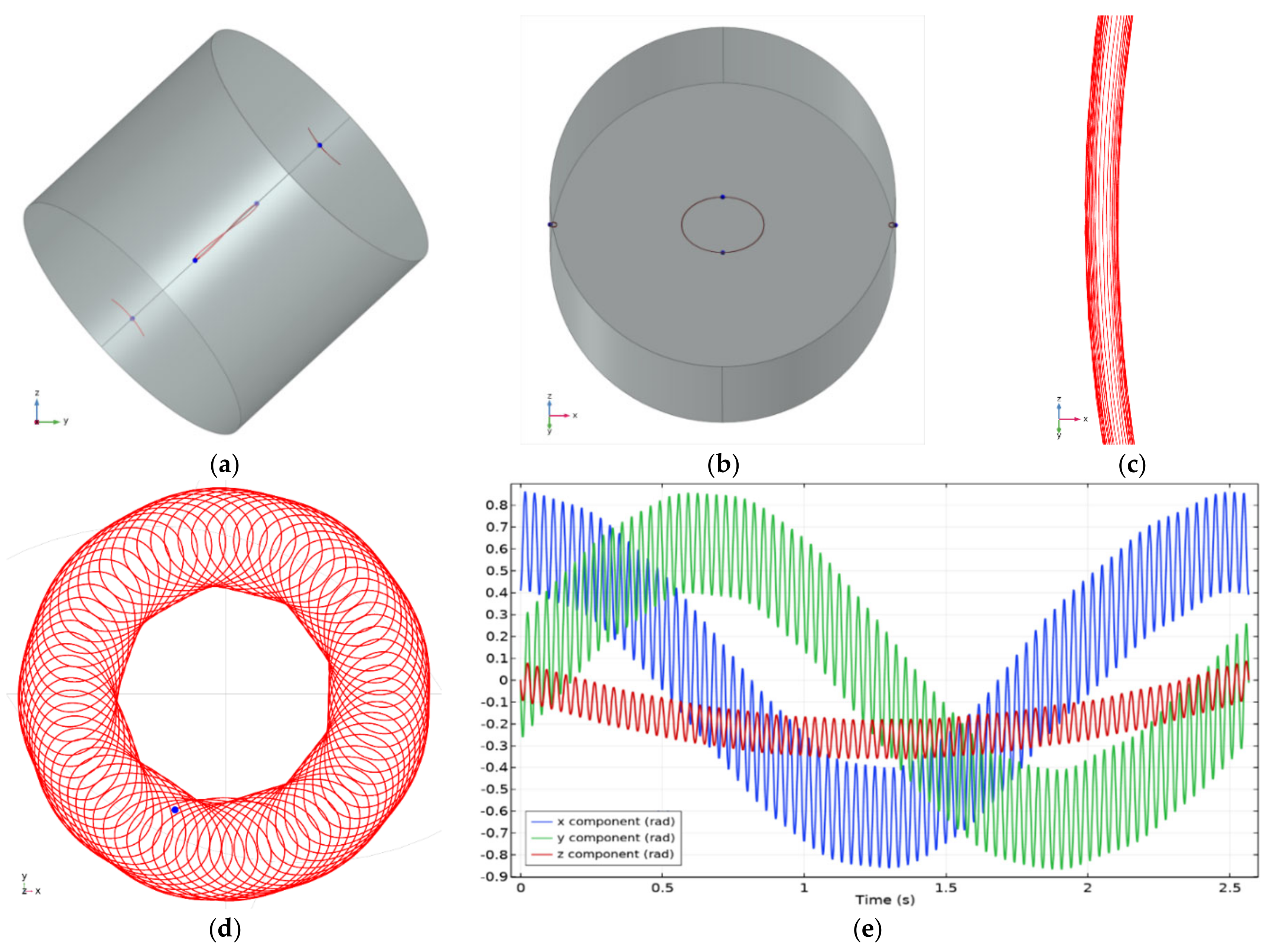
Figure 6.
Simulations of motion of a cylindrical body with equal principal MoI where static field strength BS is below the minimum BS/BC ratio (0.158) based by Equation (51) for the body to have stable motion around the axis-z. This condition shifts the axis of the conical motion from axis-z by angle called λ and the circular angular motion becomes elliptic. In the first simulation (top figures), BS/BC is 0.0944 and the motion finds an equilibrium at λ = 0.852 rad (48.8°). Simulation run about 0.5 s and motion is found stable without any drift thanks to precise initial conditions. (a) The body shown in an instance where rotation λ is aligned with axis-x. (b) Same as (a) but with a camera angle close to λ where traces of top and bottom center points overlap. (c) Zoomed part of the elliptical trace at (b). This shows the characteristics of the stability where traces are bounded in a narrow limit. Amplitude of the elliptical motion on axes x and y are 0.186 and 0.263 rad, giving an ellipticity about 0.292. In the second simulation (bottom figures), BS/BC is 0.115 and the motion finds an equilibrium at λ = 0.64 rad. Here, an excess angular velocity of 1 rad/s on axis-y is given on initial condition to obtain the drift of the motion around axis-z in CCW direction. (d) The trace of the top center point of the body on projection to the xy plane. Here the crossed hairlines mark xy axes. This snapshot is taken at t = 2570 ms. The ring has a decagon shape (10 sides) due to nutation of the motion due to initial conditions. It is observed that the angular drift of the axis of conical motion has a small acceleration which progressively decreases and switches to deceleration at about t = 1760 ms. This non-zero acceleration is found to be a simulation artefact and vanishes when time-step is reduced from 0.4 ms to 0.2 ms. (e) Plot of orientation of the body in terms of rotations around axes x, y and z. Parameters and initial conditions of simulation 1 are: I1 = I2 = I3 = 0.999 × 10−7 Nm2, τC = 1 × 10−7 Nm, τS = 9.94 × 10−5 Nm, ω = 60 π rad/s, φ0 = −1.038 rad, = [0, −47.9, −4.891] rAd/S.
Figure 6.
Simulations of motion of a cylindrical body with equal principal MoI where static field strength BS is below the minimum BS/BC ratio (0.158) based by Equation (51) for the body to have stable motion around the axis-z. This condition shifts the axis of the conical motion from axis-z by angle called λ and the circular angular motion becomes elliptic. In the first simulation (top figures), BS/BC is 0.0944 and the motion finds an equilibrium at λ = 0.852 rad (48.8°). Simulation run about 0.5 s and motion is found stable without any drift thanks to precise initial conditions. (a) The body shown in an instance where rotation λ is aligned with axis-x. (b) Same as (a) but with a camera angle close to λ where traces of top and bottom center points overlap. (c) Zoomed part of the elliptical trace at (b). This shows the characteristics of the stability where traces are bounded in a narrow limit. Amplitude of the elliptical motion on axes x and y are 0.186 and 0.263 rad, giving an ellipticity about 0.292. In the second simulation (bottom figures), BS/BC is 0.115 and the motion finds an equilibrium at λ = 0.64 rad. Here, an excess angular velocity of 1 rad/s on axis-y is given on initial condition to obtain the drift of the motion around axis-z in CCW direction. (d) The trace of the top center point of the body on projection to the xy plane. Here the crossed hairlines mark xy axes. This snapshot is taken at t = 2570 ms. The ring has a decagon shape (10 sides) due to nutation of the motion due to initial conditions. It is observed that the angular drift of the axis of conical motion has a small acceleration which progressively decreases and switches to deceleration at about t = 1760 ms. This non-zero acceleration is found to be a simulation artefact and vanishes when time-step is reduced from 0.4 ms to 0.2 ms. (e) Plot of orientation of the body in terms of rotations around axes x, y and z. Parameters and initial conditions of simulation 1 are: I1 = I2 = I3 = 0.999 × 10−7 Nm2, τC = 1 × 10−7 Nm, τS = 9.94 × 10−5 Nm, ω = 60 π rad/s, φ0 = −1.038 rad, = [0, −47.9, −4.891] rAd/S.
![Symmetry 13 00442 g006 Symmetry 13 00442 g006]()
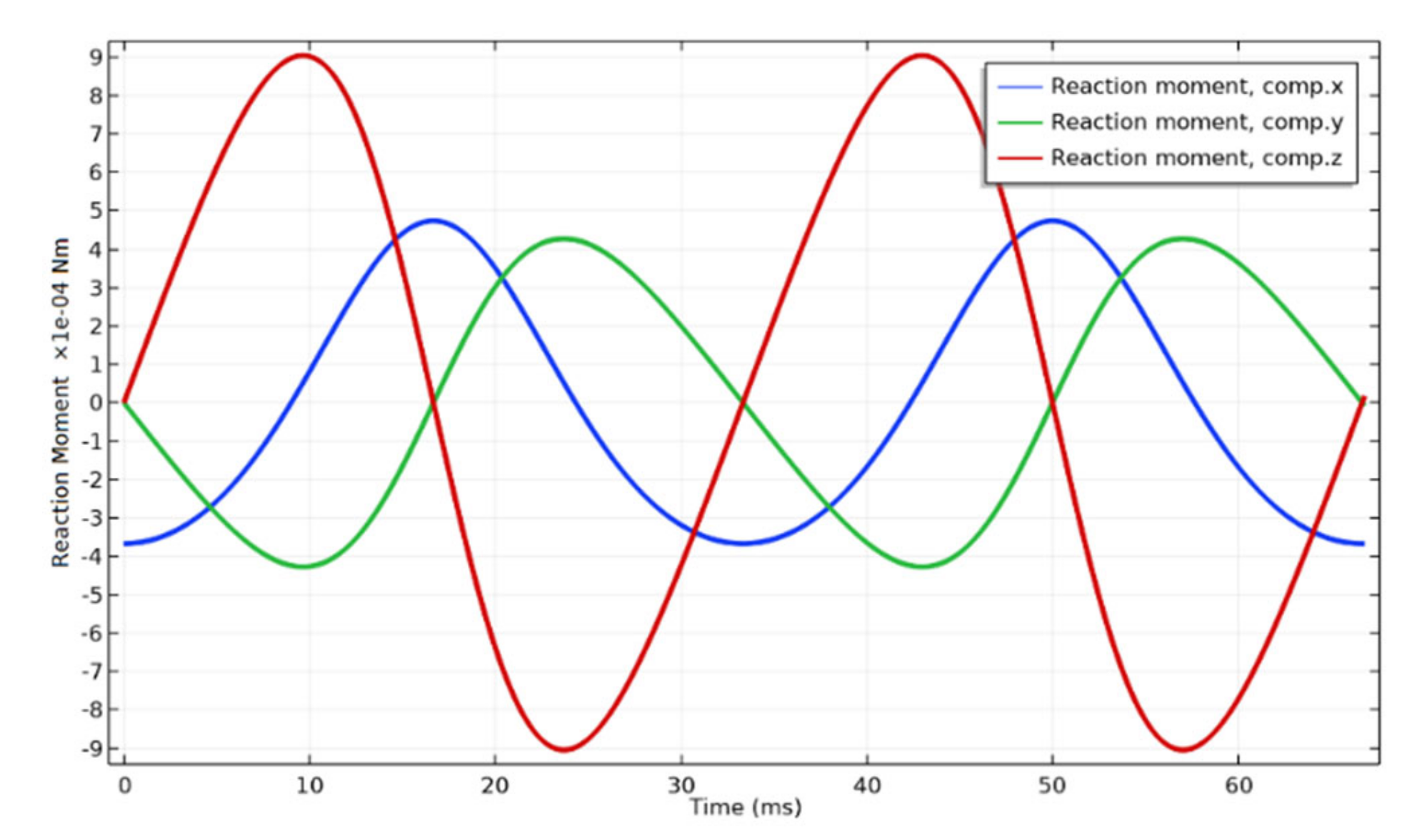
Figure 7.
Simulation result showing reaction moment receives a body for two cycles of the rotation field. In this specific case, body’s conical motion is elliptical (ellipticity = 0.52) and motion axis is off the axis-z (λ = 0.114 rad) due to static field strength not being sufficient for keeping motion axis on z (BS/BC = 0.06) while the minimum ratio calculated from Equation (51) is 0.144 and this value should be between 0.14 and 0.15 according to simulations.
Figure 7.
Simulation result showing reaction moment receives a body for two cycles of the rotation field. In this specific case, body’s conical motion is elliptical (ellipticity = 0.52) and motion axis is off the axis-z (λ = 0.114 rad) due to static field strength not being sufficient for keeping motion axis on z (BS/BC = 0.06) while the minimum ratio calculated from Equation (51) is 0.144 and this value should be between 0.14 and 0.15 according to simulations.
Figure 8.
Variation of angle
λ and the ellipticity of angular motion of the body by the strength of the static field according to simulations results where the body has uniform MoI
I = 0.998 × 10
−7 Nm
2,
τC = 1 × 10
−3 Nm and rotating field velocity
ω = 60π rad/s. Semi-axis lengths are denoted by
RX and
RY in radians. Ellipticity is calculated by formula 1−
RX/
RY. It should be noted the elliptical shape gains some asymmetry with respect to the major axis by increasing the angle
λ. Performed simulations are similar to given in
Figure 6.
Figure 8.
Variation of angle
λ and the ellipticity of angular motion of the body by the strength of the static field according to simulations results where the body has uniform MoI
I = 0.998 × 10
−7 Nm
2,
τC = 1 × 10
−3 Nm and rotating field velocity
ω = 60π rad/s. Semi-axis lengths are denoted by
RX and
RY in radians. Ellipticity is calculated by formula 1−
RX/
RY. It should be noted the elliptical shape gains some asymmetry with respect to the major axis by increasing the angle
λ. Performed simulations are similar to given in
Figure 6.
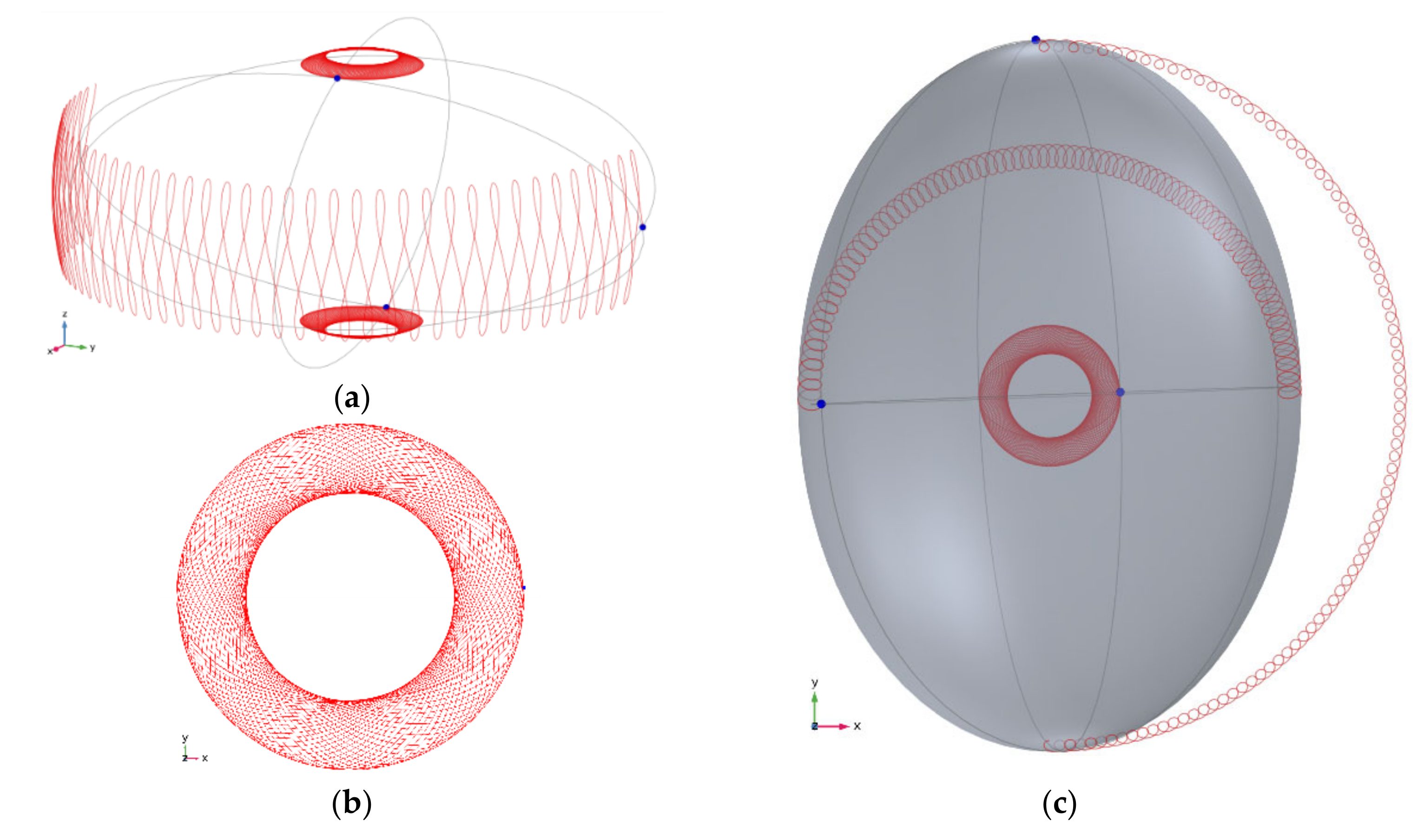
Figure 9.
Simulation about angular motion of an ellipsoid shaped body with unequal principal MoI. As IX and IY are different, the conical motion is elliptical, elongated in the direction of the axis of smaller MoI (Ix). The ratio BS /BC is equal to 0.24, enough to obtain a stable motion centered on axis-z where zenith angle φ of the body varies according to the ellipticity. The CCW rotation of the body around axis-z is mainly caused by the initial angular velocity υz = 1.53 rad/s. Body also has an angular acceleration in the same direction about 0.56 rad/s2. This acceleration can be seen on peripheral traces where these small loops get separated as the traces move CCW. Simulation time is about 1.492 sec, meanwhile the body completes a half rotation around axis-z at T = 1.475 s This acceleration is attributed to simulation artefact as it vanishes when the time step is reduced from 0.4 ms to 0.2 ms. Relevant physical properties and simulation parameters are: Semi axes lengths (x, y, z): 6, 8.5, 4 mm; Mass: 6.385 g; Principal moments of inertia: 1.123736 × 10−7, 6.623701 × 10−8, 1.3780954 × 10−7 Nm2; Torque coefficients (τC, τS): 1 × 10−3 Nm, 2.4 × 10−4 Nm; Rotating field velocity (ω): 60 π rAd/S; Initial zenith angle (φ0): −0.254 rad, Initial angular velocity vector : −[0.002 80.95 6.858] rad/s.
Figure 9.
Simulation about angular motion of an ellipsoid shaped body with unequal principal MoI. As IX and IY are different, the conical motion is elliptical, elongated in the direction of the axis of smaller MoI (Ix). The ratio BS /BC is equal to 0.24, enough to obtain a stable motion centered on axis-z where zenith angle φ of the body varies according to the ellipticity. The CCW rotation of the body around axis-z is mainly caused by the initial angular velocity υz = 1.53 rad/s. Body also has an angular acceleration in the same direction about 0.56 rad/s2. This acceleration can be seen on peripheral traces where these small loops get separated as the traces move CCW. Simulation time is about 1.492 sec, meanwhile the body completes a half rotation around axis-z at T = 1.475 s This acceleration is attributed to simulation artefact as it vanishes when the time step is reduced from 0.4 ms to 0.2 ms. Relevant physical properties and simulation parameters are: Semi axes lengths (x, y, z): 6, 8.5, 4 mm; Mass: 6.385 g; Principal moments of inertia: 1.123736 × 10−7, 6.623701 × 10−8, 1.3780954 × 10−7 Nm2; Torque coefficients (τC, τS): 1 × 10−3 Nm, 2.4 × 10−4 Nm; Rotating field velocity (ω): 60 π rAd/S; Initial zenith angle (φ0): −0.254 rad, Initial angular velocity vector : −[0.002 80.95 6.858] rad/s.
![Symmetry 13 00442 g009 Symmetry 13 00442 g009]()
Figure 10.
Curve fitting of angular motion of a body obtained from a simulation data over one cycle using Fourier analysis. In this simulation, a cylindrical body having magnetic moment in axial direction and having MoI as IR = IA = 0.999 × 10−7 kg m2 with main axis on xy plane is subject a homogeneous rotating magnetic with constant amplitude and velocity ω = 60 π rad/s on axis-z. The torque with maximum amplitude of 1 × 10−3 Nm induced by the magnetic interaction forces the body to a periodic motion. Resulting motion is sinusoidal with additional small harmonics. The top trace has cosine appearance (instead of sine) because sample data are evaluated about 8 ms after the simulation starts.
Figure 10.
Curve fitting of angular motion of a body obtained from a simulation data over one cycle using Fourier analysis. In this simulation, a cylindrical body having magnetic moment in axial direction and having MoI as IR = IA = 0.999 × 10−7 kg m2 with main axis on xy plane is subject a homogeneous rotating magnetic with constant amplitude and velocity ω = 60 π rad/s on axis-z. The torque with maximum amplitude of 1 × 10−3 Nm induced by the magnetic interaction forces the body to a periodic motion. Resulting motion is sinusoidal with additional small harmonics. The top trace has cosine appearance (instead of sine) because sample data are evaluated about 8 ms after the simulation starts.
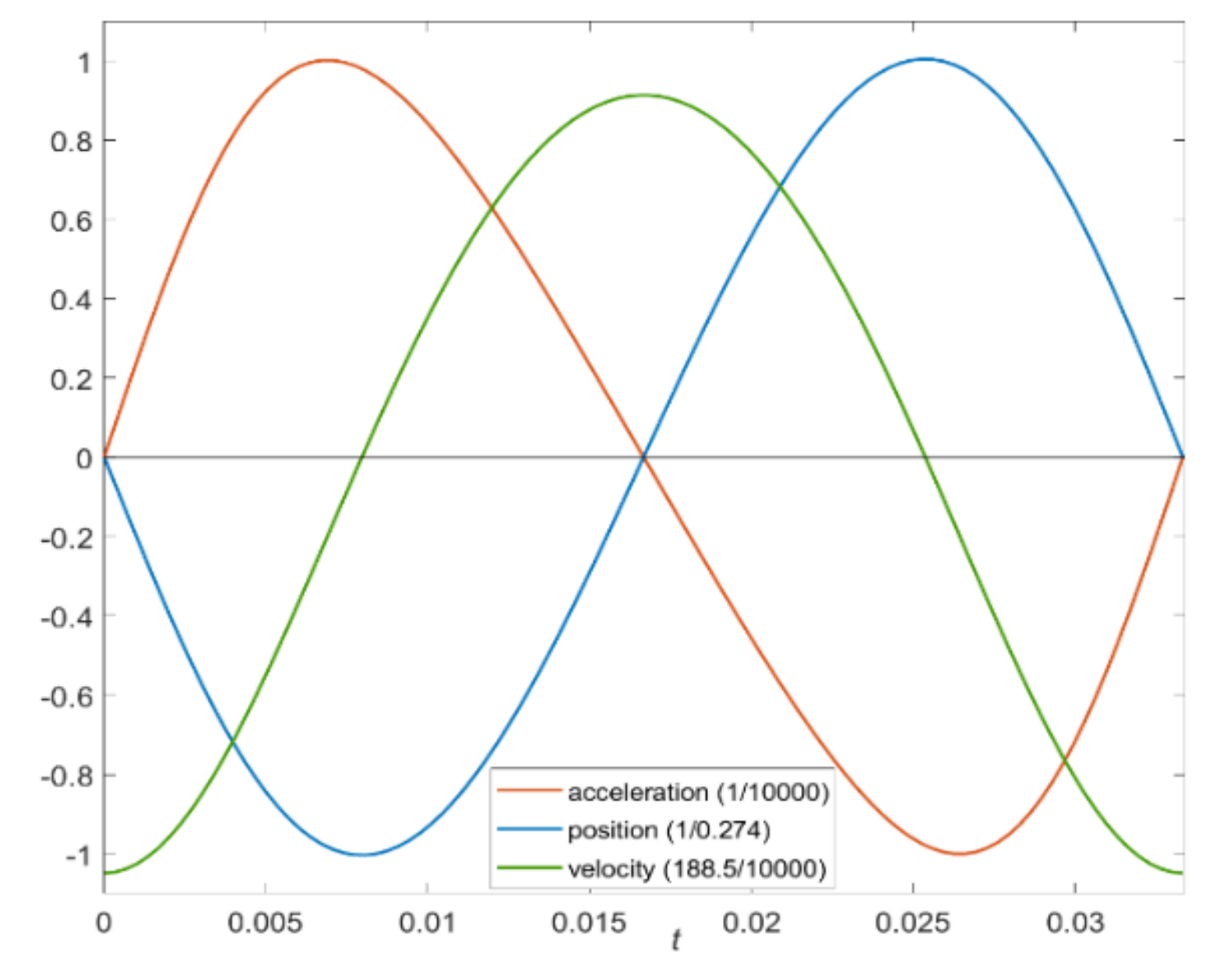
Figure 11.
Normalized plot of azimuthal position, angular velocity and acceleration of the body over one cycle of rotating field derived from data of numerical solution 1 from
Table 2.
Figure 11.
Normalized plot of azimuthal position, angular velocity and acceleration of the body over one cycle of rotating field derived from data of numerical solution 1 from
Table 2.
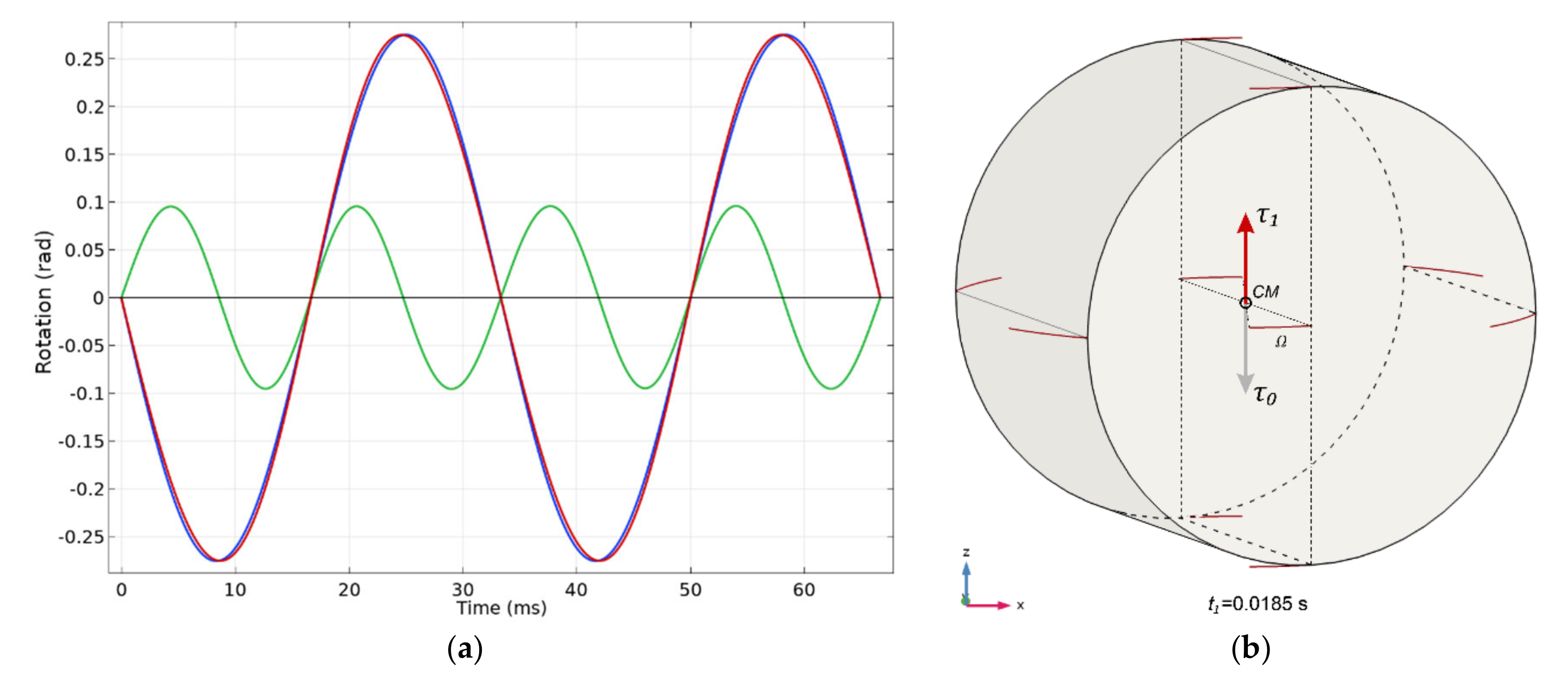
Figure 12.
(a) Angular motion (θ) of a body around the axis-z subject to a rotating field defined in Equation (70) with velocity ω = 88.5 rad/s covering two cycles of the rotating field obtained through a simulation. The amplitude τC of the torque is 1 × 10−3 Nm. Body is a cylinder with equal MoI of 0.998 × 10−7 kg m2 endowed with a magnetic moment at CM along the cylinder axis. Body rotation is shown by the red trace having amplitude 0.2756 rad. Blue trace corresponds to a pure sine curve with amplitude 0.27565 rad and the green curve is their differences amplified by 10 times. This shows the presence of a second harmonic with an amplitude 0.03453 of the first. This fits well to the ratio (0.03475) obtained through numerical solution where body’s MoI is 1 × 10−7 kg m2 instead of 0.998 × 10−7. (b) An overview of a similar simulation where the motion of the cylindrical body is shown with red colored traces. Here, the rotating field axis, body rotation axis and torque vector are aligned with the axis-z. The torque vector is shown at instances T0 and T1 near to the half cycle of the rotating field.
Figure 12.
(a) Angular motion (θ) of a body around the axis-z subject to a rotating field defined in Equation (70) with velocity ω = 88.5 rad/s covering two cycles of the rotating field obtained through a simulation. The amplitude τC of the torque is 1 × 10−3 Nm. Body is a cylinder with equal MoI of 0.998 × 10−7 kg m2 endowed with a magnetic moment at CM along the cylinder axis. Body rotation is shown by the red trace having amplitude 0.2756 rad. Blue trace corresponds to a pure sine curve with amplitude 0.27565 rad and the green curve is their differences amplified by 10 times. This shows the presence of a second harmonic with an amplitude 0.03453 of the first. This fits well to the ratio (0.03475) obtained through numerical solution where body’s MoI is 1 × 10−7 kg m2 instead of 0.998 × 10−7. (b) An overview of a similar simulation where the motion of the cylindrical body is shown with red colored traces. Here, the rotating field axis, body rotation axis and torque vector are aligned with the axis-z. The torque vector is shown at instances T0 and T1 near to the half cycle of the rotating field.
![Symmetry 13 00442 g012 Symmetry 13 00442 g012]()
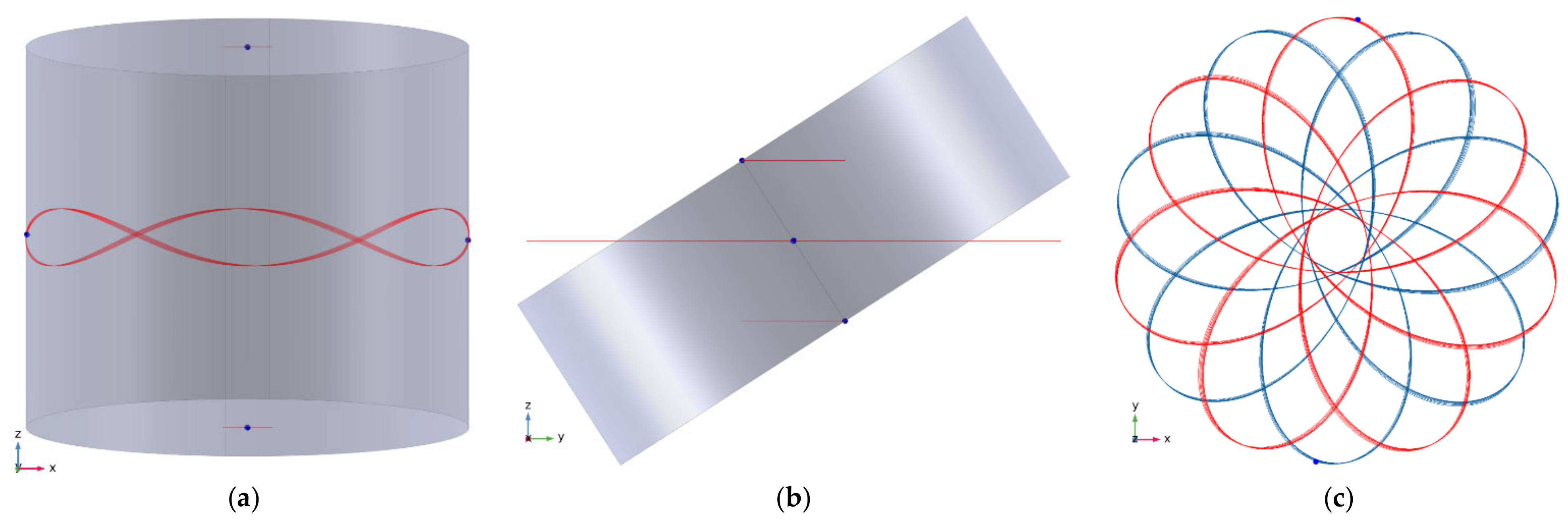
Figure 13.
(a) A simulation showing motion of a spinning cylindrical body (⌀5.245 × 9.087 mm) having magnetic moment aligned on axis-z and having uniform MoI (8.1 × 10−8 kg m2) is subject a rotating field (ω = 80 π rad/s CCW) having no z component (τC = 1 × 10−3 Nm, τS = 0). Body’s initial conditions are: φ = 0.12962 rad, = 48.71 j +122.28 k. The vector is chosen in order the body obtains a symmetric angular motion around axis-z while its spin is half of the rotating field but in the opposite direction (q = −0.5). The ribbon like trace corresponds to overlapped trajectories of middle side points (blue dots) of the cylinder. Traces of top and bottom centers are also visible as flat lines which are precise circles on the xy projection. This simulation runs about 450 ms, corresponding to 22.5 cycles of the rotating field. Simulation shows that the body obtains a symmetric angular motion around axis-z despite absence of static component of the rotating field. (b) A similar simulation where body size is ⌀7 × 5 mm, MoI’s IA = 1.4127 × 10−7, IR = 8.2654 × 10−8, υ = ω = 80 π rad/s CCW. Motion is found stable and symmetric around axis-z where angle φ is −0.5706 rad. Simulation ran for 275 ms. Trajectories of selected points (actually any point belong to the body) draw circles parallel to the xy plane since the body has a simple motion around axis-z (q = 1). (c) Motion of the same body but with different initial conditions where = −30.28 j − 373.29 k (rad/s), φ0 = 0.24337 rad and ω = 253.15 rad/s. While the motion appears stable (run time = 348 ms), the body speeds up about 0.5 rad/s during this period. Red and blue traces correspond to top and bottom centers points, respectively. In both simulations, the stability of the motion around axis-z is obtained by the spin of the body since the rotating field has no static component.
Figure 13.
(a) A simulation showing motion of a spinning cylindrical body (⌀5.245 × 9.087 mm) having magnetic moment aligned on axis-z and having uniform MoI (8.1 × 10−8 kg m2) is subject a rotating field (ω = 80 π rad/s CCW) having no z component (τC = 1 × 10−3 Nm, τS = 0). Body’s initial conditions are: φ = 0.12962 rad, = 48.71 j +122.28 k. The vector is chosen in order the body obtains a symmetric angular motion around axis-z while its spin is half of the rotating field but in the opposite direction (q = −0.5). The ribbon like trace corresponds to overlapped trajectories of middle side points (blue dots) of the cylinder. Traces of top and bottom centers are also visible as flat lines which are precise circles on the xy projection. This simulation runs about 450 ms, corresponding to 22.5 cycles of the rotating field. Simulation shows that the body obtains a symmetric angular motion around axis-z despite absence of static component of the rotating field. (b) A similar simulation where body size is ⌀7 × 5 mm, MoI’s IA = 1.4127 × 10−7, IR = 8.2654 × 10−8, υ = ω = 80 π rad/s CCW. Motion is found stable and symmetric around axis-z where angle φ is −0.5706 rad. Simulation ran for 275 ms. Trajectories of selected points (actually any point belong to the body) draw circles parallel to the xy plane since the body has a simple motion around axis-z (q = 1). (c) Motion of the same body but with different initial conditions where = −30.28 j − 373.29 k (rad/s), φ0 = 0.24337 rad and ω = 253.15 rad/s. While the motion appears stable (run time = 348 ms), the body speeds up about 0.5 rad/s during this period. Red and blue traces correspond to top and bottom centers points, respectively. In both simulations, the stability of the motion around axis-z is obtained by the spin of the body since the rotating field has no static component.
![Symmetry 13 00442 g013 Symmetry 13 00442 g013]()
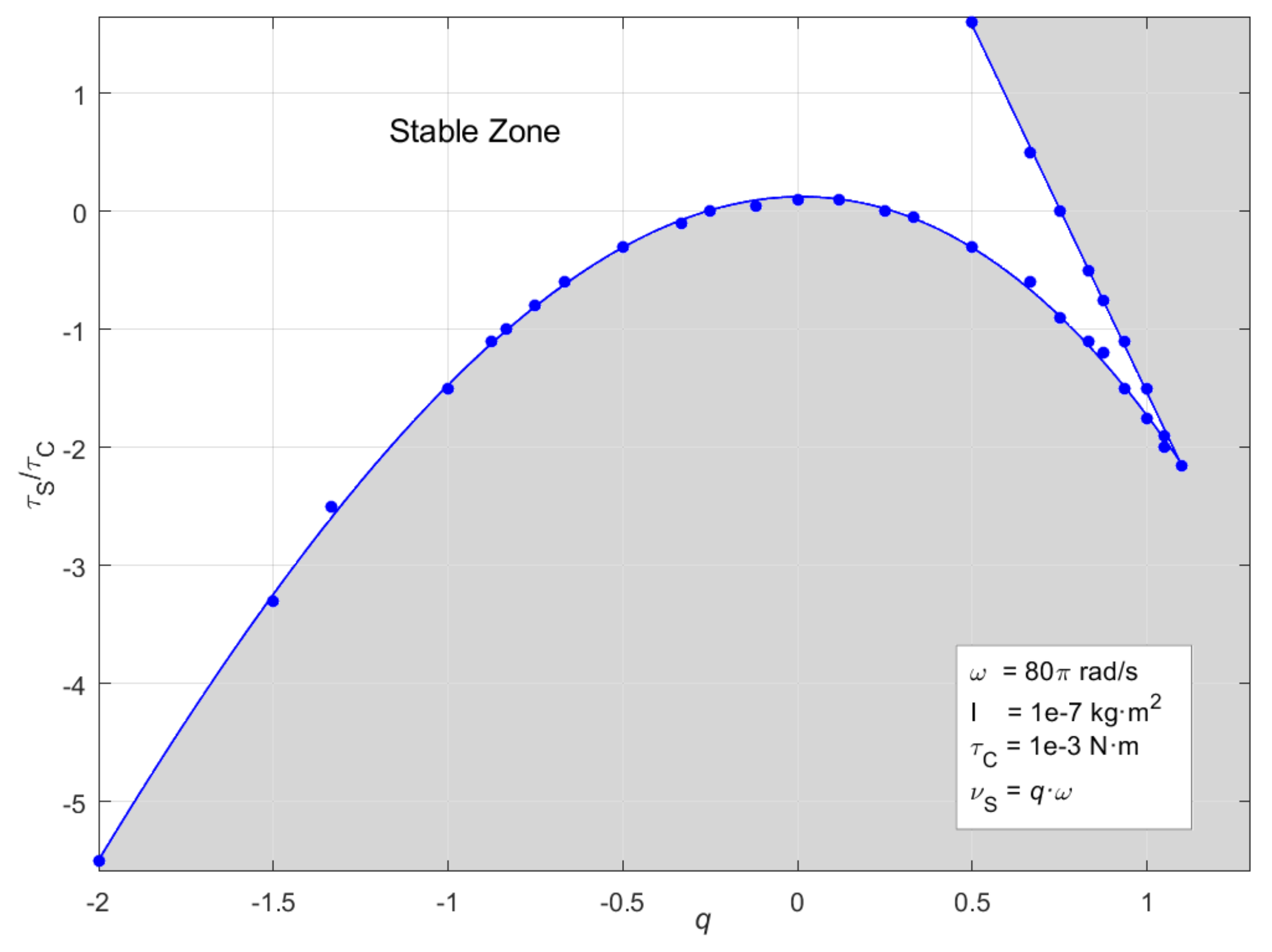
Figure 14.
Dependence of the motion stability of a rotating body subject a rotating torque to the body spin and to the static component of the torque for a configuration where the body is a homogeneous cylindrical object having equal principal MoI equal to 1 × 10−7 Nm2. The rotating torque assumed be obtained by a homogeneous rotating magnetic field around axis-z with an angular velocity 80 π rad/s interacting with the magnetic moment of the body centered at origin. This torque is defined by cyclic and static torque coefficients τC and τS. This chart is obtained by running the simulation for various values of parameter τS and body spin velocity υS which are presented by parameter q corresponding to ratio υS /ω. Each data point on the curve which separates stable and unstable zones correspond to parameter pairs providing stable motion. These stable data points are paired with unstable data points at proximity but residing in the unstable region (not shown). This chart only covers cases where the angular motion of the body is in the opposite phase of the driving field, conforming the PFR scheme. There are also cases where body motion is stable but in the same phase of the rotating field where parameter q is greater than one. These cases also cover negative τS values. The parabolic part of the curve fits to a polynomial function of third degree with R-square better than 0.999 where coefficients A0 to A3 are (0.12, 0.04, −1.72, −0.17).
Figure 14.
Dependence of the motion stability of a rotating body subject a rotating torque to the body spin and to the static component of the torque for a configuration where the body is a homogeneous cylindrical object having equal principal MoI equal to 1 × 10−7 Nm2. The rotating torque assumed be obtained by a homogeneous rotating magnetic field around axis-z with an angular velocity 80 π rad/s interacting with the magnetic moment of the body centered at origin. This torque is defined by cyclic and static torque coefficients τC and τS. This chart is obtained by running the simulation for various values of parameter τS and body spin velocity υS which are presented by parameter q corresponding to ratio υS /ω. Each data point on the curve which separates stable and unstable zones correspond to parameter pairs providing stable motion. These stable data points are paired with unstable data points at proximity but residing in the unstable region (not shown). This chart only covers cases where the angular motion of the body is in the opposite phase of the driving field, conforming the PFR scheme. There are also cases where body motion is stable but in the same phase of the rotating field where parameter q is greater than one. These cases also cover negative τS values. The parabolic part of the curve fits to a polynomial function of third degree with R-square better than 0.999 where coefficients A0 to A3 are (0.12, 0.04, −1.72, −0.17).
![Symmetry 13 00442 g014 Symmetry 13 00442 g014]()
Figure 15.
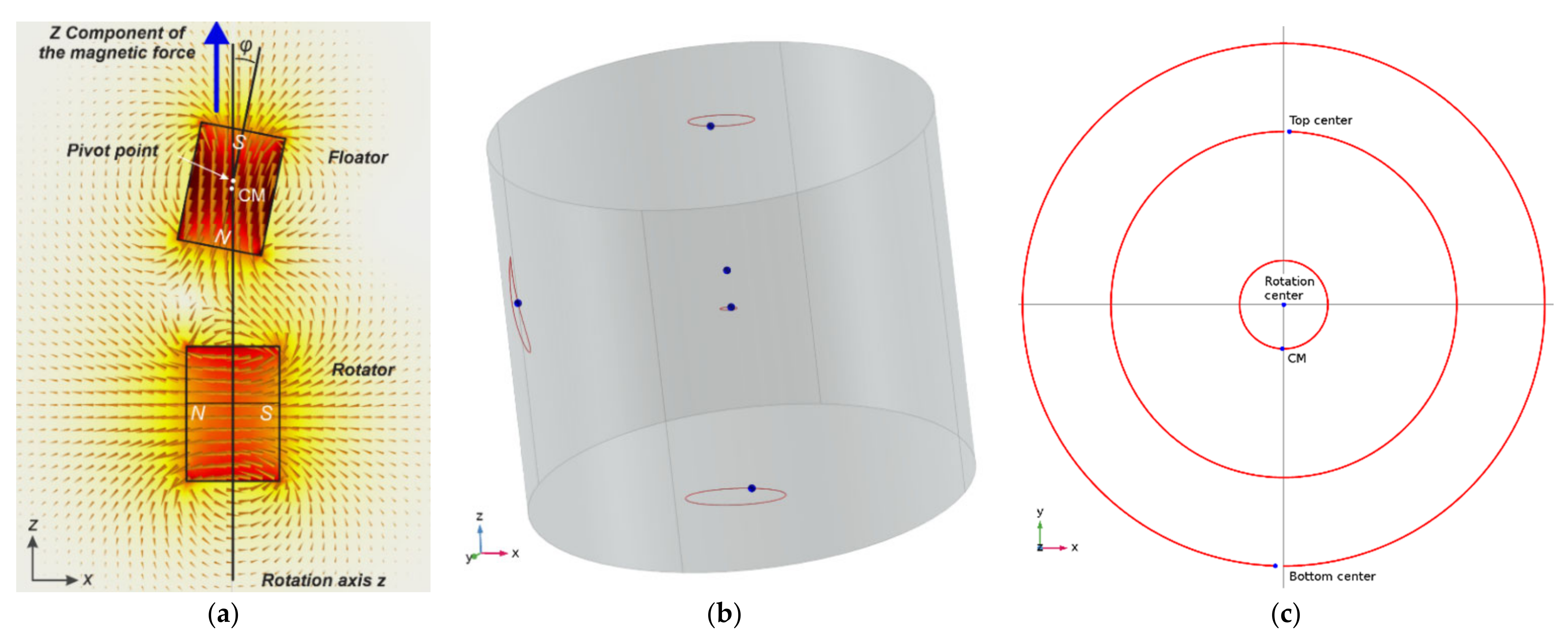
(a) A visualization of magnetic field and alignment of the floator in the interaction with the rotator in a basic configuration shown on the plane where magnetic moments lies. Due to the synchronized angular motion of the floator with the rotator rotation, this alignment is constant while this plane rotates around axis-z. The floator angular motion is accompanied with a translational motion since the rotator field also induce a force. These combined motions cause the floator’s rotation center (denoted as pivot point) to shift in z direction. In this alignment, floator’s N pole is always held toward rotator’s N pole and cause a steady repulsion in +z direction. Here, it can be also seen that effects of the angle φ and the shift of the floator’s CM (CM coincides by its magnetic moment) add up on this repulsion force. The motion of floator is called conical motion and the angle φ is retained all the time when the motion is have axis-z symmetry. This instance corresponds to ωt = π/2 of Equation (30), with reversed mAgneTIC poleS And to angle γ = 0. (b,c) Simulation result of a configuration similar to (a) where floator and rotator magnetic models are approximated as point dipoles. On this configuration, rotator is tilted around axis-y with a relatively large angle γ about 0.159 rad (9°), which induce a static field component (BS in direction of axis-z), corresponding to ratio BS/BC equal to 0.16 according to Equation (32). This ratio is above the minimum ratio 0.107 (Equation (51)) to keep the axis of the conical motion on axis-z Floator’s conical motion is characterized by angle φ equal to 0.2154 rad and by upward shift of the RC by 0.964 mm from CM. This shift can be seen also in these figures where CM circles around axis-z and by circle of bottom center point being larger than of the top center point. Rotating field velocity is 60 π rAd/s and torque coefficients τC and τS are 7.5 × 10−4 and 1.2 × 10−4 Nm, respectively. Body has equal principal moments of inertia as 0.999 × 10−8 kg m2. Initial angular velocity vector of the body for obtaining this motion is ωF = 0.0045 I + 40.295 j + 4.355 k rad/s. The simulation ran about 683 ms. Since the position and orientation of the floator’s magnetic moment is constant in a co-rotating reference frame with the field, torque and force received from the field are also constant.
Figure 15.
(a) A visualization of magnetic field and alignment of the floator in the interaction with the rotator in a basic configuration shown on the plane where magnetic moments lies. Due to the synchronized angular motion of the floator with the rotator rotation, this alignment is constant while this plane rotates around axis-z. The floator angular motion is accompanied with a translational motion since the rotator field also induce a force. These combined motions cause the floator’s rotation center (denoted as pivot point) to shift in z direction. In this alignment, floator’s N pole is always held toward rotator’s N pole and cause a steady repulsion in +z direction. Here, it can be also seen that effects of the angle φ and the shift of the floator’s CM (CM coincides by its magnetic moment) add up on this repulsion force. The motion of floator is called conical motion and the angle φ is retained all the time when the motion is have axis-z symmetry. This instance corresponds to ωt = π/2 of Equation (30), with reversed mAgneTIC poleS And to angle γ = 0. (b,c) Simulation result of a configuration similar to (a) where floator and rotator magnetic models are approximated as point dipoles. On this configuration, rotator is tilted around axis-y with a relatively large angle γ about 0.159 rad (9°), which induce a static field component (BS in direction of axis-z), corresponding to ratio BS/BC equal to 0.16 according to Equation (32). This ratio is above the minimum ratio 0.107 (Equation (51)) to keep the axis of the conical motion on axis-z Floator’s conical motion is characterized by angle φ equal to 0.2154 rad and by upward shift of the RC by 0.964 mm from CM. This shift can be seen also in these figures where CM circles around axis-z and by circle of bottom center point being larger than of the top center point. Rotating field velocity is 60 π rAd/s and torque coefficients τC and τS are 7.5 × 10−4 and 1.2 × 10−4 Nm, respectively. Body has equal principal moments of inertia as 0.999 × 10−8 kg m2. Initial angular velocity vector of the body for obtaining this motion is ωF = 0.0045 I + 40.295 j + 4.355 k rad/s. The simulation ran about 683 ms. Since the position and orientation of the floator’s magnetic moment is constant in a co-rotating reference frame with the field, torque and force received from the field are also constant.
![Symmetry 13 00442 g015 Symmetry 13 00442 g015]()
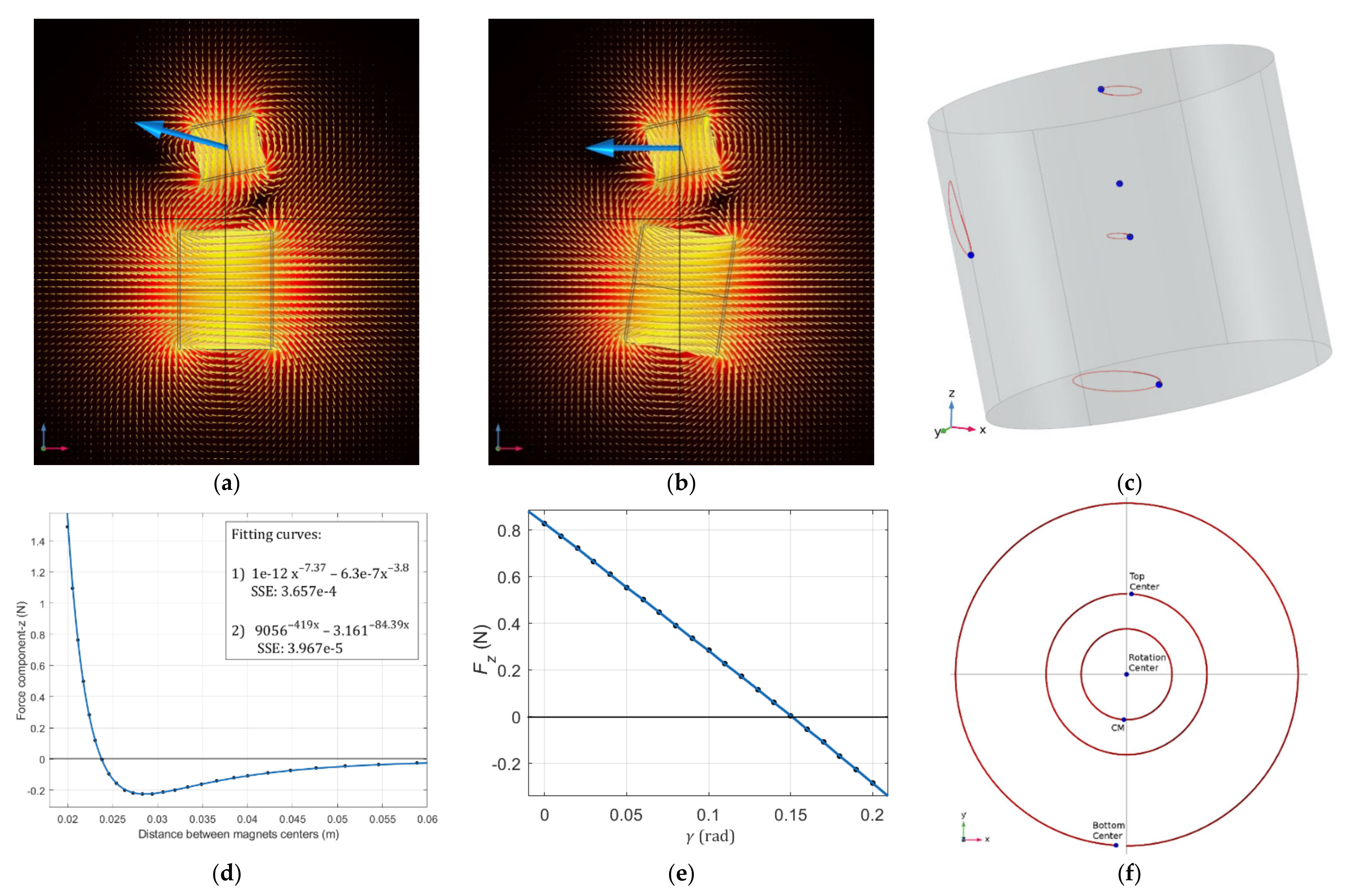
Figure 16.
An integrated magnetic (
a–
e) and rigid body dynamics simulation (
c,
f) of PFR and MBS. Alignment of bodies, torque and component-
x of the forces are shared between simulations. (
a) Floator (top magnet) experiences torque and force (blue arrow) from the rotator (bottom magnet) which is a dipole on the
xy plane supposed to rotate around axis-
z. The induced rotating torque generates the conical motion with angle
φ = 0.213 rad. This motion also has a lateral component
β (0.37 mm in amplitude) due the force component rotating on the
xy plane. This has an effect to shift the center of the angular motion (RC) away from rotator about 0.18 times of the body height from CM as 1.7 mm. The phase lag condition can be seen here within lateral and angular positions and corresponding acceleration vectors where the bottom pole of the floator approaches the pole of the rotator having the same polarity despite forces and the torque trying the opposite. As a result, the component-
z of the force get positive sign; that is, away from rotator. (
b) The requirement of static field for alignment of the axis of the conical motion with axis-
z is obtained by the tilt (angle
γ) of the rotator, causing one pole to look slightly up and the other down. The effect of this tilt is the generation of a magnetic moment in
z direction, constant in time. This moment generates the static field
BS responsible for static torque
τS and also generates an attractive force in
z direction when the floator is aligned to it in parallel. In the simulation (
b), the angle
γ is set to 0.151 rad (6.3°) in order to obtain component-
z of the force between magnets as zero on this specific distance (
r = 2.38 mm) between magnets centers. Complete parameters of this simulation can be found in
Table 4, No. 5. (
c,
f) Motion figures of the floator. The torque and the force responsible for this motion is obtained by its interaction with the rotator through magnetic simulation where orientation and position data is carried from simulation of rigid body dynamics. Red traces are trajectories of selected points (blue dots) on the floator projected on
xz and
xy planes. (
d) Variation of component-
z of the magnetic force versus distance between body centers in configuration b where the tilt angle and
x offset of the floator satisfying both simulations. (
e) Variation of component-
z of the force with the tilt angle
γ of the rotator where configurations corresponding to
γ = 0 and 0.151 rad are shown in figures (
a) and (
b), respectively.
Figure 16.
An integrated magnetic (
a–
e) and rigid body dynamics simulation (
c,
f) of PFR and MBS. Alignment of bodies, torque and component-
x of the forces are shared between simulations. (
a) Floator (top magnet) experiences torque and force (blue arrow) from the rotator (bottom magnet) which is a dipole on the
xy plane supposed to rotate around axis-
z. The induced rotating torque generates the conical motion with angle
φ = 0.213 rad. This motion also has a lateral component
β (0.37 mm in amplitude) due the force component rotating on the
xy plane. This has an effect to shift the center of the angular motion (RC) away from rotator about 0.18 times of the body height from CM as 1.7 mm. The phase lag condition can be seen here within lateral and angular positions and corresponding acceleration vectors where the bottom pole of the floator approaches the pole of the rotator having the same polarity despite forces and the torque trying the opposite. As a result, the component-
z of the force get positive sign; that is, away from rotator. (
b) The requirement of static field for alignment of the axis of the conical motion with axis-
z is obtained by the tilt (angle
γ) of the rotator, causing one pole to look slightly up and the other down. The effect of this tilt is the generation of a magnetic moment in
z direction, constant in time. This moment generates the static field
BS responsible for static torque
τS and also generates an attractive force in
z direction when the floator is aligned to it in parallel. In the simulation (
b), the angle
γ is set to 0.151 rad (6.3°) in order to obtain component-
z of the force between magnets as zero on this specific distance (
r = 2.38 mm) between magnets centers. Complete parameters of this simulation can be found in
Table 4, No. 5. (
c,
f) Motion figures of the floator. The torque and the force responsible for this motion is obtained by its interaction with the rotator through magnetic simulation where orientation and position data is carried from simulation of rigid body dynamics. Red traces are trajectories of selected points (blue dots) on the floator projected on
xz and
xy planes. (
d) Variation of component-
z of the magnetic force versus distance between body centers in configuration b where the tilt angle and
x offset of the floator satisfying both simulations. (
e) Variation of component-
z of the force with the tilt angle
γ of the rotator where configurations corresponding to
γ = 0 and 0.151 rad are shown in figures (
a) and (
b), respectively.
![Symmetry 13 00442 g016 Symmetry 13 00442 g016]()
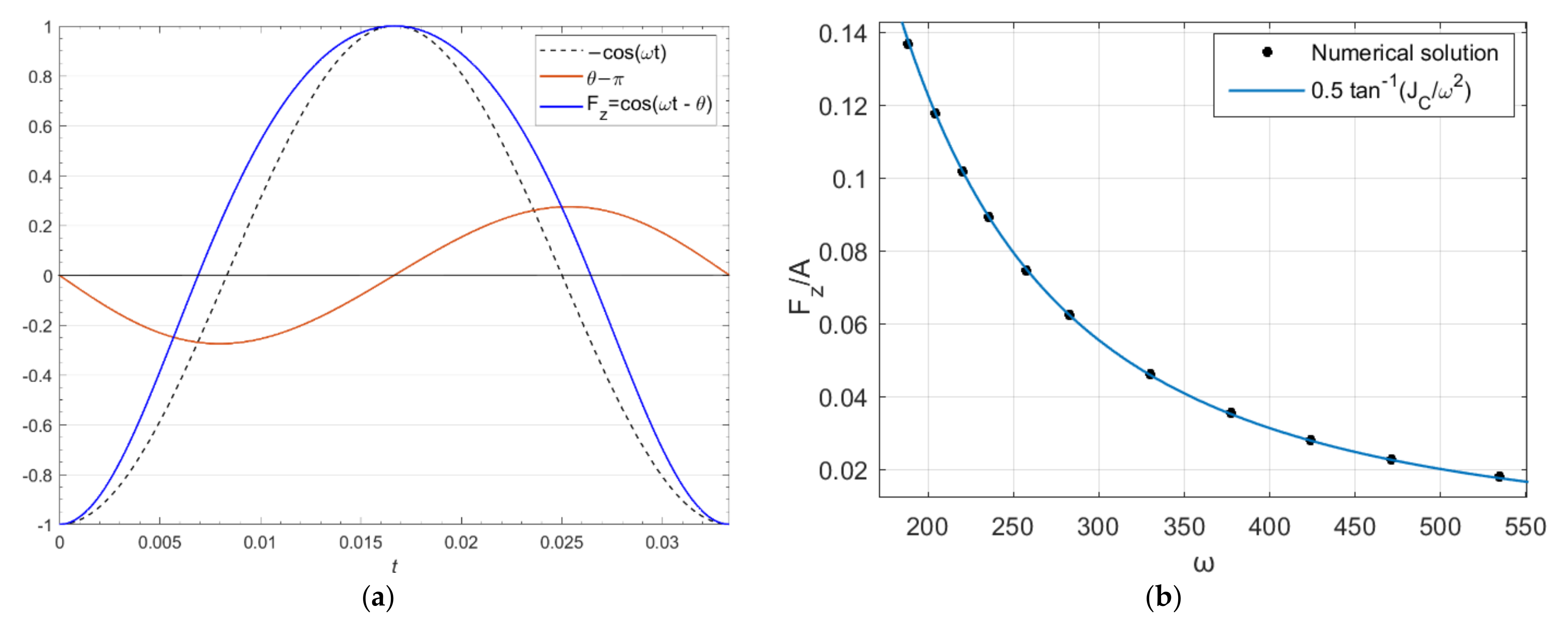
Figure 17.
(
a) Plot of floator azimuthal motion
θ (
T) and the
z component of the force
Fz (
T) it receives for the configuration 1 at
Figure 4. Red curve corresponds to angle
θ which varies between π ± 0.275. The force
Fz marked by the blue curve is a deformed cosine curve which leaves its negative region early and the positive region late. As a result, the integral of this force becomes positive, corresponding to a force in direction of the rotator weak field. A reference cosine curve is plotted with a dashed line. The value +1 of the
Fz in this plot corresponds to the force when dipoles are parallel (
θ =
ωT =
π). (
b) A curve showing variation of F
Z/A by
ω which fits well to the formula
.
Figure 17.
(
a) Plot of floator azimuthal motion
θ (
T) and the
z component of the force
Fz (
T) it receives for the configuration 1 at
Figure 4. Red curve corresponds to angle
θ which varies between π ± 0.275. The force
Fz marked by the blue curve is a deformed cosine curve which leaves its negative region early and the positive region late. As a result, the integral of this force becomes positive, corresponding to a force in direction of the rotator weak field. A reference cosine curve is plotted with a dashed line. The value +1 of the
Fz in this plot corresponds to the force when dipoles are parallel (
θ =
ωT =
π). (
b) A curve showing variation of F
Z/A by
ω which fits well to the formula
.
Figure 18.
(a–c) Configuration and motion characteristics of a cylindrical (⌀35 × 10) magnet (floator) trapped in air over a rotating magnet assembly (a stack of four 10 × 25 × 50) and by the help of a static field of an overhang magnet having horizontal dipole orientation (partially visible in (a), at top). The trapped magnet which having also horizontal dipole alignment is subject to angular oscillation on the axis-z. This oscillation can be seen on (b) from the fuzzy profile and from the elliptical light traces. On these traces, the major (horizontal) axis corresponds to an angular oscillation (peak-to-peak ~0.14 rad.) and the minor (vertical) likely to a translational oscillation (peak-to-peak ~1.5 mm). These oscillations further increase when floator get lowered by decreasing the pulling force of the static field. (c) The close-up of (a). On this camera view, angular oscillations become almost invisible, allowing to check presence of oscillations on the other DoF. (d) A similar configuration shown from top (about axis-z) where the floator consist of two stacked 25 × 10 × 10 magnets. Angular oscillations on axis-z can be clearly identified. Dimensions are in mm.
Figure 18.
(a–c) Configuration and motion characteristics of a cylindrical (⌀35 × 10) magnet (floator) trapped in air over a rotating magnet assembly (a stack of four 10 × 25 × 50) and by the help of a static field of an overhang magnet having horizontal dipole orientation (partially visible in (a), at top). The trapped magnet which having also horizontal dipole alignment is subject to angular oscillation on the axis-z. This oscillation can be seen on (b) from the fuzzy profile and from the elliptical light traces. On these traces, the major (horizontal) axis corresponds to an angular oscillation (peak-to-peak ~0.14 rad.) and the minor (vertical) likely to a translational oscillation (peak-to-peak ~1.5 mm). These oscillations further increase when floator get lowered by decreasing the pulling force of the static field. (c) The close-up of (a). On this camera view, angular oscillations become almost invisible, allowing to check presence of oscillations on the other DoF. (d) A similar configuration shown from top (about axis-z) where the floator consist of two stacked 25 × 10 × 10 magnets. Angular oscillations on axis-z can be clearly identified. Dimensions are in mm.
![Symmetry 13 00442 g018 Symmetry 13 00442 g018]()
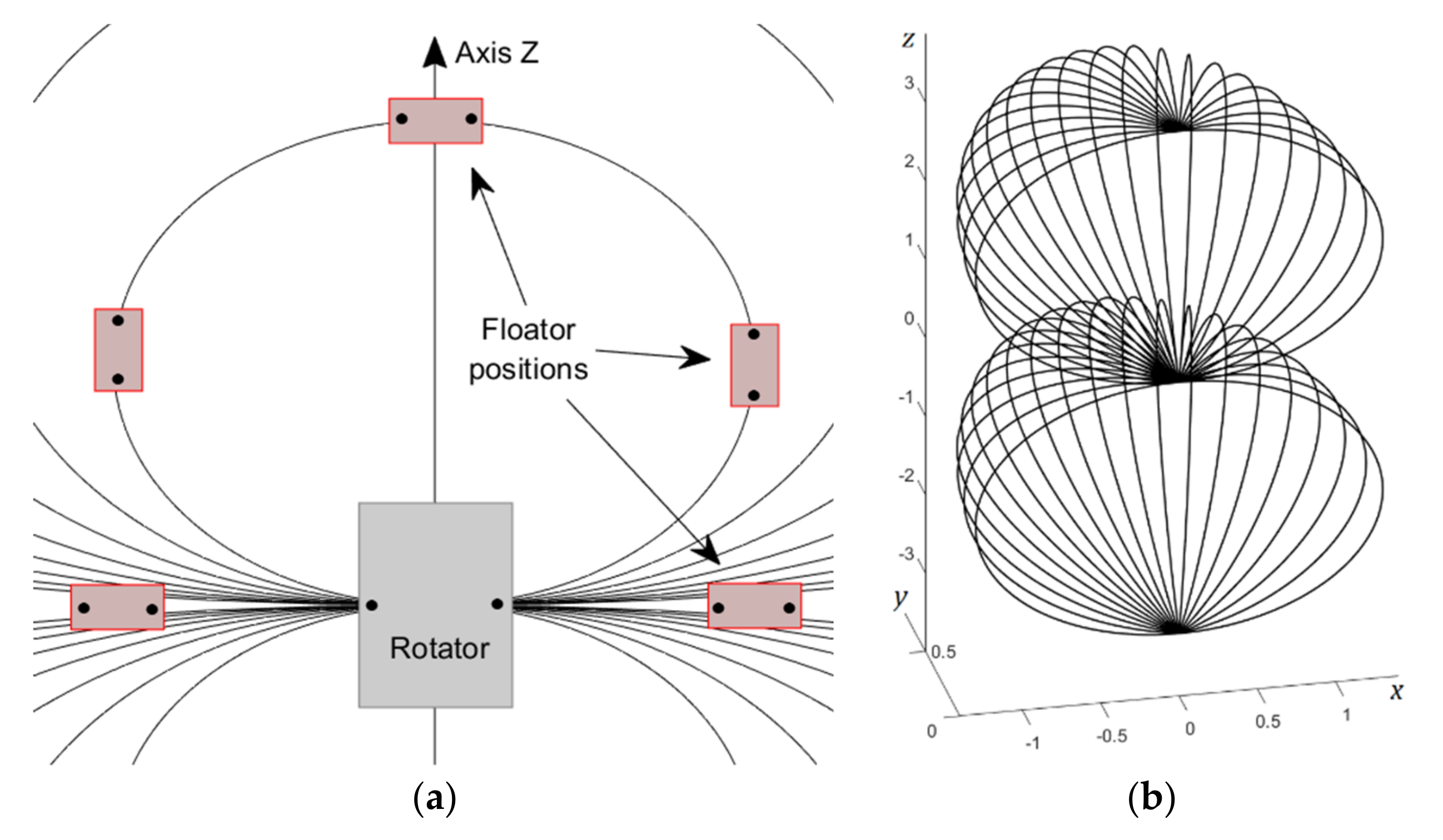
Figure 19.
(a) Diagram about alignment of floator with ‘guide-lines’. Pole positions are marked with dots. As the rotator spins around the axis-z, marks showing its polar orientation just means poles are on the side but not at the top/bottom. This is true also for the floator position aligned with axis-z, because in this position it has freedom to rotate on axis-z. (b) A 3D visualization of a single layer of guide-lines under xz cross section. The rotator (not shown) resides at the origin, poles in horizontal alignment. When the floator moment is aligned with a guide-line, the torque-phi becomes zero, therefore an angular equilibrium is found in absence of external fields.
Figure 19.
(a) Diagram about alignment of floator with ‘guide-lines’. Pole positions are marked with dots. As the rotator spins around the axis-z, marks showing its polar orientation just means poles are on the side but not at the top/bottom. This is true also for the floator position aligned with axis-z, because in this position it has freedom to rotate on axis-z. (b) A 3D visualization of a single layer of guide-lines under xz cross section. The rotator (not shown) resides at the origin, poles in horizontal alignment. When the floator moment is aligned with a guide-line, the torque-phi becomes zero, therefore an angular equilibrium is found in absence of external fields.
Figure 20.
Trapping configurations where various shaped floators are kept above rotators by the help of overhead magnets (shown on (d)) and the gravity in configurations where the rotator axis is not vertical. Rotators magnetic configurations do not generate static magnetic components and these can be seen in Figure 36g,h. In the configuration (d), overhead magnet position and orientation is hard to predict. Note: Background of this picture is erased for clarity.
Figure 20.
Trapping configurations where various shaped floators are kept above rotators by the help of overhead magnets (shown on (d)) and the gravity in configurations where the rotator axis is not vertical. Rotators magnetic configurations do not generate static magnetic components and these can be seen in Figure 36g,h. In the configuration (d), overhead magnet position and orientation is hard to predict. Note: Background of this picture is erased for clarity.
Figure 21.
(a) Circular angular motion trace obtained by reflecting a laser beam from mirror like polar face of a cylindrical magnet of dimension ⌀4 × 2.5 mm trapped horizontally in air, close to axis of a rotating field. Laser beam emanates from the hole at the center of the screen. The fuzzy halo is caused by the excessive intensity of light received by the camera and by the roughness of the magnet nickel coating. The rotating field is provided by a ⌀6 × 3 mm magnet attached to a micro motor by the plastic part of a syringe needle. This magnet provides also the required static field. Motor speed is in 22,000–28,000 RPM range. Magnets are type NdFeB/N35. As the floator is trapped horizontally, gravity pulls it in a radial direction which slightly shifts the floator off the axis; however, a deviation from the circle pattern is not noticeable here. It should be noted the circular oscillation is only one of the available of oscillation patterns which can be obtained in same or in similar configurations. (b) Similar configuration using floator as a 1/8” cube magnet (grade N52) which is partially visible behind the rotator. (c) The rotator assembly. Note that the magnet axis is tilted by angle γ from the rotation plane, generating a static dipole aligned with the rotation axis.
Figure 21.
(a) Circular angular motion trace obtained by reflecting a laser beam from mirror like polar face of a cylindrical magnet of dimension ⌀4 × 2.5 mm trapped horizontally in air, close to axis of a rotating field. Laser beam emanates from the hole at the center of the screen. The fuzzy halo is caused by the excessive intensity of light received by the camera and by the roughness of the magnet nickel coating. The rotating field is provided by a ⌀6 × 3 mm magnet attached to a micro motor by the plastic part of a syringe needle. This magnet provides also the required static field. Motor speed is in 22,000–28,000 RPM range. Magnets are type NdFeB/N35. As the floator is trapped horizontally, gravity pulls it in a radial direction which slightly shifts the floator off the axis; however, a deviation from the circle pattern is not noticeable here. It should be noted the circular oscillation is only one of the available of oscillation patterns which can be obtained in same or in similar configurations. (b) Similar configuration using floator as a 1/8” cube magnet (grade N52) which is partially visible behind the rotator. (c) The rotator assembly. Note that the magnet axis is tilted by angle γ from the rotation plane, generating a static dipole aligned with the rotation axis.
![Symmetry 13 00442 g021 Symmetry 13 00442 g021]()
Figure 22.
A dipole body consisting of a small cylindrical magnet (⌀4 × 2.5 mm) and a non magnetic needle section glued together (c) is trapped horizontally by a rotating dipole field produced by a rotating magnet (⌀6 × 3 mm). In (a), the trapping is seen from the top and from front on (b). The body’s MoI in directions orthogonal to needle orientation is increased due to the needle. From (b), it can be seen the body sits little below of the rotation axis because of its weight. This asymmetric position forces the needle orientation to horizontal, matching to the direction of the lower MoI. By defining xyz coordinates, z as main rotation axis, x as horizontal and y as vertical, angular oscillation consists of x and y components where amplitude of x component is several times larger than y. The fuzziness of the needle can be seen in (a) corresponds to the y component and the absence of z component from (b). (d) The elliptical pattern of angular oscillation obtained by a laser beam reflection from xy face of a body from a similar setup. It should be noted that oscillations on x and y axes correspond to deviation of the beam in y and x directions, respectively. (e) A similar configuration with a single arm based on a floator spherical magnet having diameter 1/8”, NdFeB/N42.
Figure 22.
A dipole body consisting of a small cylindrical magnet (⌀4 × 2.5 mm) and a non magnetic needle section glued together (c) is trapped horizontally by a rotating dipole field produced by a rotating magnet (⌀6 × 3 mm). In (a), the trapping is seen from the top and from front on (b). The body’s MoI in directions orthogonal to needle orientation is increased due to the needle. From (b), it can be seen the body sits little below of the rotation axis because of its weight. This asymmetric position forces the needle orientation to horizontal, matching to the direction of the lower MoI. By defining xyz coordinates, z as main rotation axis, x as horizontal and y as vertical, angular oscillation consists of x and y components where amplitude of x component is several times larger than y. The fuzziness of the needle can be seen in (a) corresponds to the y component and the absence of z component from (b). (d) The elliptical pattern of angular oscillation obtained by a laser beam reflection from xy face of a body from a similar setup. It should be noted that oscillations on x and y axes correspond to deviation of the beam in y and x directions, respectively. (e) A similar configuration with a single arm based on a floator spherical magnet having diameter 1/8”, NdFeB/N42.
![Symmetry 13 00442 g022 Symmetry 13 00442 g022]()
Figure 23.
Various configurations where magnets held in air by interaction of a rotating magnets. (
a) A stack of six ⌀10 × 10 mm magnets is trapped under a rotator assembly with a gap less than 4 mm. Here, the repulsive action is mostly generated by the lateral translational oscillation of the floator because the angular oscillation is too small to generate an effective repulsive action due to the large MoI of the floator in radial direction. Bottom figure shows the rotator assembly where two stacked ⌀25 × 4 mm magnets covered by a tape are housed in a plastic frame. (
b) A floator assembly consisting a 10 mm cube magnet sandwiched between two ⌀10 × 10 mm magnets hovers over a rotator assembly embedding an disk magnet ⌀30 × 5 mm rotating at 5530 RPM (579 rad/s) CWW. An overhead magnet help to keep rotator upright and partially compensate its weight. The Pizza tower appearance of the floator is behavior of long floators. From these pictures, the outcome of combined angular and translational motions which set rotation center of the body off the CM can be seen. This point is about 1/6 of the height of the body higher than CM. The unique outcome of this configuration is the sustained spin of the rotator at same speed of the rotator but in the opposite direction (CW). In order to obtain this result, floator is speeded-up this way by an air-jet until it reaches this speed. After cutting the air-jet, floator keeps indefinitely this speed and even anticipates some frictions (a touch of a soft brush). This counterintuitive behavior reminds the Rattleback effect [
22]. The misalignment of the floator rotation axis with rotator axis might allow to this effect be happens. The detail of the rotator assembly can be seen at Figure 47c. (
c) A ⌀10 × 10 mm, diametrically magnetized cylindrical floator magnet is held in air in a horizontal setup. The separation between magnets is about 10–12 mm. The floator equilibrium position is off the axis-
z since the gravity acts in radial direction. This produces the same angular alignment effect explained for the experiments shown in
Figure 22 since the floator is not axisymmetric with respect to dipole axis. Relatively large amplitude of the elliptical angular oscillation is visible for the minor axis (vertical). (
d) An asymmetric assembly of floator consisting of a rectangular magnet (15 × 10 × 5 mm, magnetized in thickness) and an axially magnetized cylindrical magnet (⌀10 × 10 mm) held in air by a rotator assembly hung by a thread, allowing five DoF. The sixth DoF (vertical) is also effective here because elasticity of thread allows small vertical motions of the rotator. The amplitude of angular oscillation on the axis of the camera angle at the bottom picture is larger than the top one as can be perceived. The rotator assembly consists of two stacked 20 × 10 × 10 mm magnets glued on the top face of a thin brass disk and a small ⌀9.5 × 1 mm disk magnet glued to the bottom face which provides the attractive static field. The brass disk (⌀44 mm) weights 13.8 g and have MoI figures as
IR = 2.152 × 10
−6 Nm
2,
IA = 4.292 × 10
−6 Nm
2. The purpose of this disk is to provide resistance or anticipate the magnetic torque caused by the floator. This subject is evaluated in
Section 6.
Figure 23.
Various configurations where magnets held in air by interaction of a rotating magnets. (
a) A stack of six ⌀10 × 10 mm magnets is trapped under a rotator assembly with a gap less than 4 mm. Here, the repulsive action is mostly generated by the lateral translational oscillation of the floator because the angular oscillation is too small to generate an effective repulsive action due to the large MoI of the floator in radial direction. Bottom figure shows the rotator assembly where two stacked ⌀25 × 4 mm magnets covered by a tape are housed in a plastic frame. (
b) A floator assembly consisting a 10 mm cube magnet sandwiched between two ⌀10 × 10 mm magnets hovers over a rotator assembly embedding an disk magnet ⌀30 × 5 mm rotating at 5530 RPM (579 rad/s) CWW. An overhead magnet help to keep rotator upright and partially compensate its weight. The Pizza tower appearance of the floator is behavior of long floators. From these pictures, the outcome of combined angular and translational motions which set rotation center of the body off the CM can be seen. This point is about 1/6 of the height of the body higher than CM. The unique outcome of this configuration is the sustained spin of the rotator at same speed of the rotator but in the opposite direction (CW). In order to obtain this result, floator is speeded-up this way by an air-jet until it reaches this speed. After cutting the air-jet, floator keeps indefinitely this speed and even anticipates some frictions (a touch of a soft brush). This counterintuitive behavior reminds the Rattleback effect [
22]. The misalignment of the floator rotation axis with rotator axis might allow to this effect be happens. The detail of the rotator assembly can be seen at Figure 47c. (
c) A ⌀10 × 10 mm, diametrically magnetized cylindrical floator magnet is held in air in a horizontal setup. The separation between magnets is about 10–12 mm. The floator equilibrium position is off the axis-
z since the gravity acts in radial direction. This produces the same angular alignment effect explained for the experiments shown in
Figure 22 since the floator is not axisymmetric with respect to dipole axis. Relatively large amplitude of the elliptical angular oscillation is visible for the minor axis (vertical). (
d) An asymmetric assembly of floator consisting of a rectangular magnet (15 × 10 × 5 mm, magnetized in thickness) and an axially magnetized cylindrical magnet (⌀10 × 10 mm) held in air by a rotator assembly hung by a thread, allowing five DoF. The sixth DoF (vertical) is also effective here because elasticity of thread allows small vertical motions of the rotator. The amplitude of angular oscillation on the axis of the camera angle at the bottom picture is larger than the top one as can be perceived. The rotator assembly consists of two stacked 20 × 10 × 10 mm magnets glued on the top face of a thin brass disk and a small ⌀9.5 × 1 mm disk magnet glued to the bottom face which provides the attractive static field. The brass disk (⌀44 mm) weights 13.8 g and have MoI figures as
IR = 2.152 × 10
−6 Nm
2,
IA = 4.292 × 10
−6 Nm
2. The purpose of this disk is to provide resistance or anticipate the magnetic torque caused by the floator. This subject is evaluated in
Section 6.
![Symmetry 13 00442 g023a Symmetry 13 00442 g023a]()
![Symmetry 13 00442 g023b Symmetry 13 00442 g023b]()
Figure 24.
2D simulations of a spinning dipole body scattering from a static field using MagPhyx application. While the static field is produced by the central point dipole, rotating dipole body is shown by the other circle. The embedded arrows show the instantaneous direction of the dipole moment. Red traces show the travelled path of the spinning free body.
Figure 24.
2D simulations of a spinning dipole body scattering from a static field using MagPhyx application. While the static field is produced by the central point dipole, rotating dipole body is shown by the other circle. The embedded arrows show the instantaneous direction of the dipole moment. Red traces show the travelled path of the spinning free body.
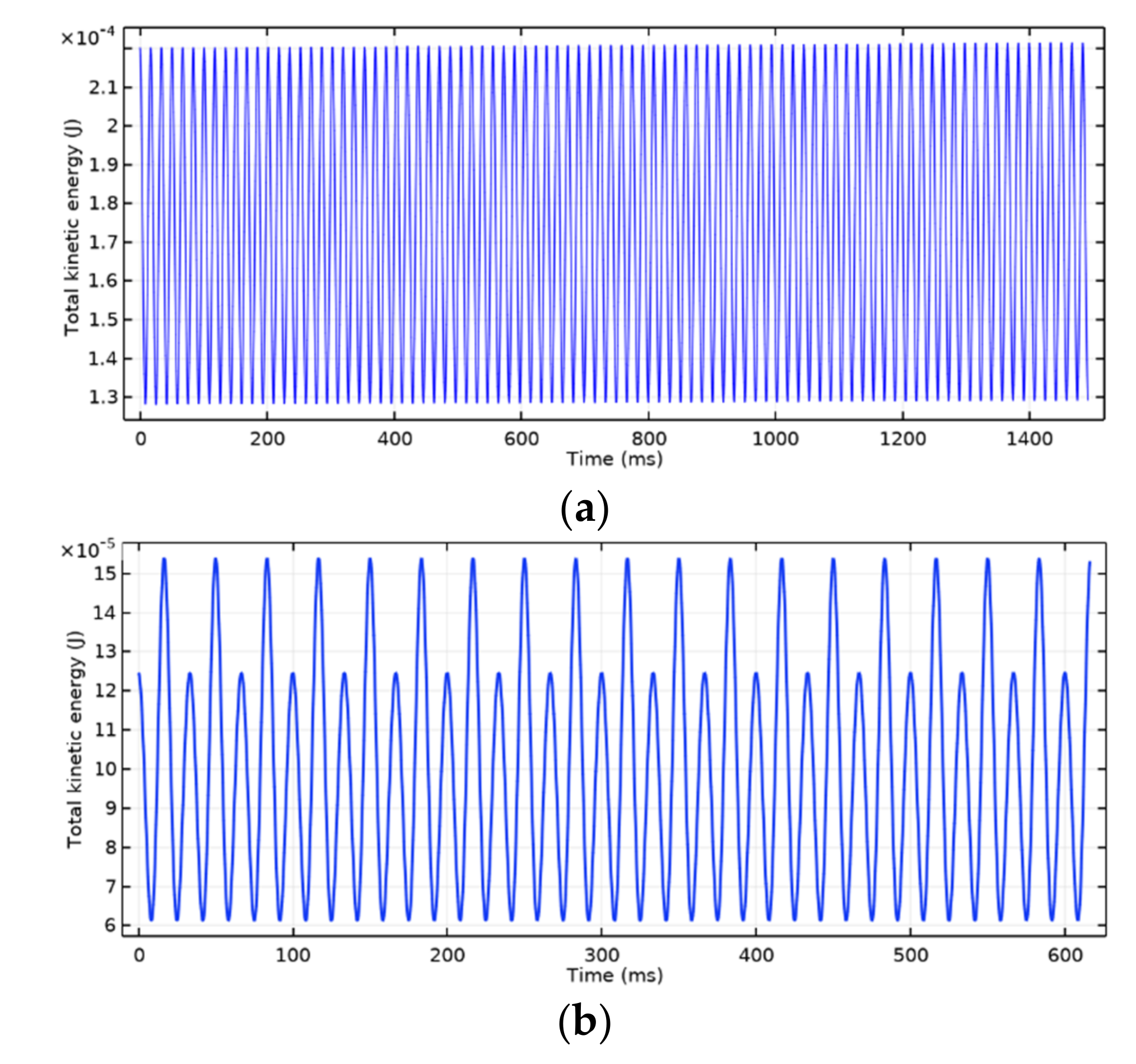
Figure 25.
(
a) The plot of kinetic energy of the floator corresponding to simulation at
Figure 9 where body is an ellipsoid. Kinetic energy oscillates around 1.74 × 10
−4 J with a constant amplitude 4.6 × 10
−5 J during the simulation time (1.5 s). This oscillation corresponds to harmonic angular motion of the body. The slight increase of energy is the simulation artefact, which is corrected later by reducing the time step. (
b) A similar plot of a simulation at
Figure 6, except the angle
λ is 45° instead of 48.8°. Kinetic energy oscillates in this case due to the axis of the conical motion not aligned with axis-
z but having the angle λ where the conical motion is elliptic. Frequency of the rotating field in both simulations is 60 π rad/s.
Figure 25.
(
a) The plot of kinetic energy of the floator corresponding to simulation at
Figure 9 where body is an ellipsoid. Kinetic energy oscillates around 1.74 × 10
−4 J with a constant amplitude 4.6 × 10
−5 J during the simulation time (1.5 s). This oscillation corresponds to harmonic angular motion of the body. The slight increase of energy is the simulation artefact, which is corrected later by reducing the time step. (
b) A similar plot of a simulation at
Figure 6, except the angle
λ is 45° instead of 48.8°. Kinetic energy oscillates in this case due to the axis of the conical motion not aligned with axis-
z but having the angle λ where the conical motion is elliptic. Frequency of the rotating field in both simulations is 60 π rad/s.
Figure 26.
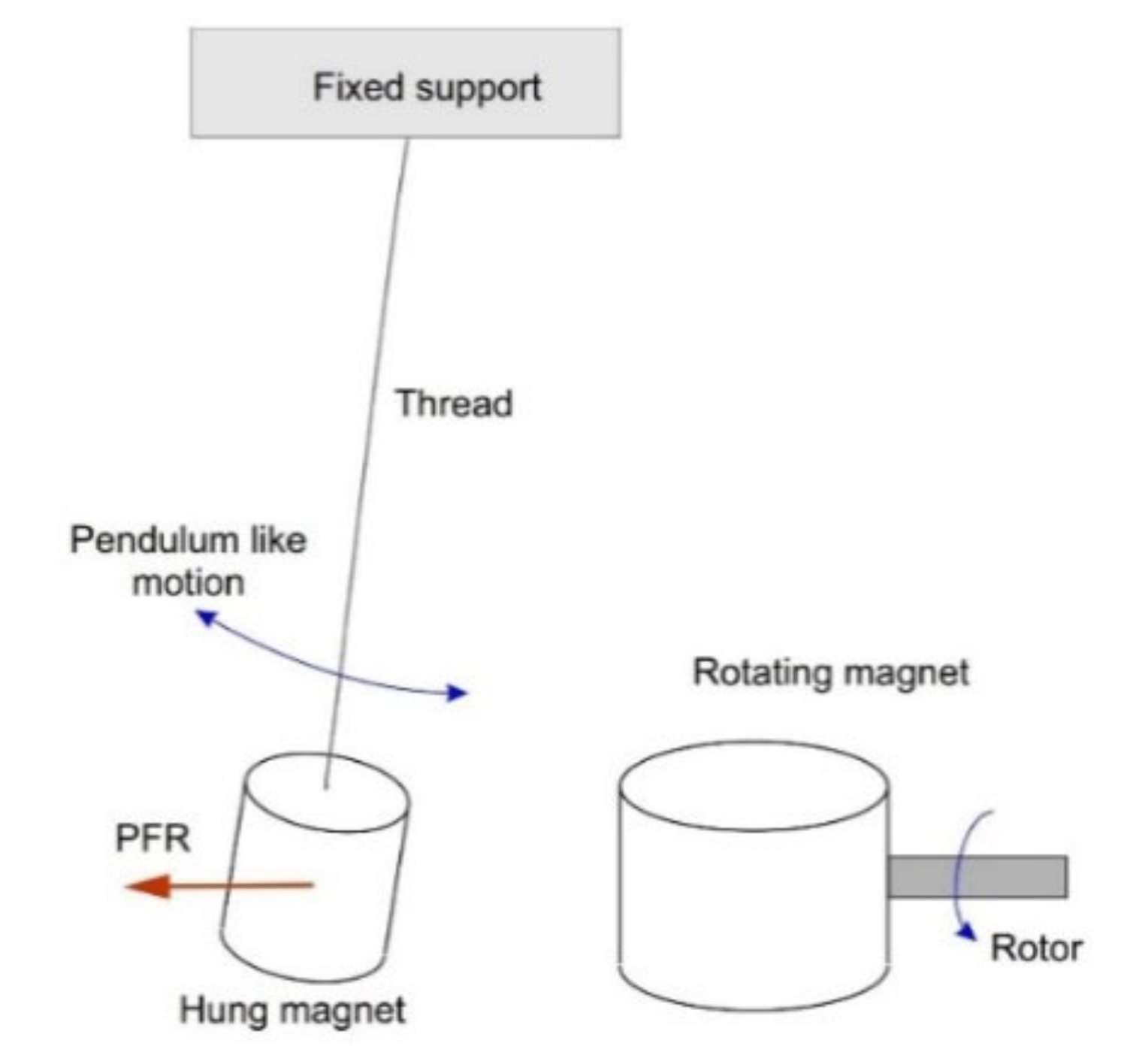
Pendulum like configuration where a dipole magnet attached to a thread experiences PFR from another dipole magnet rotating on an axis orthogonal to dipole axis. The orientation and fixture point of the hung magnet is not important. Rotor velocity can be chosen in the 5000–15,000 RPM range for a pendulum magnet of ⌀10 × 10 mm in size.
Figure 26.
Pendulum like configuration where a dipole magnet attached to a thread experiences PFR from another dipole magnet rotating on an axis orthogonal to dipole axis. The orientation and fixture point of the hung magnet is not important. Rotor velocity can be chosen in the 5000–15,000 RPM range for a pendulum magnet of ⌀10 × 10 mm in size.
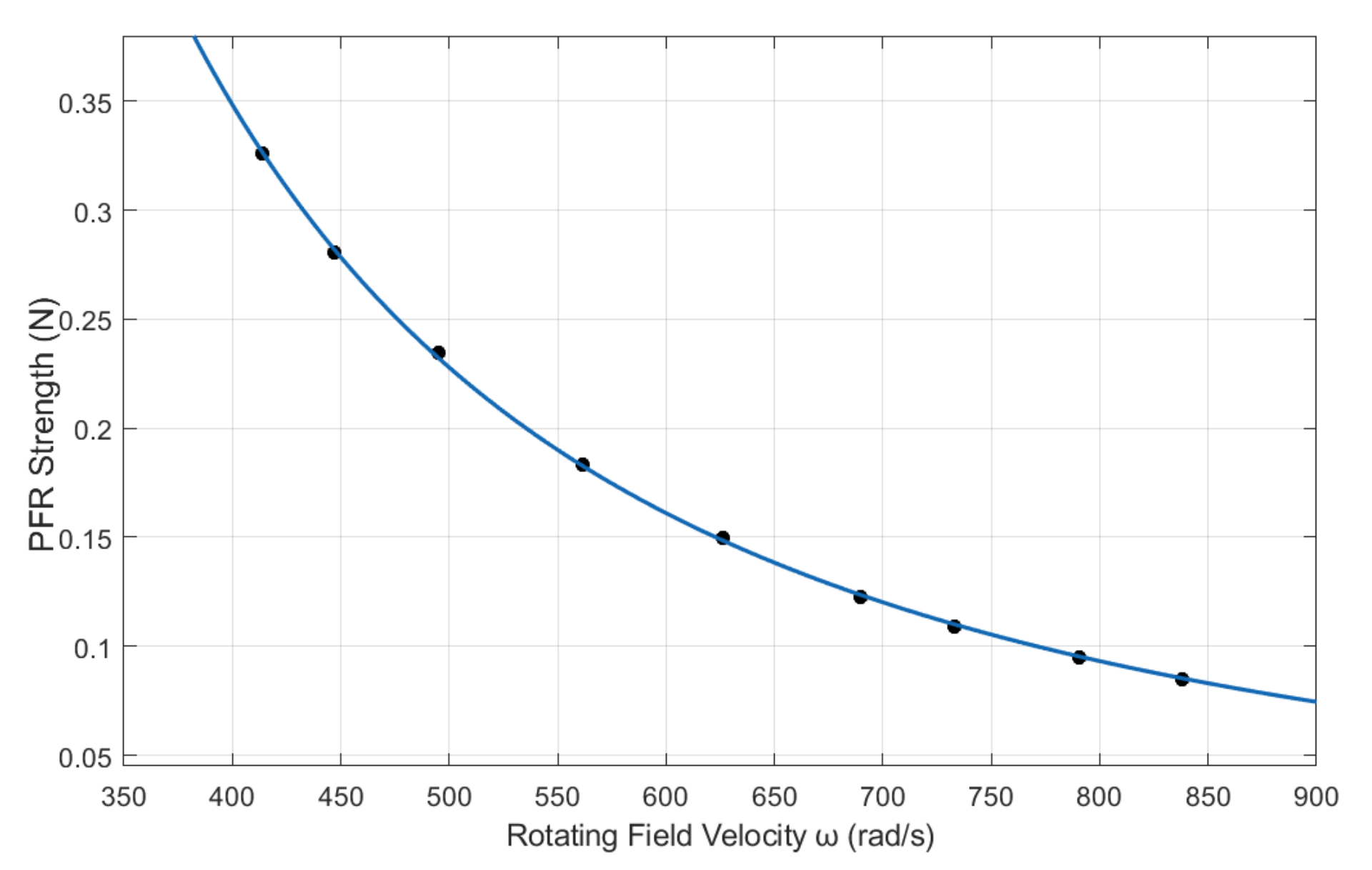
Figure 27.
Strength of polarity free repulsion varying with rotation speed of a dipole magnet acted on a magnet cushioned on a balance. Sample points fit well to function y = 224 × 106 x−1.9.
Figure 27.
Strength of polarity free repulsion varying with rotation speed of a dipole magnet acted on a magnet cushioned on a balance. Sample points fit well to function y = 224 × 106 x−1.9.
Figure 28.
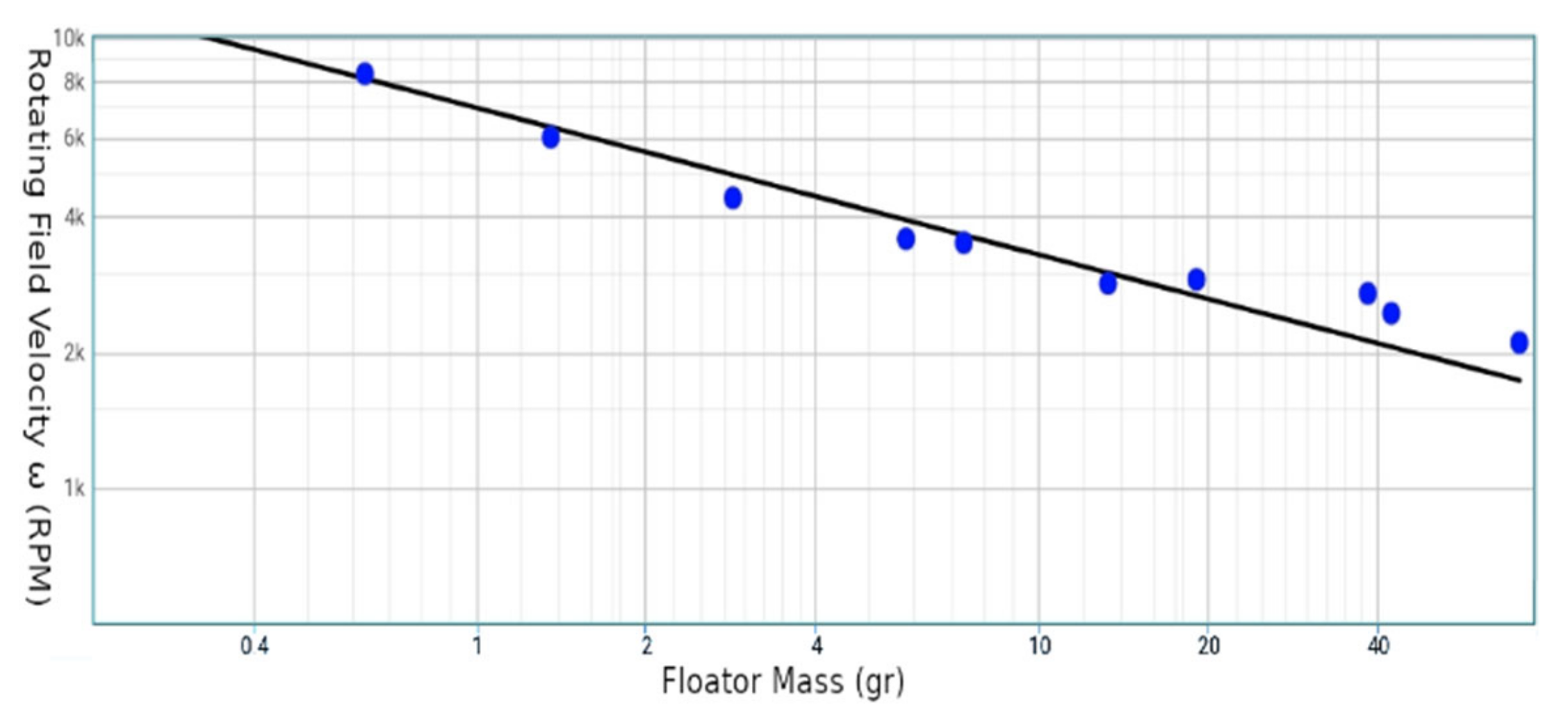
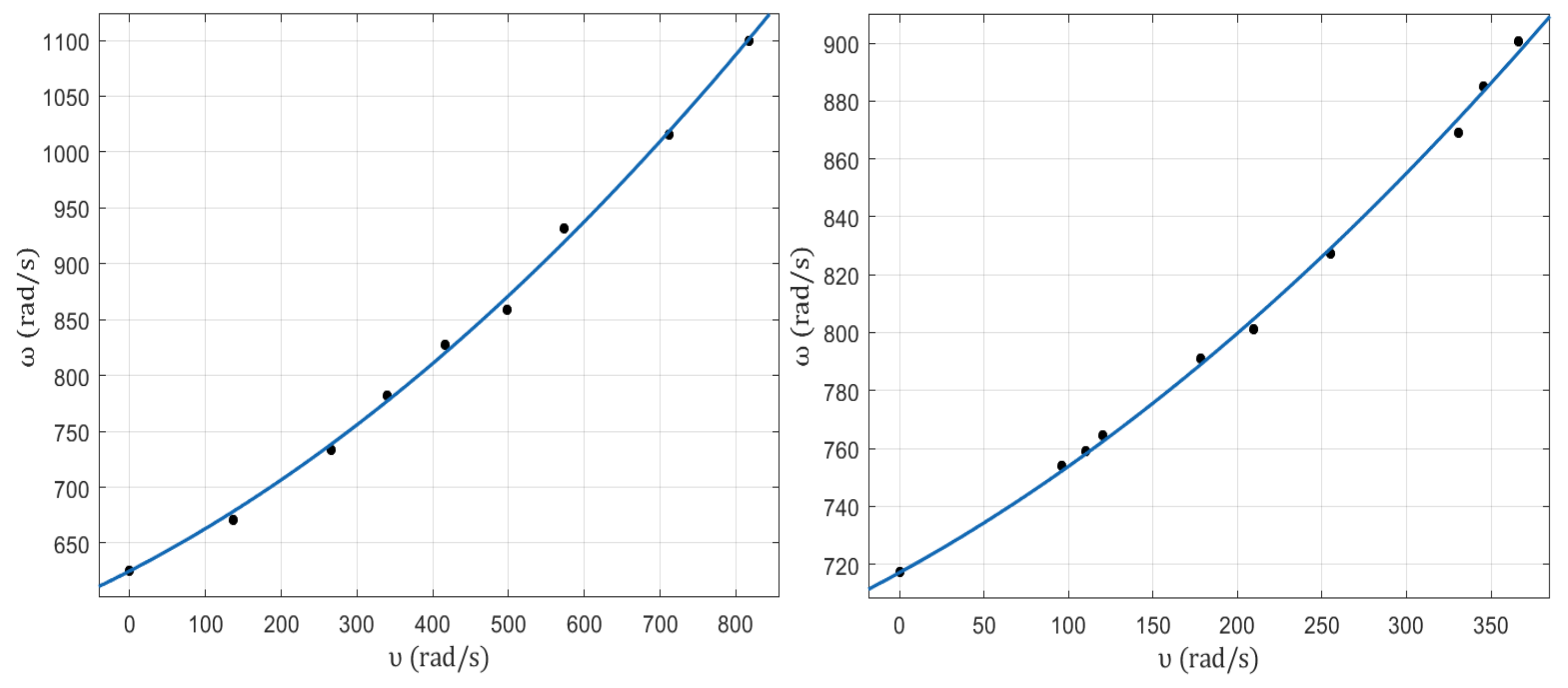
Minimum frequency required for stability for levitating bodies obtained by tests using the same rotator configuration and using floators of different masses m but having similar geometries. This relation is reflected by the function ω = a mb by curve fitting method where the exponent b = −0.326. This shows a possible relation between ω and body mass by its inverse cube root (b = −0.333).
Figure 28.
Minimum frequency required for stability for levitating bodies obtained by tests using the same rotator configuration and using floators of different masses m but having similar geometries. This relation is reflected by the function ω = a mb by curve fitting method where the exponent b = −0.326. This shows a possible relation between ω and body mass by its inverse cube root (b = −0.333).
Figure 29.
Images showing a bound state of small magnets held horizontally. (a) A magnet fragment about 1.3 mm in size trapped by a rotating dipole magnet of ⌀4 × 2.5 mm in size attached to a micro motor running about 1500 rev/s (b) A 1/8” cube magnet bound to a rotating dipole magnet of size ⌀6 × 3 mm rotating about 420 rev/s (c) Picture of a floator and a rotator assembly mount to a micro motor having dimensions ⌀4 × 10 mm. Both magnets are irregular NdFeB type fragments. Vertical lines are 8 mm apart.
Figure 29.
Images showing a bound state of small magnets held horizontally. (a) A magnet fragment about 1.3 mm in size trapped by a rotating dipole magnet of ⌀4 × 2.5 mm in size attached to a micro motor running about 1500 rev/s (b) A 1/8” cube magnet bound to a rotating dipole magnet of size ⌀6 × 3 mm rotating about 420 rev/s (c) Picture of a floator and a rotator assembly mount to a micro motor having dimensions ⌀4 × 10 mm. Both magnets are irregular NdFeB type fragments. Vertical lines are 8 mm apart.
Figure 30.
Realization (top) of split dipoles (a,b) and quadrupole (c) and their experimental outcomes (bottom). No levitation can be obtained with quadrupole configuration (c) but only a radial inward force. Magnets used in rotator setups (a,b) are 25 × 20 × 5 mm, in (c) is 25 × 10 × 10 mm, all of them magnetized in thickness. Floators dimensions are (a): ⌀10 × 10 mm, (b): ⌀15 mm, (c): (⌀19.7–8) × 3.9 mm.
Figure 30.
Realization (top) of split dipoles (a,b) and quadrupole (c) and their experimental outcomes (bottom). No levitation can be obtained with quadrupole configuration (c) but only a radial inward force. Magnets used in rotator setups (a,b) are 25 × 20 × 5 mm, in (c) is 25 × 10 × 10 mm, all of them magnetized in thickness. Floators dimensions are (a): ⌀10 × 10 mm, (b): ⌀15 mm, (c): (⌀19.7–8) × 3.9 mm.
Figure 31.
Various trapping solutions. (a) A spherical dipole magnet ⌀15 mm is levitating over a large rotating dipole magnet assembly by the help of an overhang magnet and gravity. In this configuration, magnetic forces are upward and are balanced by the weight of the floating magnet. (b,c) A cube dipole magnet is trapped by a rotating magnetic assembly consisting of five stacked 20 × 20 × 5 mm magnets housed in a cylindrical aluminum block and having dipole orientation orthogonal to rotation axis. A small magnet (a stack of two ⌀6 × 3 mm) fixed on the top face and aligned with rotation axis provides the attractive field. Stable equilibrium is possible despite the attractive magnet being closer to the trapped magnet because the slope of the PFR vs. distance is still larger than of the attractive force.
Figure 31.
Various trapping solutions. (a) A spherical dipole magnet ⌀15 mm is levitating over a large rotating dipole magnet assembly by the help of an overhang magnet and gravity. In this configuration, magnetic forces are upward and are balanced by the weight of the floating magnet. (b,c) A cube dipole magnet is trapped by a rotating magnetic assembly consisting of five stacked 20 × 20 × 5 mm magnets housed in a cylindrical aluminum block and having dipole orientation orthogonal to rotation axis. A small magnet (a stack of two ⌀6 × 3 mm) fixed on the top face and aligned with rotation axis provides the attractive field. Stable equilibrium is possible despite the attractive magnet being closer to the trapped magnet because the slope of the PFR vs. distance is still larger than of the attractive force.
Figure 32.
A ⌀6 × 3 mm dipole magnet is trapped by a rotating magnetic assembly consisting of a pair of the same magnet arranged like propeller blades and may having asymmetry with respect to rotation axis. Since magnets have opposite alignments with respect to rotation axis, this causes near zero static field on this axis. This way, trapping occurs in radial direction of the rotating field.
Figure 32.
A ⌀6 × 3 mm dipole magnet is trapped by a rotating magnetic assembly consisting of a pair of the same magnet arranged like propeller blades and may having asymmetry with respect to rotation axis. Since magnets have opposite alignments with respect to rotation axis, this causes near zero static field on this axis. This way, trapping occurs in radial direction of the rotating field.
Figure 33.
(a) A small dipole magnet trapped in air by a rotating circular track of lined up magnets, which their dipoles are in radial direction, alternately inward and outwards shown on (b). It looks like the trapping occurs over this track due to a possible local minimum of the alternating field present at this zone.
Figure 33.
(a) A small dipole magnet trapped in air by a rotating circular track of lined up magnets, which their dipoles are in radial direction, alternately inward and outwards shown on (b). It looks like the trapping occurs over this track due to a possible local minimum of the alternating field present at this zone.
Figure 34.
A cylindrical magnet (the small object at the center of the frame) is floating in air at the center of the equilateral triangular formation of large rotating magnet assemblies providing only AC fields (a cyclic field without static component).
Figure 34.
A cylindrical magnet (the small object at the center of the frame) is floating in air at the center of the equilateral triangular formation of large rotating magnet assemblies providing only AC fields (a cyclic field without static component).
Figure 35.
Similar experiment of the left picture but with isosceles triangular formation. Rotating unit at right has opposite rotation direction of the units at left.
Figure 35.
Similar experiment of the left picture but with isosceles triangular formation. Rotating unit at right has opposite rotation direction of the units at left.
Figure 36.
Dipole bodies trapped by various configurations of two rotating dipole units. Floating magnets dimensions (in mm) are (a) = ⌀9.5 × 1, (b) = ⌀25 × 5, (c,e) = ⌀10 × 10, (d) = ⌀15, (f) = ⌀12 × 10. Rotating assemblies embeds stacked magnets of dimensions 10 × 25 × 50, magnetized in thickness, four for all them, except three for units at (c). Rotating units are synchronized autonomously by the magnetic coupling mechanism. (g,h) Magnet arrangements of rotators.
Figure 36.
Dipole bodies trapped by various configurations of two rotating dipole units. Floating magnets dimensions (in mm) are (a) = ⌀9.5 × 1, (b) = ⌀25 × 5, (c,e) = ⌀10 × 10, (d) = ⌀15, (f) = ⌀12 × 10. Rotating assemblies embeds stacked magnets of dimensions 10 × 25 × 50, magnetized in thickness, four for all them, except three for units at (c). Rotating units are synchronized autonomously by the magnetic coupling mechanism. (g,h) Magnet arrangements of rotators.
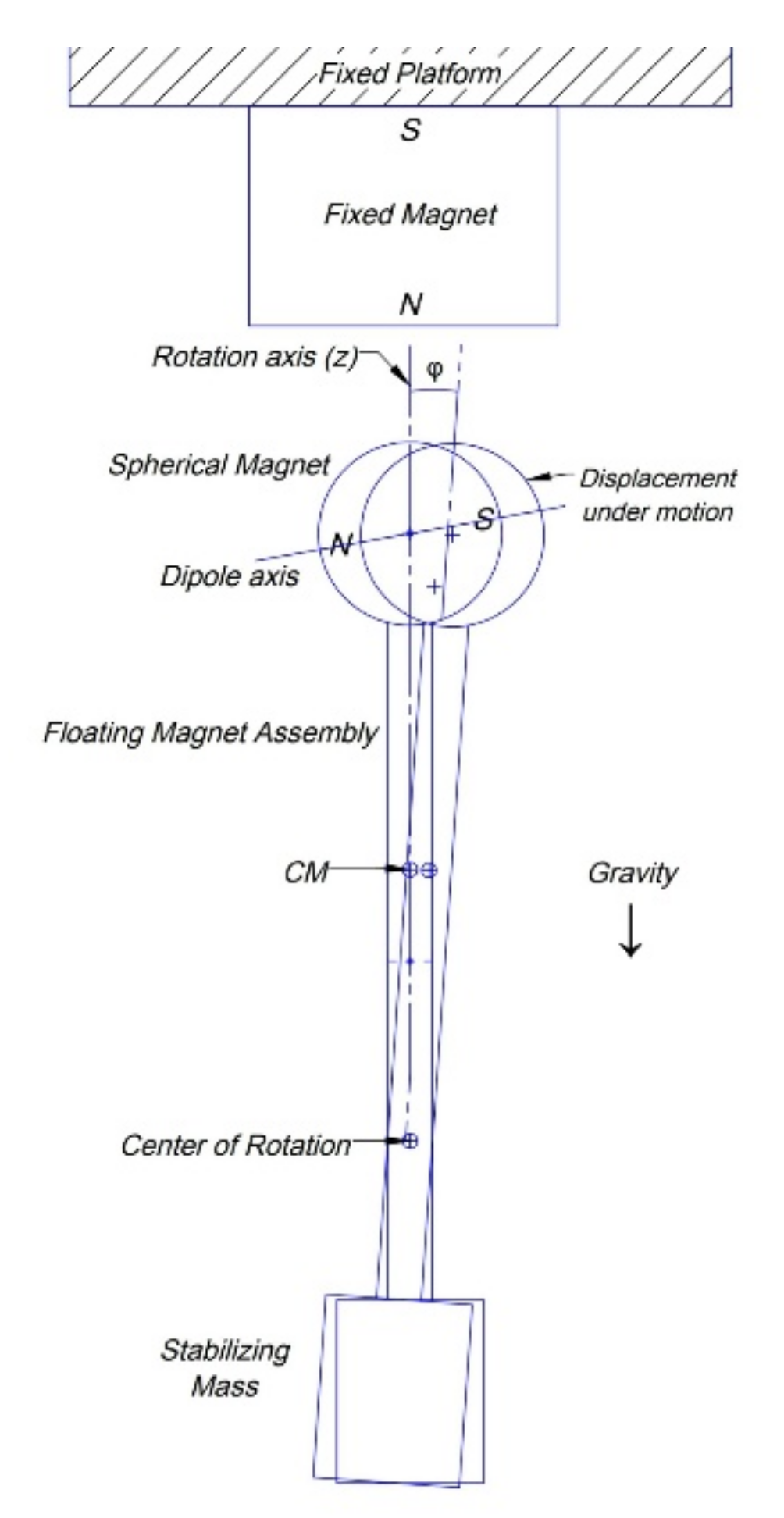
Figure 37.
Bound state of a floating assembly with a static magnetic field. The assembly rotates on the vertical axis by a given initial angular motion. The torque and force it receives from the magnetic field of the fixed magnet causes the assembly to oscillate around the point denoted as center of rotation. The magnet within the assembly is tilted from the rotation axis in order to obtain an attractive force from the fixed magnet. This force is balanced by PFR, resulting in the assembly kept trapped in air. The gravitational force stabilizes the orientation of the assembly. The displacement shown corresponds an instance of the motion, which can be shown in spherical coordinates where the origin is center point of rotation, φ is the zenith angle which kept constant and the azimuthal angle θ equal to ⍵.t where ⍵ is the angular speed of the system.
Figure 37.
Bound state of a floating assembly with a static magnetic field. The assembly rotates on the vertical axis by a given initial angular motion. The torque and force it receives from the magnetic field of the fixed magnet causes the assembly to oscillate around the point denoted as center of rotation. The magnet within the assembly is tilted from the rotation axis in order to obtain an attractive force from the fixed magnet. This force is balanced by PFR, resulting in the assembly kept trapped in air. The gravitational force stabilizes the orientation of the assembly. The displacement shown corresponds an instance of the motion, which can be shown in spherical coordinates where the origin is center point of rotation, φ is the zenith angle which kept constant and the azimuthal angle θ equal to ⍵.t where ⍵ is the angular speed of the system.
Figure 38.
Free spinning dipole bodies trapped by a static magnetic field of stacked permanent magnets fixed to a motionless platform. A spherical magnet (⌀15 mm) and a small magnet stuck to its side constitute the body’s dipole. These side magnets are 10 × 10 × 3 mm except setup (d). Their presences cause asymmetry on the magnetic field and on mass distribution of the body along its axis. However, this factor strengthens the bound state both providing extra attractive force and extra PFR strength by increasing the lateral oscillation of the dipole (center) in the same time zeroing the lateral oscillation of the body by providing counteracting inertial force to the lateral magnetic force. As a result, the body spins on its predetermined axis without vibration in a specific rotation velocity. The steady velocity of the body is provided by its coupling to a rotating dipole field belonging to assembly at the side of the frame in (a–c) and at top of (d). This coupling is found to introduce instability to the system by low frequency oscillations which are damped by approaching a copper or an aluminum block.
Figure 38.
Free spinning dipole bodies trapped by a static magnetic field of stacked permanent magnets fixed to a motionless platform. A spherical magnet (⌀15 mm) and a small magnet stuck to its side constitute the body’s dipole. These side magnets are 10 × 10 × 3 mm except setup (d). Their presences cause asymmetry on the magnetic field and on mass distribution of the body along its axis. However, this factor strengthens the bound state both providing extra attractive force and extra PFR strength by increasing the lateral oscillation of the dipole (center) in the same time zeroing the lateral oscillation of the body by providing counteracting inertial force to the lateral magnetic force. As a result, the body spins on its predetermined axis without vibration in a specific rotation velocity. The steady velocity of the body is provided by its coupling to a rotating dipole field belonging to assembly at the side of the frame in (a–c) and at top of (d). This coupling is found to introduce instability to the system by low frequency oscillations which are damped by approaching a copper or an aluminum block.
![Symmetry 13 00442 g038 Symmetry 13 00442 g038]()
Figure 39.
(a) A spherical dipole magnet (⌀15 mm) attached to a DC motor trapped by the field of a dipole magnet (⌀15 × 15 mm) fixed to a motionless platform. The z component of the rotating magnetic moment is large enough to keep the whole assembly in air. (b) A similar scheme where a cylindrical magnet (⌀15 × 10 mm) mounted in a plastic housing is trapped by a long strip of magnets of segments (50 × 10 × 5 mm) magnetized in thickness mounted in an acrylic transparent track. This allow the rotating magnet assembly to move freely along the track (x direction) but not on y and z.
Figure 39.
(a) A spherical dipole magnet (⌀15 mm) attached to a DC motor trapped by the field of a dipole magnet (⌀15 × 15 mm) fixed to a motionless platform. The z component of the rotating magnetic moment is large enough to keep the whole assembly in air. (b) A similar scheme where a cylindrical magnet (⌀15 × 10 mm) mounted in a plastic housing is trapped by a long strip of magnets of segments (50 × 10 × 5 mm) magnetized in thickness mounted in an acrylic transparent track. This allow the rotating magnet assembly to move freely along the track (x direction) but not on y and z.
Figure 40.
A rotating dipole magnet attached to a DC motor hung from cables is trapped horizontally (a) and by an angle (b) by a dipole magnet stack fixed to a motionless platform. Items attached to the cable serve to suppress vibrations.
Figure 40.
A rotating dipole magnet attached to a DC motor hung from cables is trapped horizontally (a) and by an angle (b) by a dipole magnet stack fixed to a motionless platform. Items attached to the cable serve to suppress vibrations.
Figure 41.
A simulation (first run) of MBS where bodies are released very close to their equilibrium distance. During the simulation time, rotation point of the floator varied in this range: z: 24,517 ± 7 μm, x: −0.5 ± 0.75 μm, y: 1.6 ± 1.6 μm. (a) Overview of the simulation. Top object is the floator, N pole looking up, bottom object is the rotator where it N pole is looking right on this instance, marked with small indentation on the ring. (b) Trajectories of reference points of bodies projected on xy plane at the end of simulations. Red traces are belong to floator (F) and green ones to the rotator (R). From outside to inside these traces are F: bottom center, top center, CM, R: magnetic top center, body top center, CM. (c,d) Trajectories of floator’s rotation center (blue) and rotator (red) projected on xz and on xy planes.
Figure 41.
A simulation (first run) of MBS where bodies are released very close to their equilibrium distance. During the simulation time, rotation point of the floator varied in this range: z: 24,517 ± 7 μm, x: −0.5 ± 0.75 μm, y: 1.6 ± 1.6 μm. (a) Overview of the simulation. Top object is the floator, N pole looking up, bottom object is the rotator where it N pole is looking right on this instance, marked with small indentation on the ring. (b) Trajectories of reference points of bodies projected on xy plane at the end of simulations. Red traces are belong to floator (F) and green ones to the rotator (R). From outside to inside these traces are F: bottom center, top center, CM, R: magnetic top center, body top center, CM. (c,d) Trajectories of floator’s rotation center (blue) and rotator (red) projected on xz and on xy planes.
Figure 42.
A simulation (second run) of MBS where bodies are released at 3 mm off from their equilibrium distance in direction of rotator’s rotation axis (z). This causes bodies to oscillate around the equilibrium point stably. (a) A screenshot of the simulation while bodies are in motion. The horizontal trace around the rotator is belong to trajectory of a point on the edge of ring (notice the small blue dot, marking this point) coinciding to the N pole orientation. While the trace spirals by the motion of the rotator on z, it keep its parallel alignment to the xy plane despite the ring plane is not. Floator top face is belong to its N pole. Its conical motion is synchronized with the rotator and its S pole is always looking toward S pole of the rotator despite it is attracted by the N pole. (b) Profile of the force-z between bodies vs. distance while the bodies traverse this distance two times within a cycle. The undulated trace is belong the second half of the cycle where bodies are returning back to their initial position. This trace is undulated due to quick changes on torques they experience at the bounce instance. Due to this quick change, the tilt angles of bodies adapt to these changes in a oscillatory manner which is reflected on forces. Trace cross zero at equilibrium distance at 24.5 mm. The variation of the force by distance have a curve matching to where residuals are shown in the embedded figure for the approaching sequence of the motion. (c) The projection of the trajectory of floator (CM) on YZ plane after completing its first cycle of the motion where blue dot marks its actual position. (d) Time profile of the velocity-z of the floator. The curve have significantly high slope where it cross zero at the bounce instance. (e) Time profile of kinetic energy of the floator detailed as angular and translational energies within one cycle of the motion along z. The trace shows that the initial energies levels are restored at the end of the cycle. Most of the translational kinetic energy belongs to lateral circular motion of the body and maximized at the shortest distance.
Figure 42.
A simulation (second run) of MBS where bodies are released at 3 mm off from their equilibrium distance in direction of rotator’s rotation axis (z). This causes bodies to oscillate around the equilibrium point stably. (a) A screenshot of the simulation while bodies are in motion. The horizontal trace around the rotator is belong to trajectory of a point on the edge of ring (notice the small blue dot, marking this point) coinciding to the N pole orientation. While the trace spirals by the motion of the rotator on z, it keep its parallel alignment to the xy plane despite the ring plane is not. Floator top face is belong to its N pole. Its conical motion is synchronized with the rotator and its S pole is always looking toward S pole of the rotator despite it is attracted by the N pole. (b) Profile of the force-z between bodies vs. distance while the bodies traverse this distance two times within a cycle. The undulated trace is belong the second half of the cycle where bodies are returning back to their initial position. This trace is undulated due to quick changes on torques they experience at the bounce instance. Due to this quick change, the tilt angles of bodies adapt to these changes in a oscillatory manner which is reflected on forces. Trace cross zero at equilibrium distance at 24.5 mm. The variation of the force by distance have a curve matching to where residuals are shown in the embedded figure for the approaching sequence of the motion. (c) The projection of the trajectory of floator (CM) on YZ plane after completing its first cycle of the motion where blue dot marks its actual position. (d) Time profile of the velocity-z of the floator. The curve have significantly high slope where it cross zero at the bounce instance. (e) Time profile of kinetic energy of the floator detailed as angular and translational energies within one cycle of the motion along z. The trace shows that the initial energies levels are restored at the end of the cycle. Most of the translational kinetic energy belongs to lateral circular motion of the body and maximized at the shortest distance.
![Symmetry 13 00442 g042 Symmetry 13 00442 g042]()
Figure 43.
A simulation (third run) of MBS where bodies are released at off 10 mm from their equilibrium distance in the direction of rotator’s rotation axis (z). (a) The trajectory of the floator projected on xz plane when the floator bounced back to its initial position. The zoomed part corresponds to top of this trajectory where the floator returns to its initial position at the end of cycle with a +0.03 mm offset. Same trajectory (in a different scale) is shown on Figure (b) as a projection on the yz plane. The undulation in the trace corresponds to a circular motion on the xy plane where amplitude of lateral motion gets several times larger at the bounce distance. (c) Time profiles of the force component-z and the z distance between bodies. (d) Displacement of rotation center of the floator in x and y directions. The rotation center varies as torque and forces varies by distance and this is reflected by varied amplitude of traces.
Figure 43.
A simulation (third run) of MBS where bodies are released at off 10 mm from their equilibrium distance in the direction of rotator’s rotation axis (z). (a) The trajectory of the floator projected on xz plane when the floator bounced back to its initial position. The zoomed part corresponds to top of this trajectory where the floator returns to its initial position at the end of cycle with a +0.03 mm offset. Same trajectory (in a different scale) is shown on Figure (b) as a projection on the yz plane. The undulation in the trace corresponds to a circular motion on the xy plane where amplitude of lateral motion gets several times larger at the bounce distance. (c) Time profiles of the force component-z and the z distance between bodies. (d) Displacement of rotation center of the floator in x and y directions. The rotation center varies as torque and forces varies by distance and this is reflected by varied amplitude of traces.
Figure 44.
(a) Configuration and 3D field plot of two interacting cylindrical dipole magnets assumed under bound state shown in cross section xz. In this configuration, the top magnet rotates around the z-axis and is tilted by an angle γ = 5° between its dipole and x-axis. Bottom magnet is assumed to have full DoF and its tilt varies by the distance proportional to the y component of torque it receives but in the opposite direction due to phase lag. (b) Plots of z component of forces as function of distance between centers of magnets. Black curve corresponds to an external force which balances magnetic forces. The external force has positive sign when it pushes magnets into each other. It is zero at 3.95 cm, which corresponds to the equilibrium distance of the bound state in absence of external forces. This equilibrium is stable because magnets repel each other when getting closer than this and attract otherwise. Red curve corresponds to the strength of the PFR force, which is obtained by the simulation by setting the angle γ to zero which cancels the attraction between magnets when the top magnet rotates around the z-axis. Blue curve is obtained by subtracting black curve from red. This curve corresponds to the attraction factor determined by angle γ. Red (PFR) and blue (AF) curves are in the form of y = axb with a, b values (7754, −8.0) and (107, −4.88,), respectively. (c,d,e) Similar analysis for interacting two spherical dipole magnets having same size (⌀10 mm) and magnetizations M = 1 × 106 A/m, corresponding to Br = 1.256 T (NdFeB/N38). Values a, b of repulsive (PFR) and attractive (AF) force functions are obtained as PFR (3950, −7.0) and AF (89.5, −4.0) when the tilt angle γ of the rotator is set to 5°. These parameters are obtained by curve fitting method and power factor terms have an uncertainty about ±0.3 in general. Potential energy of this configuration is shown in plot (e).
Figure 44.
(a) Configuration and 3D field plot of two interacting cylindrical dipole magnets assumed under bound state shown in cross section xz. In this configuration, the top magnet rotates around the z-axis and is tilted by an angle γ = 5° between its dipole and x-axis. Bottom magnet is assumed to have full DoF and its tilt varies by the distance proportional to the y component of torque it receives but in the opposite direction due to phase lag. (b) Plots of z component of forces as function of distance between centers of magnets. Black curve corresponds to an external force which balances magnetic forces. The external force has positive sign when it pushes magnets into each other. It is zero at 3.95 cm, which corresponds to the equilibrium distance of the bound state in absence of external forces. This equilibrium is stable because magnets repel each other when getting closer than this and attract otherwise. Red curve corresponds to the strength of the PFR force, which is obtained by the simulation by setting the angle γ to zero which cancels the attraction between magnets when the top magnet rotates around the z-axis. Blue curve is obtained by subtracting black curve from red. This curve corresponds to the attraction factor determined by angle γ. Red (PFR) and blue (AF) curves are in the form of y = axb with a, b values (7754, −8.0) and (107, −4.88,), respectively. (c,d,e) Similar analysis for interacting two spherical dipole magnets having same size (⌀10 mm) and magnetizations M = 1 × 106 A/m, corresponding to Br = 1.256 T (NdFeB/N38). Values a, b of repulsive (PFR) and attractive (AF) force functions are obtained as PFR (3950, −7.0) and AF (89.5, −4.0) when the tilt angle γ of the rotator is set to 5°. These parameters are obtained by curve fitting method and power factor terms have an uncertainty about ±0.3 in general. Potential energy of this configuration is shown in plot (e).
![Symmetry 13 00442 g044 Symmetry 13 00442 g044]()
Figure 45.
Various bound state realizations and assemblies generating rotating fields. Assembly (g) which has asymmetric split dipole configuration obtained by four square magnets is used in realizations shown at (a,b). At Figure (c), a small magnet (⌀6 × 3) is trapped below the sphere magnet (⌀15) in ‘tilted’ configuration. At (d), the floating magnet assembly consists of two stacked small magnets (⌀6 × 3) and a non magnetic nut is held by a rotating magnet of same size in side the cylindrical container attached to a rotor. In (e), a rotating body (top) is hung from a rotor by a thin string allowing five DoF. Dimensions are given in mm. (f) A bound state anticipating external force in radial direction (the weigt of the floator) by using the offset scheme in the rotator magnet in order to obtain static field component providing the attraction. Assembly (g) consists of four 10 × 10 × 3 magnets where an air gap is present between the third and fourth. Figure (h) shows an off center dipole configuration consists of four stacked magnets (12 × 12 × 3) and a counterbalance weights. The round mark on the third magnet from the left shows the rotation center. Assembly shown at (i) is a tilted dipole configuration as the bottom face of the magnet becomes visible because of the tilt. Magnets dimensions are ⌀50 × 10. The tilt amount can be also seen from the small dot visible on the bottom magnet marking the rotation center. Figure (j) shows a large assembly of eight 50 × 25 × 10 magnets where vertically stacked six magnets form a dipole and two side magnets in anti-Helmholtz configuration provides the static field along the rotation axis.
Figure 45.
Various bound state realizations and assemblies generating rotating fields. Assembly (g) which has asymmetric split dipole configuration obtained by four square magnets is used in realizations shown at (a,b). At Figure (c), a small magnet (⌀6 × 3) is trapped below the sphere magnet (⌀15) in ‘tilted’ configuration. At (d), the floating magnet assembly consists of two stacked small magnets (⌀6 × 3) and a non magnetic nut is held by a rotating magnet of same size in side the cylindrical container attached to a rotor. In (e), a rotating body (top) is hung from a rotor by a thin string allowing five DoF. Dimensions are given in mm. (f) A bound state anticipating external force in radial direction (the weigt of the floator) by using the offset scheme in the rotator magnet in order to obtain static field component providing the attraction. Assembly (g) consists of four 10 × 10 × 3 magnets where an air gap is present between the third and fourth. Figure (h) shows an off center dipole configuration consists of four stacked magnets (12 × 12 × 3) and a counterbalance weights. The round mark on the third magnet from the left shows the rotation center. Assembly shown at (i) is a tilted dipole configuration as the bottom face of the magnet becomes visible because of the tilt. Magnets dimensions are ⌀50 × 10. The tilt amount can be also seen from the small dot visible on the bottom magnet marking the rotation center. Figure (j) shows a large assembly of eight 50 × 25 × 10 magnets where vertically stacked six magnets form a dipole and two side magnets in anti-Helmholtz configuration provides the static field along the rotation axis.
![Symmetry 13 00442 g045 Symmetry 13 00442 g045]()
Figure 46.
(a) Tilting a dipole magnet with respect to its axis produces a dipole moment in this axis direction. This tilt produces a static z component of the rotating field. (b) Rotating a dipole magnet on an axis off its dipole center generates a static component of the rotating field having gradient which can serve to obtain an attractive force on the floator in direction-z. Figures (c) and (d) show rotator assemblies based on the offset scheme. Assemblies are balanced by non-magnetic counter-weights. Magnets used in Figure (c) are two 20 × 20 × 5 mm and one half and in Figure (d) is a ½” cube where the rotation center of the assembly is marked by a dot.
Figure 46.
(a) Tilting a dipole magnet with respect to its axis produces a dipole moment in this axis direction. This tilt produces a static z component of the rotating field. (b) Rotating a dipole magnet on an axis off its dipole center generates a static component of the rotating field having gradient which can serve to obtain an attractive force on the floator in direction-z. Figures (c) and (d) show rotator assemblies based on the offset scheme. Assemblies are balanced by non-magnetic counter-weights. Magnets used in Figure (c) are two 20 × 20 × 5 mm and one half and in Figure (d) is a ½” cube where the rotation center of the assembly is marked by a dot.
Figure 47.
Bound state of dipole magnets. (a) A spherical magnet (⌀15) is trapped by a rotating magnet assembly visible at top edge of the image consisting of a disk magnet (⌀40 × 10) mounted inside of an aluminum cylindrical block. (b) attached to a rotor. The small translational motion of the floator can be seen on its fuzzy edge, zoomed at the embedded rectangle. The small tilt angle of the rotator (~3°), suffices to balance the PFR and the weight of the trapped magnet. (d) The floator is a cube of edge 10 mm and the rotator is a disk of ⌀30 × 5 having a tilt about 4° as shown on (c) right picture. Floators in tests (a,d) also spin around their dipole axes and obtained a constant spin velocities equal to an integer fraction of the rotator velocity. This fraction is typically 1/2 for spherical shaped floators. (e) A cylindrical magnet (⌀7 × 15) is held horizontally by the by a rotating spherical magnet (⌀25.4) attached to a rotor using an plastic housing. The torque-phi effect is efficient on this configuration due to elongated shape of the floator and play role on it orientation combined by the force of the gravity which shift it position down from the rotor axis. This floator does not spin due to large misalignment/inhomogeneities of its magnetic field combined with its off axis position condition. (f) An assembly (floator) containing a spherical dipole magnet (⌀15) shown under bound state with a rotating dipole magnet of same attached to a motor swinging through its cables. Motor speed is about 100 rev/s The floator assembly is actually another rotator assembly but used as floator here. Dimensions are given in mm.
Figure 47.
Bound state of dipole magnets. (a) A spherical magnet (⌀15) is trapped by a rotating magnet assembly visible at top edge of the image consisting of a disk magnet (⌀40 × 10) mounted inside of an aluminum cylindrical block. (b) attached to a rotor. The small translational motion of the floator can be seen on its fuzzy edge, zoomed at the embedded rectangle. The small tilt angle of the rotator (~3°), suffices to balance the PFR and the weight of the trapped magnet. (d) The floator is a cube of edge 10 mm and the rotator is a disk of ⌀30 × 5 having a tilt about 4° as shown on (c) right picture. Floators in tests (a,d) also spin around their dipole axes and obtained a constant spin velocities equal to an integer fraction of the rotator velocity. This fraction is typically 1/2 for spherical shaped floators. (e) A cylindrical magnet (⌀7 × 15) is held horizontally by the by a rotating spherical magnet (⌀25.4) attached to a rotor using an plastic housing. The torque-phi effect is efficient on this configuration due to elongated shape of the floator and play role on it orientation combined by the force of the gravity which shift it position down from the rotor axis. This floator does not spin due to large misalignment/inhomogeneities of its magnetic field combined with its off axis position condition. (f) An assembly (floator) containing a spherical dipole magnet (⌀15) shown under bound state with a rotating dipole magnet of same attached to a motor swinging through its cables. Motor speed is about 100 rev/s The floator assembly is actually another rotator assembly but used as floator here. Dimensions are given in mm.
![Symmetry 13 00442 g047 Symmetry 13 00442 g047]()
Figure 48.
Four sequences of a test showing a bound state anticipating gravitational force regardless of its direction. Floator is a stack of three ⌀6 × 3 mm magnets and rotator is an assembly of five 10 × 10 × 3 mm magnets where four of them are stacked and one at behind them. In this assembly, magnets have room to move to sides of the housing and once rotator starts to rotate in high speed, a gap about 0.6 mm develops between two middle magnets. Rotation speed is 230 rev/s.
Figure 48.
Four sequences of a test showing a bound state anticipating gravitational force regardless of its direction. Floator is a stack of three ⌀6 × 3 mm magnets and rotator is an assembly of five 10 × 10 × 3 mm magnets where four of them are stacked and one at behind them. In this assembly, magnets have room to move to sides of the housing and once rotator starts to rotate in high speed, a gap about 0.6 mm develops between two middle magnets. Rotation speed is 230 rev/s.
Figure 49.
An assembly (a,b) consists of two dipole magnets, the top, having ring shape aligned in axial direction providing DC (static) component and the other, large one in radial direction generating AC (cyclic) field. The assembly (c) is similar except the magnet providing attractive force is at the bottom and the attached non-magnetic metal disk is aimed to increase the MoI in the rotation axis direction. The assembly (d) have same magnets configurations of a, b and have an additional brass disk. As assemblies designed to have major principal MoI on rotation axis, they can spin stably on this axis with a small deviation. Assemblies are driven through threads in order to allow most of their DoF and to exhibit characteristics of bound state of two free bodies.
Figure 49.
An assembly (a,b) consists of two dipole magnets, the top, having ring shape aligned in axial direction providing DC (static) component and the other, large one in radial direction generating AC (cyclic) field. The assembly (c) is similar except the magnet providing attractive force is at the bottom and the attached non-magnetic metal disk is aimed to increase the MoI in the rotation axis direction. The assembly (d) have same magnets configurations of a, b and have an additional brass disk. As assemblies designed to have major principal MoI on rotation axis, they can spin stably on this axis with a small deviation. Assemblies are driven through threads in order to allow most of their DoF and to exhibit characteristics of bound state of two free bodies.
Figure 50.
Dynamics of free rotating body (rotator) subject to magnetic forces and torque of a floator (not shown) residing on axis z and N pole up. Rotator consists of a spherical magnet and an enveloping ring made by a nonmagnetic and nonconductive material. This ring determines the principal axes of inertia of the body by setting the major principal axis orthogonal to the dipole axis. In absence of external forces, bodies spin on this axis but when a magnetic torque is applied on axis-y, it gets tilted by angle σ and might be balanced by the inertial torque. In this tilted configuration, the S pole always stays below the xy plane and N pole above. It should be noted that this figure shows an instance of the motion, which can be described with Equation (144). Torque vectors are on axis-y in this instance. Vectors denoted as inertial torques represent force vectors instead, in the logic of force × distance.
Figure 50.
Dynamics of free rotating body (rotator) subject to magnetic forces and torque of a floator (not shown) residing on axis z and N pole up. Rotator consists of a spherical magnet and an enveloping ring made by a nonmagnetic and nonconductive material. This ring determines the principal axes of inertia of the body by setting the major principal axis orthogonal to the dipole axis. In absence of external forces, bodies spin on this axis but when a magnetic torque is applied on axis-y, it gets tilted by angle σ and might be balanced by the inertial torque. In this tilted configuration, the S pole always stays below the xy plane and N pole above. It should be noted that this figure shows an instance of the motion, which can be described with Equation (144). Torque vectors are on axis-y in this instance. Vectors denoted as inertial torques represent force vectors instead, in the logic of force × distance.
Figure 51.
Bipolar bound states of approximated free bodies. (a) A rotating assembly consists of ¾’’ dipole sphere magnet and a plastic ring surrounding it and attached to a rotor by a thread, approximating a free rotating body. The MoI of the magnet in direction orthogonal to its dipole is increased by this ring in order for the dipole to be aligned with the rotation plane while it spins. Under this body, a trapped magnetic assembly is found, consisting of a cube magnet of 10 mm in size extended by two square magnets in polar direction. (b) A spherical magnet is trapped by a rotating assembly similar to the one used in setup (a), making BBS of two spherical magnets. The equilibrium is in the limits and bound state only persists for a short time because trapped magnet quickly gains spin causing an increase of the repulsion factor, which cannot be balanced by the attractive factor. It should be noted that rotating assemblies having spherical magnets may have small misalignments up to 0.3° between the dipole axis and the rotation plane. (c,d) A floator consisting of two ⌀15 × 15 cylindrical and a ⌀16 × 2 disk magnet in between is trapped in both polarities by a rotator satisfying bipolar bound state scheme. Rotator consists of a 1” spherical magnet mounted in an acrylic made ring (e) where its dipole is aligned with the ring plane. Stability is marginal in this test, possibly due to the weight of the floator (~40 g) plays a negative role. Additionally, rotator−floator matching might be not good enough. (f,g) Rotating assemblies based on ¾’’ and 1’’ diameter sphere magnets used in tests while spinning stand-alone. Rings are made from nonmagnetic and nonconductive materials. Rings are finely tuned by wrapping a ribbon (f) and tape (g) around in order to obtain proper MoI figures for matching to specific floators.
Figure 51.
Bipolar bound states of approximated free bodies. (a) A rotating assembly consists of ¾’’ dipole sphere magnet and a plastic ring surrounding it and attached to a rotor by a thread, approximating a free rotating body. The MoI of the magnet in direction orthogonal to its dipole is increased by this ring in order for the dipole to be aligned with the rotation plane while it spins. Under this body, a trapped magnetic assembly is found, consisting of a cube magnet of 10 mm in size extended by two square magnets in polar direction. (b) A spherical magnet is trapped by a rotating assembly similar to the one used in setup (a), making BBS of two spherical magnets. The equilibrium is in the limits and bound state only persists for a short time because trapped magnet quickly gains spin causing an increase of the repulsion factor, which cannot be balanced by the attractive factor. It should be noted that rotating assemblies having spherical magnets may have small misalignments up to 0.3° between the dipole axis and the rotation plane. (c,d) A floator consisting of two ⌀15 × 15 cylindrical and a ⌀16 × 2 disk magnet in between is trapped in both polarities by a rotator satisfying bipolar bound state scheme. Rotator consists of a 1” spherical magnet mounted in an acrylic made ring (e) where its dipole is aligned with the ring plane. Stability is marginal in this test, possibly due to the weight of the floator (~40 g) plays a negative role. Additionally, rotator−floator matching might be not good enough. (f,g) Rotating assemblies based on ¾’’ and 1’’ diameter sphere magnets used in tests while spinning stand-alone. Rings are made from nonmagnetic and nonconductive materials. Rings are finely tuned by wrapping a ribbon (f) and tape (g) around in order to obtain proper MoI figures for matching to specific floators.
![Symmetry 13 00442 g051 Symmetry 13 00442 g051]()
Figure 52.
Variation angles σF (black) And σT (red) vs. distance for a given configuration. Red plots correspond to a range of inertia figures of the rotator where the term (IA–IR) varies between 0.181 × 10−6 to 2.96 × 10−6 kg m2 in ten steps, top to bottom. Stable equilibrium of bodies are obtained at cross of a red and the black curve. The rotator of the last red curve cannot obtain enough tilt for the equilibrium and the interaction becomes always repulsive since red and black lines never cross. As a note, equations about these curves omits the lateral offsets of bodies caused by translational oscillations of motion. These offsets have effects on profile on forces and marginally on torques. In bipolar bound state, these effects gain importance since the equilibrium can be marginal.
Figure 52.
Variation angles σF (black) And σT (red) vs. distance for a given configuration. Red plots correspond to a range of inertia figures of the rotator where the term (IA–IR) varies between 0.181 × 10−6 to 2.96 × 10−6 kg m2 in ten steps, top to bottom. Stable equilibrium of bodies are obtained at cross of a red and the black curve. The rotator of the last red curve cannot obtain enough tilt for the equilibrium and the interaction becomes always repulsive since red and black lines never cross. As a note, equations about these curves omits the lateral offsets of bodies caused by translational oscillations of motion. These offsets have effects on profile on forces and marginally on torques. In bipolar bound state, these effects gain importance since the equilibrium can be marginal.
Figure 53.
Simulation of bipolar bound state of free bodies. Configuration parameters are mR = 20.56 g, mF = 6.666 g, IR1 = 9.944 × 10−7, IR2 = 7.081 × 10−7, IF1 = IF2 = 9.96 × 10−8 kg m2, ω = 857 rad/s where subscript letters R and F denote rotator and floator. Bodies are released near (25.65 mm) to the equilibrium position (25.47 mm), slowly get closer, bouncing at 25.3 mm while the simulation is ended before bodies return to their initial position. In a continuation of the simulation, the distance reached to 25.67 mm as maximum. The conical motions of bodies have some irregularities and a small drift (5 × 10−5 m) in lateral directions due to non-precise initial and non-equilibrium conditions resulting in some fluctuations in forces. The thick horizontal line corresponds to circular trajectory (seen from edge) of a point at the edge of the ring in orientation of the rotator’s N pole. The line thickens as the rotator goes forth and back on axis-z. (a) Overview of the simulation at the end (t = 131 ms). The magenta dot on the rotator marks its rotation center little above the CM (green dot). Rotation center of the floator is about 1.7 mm above the CM. (b) Plot of the distance in direction-z between bodies by a superimposed sinusoidal curve defined as f(x) = a0 + a1 cos ωT + b1 sin ωT, a0 = 25.47, a1 = 0.177, b1 = 0.01048, ω = 0.03796. Based on this curve, peak acceleration of the floator is calculated as ±0.193 m/s2, corresponding to forces ±0.00128 N. Due to irregularities in angular motions of bodies, actual forces varies by ±0.02 N in this course, more than 10 times than should be as shown in (d). (c) Trajectory of the floator’s rotation center projected on the yz plane. The amplitude of lateral force between bodies starts with 1.197 N, peaks as 1.265 N at the closest distance. Averages of angles φ and σ are 8.46° and 5.77°, respectively.
Figure 53.
Simulation of bipolar bound state of free bodies. Configuration parameters are mR = 20.56 g, mF = 6.666 g, IR1 = 9.944 × 10−7, IR2 = 7.081 × 10−7, IF1 = IF2 = 9.96 × 10−8 kg m2, ω = 857 rad/s where subscript letters R and F denote rotator and floator. Bodies are released near (25.65 mm) to the equilibrium position (25.47 mm), slowly get closer, bouncing at 25.3 mm while the simulation is ended before bodies return to their initial position. In a continuation of the simulation, the distance reached to 25.67 mm as maximum. The conical motions of bodies have some irregularities and a small drift (5 × 10−5 m) in lateral directions due to non-precise initial and non-equilibrium conditions resulting in some fluctuations in forces. The thick horizontal line corresponds to circular trajectory (seen from edge) of a point at the edge of the ring in orientation of the rotator’s N pole. The line thickens as the rotator goes forth and back on axis-z. (a) Overview of the simulation at the end (t = 131 ms). The magenta dot on the rotator marks its rotation center little above the CM (green dot). Rotation center of the floator is about 1.7 mm above the CM. (b) Plot of the distance in direction-z between bodies by a superimposed sinusoidal curve defined as f(x) = a0 + a1 cos ωT + b1 sin ωT, a0 = 25.47, a1 = 0.177, b1 = 0.01048, ω = 0.03796. Based on this curve, peak acceleration of the floator is calculated as ±0.193 m/s2, corresponding to forces ±0.00128 N. Due to irregularities in angular motions of bodies, actual forces varies by ±0.02 N in this course, more than 10 times than should be as shown in (d). (c) Trajectory of the floator’s rotation center projected on the yz plane. The amplitude of lateral force between bodies starts with 1.197 N, peaks as 1.265 N at the closest distance. Averages of angles φ and σ are 8.46° and 5.77°, respectively.
![Symmetry 13 00442 g053 Symmetry 13 00442 g053]()
Figure 54.
Approximated BBS of two free bodies having dipole moment realized by permanents magnets. The upper magnet (rotator) having equal diameter and length of 20 mm is suspended by a thread attached to a rotor providing five DoF to approximate a free body (b). This geometry provides a larger MoI in radial directions of the cylinder corresponding to the rotation axis (z) of the motion by a ratio of 7/6, forcing the body to rotate on this axis, therefore orienting its dipole orthogonal to it. The lower magnet (floator) consists of four stacked pieces which allowed to adjust properties precisely, in order to obtain a stable equilibrium. The floator is held in air stably while exhibiting angular motion synchronized by the rotation of the rotator. Figure (a) shows the bound state as seen by naked eye where rotation of rotator and oscillation of floator cause the motion blur. While the rotator is forced to rotate its dipole axis orthogonal to rotation axis by the inertial torque, the magnetic torque it receives from the floator cause to oppose this orientation, resulting in a tilt angle where these two opposing torques find an equilibrium. This tilt which can be seen from (c,d), produces a dipole moment in the direction of rotation axis which attracts the floator. On the other hand, magnets do not collapse because this attraction force is balanced by the PFR generated by the rotating magnetic field. However, this equilibrium can be only stable if magnetic and inertial properties of these bodies are adjusted well. From figures (c,d) which correspond two instances of motions of bodies taken by an interval of half cycle using camera 1/2000 s shuttle speed, it can be seen that their motions are synchronized and the floator is tilted from the vertical orientation, but its top pole pointing to the other magnet pole having the same polarity due to phase lag condition. BBS ensures that floator can be trapped regardless of the pole is facing to the rotator because rotator gets tilted automatically in order to generate a dipole moment parallel to the floator dipole. (e) These magnets are shown in two phases (red and blue) of rotation of the rotator by half cycle difference.
Figure 54.
Approximated BBS of two free bodies having dipole moment realized by permanents magnets. The upper magnet (rotator) having equal diameter and length of 20 mm is suspended by a thread attached to a rotor providing five DoF to approximate a free body (b). This geometry provides a larger MoI in radial directions of the cylinder corresponding to the rotation axis (z) of the motion by a ratio of 7/6, forcing the body to rotate on this axis, therefore orienting its dipole orthogonal to it. The lower magnet (floator) consists of four stacked pieces which allowed to adjust properties precisely, in order to obtain a stable equilibrium. The floator is held in air stably while exhibiting angular motion synchronized by the rotation of the rotator. Figure (a) shows the bound state as seen by naked eye where rotation of rotator and oscillation of floator cause the motion blur. While the rotator is forced to rotate its dipole axis orthogonal to rotation axis by the inertial torque, the magnetic torque it receives from the floator cause to oppose this orientation, resulting in a tilt angle where these two opposing torques find an equilibrium. This tilt which can be seen from (c,d), produces a dipole moment in the direction of rotation axis which attracts the floator. On the other hand, magnets do not collapse because this attraction force is balanced by the PFR generated by the rotating magnetic field. However, this equilibrium can be only stable if magnetic and inertial properties of these bodies are adjusted well. From figures (c,d) which correspond two instances of motions of bodies taken by an interval of half cycle using camera 1/2000 s shuttle speed, it can be seen that their motions are synchronized and the floator is tilted from the vertical orientation, but its top pole pointing to the other magnet pole having the same polarity due to phase lag condition. BBS ensures that floator can be trapped regardless of the pole is facing to the rotator because rotator gets tilted automatically in order to generate a dipole moment parallel to the floator dipole. (e) These magnets are shown in two phases (red and blue) of rotation of the rotator by half cycle difference.
![Symmetry 13 00442 g054 Symmetry 13 00442 g054]()
Figure 55.
(
a–
d) An approximated BBS configuration similar to
Figure 54 where the rotating magnet is extended axially by stacking thin disk magnets to both ends. This extension increases its MoI on the rotation axis approximately by 2.6 times and increases its tilt stiffness by this ratio. As a result, the required magnetic torque provided by the floating magnet needs to be increased by this ratio to obtain the same tilt. In this configuration, the rotating magnet is suspended by an elastic thread in order to approximate better full DoF. In this realization, a larger distance between bodies is also observed. Figure (
c,
d) show two instances separated approximately by half cycle where the floating magnet performs a synchronized conical motion on the rotation axis of the upper body. (
e) Another configuration where rotating assembly consists of two stacked cube magnets same as the ones used on the floating body which is heavier than the rotating body by 4/3 ratio. (
f,
g) A ring ((⌀19.7–8) × 3.9 mm) shaped axially magnetized floator magnet having an adjustment mass is held at short distance by the rotator consisting a 1/2” cube magnet housed in a cylindrical block. This adjustment mass mainly has an effect on the moments of inertia for obtaining appropriate PFR slope vs. distance for stable equilibrium. The material used in this block have density about 1.75 g/cm
3 and provides rather a large MoI factor (
IA–
IR) resulting a small angle σ about 5° at ω = 220 rev/s and can be increased up to 10° by lowering the speed permitted by the stability in this configuration. Figure (
g) shows that the rotator does not wobble (σ = 0) in absence of the floator.
Figure 55.
(
a–
d) An approximated BBS configuration similar to
Figure 54 where the rotating magnet is extended axially by stacking thin disk magnets to both ends. This extension increases its MoI on the rotation axis approximately by 2.6 times and increases its tilt stiffness by this ratio. As a result, the required magnetic torque provided by the floating magnet needs to be increased by this ratio to obtain the same tilt. In this configuration, the rotating magnet is suspended by an elastic thread in order to approximate better full DoF. In this realization, a larger distance between bodies is also observed. Figure (
c,
d) show two instances separated approximately by half cycle where the floating magnet performs a synchronized conical motion on the rotation axis of the upper body. (
e) Another configuration where rotating assembly consists of two stacked cube magnets same as the ones used on the floating body which is heavier than the rotating body by 4/3 ratio. (
f,
g) A ring ((⌀19.7–8) × 3.9 mm) shaped axially magnetized floator magnet having an adjustment mass is held at short distance by the rotator consisting a 1/2” cube magnet housed in a cylindrical block. This adjustment mass mainly has an effect on the moments of inertia for obtaining appropriate PFR slope vs. distance for stable equilibrium. The material used in this block have density about 1.75 g/cm
3 and provides rather a large MoI factor (
IA–
IR) resulting a small angle σ about 5° at ω = 220 rev/s and can be increased up to 10° by lowering the speed permitted by the stability in this configuration. Figure (
g) shows that the rotator does not wobble (σ = 0) in absence of the floator.
![Symmetry 13 00442 g055 Symmetry 13 00442 g055]()
Figure 56.
Floating bodies having anti-Helmholtz type quadrupolar field bound to a rotating dipole field provided by three different rotator assemblies above them. This scheme generates single axis angular oscillation of floators allowing to a simple coupling that can isolate vibration. A close-up image of floator can be seen on rightmost image where its angular oscillation becomes apparent. The attached wire does not vibrate because its pass through the axis of the motion. (a) Positioning and magnetic diagram of the configuration on the xz plane at instance t0. Floator magnets are arranged in anti-Helmholtz configuration and generates a quadrupole field. By calling next instances by each π/2 rotation of the rotator, at t1 and t3, the floator axis is aligned to axis-x and the diagram at t2 is mirror of t0. (b) A floator assembly consisting two axially polarized ring magnets (ring (⌀19.7–8) × 3.9 mm) mounted on a plastic rod as anti-parallel with a distance of ~5–6 mm trapped by a spherical magnet (⌀3/4”) mounted to a rotor. (c,d) The configurations of floator where the distance between ring magnets is smaller at the right configuration. (e) A similar configuration where floator magnets are doubled. The image is a slow motion video snapshot where the rolling shutter artefact deforms the shape of moving objects as the floator frame appears bend. At this instance, the rotator’s N pole (marked by the reflective sticker) is in camera direction, and the floator frame is horizontal in accordance with the model.
Figure 56.
Floating bodies having anti-Helmholtz type quadrupolar field bound to a rotating dipole field provided by three different rotator assemblies above them. This scheme generates single axis angular oscillation of floators allowing to a simple coupling that can isolate vibration. A close-up image of floator can be seen on rightmost image where its angular oscillation becomes apparent. The attached wire does not vibrate because its pass through the axis of the motion. (a) Positioning and magnetic diagram of the configuration on the xz plane at instance t0. Floator magnets are arranged in anti-Helmholtz configuration and generates a quadrupole field. By calling next instances by each π/2 rotation of the rotator, at t1 and t3, the floator axis is aligned to axis-x and the diagram at t2 is mirror of t0. (b) A floator assembly consisting two axially polarized ring magnets (ring (⌀19.7–8) × 3.9 mm) mounted on a plastic rod as anti-parallel with a distance of ~5–6 mm trapped by a spherical magnet (⌀3/4”) mounted to a rotor. (c,d) The configurations of floator where the distance between ring magnets is smaller at the right configuration. (e) A similar configuration where floator magnets are doubled. The image is a slow motion video snapshot where the rolling shutter artefact deforms the shape of moving objects as the floator frame appears bend. At this instance, the rotator’s N pole (marked by the reflective sticker) is in camera direction, and the floator frame is horizontal in accordance with the model.
![Symmetry 13 00442 g056 Symmetry 13 00442 g056]()
Figure 57.
A rotating assembly where a dipole magnet is inserted between two ring magnets in anti-Helmholtz configuration. The central magnet is polarized in thickness. When the assembly rotates it produces a rotating dipole field along a static quadrupole field. While the rotating dipole field generates PFR while interacting with a dipole field, the inner pole of the quadrupole provides the attractive force and the outer poles ensure angular stability.
Figure 57.
A rotating assembly where a dipole magnet is inserted between two ring magnets in anti-Helmholtz configuration. The central magnet is polarized in thickness. When the assembly rotates it produces a rotating dipole field along a static quadrupole field. While the rotating dipole field generates PFR while interacting with a dipole field, the inner pole of the quadrupole provides the attractive force and the outer poles ensure angular stability.
Figure 58.
Two series of measurements for showing relation of rotating field speed and floating body spin velocity υS (denoted as υ in this figure) for obtaining the same PFR strength. As the PFR is inversely proportional to square of the field rotation speed, It can be seen this relation is approximately inverse for floating body spin. First series corresponds to the bound state of a spherical magnet of 15 mm of diameter (m = 13.36 g, I = 3 × 10−7 kg m2) and the second to a cylindrical magnet having both 10 mm diameter and length. (m = 5.64 g, IR = 8.225 × 10−8 kg m2, IA = 7.05 × 10−8 kg m2).
Figure 58.
Two series of measurements for showing relation of rotating field speed and floating body spin velocity υS (denoted as υ in this figure) for obtaining the same PFR strength. As the PFR is inversely proportional to square of the field rotation speed, It can be seen this relation is approximately inverse for floating body spin. First series corresponds to the bound state of a spherical magnet of 15 mm of diameter (m = 13.36 g, I = 3 × 10−7 kg m2) and the second to a cylindrical magnet having both 10 mm diameter and length. (m = 5.64 g, IR = 8.225 × 10−8 kg m2, IA = 7.05 × 10−8 kg m2).
Figure 59.
(
a–
f) Various epitrochoidal/hypotrochoidal patterns of small angular oscillations generated spinning dipole bodies trapped in air. Patterns are obtained by reflection of a laser beam from a polar face of floating magnet. (
a,
b) A three armed hypotrochoidal angular pattern of a spinning rectangular floator. The small plot is obtained by settings
a = −1/3 and
b = 0.82 in the equation at footnote 8. (
d) A tiny 1/8” cube magnet trapped in air in a position along axis of a rotation of a small magnet visible at right edge of the image and the reflection of laser beam emanating from the small hole on the screen reflected back from a face of the cube belong a pole. The pattern consists of one outer and two overlapping inner loops. On the center images, trapped magnets and their angular oscillations can be seen. They gave both single inner loops, large on the left image and point like on the right. At image (
f), the pattern has four inner loops. The amplitude of the angular oscillation can be barely seen by X shaped light lines on the face of three stacked square small magnets. Here the lateral angle of the cross, which appears close to 30°, corresponds to peak-to-peak amplitude of oscillation. (
g) A setup where the floator rotates in opposite direction of the rotator at same speed without an enforcement. This floator consist of stack of two cylinders of ⌀10 × 10 mm. The same effect is present in the experiment in
Figure 23b.
Figure 59.
(
a–
f) Various epitrochoidal/hypotrochoidal patterns of small angular oscillations generated spinning dipole bodies trapped in air. Patterns are obtained by reflection of a laser beam from a polar face of floating magnet. (
a,
b) A three armed hypotrochoidal angular pattern of a spinning rectangular floator. The small plot is obtained by settings
a = −1/3 and
b = 0.82 in the equation at footnote 8. (
d) A tiny 1/8” cube magnet trapped in air in a position along axis of a rotation of a small magnet visible at right edge of the image and the reflection of laser beam emanating from the small hole on the screen reflected back from a face of the cube belong a pole. The pattern consists of one outer and two overlapping inner loops. On the center images, trapped magnets and their angular oscillations can be seen. They gave both single inner loops, large on the left image and point like on the right. At image (
f), the pattern has four inner loops. The amplitude of the angular oscillation can be barely seen by X shaped light lines on the face of three stacked square small magnets. Here the lateral angle of the cross, which appears close to 30°, corresponds to peak-to-peak amplitude of oscillation. (
g) A setup where the floator rotates in opposite direction of the rotator at same speed without an enforcement. This floator consist of stack of two cylinders of ⌀10 × 10 mm. The same effect is present in the experiment in
Figure 23b.
![Symmetry 13 00442 g059 Symmetry 13 00442 g059]()
Figure 60.
A sequence of video frames of spinning a square floating magnet (3 × 10 × 10 mm) under an epitrochoidal motion having two loops. Each row corresponds to one cycle of rotating spherical magnet used for trapping the above magnet in the air. While frames are taken by 66 ms apart, each corresponds to motion advancement of about 4 milliseconds and by 31 degrees of rotation of driving magnet spinning 240 rev/s According to the epitrochoid geometry, large angles correspond to the outer loop and small angles to the inner loop. Frames also show the floating magnet is also spinning around its dipole axis, however, not synchronized with its epitrochoidal pattern. In many cases, as occurs in this experiment, the floating magnet position is off the main axis. This can be relied to the torque-phi effect which enforces the position for the average dipole moment direction of the body while the static dipole moment of the rotating field which tries to keep the body on axis becomes less effective within large angular oscillation of the body. The deformed appearance of the floating magnet is caused by the rolling shutter effect of the camera which scans the frame from top to bottom.
Figure 60.
A sequence of video frames of spinning a square floating magnet (3 × 10 × 10 mm) under an epitrochoidal motion having two loops. Each row corresponds to one cycle of rotating spherical magnet used for trapping the above magnet in the air. While frames are taken by 66 ms apart, each corresponds to motion advancement of about 4 milliseconds and by 31 degrees of rotation of driving magnet spinning 240 rev/s According to the epitrochoid geometry, large angles correspond to the outer loop and small angles to the inner loop. Frames also show the floating magnet is also spinning around its dipole axis, however, not synchronized with its epitrochoidal pattern. In many cases, as occurs in this experiment, the floating magnet position is off the main axis. This can be relied to the torque-phi effect which enforces the position for the average dipole moment direction of the body while the static dipole moment of the rotating field which tries to keep the body on axis becomes less effective within large angular oscillation of the body. The deformed appearance of the floating magnet is caused by the rolling shutter effect of the camera which scans the frame from top to bottom.
![Symmetry 13 00442 g060 Symmetry 13 00442 g060]()
Figure 61.
Complex angular motions of floators involving large variations of angle φ while they spin around their dipole axes. Floator is a stack of two square 10 × 10 × 3 and one ⌀9.5 × 1 magnets. This setup includes an overhead magnet assembly consisting of a stack of two ⌀10 × 10, visible on the top of (c) which allows complex motions of trapped magnets. Pictures covers a frame about 1/30 s where the floators perform several cycles of motion in this time window. Floators can ever reach to larger variations of φ by increasing the rotation speed of the motor. Dimensions are in mm.
Figure 61.
Complex angular motions of floators involving large variations of angle φ while they spin around their dipole axes. Floator is a stack of two square 10 × 10 × 3 and one ⌀9.5 × 1 magnets. This setup includes an overhead magnet assembly consisting of a stack of two ⌀10 × 10, visible on the top of (c) which allows complex motions of trapped magnets. Pictures covers a frame about 1/30 s where the floators perform several cycles of motion in this time window. Floators can ever reach to larger variations of φ by increasing the rotation speed of the motor. Dimensions are in mm.
Figure 62.
Sequences from a test about capturing a spherical dipole magnet (⌀15 mm) by a rotating dipole magnet assembly from a container filled with water, initially staying at the bottom, raising it and taking out without making contact with the container. The rotating assembly consists of two stacked 1/2” cube magnets grade N50 having dipoles aligned to the rotation plane, placed asymmetrically with respect to the rotation axis inside a plastic cylindrical housing having ⌀29.6 mm inner diameter as shown on the right picture. The small circle in violet color on the right magnet marks the rotation axis. The attraction factor is obtained solely by this offset in this configuration since the dipole of these stacked magnets lies on the rotation plane.
Figure 62.
Sequences from a test about capturing a spherical dipole magnet (⌀15 mm) by a rotating dipole magnet assembly from a container filled with water, initially staying at the bottom, raising it and taking out without making contact with the container. The rotating assembly consists of two stacked 1/2” cube magnets grade N50 having dipoles aligned to the rotation plane, placed asymmetrically with respect to the rotation axis inside a plastic cylindrical housing having ⌀29.6 mm inner diameter as shown on the right picture. The small circle in violet color on the right magnet marks the rotation axis. The attraction factor is obtained solely by this offset in this configuration since the dipole of these stacked magnets lies on the rotation plane.
Table 1.
Summary of stability tests of conical motion of the body through simulations. Most of the configurations are tested using multiple static field strengths in order to evaluate their stability using this factor. Angular motion deviates from the equilibrium angle φ when the static torque coefficient τS is below a certain value. In this case, the motion axis still finds an equilibrium at a zenith angle λ with proper initial conditions. However, in these tests, initial conditions are given for the motion for λ = 0. For this reason, the motion cannot settle to the equilibrium angle λ, but oscillates around it since there is no friction. These oscillations are considered as an instability factor here. The data fits very well to the criterion for obtaining symmetric conical motion around axis-z given by Equation (51) where the values at column “Min. τS/τC” correspond to this equation. Results are characterized by the following criteria: (1) φ is constant (λ = 0) or has a sinusoidal curve, (2) φ varies with a complex cyclic curve, (3) φ ever increases, (4) φ oscillates with ever increasing amplitude, (5) φ varies but the simulation ran short for obtaining exact criterion.
Table 1.
Summary of stability tests of conical motion of the body through simulations. Most of the configurations are tested using multiple static field strengths in order to evaluate their stability using this factor. Angular motion deviates from the equilibrium angle φ when the static torque coefficient τS is below a certain value. In this case, the motion axis still finds an equilibrium at a zenith angle λ with proper initial conditions. However, in these tests, initial conditions are given for the motion for λ = 0. For this reason, the motion cannot settle to the equilibrium angle λ, but oscillates around it since there is no friction. These oscillations are considered as an instability factor here. The data fits very well to the criterion for obtaining symmetric conical motion around axis-z given by Equation (51) where the values at column “Min. τS/τC” correspond to this equation. Results are characterized by the following criteria: (1) φ is constant (λ = 0) or has a sinusoidal curve, (2) φ varies with a complex cyclic curve, (3) φ ever increases, (4) φ oscillates with ever increasing amplitude, (5) φ varies but the simulation ran short for obtaining exact criterion.
| No. | IA (axial)
(kg m2) | IR (radial)
(kg m2) | Ω
(rad/s) | τC
(Nm) | τS/τC | Min τS/τC | Bias υY (rad/s) | φ0
(rad) | φ-calc
(rad) | λ
(rad) | Criterion |
|---|
| 1 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.30 | 0.101 | 0.5 | 0.2100 | 0.2102 | 0 | 1 |
| 2 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.25 | 0.101 | 0.5 | 0.2080 | 0.2080 | 0 | 1 |
| 3 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.25 | 0.101 | 0.5 | 0.2069 | 0.2069 | 0 | 1 |
| 4 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.22 | 0.101 | 0.5 | 0.2066 | 0.2067 | 0 | 1 |
| 5 | 8.100 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.20 | 0.101 | 0.5 | 0.2055 | 0.2059 | 0 | 1 |
| 6 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.18 | 0.101 | 0.5 | 0.2049 | 0.2050 | 0 | 1 |
| 7 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.10 | 0.101 | 0.5 | 0.2013 | 0.2018 | 0 | 1 |
| 8 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.08 | 0.101 | 0.5 | 0.2008 | 0.2010 | >0 | 5 |
| 9 | 8.099 × 10−8 | 1.058 × 10−7 | 60 π | 7.5 × 10−4 | 0.05 | 0.101 | 0.5 | 0.1996 | 0.1998 | >0 | 3 |
| 10 | 8.099 × 10−8 | 1.058 × 10−7 | 80 π | 7.5 × 10−4 | 0.06 | 0.056 | 0.2 | 0.1123 | 0.1127 | 0 | 1 |
| 11 | 8.099 × 10−8 | 1.058 × 10−7 | 80 π | 7.5 × 10−4 | 0.05 | 0.056 | 0.0 | 0.1121 | 0.1125 | >0 | 5 |
| 12 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.5 × 10−3 | 0.55 | 0.221 | 0.0 | 0.5027 | 0.5027 | >0 | 4 |
| 13 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.20 | 0.159 | 0.0 | 0.3188 | 0.3188 | 0 | 1 |
| 14 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.17 | 0.159 | 0.0 | 0.3158 | 0.3158 | 0 | 1 |
| 15 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.155 | 0.159 | 0.0 | 0.3144 | 0.3144 | 0 | 1 |
| 16 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.150 | 0.159 | 0.0 | 0.3139 | 0.3139 | >0 | 2 |
| 17 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.145 | 0.159 | 0.0 | 0.3133 | 0.3134 | >0 | 2 |
| 18 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.140 | 0.159 | 0.5 | 0.313 | 0.3133 | >0 | 2 |
| 19 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.1 × 10−3 | 0.15 | 0.159 | 0.0 | 0.3137 | 0.3139 | >0 | 2 |
| 20 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.2 × 10−3 | 0.40 | 0.174 | 0 | 0.3721 | 0.3723 | 0 | 1 |
| 21 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.2 × 10−3 | 0.18 | 0.174 | 1.0 | 0.3455 | 0.3452 | 0 | 1 |
| 22 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.2 × 10−3 | 0.17 | 0.174 | 0 | 0.3431 | 0.3440 | 0 | 1 |
| 23 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.2 × 10−3 | 0.16 | 0.174 | 0 | 0.3429 | 0.3429 | >0 | 2 |
| 24 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 1.2 × 10−3 | 0.115 | 0.174 | 1.0 | 0.4095 | n/a | >0 | 2 |
| 25 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 2.5 × 10−4 | 0.04 | 0.035 | 0.2 | 0.070 | 0.070 | 0 | 1 |
| 26 | 1.000 × 10−7 | 1.000 × 10−7 | 60 π | 2.5 × 10−4 | 0.02 | 0.035 | 0.2 | 0.070 | 0.070 | >0 | 5 |
| 27 | 2.500 × 10−8 | 3.750 × 10−8 | 60 π | 2.5 × 10−4 | 0.20 | 0.095 | 0.0 | 0.1938 | 0.1938 | 0 | 1 |
| 28 | 2.500 × 10−8 | 3.750 × 10−8 | 60 π | 3.75 × 10−4 | 0.20 | 0.144 | 0.0 | 0.2940 | 0.2940 | 0 | 1 |
| 29 | 2.500 × 10−8 | 3.750 × 10−8 | 60 π | 3.75 × 10−4 | 0.15 | 0.144 | 0.5 | 0.2896 | 0.2898 | 0 | 1 |
| 30 | 2.500 × 10−8 | 3.750 × 10−8 | 60 π | 3.75 × 10−4 | 0.13 | 0.144 | 0.5 | 0.2874 | 0.2881 | >0 | 2 |
| 31 | 2.500 × 10−8 | 3.750 × 10−8 | 60 π | 3.75 × 10−4 | 0.10 | 0.144 | 0.0 | 0.2854 | 0.2856 | >0 | 3 |
| 32 | 2.000 × 10−7 | 1.125 × 10−7 | 60 π | 1.0 × 10−3 | 0.13 | 0.127 | 0.0 | 0.2472 | 0.2472 | 0 | 1 |
| 33 | 2.000 × 10−7 | 1.125 × 10−7 | 60 π | 1.0 × 10−3 | 0.12 | 0.127 | 0.0 | 0.2466 | 0.2466 | >0 | 5 |
| 34 | 2.000 × 10−7 | 1.125 × 10−7 | 60 π | 1.0 × 10−3 | 0.11 | 0.127 | 0.0 | 0.2461 | 0.2461 | >0 | 5 |
| 35 | 1.000 × 10−7 | 1.000 × 10−7 | 80 π | 3.0 × 10−3 | 0.25 | 0.253 | 0.0 | 0.4943 | 0.4943 | >0 | 4 |
| 36 | 1.000 × 10−7 | 1.000 × 10−7 | 80 π | 3.0 × 10−3 | 0.267 | 0.253 | 0.0 | 0.498 | 0.498 | 0 | 1 |
Table 2.
Some numerical solutions of Equation (72).
Table 2.
Some numerical solutions of Equation (72).
| No. | JC | θ0 | | θ (t) |
|---|
| 1 | −1 × 104
1 × 104 | 0
π | −55.664 | |
| 2 | 1 × 104
−1 × 104 | 0
π | 48.45 | |
| 3 | 1 × 104 | π/2−0.206 | 0 | |
Table 3.
Results of curve fitting based on Equation (95) where x and f (x) data are, respectively the distance r and sin φ for data points corresponding to φ range. Force columns give normalized figures for the exact formula and the approximate formula for comparison purpose. Overall, the deviations are less than 0.5%.
Table 3.
Results of curve fitting based on Equation (95) where x and f (x) data are, respectively the distance r and sin φ for data points corresponding to φ range. Force columns give normalized figures for the exact formula and the approximate formula for comparison purpose. Overall, the deviations are less than 0.5%.
| No | φ Range (rad) | φ Range (deg) | Multiplier a | Exponent b | Relative
Distance | Force (z)
(Equation (93)) | Force (z)
(Equation (97)) |
|---|
| 1 | 0.60–0.40 | 34.4–22.9 | 1.3 | 2.30 | 0.53–0.62 | 71– 26 | 71–26 |
| 2 | 0.40–0.25 | 22.9–14.3 | 1.072 | 2.69 | 0.62–0.73 | 26.3–8.8 | 26.2–8.8 |
| 3 | 0.25–0.15 | 14.3–8.6 | 1.007 | 2.88 | 0.73–0.87 | 8.8–2.6 | 8.8–2.6 |
| 4 | 0.25–0.10 | 14.3–5.73 | 1.001 | 2.91 | 0.73–1.00 | 8.8–1.0 | 8.8–1.0 |
| 5 | 0.15–0.05 | 8.6–2.86 | 1.000 | 2.97 | 0.87–1.26 | 2.6–0.2 | 2.6–0.2 |
| 6 | 0.10–0.02 | 5.73–1.15 | 1.000 | 2.99 | 1.00–1.71 | 1.0–0.0235 | 1.0–0.0235 |
Table 4.
Integration data of simulations of interaction of rotator and floator within conical motions. Col. 14 gives the force between magnets in coaxial configuration as a reference figure for a comparison with the PFR force (Col. 13). Col.15 gives
FZ values based on point dipole formula. Col. 12 gives values for the
x component of the force for two rotator tilt configurations such as shown in
Figure 16a,b.
Table 4.
Integration data of simulations of interaction of rotator and floator within conical motions. Col. 14 gives the force between magnets in coaxial configuration as a reference figure for a comparison with the PFR force (Col. 13). Col.15 gives
FZ values based on point dipole formula. Col. 12 gives values for the
x component of the force for two rotator tilt configurations such as shown in
Figure 16a,b.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|
| | R × H
(mm) | Mass
(g) | I
(Nm2) | Moment
(Am2) | ω
(rad/s) | Dist.
(mm) | φ, γe
(rad) | β
(mm) | τC, τS
(N·m) | τS/τC,
RMIN | FX γ=0, γe (N) | FZγ=0(N) | Ref. F
(N) | FZ (DP)
(N) |
|---|
| 1 | Flo | 5.47 × 9.48 | 6.67 | 10−7 | 0.8 | 589.2 | 33 | 0.2 | 0.25 | 0.00674 | 0.2 | −0.622 | 0.145 | 0.972 | 0.131 |
| Rot | 10 × 10 | 23.5 | - | 2.83 | 0.104 | 0.00135 | 0.1 | −0.632 |
| 2 | Flo | 5.47 × 9.48 | 6.67 | 10−7 | 0.8 | 1100 | 28 | 0.0946 | 0.156 | 0.01135 | 0.1027 | −1.264 | 0.148 | 1.76 | 0.129 |
| Rot | 10 × 10 | 23.5 | - | 2.83 | 0.0513 | 0.001166 | 0.0471 | −1.272 |
| 3 | Flo | 5.47 × 9.48 | 6.67 | 10−7 | 0.8 | 837.33 | 38 | 0.1 | 0.113 | 0.00694 | 0.114 | −0.5213 | 0.059 | 1.00 | 0.052 |
| Rot | 10 × 16 | 37.7 | - | 4.52 | 0.0569 | 0.000791 | 0.050 | −0.5243 |
| 4 | Flo | 5.47 × 9.48 | 6.67 | 10−7 | 0.8 | 995.6 | 28 | 0.18 | 0.27 | 0.01728 | 0.229 | −1.75 | 0.3715 | 3.17 | 0.407 |
| Rot | 10 × 16 | 37.7 | - | 4.52 | 0.114 | 0.003957 | 0.088 | −1.71 |
| 5 | Flo | 5.47 × 9.48 | 6.67 | 10−7 | 0.8 | 1129 | 23.8 | 0.213 | 0.362 | 0.0258 | 0.304 | −3.15 | 0.852 | 5.69 | 0.919 |
| Rot | 10 × 16 | 37.7 | - | 4.52 | 0.151 | 0.00785 | 0.102 | −3.28 |
Table 5.
Solutions of Equation (72) in form Equation (73) for various rotating field speeds and forces obtained using Equation (107).
Table 5.
Solutions of Equation (72) in form Equation (73) for various rotating field speeds and forces obtained using Equation (107).
| No | JC | ω (rad/s) | θ0 (rad) | θ’0 (rad/s) | |θ| (rad) | Fav/A |
|---|
| 1 | 10000 | 60 π | π | −55.666 | 0.2750 | 0.13688 |
| 2 | 10000 | 65 π | π | −51.15 | 0.2358 | 0.11775 |
| 3 | 10000 | 70 π | π | −47.31 | 0.2042 | 0.10183 |
| 4 | 10000 | 75 π | π | −43.99 | 0.1784 | 0.08926 |
| 5 | 10000 | 82 π | π | −40.05 | 0.1497 | 0.07472 |
| 6 | 10000 | 90 π | π | −36.33 | 0.1245 | 0.06228 |
| 7 | 10000 | 105 π | π | −30.945 | 0.0917 | 0.04623 |
| 8 | 10000 | 120 π | π | −26.96 | 0.0703 | 0.03553 |
| 9 | 10000 | 135 π | π | −23.89 | 0.0555 | 0.02809 |
| 10 | 10000 | 150 π | π | −21.45 | 0.0450 | 0.02275 |
| 11 | 10000 | 170 π | π | −18.88 | 0.0350 | 0.01793 |