Abstract
We present a fully second-quantized calculation showing the emergence of spontaneous coherent configurations of the electromagnetic field interacting with charged bosons in a regular lattice. The bosons tend to oscillate at their plasma frequency, and in addition are subjected to electrostatic forces which keep them confined close to the lattice sites while causing a frequency shift in the oscillation. Under certain conditions upon these frequencies, we find that a suitably defined set of coherent states (coherent both in the field and matter degrees of freedom) exhibit a negative energy gap with respect to the perturbative ground state. This is true in the RWA approximation and for position-independent fields to both the first and second order in the interaction Hamiltonian. We compare this result with other recent findings from cavity QED, and note that (1) consideration of full 3D wavefunctions and a careful definition of the coherent states are essential for obtaining the energy gap, and (2) although our calculation is made in reference to bosons, it may apply to protons bound in a crystal matrix as well if their density is very low compared to the density of available states.
1. Introduction
The stability of the perturbative ground state in single-mode cavity QED has been intensively studied under broad conditions for quantum gases and electron systems [,,,,,,,,], when the diamagnetic term proportional to is taken into account or not (the so-called “no-go theorem” for the superradiant transition in its various versions; see [,]). The control, at a microscopic level, of coherent interactions between light and matter is one of the main focus points of quantum technologies. In this context, methods for increasing the light—matter coupling strength acquire special importance. As long as the coupling strength remains much smaller than the frequency of the cavity mode, only the resonant terms in the interaction Hamiltonian play a significant role. The remaining counter-rotating terms couple states with contributions that can be neglected. The so-called rotating-wave approximation (RWA) provides an accurate picture of atom–photon interaction processes in this regime [,,].
There are other important cases in quantum field theory in which the perturbative ground state is unstable, e.g., in QCD [,,] and quantum gravity [,,,,]. Such instabilities are usually related to complex dynamical behavior not reducible to single-particle excitations. This can lead to the formation of so-called “kinetic condensates”, differing from the more common translationally invariant potential condensates related to the conventional Higgs mechanism.
In this work, we consider an idealized physical system of localized oscillating charges coupled to a multi-mode monochromatic electromagnetic field in which a finite energy gap develops at zero temperature; we compute it rigorously using a set of trial states which are coherent in both the matter and field sectors. In this calculation, the term is included and no-go theorems are avoided, as we consider electromagnetic modes with their momenta quantized in all possible directions. These modes are confined in the material due to a dispersion relation that prevents them from escaping even in the absence of an external cavity.
Of course, there are conditions that need to be satisfied for a negative gap, especially concerning the relation between the plasma frequency and another characteristic frequency that defines the strength of the electrostatic potential binding the charges to the lattice sites.
In Section 2, we introduce the Hamiltonian of the system, which contains the kinetic term of the bosons in the presence of a vector potential, plus the Hamiltonian of free cavity photons of momentum (with ) and a harmonic potential due to the combined effect of plasma oscillations and of local electrostatic “cages” near each lattice site. In real systems, these cages typically correspond to tetrahedral or octahedral holes []. In agreement with standard approaches for handling the diamagnetic term [,], we define new photon operators with the same momentum and a shifted or “dressed” frequency equal to the oscillation frequency of the matter field (see Appendix B). The interaction term is written employing the dipole approximation, i.e., with the vector potential constant in space.
In Section 3, we define photon operators which project along the three space directions via a canonical transformation in preparation for the introduction of trial coherent states in which matter oscillations occur in one specific direction (Section 4). The full Hamiltonian, when evaluated on these trial states in the rotating wave approximation (RWA), reduces to an effective Hamiltonian with a minimum that exhibits an energy gap per particle of the form , where , meaning that the perturbative vacuum becomes unstable at the first order when .
The factor in the gap formula controls the oscillation amplitude in the trial coherent state, which is physically limited by the lattice spacing (Section 5). In Section 6 and Section 7, we compute the contribution to the energy gap provided by the second perturbative order in the interaction Hamiltonian describing processes in which photons are emitted and re-absorbed at different lattice sites. The resulting expression for the gap up to second order is very similar, namely, , implying condensation for even lower values of the coupling constant .
In Appendix D, we provide a numerical estimate of the condensation threshold and of the energy gap for a realistic case, namely, for protons absorbed into an FCC metallic matrix, when their density is so low that they can be described by a bosonic wavefunction. Supposing one proton per lattice site and a lattice spacing , we obtain a coupling constant . Thus, the system is over threshold and condensation occurs under robust conditions. Assuming that the amplitude of the oscillation is fixed by the size of the octahedral sites of the crystal, the average energy gap per particle is eV and the frequencies and are in the THz range, which is in good agreement with the values of the largest phonon frequencies adapted to the proton mass [].
In Section 8, we estimate the spatial dependence of the field and argue that coherence domains form, at the boundary of which the field decreases in keeping with the spherical Bessel function .
Section 9 contains a final discussion and outlook on future work. From the historical point of view, we point out that extensive pioneering work on e.m. coherence in condensed matter was carried out in the 1990s by G. Preparata [], who introduced the concept of coherence domains. Our present approach was inspired by Preparata’s work; however, it is independent from it and completely self-consistent.
The main results of this paper are summarized in Section 10.
In addition to the mentioned Appendix B and Appendix D, Appendix C and Appendix E contain technical details of the calculation. In Appendix A, a static charge distribution is defined which reproduces the almost-harmonic potential used in the Hamiltonian.
2. Hamiltonian
Let us consider a system of charged identical quantum oscillators placed at the vertices of a simple cubic three-dimensional lattice with spacing d. Here, we suppose that the oscillator n is in its equilibrium position at site n of the lattice, meaning that there are N oscillators in a lattice with N elementary cells (Figure 1). Oscillator n is kept in its equilibrium position by a potential , which is harmonic with frequency when is small enough and becomes stiffer when the oscillation approaches the boundary of the elementary cell. This requirement guarantees that the oscillation does not interfere with the adjacent elementary cells and remains confined in the nth cell.
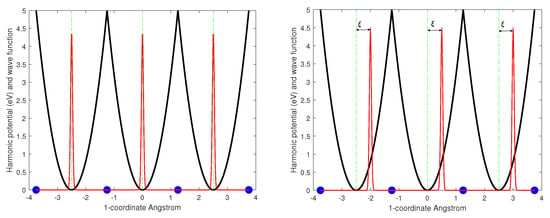
Figure 1.
Periodic harmonic potential in the 1—direction with square modulus of the wave functions of the oscillators in their ground state (left) and elongated by due to their coherent oscillation (right).
The Hamiltonian of the single harmonic oscillator is as follows (we use natural units with ):
where e, m, and are the charge, mass, and oscillation frequency of the oscillator at position , while is the electromagnetic vector potential.
Due to the self-generated electrostatic interaction, the particles experience an additional potential provided by , where is the free plasma frequency.
Therefore, the total Hamiltonian describing the oscillators in interaction with the electromagnetic field is
where is the equilibrium position of the nth oscillator.
By adding to (2) the free electromagnetic Hamiltonian, the total Hamiltonian can be rewritten in second-quantized terms as
where
and where we have defined the shifted oscillation frequency as
Note that for the electromagnetic field we have selected the modes with frequency only, as we are interested in the modes that have a relevant dynamical impact on the system under study in a way that becomes clear in the following. The neglected modes interact with the system only perturbatively.
The destruction and creation operators , , and are in the interaction picture, meaning that
and the radiation field operator is given by
where , and . Here p is a polarization index and the e.m. wave unit vector spans all possible 3D directions. In order to get rid of the diamagnetic term we will proceed in the context of the dipole approximation. Following the lines described in Appendix B [], we can recast Equation (4c) in terms of new photon operators so that
Equation (8) shows that the transformation (A14) makes the diamagnetic term disappear, making the electromagnetic Hamiltonian diagonal. The oscillation frequency is shifted to the new value , equal to that of the matter field. Moreover, the electromagnetic modes acquire a mass and their dispersion relation is modified such that the electromagnetic field is not able to propagate through the vacuum and cannot escape from the material.
The last term of the Hamiltonian can now be written in terms of the new operators. By means of the canonical transformations
and
where we have defined , we can recast Equation (4b) as
Because we are considering e.m. modes for which the wavelength is much larger than the lattice constant, we may neglect the spatial dependence of the electromagnetic field (dipole approximation, DA); thus, Equation (11) becomes
where the coupling strength turns out to be proportional to the plasma frequency .
3. Selection of the Quantum State for the Electromagnetic Field
The modes of the electromagnetic field that are eligible for resonant interaction with the oscillators are those with frequencies that equal , more precisely, those selected in Equation (12). The number of such independent modes is , distributed along the possible directions of the electromagnetic momentum and the electric polarization. We note here that we are now diverging from the usual treatment of the electromagnetic field in resonant cavities, as our analysis is not limited to the wave vectors in a single direction; rather, we consider the contribution of all the wave vectors with moduli . This fact is bound to have dramatic consequences on the final result.
Assuming, without loss of generality, that the oscillation of the charges is along the direction , we can define the photon states
where the integral is performed over the directions of the unit vector . These states are properly normalized thanks to the relation
The states are created and annihilated by the operators
By introducing the operators
the commutation relations for the new operators are
meaning that Equations (15) and (16) are canonical transformations. The vector potential after the DA can be rewritten in terms of these operators as
We can now express the interaction and photon Hamiltonians in terms of the new operators. Immediately, from Equation (12) we obtain
and from Equation (8) we obtain
Equations (19) and (20) tell us that the different modes of the electromagnetic field contribute to an increase in the coupling with the matter field, and such an interaction does not affect the energy density of the electromagnetic field. It will be seen in the next sections how this fact avoids the no-go theorem [,] while leading to the instability of the perturbative vacuum and to the migration of the field to a new stable and coherent configuration.
4. Effective Hamiltonian
Let us consider the trial coherent state
with the definitions
The state is a coherent state with a vector order parameter for the matter sector and for the electromagnetic sector. We make a further choice in setting such that
The two order parameters and are complex functions that are treated as both variational parameters and as the solution of the emerging dynamical equations. The all-important feature of the state is that the parameter is the same for all n, allowing us to drop the index n from the operators such that Equations (4a), (12), and (20) can be rewritten as
Equation (24) lead to the Schrödinger-like equation
By setting , and , Equation (24) add up to
where
are the counter-rotating terms that wildly oscillate at the double of the frequency and where the superscript indicates that the calculation is at first order in perturbation theory.
We now introduce the rotating wave approximation (RWA), consisting in neglecting the term in the effective Hamiltonian. We note that the counter-rotating terms of the type and , after being evaluated on the trial state, produce terms proportional to and which have a time dependence of the type and are averaged to zero over an oscillation period. This does not happen for the retained terms, which have a temporal dependence of type and . They are time-independent, and as such are the only ones that make a contribution to the trial state’s energy. For this reason, it is legitimate to apply the RWA approximation in our calculation, even though it is generally not valid in cavity QED in the presence of ultra-strong coupling [].
Equation (25) then leads to
We are now equipped with a set of legitimate matter–field quantum states that satisfy the dynamical equations depending parametrically on and . Our goal is to look for solutions with energy contents lower than that of the perturbative vacuum . To this end, we define the energy gap per particle as and find the minimum with respect to the parameter by requiring
The minimum is found for , and the minimum of the energy gap is
Equation (30) shows that the vacuum becomes unstable when
which is well within the allowed range .
This result reveals the existence of a phase transition to a new vacuum of the system. However, when looking at Equation (30) it appears that the new vacuum has a negatively diverging gap due to the freedom of the variational parameter , which is clearly a non-physical situation. Fortunately, due to the intervention of other factors not considered in the Hamiltonian that limit the oscillations of the charges outside their reticular cages, the parameter cannot assume arbitrarily large values, making the result of Equation (30) meaningful and rich of physical consequences.
To be more specific, we must consider that the Hamiltonian (4a) is a quadratic approximation of the true Hamiltonian that is valid for small oscillations around the equilibrium positions of the oscillating charges and fails when the oscillation amplitude exceeds a certain value. The complete Hamiltonian contains terms that prevent the oscillations from exceeding the dimensions of the reticular cage. The detailed form of such terms is unknown, as it depends on the details of the charge distributions of the host lattice. Here, we introduce the effect of these terms by imposing a maximum value on the amplitude of oscillation of the charges, which is fixed by the size and shape of the lattice cells. We address these topics in the following paragraphs.
It is important to note that symmetry-breaking of the vacuum is made possible by the synergistic cooperation of the various modes of the electromagnetic field, which make the coupling to the matter field times that of the single mode (Equation (19)). As far as we know, to date this feature represents a novelty in the literature dedicated to the study of the strong coupling regime. Had we only considered the two polarization modes and the two directions and along a fixed axis of the field, we would not have obtained sufficiently intense coupling with the matter to induce the transition. In fact, the factor would have been substituted by (provided by the two polarizations and the two directions), and Equation (30) would have been substituted by the similar equation
which displays no instability for in the allowed range and reproduces the result of various no-go theorems in the literature [,]. It is therefore imperative to consider the photon state (13) in order to achieve symmetry-breaking.
5. Lower Bound of the Energy Gap for the Coherent Phase
When condition (31) is met, Equation (30) is unbounded from below because can assume any value, which is an obviously non-physical condition. Little thought is required to spot the direction we need to take in order to recover a physically sound result; the parameter is related to the maximum amplitude of the plasma oscillation of the charges, and it is clear that such an oscillation cannot take arbitrarily large values because it is limited by the linear size of the lattice “cages” with spacing d. Mathematically, this may be formulated by introducing anharmonic terms into the matter Hamiltonian that are negligible for small plasma oscillations and become predominant when the oscillation exceeds the cage dimension. To implement this condition, we need to fix a maximum value of the oscillation amplitude of the matter field, which in general is provided by a fraction f of the linear dimension d of the electrostatic cages. Indeed, using Equation (10) we must have
which, recalling Equation (23a), becomes
In all practical situations, the last term in Equation (34) stemming from the indetermination principle can be neglected (being ) and the energy gap per particle has the form
It is important to note that, had we used plane wave functions in place of coherent states, we would not have been able to use any arguments relating to the non-divergence of the energy gap, obliging us to declare the resulting solutions to be non-physical.
To summarize this section, we have found that when an ensemble of charged particles embedded in a neutralizing charge density of opposite charges reaches a critical density, it is subjected to a spontaneous quantum phase transition to a stable, collective, and coherent state that is strongly and resonantly coupled to a coherent electromagnetic field with a total energy lower than that of the incoherent state (i.e., uncorrelated particles and no macroscopic electromagnetic field) by a finite amount.
This configuration involves a very large number of particles and has a spatial extension much larger than the typical atomic radius. In Section 8, we estimate the spatial structure and introduce the key concept of coherence domain (CD).
6. Second-Order Perturbation Theory for Composite Coherent States
We now proceed with the analysis of the energy content of the trial state (21) by studying the second order contribution of the perturbative expansion of the ground state energy. In physical terms, the first order contribution takes into account the contribution to the energy of the photons emitted by the oscillators and reabsorbed by the same oscillators, whereas the second order contribution considers the dispersive contribution of photons emitted by an oscillator and absorbed by a different oscillator. As we show below, it turns out that the two terms contribute the same amount, thereby doubling the term of negative interaction and strengthening the condensation mechanism.
To apply the second order perturbation theory, we need an orthonormal basis over which we can expand our trial state. To this end, we use the property of the interaction term to preserve the sum of the number of photons and the excitation number of the oscillators (the creation of a photon involves the reduction of the excitation state of the oscillator and vice versa), then define the new normalized basis as
where we have defined such that the trial state can be rewritten as
The properties of the states are as follows:
- The expectation value of the unperturbed Hamiltonian (see Appendix C) is
We are now ready to compute the second-order contribution to the energy.
7. The Second-Order Contribution
We start from the well-known second order perturbation theory in the Brillouin–Wigner approximation []:
where, for simplicity, we have indicated , and .
Strictly speaking, the numerator of Equation (40) should be , as the sum over the unperturbed states should exclude the diagonal terms; however, as N is very large, here we may set .
The solutions of Equation (40) are
and the lowest energy per particle of the states is . Substitution of Equations (38) and (39) into Equation (3) at the second order yields
Equation (42) shows that at the second order the contribution of the negative interaction term is twice the contribution at the first order, meaning that the coupling threshold is further lowered compared to the first order calculation. By repeating the procedure already performed in Section 4, we find
As anticipated at the beginning of Section 6, the threshold for the onset of coherence is significantly lowered and the energy gap is more pronounced compared to the calculation at first order.
8. Spatial Dimension of the Coherent States and Concept of Natural Resonating Cavity
We have shown that the dynamical relevance of quantum states is composed of a very large number of elementary charged particles plus a macroscopic (classical) electromagnetic field with an energy content lower than that of the perturbative state.
The properties of the coherent state (21) allow us to identify two vector order parameters, and , for which the temporal evolution is
where and . The choice of a spatial direction of 1 is arbitrary.
Thus far, we have neglected the spatial properties of the problem. The reason for this is the very long wavelength of the radiation field compared to the scale of the lattice. We now wish to obtain more insight into the nature of the spatial properties of the lowest-energy state. The wave number of the radiation field is unaffected by the coherent transition, and is provided by
where it is reasonable to expect that the spatial region in which a coherent condensation can occur has a minimum radius on the order of the half-wavelength . We refer to this region as the coherence domain (CD).
Returning to the definition of the photon field (7), we can reformulate the expansion in plane waves in terms of spherical harmonics provided by []
By substitution, we obtain
where
It can be shown (see Appendix E) that
therefore, the intensity profile of the vector potential is provided by the zeroth-order expansion in spherical harmonics of the exponentials in Equation (7). Denoting as r the distance from the center of the CD, we can write
where is the spherical Bessel function of order 0. The density must be constant throughout the whole CD in order to maintain the frequency, and consequently the quantum phase, as spatially constant; given that is proportional to (see Equation (43a)), the profile of is modulated spatially by . If we consider a volume in which the charges are distributed uniformly in a sphere of radius with density , the electromagnetic field is zero on the surface of the sphere and varies with the distance from the center following the profile (50). Thanks to Equation (43a), the matter amplitude has to be proportional to throughout the CD such that the profile of the matter amplitude is provided by
and the profile of the energy gap turns out to be modulated by (see Figure 2).
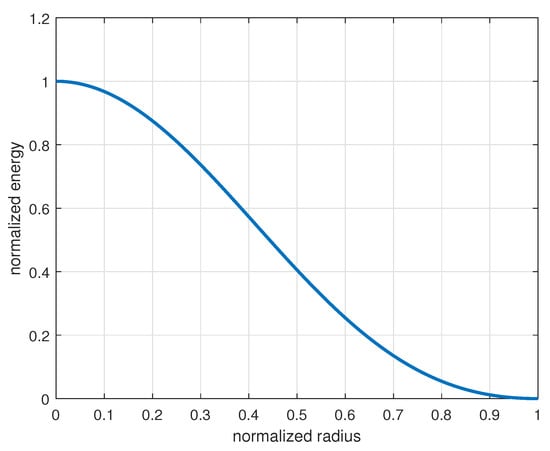
Figure 2.
Normalized energy profile as a function of the normalized radius of the coherence domain.
Now, we make a number of further considerations beyond the exact calculation carried out thus far, allowing the density of the oscillating charges and its neutralizing background charge density to vary to a certain extent, while maintaining its uniformity inside the CD through migration within the material. We realize that the spatial modulation of the energy gap inside the CD produces a gradient that pulls the charges towards the center of the CD, thereby increasing the density to the maximum value compatible with the other terms of the energy per particle (which have been neglected in our previous calculation), namely, the electrostatic Coulomb repulsion among particles and Pauli repulsion in case of fermions. As a final result, the system reaches an equilibrium density at which the attractive coherent potential is counterbalanced by the repulsive short-range terms.
The density on the outside is lower than that inside the CD due to the equilibrium of the chemical potential, while a sharp variation of the density is present at the boundary of the CD, implying a difference between the plasma frequency inside and outside the CD. The mismatch of the dispersion relations inside and outside the CD implies the total reflection of the EM field at the interface. Thus, a natural resonating cavity is generated.
In particular, as the dispersion relation of the renormalized radiating field is different from Equation (45), the electromagnetic field cannot propagate through the vacuum and remains trapped inside the material. In other words, the described mechanism accounts for the formation of a self-generated natural QED cavity after the density of the charges overcomes a certain threshold.
Such configurations may well be identified as new emerging mesoscopic structures able to justify particular properties of matter that display intrinsic quantum features.
The spatial modulation of the fields implies that the average energy gap throughout the CD is provided by
9. Discussion
Most extant theories of condensed matter do not consider the radiative component of the electromagnetic field to play a central role, due to its being strongly shielded by the high density of the charges and the conception that only those electrostatic forces generated by the constituents of matter are important. This is indeed true at most times, as the attenuation length for the electromagnetic field is typically much smaller than the wavelength of the radiating field. However, in certain circumstances the attenuation can be compensated by a positive optical gain of the material, as happens, for instance, in solid state lasers and optical microcavities in which exciton-polaritons are formed [,,]. A similar mechanism is at play in the problem under study.
In the previous sections, we have shown how, via instability of the QED vacuum, when the temperature is low enough a spontaneous phase transition is possible for a system of charges oscillating around equilibrium positions and immersed in a spatially modulated neutralizing charge density of opposite sign.
In Section 8, we reported that the typical spatial dimension of the coherence domains is fixed by the wavelength of the radiation field trapped inside the domains. However, this dimension is usually much smaller than the typical dimension of bulk material, meaning that we should expect the bulk material to contain a collection of coherence domains. Such domains are characterized by a single macroscopic wave function, an order parameter, and a well-determined quantum phase, which together confer intrinsically macroscopic quantum properties on the domains.
The arguments developed in the present work are valid for bosonic states of matter and remain valid for fermion systems when a trial state incorporating the anti-symmetry of the global wave function has been defined. This theoretical development will be addressed in a future work.
Regarding the energetic stability of the solutions, and considering the fact that in [] the spatial distribution of matter is two-dimensional, while in our case it is three-dimensional, a substantial difference between the results reached in [] and ours lies in the fact that the states considered in [] are plane waves, whereas in the present work we have considered coherent states with spatial size and oscillation that remain limited thanks to the intervention of nonlinear forces. This fact avoids a divergent energy gap associated with such coherent states.
The physical system analyzed in this work is at zero temperature. A next step will be to consider its thermal properties. While this topic will be addressed in a future work, we can anticipate that thermal excitations cause a portion of the particles forming the coherent state to populate the levels of the single quasi-particle spectrum. The net result is the formation of a two-fluid system similar to that proposed for superfluid helium []. Within this theoretical framework, all the properties associated with the degrees of freedom of the quasi-particles of the consolidated condensed matter theory involve the incoherent fraction, and only at low temperatures does the coherent fraction macroscopically manifest its intrinsically coherent characteristics.
A similar coherent condensation mechanism produced by the electromagnetic field can occur in atomic or molecular systems with an electric dipole. In this case, the electromagnetic field couples to two electronic levels displaying a sufficiently large electric dipole. A very interesting example is represented by liquid water [,].
In general, in a physical system made up of different types of charges with sufficiently high density, various types of electrodynamic coherence associated with different degrees of freedom of the charges can coexist. For instance, in a crystal the valence or conduction electrons and ions can form their own coherent states, each one resonating with the electromagnetic field at their specific plasmon polariton frequency.
10. Conclusions
In this work, we have defined and mathematically solved the problem of determining the lowest energy state of a large number of charged bosons coupled to selected modes of the electromagnetic field and harmonically oscillating around their equilibrium positions defined by the vertices of a crystal with lattice spacing much smaller than the wavelength of the modes of the electromagnetic field.
The equilibrium positions are determined by a periodic electrostatic potential, which we have called the jellium crystal, which implements global charge neutrality and localization.
The solution we have found corresponds to a state in which both the electromagnetic and matter fields are coherent and oscillate in quadrature and with a renormalized frequency with respect to the perturbative solution.
The energy content of this state is lower than that of the perturbative state. This is not in contrast with the no-go theorems mentioned in the introduction, as our calculation takes into account the contribution of the wave vectors in all directions. The aforementioned theorems consider only a single wave vector, and as such do not apply to our case.
The calculated energetic gap is not divergent, as it depends on the maximum oscillation that the charges can perform, which is limited by the finite size of the elementary cells of the crystal.
From a heuristic analysis of the solutions we found, we have defined a spatial region called the coherence domain (CD), the size of which is provided by the wavelength of the field and in which both the matter and electromagnetic fields are described by single macroscopic wave functions spatially modulated by the spherical harmonic , where r is the distance from the center of the domain and is the modulus of the wave vectors of the e.m. field. Due to the modulation of the fields, the energy gap depends on r, resulting in an average gap over the coherence domain which is about 15% of the maximum gap . We numerically evaluated this average value for a case involving protons loaded in the octahedral voids of a typical FCC crystal, resulting in a gap of eV per particle.
The coherent electromagnetic field remains confined within the domain due to the mismatch of the dispersion relation on the edge of the domain, and as such cannot propagate, forming a natural QED cavity. If the crystal is spatially larger than the size of a single coherence domain, the material is filled with a collection of CDs.
It should be noted that the present analysis was performed at zero temperature; the thermodynamics of the coherence domains will be presented in a future work.
Although our calculation is in reference to bosons, it may apply to protons bound in a crystal matrix as well if their density is very low compared to the density of available states. Indeed, the overlap of the single particle wave functions of the protons located in different lattice cells is negligible, implying a negligible contribution to the exchange integrals, and the antisymmetrization of the global wave function of protons has practically no effect.
Author Contributions
Conceptualization, L.G. and G.M.; formal analysis, L.G. and G.M.; software: L.G.; writing—original draft preparation, L.G. and G.M.; writing—review and editing, L.G. and G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article, as no datasets were generated or analysed during the current study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Jellium Crystal
In this Appendix, we define a static charge distribution able to reproduce the almost-harmonic potential used in our Hamiltonian.
As was the case in the Jellium model [], we assume that the neutralizing charge distribution is static and not perturbed by the presence of the oscillating charges.
In order to simplify the calculation, we approximate the cubic cell to a spherical cell with diameter d and assume that the charge density in the interstitial regions is zero. In addition, we assume a uniform negative charge distribution due to the conduction electrons of the metal present in the cell, contributing with a total negative charge of . We further assume that the oscillating charges contribute a positive charge for each cell, where x is the hydrogen loading ratio of the metal.
Here, we want to implement charge neutrality and the approximated harmonic potential through a charge distribution , where is the distance from the center of the cell, such that
with being the charge of the single oscillator.
The presence of the oscillators in the centers of the cells represents a localized positive charge that tends to attract the neutralizing charges, forming an atomic-like distribution of electrons around the equilibrium positions of the oscillators. We model such a distribution with a hydrogen-like plus uniform charge distribution. The charge density that satisfies these requirements (nte that is the Bohr radius and with for a typical metal lattice) is
In the approximation of the small oscillation , the solution of the Poisson equation in spherical symmetry yields a harmonic potential provided by
meaning that the electrostatic frequency is
and the coupling is computed to be
Using these numbers with and , we find , , and .
Appendix B. Renormalization of the Photon Field
We define a canonical transformation for the photon creation operators through a diagonalization procedure. The starting Hamiltonian is
where we have made the substitution . In our approximation, Equation (A6) can be written as
where
By defining the vector operators
and the matrix
Equation (A8) can be written in a compact form as
By diagonalizing W, we can find the matrix of the eigenvalues and eigenvectors
where the normalization of the eigenvectors is chosen such that ; by defining
we arrive at the “dressed” destruction and creation operators
meaning that Equation (A11) can be finally written as
and Equation (A6) becomes
The transformations (A14) are canonical, and the vector potential can be written in terms of the new operators as
with a dispersion relation which is different from that of the vacuum ().
Appendix C. Detailed Calculation of the Expectation Values of the States
For simplicity of notation, we set and here such that
and, after action of the operators,
By shifting the indexes, we obtain
and the expectation value of becomes
The expectation values of the matter Hamiltonian in n sector is
while for the photon Hamiltonian it is
Appendix D. Estimate of the Numerical Value of the Energy Gap
Here, let us make an estimate of the energy gap per particle for an ensemble of protons adsorbed into a metallic matrix. The Fermionic nature of protons can be neglected, as the Fermi energy at the density we are considering is negligible. Assume that the lattice spacing is eV eV and that there is one proton for each cell. The mass of a proton is MeV and the coupling with the electromagnetic field is , as computed in Appendix A. As the system is above the threshold, it is coherent. Finally, we choose in (35) and (43b), which is the typical relative dimension of the octahedral voids in a metallic lattice. Inserting the numerical values, we obtain
The computed energy gap is in the range of the chemical energies, and is a good candidate for the description of the spontaneous hydrogen absorption observed in many metals. Moreover, when this analysis is extended to electrons, for which their full Fermionic nature must be taken into account, this mechanism could have relevance to theoretical description of the work function.
Appendix E. Calculation of
Starting from the definition (7), we expand the exponentials in the spherical harmonics such that
where we define
We now compute the expectation value of on the coherent state . We need to evaluate the expectation value of the nth term of the sum of Equation (22b)
After performing the contractions, the only term of the sum that survives is the th, which is proportional to , yielding zero for thanks to the orthogonality of the spherical harmonic functions.
Likewise, following the same argument, we find that for
and finally we obtain
References
- Rokaj, V.; Welakuh, D.; Ruggenthaler, M.; Rubio, A. Light–matter interaction in the long-wavelength limit: No ground-state without dipole self-energy. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 034005. [Google Scholar] [CrossRef]
- Andolina, G.; Pellegrino, F.; Giovannetti, V.; MacDonald, A.; Polini, M. Cavity quantum electrodynamics of strongly correlated electron systems: A no-go theorem for photon condensation. Phys. Rev. B 2019, 100, 121109. [Google Scholar] [CrossRef]
- Andolina, G.; Pellegrino, F.; Giovannetti, V.; MacDonald, A.; Polini, M. Theory of photon condensation in a spatially varying electromagnetic field. Phys. Rev. B 2020, 102, 125137. [Google Scholar] [CrossRef]
- Ashida, Y.; İmamoğlu, A.; Faist, J.; Jaksch, D.; Cavalleri, A.; Demler, E. Quantum electrodynamic control of matter: Cavity-enhanced ferroelectric phase transition. Phys. Rev. X 2020, 10, 041027. [Google Scholar] [CrossRef]
- Guerci, D.; Simon, P.; Mora, C. Superradiant phase transition in electronic systems and emergent topological phases. Phys. Rev. Lett. 2020, 125, 257604. [Google Scholar] [CrossRef]
- Stokes, A.; Nazir, A. Uniqueness of the phase transition in many-dipole cavity quantum electrodynamical systems. Phys. Rev. Lett. 2020, 125, 143603. [Google Scholar] [CrossRef]
- Mivehvar, F.; Piazza, F.; Donner, T.; Ritsch, H. Cavity QED with quantum gases: New paradigms in many-body physics. Adv. Phys. 2021, 70, 1–153. [Google Scholar] [CrossRef]
- Román-Roche, J.; Luis, F.; Zueco, D. Photon condensation and enhanced magnetism in cavity QED. Phys. Rev. Lett. 2021, 127, 167201. [Google Scholar] [CrossRef]
- Rokaj, V.; Ruggenthaler, M.; Eich, F.; Rubio, A. Free electron gas in cavity quantum electrodynamics. Phys. Rev. Res. 2022, 4, 013012. [Google Scholar] [CrossRef]
- Nataf, P.; Ciuti, C. No-go theorem for superradiant quantum phase transitions in cavity QED and counter-example in circuit QED. Nat. Commun. 2010, 1, 510–532. [Google Scholar] [CrossRef]
- Le Boité, A. Theoretical methods for ultrastrong light–matter interactions. Adv. Quantum Technol. 2020, 3, 1900140. [Google Scholar] [CrossRef]
- Ashida, Y.; İmamoğlu, A.; Demler, E. Cavity quantum electrodynamics at arbitrary light-matter coupling strengths. Phys. Rev. Lett. 2021, 126, 153603. [Google Scholar] [CrossRef]
- Schlawin, F.; Kennes, D.M.; Sentef, M.A. Cavity quantum materials. Appl. Phys. Rev. 2022, 9, 011312. [Google Scholar] [CrossRef]
- Savvidy, G. Infrared instability of the vacuum state of gauge theories and asymptotic freedom. Phys. Lett. B 1977, 71, 133–134. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M.; Wetterich, C. Rotation symmetry breaking condensate in a scalar theory. Phys. Rev. D 2000, 62, 125021. [Google Scholar] [CrossRef]
- Branchina, V.; Mohrbach, H.; Polonyi, J. Antiferromagnetic φ4 model. I. The mean-field solution. Phys. Rev. D 1999, 60, 045006. [Google Scholar] [CrossRef]
- Modanese, G. Stability issues in Euclidean quantum gravity. Phys. Rev. D 1998, 59, 024004. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Modulated ground state of gravity theories with stabilized conformal factor. Phys. Rev. D 2013, 87, 084019. [Google Scholar] [CrossRef]
- Bonanno, A. On the Structure of the Vacuum in Quantum Gravity: A View from the Asymptotic Safety Scenario. Universe 2019, 5, 182. [Google Scholar] [CrossRef]
- Modanese, G. Quantum metrics with very low action in R+R2 gravity. Phys. Rev. D 2021, 103, 106020. [Google Scholar] [CrossRef]
- Chernodub, M.N.; Ferreiros, Y.; Grushin, A.G.; Landsteiner, K.; Vozmediano, M.A. Thermal transport, geometry, and anomalies. Phys. Rep. 2022, 977, 1–58. [Google Scholar] [CrossRef]
- Burns, R. Mineralogical Applications of Crystal Field Theory; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Faisal, F. Theory of Multiphoton Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Wang, Y.; Liu, Z.K.; Chen, L.Q. Thermodynamic properties of Al, Ni, NiAl, and Ni3Al from first-principles calculations. Acta Mater. 2004, 52, 2665–2671. [Google Scholar] [CrossRef]
- Preparata, G. QED Coherence in Matter; World Scientific: Singapore, 1995. [Google Scholar]
- Frisk Kockum, A.; Miranowicz, A.; De Liberato, S.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Morse, P.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill Book Company Inc.: New York, NY, USA, 1953; Volume II, p. 999. [Google Scholar]
- Messiah, A. Quantum Mechanics; Courier Corporation: Chelmsford, MA, USA, 2014. [Google Scholar]
- Byrnes, T.; Kim, N.; Yamamoto, Y. Exciton–polariton condensates. Nat. Phys. 2014, 10, 803–813. [Google Scholar] [CrossRef]
- Keeling, J.; Kéna-Cohen, S. Bose–Einstein condensation of exciton-polaritons in organic microcavities. Annu. Rev. Phys. Chem. 2020, 71, 435–459. [Google Scholar] [CrossRef]
- McGhee, K.; Putintsev, A.; Jayaprakash, R.; Georgiou, K.; O’Kane, M.; Kilbride, R.; Cassella, E.; Cavazzini, M.; Sannikov, D.; Lagoudakis, P.; et al. Polariton condensation in an organic microcavity utilising a hybrid metal-DBR mirror. Sci. Rep. 2021, 11, 20879. [Google Scholar] [CrossRef]
- Tilley, D.; Tilley, J. Superfluidity and Superconductivity; Routledge: London, UK, 2019. [Google Scholar]
- del Giudice, E.; Galimberti, A.; Gamberale, L.; Preparata, G. Electrodynamical coherence in water: A possible origin of the tetrahedral coordination. Mod. Phys. Lett. B 1995, 9, 953–961. [Google Scholar] [CrossRef]
- Bono, I.; Del Giudice, E.; Gamberale, L.; Henry, M. Emergence of the Coherent Structure of Liquid Water. Water 2012, 4, 510–532. [Google Scholar] [CrossRef]
- Hughes, R. Theoretical practice: The Bohm-Pines quartet. Perspect. Sci. 2006, 14, 457–524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).